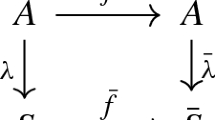Permutation polynomials of the type $x^rg(x^{s})$ over ${\mathbb {F}}_{q^{2n}}$

Abstract

We provide some new families of permutation polynomials of ${\mathbb {F}}_{q^{2n}}$ of the type $x^rg(x^{s})$, where the integers r, s and the polynomial $g \in {\mathbb {F}}_q[x]$ satisfy particular restrictions. Some generalizations of known permutation binomials and trinomials that involve a sort of symmetric polynomials are given. Other constructions are based on the study of algebraic curves associated to certain polynomials. In particular we generalize families of permutation polynomials constructed by Gupta–Sharma, Li–Helleseth, Li–Qu–Li–Fu.

1 Introduction

Let $q=p^h$ be a prime power. A polynomial $f(x)\in {\mathbb {F}}_q[x]$ is a permutation polynomial (PP) if it is a bijection of the finite field ${\mathbb {F}}_q$. On the other hand, each permutation of ${\mathbb {F}}_q$ can be expressed as a polynomial over ${\mathbb {F}}_q$.

In general it is not difficult to construct a random PP for a given ${\mathbb {F}}_q$. Particular simple structures or additional extraordinary properties are usually required in applications of PPs in other areas of mathematics and engineering, such as cryptography, coding theory, or combinatorial designs. Permutation polynomials meeting these criteria are usually difficult to find. For a deeper introduction on the connections between PPs and other fields of mathematics we refer to [7, 14] and the references therein.

A PP f(x) is said to be a complete permutation polynomial (CPP) if $f(x)+x$ is also a PP; see for instance [2] and the references therein. CPPs are also related to bent and negabent functions which are studied for a number of applications in cryptography, combinatorial designs, and coding theory; see for instance [8, 13, 17]. Recently monomial CPPs have been related to exceptional polynomials; see [3].

The aim of this paper is to provide some new families of PPs of ${\mathbb {F}}_q$ of the type $x^rg(x^s)$, where the integers r, s and the polynomial g satisfy particular restrictions. We are interested in some constructions arising from a well known criterion due to Park and Lee [15] (a shorter proof can be found in [18]), given in the following lemma.

Lemma 1.1

[15, 18] Let $g(x) \in {\mathbb {F}}_{q^n}[x]$. If $d,s,r >0$ are integers such that $q^n-1=sd$, then $x^rg(x^s)$ is a permutation over ${\mathbb {F}}_{q^n}$ if and only if

• (i) $\gcd (r,s)=1$, and

• (ii) $x^rg(x)^s$ permutes $U_d=\{ x \in {\mathbb {F}}_{q^n} \mid x^d=1 \}$, the group of d-th roots of unity in ${\mathbb {F}}_{q^n}$.

This criterion has been used in several papers in recent years, especially in even characteristic and for polynomials g having a small number of terms in general (binomials or trinomials). In the following we summarize some known constructions.

• (i) In [9] the authors determine permutation trinomials of ${\mathbb {F}}_{2^{2m}}$, of the type $f(x) = x + x^{s(q-1)+1} + x^{t(q-1)+1}$, where

  • $(s,t)=\left( \frac{2^k}{2^k-1},\frac{-1}{2^k-1}\right)$, and $\gcd (2^k- 1, 2^m + 1) = 1$, or

  • $(s,t)=\left( \frac{1}{2^k+1},\frac{2^k}{2^k+1}\right)$, and $\gcd (2^k+ 1, 2^m + 1) = 1$.

  Here negative or fractional numbers should be interpreted modulo $q+1$.

• (ii) In [12, 19] PPs of ${\mathbb {F}}_q$ of the type $f(x) = x^r \left( bx^{k(q-1)/d} + g(x^{(q-1)/d})\right)$, where the polynomial $g(x)\in {\mathbb {F}}_q[x]$ is divisible by $x^{d-1}+x^{d-2}+\cdots +x+1$, are studied.

• (iii) In [6, 7] the author determines all permutation trinomials of ${\mathbb {F}}_{q^2}$ of the form $ax +bx^q+x^{2q-1} \in \mathbb F_{q^2}[x]$.

• (iv) Many families of permutation trinomials are determined in [10]. In particular, if q is even they provide some sufficient conditions for the trinomials

  $$\begin{aligned} \begin{array}{l} x^{\ell q+\ell +3}+x^{(\ell +4)q+\ell -1}+x^{(\ell -1)q+\ell +4},\\ x^{\ell q+\ell +2}+x^{(\ell +2)q+\ell }+x^{(\ell -1)q+\ell +3},\\ x^{\ell q+\ell +2}+x^{(\ell +4)q+\ell -2}+x^{(\ell -1)q+\ell +3},\\ x^{\ell q+\ell +3}+x^{(\ell +3)q+\ell }+x^{(\ell -1)q+\ell +4},\\ x^{\ell q+\ell +1}+x^{(\ell +3)q+\ell -2}+x^{(\ell -1)q+\ell +2},\\ x^{\ell q+\ell +1}+x^{(\ell +4)q+\ell -3}+x^{(\ell -2)q+\ell +3} \end{array} \end{aligned}$$

  to be PPs in ${\mathbb {F}}_{q^2}$.

• (v) The author in [18] gives many sufficient conditions for a polynomial $x^rg(x^s)$ to be a PP.

• (vi) A survey on other results on PP obtained using Lemma 1.1 can be found in [7, Sect. 3].

In this paper we investigate some families of PPs of ${\mathbb {F}}_{q^{2n}}$ of the type $x^rg(x^{\frac{q^{2n}-1}{q+1}})$ arising from polynomials $g(x) \in {\mathbb {F}}_q[x]$ of particular shapes. In Sect. 2 we work with the notion of a symmetric polynomial (Definition 2.1) in order to obtain permutation polynomials with many terms and, in particular, generalizations of some known permutation binomials and trinomials in [4, 9]; see Theorem 2.3. For instance, in Theorem 2.10 we show that for

$$\begin{aligned} g(x)&=\left( x^{t_1/2}+x^{q+1-t_1/2}\right) \cdots \left( x^{t_k/2}+x^{q+1-t_k/2}\right) \left( 1+x^{s_1}+x^{q+1-s_1}\right) \cdots \\&\quad \left( 1+x^{s_j}+x^{q+1-s_j}\right) , \end{aligned}$$

a carefully chosen polynomial over ${\mathbb {F}}_q$, $f(x)=x^rg(x^{\frac{q^{2n}-1}{q+1}}) \in {\mathbb {F}}_{q}[x]$ permutes ${\mathbb {F}}_{q^{2n}}$ for any r coprime with $q^{2n}-1$.

In Sect. 3 we examine polynomials $g(x)=x^3+ bx+c \in {\mathbb {F}}_q[x]$, $bc \ne 0$, and obtain PPs of ${\mathbb {F}}_{q^2}$ of the type $x^3g(x^{q-1})$, where $\gcd (3, q-1)=1$. Our approach involves the study of the points $(x,y) \in U_{q+1} \times U_{q+1}$ in the algebraic curve

$$\begin{aligned} -bx^2y^2 +bc (x^2y +xy^2) +(c^2-1)(x^2+y^2) +(c^2+b^2-1)xy+bc(x+y)-b=0 \end{aligned}$$

associated to g(x). In particular we generalize some families of permutation polynomials in [4, 9, 10].

Finally in Sect. 4 we give a generalization of a recent result by Helleseth and Li in [9, Theorem 1] where the authors present classes of permutation polynomials of ${\mathbb {F}}_{2^{2m}}$ of the type $x(1+x^{s(2^m-1)}+x^{t(2^m-1)})$ for suitable pairs (s, t). We extend their result by showing that the polynomial $x(1+Ax^{s(2^m-1)}+Ax^{t(2^m-1)})$ is a PP of ${\mathbb {F}}_{2^{2m}}$ with exactly the same conditions on the pair (s, t), for many suitable parameters $A\in {\mathbb {F}}_{2^m}$.

2 Permutation polynomials arising from “symmetric” polynomials

In this section if an integer t is written as a fraction or as a negative integer, then it should be interpreted as modulo $q+1$. For instance, $t=-3=q+1-3 \ge 1$.

Definition 2.1

A polynomial $f(x) \in {\mathbb {F}}_q[x]$ is said to be symmetric if

$$\begin{aligned} f(x^q)=f(x) \qquad \forall x \in U_{q+1}=\{ x \in {\mathbb {F}}_{q^{2}} \mid x^{q+1}=1 \}. \end{aligned}$$

Notice that if $f(x) \in {\mathbb {F}}_q[x]$ is symmetric and $f(x) \ne 0$ for each $x\in U_{q+1}$, then $f(x)^{q-1}=1$ for each $x\in U_{q+1}$, that is f(x) satisfies the following theorem.

Theorem

[1, Theorem 3.1] Let $q - 1 = \ell s$. Assume that $f(t)^s = 1$ for any $t \in U_{\ell }$. Then $P(x) = x^rf(x^s)$ is a permutation polynomial of ${\mathbb {F}}_q$ if and only if $(r, q - 1) = 1$.

We just point out that by definition we require that $f(x) \in {\mathbb {F}}_q[x]$, whereas in [1, Theorem 3.1] the polynomial $f(x)\in {\mathbb {F}}_{q^2}[x]$. Similar results can be found in [8, Theorem 3.1] and [11, Theorem 7.10]. Also, observe that the symmetric property is closed under multiplication and, for any symmetric polynomial $f(x) \in {\mathbb {F}}_q[x]$ and $\xi \in {\mathbb {F}}_q$, $f(x)+\xi$ is still a symmetric polynomial. For instance, for any $t\le q$, the polynomials $a+bx^t+bx^{-t} \in {\mathbb {F}}_q[x]$ are symmetric.

We also observe that a polynomial $f(x) \in {\mathbb {F}}_q[x]$ is symmetric if and only if $f(x) \bmod (x^{q+1}-1)$ is symmetric, and we can restrict ourselves to the study of symmetric polynomials of degree less than $q+1$.

Proposition 2.2

Let $q>3,$ and $f(x) \in {\mathbb {F}}_q[x]$ be a symmetric polynomial. Then there exists a $\xi \in {\mathbb {F}}_q$ such that $\xi + f(x)$ has no roots in $U_{q+1}$.

Proof

Since $f(x)^q=f(x^q)=f(x)$, the polynomial f(x) defines a function from $U_{q+1}$ to ${\mathbb {F}}_q$. For any $x \in U_{q+1}, f(x)=f(1/x)$ and we conclude that f is not a surjective function, i.e. there exists a $\xi \in {\mathbb {F}}_q$ such that $f(x)+\xi \ne 0 , \forall x \in U_{q+1}.$ $\square$

We now present a general construction of permutation polynomials of the type $x^rg(x^s)$ over ${\mathbb {F}}_{q^{2n}}$ using symmetric polynomials over ${\mathbb {F}}_q$ and Proposition 2.2.

Theorem 2.3

Let $f(x) \in {\mathbb {F}}_q[x]$ be a symmetric polynomial and $\xi \in {\mathbb {F}}_q$ as in Proposition 2.2. For $g(x)=f(x)+\xi , s=\frac{q^{2n}-1}{q+1}$ and r co-prime with $q^{2n}-1$, the polynomial $x^rg(x^s)$ is a permutation polynomial of ${\mathbb {F}}_{q^{2n}}$.

Proof

Since $\gcd (r, s)=1$ from Lemma 1.1 it is enough to prove that $x^rg(x)^{s}$ permutes the set $U_{q+1}$. Let $s=(q-1)s_1$, where $s_1=\sum _{i=1}^{2n} q^{2n-2i}$. By the choice of $\xi$ for any $x \in U_{q+1}$ we have that $g(x) \ne 0$ and we can write

$$\begin{aligned} x^rg(x)^{s}=x^r(g(x)^{q-1})^{s_1}=x^r\left( \frac{g(x)^q}{g(x)}\right) ^{s_1}=x^r, \end{aligned}$$

since g(x) is symmetric. From the hypothesis $\gcd (r,q+1)=1,$ the monomial $x^r$ permutes $U_{q+1}$. $\square$

Remark 2.4

We point out that Theorem 2.3 is a special case of the multiplicative version of the following theorem; see [16, Theorem 5.1].

Theorem

Assume that A is a finite field and S is a subset of A such that the map $\lambda : A \rightarrow S$ is surjective. Let $g : A \rightarrow A, h : S \rightarrow S,$ and $f : A \rightarrow A$ be maps such that the following diagram commutes:

Then the map $p(x)= f(x)g(\lambda (x))$ permutes A if and only if the following conditions hold.

• (i) h is a bijection from $\lambda (A)$ to $\lambda (A)$.

• (ii) $g(y) \ne 0$ for every $y \in \lambda (A)$ with $\sharp \lambda ^{-1}(y) > 1$.

• (iii) f(x) is injective on each $\lambda ^{-1}(y)$ for all $y \in \lambda (A)$.

In our case, $A= {\mathbb {F}}_{q^{2n}}$, $S=U_{q+1}\cup \{0\}$, $\lambda (x)=x^s, f(x)=x^r, h(x)=x^rg(x)^s$ and $g(x) \in {\mathbb {F}}_{q}[x]$ is symmetric with no roots in $U_{q+1}$.

We finish this section showing how we can obtain a PP over ${\mathbb {F}}_{q^n}, n=2k$ from a PP over ${\mathbb {F}}_{q^2}$ using Lemma 1.1.

Theorem 2.5

Let q be a prime power, $n=2k$, $q^n-1=sd$, $d=q+1$. Let $r\in \mathbb {N}$ and $f\in {\mathbb {F}}_q[x]$ be such that $\gcd (kr,s)=\gcd (k,d)=1$ and $h(x)=x^{r} f(x^{q-1})$ is a PP of ${\mathbb {F}}_{q^2}$. Then the polynomial $x^{kr}f(x^s)$ is a PP of ${\mathbb {F}}_{q^n}$.

Proof

Since h(x) is a PP of ${\mathbb {F}}_{q^2}$, in particular $x^{r} f(x)^{q-1}$ permutes $U_d$. Consider the polynomial $\overline{h} (x)= x^{kr}f(x^s)$. Since $\gcd (kr, s)=1$ we only have to show that $x^{kr} f(x)^s$ permutes $U_d$. Note that $f(x)^q=f(1/x)$ and $f(x)^{q^2}=f(x)$, if $x\in U_d$. Therefore, if $x \in U_d$ then

$$\begin{aligned} f(x)^s&= f(x)^{q^{n-1}-q^{n-2}+ \dots +q-1}=f(x)^{(q-1)(q^{n-2}+q^{n-4}+\cdots +q^2+1)}\\&=\left( f(x)^{q^{n-2}+q^{n-4}+\cdots +q^2+1}\right) ^{q-1}=\left( f(x)^{n/2}\right) ^{q-1}=\left( f(x)^{q-1}\right) ^{k}. \end{aligned}$$

Hence $x^{kr}f(x)^s$ permutes $U_d$ if and only if $x^{kr}\left( f(x)^{q-1}\right) ^{k}=\left( x^{r}f(x)^{q-1}\right) ^{k}$ permutes $U_d$. Since $x^{r}f(x)^{q-1}$ permutes $U_d$ by assumption and $\gcd (k,d)=1$, the assertion follows. $\square$

2.1 Permutation polynomials over ${\mathbb {F}}_{q^{2n}}, n \ge 1$

Next we present symmetric polynomials over ${\mathbb {F}}_q$ with no roots in $U_{q+1}$ and construct many families of permutation polynomials of ${\mathbb {F}}_{q^{2n}}$.

Lemma 2.6

Let q be an odd prime power and $q+1=2^\alpha m$, m odd, and $t_1, \dots , t_k$ be positive integers such that $2^\alpha \mid t_i, i=1, \dots , k$. Consider $h(x)=(x^{t_1}+1)\cdots (x^{t_k}+1) \in {\mathbb {F}}_q[x].$ If $x \in U_{q+1}$, then $h(x) \ne 0$.

Proof

If $x \in U_{q+1}$ and $h(x)=0$, then $x^{q+1}=1$ and $x^{2t_i}=1$ for some $i=1, \dots , k$. Since $\gcd (2t_i, q+1)=\gcd (t_i, q+1)$ we have that $\gcd (x^{q+1}-1,x^{t_i}+1)=1$, which is a contradiction. $\square$

Proposition 2.7

Let q be an odd prime power and $q+1=2^\alpha m$, m odd, $t_1, \dots , t_k$ be positive integers such that $2^\alpha \mid t_i$ for $i=1, \dots , k$ and $t_1 + \dots + t_k < 2(q+1)$. For $s=\frac{q^{2n}-1}{q+1}$, r co-prime with $q^{2n}-1$, and

$$\begin{aligned} g(x)=\left( x^{t_1/2}+x^{-t_1/2}\right) \cdots \left( x^{t_k/2}+x^{-t_k/2}\right) , \end{aligned}$$

the polynomial $f(x)=x^rg(x^s) \in {\mathbb {F}}_{q}[x]$ permutes ${\mathbb {F}}_{q^{2n}}$.

Proof

Let $x \in U_{q+1}$. Since $x \ne 0$, $g(x)= x^{-(t_1+ \cdots +t_k)/2}(x^{t_1}+1)\cdots (x^{t_k}+1) \ne 0$ by Lemma 2.6. The polynomial g(x) is clearly symmetric and the result follows from Theorem 2.3. $\square$

Lemma 2.8

Suppose the characteristic of ${\mathbb {F}}_q$ is different from 3. For any $t < q+1$ with $\gcd (3t, q+1)=1$, the polynomial $g(x)=1+x^t+x^{-t}$ has no roots in $U_{q+1}$.

Proof

Let $1+x^t+x^{-t}=0$, then $x^{3t}=1$. Since $\gcd (3t, q+1)=1$ and the characteristic is not 3, the polynomials g(x) and $x^{q+1}-1$ have no roots in common. $\square$

The following result is similar to [4, Theorem 3.4], where the authors give necessary and sufficient conditions for the trinomial $x(1+x^{k(q-1)}+x^{-k(q-1)})$ to be a PP of ${\mathbb {F}}_{q^2}$.

Proposition 2.9

Suppose the characteristic of ${\mathbb {F}}_q$ is different from 3 and consider $t_1, \dots ,t_k$ positive integers such that $t_i <q+1$ and $\gcd (3t_i, q+1)=1$ for $i=1, \dots , k$. Let $s=\frac{q^{2n}-1}{q+1}$, r co-prime with $q^{2n}-1$, and

$$\begin{aligned} g(x)=\left( 1+x^{t_1}+x^{-t_1}\right) \cdots \left( 1+x^{t_k}+x^{-t_k}\right) , \deg g(x) < q+1,. \end{aligned}$$

Then $f(x)=x^rg(x^s)$ permutes ${\mathbb {F}}_{q^{2n}}$.

Proof

The polynomial g(x) is clearly symmetric since it is the product of symmetric polynomials and, by Lemma 2.8 it has no root in $U_{q+1}$. The result follows from Theorem 2.3. $\square$

Theorem 2.10

Let $q=p^h$, $p>3$ prime, and $q+1=2^\alpha m$, m odd. Let $t_1, \dots , t_k$ be positive integers such that $2^\alpha \mid t_i$ for $i=1, \dots , k$ and $t_1 + \dots + t_k < 2(q+1)$. Let $s_1, \dots , s_j$ be positive integers such that $s_i <q+1$ and $\gcd (3s_i, q+1)=1$, $i=1, \dots , j$. For $s=\frac{q^{2n}-1}{q+1}$, r co-prime with $q^{2n}-1$, and

$$\begin{aligned} g(x)=\left( x^{t_1/2}+x^{-t_1/2}\right) \cdots \left( x^{t_k/2}+x^{-t_k/2}\right) \left( 1+x^{s_1}+x^{-s_1}\right) \cdots \left( 1+x^{s_j}+x^{-s_j}\right) , \end{aligned}$$

$\deg g(x) < q+1$, the polynomial $f(x)=x^rg(x^s) \in {\mathbb {F}}_{q}[x]$ permutes ${\mathbb {F}}_{q^{2n}}$.

Proof

It follows directly from Propositions 2.7 and 2.9 and by considering $\xi =0$ in Theorem 2.3. $\square$

3 Permutation polynomials from $g(x)=x^3+bx+c, bc \ne 0$

In this section we give generalizations of some families that appear in [4, 5, 9, 10]. For instance, in [10, Theorem 2.3] the authors use the fact that $1+x+x^3$ has no roots in $U_{2^m+1}$ and that the polynomial $x^3(1+x+x^3)^{2^m-1}$ permutes the set $U_{2^m+1}$ to construct PPs over ${\mathbb {F}}_{2^{2m}}$ of the type $x^3(1+x^{2^m-1}+x^{3.2^m-3})$ whenever $3 \not \mid m$. In characteristics 2 and 3 the authors in [4] work with trinomials $g_1(x)=1+x^s+x^t, 1<s<t$ with no roots in $U_{q+1}$ in order to obtain PPs of ${\mathbb {F}}_{q^2}$ of the type $x^rg_1(x^{q-1})$.

We are going to analyze trinomials of the type $g(x)=x^3+ bx+c \in {\mathbb {F}}_q,$ with $bc \ne 0$ in order to obtain PPs of ${\mathbb {F}}_{q^2}$ of the type $x^3g (x^{q-1})$, where $\gcd (3, q-1)=1$. Many constructions will work in any characteristic. Following the criterion in Lemma 1.1, we need to show that $x^3g(x)^{q-1}$ permutes $U_{q+1}$. Suppose that g(x) has no roots in $U_{q+1}$. Then for any $x \in U_{q+1}$ we have that

$$\begin{aligned} x^3g(x)^{q-1}= x^3 \frac{g(x)^q}{g(x)}=x^3\frac{x^{3q}+ bx^q+c}{x^3+ bx+c}=x^3\frac{x^{-3}+ bx^{-1}+c}{x^3+ bx+c}=\frac{cx^3+bx^2+1}{x^3+bx+c}. \end{aligned}$$

Given the rational function $f(x)= \frac{cx^3+bx^2+1}{x^3+bx+c}$, we associate the algebraic curve $\mathcal {C}_f$ with equation $\frac{f(x)-f(y)}{x-y}=0$:

$$\begin{aligned} \mathcal {C}_f: -bx^2y^2 +bc (x^2y +xy^2) +(c^2-1)(x^2+y^2) +(c^2+b^2-1)xy+bc(x+y) - b=0. \end{aligned}$$

(1)

The rational function f(x) permutes $U_{q+1}$ if and only if for all $x \ne y \in U_{q+1},\ \mathcal {C}_f (x,y) \ne 0$. First we require that a polynomial of the type $x^3+bx+c \in {\mathbb {F}}_q[x]$ has no roots in $U_{q+1}$.

Proposition 3.1

Let $g(x)=x^3+ bx+c \in {\mathbb {F}}_q[x]$, with $bc \ne 0$. Then g(x) has no roots in $U_{q+1}$ in the following cases:

• (i) $c^2+b-1 \ne 0$ and $(b+1-c^2)^3+b^3c^2(b+1-c^2)+b^3c^4 \ne 0$;

• (ii) $c^2+b-1=0$ and $T^2-cT+1$ has no roots in $U_{q+1}$.

Proof

Let $x \in U_{q+1}$ and $g(x)=0$. By raising the equality $g(x)=0$ to the power q and multiplying the result by $x^3$ gives that

$$\begin{aligned} x^{3q}+bx^q+c=0 \Rightarrow x^{-3}+bx^{-1}+c=0 \Rightarrow cx^3+bx^2+1=0. \end{aligned}$$

By multiplying $g(x)=0$ by c and comparing the result with $cx^3+bx^2+1=0$, we obtain that

$$\begin{aligned} bx^2-bcx+1-c^2=0. \end{aligned}$$

Now we raise this equation to the power q and multiply the result by $x^2$ to get

$$\begin{aligned} (1-c^2)x^2-bcx+b=0. \end{aligned}$$

From these two last equations, we get

$$\begin{aligned} b^2-(1-c^2)^2=bc(c^2+b-1)x. \end{aligned}$$

If $b-1+c^2\ne 0$ then $x= \frac{b+1-c^2}{bc}$ has to be a root of g(x) and we get i). If $b-1+c^2= 0$ then $bx^2-bcx+1-c^2=0$ implies $x^2-cx+1=0$. $\square$

Proposition 3.2

Let q be even. Suppose $x^3+bx+c\in \mathbb F_q[x]$, with $bc \ne 0$, has no roots in $U_{q+1}$. Then the fractional polynomial $f(x)= \frac{cx^3+bx^2+1}{x^3+bx+c}$ permutes $U_{q+1}$ in the following cases

• (i) $c=k+k^{-1}$ and $b=c^2+1$, where $k\in {\mathbb {F}}_q\setminus \{0,1\}$;

• (ii) $b=1$ and c is such that $Tr_{{\mathbb {F}}_q | {\mathbb {F}}_2}(1+1/c^2)=0$ and the roots of $T^2+c T+1\in {\mathbb {F}}_q[T]$ belong to ${\mathbb {F}}_{q^2}\setminus U_{q+1}$.

Proof

We are going to show that with the given conditions on b and c the curve $\mathcal {C}_f$ has no points $(x,y) \in U_{q+1} \times U_{q+1}.$ In the first case the curve $\mathcal {C}_f$ defined in (1) splits into

$$\begin{aligned} (x+k)(y+k)(x+k^{-1})(y+k^{-1})=0. \end{aligned}$$

Since $k\in {\mathbb {F}}_q\setminus \{0,1\}$, $k\notin U_{q+1}$ and therefore $-k,-k^{-1} \notin U_{q+1}$. In the second case the curve $\mathcal {C}_f$ factors as

$$\begin{aligned} (xy+\alpha x+\beta y+1)(xy+\beta x+\alpha y+1)=0, \end{aligned}$$

where $\alpha , \beta$ are the roots of $T^2+c T+c^2+1$. By the assumption $Tr_{{\mathbb {F}}_q | {\mathbb {F}}_2}(1+1/c^2)=0$, we have that $\alpha , \beta \in {\mathbb {F}}_q$. The roots of $T^2+c T+c^2+1$ belong to $U_{q+1}$ if and only if $c^2+c+1=0$ and in this case $\{\alpha ,\beta \}=\{0,1\}$: the two factors of $\mathcal {C}_f$ are $xy+x+1=0$ and $xy+y+1=0$. It is easily seen that they do not have points belonging to $U_{q+1}\times U_{q+1}$. Suppose that $c^2+c+1\ne 0$. Then $\alpha ,\beta \notin U_{q+1}$ and for any $x\in U_{q+1}$ we have that

$$\begin{aligned} y^q=\left( \frac{\alpha x+1}{x+\beta }\right) ^q=\frac{\alpha +x}{\beta x+1}. \end{aligned}$$

Then $y^{q+1}=1$ if and only if

$$\begin{aligned} \frac{\alpha +x}{\beta x+1}=\left( \frac{\alpha x+1}{\beta +x}\right) ^{-1}\iff & {} \alpha ^2x+\alpha x^2+\alpha +x=\beta ^2x+\beta x^2+\beta +x\\\iff & {} x^2+cx+1=0. \end{aligned}$$

$\square$

Remark 3.3

Note that if $Tr_{{\mathbb {F}}_q| {\mathbb {F}}_2}(1+1/c^2)=1$ then $\alpha ,\beta \in {\mathbb {F}}_{q^2}\setminus {\mathbb {F}}_q$. In this case, for any $x\in U_{q+1}$, we have that

$$\begin{aligned} y^q=\left( \frac{\alpha x+1}{x+\beta }\right) ^q=\frac{\beta +x}{\alpha x+1}=y^{-1}. \end{aligned}$$

We now combine the results from Propositions 3.1 and 3.2 to present families of permutation polynomials in even characteristic.

Theorem 3.4

Let $q=2^{2h+1}$, where $h\in \mathbb {N}$. Consider $g(x)=x^3+bx+c$, with $b,c\in {\mathbb {F}}_q^*$. Then $x^3g(x^{q-1})$ is a PP of ${\mathbb {F}}_{q^2}$ in the following cases:

• (i) $c=k+k^{-1}$, $b=c^2+1$, where $k\in {\mathbb {F}}_q \setminus \{0,1\}$ and $T^2+cT+1$ has no roots in $U_{q+1}$;

• (ii) $b=1$, $Tr_{{\mathbb {F}}_q | {\mathbb {F}}_2}(1+1/c^2)=0$ and the polynomial $T^2+c T+1$ has no roots in $U_{q+1}$.

Proof

The conditions on b and $c \in {\mathbb {F}}_q$ guarantee that g(x) has no roots in $U_{q+1}$ and $f(x)= \frac{cx^3+bx^2+1}{x^3+bx+c}$ permutes $U_{q+1}$. Since $q=2^{2h+1}$ we have that $\gcd (3, q-1)=1$. Now apply the criterion in Lemma 1.1. $\square$

Proposition 3.5

Let $q=p^h$ and $p\ne 3$ be an odd prime. Suppose $x^3+bx+c\in \mathbb F_q[x]$, $bc \ne 0$, has no roots in $U_{q+1}$. Then the fractional polynomial $f(x)= \frac{cx^3+bx^2+1}{x^3+bx+c}$ permutes $U_{q+1}$ in the following cases

• (i) $c^2 \ne 1, b=-c^2+1$, $T^2 - cT + 1$ has no roots in $U_{q+1}$;

• (ii) $(b,c)=(-3,1)$ and $T^2 - T + 1$ has no roots in $U_{q+1}$;

• (iii) $(b,c)=(-3,-1)$ and $T^2 + T + 1$ has no roots in $U_{q+1}$;

• (iv) $b=-3$, $c\notin \{\pm 1,\pm 2\}$, and $T^2 -cT + 1$ has no roots in $U_{q+1}$.

Proof

We are going to show that with the given conditions on b and c the curve $\mathcal {C}_f$ has no points $(x,y) \in U_{q+1} \times U_{q+1}.$ In the first case the curve $\mathcal {C}_f$ splits in

$$\begin{aligned} (y^2 - cy + 1) (x^2 - cx + 1)=0 \end{aligned}$$

and we require that the roots of $x^2 - cx + 1$ and $y^2 - cy + 1$ are not in $U_{q+1}$. In the second and third case we get the following decompositions:

$$\begin{aligned} (x y - y + 1)(x y -x + 1)=0 \text { and }(x y +y + 1)(x y + x + 1)=0, \end{aligned}$$

respectively. In the second case let $x \in U_{q+1}$ and $(x,y) \in \mathcal {C}_f$, then $y=-1/(x-1)$ and we have that $y \in U_{q+1}$ if and only if $x^2-x+1=0$. For the third case an analogous argument works.

Finally, in the last case the curve factors as

$$\begin{aligned} (x y+k x+j y+1)(x y+j x+k y+1)=0, \end{aligned}$$

where j and k are the roots of $3T^2+3cT+c^2-1=0$. The curve $\mathcal {C}_f$ has a point $(x,y)\in U_{q+1}\times U_{q+1}$ if and only if

$$\begin{aligned} \frac{jx+1}{x+k}\in U_{q+1}. \end{aligned}$$

If k and j do not belong to ${\mathbb {F}}_q$ then $k=j^q$ and $\frac{jx+1}{x+k}\in U_{q+1}$. We conlude that k and j are in ${\mathbb {F}}_q$. Note that $k,j \in U_{q+1}$ if and only if $k,j \in \{\pm 1 \}$, that is $c\in \{\pm 1,\pm 2\}$, impossible. Therefore $x+k\ne 0$. Finally,

$$\begin{aligned} \left( \frac{jx+1}{x+k}\right) ^q=\frac{j+x}{kx+1} \end{aligned}$$

equals $\frac{x+k}{jx+1}$ if and only if $x^2+(j+k)x+1=0$, that is $T^2-cT+1$ has roots in $U_{q+1}$. $\square$

We now combine the results from Propositions 3.1 and 3.5 to present families of permutation polynomials in odd characteristic different from 3.

Theorem 3.6

Let q be odd, $q \equiv 2 \bmod 3$, and $g(x)=x^3+bx+c \in {\mathbb {F}}_q[x], bc \ne 0$. Then $x^3g(x^{q-1})$ is a PP of ${\mathbb {F}}_{q^2}$ in the following cases

• (i) $c^2 \ne 1, b=-c^2+1$, $T^2 - cT + 1$ has no roots in $U_{q+1}$;

• (ii) $b=-3$, $c^2\ne 4$, $-3c^2+12$ is a square in ${\mathbb {F}}_q$, and $T^2 -cT + 1$ has no roots in $U_{q+1}$.

Remark 3.7

Note that $q \equiv 2 \bmod 3$ implies that $T^2 - T + 1$ and $T^2 + T + 1$ have roots in $U_{q+1}$.

4 A generalization of PP over ${\mathbb {F}}_{2^{2m}}$

In [9, Theorem 1] the authors present classes of permutation polynomials of ${\mathbb {F}}_{q^2}$, $q=2^m$, of the type $x(1+x^{s(q-1)}+x^{t(q-1)})$ for suitable pairs (s, t). We extend their result showing that there exists a parameter A such that the polynomial $x(1+Ax^{s(q-1)}+Ax^{t(q-1)})$ is still a PP of ${\mathbb {F}}_{q^2}$ with exactly the same conditions on the pairs (s, t). In this section the pairs of integers should be interpreted as modulo $2^m+1$ when they are negative or fractions.

Lemma 4.1

Let $q=2^m$, $a\in U_{q+1}\setminus \{1\}$, $A^2(a^2+1)+a\ne 0$, $e_1=\frac{a}{A(a+1)}$, and $A \in {\mathbb {F}}_{2^k}, A \ne 0$. Suppose $x^{2^k}=\frac{e_1x+1}{x+e_1+1/A}$. Then for any $i\ge 2$

$$\begin{aligned} x^{2^{ik}}=\left\{ \begin{array}{ll} x, &{} e_{i-1}^{2^k}+e_1+1/A=0,\\ \frac{e_i x+1}{x+e_i+1/A}, &{} e_{i-1}^{2^k}+e_1+1/A\ne 0,\\ \end{array} \right. \end{aligned}$$

where $e_i = \infty$ if $e_{i-1}^{2^k}+e_1+1/A=0$, otherwise $e_i=\frac{e_{i-1}^{2^k}e_1+1}{e_{i-1}^{2^k}+e_1+1/A}$ for any $i\ge 2$.

Proof

The proof can be done by induction and is very similar to [9, Lemma 2]. $\square$

Theorem 4.2

Let $q=2^m, k \ge 1$ such that $\gcd (2^k-1,2^m+1)=1$, and $A\in {\mathbb {F}}_{2^k}^* \cap {\mathbb {F}}_q$. Then $f(x)=x(1+Ax^{s(q-1)}+Ax^{t(q-1)})$ for $(s,t)=\left( \frac{2^k}{2^k-1},\frac{-1}{2^k-1}\right)$ is a PP of ${\mathbb {F}}_{q^2}$.

Proof

The proof is very similar to [9, Theorem 1]. Following Lemma 1.1, we need to prove that $h(x)=x(1+Ax^{s}+Ax^{t})^{q-1}$, for $(s,t)=\left( \frac{2^k}{2^k-1},\frac{-1}{2^k-1}\right)$ permutes $U_{q+1}$. Since $\gcd (2^k-1,2^m+1)=1$, this is equivalent to showing that $h(x^{2^k-1})=x^{2^k-1}(1+Ax^{2^k}+Ax^{-1})^{2^m-1}$ permutes $U_{q+1}.$ First of all notice that $1+Ax^{2^k}+Ax^{-1}\ne 0$ if $x \in U_{q+1}$. Suppose the contrary. This yields $x^{2^m}=x^{-1}, Ax^{2^k+1}+x+A=0$. By raising the second equality to the power $2^m$ and multiplying the result by $x^{2^k+1}$ we get $Ax^{2^k+1}+x^{2^k}+A=0$, so $x^{2^{k}}=x$ and therefore $x=1$. Since $\gcd (2^k-1,q+1)=1$ and $1+Ax^{2^k}+Ax^{-1}=1+A+A=1\ne 0$ we obtain a contradiction. So for any $x \in U_{q+1}$ we can write $h(x^{2^k-1})= \frac{Ax^{2^k+1}+x^{2^k}+A}{Ax^{2^k+1}+x+A}.$ Now let $a\in U_{q+1}$ and consider $x\in U_{q+1}$ satisfying

$$\begin{aligned} \frac{Ax^{2^k+1}+x^{2^k}+A}{Ax^{2^k+1}+x+A}=a \iff x^{2^k}=\frac{ax+A(a+1)}{A(a+1)x+1}. \end{aligned}$$

(2)

We need to prove that (2) has at most one root $x\in U_{q+1}$ for each $a\in U_{q+1}$. Now we consider three cases depending on a.

• Case 1 $a=1$. Then $x^{2^k-1}=1$ and since $\gcd (2^k-1, 2^m+1)=1$ we get only one solution $x=1$.

• Case 2 $A^2(a^2+1)+a=0$. Then (2) yields $x^{2^k}=A(a+1)$, which has at most one solution in $U_{q+1}$.

• Case 3 $a\ne 1$ and $A^2(a^2+1)+a \ne 0$. Then (2) reads

  $$\begin{aligned} x^{2^k}=\frac{ax+A(a+1)}{A(a+1)x+1}=\frac{e_1x+1}{x+e_1+1/A}, \end{aligned}$$

  where $e_1=\frac{a}{A(a+1)}$. If k is odd then taking $i=m$ in Lemma 4.1 we obtain that $\frac{e_m x+1}{x+e_m+1/A}=\frac{1}{x}$ which implies $x^2=\frac{Ae_m+1}{Ae_m}$. We only have at most one solution. If $k=2^jk_1$, where $2 \not \mid k_1$, since $\gcd (2^k-1,2^m+1)=1$ we have that $k/\gcd (m,k)$ is odd and $2^j \mid m$. We take $i=m/2^j$ and the argument is the same as in the odd case.

$\square$

Theorem 4.3

Let $q=2^m$, $\gcd (2^k+1,2^m+1)=1$, $A\in {\mathbb {F}}_{2^k} \cap {\mathbb {F}}_q$. Then $f(x)=x(1+Ax^{s(q-1)}+Ax^{t(q-1)})$, $(s,t)=\left( \frac{2^k}{2^k+1},\frac{1}{2^k+1}\right)$ is a PP in ${\mathbb {F}}_{q^2}$.

Proof

The proof is basically the same as in [9, Theorem 2] and Theorem 4.2. $\square$