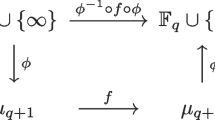Classification of permutation polynomials of the form $x^3g(x^{q-1})$ of ${\mathbb F}_{q^2}$ where $g(x)=x^3+bx+c$ and $b,c \in {\mathbb F}_q^*$

Abstract

We classify all permutation polynomials of the form $x^3g(x^{q-1})$ of ${\mathbb F}_{q^2}$ where $g(x)=x^3+bx+c$ and $b,c \in {\mathbb F}_q^*$. Moreover we find new examples of permutation polynomials and we correct some contradictory statements in the recent literature. We assume that $\gcd (3,q-1)=1$ and we use a well known criterion due to Wan and Lidl, Park and Lee, Akbary and Wang, Wang, and Zieve.

1 Introduction

Let q be a power of a prime, ${\mathbb F}_q$ be a finite field with q elements and ${\mathbb F}_q^*={\mathbb F}_q\setminus \{0\}$. A polynomial is called a permutation polynomial if it induces a bijection on ${\mathbb F}_q$. Permutation polynomials over finite fields has been studied by numerous researchers for a long time. In general it is not so hard to construct a permutation polynomial for a finite field ${\mathbb F}_q$. Researchers have been interested in permutation polynomials that looks simple, nice and have some additional properties which are practically needed by some applications in other areas such as coding theory, cryptography and combinatorial designs. Finding permutation polynomials having such properties are usually hard to find.

As far as we know, permutation polynomials were first studied by Dickson and Hermite (see [11, 13]). The books on finite fields (see [26] and Chap. 8 in [27]) together with the survey papers (see [15, 17, 33]) which review some of the recent results will be a very useful starting point for the interested reader. For further results on permutation polynomials over finite fields we refer to [4,5,6, 12, 16, 19, 20, 23,24,25, 30] and the references therein.

In order to decide whether a polynomial of the form $f\left( x\right) = x^rh\left( x^{\left( q^n-1\right) /d}\right)$ permutes ${\mathbb F}_{q^n}$ or not, there is a well known criterion due to Wan and Lidl [31], Park and Lee [28], Akbary and Wang [1], Wang [32] and Zieve [34] which is given in the following lemma.

Lemma 1

[1, 28, 31, 32, 34] Let $h\left( x\right) \in {\mathbb F}_{q^n}[x]$ and d, r be positive integers with $d\mid q^n-1$. Then $f\left( x\right) = x^rh\left( x^{\left( q^n-1\right) /d}\right)$ permutes ${\mathbb F}_{q^n}$ if and only if the following conditions hold:

• (i) $\gcd \left( r,\left( q^n-1\right) /d\right) = 1$,

• (ii) $x^rh\left( x\right) ^{\left( q^n-1\right) /d}$ permutes $U_{d}$, where $U_d=\{a\in {\mathbb F}_{q^n}^*\mid \, a^d=1\}$.

In this paper we classify all permutation polynomials of the form $x^3g(x^{q-1})$ of ${\mathbb F}_{q^2}$ where $g(x)=x^3+bx+c$ and $b,c \in {\mathbb F}_q^*$. We explain our approach in Sect. 2, which seems to go back, at least to [21, 29]. We assume that $\gcd (3,q-1)=1$ and use Lemma 1 in our classification. Our results are different in even and odd characteristics and hence we present them in separate sections.

We obtain a complete classification and we also compare our results with the related results, mainly [3], in Sects. 6 and 7.

We find it useful and interesting to obtain a complete classification. Moreover we find new examples of permutation polynomials and we show some contradictory statements in the recent literature. We refer to Sects. 6 and 7 for the details. In particular, using Theorem 4 and Theorem 8 below, we completely determine when $x^3g(x^{q-1})$ is a permutation polynomial of ${\mathbb F}_{q^2}$ (see also Remarks 3 and 5). Furthermore we present finer if and only if conditions corresponding to factorization structure of a related bivariate polynomial $C_f$ (see Sect. 2) in Theorems 1, 2, 3 in the even characteristic, and in Theorems 5, 6, 7 in the odd characteristic.

The paper is organized as follows: In Sect. 2 we determine all conditions on b and c for which the polynomial $g(x)=x^3+bx+c\in {\mathbb F}^*_q[x]$ does not have any roots in $U_{q+1}$, in Sects. 3 and 4 we give all our results with their proofs in even and odd characteristic respectively, in Sect. 5 we give our results for the case when $C_f$ (see, (13)) is absolutely irreducible and finally in Sects. 6 and 7 we compare our results with the results in [Theorem 3.4, [3]] and [Theorem 3.6, [3]] respectively.

Throughout the paper the trace function denoted by ${\text {Tr}}$ stands for the absolute trace function ${Tr_{{\mathbb F}_q/{\mathbb F}_2}}$ of ${\mathbb F}_q$ over ${\mathbb F}_2$.

2 Our approach

We plan to apply Lemma 1. Hence we need to find out $b,c\in {\mathbb F}_q^*$ for which the polynomial $g(x)=x^3+bx+c\in {\mathbb F}_q^*[x]$ does not have any roots in $U_{q+1}$. If $g(1)=0$ or $g(-1)=0$, then g(x) has a root in $U_{q+1}$ trivially, therefore we characterize all such polynomials in the next proposition under the assumptions $g(1)\ne 0$ and $g(-1)\ne 0$. Note that we present an equivalent statement giving an if and only if condition such that g(x) has a root in $U_{q+1}$, instead of g(x) has no roots in $U_{q+1}$.

Proposition 1

Let $g\left( x\right) =x^3+bx+c\in \mathbb {F}_q[x]$ where $b,c\in \mathbb {F}^*_q$ and assume that $g(1)=1+b+c\ne 0$, $g(-1)=-1-b+c\ne 0$ . Then there exists $x\in U_{q+1}$ such that $g(x)=0$ if and only if one the following conditions hold according to the characteristic of the finite field ${\mathbb F}_q$:

• (i) $char(\mathbb {F}_q)=2$: $b=1-c^2$ and ${\text {Tr}}(1/c)=1$,

• (ii) $char(\mathbb {F}_q)$ is odd: $b=1-c^2$ and $c^2-4$ is a nonsquare in ${\mathbb F}_q$.

Before proving Proposition 1 we need to prove a simple result showing that if g(x) has a root in $U_{q+1}$ then it must be in ${\mathbb F}_{q^2}\setminus {\mathbb F}_q$.

Lemma 2

Let $g\left( x\right) =x^3+bx+c\in \mathbb {F}_q[x]$ where $b,c\in \mathbb {F}^*_q$ and assume that $g(1)\ne 0$, $g(-1)\ne 0$ . If there exists $x\in U_{q+1}$ such that $g(x)=0$ then $x\in {\mathbb F}_{q^2}\setminus {\mathbb F}_q$.

Proof

Assume that there exists $x\in U_{q+1}\cap {\mathbb F}_q$ such that $g(x)=0$, then we have $x=x^q=1/x$ which implies that $x^2=1$, that is, $x=1$ or $x=-1$ both of which contradict with the assumptions $g(1)\ne 0$ and $g(-1)\ne 0$. $\square$

We are now ready to prove Proposition 1.

Proof of Proposition 1

Let $x\in U_{q+1}$ such that $g(x)=0$, that is, $x^q=1/x$ and $x^3+bx+c=0$. Taking the q-th power of the equation $x^3+bx+c=0$ and inserting $x^q=1/x$ we get

$$\begin{aligned} x^{3q}+bx^q+c=\dfrac{1}{x^3}+b\dfrac{1}{x}+c=0 \Leftrightarrow 1+bx^2+cx^3=0. \end{aligned}$$

(1)

Hence, there exists $x\in U_{q+1}$ such that $g(x)=0$ if and only if the following system

$$\begin{aligned} \left\{ \begin{array}{rl} x^3+bx+c &{}=0\\ x^3+\dfrac{b}{c}x^2+\dfrac{1}{c} &{}=0 \end{array} \right. \end{aligned}$$

(2)

holds. Subtracting the equations in the above system (2) we get:

$$\begin{aligned} \dfrac{b}{c}x^2-bx+\dfrac{1}{c}-c=0 \end{aligned}$$

(3)

and then multiplying the equation in (3) by $\dfrac{c}{b}$ we have:

$$\begin{aligned} x^2-cx+\dfrac{1}{b}-\dfrac{c^2}{b}=0. \end{aligned}$$

(4)

Letting $\varDelta =\dfrac{1-c^2}{b}$, the equation in (4) becomes

$$\begin{aligned} x^2-cx+\varDelta =0. \end{aligned}$$

(5)

Here, we note that $\varDelta \ne 0$, because otherwise the equation in (5) implies that either $x=0$ or $x=c$, which contradicts with Lemma 2 as $0,c\in {\mathbb F}_q$. Note also that $\varDelta \in {\mathbb F}_q$.

Taking the q-th power of the equation in (5) and substituting $x^q=1/x$, we obtain

$$\begin{aligned} \dfrac{1}{x^2}-\dfrac{c}{x}+\varDelta =0 \Leftrightarrow \varDelta x^2-cx+1=0 \Leftrightarrow x^2-\dfrac{c}{\varDelta }x+\dfrac{1}{\varDelta }=0. \end{aligned}$$

(6)

Now, subtracting the equations in (5) and (6) we have

$$\begin{aligned} -cx+\dfrac{c}{\varDelta }x+\varDelta -\frac{1}{\varDelta }=0, \end{aligned}$$

(7)

which is equivalent to

$$\begin{aligned} \displaystyle c\left( \dfrac{1}{\varDelta }-1\right) x+\dfrac{\varDelta ^2 -1}{\varDelta }=0 \Leftrightarrow c(1-\varDelta )x+(\varDelta ^2 -1)=0. \end{aligned}$$

(8)

If $\varDelta \ne 1$, then by the equation in (8) we get

$$\begin{aligned} cx-(\varDelta +1)=0 \Leftrightarrow x=\dfrac{\varDelta +1}{c}, \end{aligned}$$

which contradicts with Lemma 2, since $\dfrac{\varDelta +1}{c}=\dfrac{1-c^2+b}{bc}\in {\mathbb F}_q$. Thus, $\varDelta =1$, that is, $b=1-c^2$, so the proof of the first condition in both parts (i) and (ii) of the proposition is complete.

Now, assume that $char({\mathbb F}_q)=2$. Using the equation in (5) and the fact that $\varDelta =1$, we obtain

$$\begin{aligned} x^2+cx=1 \Leftrightarrow \dfrac{x^2}{c^2}+\dfrac{cx}{c^2}=\dfrac{1}{c^2} \Leftrightarrow y^2+y=\dfrac{1}{c^2}\,,\,\, \text {where}\,\,y=\dfrac{x}{c}. \end{aligned}$$

(9)

If ${\text {Tr}}(1/c^2)={\text { Tr}}(1/c)=0$ then $y=x/c\in {\mathbb F}_q$, so $x\in {\mathbb F}_q$ (see for instance Theorem 2.25 in [26]), which is not possible by Lemma 2, therefore ${\text { Tr}}(1/c)=1$ and this completes the proof of necessity in part (i).

Next, assume that $char({\mathbb F}_q)$ is odd. Using the equation in (5) and $\varDelta =1$, we obtain

$$\begin{aligned} x^2-cx+1=x^2-cx+\dfrac{c^2}{4}+1-\dfrac{c^2}{4}=0 \Leftrightarrow x^2-cx+\dfrac{c^2}{4}=\dfrac{c^2-4}{4}, \end{aligned}$$

which holds if and only if

$$\begin{aligned} \left( x-\dfrac{c}{2}\right) ^2=\dfrac{c^2-4}{4}. \end{aligned}$$

(10)

Using the equation in (10) and Lemma 2, we obtain that $\dfrac{c^2-4}{4}$ must be a nonsquare in ${\mathbb F}_q$, or equivalently $c^2-4$ must be a nonsquare in ${\mathbb F}_q$ and this completes the proof of necessity in odd characteristic.

Finally, in order to prove sufficiency in both parts (i) and (ii), let $x\in {\mathbb F}_{q^2}$ satisfying $x^2-cx+1=0$, multiplying both sides by x we get $x^3=cx^2-x$.

Substituting $x^3=cx^2-x$ and $b=1-c^2$ in the system (2) we obtain the following:

$$\begin{aligned} x^3+bx+c=cx^2-x+(1-c^2)x+c=c(x^2-cx+1)=0 \end{aligned}$$

(11)

and

$$\begin{aligned} x^3+\dfrac{b}{c}x^2+\dfrac{1}{c}=cx^2-x+\dfrac{1-c^2}{c}x^2+\dfrac{1}{c}=\dfrac{1}{c}(x^2-cx+1)=0. \end{aligned}$$

(12)

This completes the proof of sufficiency and the whole proof ends here. $\square$

There is a related result (see, Proposition 3.1,[3]) in [3], however [Proposition 3.1, [3]] is only an existence result and moreover there are some polynomials such that [Proposition 3.1, [3]] can not show that they exist. We give a detailed comparison in the following Remark.

Remark 1

In this remark we compare Proposition 1 with [Proposition 3.1, [3]]. We first note that Proposition 1 gives an if and only if condition for $g(x)=x^3+bx+c$ with $b,c\in {\mathbb F}^*_q$ to have no roots in $U_{q+1}$. However, [Proposition 3.1, [3]] provides only some of such polynomials. In Table 1 we compare the number of polynomials $g(x)=x^3+bx+c$ with $b,c\in {\mathbb F}^*_q$ such that g(x) has no roots in $U_{q+1}$ which is determined using Proposition 1 with the partial number of such polynomials provided by [Proposition 3.1, [3]].

Table 1 # of g(x) denotes the number of $g(x)=x^3+bx+c$ with $b,c\in {\mathbb F}^*_q$ which has no roots in $U_{q+1}$

For instance, let $q=8$, $w\in {\mathbb F}_8$ with $w^3+w+1=0$. Put $b=w^2, c=w^2$ and $g(x)=x^3+bx+c$. Then g(x) has no roots in $U_9$ using Proposition 1. However, [Proposition 3.1, [3]] does not imply that g(x) has no roots in $U_9$. Indeed, we have $(b+1-c^2)^3+b^3c^2(b+1-c^2)+b^3c^4=0$ and hence the conditions of [Proposition 3.1, [3]] do not hold. As another example, let $q=9$, $w\in {\mathbb F}_9$ with $w^2+2w+2=0$. Put $b=w^7, c=w^6$ and $g(x)=x^3+bx+c$. Then g(x) has no roots in $U_{10}$ using Proposition 1. Indeed, $b\ne 1-c^2$. However, [Proposition 3.1, [3]] does not imply that g(x) has no roots in $U_{10}$. As in the previous example, we have $(b+1-c^2)^3+b^3c^2(b+1-c^2)+b^3c^4=0$ and hence the conditions of [Proposition 3.1, [3]] do not hold.

Now, suppose that g(x) has no roots in $U_{q+1}$, then for any $x\in U_{q+1}$ we have

$$\begin{aligned} x^3g(x)^{q-1}=x^3\dfrac{g(x)^q}{g(x)}=x^3\dfrac{x^{3q}+bx^q+c}{x^3+bx+c}=x^3\dfrac{x^{-3}+bx^{-1}+c}{x^3+bx+c}=\dfrac{cx^3+bx^2+1}{x^3+bx+c}. \end{aligned}$$

Let $f(x)=\dfrac{cx^3+bx^2+1}{x^3+bx+c}$ and note that f(x) permutes $U_{q+1}$ if and only if $f(x)\ne f(y)$ for all $x\ne y\in U_{q+1}$. Computing $\dfrac{f(x)-f(y)}{x-y}$, one gets the following

$$\begin{aligned} C_f: x^2y^2-c(x^2y+xy^2)+\dfrac{(1-c^2)}{b}(x^2+y^2)+\dfrac{(1-c^2-b^2)}{b}xy-c(x+y)+1 \end{aligned}$$

(13)

That is, f(x) permutes $U_{q+1}$ if and only $C_f$ defined in (13) is not zero for any $x,y\in U_{q+1}$ with $x\ne y$. This approach seems to go back, at least, to [21] and [29]. There are further applications of this method, for instance in [2, 7, 9, 10, 14, 22, 35]. Thus, in order to solve this problem we need to check all decompositions of the bivariate polynomial in (13) into absolutely irreducible factors in $\overline{{\mathbb F}}_q$, where $\overline{{\mathbb F}}_q$ stands for an algebraic closure of the finite field ${\mathbb F}_q$.

Remark 2

Note that all possible decompositions of $C_f$ defined in (13) into absolutely irreducible factors are the following:

• (a) $(xy+\alpha _1x+ \alpha _2y+\mu )(xy+\alpha _3x+\alpha _4y+1/\mu )$,

• (b) $(x^2+\alpha _1x+\mu )(y^2+\alpha _2y+1/\mu )$,

• (c) $(x+\alpha _1)(x+\alpha _2)(y+\alpha _3)(y+\alpha _4)$,

• (d) $C_f$ is absolutely irreducible.

3 Results in characteristic two

Throughout this section assume that ${\mathbb F}_q$ is a finite field of characteristic two. Note that if $char({\mathbb F}_q)$ is even then in order to have $\gcd (3,q-1)=1$, q must be of the form $q=2^{2k+1}$, for some $k\in {\mathbb N}$.

In this section we exhibit all the results whenever $C_f$ is not absolutely irreducible in the even characteristic case. We deal with the possible decompositions given in Remark 2 parts (a), (b) and (c) in Theorems 1, 2 and 3, respectively and combine all these results in Theorem 4.

Theorem 1

Let $g(x)=x^3+bx+c$ with $b,c\in {\mathbb F}_q^*$, where $q=2^{2k+1}$, for some $k\in {\mathbb N}$. Assume that $C_f$ is decomposed into absolutely irreducible factors in the form

$$\begin{aligned} (xy+\alpha _1x+ \alpha _2y+\mu )(xy+\alpha _3x+\alpha _4y+1/\mu ), \end{aligned}$$

where $\alpha _1, \alpha _2, \alpha _3, \alpha _4, \mu \in \overline{{\mathbb F}}_q$. Then $x^3g(x^{q-1})$ is a permutation polynomial of ${\mathbb F}_{q^2}$ iff either $b=1$ and ${\text {Tr}}(1/c)=1$ or $b=1+c^2$ and ${\text { Tr}}(1/c)=0$.

Proof

Assume that $C_f$ decomposes in the following form

$$\begin{aligned} (xy+\alpha _1x+ \alpha _2y+\mu )(xy+\alpha _3x+\alpha _4y+1/\mu )=0, \end{aligned}$$

(14)

where $\mu \ne 0$.

First, assume that the factors in (14) remain invariant under the map $(x,y)\mapsto (y,x)$, that is, $C_f$ decomposes in the following form

$$\begin{aligned} (xy+\alpha _1x+ \alpha _1y+\mu )(xy+\alpha _3x+\alpha _3y+1/\mu )=0 \end{aligned}$$

(15)

since $\alpha _1=\alpha _2$ and $\alpha _3=\alpha _4$ in this case. In order to simplify the notation a little bit let us define $\alpha :=\alpha _1$ and $\beta :=\alpha _3$. After computing the product of the factors in (15) and comparing the coefficients with the coefficients of $C_f$ defined in (13) we obtain the following

$$\begin{aligned}&\alpha&+\beta = c \end{aligned}$$

(16)

$$\begin{aligned}&\alpha \beta&= \dfrac{1+c^2}{b} \end{aligned}$$

(17)

$$\begin{aligned}&\mu&+\dfrac{1}{\mu } = \dfrac{1+b^2+c^2}{b} \end{aligned}$$

(18)

$$\begin{aligned}&\dfrac{\alpha }{\mu }&+\beta \mu = c \end{aligned}$$

(19)

By the equations in (16) and (19) we get

$$\begin{aligned} c=\alpha +\beta =\dfrac{\alpha }{\mu }+\beta \mu \iff (\mu +1)\left( \dfrac{\alpha }{\mu }+\beta \right) =0 \end{aligned}$$

(20)

Thus, two possibilities occur: either $\mu =1$ or $\alpha =\mu \beta$. If $\mu =1$, then by equation (18) we obtain $b^2+c^2=1$ which implies $b+c=1$ since q is even. Thus $g(x)=x^3+bx+b+1$ and $g(1)=0$ and we conclude that the polynomial $x^g(x)^{q-1}$ does not permute $U_{q+1}$. Now, suppose that $\alpha =\mu \beta$. Substituting $\alpha =\mu \beta$ in equation (19) we obtain that $\beta =\dfrac{c}{\mu +1}$ and thus $\alpha =\dfrac{c\mu }{\mu +1}$.

Let

$$\begin{aligned} \varDelta :=\mu +\dfrac{1}{\mu }=\dfrac{1+b^2+c^2}{b} \end{aligned}$$

On the other hand, substituting $\alpha =\dfrac{c\mu }{\mu +1}$ and $\beta =\dfrac{c}{\mu +1}$ in equation (17), we also obtain that $\varDelta =\dfrac{c^2b}{1+c^2}.$ Thus $\varDelta =\dfrac{c^2b}{1+c^2}=\dfrac{1+b^2+c^2}{b}$ gives us the following

$$\begin{aligned} (c^2+b)^2=1 \Rightarrow b=1+c^2, \end{aligned}$$

(21)

and so $\varDelta =c^2$.

On the other hand, $\varDelta =\mu +\dfrac{1}{\mu }$ implies that

$$\begin{aligned} \mu ^2+\varDelta \mu +1=0 \end{aligned}$$

(22)

It follows that $\mu \in {\mathbb F}^*_q$ iff ${\text {Tr}}\left( \frac{1}{\varDelta }\right) =0$ and $\mu \in {\mathbb F}_{q^2}\setminus {\mathbb F}_q$ iff ${\text {Tr}}\left( \frac{1}{\varDelta }\right) =1$ (by Theorem 2.25 in [26]). As $\varDelta =c^2$, we have ${\text {Tr}}\left( \frac{1}{\varDelta }\right) ={\text {Tr}}\left( \frac{1}{c^2}\right) ={\text {Tr}}\left( \frac{1}{c}\right)$. Moreover $b=1+c^2$ by (21). Using Proposition 1 we obtain that $x^3g(x^{q-1})$ is not a permutation polynomial of ${\mathbb F}_{q^2}$ if ${\text {Tr}}\left( \frac{1}{c}\right) =1$ as in the case $b=1+c^2$ and ${\text {Tr}}\left( \frac{1}{c}\right) =1$ there exists $x\in U_{q+1}$ with $g(x)=0$. Hence we assume that ${\text {Tr}}\left( \frac{1}{c}\right) =0$ without loss of generality. Then we obtain

$$\begin{aligned} {\text {Tr}}\left( \dfrac{1}{\varDelta }\right) ={\text {Tr}}\left( \dfrac{1}{c^2}\right) ={\text {Tr}}\left( \dfrac{1}{c}\right) =0, \end{aligned}$$

(23)

and hence $\mu \in {\mathbb F}^*_q$. This also imply that $\alpha ,\beta \in {\mathbb F}^*_q$ as $\alpha =\frac{c\mu }{\mu +1}$ and $\beta =\frac{c}{\mu +1}$.

Assume that $xy+\alpha x+\alpha y+ \mu =0$ for some $x,y\in U_{q+1}$, then together with its qth power we get the following system of equations

$$\begin{aligned} xy+\alpha x+\alpha y+ \mu =0 \end{aligned}$$

(24)

$$\begin{aligned} \mu xy+\alpha x+\alpha y+ 1=0 \end{aligned}$$

(25)

Subtracting the above equations we obtain, $(1+\mu )(xy+1)=0$, thus, $xy=1$ as we assumed that $\mu \ne 1$. Substituting $xy=1$ in $xy+\alpha x+\alpha y+\mu =0$ we obtain $x+y=\dfrac{\mu +1}{\alpha }=\dfrac{1}{c}(b+1)=c$ as $\alpha =\dfrac{c\mu }{\mu +1}$ and $\varDelta =b+1=c^2$ in this case. Now, substituting $y=\dfrac{1}{x}$ in $x+y=c$, we obtain $x^2+cx+1=0$. That is, $xy+\alpha x+\alpha y+\mu \ne 0$ for $x,y\in U_{q+1}$ iff the polynomial $x^2+cx+1$ has no roots in $U_{q+1}$.

Moreover, if $xy+\beta x+\beta y+ 1/\mu =0$ for some $x,y\in U_{q+1}$, then together with its qth power we get the following system of equations

$$\begin{aligned} xy+\beta x+\beta y+ 1/\mu =0 \end{aligned}$$

(26)

$$\begin{aligned} (1/\mu ) xy+\beta x+\beta y+ 1=0 \end{aligned}$$

(27)

Subtracting the above equations we obtain, $(1+\dfrac{1}{\mu })(xy+1)=0$, thus, $xy=1$ as we assumed that $\mu \ne 1$.

Substituting $xy=1$ in $xy+\beta x+\beta y+\dfrac{1}{\mu }=0$ we obtain

$x+y=\dfrac{\mu +1}{\mu \beta }=\dfrac{\mu ^2+1}{c\mu }=\dfrac{1}{c}\left( \mu +\dfrac{1}{\mu }\right)$ as $\beta =\dfrac{c}{\mu +1}$.

Now, substituting $y=\dfrac{1}{x}$ in the above equation, we obtain

$x^2+\dfrac{(b+1)}{c}x+1=x^2+cx+1=0$, since $b=1+c^2$. That is, $xy+\beta x+\beta y+\dfrac{1}{\mu }=0$ for $x,y\in U_{q+1}$ iff the polynomial $x^2+cx+1$ has roots in $U_{q+1}$. But we have

$$\begin{aligned} x^2+cx+1=0 \Leftrightarrow \dfrac{x^2}{c^2}+\dfrac{cx}{c^2}=\dfrac{1}{c^2} \Leftrightarrow y^2+y=\dfrac{1}{c^2}\,,\,\, \text {where}\,\,y=\dfrac{x}{c}. \end{aligned}$$

(28)

If ${\text {Tr}}(1/c^2)={\text { Tr}}(1/c)=0$ then $y=x/c\in {\mathbb F}_q$, so $x\in {\mathbb F}_q$ (see for instance Theorem 2.25 in [20]), so we obtain that $x\in U_{q+1}\cap {\mathbb F}_q$, which implies $x=1$ by Lemma 2 and $x=1$ can not be a root of the polynomial $x^2+cx+1$ as $c\ne 0$.

For $g(1)\ne 0$, we must have $1+b+c\ne 0$ but this is already satisfied since $b=1+c^2$ and b, c are nonzero. In this case, we proved that $x^3g(x^{q-1})$ is a permutation polynomial of ${\mathbb F}_{q^2}$ iff $b=1+c^2$ and ${\text { Tr}}(1/c)=0$.

Next, assume that the factors in (14) are mapped to each other under the map $(x,y)\mapsto (y,x)$, that is $C_f$ decomposes in the following form

$$\begin{aligned} (xy+\alpha _1x+ \alpha _2y+\mu )(xy+\alpha _2x+\alpha _1y+1/\mu )=0 \end{aligned}$$

(29)

since $\alpha _1=\alpha _4$ and $\alpha _2=\alpha _3$ in this case. We also have $\mu =1/\mu$ which implies that $\mu =1$. In order to simplify the notation let us define $\alpha :=\alpha _1$ and $\beta :=\alpha _2$.

Thus the equation in (29) is actually the following

$$\begin{aligned} (xy+\alpha x+ \beta y+1)(xy+\beta x+\alpha y+1)=0 \end{aligned}$$

(30)

After computing the product of the factors in (30) and comparing the coefficients with the coefficients of $C_f$ defined in (13) we obtain the following equations:

$$\begin{aligned} \alpha +\beta= & {} c \end{aligned}$$

(31)

$$\begin{aligned} \alpha \beta= & {} \dfrac{1+c^2}{b} \end{aligned}$$

(32)

$$\begin{aligned} \alpha ^2+\beta ^2= & {} \dfrac{1+c^2+b^2}{b} \end{aligned}$$

(33)

Substituting $\alpha \beta = \dfrac{1+c^2}{b}$ in (33) we obtain that

$$\begin{aligned} b=\alpha ^2+\beta ^2+\alpha \beta \end{aligned}$$

(34)

and then substituting both $b=\alpha ^2+\beta ^2+\alpha \beta$ and $c=\alpha +\beta$ in equation (32) we end up with the following equation

$$\begin{aligned} \alpha ^3\beta +\alpha \beta ^3+\alpha ^2\beta ^2+\alpha ^2+\beta ^2+1 = 0 \end{aligned}$$

which implies that

$$\begin{aligned} (\alpha \beta +1)(\alpha ^2+\beta ^2+\alpha \beta +1) = 0 \end{aligned}$$

Thus either $\alpha \beta =1$ or $\alpha ^2+\beta ^2+\alpha \beta +1 = 0$. Note that, if $\alpha \beta =1$ then the equation in (30) is of the following form

$$\begin{aligned}&(xy+\alpha x+ \dfrac{1}{\alpha } y+1)(xy+\dfrac{1}{\alpha } x+\alpha y+1)\nonumber \\&\quad = (x(y+\alpha )+\dfrac{1}{\alpha }(y+\alpha ))(y(x+\alpha )+\dfrac{1}{\alpha }(x+\alpha ))\nonumber \\&\quad = (x+\dfrac{1}{\alpha })(y+\alpha )(y+\dfrac{1}{\alpha })(x+\alpha )=0, \end{aligned}$$

(35)

and we consider this case in Theorem 3. Thus, assume that $\alpha \beta \ne 1$, that is, $\alpha ^2+\beta ^2+\alpha \beta +1 = 0$. Then using the equations in (32) and (33) we get

$$\begin{aligned} \dfrac{1+c^2+b^2}{b}=\alpha ^2+\beta ^2=\alpha \beta +1=\dfrac{1+c^2}{b}+1=\dfrac{1+c^2+b}{b} \end{aligned}$$

which implies that $b(b+1)=0$. Thus, since $b\ne 0$, we obtain that $b=1$. Since $\alpha \beta \ne 1$ then $b\ne 1-c^2$ by (32), so by Proposition 1, g(x) will have no roots in $U_{q+1}$ if $g(1)\ne 0$ is satisfied. Substituting $b=1$ in $g(1)=1+b+c\ne 0$ we just obtain that $c\ne 0$ which is already our assumption. Now, substituting $\alpha =\beta +c$ in the equation $\alpha ^2+\beta ^2+\alpha \beta +1=0$ we get $\beta ^2+c\beta +c^2+1=0$ implying that

$$\begin{aligned} \left( \dfrac{\beta }{c}\right) ^2+\dfrac{\beta }{c}=1+\dfrac{1}{c^2} \end{aligned}$$

which holds if and only if ${\text {Tr}}\left( 1+\dfrac{1}{c^2}\right) =0$, for some $\beta \in {\mathbb F}_q$. Since, $q=2^{2k+1}$, we have

$$\begin{aligned} 0={\text {Tr}}\left( 1+\dfrac{1}{c^2}\right) ={\text {Tr}}(1)+{\text {Tr}}\left( \dfrac{1}{c^2}\right) =1+{\text {Tr}}\left( \dfrac{1}{c}\right) \end{aligned}$$

implying that ${\text {Tr}}\left( \dfrac{1}{c}\right) =1$.

Now, substituting $\alpha =c+\beta$ in the factor $xy+\alpha x+\beta y+1$ we get $xy+(c+\beta )x+\beta y+1$. If $xy+(c+\beta )x+\beta y+1=0$ for some $x,y\in U_{q+1}$ then taking the q-th power of this equation we obtain $1+(c+\beta )y+\beta x+xy=0$. So we have the following system of equations:

$$\begin{aligned} xy+(c+\beta )x+\beta y+1=0\\ xy+\beta x+(c+\beta )y+1=0 \end{aligned}$$

Subtracting the equations in the above system we obtain

$$\begin{aligned} c(y-x)=0. \end{aligned}$$

It follows that the only solution to the above equation is $x=y$ since $c\ne 0$. Similarly, substituting $\alpha =c+\beta$ in the second factor $xy+\beta x+\alpha y+1$ we obtain the same result. Thus we proved that in this case $x^3g(x^{q-1})$ is a permutation polynomial of ${\mathbb F}_{q^2}$ iff $b=1$ and ${\text {Tr}}(1/c)=1$.

On the other hand, if ${\text {Tr}}\left( 1/c\right) =0$ then this implies that $\beta \in {\mathbb F}_{q^2}\setminus {\mathbb F}_q$ and we observe that the factors in the decomposition (30) must be mapped to each other when we apply the map $a\mapsto a^q$ to the coefficients of the factors, that is, $xy+\alpha ^q x+\beta ^q y+1=xy+\beta x+\alpha y+1$ and $xy+\beta ^q x+\alpha ^q y+1=xy+\alpha x+\beta y+1$. As a result we obtain $\beta =\alpha ^q$ and $\alpha =\beta ^q$. Now, if $xy+\alpha x+\beta y+1=xy+\beta ^q x+\beta y+1=0$ for some $x,y\in U_{q+1}$ then this implies that $x=\dfrac{\beta y+1}{y+\beta ^q}=\dfrac{\beta y+1}{y+\beta +c}$ since $\alpha +\beta =\beta ^q+\beta =c$. Thus $x=y\in U_{q+1}$ iff $y^2+cy+1=0$ which is iff ${\text {Tr}}\left( 1/c\right) =0$ for some $y\in {\mathbb F}_q$, that is $y\in U_{q+1}\cap {\mathbb F}_q$, that is, $y=1$ or $y=-1$ by Lemma 2, but in both cases $x\ne y$ since $c\ne 0$. Therefore if $x=\dfrac{\beta y+1}{y+\beta ^q}$ then $C_f$ is zero for some $x,y\in U_{q+1}$ with $x\ne y$, which implies that $x^3g(x)^{q-1}$ does not permute $U_{q+1}$. $\square$

Theorem 2

Let $g(x)=x^3+bx+c$ with $b,c\in {\mathbb F}_q^*$, where $q=2^{2k+1}$, for some $k\in {\mathbb N}$. Assume that $C_f$ is decomposed into absolutely irreducible factors in the form

$$\begin{aligned} (x^2+\alpha _1x+\mu )(y^2+\alpha _2y+1/\mu ), \end{aligned}$$

where $\alpha _1, \alpha _2, \mu \in \overline{{\mathbb F}}_q$. Then $x^3g(x^{q-1})$ is a permutation polynomial of ${\mathbb F}_{q^2}$ iff $b=1+c^2$ and ${\text {Tr}}(1/c)=0$.

Proof

Assume that $C_f$ decomposes in the following form

$$\begin{aligned} (x^2+\alpha _1 x+\mu )(y^2+\alpha _2 y+1/\mu )=0, \end{aligned}$$

(36)

where $\mu \ne 0$. First of all, we observe that the factors in (36) must be mapped to each other under the map $(x,y)\mapsto (y,x)$ so we obtain $\alpha _1=\alpha _2$ and $\mu ^2=1$ which implies that $\mu =1$, that is, the equation in (36) is actually the following

$$\begin{aligned} (x^2+\alpha x+1)(y^2+\alpha y+1)=0, \end{aligned}$$

(37)

where $\alpha :=\alpha _1=\alpha _2$. After computing the product of the factors in (37) and comparing the coefficients of the equation in (37) with the coefficients of $C_f$ defined in (13) we obtain the following

$$\begin{aligned} \alpha= & {} c \end{aligned}$$

(38)

$$\begin{aligned} \dfrac{1+c^2}{b}= & {} 1 \end{aligned}$$

(39)

$$\begin{aligned} \dfrac{1+b^2+c^2}{b}= & {} \alpha ^2. \end{aligned}$$

(40)

By (39) we have $b=1+c^2$ and thus by (40) we have $\alpha ^2=1+b$. Now, assume that the first factor in (37) is zero for some $x\in U_{q+1}$, that is, $x^2+\alpha x+1=0$ for some $x\in U_{q+1}$. Dividing both sides by $\alpha ^2$ we obtain

$$\begin{aligned} \dfrac{x^2}{\alpha ^2}+\dfrac{x}{\alpha }+\dfrac{1}{\alpha ^2}=0 \iff \dfrac{x^2}{\alpha ^2}+\dfrac{x}{\alpha }=\dfrac{1}{\alpha ^2}. \end{aligned}$$

Recall that $b=1+c^2$ and hence ${\text {Tr}}(1/c)=0$ by Proposition 1 for $x^3g(x^{q-1})$ to be a permutation polynomial of ${\mathbb F}_{q^2}$. Using the last equation (see for instance [26, Theorem 2.25]) we conclude that ${\text {Tr}}(1/\alpha ^2)={\text {Tr}}(1/c^2)={\text {Tr}}(1/c)=0$ and hence $x/\alpha \in {\mathbb F}_q$ which implies that $x\in {\mathbb F}_q$ as $\alpha =c\in {\mathbb F}^*_q$, so $x\in {\mathbb F}_q\cap U_{q+1}\setminus \{1\}=\emptyset$ by Lemma 2 which means that $x^2+\alpha x+1$ has no roots in $U_{q+1}$. Similarly the second factor $y^2+\alpha y+1$ in (37) does not have any roots in $U_{q+1}$. Moreover, by Proposition 1 we also need that $g(1)=1+b+c\ne 0$ be satisfied. The proof is completed. $\square$

The proof of Theorem 3 is given below.

Theorem 3

Let $g(x)=x^3+bx+c$ with $b,c\in {\mathbb F}_q^*$, where $q=2^{2k+1}$, for some $k\in {\mathbb N}$. Assume that $C_f$ is decomposed into absolutely irreducible factors in the form

$$\begin{aligned} (x+\alpha _1)(x+\alpha _2)(y+\alpha _3)(y+\alpha _4), \end{aligned}$$

where $\alpha _1, \alpha _2, \alpha _3, \alpha _4\in \overline{{\mathbb F}}_q$. Then $x^3g(x^{q-1})$ is a permutation polynomial of ${\mathbb F}_{q^2}$ iff there exists $\alpha \in {\mathbb F}_{q^2}^*\setminus U_{q+1}$ such that $c=\alpha +\dfrac{1}{\alpha }$ and $b=1+c^2$.

Proof

Let $g(x)=x^3+bx+c$ with $b,c\in {\mathbb F}_q^*$. Assume that $C_f$ is decomposed in the form

$$\begin{aligned} (x+\alpha _1)(x+\alpha _2)(y+\alpha _3)(y+\alpha _4), \end{aligned}$$

(41)

where $\alpha _1, \alpha _2, \alpha _3, \alpha _4\in \overline{{\mathbb F}}_q$, since $C_f$ is fixed under the map $(x,y)\mapsto (y,x)$, we obtain $\alpha _1=\alpha _3$ and $\alpha _2=\alpha _4$. Now, comparing the coefficients of (41) with the coefficients of $C_f$ we get the following:

$$\begin{aligned} \alpha _1+\alpha _2= & {} c \end{aligned}$$

(42)

$$\begin{aligned} \alpha _1\alpha _2= & {} \dfrac{1+c^2}{b} \end{aligned}$$

(43)

$$\begin{aligned} (\alpha _1+\alpha _2)^2= & {} \dfrac{1+b^2+c^2}{b} \end{aligned}$$

(44)

$$\begin{aligned} (\alpha _1+\alpha _2)\alpha _1\alpha _2= & {} c \end{aligned}$$

(45)

$$\begin{aligned} \alpha _1^2\alpha _2^2= & {} 1. \end{aligned}$$

(46)

From (42) and (45) we get that $\alpha _1\alpha _2=1$. Let $\alpha \in {\mathbb F}_{q^2}^*\setminus U_{q+1}$, with $\alpha _1=\alpha$ and $\alpha _2=\dfrac{1}{\alpha }$, then, by (42) we get $c=\alpha +\dfrac{1}{\alpha }$ and $b=1+(\alpha ^2+\dfrac{1}{\alpha ^2})$ which satisfy $b=1+c^2$. Thus, by Proposition 1, for g(x) not to have any roots in $U_{q+1}$ we must have $g(1)=1+b+c\ne 0$ and ${\text {Tr}}(1/c)=0$. We have

$$\begin{aligned} g(1)= & {} 1+b+c=1+1+(\alpha ^2+\dfrac{1}{\alpha ^2})+(\alpha +\dfrac{1}{\alpha })\\= & {} \alpha ^2+\dfrac{1}{\alpha ^2}+\alpha +\dfrac{1}{\alpha }\\= & {} \dfrac{\alpha ^4+1+\alpha ^3+\alpha }{\alpha ^2} \end{aligned}$$

Thus, by Proposition 1, $\alpha \in {\mathbb F}_{q^2}^*\setminus U_{q+1}$ must be such that $\alpha ^4+\alpha ^3+\alpha +1\ne 0$. Note that $\alpha ^4+\alpha ^3+\alpha +1=(\alpha +1)^2(\alpha ^2+\alpha +1)\ne 0$ holds automatically as $\alpha \ne 1$ and $\alpha ^2+\alpha +1\ne 0$ since otherwise $\alpha \in {\mathbb F}_4\setminus {\mathbb F}_2$ which is not possible as $q=2^{2k+1}$, that is, q is an odd power of 2. Moreover, $c=\alpha +\dfrac{1}{\alpha }=\dfrac{\alpha ^2+1}{\alpha }$, then taking $\theta :=\alpha +1$ we get the following

$$\begin{aligned} \dfrac{1}{c}=\dfrac{\alpha }{\alpha ^2+1}=\dfrac{\theta +1}{\theta ^2}=\dfrac{1}{\theta }+\dfrac{1}{\theta ^2}, \end{aligned}$$

and thus we have

$$\begin{aligned} {\text { Tr}}(\dfrac{1}{c})={\text { Tr}}(\dfrac{1}{\theta }+\dfrac{1}{\theta ^2})={\text { Tr}}(\dfrac{1}{\theta })+{\text { Tr}}(\dfrac{1}{\theta ^2})={\text { Tr}}(\dfrac{1}{\theta })+{\text { Tr}}(\dfrac{1}{\theta })=0. \end{aligned}$$

That is, whenever $c=\alpha +\dfrac{1}{\alpha }$, where $\alpha \in {\mathbb F}_{q^2}^*\setminus U_{q+1}$, the condition ${\text { Tr}}(1/c)=0$ in Proposition 1 is already satisfied, which implies that g(x) has no roots in $U_{q+1}$ in this case. Thus, the proof is completed. $\square$

The following theorem is the main result of this section, where we combine all results in even characteristic case.

Theorem 4

Let $g(x)=x^3+bx+c$ with $b,c\in {\mathbb F}_q^*$, where $q=2^{2k+1}$, for some $k\in {\mathbb N}$. Assume that $C_f$ is not absolutely irreducible. Then $x^3g(x^{q-1})$ is a permutation polynomial of ${\mathbb F}_{q^2}$ iff one of the following conditions hold:

• (i) $b=1+c^2$ and ${\text {Tr}}(1/c)=0$.

• (ii) $b=1$ and ${\text {Tr}}(1/c)=1$.

Proof

In this Theorem we just combine all results in Theorems 1, 2 and 3. Thus, it is enough to simply prove that under the assumptions $b,c\in {\mathbb F}^*_q$ and $b=1+c^2$ the following conditions are equivalent:

• (a) There exists $\alpha \in {\mathbb F}_{q^2}^*\setminus U_{q+1}$ such that $c=\alpha +\dfrac{1}{\alpha }$,

• (b) ${\text { Tr}}(1/c)=0$.

Consider the equation

$$\begin{aligned} x^2+cx+1=0. \end{aligned}$$

(47)

The equation in (47) has a solution $\alpha \in {\mathbb F}^*_{q^2}$ iff $c=\alpha +\dfrac{1}{\alpha }$. Moreover, by (47), $\alpha \in {\mathbb F}_q$ iff ${\text {Tr}}(1/c)=0$. Also, if $\alpha \in {\mathbb F}_{q^2}\setminus {\mathbb F}_q$, that is, if ${\text {Tr}}(1/c)\ne 0$, then the roots of the equation in (47) are $\alpha$ and $\alpha ^q$. Thus, this implies that $x^2+cx+1=(x-\alpha )(x-\alpha ^q)$. Considering the coefficient of 1 on both sides we obtain that $\alpha ^{q+1}=1$. This completes the proof. $\square$

Remark 3

In Sect. 5 we prove that there is no permutation polynomial of the form $x^3g(x^{q-1})$ of ${\mathbb F}_{q^2}$ if $C_f$ is absolutely irreducible. Hence we complete the classification when the characteristic is even.

4 Results in odd characteristic

In this section we exhibit all the results whenever $C_f$ is not absolutely irreducible in the odd characteristic case. We deal with the possible decompositions given in Remark 2 parts (a), (b) and (c) in Theorems 5, 6 and 7 respectively and combine all these results in Theorem 8.

Theorem 5

Let ${\mathbb F}_q$ be a finite field of odd characteristic, where $gcd(3,q-1)=1$. Let $g(x)=x^3+bx+c$ with $b,c\in {\mathbb F}_q^*$. Assume that $C_f$ is decomposed into absolutely irreducible factors in the form

$$\begin{aligned} (xy+\alpha _1x+ \alpha _2y+\mu )(xy+\alpha _3x+\alpha _4y+1/\mu ), \end{aligned}$$

where $\alpha _1, \alpha _2, \alpha _3, \alpha _4, \mu \in \overline{{\mathbb F}}_q$. Then $x^3g(x^{q-1})$ is a permutation polynomial of ${\mathbb F}_{q^2}$ iff either $char({\mathbb F}_q)\ne 3$, $b=-3$, $c\ne -2,2$ and $\dfrac{(4-c^2)}{3}$ is a square in ${\mathbb F}_q$ or $b=1-c^2$ and $c^2-4$ is a nonzero square in ${\mathbb F}_q$.

Using the same arguments and similar computations as in Theorem 1 one can prove Theorem 5. Therefore, in order not to repeat the long and complicated computations we omit the proof of Theorem 5.

Theorem 6

Let ${\mathbb F}_q$ be a finite field of odd characteristic, where $gcd(3,q-1)=1$. Let $g(x)=x^3+bx+c$ with $b,c\in {\mathbb F}_q^*$. Assume that $C_f$ is decomposed into absolutely irreducible factors in the form

$$\begin{aligned} (x^2+\alpha _1x+\mu )(y^2+\alpha _2y+1/\mu ), \end{aligned}$$

where $\alpha _1, \alpha _2, \mu \in \overline{{\mathbb F}}_q$. Then $x^3g(x^{q-1})$ is a permutation polynomial of ${\mathbb F}_{q^2}$ iff $b=1-c^2$ and $c^2-4$ is a nonzero square in ${\mathbb F}_q$.

Proof

Assume that $C_f$ decomposes in the following form

$$\begin{aligned} (x^2+\alpha x+\mu )(y^2+\beta y+1/\mu )=0, \end{aligned}$$

(48)

where $\mu \ne 0$. First of all, we observe that the factors in (48) must be mapped to each other under the map $(x,y)\mapsto (y,x)$ so we obtain $\alpha =\beta$ and $\mu ^2=1$ which implies that either $\mu =1$ or $\mu =-1$. If $\mu =-1$, then the equation in (48) becomes

$$\begin{aligned} (x^2+\alpha x-1)(y^2+\alpha y-1)=0. \end{aligned}$$

(49)

After computing the product of the factors in (49) and comparing the coefficients with the coefficients of $C_f$ defined in (13) we obtain the following

$$\begin{aligned} \alpha= & {} -c \end{aligned}$$

(50)

$$\begin{aligned} \dfrac{1-c^2}{b}= & {} -1 \end{aligned}$$

(51)

$$\begin{aligned} \dfrac{1-b^2-c^2}{b}= & {} \alpha ^2 \end{aligned}$$

(52)

$$\begin{aligned} -c= & {} -\alpha . \end{aligned}$$

(53)

By (50) and (53) we obtain $\alpha =-c=0$ which gives a contradiction since $c\ne 0$. Thus $\mu =1$ and we have only the following decomposition in odd characteristic case

$$\begin{aligned} (x^2+\alpha x+1)(y^2+\alpha y+1)=0. \end{aligned}$$

(54)

After computing the product of the factors in (49) and comparing the coefficients with the coefficients of $C_f$ defined in (13) we obtain the following

$$\begin{aligned} \alpha= & {} -c \end{aligned}$$

(55)

$$\begin{aligned} \dfrac{1-c^2}{b}= & {} 1 \end{aligned}$$

(56)

$$\begin{aligned} \dfrac{1-b^2-c^2}{b}= & {} \alpha ^2 \end{aligned}$$

(57)

Substituting (56) in the equation (57) we obtain $b=1-\alpha ^2$ which implies that $b=1-c^2$ by (55). Now, the polynomial $x^2+\alpha x+1=x^2-cx+1=0$ has a root $x\in {\mathbb F}_q$ iff $c^2-4$ is a square in ${\mathbb F}_q$. So, if $c^2-4$ is a square in ${\mathbb F}_q$ and $x\in U_{q+1}$ is such that $x^2-cx+1=0$ we get $x=\pm 1$. Since $c^2-4$ is a square in ${\mathbb F}_q$, g(x) does not have any roots in $U_{q+1}$ by Proposition 1 whenever $g(1)\ne 0$ and $g(-1)\ne 0$. Note that for $g(1)=1+b+c=2-c^2+c\ne 0$ and $g(-1)=-1-b+c=c^2+c-2\ne 0$ we must have $c\notin \{-1,2,-2,1\}$. The proof of the theorem is completed here. $\square$

Theorem 7

Let ${\mathbb F}_q$ be a finite field of odd characteristic, where $gcd(3,q-1)=1$. Let $g(x)=x^3+bx+c$ with $b,c\in {\mathbb F}_q^*$. Assume that $C_f$ is decomposed into absolutely irreducible factors in the form

$$\begin{aligned} (x+\alpha _1)(x+\alpha _2)(y+\alpha _3)(y+\alpha _4), \end{aligned}$$

where $\alpha _1, \alpha _2, \alpha _3, \alpha _4\in \overline{{\mathbb F}}_q$. Then $x^3g(x^{q-1})$ is a permutation polynomial of ${\mathbb F}_{q^2}$ iff there exists $\alpha \in {\mathbb F}_{q^2}^*\setminus U_{q+1}$ such that $(\alpha ^2+\alpha +1)(\alpha ^2-\alpha +1)\ne 0$, $c=-\left( \alpha +\dfrac{1}{\alpha }\right)$ and $b=1-c^2$.

Proof

Let $g(x)=x^3+bx+c$ with $b,c\in {\mathbb F}_q^*$. Assume that $C_f$ is decomposed in the form

$$\begin{aligned} (x+\alpha _1)(x+\alpha _2)(y+\alpha _3)(y+\alpha _4), \end{aligned}$$

(58)

where $\alpha _1, \alpha _2, \alpha _3, \alpha _4\in \overline{{\mathbb F}}_q$, since $C_f$ is fixed under the map $(x,y)\mapsto (y,x)$, we obtain $\alpha _1=\alpha _3$ and $\alpha _2=\alpha _4$. Now, comparing the coefficients of (58) with the coefficients of $C_f$ we get the following:

$$\begin{aligned} \alpha _1+\alpha _2= & {} -c \end{aligned}$$

(59)

$$\begin{aligned} \alpha _1\alpha _2= & {} \dfrac{1-c^2}{b} \end{aligned}$$

(60)

$$\begin{aligned} (\alpha _1+\alpha _2)^2= & {} \dfrac{1-b^2-c^2}{b} \end{aligned}$$

(61)

$$\begin{aligned} (\alpha _1+\alpha _2)\alpha _1\alpha _2= & {} -c \end{aligned}$$

(62)

$$\begin{aligned} \alpha _1^2\alpha _2^2= & {} 1. \end{aligned}$$

(63)

From (59) and (62) we get that $\alpha _1\alpha _2=1$. Let $\alpha \in {\mathbb F}_{q^2}^*\setminus U_{q+1}$, with $\alpha _1=\alpha$ and $\alpha _2=\dfrac{1}{\alpha }$, then, by (59) we get $c=-(\alpha +\dfrac{1}{\alpha })$ and $b=-1-(\alpha ^2+\dfrac{1}{\alpha ^2})$ which satisfy $b=1-c^2$. Thus, by Proposition 1, for g(x) not to have any roots in $U_{q+1}$ we must have $g(1)=1+b+c\ne 0$, $g(-1)=-1-b+c\ne 0$ and moreover $c^2-4$ must be a square in ${\mathbb F}_q$. For $g(1)\ne 0$, $\alpha \in {\mathbb F}_{q^2}^*\setminus U_{q+1}$ must satisfy $\alpha ^4+\alpha ^3+\alpha +1\ne 0$. Note that $\alpha ^4+\alpha ^3+\alpha +1=(\alpha +1)^2(\alpha ^2-\alpha +1)\ne 0$ so it is enough to assume that $\alpha ^2-\alpha +1\ne 0$, since $\alpha \ne -1$.

Similarly,

$$\begin{aligned} g(-1)= & {} -1-b+c=-1+1+(\alpha ^2+\dfrac{1}{\alpha ^2})-(\alpha +\dfrac{1}{\alpha })\\= & {} \alpha ^2+\dfrac{1}{\alpha ^2}-\alpha -\dfrac{1}{\alpha }\\= & {} \dfrac{\alpha ^4+1-\alpha ^3-\alpha }{\alpha ^2}\ne 0 \end{aligned}$$

Thus $\alpha \in {\mathbb F}_{q^2}^*\setminus U_{q+1}$ must be such that $\alpha ^4-\alpha ^3-\alpha +1\ne 0$. Note that $\alpha ^4-\alpha ^3-\alpha +1=(\alpha -1)^2(\alpha ^2+\alpha +1)\ne 0$, so it is enough to assume that $\alpha ^2+\alpha +1\ne 0$, since $\alpha \ne 1$.

Moreover, $c=-(\alpha +\dfrac{1}{\alpha })$ implies that

$$\begin{aligned} c^2=\alpha ^2+2+\dfrac{1}{\alpha ^2} \Longrightarrow c^2-4=\left( \alpha -\dfrac{1}{\alpha }\right) ^2, \end{aligned}$$

so $c^2-4$ is already a square in ${\mathbb F}_q$. The proof is completed. $\square$

Remark 4

The conditions in the statement of Theorem 7 do not seem to appear in the statement of Theorem 8 which is the main result in odd characteristic case. Note that in the proof of Theorem 8 we show that under the assumptions $b,c\in {\mathbb F}^*_q$ and $b=1-c^2$ the following conditions are equivalent:

• (a) There exists $\alpha \in {\mathbb F}_{q^2}^*\setminus U_{q+1}$ such that $c=-\left( \alpha +\dfrac{1}{\alpha }\right)$, $\alpha ^2+\alpha +1\ne 0$ and $\alpha ^2-\alpha +1\ne 0$,

• (b) $c^2-4$ is a square in ${\mathbb F}_q$, where $c\notin \{-2,-1,1,2\}$.

Therefore, the conditions in the statement of Theorem 7 are actually involved in Theorem 8.

The following theorem is the main result of this section, where we combine all results in odd characteristic case.

Theorem 8

Let ${\mathbb F}_q$ be a finite field of odd characteristic, where $gcd(3,q-1)=1$. Let $g(x)=x^3+bx+c$ with $b,c\in {\mathbb F}_q^*$. Assume that $C_f$ is not absolutely irreducible. Then $x^3g(x^{q-1})$ is a permutation polynomial of ${\mathbb F}_{q^2}$ iff one of the following conditions hold:

• (i) $b=1-c^2$ and $c^2-4$ is a nonzero square in ${\mathbb F}_q$,

• (ii) $char({\mathbb F}_q)\ne 3$, $b=-3$ and $\dfrac{4-c^2}{3}$ is a nonzero square in ${\mathbb F}_q$.

Proof

In this Theorem we just combine all results in Theorems 5, 6 and 7. Thus, it is enough to simply prove that under the assumptions $b,c\in {\mathbb F}^*_q$ and $b=1-c^2$ the following conditions are equivalent:

• (a) There exists $\alpha \in {\mathbb F}_{q^2}^*\setminus U_{q+1}$ such that $c=-\left( \alpha +\dfrac{1}{\alpha }\right)$, $\alpha ^2+\alpha +1\ne 0$ and $\alpha ^2-\alpha +1\ne 0$,

• (b) $c^2-4$ is a square in ${\mathbb F}_q$, where $c\notin \{-2,-1,1,2\}$.

The equation $x^2-cx+1=0$ has a solution in ${\mathbb F}_q$ (i.e. all solutions) iff $c^2-4$ is a square in ${\mathbb F}_q$. Otherwise, $\alpha$ and $\alpha ^q$ are solutions with $\alpha ,\alpha ^q\in {\mathbb F}_{q^2}\setminus {\mathbb F}_q$ and we have $(x-\alpha )(x-\alpha ^q)=x^2-cx+1$. Considering the coefficient of 1 on both sides we obtain $\alpha ^{q+1}=1$ which gives a contradiction since $\alpha \notin U_{q+1}$. Assume that $\alpha ^2-c\alpha +1=0$. Note that $\alpha ^2-\alpha +1=0$ iff $(-c+1)\alpha =0$ which is iff $c=1$. Similarly, $\alpha ^2+\alpha +1=0$ iff $(c+1)\alpha =0$ which is iff $c=-1$. Now, assume that $c^2-4$ is a square, then $\alpha ^2-c\alpha +1=0$ and $\alpha ^{q+1}=\alpha ^2=1$ iff $\alpha =-1$ or $\alpha =1$ and $\alpha ^2-c\alpha +1=0$ which is iff $c=2$ or $c=-2$. This completes the proof. $\square$

Remark 5

In Sect. 5 we prove that there is no permutation polynomial of the form $x^3g(x^{q-1})$ of ${\mathbb F}_{q^2}$ if $C_f$ is absolutely irreducible. Hence we complete the classification when the characteristic is odd.

5 The case when $C_f$ is absolutely irreducible

In this section, we consider all $b,c\in {\mathbb F}^*_q$ so that $C_f$ is absolutely irreducible and we prove that in this case $x^3g(x^{q-1})$ is not a permutation polynomial of ${\mathbb F}_{q^2}$. For this purpose we will make use of the Hasse-Weil bound. In order to be able to use the Hasse-Weil bound (see [18, Theorem 5.28]), we need to apply the following idea:

Let z be any element in $\mathbb {F}_{q^2}\setminus \mathbb {F}_{q}$ and define $\phi \left( x\right) =\frac{x+z}{x+z^q}$ for any $x\in \mathbb {F}_q$ with $\phi \left( \infty \right) =1$. Note that it is easy to observe that $\phi$ is one to one from $\mathbb {F}_q \cup \{\infty \}$ to $U_{q+1}$ and thus onto. Moreover, $\phi ^{-1}\left( x\right) = \frac{xz^q-z}{1-x}$ for any $x\ne 1$ with $\phi ^{-1}\left( 1\right) =\infty$. In this setting, $f(x)=\frac{cx^3+bx^2+1}{x^3+bx+c_{}}$ is one to one on $U_{q+1}$ if and only if the map $\left( \phi ^{-1} \circ f \circ \phi \right)$ is one to one on $\mathbb {F}_q\cup \{\infty \}$.

First assume that ${\mathbb F}_q$ is of even characteristic, where $q=2^{2k+1}$. Let $F(x)=\left( \phi ^{-1} \circ f \circ \phi \right) (x)$, $z^q+z=\alpha$, for some $\alpha \in {\mathbb F}_q$ and moreover assume without loss of generality that $\alpha =1$ and $z^2+z+1=0$ then we obtain $F(x)=\frac{x^3(b+c+1)+x^2(b+1)+x(b+c)+c+1}{x^2(b+c+1)+x(b+c+1)+b}$. Here we first assume that ${\text {Tr}}\left( \frac{b}{b+c+1}\right) \ne 0$ so for any $x\in {\mathbb F}_q$ the denominator of F(x) is nonzero. Computing $\frac{F(x)-F(y)}{x-y}$ one gets the following

$$\begin{aligned} \chi _F: x^2y^2+B_1(x^2y+xy^2)+C_2(x^2+y^2)+xy+C_1(x+y)+C_0, \end{aligned}$$

(64)

where $B_1=1, C_2=\frac{b}{b+c+1}, C_1=1+\frac{bc}{b^2+c^2+1}$ and $C_0=1+\frac{b}{b^2+c^2+1}$. We obtain that if the conditions of Theorem 4 do not hold, namely $b,c\in {\mathbb F}^*_q$ such that none of the following conditions hold:

• (i) $b=1+c^2$ and ${\text {Tr}}(1/c)=0$,

• (ii) $b=1$ and ${\text {Tr}}(1/c)=1$,

then $\chi _F$ is absolutely irreducible. Next we consider the case where ${\text {Tr}}\left( \frac{b}{b+c+1}\right) =0$. Note that $b+c+1\ne 0$ as we assume $g(1)\ne 0$. Note that the polynomial $x^2+x+\frac{b}{b+c+1}$ corresponds to the denominator of the rational function F(x) and $x^3(b+c+1)+x^2(b+1)+x(b+c)+c+1$ is the numerator of F(x). It is easy to observe that the numerator and denominator of F(x) are coprime if $\frac{c+1}{c}\ne \frac{b}{b+c+1}$. Note that $\frac{c+1}{c}= \frac{b}{b+c+1}$ if and only if $b=1+c^2$. First consider the subcase where $b\ne 1+c^2$ and ${\text {Tr}}\left( \frac{b}{b+c+1}\right) =0$. As the numerator and denominator of F(x) are coprime and the denominator has a root $x_0\in {\mathbb F}_q$, the composite map $\phi ^{-1} \circ f \circ \phi$ is not one to one on $\mathbb {F}_q\cup \{\infty \}$. In particular both $\infty$ and $x_0$ are mapped to $\infty$ by the composite map $\phi ^{-1} \circ f \circ \phi$. Next we consider the remaining subcase where $b=1+c^2$ and ${\text {Tr}}\left( \frac{b}{b+c+1}\right) =0$. These conditions imply that $b=1+c^2$ and ${\text {Tr}}(1/c)=1$ as ${\text {Tr}}(1)=1$. This gives a contradiction to the assumption that g(x) has no roots in $U_{q+1}$ by Proposition 1. Consequently we can assume without loss of generality that ${\text {Tr}}\left( \frac{b}{b+c+1}\right) =1$ whenever $x^3g(x^{q-1})$ is a permutation polynomial of ${\mathbb F}_{q^2}$.

Next, we consider the case ${\mathbb F}_q$ has odd characteristic. Choose a nonsquare $u\in {\mathbb F}^*_q$ and let $z^2=u$ then note that $z+z^q=0$ and $z^{q+1}=-u$. Here we first assume that $b+3c-3\ne 0$ and similarly let $F(x)=\left( \phi ^{-1} \circ f \circ \phi \right) (x)$ be the composite map on ${\mathbb F}_q\cup \{\infty \}$. Using the chosen value of z we obtain that $F(x)=\frac{x^3+Ax}{x^2+B}$, where $A=u\frac{(-b+3c+3)}{b+c+1}, B=u\frac{(-b+c-1)}{b+3c-3}$. Computing $\frac{F(x)-F(y)}{x-y}$ one gets the following

$$\begin{aligned} \chi _F: x^2y^2+B(x^2+y^2)+(B-A)xy+AB. \end{aligned}$$

(65)

We obtain that if the conditions of Theorem 8 do not hold, namely $b,c\in {\mathbb F}^*_q$ such that none of the following conditions hold:

• (i) $b=1-c^2$ and $c^2-4$ is a nonzero square in ${\mathbb F}_q$,

• (ii) $char({\mathbb F}_q)\ne 3$, $b=-3$ and $\frac{4-c^2}{3}$ is a nonzero square in ${\mathbb F}_q$,

then $\chi _F$ is absolutely irreducible. Next, we consider the case where $b+3c-3=0$. In this case F(x) becomes $F(x)=x^3+Ax$ where $A=\frac{3c}{2-c}$. Computing $\frac{F(x)-F(y)}{x-y}$ one gets the following

$$\begin{aligned} \chi _F: x^2+xy+y^2+A. \end{aligned}$$

(66)

Similarly we obtain that if the conditions of Theorem 8 do not hold then $\chi _F$ is absolutely irreducible.

Now assume that $\chi _F$ in both (64) and (65) is absolutely irreducible. Homogenizing the polynomial in (64) (respectively in (65)) with $x=\frac{X}{Z}$ and $y=\frac{Y}{Z}$ we obtain a homogeneous polynomial of degree $d=4$. Then by the Hasse-Weil bound (see [18, Theorem 5.28]) we have the following:

$c(d)=\frac{1}{2}d(d-1)^2+1$, note that $c(d)=19$ if $d=4$ and $c(d)=2$ if $d=2$ (namely, $d=4$ except when q is odd and $b+3c-3=0$), hence $c(d)\le 19$ and

$$\begin{aligned} \big | N - q \big | \le (d-1)(d-2)q^{1/2}+c(d)\le 6q^{1/2}+ 19, \end{aligned}$$

where N is the number of affine ${\mathbb F}_q$-rational points of $\chi _F$. This implies that if $q- 6q^{1/2}-19> 4$ then both (64) and (65) have an ${\mathbb F}_q$-rational point off the line $x=y$. As q is a prime power, we note that $q- 6q^{1/2}-19> 4$ for any such q provided that $q\ge 79$. Consequently, we complete the proof of the statement $x^3g(x^{q-1})$ is not a permutation polynomial of ${\mathbb F}_{q^2}$ if $C_f$ is absolutely irreducible and $q\ge 79$. It remains to consider $q<79$. If characteristic of ${\mathbb F}_q$ is even then q is in the form $q=2^{2k+1}$ in our case and so we need to consider only $q\in \{2,8,32\}$ and if characteristic of ${\mathbb F}_q$ is odd, then since we need to consider only $q\in \{3,5,9,11,17,23,27,29,41,47,53,59,71\}$. Using MAGMA [8] we observed that there are no other permutation polynomials of the form $x^3g(x^{q-1})$ other than the ones obtained by Theorems 4 and 8. As these correspond to the cases that $C_f$ is not absolutely irreducible, we complete the proof of the statement that $x^3g(x^{q-1})$ is not a permutation polynomial of ${\mathbb F}_{q^2}$ if $C_f$ is absolutely irreducible for any finite field ${\mathbb F}_q$.

Consequently, combining all the results we attained in the absolutely irreducible case, we have the following theorem.

Theorem 9

Let ${\mathbb F}_q$ be a finite field and $g(x)=x^3+bx+c$ with $b,c\in {\mathbb F}_q^*$. Assume that $C_f$ is absolutely irreducible. Then $x^3g(x^{q-1})$ is not a permutation polynomial of ${\mathbb F}_{q^2}$.

Hence, using Theorems 4, 8 and 9 we completely classify all permutation polynomial of the form $x^3g(x^{q-1})$ of ${\mathbb F}_{q^2}$, where $g(x)=x^3+bx+c$ with $b,c\in {\mathbb F}_q^*$.

6 Comparison of Theorem 4 with Theorem 3.4 in [3]

We first consider [Theorem 3.4, [3]], item (ii). As $q=2^{2k+1}$, we obtain that the conditions of [Theorem 3.4, [3]], item (ii) imply

$$\begin{aligned} {\text {Tr}}(\dfrac{1}{c})=1 \,\, \text {and}\,\, T^2+cT+1 \,\, \text {has no roots in}\,\, U_{q+1}. \end{aligned}$$

(67)

However, these two conditions are contradictory. Using Hilbert’s Theorem 90 (see, for instance, Theorem 2.25 in [26]), as ${\text {Tr}}(\dfrac{1}{c})=1$, we obtain that the polynomial $T^2+cT+1$ is irreducible over ${\mathbb F}_q$ and hence its roots are $\alpha ,\alpha ^q\in {\mathbb F}_{q^2}\setminus {\mathbb F}_q$, that is, $T^2+cT+1=(T-\alpha )(T-\alpha ^q)$. Considering the coefficient of $T^0$ on both sides we conclude that $\alpha ^{q+1}=1$ which gives a contradiction to (67). Hence [Theorem 3.4, [3]], item (ii) is an empty condition. On the other hand, Theorem 4, item (ii) gives exactly q/2 polynomials of the form $g(x)=x^3+x+c$ such that $x^3g(x^{q-1})$ is a permutation polynomial of ${\mathbb F}_{q^2}$. Indeed, as $|\{u : {\text {Tr}}(u)=1 \}|=q/2$, choosing $c\in {\mathbb F}_q$ with $1/c\in \{u : {\text {Tr}}(u)=1 \}$, we obtain exactly q/2 distinct polynomials of the form $g(x)=x^3+x+c$ satisfying the conditions of Theorem 4, item (ii).

We also indicate an unnecessary phrase in [Theorem 3.4, [3]], item (i). Indeed, if $c=\alpha +\dfrac{1}{\alpha }$ with $\alpha \in {\mathbb F}_q$, then putting $\alpha =\theta +1$ we obtain that ${\text {Tr}}(\dfrac{1}{c})={\text {Tr}}\left( \dfrac{1}{\theta }+\dfrac{1}{\theta ^2}\right) =0$ and hence the polynomial $T^2+cT+1$ has no roots in $U_{q+1}$ automatically.

The last but not the least comparison we need to underline is the following:

Theorem 4 gives an if and only if statement provided that $C_f$ is not absolutely irreducible. However, [Theorem 3.4, [3]] is only an existence result, which is far from complete, as explained above.

7 Comparison of Theorem 8 with Theorem 3.6 in [3]

We first consider [Theorem 3.6, [3]], item (ii). Let p be the characteristic of the finite field ${\mathbb F}_q$ and $q=p^m$. As $q\equiv 2 \,(mod \,\,3)$, this implies that $p\equiv 2\,(mod \,\,3)$ and m is odd. Note that if the polynomial $T^2-cT+1$ has no roots in $U_{q+1}$ then $c^2-4$ must be a square in ${\mathbb F}_q$. Hence the assumptions of [Theorem 3.6, [3]], item (ii) hold if and only if $-3c^2+12$ and $c^2-4$ are both squares in ${\mathbb F}_q$. As $-3c^2+12=-3(c^2-4)$, we obtain that if the assumptions of [Theorem 3.6, [3]], item (ii) hold, then

$$\begin{aligned} p\equiv 2\,(mod \,\,3) \,\,\text {and}\, -3 \,\,\text {is a square in}\,\,{\mathbb F}_p. \end{aligned}$$

(68)

However, there are many examples in which the conditions in (68) do not hold. For instance, $p=5\equiv 2 \,(mod \,\,3)$ and $-3=2$ is not a square in ${\mathbb F}_5$. In fact, we have checked for all primes $p\le 10000$ and observed that there is no prime p satisfying the conditions in (68). Hence [Theorem 3.6, [3]], item (ii) is empty for many (if not all) cases. However, Theorem 8 gives examples for any finite field ${\mathbb F}_q$ of odd characteristic, where $q\equiv 2 \,(mod \,\,3)$. For instance, if $q=5$, then for $g(x)=x^3-3x+1$ and $g(x)=x^3-3x+4$, we obtain that $x^3g(x^{q-1})$ is a permutation polynomial of ${\mathbb F}_{q^2}$.

Next, we consider [Theorem 3.6, [3]], item (i) and observe that [Theorem 3.6, [3]], item (i) does not hold when $char({\mathbb F}_q)=3$. However, Theorem 8, item (i) holds when $char({\mathbb F}_q)=3$ as well. For instance, if $q=9$, then for $g(x)=x^3+(1-w^2)x+w^2$ and $g(x)=x^3+(1-w^6)x+w^6$, where $w^2+2w+2=0$, $w\in {\mathbb F}_9\setminus {\mathbb F}_3$, we obtain that $x^3g(x^{q-1})$ is a permutation polynomial of ${\mathbb F}_{q^2}$.

Finally, the last but not the least comparison we want to underline is the following: Theorem 8 gives an if and only if statement provided that $C_f$ is not absolutely irreducible. However, [Theorem 3.6, [3]] is only an existence result, which is far from complete as explained above.