Option Pricing and Local Volatility Surface by Physics-Informed Neural Network

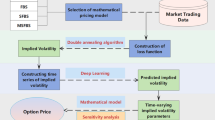
Abstract

We use an artificial neural network for finance in two directions: to estimate prices and Greeks based on the geometric Brownian motion and the constant elasticity of variance model for European options, and to construct a local volatility surface. To show the efficiency and successful usage of the network, we compare prices and Greeks obtained by a solution formula and by the artificial neural network when there is a solution formula is known. Then, we calculate Dupire’s equations to construct a local volatility surface by the network.

1 Introduction

The Black–Scholes equation (BSE) Black and Scholes (1973) is the most widely used option pricing model. The assumption that the price of the underlying asset follows a log-normal process with a constant volatility, is useful for practitioners because there are closed-form solutions for European options. However, the constant volatility assumption is not realistic in the real world. In such a sense, several approaches to the volatility have been developed as four categroies: historical, local, implied and stochastic volatilities, for example in Ref. Ahn et al. (2013), Derman and Kani (1994), Dupire (1994), Heston (1993), Hull (2003), Mayhew (1995), Poon and Granger (2005). Dupire’s local volatility model is useful in practice and important to calculate prices and Greeks.

In practice, estimating the volatility surface is important for pricing exotic options or hedging derivatives. Since different implied volatilities are observed depending on maturity and strike price in the market, after works by Derman and Kani (1994), Dupire (1994) many studies have been conducted to estimate the volatility surface via the local volatility model (Carr & Lee, 2009; Coleman et al., 2001; Gatheral, 2011; Larguinho et al., 2013; Lim & Bae, 2019).

For option pricing based on a local volatilty model, people use the Monte-Carlo method and the finite difference method most popularly. However, these have some disadvantages. Typically, price and Greeks cannot be obtained at the same time. In Ref. Kim et al. (2014), the mesh-free point collocation method is used to calculate option price and their Greeks simultaneously. Artificial neural networks can be used in a sense similar to the mesh-free method. It also solves parametric partial differential equations (PDEs), and approximates even differentiations (see Sect. 4). Furthermore, one of the advantages of the artificial neural network is that people first train the network in advance for a problem, then when predicting and/or pricing are needed, people can use the trained network quickly.

Research on solving PDE using artificial neural networks has been in progress for several decades (Lee & Kang, 1990; Lagaris et al., 1998; Meade & Fernandez, 1994; Yentis & Zaghloul, 1996), and many studies (Sirignano & Spiliopoulos, 2018; Raissi et al., 2019; Glau & Wunderlich, 2022; Berner et al., 2020) have shown the deep learning as an interesting tool. PDEs usually come from physical or social phenomena and laws. In Ref. Raissi et al. (2019), a deep learning framework for solving nonlinear PDEs is proposed, called the physics-informed neural network (PINN). In a usual deep learning, providing data is so important to predict, and the automatic differentiation technique is used to only the back propagation process. Owing to the fact that a physical modeling is given in advance as a form of PDE instead of providing data, it is different from usual machine learning algorithms treated as black box tools. PINN also use the automatic differentiation to calculate partial derivatives included in a PDE where a physical information is described. In the financial market, data is rarely observed, to overcome this we take PINN to solve financial problems. As a result, in finance we can calculate prices, Greeks and Dupire’s equation simultaneously.

In Ref. Gogas and Papadimitriou (2021) there is a survey on machine learning to finance. In Ref. Liu et al. (2022) deep learning techniques are used to better predict the risks of the Internet. For usual deep learnings, to get a better prediction, many data are needed. Even though PINN does not require data, if there are data, the prediction is better. In Ref. Wang et al. (2022) to estimate various option prices, PINN is used. In Ref. Kim et al. (2022) introducing physics-informed convolutional transformer, a volatility surface is estimated. In Ref. Bae et al. (2023) based on a few observed volatility data, and moneyness and maturity data in the market, we construct the implied volatility surface and option price surface using PINN.

In this article, using PINN as a neural network approach, we calculate solutions of BSE, Constant Elasticity of Variance (CEV), Dupire’s PDE, related volatilities and prices for European options. We also calculate price and Greeks.

The contributions of this article are the following:

• 1. We adopt PINN algorithm to solve a family of extended BSEs, for example, CEV and Dupire’s local volatility model. Like a usual neural network, there is a training process and a predictin process. We first train the network for a sufficient time by using PDE, initial and boundary conditions, and then the trained network predicts solutions (prices, Greeks, volatilties, and so on) for different parameter values immediately.

• 2. To show the performance of the method, we estimate errors in the option price, and solve Dupire’s equation to construct a local volatility model, of which solution is not known.

2 Black–Scholes Equation with Local Volatility

2.1 Local Volatility Model

Implied volatilities in market depend on the strike price and the time to maturity. Implied volatility tends to be higher in deep OTM options and deep ITM options than ATM options. It is explained by a phenomenon called volatility smile or skew (refer to Derman and Kani (1994), Dupire (1994)). In the local volatility model, in a risk-neutral world, the volatility is assumed as a deterministic function of time and stock price in the spreading period of the stock price process as follows:

$$\begin{aligned} dS_t/S_t = rdt + \sigma (S_t,t) dW_t, \end{aligned}$$

(1)

where $S_t$ is a stock price at time t, r is a constant risk-free rate, and $dW_t$ is the standard Wiener process in the risk-neutral world. The local volatility $\sigma (S_t,t)$ is a function of the underlying asset price $S_t$ and the time t.

In Ref. Cox and Ross (1976) is denoted by $V(S_t,t)$ a price function of a derivative with underlying asset $S_t$. The extended BSE under the no arbitrage condition is as follows:

$$\begin{aligned} \frac{\partial V}{\partial t} + \frac{1}{2} \sigma ^2(S_t,t) S_t^2 \frac{\partial ^2 V}{\partial S_t^2} + rS_t\frac{\partial V}{\partial S_t} - rV = 0. \end{aligned}$$

Assuming that the price of the underlying asset follows (1), the price of a European call option is given by

$$\begin{aligned} c(S_0,K,T) = e^{-rT}{\mathbb {E}}[(S_T-K)^+], \end{aligned}$$

where K is the strike price of the option, T is the maturity and ${\mathbb {E}}$ is the expectation. In Ref. Dupire (1994), a volatility function is obtained by solving the following Dupire’s equation:

$$\begin{aligned} \sigma ^2(K,T) = 2\frac{ \frac{\partial c}{\partial T} + rK\frac{\partial c}{\partial K} }{ K^2\frac{\partial ^2 c}{\partial K^2} } = 2\frac{ \frac{\partial p}{\partial T} + rK\frac{\partial p}{\partial K} }{ K^2\frac{\partial ^2 p}{\partial K^2} }, \end{aligned}$$

(2)

where p is the correspoding put option price. If the local volatility is constant, then (1) is reduced to the geometric Brownian motion (or called the Black–Scholes model in practice). A model leading to the skew of implied volatility is the CEV model (Cox, 1975; Cox & Ross, 1976).

2.2 Geometric Brownian Motion

The geometric Brownian motion (GBM) follows log-normal, and has the advantage that the existence of closed-form solutions for various options is well known. It can be seen as the simplest model of the local volatility model as flat surface. The stochastic differential equation for GBM is the following:

$$\begin{aligned} dS_t/S_t = rdt + \sigma dW_t, \end{aligned}$$

where $\sigma$ is a constant volatility. The solutions for European options are known as the Black–Scholes formula:

$$\begin{aligned} c(S_t,t,K,r,\sigma )&= S_tN(d_1) - Ke^{-r(T-t)}N(d_2),\\p(S_t,t,K,r,\sigma )&= Ke^{-r(T-t)}N(-d_1) - S_tN(-d_2), \end{aligned}$$

where $d_1:=\frac{\log (S_t/K)+(r+\sigma ^2/2)(T-t)}{\sigma \sqrt{T-t}}$, $d_2:=d_1-\sigma \sqrt{T-t}$ and N(x) is the cumulative normal distribution. The advantage of a model with a closed solution is that Greeks can be found analytically. Greeks’ analytic formula are used for model evaluation. For Greeks, we refer to Larguinho et al. (2013) which contains many formula.

2.3 Constant Elasticity of Variance Model

The constant elasticity of variance (CEV) model (Cox, 1975) with the local volatility $\sigma (S_t,t)=\sigma S_t^{(\beta -2)/2}$, $\beta \in {\mathbb {R}}$, explains the negative skew on the underlying asset’s price, and there are closed-form solutions for European vanilla options. CEV model is the same as GBM when $\beta =2$, and the square-root diffusion model in Ref. Cox and Ross (1976) when $\beta =1$. In Ref. Emanuel and MacBeth (1982) the closed-form solution is provided for European call option of $\beta >2$. In Ref. Cox and Ross (1976) denoted by $V(S_t,t)$ a price function of a derivative with underlying asset $S_t$. Equations for CEV model are as follows: for short, with notations $\partial _t V:=\frac{\partial V}{\partial t}$, $\partial _{S_t}V:=\frac{\partial V}{\partial _{S_t}}$,

$$\begin{aligned}&dS_t = rS_tdt + \sigma S_t^{\beta /2}dW_t, \\ \nonumber&\partial _t V + \frac{1}{2}\sigma ^2S_t^\beta \partial ^2_{S_t} V + rS_t\partial _{S_t} V - rV = 0, \end{aligned}$$

(3)

where $\sigma$ is constant. The solution for European put option $p(S_t,t,K,r,\sigma )$ is

$$\begin{aligned}&p(S_t,t,K,r,\sigma ) \nonumber \\&= {\left\{ \begin{array}{ll} Ke^{-r(T-t)}Q(2x;\frac{2}{2-\beta },2y) -S_t\big [1{-}Q(2y;2 + \frac{2}{2-\beta },2x)\big ], &{} \text {for } \beta <2, \\ Ke^{-r(T-t)}Q(2y;2 + \frac{2}{\beta -2},2x) -S_t\big [1{-}Q(2x;\frac{2}{\beta -2},2y)\big ], &{} \text {for } \beta >2, \end{array}\right. } \end{aligned}$$

(4)

where $Q(w;v,\lambda )$ is the complementary distribution function of a non-central chi-square law, v is the degree of freedom, $\lambda$ is a non-centrality parameter, and

$$\begin{aligned}&x = S_t^{2-\beta }e^{r(2-\beta )(T-t)}d,{} & {} y = K^{2-\beta }d,\\&d = \frac{2r}{ \delta ^2(2-\beta )[e^{r(2-\beta )(T-t)}-1]},{} & {} \delta ^2 = \sigma _0^2S_0^{2-\beta }. \end{aligned}$$

These values are given in Ref. Lagaris et al. (1998).

3 Artificial Neural Network for PDE solver

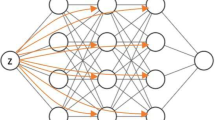
Artificial neural networks are essentially functions that map from input variables to output values. The layers in the neural network consist of composite functions of affine mapping (weighted sum) and nonlinear mapping (activation function). Usual artificial neural networks require many data, and are used in various areas, for examples, pattern classification, clustering, function approximation, prediction, optimization, and many others. Refer to Jain et al. (1996) for a tutorial.

Among artificial neural networks, deep neural networks (DNNs) are popularly used, which contains many hidden layers between input and output layers. Between layers, there are parameters (or weights) used for weighted sum, activation functions and optimizers. In our case, we use $\tau {:=}T{-}t, s, k$ as inputs, $u^\theta$ as an output option price. We also denoted by $\theta$ parameters between input and a hidden layer, between hidden layers, and between a hidden layer and output. We describe these more details in Sect. 3.1.

The universal approximation theorem has been demonstrated in Cybenko (1989) that a neural network with one hidden layer can approximate an arbitrary continuous function. This shows the neural network is a kind of function approximation, and as a result, it can be used as a method to solve PDEs. Recently, neural network techniques to solve PDEs has been developed actively. The automatic differentiation technique, which contributes greatly to the efficient learning of network weights and biases, provides partial derivatives of the neural network analytically. Therefore, this plays an important role in constructing a PDE for an objective function.

In Ref. Raissi et al. (2019), PINN is proposed to solve PDEs as a DNN, which does not require data, differently from usual DNNs.

3.1 PINN for BSE with Local Volatility

Consider parametric BSE for $V(\tau ,s,k)$ under the local volatility model:

$$\begin{aligned} \begin{aligned}&\partial _\tau V - \sigma ^2(\tau ,s)s^2\partial ^2_s V/2 - rs\partial _s V + rV = 0\quad \text { in }[0,T] \times \Omega _S \times \Omega _K, \\&V(0,s,k) = V_0(s,k), \qquad (s,k) \in \Omega _S \times \Omega _K, \\&V(\tau ,s,k) = g(\tau ,s,k), \qquad (\tau ,s,k) \in [0,T] \times \partial \Omega _S \times \Omega _K, \end{aligned} \end{aligned}$$

where $\tau :=T-t$ is time to maturity, $\Omega _S,\Omega _K \subset [0,\infty )$ are closed sets of stock price S, of strike price K, respectively. The boundary of $\Omega _S$ is denoted by $\partial \Omega _S$, and $V_0, g$ are given initial and boundary conditions, respectively.

We denote by $u^\theta (\tau ,s,k) \in {\mathbb {R}}$ a functional form of artificial neural network for option price with respect to $\tau$, stock price s, and strike price k. The artificial neural network $u^\theta (\tau ,s,k)$ approximates $V(\tau ,s,k)$, where $\theta$ is the neural network’s parameter.

Construct the objective function for BSE under the local volatility model as a summation of mean square error losses for the equation, initial and boundary conditions:

$$\begin{aligned} \begin{aligned}&{\mathcal {L}}_{pde}(u^\theta ) := \big \Vert \partial _\tau u^\theta - \sigma ^2(\tau ,s)s^\beta \partial ^2_s u^\theta /2 - rs\partial _2 u^\theta + ru^\theta \big \Vert ^2,\qquad \beta =2,\\&{\mathcal {L}}_{ic}(u^\theta ) := \Vert u^\theta (0,\cdot ,\cdot ) - V_0(\cdot ,\cdot ) \Vert ^2, \\&{\mathcal {L}}_{bc}(u^\theta ) := \Vert u^\theta (\cdot ,s,\cdot ) - g(\cdot ,s,\cdot ) \Vert ^2 \qquad \text { for } s\in \partial \Omega _S,\\&{\mathcal {L}}_{total}(u^\theta ) := {\mathcal {L}}_{pde}(u^\theta ) + {\mathcal {L}}_{ic}(u^\theta ) + {\mathcal {L}}_{bc}(u^\theta ), \end{aligned} \end{aligned}$$

(5)

where ${\mathcal {L}}_{total}(u^\theta )$ is the objective or total loss function. The notation $\Vert \cdot \Vert$ means the mean square error with respect to the discretizations of $\tau$, s and k in (5)$_1$, of s and k in (5)$_2$, and of $\tau$ and k in (5)$_3$. Using the neural network technique we try to find a minimizer of $\mathcal{L}_{total}$, which approximates a solution V of the equation. If ${\mathcal {L}}_{total}(u^\theta )=0$, then $u^\theta (\tau ,s,k)$ is a solution of BSE.

In Ref. Cybenko (1989); Sirignano and Spiliopoulos (2018), define by ${\mathbb {C}}^n$ the class of neural networks with a single hidden layer and n hidden units. Let $u^n$ be a neural network with n hidden units which minimizes ${\mathcal {L}}_{total}(u^n)$. It is proved that, under certain conditions,

$$\begin{aligned} \begin{aligned}&\text {there exists }u^n \in {\mathbb {C}}^n \text {such that } {\mathcal {L}}_{total}(u^n) \rightarrow 0, \text { as } n \rightarrow \infty , \text { and} \\&u^n \rightarrow V \text { as } n \rightarrow \infty . \end{aligned} \end{aligned}$$

(6)

The goal of training neural network is to find a set of parameter $\theta$ such that the function $u^\theta (\tau ,s,k)$ minimizes the total loss function ${\mathcal {L}}_{total} (u^\theta )$. The algorithm is following:

Algorithm 1

Algorithm of PINN for local volatility BSE

4 Numerical results

We implement the neural networks of local volatility models (1), and (3) in TensorFlow2 on a GeForce RTX 3070. We describe our result in two ways: the cases that a solution formula is known, and not.

• (1). For the case that a local volatility model allows a closed form solution of European put option, we evaluate the option’s price and Greeks (Delta, Gamma, Theta) via a neural network. We compare the values obtained by the solution formula and by PINN to show the PINN technique is good.

• (2). For the case that there does not exist a closed form solution of European put option, we evaluate Dupire’s equation (2) via the neural network in the following way:

  $$\begin{aligned} \sigma ^2_{NN} = 2 \big ( \partial _T u^\theta + rK\partial _K u^\theta \big ) / \big (K^2 \partial ^2_K u^\theta \big ), \end{aligned}$$

  (7)

where $u^\theta$ is obtained via PINN.

If the neural network $u^\theta (\tau ,s,k)$ is well trained with the object function (5) for European put options, then (7) should be equal to the local volatility function. Instead of the price of the underlying asset, moneyness is used and the maturity is fixed at one year $T=1$. Risk-free interest rate is $r=0.01$, volatility is $\sigma =0.3$, strike price fixed $k=1$, and for CEV model we consider $\beta =1,3$.

In this section, for a volatility surface model, we use the market European option data consisting of several maturities and strike prices of which underlying asset is EUROSTOXX50 in January 15, 2016. In Ref. Woo et al. (2016), by using the parameters obtained by calibration and the implied volatility formula under SABR model, the authors provide several quantitative properties of volatility by drawing volatility surface. We adopt (Woo et al., 2016) to derive volatility surface from market data (see Fig. 12a). Based on the volatility surface in Fig. 12a as a local volatility $\sigma (S_t,t)$ in (1), we calculate all prices and Greeks.

According to (6), the larger the number of hidden units, the better the approximation. We have adopted the number of hidden units 20,000. We have used the softplus function as an activation function.

4.1 GBM

Here, we test the efficiency of PINN computation by comparing wth Black–Scholes solution formula. For PINN we use the objective function (5) with $\beta =2$.

For GBM, we fix $\sigma =0.3$ as a plane volatility surface. Figure 1 show prices, Deltas, Gammas and Thetas of European put option with GBM. Figure 1a is obtained from the solution formula, and Fig. 1b by PINN. In Fig. 2, we evaluate pointwise absolute errors of price, Delta, Gamma and Theta. For example, for each $s,\tau$, we consider the absolute value of the difference between two solutions obtained by the formula and PINN. Table 1 shows errors of price and Greeks, which show the computational errors are sufficiently small.

Table 1 GBM Neural network’s pointwise absolute errors between solutions obtained by formula and by PINN for prices and Greeks

Fig. 1

European put option price and Greeks with GBM, and their PINN approximations: price(left top), Delta(right top), Gamma(left bottom), Theta(right bottom)

Fig. 2

Pointwise absolute errors of GBM via PINN: price(left top), Delta(right top), Gamma(left bottom), Theta(right bottom). Maximum errors are given in Table 1

We also provide two dimensional comparisions of the results in Fig. 3, which are cross sections of the 3 dimensional surface in Fig. 1. The blue graphs are cross sections of Fig. 1a and the red graphs are those of Fig. 1b. As we can see, the computational results obtained by the solution formula and by the neural network are almost the same.

Fig. 3

Two dimensional comarision of results by solution formula and by PINN: Obtained by formula (blue) and by PINN(red)

Figure 4 shows the volatility surfaces: Fig. 4a is the given constant volatility $\sigma =0.3$, and Fig. 4b is the local volatility surface directly obtained by solving Dupire’s equation (7) via PINN without the information $\sigma =0.3$. This local volatility surface approximates the constant volatility with an error.

Fig. 4

(Left) Constant volatility $\sigma =0.3$, and (Right) volatility surface obtained by PINN (7) which approximates the constant volatility surface

Based on the above computational results, we infer that PINN computations provide good accuracies in prices and Greeks, even in a volatility.

4.2 CEV

We compute CEV model for $\beta =1$ and $\beta =3$ and Dupire’s equation via PINN. The objective function for CEV is similar to (5) with $\beta =1,3$. From our results, we show that the neural network approximates the parametric PDE as well as its derivatives simultaneously, and efficiently.

With fixed $\sigma =0.3$, (4) is used to evaluate. Volatility surfaces of CEV model with $\beta =1,3$ are shown in Fig. 5. Figure 6 shows neural network Dupire’s equation (7) of both CEV models. Dupire’s equations of the CEV neural networks in Fig. 6 have a similar shape to the local volatility functions of CEV in Fig. 5, indicating that the approximation of the parametric PDE is well done.

Fig. 5

Volatility surfaces of CEV model: $\sigma (S_t,t)=\sigma S_t^{(\beta -2)/2}$ with $\sigma =0.3$, $\beta =1$ and $\beta =3$

Fig. 6

Volatility surfaces of CEV $(\beta {=}1,3)$ obtained via PINN

Prices, Deltas, Gammas, Thetas of European put option with CEV obtained from the solution formula are provided in Fig. 7, in Fig. 7a for $\beta =1$, and in Fig. 7b for $\beta =3$. In. 8, prices, Deltas, Gammas and Thetas of European put option with CEV model approximated by PINN are shown, in Fig. 8a for $\beta {=}1$, and in Fig. 8b for $\beta {=}3$. In Fig. 9, we evaluate pointwise absolute errors of prices, Deltas, Gammas and Thetas for CEV model.

Table 2 provides absolute errors of prices and Greeks obtained by solution formula and by PINN, which shows PINN approximates prices and Greeks with high accuracy.

Table 2 CEV PINN’s pointwise absolute errors of price and Greeks

Fig. 7

European put option price and Greeks with CEV for $\beta =1,3$: price(left top), Delta(right top), Gamma(left bottom), Theta(right bottom)

Fig. 8

PINN approximation of European put option price and Greeks with CEV model: price(left top), Delta(right top), Gamma(left bottom), Theta(right bottom)

Fig. 9

Pointwise absolute errors of PINN approximations to CEV for $\beta =1,3$: price(left top), Delta(right top), Gamma(left bottom), Theta(right bottom). Maximum errors are given in Table 2

Two dimesional comparisions of the results obtained by the formula and by PINN are provided in Fig. 10. The blue graphs are cross sections of Fig. 7, and the red graphs are those of Fig. 8. As we can see, the computational results obtained by the solution formula and by the neural network are almost the same.

Fig. 10

Two dimensinal comparison of results obtained by CEV solution formula(blue) and by PINN(red): price(left top), Delta(right top), Gamma(left bottom), Theta(right bottom)

4.3 Local Volatility Model

SABR local volatility model using volatility data in the market does not have a closed form solution. Using PINN we calcualte BSE under the local volatility model, which does not have a closed form solution. We have used the volatility surface in Fig. 12a as the local volatility function. Figure 11 shows prices, Deltas, Gammas and Thetas of European put options with the volatility surface approximated by the neural network. Figure 12b shows the local volatility surface obtained by the neural network, PINN (7).

Fig. 11

Volatility surface PINN approximation of European put option price and Greeks: price(left top), Delta(right top), Gamma(left bottom) and Theta(right bottom)

Fig. 12

Local volatility surfaces are obtained by SABR local volatility (Left), and by PINN (Right)

Two dimensional comparision of volatilities is provided in Fig. 13. SABR local volatility is in blue, and PINN local volatility is in red. Figures are cross sections of the surfaces in Fig. 12a and b. Each figure is drawn at each time to maturity: $\tau =0.0$ (top left), $\tau =0.3$(top right), $\tau =0.6$(bottom left), and $\tau =0.9$(bottom right). As we can see, at $\tau =0$ the error is biggest even though small. One of the reason is that PINN may not catch the initial conditon efficiently, and the other reason is that at $\tau =0$ volatility is skewed more seriously.

Fig. 13

Comparision of volatilities obtained by SABR local volatility(Blue), and by PINN local volatility(Red). Figures are drawn at each time to maturity: $\tau =0.0$ (top left), $\tau =0.3$(top right), $\tau =0.6$(bottom left), and $\tau =0.9$(bottom right)

5 Conclusion

We focus on the power of artificial neural networks as function approximations. We have implemented neural networks to solve parametric BSEs under local volatility models.

We use algorithms to improve the performance of BSE approximation. Data random generation scheme is used for the approximation performance. As a result in Sect. 4, the approximation performance of local volatility models is evaluated through closed-form solutions and Dupire’s equation. Prices and Greeks are approximated well in measurement. It is verified by Dupire’s equation that the parametric BSE is well approximated.

It is expected that this study can contribute to practitioners as a tool for the local volatility model. Based on the comparion of the computional results, we conclude that the neural network, PINN, provides high efficiency, as a result, we can use PINN to compute prices and Greeks when the solution formulae is not known. And our ongoing projects are twofolds: (1) to compute more complicated exotic options like the equity-linked securities (ELS), and their Greeks, and (2) to construct a volatility surface based on a few volatility data. For the second problem, we have constructed a volatility surface by the thin plate spline function (Lim & Bae, 2019). We have also constructed a volatility surface by using PINN based on a few observed data in the market in Ref. Bae et al. (2023).