Calibration of Agent-Based Models by Means of Meta-Modeling and Nonparametric Regression

Abstract

Taking agent-based models to the data is still very challenging for researchers. In this paper we propose a new method to calibrate the model parameters based on indirect inference, which consists in minimizing the distance between real and artificial data. Basically, we first introduce a nonparametric regression meta-model to approximate the relationship between model parameters and distance. Then the meta-model is estimated by local polynomial regression estimation on a small sample of parameter vectors drawn from the parameter space of the ABM. Finally, once the distance has been estimated we can pick the parameter vector minimizing it. One innovative feature of the method is the sampling scheme, based on sampling at the same time both the parameter vectors and the seed of the random numbers generator in a random fashion, which permits to average out the effect of randomness without resorting to Monte Carlo simulations. A battery of simple calibration exercises performed on an agent-based macro model shows that the method allows to minimize the distance with good precision using relatively few simulations of the model.

1 Introduction

The acknowledgment that real-world economies are intrinsically complex systems has pushed an increasing number of economists to turn in the last few decades to agent-based models (ABMs).

ABMs are generally large systems of stochastic difference equations whose properties cannot be analytically understood because of their complexity. Consequently, ABMs are first translated into software and then analyzed numerically through computer simulations. Examples of applications of ABMs to economics (or agent-based computational economics, a.k.a. ACE, Judd and Tesfatsion 2006) are now uncountable and range from the study of single markets, such as the financial market and the labor market, to the study of entire multi-market economies.

A crucial and still problematic phase of ABMs analysis is the assessment of their degree of realism. This phase is generally called empirical validation, which consists in comparing the model output with analogous empirical data (Fagiolo et al. 2007). Basically, there are three broad categories of empirical validation (Judd and Tesfatsion 2006; Bianchi et al. 2007):

• 1. Input or ex ante validation, ensuring that the model characteristics exogenously input by the modeler (such as agents’ behavioral equations, initial conditions, random-shock realizations, etc.) are empirically meaningful and broadly consistent with the real system being studied through the model.

• 2. Descriptive output validation, assessing how well the model output matches the properties of pre-selected empirical data.

• 3. Predictive output validation, assessing how well the model output is able to forecast properties of new data (out-of-sample forecasting).

The most common typology of validation procedure is the descriptive one, which is carried out by evaluating the model’s ability to replicate some set of stylized facts. However, descriptive validation procedures are still eminently qualitative and consequently no consensus has emerged so far on the best way to evaluate ABMs.¹

Taking ABMs to the data is made tricky also by the estimation of the model parameters. The outcome of validation procedures depends in fact also on the model parameter configuration. As a consequence, to increase the model’s degree of realism the researcher may want to resort to some calibration procedure to choose optimal parameter values. Calibration is however one of the major challenges posed by agent-based models. The reason is that in general ABMs cannot be analytically solved and so it is not possible to obtain some closed-form equilibrium relationship depending on the model parameters (e.g. equilibrium GDP as function of the marginal propensity to consume) to estimate directly on real data through common statistical techniques.² Hence, because of the difficulties encountered in calibrating the parameters by direct estimation, indirect methods such as indirect inference (Gourieroux et al. 1993) and the method of simulated moments (McFadden 1989) have become popular to calibrate ABMs. Many different variants of calibration through indirect methods exist in ACE literature, including among the others those proposed by Gilli and Winker (2003), (Bianchi et al. 2007, 2008), Fabretti (2013), Recchioni et al. (2015), Grazzini and Richiardi (2015) and Lamperti (2018).³ In spite of their differences, however, all indirect calibration methods feature the same three phases:

• 1. Choosing a set of real data $D_r$ and analogous simulated data $D_m$ produced by the model.⁴

• 2. Choosing a metric $d(\cdot )$ to measure the distance between $D_r$ and $D_m$, representing the degree of realism of the model.

• 3. Choosing by simulations the model parameters that minimize the distance $d(D_r,D_m)$.

Such a general framework has been labeled simulated minimum distance approach (Grazzini and Richiardi 2015), of which the first two phases basically constitute the criterion used to validate the model, and the third phase is the very calibration process. The goal of this paper is precisely to propose a new indirect calibration method.

Indirect calibration in principle would require repeated simulations of the ABM to compute the value of the objective function $d(D_r,D_m)$ for each point of the parameter space. By the brute force of calculations the modeler can therefore find the minimum-distance parameter vector. Unfortunately, for most of ABMs a complete exploration of the parameter space cannot be carried out at reasonable computational costs because of well-known issues:

• 1. Complexity: a single simulation of a sufficiently large ABM may take a long time to be run even for a small number of periods.

• 2. ‘Curse of dimensionality’: ABMs are usually over-parametrized, i.e. their parameter space is large.

• 3. Randomness: normally ABMs are stochastic. Thus, Monte Carlo replications are needed to average out the noise caused by random numbers, that is for each point of the parameter space simulations must be repeated with different seeds of the random numbers generator.

To overcome these problems, calibration methods are usually constructed around search algorithms that explore only sub-sets of the parameter space, like for instance genetic algorithms (e.g. as in Fabretti 2013) and gradient-based search algorithms (e.g. as in Gilli and Winker 2003; Recchioni et al. 2015). Because of the typical complexity of ABMs, however, a major drawback of search algorithms is that they may find a solution that is only a local minimum. This means that such methods may still require many runs of the model because to find the global minimum the search needs to be repeated for different starting points (and for different seeds of the random numbers generator).

A totally different approach to calibration which allows to avoid the complete exploration of the parameter space is the one based on the concept of meta-modeling. Meta-modeling is the process of approximation of an unknown complicated relationship between input factors (the parameters or other initial conditions) and model output with a simpler one of known shape, called ‘meta-model’ (Saltelli et al. (2008), ch. 5). In the context of calibration a meta-model could be specified for example to approximate the relationship between the distance $d(\cdot )$ and the ABM parameters. The advantage of this approach is that the distance is not computed point by point but is estimated using only a limited number of observed points of the parameter space, for which therefore the ABM needs to be simulated. Subsequently, the estimated meta-model is used to calculate an approximated distance ${\hat{d}}$ for the whole parameter space without further simulations of the agent-based model. Calibration procedures based on meta-modeling are therefore aimed to increase the speed of the calibration process at the expenses of its accuracy, because the distance is approximated by the fitted values of the meta-model. Hence, calibration through meta-modeling seems to be particularly suitable for computationally demanding large-scale ABMs, in which case a loss in accuracy is well compensated by gains in execution time. Moreover, methods based on meta-modeling have potentially also another merit: as in fact the approximated distance is smoother than the actual one, in general they have the tendency to eliminate local minima, which are one of the main problems afflicting methods based on search algorithms.

Among the few examples of the meta-modeling approach in ACE literature are Salle and Yildizoglu (2014), Barde and van der Hoog (2017) and Bargigli et al. (2020), who employ a kriging meta-model estimated on a sample constructed by the nearly-orthogonal Latin hypercube method. Another one is Chen and Desiderio (2021), who propose a novel sampling strategy of the parameter space which allows to estimate meta-models without resorting to Monte Carlo replications. All of these works are based on parametric regression meta-models, which can be easily estimated by such standard regression techniques as OLS and GLS but which may provide a poor approximation of the distance if this is a highly non-linear function of the model parameters. Thus, to overcome such a limitation in the present paper we will introduce a new calibration method still based on the sampling scheme of Chen and Desiderio (2021), but with the crucial difference that we will not specify the functional form of the meta-model used to approximate the distance. The unspecified meta-model will be therefore estimated by nonparametric regression techniques, namely local polynomial estimation. As for the parametric case, the main advantage of our method over other calibration procedures is that the ABM is simulated relatively few times. In addition, its high degree of flexibility makes it fitter than the parametric counterparts when the distance function is highly non-linear. Clearly, the inevitable drawback is that it requires less common estimation techniques.

To our knowledge, our method is the first of its kind. Another recent calibration method for ABMs based on nonparametric meta-modeling is Lamperti et al. (2018), which use machine learning algorithms in place of regression meta-models. Although very similar in spirit, our work is however totally different as for the technique adopted, and is probably of greater ease of implementation. Other recent works quite different from ours but also employing some typology of nonparametric estimation techniques are Kukacka and Barunik (2017) and Grazzini et al. (2017).

The paper continues as follows: in Sect. 2 we briefly introduce nonparametric regression, in Sect. 3 we present the calibration procedure and in Sect. 4 we apply it to calibrate the ABM presented in Chen and Desiderio (Chen and Desiderio 2018, 2020). Section 5 concludes.

2 Nonparametric Regression

In this section we briefly introduce nonparametric regression methods. Unlike parametric regression, the general idea is to estimate the relationship between a dependent variable Y (the output) and a set of independent variables X (the input) without specifying a particular functional form for it. Many techniques exist that perform this task, such as kernel smoothing, splines and wavelets, but we will focus on the relatively simple local polynomial estimators (e.g. ch. 1, Tsybakov (2009)), which will constitute the basis of our calibration procedure. Local polynomial estimators possess good statistical properties in the case of both random inputs and fixed inputs. Below we will consider only the former case as it is more consistent with the sampling strategy we are going to use in Sect. 3.

2.1 Local Polynomial Regression

Given the random vector $(X,Y)\in R^k \times R$, the regression function of Y on X is defined as

$$\begin{aligned} f(x)=E(Y|X=x). \end{aligned}$$

(1)

The goal in nonparametric regression is to estimate the unspecified relationship f(x) using a random sample $(x_1,y_1),...,(x_n,y_n)$ drawn from (X, Y). Hence, under the hypothesis of random sampling we have

$$\begin{aligned} y_i=f(x_i)+\epsilon _i, \; \; i=1,...,n, \end{aligned}$$

(2)

where $\epsilon _1,...,\epsilon _n$ are i.i.d. random errors with $E(\epsilon _i)=0$. Moreover, we assume independence between $\epsilon _i$ and $x_i$. This is generally a strong assumption but, as we will see in Sect. 3, it is satisfied in the context of our calibration method.

For simplicity, assume that the input X is univariate. So, given an arbitrary evaluation point $x_0$ belonging to the domain of X, we want to estimate $f(x_0)$ using the information available for f(x) at the observed points $x_i$, where each point is given a different weight according to its distance from $x_0$. Loosely speaking, if $x_0$ is closer to $x_i$, then the estimate ${\hat{f}}(x_0)$ will be closer to $y_i$.

The weights assigned to each observation i are determined by a kernel function $K \, : R \rightarrow R$, which should satisfy regularity conditions such as

$$\begin{aligned} \int K(z)dz=1, \; \int zK(z)dz=0, \; \; 0<\int z^2 K(z)dz< +\infty . \end{aligned}$$

(3)

There are many options available for K. In the following we will use the popular parabolic or Epanechnikov kernel

$$\begin{aligned} K(z)= {\left\{ \begin{array}{ll} 3/4(1-z^2) \; {\text {if}} \; \; |z|\le 1 \\ 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\text {otherwise}} \end{array}\right. }. \end{aligned}$$

(4)

Hence, given the evaluation point $x_0$, a bandwidth $h>0$ and a polynomial degree $p\ge 1$, the local polynomial regression⁵ estimate of $f(x_0)$ is

$$\begin{aligned} {\hat{f}}(x_0)={\hat{\beta }}_0 + \sum _{j=1} ^p \, {\hat{\beta }}_j x_0^j, \end{aligned}$$

(5)

where the ${\hat{\beta }}_0,...,{\hat{\beta }}_p$ solve the following problem:

$$\begin{aligned} {\text {min}} \; \; Q(\beta _0,...,\beta _p)=\sum _{i=1}^n K \Bigl (\frac{x_0-x_i}{h}\Bigr ) \Bigl (y_i -\beta _0 - \sum _{j=1} ^p \, \beta _j x_i^j\Bigr )^2. \end{aligned}$$

(6)

Problem (6) is basically a weighted least squares estimation where squared residuals are weighted by the kernel function. Upon resolving it, we can in fact write

$$\begin{aligned} {\hat{f}}(x_0)=b(x_0)(B' \Sigma B)^{-1} B' \Sigma \, y, \end{aligned}$$

(7)

where $b(x_0)=(1, x_0, x_0^2,...,x_0^p)$, B is an $n \times (p+1)$ matrix whose ith row is $b(x_i)=(1, x_i, x_i^2,...,x_i^p)$, $\Sigma$ is an $n \times n$ diagonal matrix whose element (i, i) is given by $K ((x_0-x_i)/h)$, and $y=(y_1,...,y_n)'$. Hence, the local polynomial regression estimator is a linear smoother, as it can be written as

$$\begin{aligned} {\hat{f}}(x_0)= \sum _{i=1}^n \, w_i (x_0;x_1,...,x_n;h) y_i. \end{aligned}$$

(8)

A crucial aspect of this method is the choice of the bandwidth h. In fact, from Eq. (4) we can see that the higher $|x_0-x_i|/h$, the lower is the weight assigned to observation i by the kernel function. In particular, if $|x_0-x_i|/h>1$ the weight is zero. Thus, for larger values of h the local polynomial regression will be smoother, because also points that are distant from $x_0$ will be taken into account (oversmoothing). Conversely, when h is smaller the estimated function ${\hat{f}}(\cdot )$ will track more closely the observed values of Y (undersmoothing).

Local polynomial regression estimators have good statistical properties. It can be shown that ${\hat{f}}(x_0)$ is correct for $f(x_0)$ up to an error which is decreasing with the polynomial order p in Eq. (5), which means that the higher p, the smaller the bias (even though the variance increases with p). Moreover, under certain regularity conditions the bias of ${\hat{f}}(x_0)$ has an upper bound proportional to the bandwidth h, whereas its variance has un upper bound proportional to 1/h. This implies that decreasing h will reduce the bias but will increase the variance (Tsybakov (2009), ch. 1).

The technique extends easily to higher dimensions. In Sect. 4 we will consider the case of a bivariate input X in which the residuals at problem (6) depend on the powers of both elements of X and the weights are computed as $K(||x_0-x_i||/h)$, where $||x_0-x_i||$ is the Euclidean norm of the difference vector $x_0-x_i$.

3 The Calibration Method

The method we are going to expose can be applied to the calibration of the structural parameters of an ABM for any choice of the data D and metric $d(\cdot )$.

Unless the ABM is deterministic, the artificial data $D_m$ computed on the output of a single simulation of the model are not only a function of the model parameters $\theta \in \Theta$,⁶ but also of random numbers r.⁷ As a consequence, the distance between real and simulated data for a single run of the ABM can be written as

$$\begin{aligned} d(D_r, D_m(\theta ,r))\equiv d(\theta ,r). \end{aligned}$$

(9)

Hence, given the set of data, the metric and the parameter space $\Theta$, we can define the regression function of $d(\cdot )$ on $\Theta$ as

$$\begin{aligned} d(\theta )=E_r(d(\theta ,r)|\Theta =\theta ). \end{aligned}$$

(10)

Definition (10) represents the average distance between the real data and the artificial data produced by the ABM when we initialize it with the parameter vector $\theta \in \Theta$. Thus, our goal is to find the vector $\theta ^*$ that minimizes such a distance.

To achieve this goal the ABM has to be run for different parameter vectors $\theta$. The process, however, is made more complicated by randomness. To compute distance (10) (and its minimum) we could therefore use Monte Carlo replications, that is for each $\theta \in \Theta$ we could run the model k times with the same parameter vector but with different streams of random numbers, thus obtaining k instances of the distance $d(\theta ,r_k)$, and then take the Monte Carlo average ${\hat{d}}(\theta )=k^{-1}\sum _k d(\theta ,r_k)$ to average out the influence of random numbers. However, to avoid the enormous computational costs necessary to compute Monte Carlo averages for every point of $\Theta$, we will instead estimate the regression function (10) through a nonparametric regression meta-model using few parameter vectors $\theta _i$ drawn from $\Theta$.⁸

3.1 Estimating the Distance

Given the output of a single run of the ABM, we can represent the associated distance (9) by an auxiliary meta-model such as

$$\begin{aligned} d(\theta ,r)=f(\theta ) +u(r). \end{aligned}$$

(11)

Equation (11) represents the essence of the meta-modeling approach we are following (Saltelli et al. 2008, ch. 5): we basically approximate the unknown and surely complicated relationship between the model parameters and the distance with a simpler one upon which we decide to place certain reasonable restrictions. The convenience of this representation of the distance is that it allows to split it into two parts: a systematic part $f(\theta )$ that depends on the structural parameters and a unsystematic part u(r) (the error) that depends only on the stream of random numbers. The central point of our approach is that we treat the numbers r in Eq. (11) just as omitted explanatory variables influencing $d(\cdot )$ through the error term. If a parametric model is chosen for $f(\theta )$, the hypothesis of errors not depending on the parameters would be equivalent to assuming that the meta-model (11) be correctly specified. Although the meta-model can be augmented with as many non-linear functions of $\theta$ as we want and functional form misspecification can be tested (for instance by Ramsay’s RESET), the assumption of correct specification may still be likely to fail if function $d(\theta )$ is highly non-linear. Hence, in the present paper we propose a radical solution to this problem: we simply leave the function $f(\theta )$ unspecified, basically moving to a nonparametric setting. Consequently, we can always assume that the function $f(\theta )$ is correctly specified and that the error u depends only on the stream of random numbers r. Moreover, if $Cov(\theta ,u)=0$ we have

$$\begin{aligned} E_r(d|\theta )&= {} E_r(f(\theta )|\theta )+E_r(u(r)|\theta )\nonumber \\ E_r(d|\theta )&= {} f(\theta ), \end{aligned}$$

(12)

showing that the meta-model $f(\theta )$ is exactly the regression function of d on $\theta$ expressed by Eq. (10). As we are allowed to assume that the errors do not directly depend on $\theta$, the validity of $Cov(\theta ,u)=0$ will depend entirely on the sampling scheme used to draw the parameter vectors $\theta _i$ and the stream of numbers $r_i$.

Following Chen and Desiderio (2018), to estimate the meta-model we randomly generate from uniform distributions n couples $(\theta _i,r_i)$, where $\theta _i$ is a parameter vector sampled from the parameter space $\Theta$ and $r_i$ is a stream of random numbers. Practically speaking, to generate a random stream $r_i$ we have to randomly select the seed of the random number generator when we run a simulation of the ABM with a given $\theta _i$. Hence, we are basically treating the seed of the random number generator as an additional parameter that needs to be sampled along with $\theta$. Then, for each vector $\theta _i$ and stream $r_i$ we simulate the agent-based model once, thus obtaining n values $D_m(i)$ for the simulated data.

After that, for each of the n values $D_m(i)$ we calculate the corresponding distance from the real data $D_r$:

$$\begin{aligned} d(D_r,D_m(i))=d(\theta _i,r_i)\equiv d_i. \end{aligned}$$

(13)

Finally, given a bandwidth $h>0$ and a polynomial order $p\ge 1$, using the samples for $d_i$ and $\theta _i$ we can estimate by local polynomial regression the relationship

$$\begin{aligned} d_i=f(\theta _i) +u(r_i), \; \; i=1,...,n. \end{aligned}$$

(14)

Thus, for all the points $\theta _0$ belonging to the parameter space we can obtain

$$\begin{aligned} {\hat{f}}(\theta _0)=\sum _{i=1}^n w_i (\theta _0; \theta _1,...,\theta _n; h) \, d_i \end{aligned}$$

(15)

as in Eq. (8), with $d_i$, $\theta _i$ and $\theta _0$ replacing respectively $y_i$, $x_i$ and $x_0$. Because of the random sampling of both $\theta _i$ and $r_i$, we have $Cov(\theta _i,r_i)=0$, which also implies $Cov(\theta _i,u_i)=0$. But then ${\hat{f}}(\theta _0)$ coincides with the estimated distance ${\hat{d}}(\theta _0)$ (see Eqs. 10 and 12). Hence, we can choose the parameter vector corresponding to the smallest ${\hat{f}}(\theta )$ as our estimate of the “best” vector $\theta ^*$ minimizing Eq. (10).

Random sampling of $\theta _i$ and $r_i$ has also another important consequence: observations are independent and, therefore, also the error terms. But this means that the assumptions of the basic setup in Sect. 2 are satisfied,⁹ with $u(r_i)$ in place of $\epsilon _i$ in Eq. (2). As a consequence, ${\hat{f}}(\theta _0)$ will possess the nice statistical properties that, under these assumptions, characterize local polynomial regression estimators.

In summary, the procedure can be described by the following algorithm (refer to Section 6 for more operational algorithms):

Algorithm 1

• 1. Define the parameter space $\Theta$.

• 2. Randomly sample n vectors $\theta _i \in \Theta$ with equal probability.

• 3. For each $\theta _i$, run the ABM for T periods. Before each simulation the seed of the random number generator is randomly selected (random sampling of the numbers $r_i$).

• 4. From the output of each simulation i, take the data $D_m(i)$ and compute the distance $d_i$ as in Eq. (13).

• 5. Using the samples $\{\theta _i\}^n_{i=1}$ and $\{d_i\}^n_{i=1}$, estimate by local polynomial regression the in-sample fitted values ${\hat{d}}_i$ to choose the best bandwidth $h^*$ (see Sect. 3.2).

• 6. Using the samples $\{\theta _i\}^n_{i=1}$ and $\{d_i\}^n_{i=1}$ and bandwidth $h^*$, estimate by local polynomial regression Eq. (14), obtaining the sample regression function ${\hat{f}}(\theta ) \; \forall \, \theta \in \Theta$.

• 7. Choose the vector ${\hat{\theta }}^*\in \Theta$ associated with the smallest estimated distance ${\hat{f}}(\theta )$.

3.2 Choosing the Bandwidth h

As already mentioned in Sect. 2, the choice of the bandwidth h is crucial for obtaining the local polynomial regression estimator. In fact, different h will produce different ${\hat{f}}(\theta )$ and, in general, different estimated minimum-distance vectors ${\hat{\theta }}^*$. There is no hard rule for choosing the bandwidth, so in Sect. 4 we will use four different methods. Basically, after generating the sample $\{\theta _i,d_i\}^n_{i=1}$, we will estimate the in-sample fitted values ${\hat{f}}(\theta )$ for all h and, based on the in-sample residuals $\{d_i-{\hat{f}}(\theta _i)\}^n_{i=1}$, assign a score to each h. This means that a bandwidth h could get different scores according to the method considered. Finally, for each method we select the h with the highest score to estimate ${\hat{f}}(\theta )$ for all $\theta \in \Theta$.

Method 1: $C_p$ criterion.

This is one of the most common approaches to choose h: the idea is to find the estimator (in practice, a bandwidth) associated with the smallest mean integrated squared error, which is a common measure of the goodness of an estimator.

For given h, the point-wise mean squared error (MSE) of the estimator at $\theta _0$ is

$$\begin{aligned} {\text {MSE}}(\theta _0)=E\bigl [({\hat{f}}(\theta _0)-d(\theta _0))^2\bigr ] \equiv [Bias({\hat{f}}(\theta _0))]^2+VAR({\hat{f}}(\theta _0)), \end{aligned}$$

(16)

and its mean integrated squared error (MISE) is defined as

$$\begin{aligned} {\text {MISE}}=\int _{\theta \in \Theta } {\text {MSE}}(\theta ) \, d \theta . \end{aligned}$$

(17)

Parameter h influences both the bias and the variance of the estimator monotonically, but in opposite ways. The presence of such a trade-off therefore implies the existence of a certain value $h^*$ which minimizes the MISE.

In practice, in applications we have to use the discretized version of the MISE

$$\begin{aligned} \frac{1}{n} \sum _{i=1}^n ({\hat{f}}(\theta _i)-f(\theta _i))^2. \end{aligned}$$

(18)

The discretized MISE however cannot be computed because it depends on the unknown $f(\theta _i)$. Hence, based on the sample $\{(d_i,\theta _i)\}^n_{i=1}$ we use the $C_p$ criterion

$$\begin{aligned} C_p(h)=\frac{1}{n} \sum _{i=1}^n (d_i-{\hat{f}}(\theta _i))^2 +\frac{2\sigma ^2}{n} \sum _{i=1}^n w(\theta _i,h), \end{aligned}$$

(19)

where $w(\theta _i,h)$ is the weight assigned to observation i when estimating ${\hat{f}}(\theta _i)$ and $\sigma ^2$ is the error variance (to be estimated from the residuals). Since $C_p(h)$ is an unbiased estimator for the discretized MISE up to a shift $\sigma ^2$ not depending upon h, the optimal bandwidth can be chosen as the one that minimizes the $C_p$ criterion (Tsybakov (2009), ch. 1.9).

Method 2: leave-one-out cross-validation criterion.

This method is also common. Given the in-sample fitted values

$$\begin{aligned} {\hat{f}}=W d \end{aligned}$$

(20)

defined as the product between the $n\times n$ matrix W and the vector of sample values for the distance d,¹⁰ we choose the bandwidth h that minimizes the leave-one-out cross-validation criterion

$$\begin{aligned} {\text {CV}}(h)=\frac{1}{n} \sum _{i=1}^n (d_i-{\hat{f}}_{-i}(\theta _i))^2, \end{aligned}$$

(21)

where ${\hat{f}}_{-i}(\theta _i)$ is the estimate of $f(\theta _i)$ without using observation i. This statistic can be conveniently re-written simply as

$$\begin{aligned} {\text {CV}}(h)=\frac{1}{n} \sum _{i=1}^n \Bigl (\frac{d_i-{\hat{f}}(\theta _i)}{1-W_{ii}}\Bigr )^2, \end{aligned}$$

(22)

where $W_{ii}$ is the diagonal element of matrix W that determines ${\hat{f}}(\theta _i)$. Basically, the statistic ${\text {CV}}(h)$ measures the ability of the estimator to correctly predict each $E(d|\theta _i)$ without using the sample value $d_i$.

Method 3: normality of the residuals.

The third method is unconventional: we pick as optimal bandwidth the one producing residuals whose distribution is closest to a normal distribution. To measure normality we will use the the Kolmogorov-Smirnov normality test, whose null hypothesis is that the residuals are normally distributed. Hence, we will choose the h for which the p-value is larger.

Method 4: averaging over h.

The last method is also unconventional: instead of searching for some ‘optimal’ h, we use several of them. We first choose a suitable set of values H for the bandwidth and compute the sample regression function ${\hat{f}}(x;h) \; \forall \, h \in H$. Then, we choose the vector $\theta ^*$ minimizing the average

$$\begin{aligned} {\bar{f}}(\theta )=\frac{1}{n_h} \sum _{h \in H} {\hat{f}}(\theta ;h), \end{aligned}$$

(23)

where $n_h$ is the cardinality of H. The reason why we employ this method is that it avoids both oversmoothing and undersmoothing.

Before turning to the illustrative examples, we suggest a heuristic way to apply our method. As in fact in true calibration exercises the minimum-distance parameter value will remain unknown, we can apply the method using different combinations of polynomial degrees and bandwidth-selection criteria getting as many estimated parameters (in the cases below we will have eight estimates). Then, for each of the estimated parameters we can calculate the actual distance by Monte Carlo simulations and select the one estimate corresponding to the lowest Monte Carlo distance. If the method works, we can be confident that among the estimated parameters there will be the actual minimum-distance parameter or some other value close to it.

4 Illustrative Examples

As a mere illustrative example, in this section we are going to apply the proposed calibration method to the agent-based model of Chen and Desiderio (Chen and Desiderio 2018, 2020), which we refer to for details.

The model represents a closed economy populated by firms, households and one commercial bank that operate on the markets for labor, consumption and credit. In the following we will focus on three parameters. The first one is the upper bound $\alpha$ of the stochastic wage increase offered by firms, the second parameter is the consumers’ marginal propensity to consume $\beta$ and the last one is the minimum interest rate $\gamma$ set by the monetary authority.¹¹ When not varying for calibration purposes, the default values of these parameters are respectively 0.05, 0.8 and 0.01. To obtain a very low execution time for a single simulation, the ABM is always run for 300 periods with only 10 firms and 60 households.

Below we perform four calibration exercises: first we calibrate the three parameters separately, and finally we calibrate at the same time $\alpha$ and $\gamma$.¹² The metric $d(\cdot )$ will be the Euclidean distance computed between real and simulated data relative to the real GDP average growth rate (g) and the average inflation rate ($\pi$), that is:

$$\begin{aligned} d(\theta ,r)=\sqrt{(g_r-g_m(\theta ,r))^2+(\pi _r-\pi _m(\theta ,r))^2}, \end{aligned}$$

(24)

where $g_m(\theta ,r)$ and $\pi _m(\theta ,r)$ are time averages computed on a single 300-period simulation of the ABM.¹³ Hence, our calibration exercises are examples of the method of simulated moments.

4.1 Univariate Case 1: $\alpha$

Here we have $\theta =\alpha$ belonging to the parameter space $A=[0.005,0.2]$, made of 100 equally-spaced points.¹⁴

To have an idea of the potentialities of our approach, before estimating the distance using our method we first compute the (pseudo) actual distance and the associated minimum point by using 100 Monte Carlo replications for each point of A. The resulting average distances $d(\alpha )=100^{-1} \sum _k^{100} d(\alpha ,r_k)$ are reported in Fig. 1 as a function of $\alpha$, with a minimum at $\alpha ^*=0.0267$.

Fig. 1

Actual distance for parameter $\alpha \in [0.005,0.2]$ obtained with 100 Monte Carlo replications. Minimum at $\alpha ^*=0.0267$

Now we are going to use our procedure. We randomly sample $n=100$ values $\alpha _i$ from $A=[0.005,0.2]$, and for each of them we run the ABM for 300 time steps, choosing randomly the seed of the random number generator at every run. Then, from each simulation i we compute the distance $d_i$ as in Eq. (24), thus obtaining our sample $\{d_i,\alpha _i\}^{100}_{i=1}$.

Just to understand the importance of the bandwidth, in Fig. 2 we report the scatter plots for both the observed $d_i$ and its estimate ${\hat{f}}(\alpha _i)$, this one obtained with bandwidth $h=0.2$ and $h=0.05$ (in both cases using a second-order polynomial degree). Comparing the two pictures with the actual distance in Fig. 1, we can see that panel (a) is probably an example of oversmoothing as the fitted distances lie almost along a straight line, while in panel (b) the fitted values follow more closely the observed distance. It is therefore clear that the search for the minimum-distance $\alpha ^*$ is strongly influenced by the choice of the bandwidth.

Fig. 2

Observed (blue dots) and in-sample estimated (red dots) distances: a with $h=0.2$; b with $h=0.05$

Now we apply our procedure using the four methods for the choice of the bandwidth h illustrated in Sect. 3. The pre-selected set $H=[0.01,0.05]$ for the bandwidth is made of 100 equally-spaced points.¹⁵ For all the four methods we try both a first-order and a second-order polynomial degree (for p larger than 2 we could not notice much difference). Results are shown in Table 1.

We can see that the first-order local polynomial regression estimator with Methods 1 and 2 performs better, producing an estimated minimum-distance $\alpha =0.0227$ which is just $15\%$ lower than the true $\alpha ^*=0.0267$. Moreover, the absolute difference between estimated and actual minimum point (i.e. 0.004) is very small if compared with the extent of the parameter space A (i.e. $0.2-0.005=0.195$). We also point out that practically speaking there is no difference between the estimated $\alpha =0.0227$ and $\alpha ^*$ because the distance attained at the former is almost equal to the minimum distance corresponding to the latter (see Fig. 1). As for the second-order local polynomial regression estimator, its estimate ($\alpha =0.0208$) is less precise but still quite close to the actual $\alpha ^*$. Thus, as far as the case of parameter $\alpha$ is concerned, we deem our calibration method successful, as we were able to get very close to the actual minimum-distance parameter value using only 100 simulations of the ABM, against the 10000 necessary to calculate Monte Carlo averages for the whole parameter space.

Table 1 Estimated minimum-distance $\alpha$. Actual $\alpha ^*=0.0267$

4.2 Univariate Case 2: $\beta$

Here we have 100 values for $\theta =\beta$ belonging to the parameter space $B=[0.1,0.9]$. In Fig. 3 we report the actual distance obtained with 100 Monte Carlo replications for all $\beta \in [0.1,0.9]$, showing a minimum at the corner value $\beta ^*=0.1$.

Fig. 3

Actual distance for parameter $\beta \in [0.1,0.9]$ obtained with 100 Monte Carlo replications. Minimum at $\beta ^*=0.1$

We now repeat our calibration procedure: we randomly sample $n=100$ values $\beta _i$ from $B=[0.1,0.9]$, for each of them we run the ABM for 300 time steps and compute the distance $d_i$, thus obtaining the sample $\{d_i,\beta _i\}^{100}_{i=1}$. Table 2 shows the results, after choosing $H=[0.05,0.2]$.

Again the local linear regression estimator performs much better than its quadratic counterpart, and correctly estimates the minimum-distance $\beta ^*$ in three cases out of four. Conversely, the second-degree estimator gets close to $\beta ^*$ in two cases but also very far in other two cases. Such inconsistent results are mainly due to the high sensitivity of the second-degree estimator to an outlier $\{d_i\}$ that unfortunately is present in our sample (whereas the linear estimator is by construction less sensitive to “noisy” data). Nonetheless, increasing the sample size to $n=200$ observations (which is still a small number of simulations) we were able to correctly estimate $\beta ^*=0.1$ also by the second-degree estimator, and this despite the actual distance function being very corrugated and studded with local minima.

Table 2 Estimated minimum-distance $\beta$. Actual $\beta ^*=0.1$

4.3 Univariate Case 3: $\gamma$

Here we have 100 values for $\theta =\gamma$ belonging to the parameter space $\Gamma =[0.001,0.05]$. In Fig. 4 we report the actual distance obtained with 100 Monte Carlo replications for all $\gamma \in [0.001,0.05]$, showing a minimum at $\gamma ^*=0.0460$.

Fig. 4

Actual distance for parameter $\gamma \in [0.001,0.05]$ obtained with 100 Monte Carlo replications. Minimum at $\gamma ^*=0.0460$

Again, with the same procedure we generate a sample $\{d_i,\gamma _i\}^{100}_{i=1}$ of 100 observations and estimate the minimum-distance $\gamma ^*$, choosing $H=[0.005,0.01]$. Table 3 shows the results: in no case we were able to find exactly the actual minimum-distance parameter value, but all the estimates are pretty close to it, specially with $p=2$ and using method 1 and method 4. In fact, the best estimate $\gamma =0.0475$ is only $3\%$ higher than $\gamma ^*$, and their difference is very small when compared with the length of the parameter space $\Gamma$. Moreover, the actual distance in $\gamma =0.0475$ is very similar to the minimum distance attained at $\gamma ^*$, which makes the two values practically equivalent.

Table 3 Estimated minimum-distance $\gamma$. Actual $\gamma ^*=0.0460$

In conclusion, the results from the univariate examples show the reliability of the proposed calibration method as in all of the three cases we were able to find either the minimum-distance parameter value (in case 2) or a very close value (cases 1 and 3).

4.4 The Bivariate Case

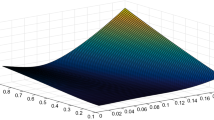
In this section we are going to show how our calibration procedure extends to a multivariate setting (see end of Sect. 2). To this scope we will simultaneously calibrate parameters $\alpha$ and $\gamma$ belonging to the parameter space $\Theta$ given by Table 4. The pseudo-actual distance surface obtained with 100 Monte Carlo replications is shown in Fig. 5, whose minimum of about 0.0019 is attained at $(\alpha ^*,\gamma ^*)=(0.0227,0.0045)$.

As the parameter space is now much larger than in the univariate cases ($10^4$ points against 100 points), to have a better coverage of it we will generate a random sample of $n=200$ observations. Thus, we apply our multivariate procedure to the random sample $\{d_i,\alpha _i,\gamma _i\}_{i=1}^{200}$ with a pre-selected set of values for the bandwidth $H=[0.03,0.1]$. Fig. 6 shows two examples of estimated distance surfaces: again, the choice of the polynomial degree and of the bandwidth turns out to be crucial for the search of the minimum-distance parameter values.

The estimates are reported in Table 5: we can see that the results obtained do not appear to be much consistent with each other, even though all the estimates indicate a small value for $\alpha$. The point $(\alpha ,\gamma )=(0.0208,0.001)$ obtained by Method 2 and $p=2$ is associated with the smallest actual distance among the eight candidates. We therefore take this point as our estimate of the optimal parameter value. Although we did not find the actual minimum-distance parameter vector, our solution is pretty close to it (in fact, the actual value 0.0227 is just the next value of 0.0208 inside the domain of $\alpha$). In addition, the distance associated with our estimate is about 0.0021, which is only slightly higher than the actual minimum distance (about 0.0019). Indeed, both points belong to a small basin of the parameter space where the actual distance is about the same for all the parameter values $(\alpha ,\gamma )$.

In conclusion, we consider our calibration procedure as successful for two reasons. First, it was able to identify a solution belonging to an area of the parameter space where the actual distance is smaller. Second, it is very efficient in terms of computational time, as it allowed to find a satisfactory solution using relatively few runs of the ABM (200 against $10^6$ necessary to compute the Monte Carlo distances). Specially in case of large-scale ABMs, this characteristic in particular may give our procedure a substantial advantage over other more time-consuming calibration methods.

Table 4 Parameter space $\Theta$

Fig. 5

Actual distance for parameters $\alpha \in [0.005, 0.2]$ and $\gamma \in [0.001,0.05]$ obtained with 100 Monte Carlo replications. Minimum at $(\alpha ^*,\gamma ^*)=(0.0227,0.0045)$

Fig. 6

Estimated distance surface for $p=2$: a with $h=0.03$; b with $h=0.1$

Table 5 Estimated minimum-distance $(\alpha ,\gamma )$

5 Conclusive Remarks

In the last few decades the application of agent-based models has become more and more popular among economists. Unlike mainstream models, however, taking ABMs to the data is still very challenging for researchers. Such an uncomfortable situation is basically due to two reasons: (1) there is still a lack of a sound validation procedure and (2) the model parameters cannot be estimated by common statistical techniques. The second issue has recently lead to the development of several indirect calibration methods based on the simulated minimum distance approach, which consists in finding those parameter values that minimize the distance between real and simulated data. However, the typical complexity characterizing ABMs makes such methods computationally demanding.

In this paper we have proposed a new indirect calibration method based on simulated minimum distance that extends the parametric technique introduced by Chen and Desiderio (2021). In essence, instead of calculating the distance over the whole parameter space we estimate a nonparametric regression meta-model introduced to approximate the relationship between model parameters and distance metric. The meta-model is estimated by local polynomial regression techniques on a small sample of parameter vectors drawn from the parameter space of the ABM. Finally, once the distance has been estimated for the whole parameter space we can pick the parameter vector minimizing it. Results are promising and pave the way for future developments of this approach.

The strategy adopted to sample the parameter vectors is the one first introduced in (Chen and Desiderio 2018, 2020) for sensitivity analysis purposes and subsequently also employed for parameter calibration (Chen and Desiderio 2021). Its innovative feature consists in sampling at the same time both the parameters and the seed of the random numbers generator in a random fashion, which allows to average out the effect of randomness without resorting to Monte Carlo simulations.

The great advantage of our method over other calibration procedures based on search algorithms is first and foremost its speed, because it requires the simulation of the ABM only for the parameter vectors used to estimate the meta-model. This feature makes the method particularly suitable for computationally demanding large-scale ABMs. In addition, the use of nonparametric estimation techniques makes it more flexible and accurate than the parametric counterparts such as kriging method (Salle and Yildizoglu 2014), and only slightly more complicated. Of course, more advanced nonparametric techniques such as wavelets may be used, but we believe local polynomial estimation to be a good compromise between precision and ease of application. Finally, it is well-known that nonparametric methods are not optimal when the number of dimensions is high. Hence, to tackle this problem refinements of our method could contemplate the use of structured regression models such as additive models that are built starting from the univariate estimators, or the use of simpler tools such as nearest-neighbors estimators. This would reduce precision but increase the speed.

Appendix

In this section we propose the general implementation of our method in pseudo-code, divided into four algorithms (Tables 6, 7, 8 and 9). The pseudo-code is intended to be completed using all the relevant formulas and equations presented in the paper.

Table 6 Algorithm A to generate samples $\{\theta _i\}^n_{i=1}$ and $\{d_i\}^n_{i=1}$

Table 7 Algorithm B to choose the optimal bandwidth $h^*$

Table 8 Algorithm C to estimate the minimum-distance $\theta ^*$

Table 9 Algorithm D to compute local polynomial estimates