Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Generalized linear mixed models (GLMMs) have been broadly used to analyze correlated data, such as clustered/familial data, longitudinal data, and multivariate data. GLMMs provide flexible tools to accommodate normally or non-normally distributed data through various link functions between the response mean and a set of predictors. For longitudinal studies, in which repeated measurements of a response variable are collected on the same subject over time, GLMMs can be used as a convenient analytic tool to account for subject-specific variations [e.g., 5].

Standard statistical analysis with GLMMs is typically developed under the assumption that all variables are precisely observed. However, this assumption is commonly violated in applications. There has been much interest in statistical inference pertaining to error-in-covariates, and a large body of methods have been developed [e.g., 3, 17, 18]. Measurement error in response, however, has received much less attention, and this is partially attributed to a misbelief that ignoring response error would still lead to valid inferences. Unfortunately, this is only true in some special cases, e.g., the response variable follows a linear regression model and is subject to additive measurement error. With nonlinear response models or nonlinear error models, inference results can be seriously biased if response error is ignored. Buonaccorsi [1] conducted numerical studies to illustrate induced biases under linear models with nonlinear response measurement error. With binary responses subject to error, several authors, such as Neuhaus [10] and Chen et al. [4], demonstrated that naive analysis ignoring measurement error may lead to incorrect inference results.

Although there is some research on this topic, systematic studies on general clustered/longitudinal data with response error do not seem available. It is the goal of this paper to investigate the asymptotic bias induced by the error in response and to develop valid inference procedures to account for such biases. We formulate the problem under flexible frameworks where GLMMs are used to feature various response processes and nonlinear models are adopted to characterize response measurement error.

Our research is partly motivated by the Framingham Heart Study, a large scale longitudinal study concerning the development of cardiovascular disease. It is well known that certain variables, such as blood pressure, are difficult to measure accurately due to the biological variability and that their values are greatly affected by the change of environment. There has been a large body of work on the analysis of data from the Framingham Heart Study, accounting for measurement error in covariates. For example, Carroll et al. [2] considered binary regression models to relate the probability of developing heart disease to risk factors including error-contaminated systolic blood pressure. Within the framework of longitudinal analysis, the impact of covariate measurement error and missing data on model parameters has been examined. Yi [16] and Yi et al. [19] proposed estimation and inference methods that account for measurement error and missing response observations. Other work can be found in [7, 20], among others. Relative to the extensive analysis of data with covariate error, there is not much work on accounting for measurement error in continuous responses using the data from the Framingham Heart Study.

The remainder of the paper is organized as follows. In Sect. 2, we formulate the response and the measurement error processes. In Sect. 3, we investigate the estimation bias in two analyses: the naive analysis that completely ignores response measurement error, and a partial-adjustment method that fits model to transformed surrogate responses. In Sect. 4, we develop likelihood-based methods to cover two useful situations: measurement error parameters are known, or measurement error parameters are unknown. In Sect. 5, we evaluate the performances of various approaches through simulation studies. In Sect. 6, we illustrate the proposed method using a real data set from the Framingham Heart Study. Discussion and concluding remarks are given in Sect. 7.

2 Model Formulation

2.1 Response Model

Suppose data from a total of n independent clusters are collected. Let Y ij denote the response for the jth subject in cluster i, i = 1, …, n, j = 1, …, m i . Let X ij and Z ij be vectors of covariates for subject j and cluster i, respectively, and write \(\mathbf{X}_{i} = (\mathbf{X}_{i1}^{\mathrm{T}},\ldots,\mathbf{X}_{im_{i}}^{\mathrm{T}})^{\mathrm{T}}\) and \(\mathbf{Z}_{i} = (\mathbf{Z}_{i1}^{\mathrm{T}},\ldots,\mathbf{Z}_{im_{i}}^{\mathrm{T}})^{\mathrm{T}}\). Here we use upper case letters and the corresponding lower case letters to denote random variables and their realizations, respectively.

Conditional on random effects b i and covariates {X i , Z i }, the Y ij ( j = 1, …, m i ) are assumed to be conditionally independent and follow a distribution from the exponential family with the probability density or mass function

$$\displaystyle\begin{array}{rcl} f_{y\vert x,z,b}(y_{ij}\vert \mathbf{x}_{ij},\mathbf{z}_{ij},\mathbf{b}_{i}) =\exp [\{y_{ij}\alpha _{ij} - a_{1}(\alpha _{ij})\}/a_{2}(\phi ) + a_{3}(y_{ij},\phi )],& &{}\end{array}$$
(1)

where functions a 1(⋅ ), a 2(⋅ ), and a 3(⋅ ) are user-specified, ϕ is a dispersion parameter, and α ij is the canonical parameter which links the conditional mean, μ ij b = E(Y ij  | X i , Z i , b i ), via the identity μ ij b = ∂ a 1(α ij )∕∂ α ij .

A generalized linear mixed model (GLMM) relates μ ij b to the covariates and random effects via a regression model

$$\displaystyle\begin{array}{rcl} g(\mu _{ij}^{b}) = \mathbf{X}_{ ij}^{\mathrm{T}}\boldsymbol{\beta } + \mathbf{Z}_{ ij}^{\mathrm{T}}\mathbf{b}_{ i},& &{}\end{array}$$
(2)

where \(\boldsymbol{\beta }\) is a vector of regression coefficients for the fixed effects, and g(⋅ ) is a link function. Random effects b i are assumed to have a distribution, say, \(f_{b}(\mathbf{b}_{i};\boldsymbol{\sigma }_{\mathbf{b}})\), with an unknown parameter vector \(\boldsymbol{\sigma }_{\mathbf{b}}\). The link function g(⋅ ) is monotone and differentiable, and its form can be differently specified for individual applications. For instance, for binary Y ij , g(⋅ ) can be chosen as a logit, probit, or complementary log-log link, while for Poisson or Gamma variables Y ij , g(⋅ ) is often set as a log link.

A useful class of models belonging to GLMMs is linear mixed models (LMM) where g(⋅ ) in (2) is set to be the identity function, leading to

$$\displaystyle\begin{array}{rcl} Y _{ij} = \mathbf{X}_{ij}^{\mathrm{T}}\boldsymbol{\beta } + \mathbf{Z}_{ ij}^{\mathrm{T}}\mathbf{b}_{ i} +\epsilon _{ij}& &{}\end{array}$$
(3)

where the error term ε ij is often assumed to be normally distributed with mean 0 and unknown variance ϕ.

Let \(\boldsymbol{\theta }= (\boldsymbol{\beta }^{\mathrm{T}},\boldsymbol{\sigma }_{b}^{\mathrm{T}},\phi )^{\mathrm{T}}\) be the vector of model parameters. In the absence of response error, estimation of \(\boldsymbol{\theta }\) is based on the likelihood for the observed data:

$$\displaystyle{\mathcal{L}(\boldsymbol{\theta }) =\prod _{ i=1}^{n}\mathcal{L}_{ i}(\boldsymbol{\theta }),}$$

where

$$\displaystyle\begin{array}{rcl} \mathcal{L}_{i}(\boldsymbol{\theta }) =\int \prod _{ j=1}^{m_{i} }f_{y\vert x,z,b}(y_{ij}\vert \mathbf{x}_{ij},\mathbf{z}_{ij},\mathbf{b}_{i};\boldsymbol{\theta })f_{b}(\mathbf{b}_{i};\boldsymbol{\sigma }_{\mathbf{b}})d\mathbf{b}_{i}& &{}\end{array}$$
(4)

is the marginal likelihood for cluster i, and \(f_{y\vert x,z,b}(y_{ij}\vert \mathbf{x}_{ij},\mathbf{z}_{ij},\mathbf{b}_{i};\boldsymbol{\theta })\) is determined by (1) in combination with (2). Maximizing \(\mathcal{L}(\boldsymbol{\theta })\) with respect to \(\boldsymbol{\theta }\) gives the maximum likelihood estimator of \(\boldsymbol{\theta }\).

2.2 Measurement Error Models

When Y ij is subject to measurement error, we observe a value that may differ from the true value; let S ij denote such an observed measurement for Y ij , and we call it a surrogate variable. In this paper we consider the case where Y ij is a continuous variable only. Let f s | y, x, z (S ij  | y i , x i , z i ) or f s | y, x, z (S ij  | y ij , x ij , z ij ) denote the conditional probability density (or mass) function for S ij given {Y i , X i , Z i } or {Y ij , X ij , Z ij }, respectively. It is often assumed that

$$\displaystyle{f_{s\vert y,x,z}(s_{ij}\vert \mathbf{y}_{i},\mathbf{x}_{i},\mathbf{z}_{i}) = f_{s\vert y,x,z}(s_{ij}\vert y_{ij},\mathbf{x}_{ij},\mathbf{z}_{ij}).}$$

This assumption says that given the true variables {Y ij , X ij , Z ij } for each subject j in a cluster i, the observed measurement S ij is independent of variables {Y ik , X ik , Z ik } of other subjects in the same cluster for k ≠ j.

Parametric modeling can be invoked to feature the relationship between the true response variable Y ij and its surrogate measurement S ij . One class of useful models are specified as

$$\displaystyle\begin{array}{rcl} S_{ij} = h(Y _{ij},\mathbf{X}_{ij},\mathbf{Z}_{ij};\boldsymbol{\gamma }_{i}) + e_{ij},& &{}\end{array}$$
(5)

where the stochastic noise term e ij has mean zero. Another class of models are given by

$$\displaystyle\begin{array}{rcl} S_{ij} = h(Y _{ij},\mathbf{X}_{ij},\mathbf{Z}_{ij};\boldsymbol{\gamma }_{i}) \cdot e_{ij},& &{}\end{array}$$
(6)

where the stochastic term e ij has mean 1. These models basically modulate the mean structure of the surrogate variable S ij :

$$\displaystyle\begin{array}{rcl} E(S_{ij}\vert \mathbf{Y}_{i},\mathbf{X}_{i},\mathbf{Z}_{i}) = h(Y _{ij},\mathbf{X}_{ij},\mathbf{Z}_{ij};\boldsymbol{\gamma }_{i}),& &{}\end{array}$$
(7)

where the function form h(⋅ ) can be chosen differently to facilitate various applications, and \(\boldsymbol{\gamma }_{i}\) is a vector of error parameters for cluster i. For cases where the measurement error process is homogeneous, e.g., same measuring system is used across clusters, we replace \(\boldsymbol{\gamma }_{i}\) with a common parameter vector \(\boldsymbol{\gamma }\).

Specification of h(⋅ ) reflects the feature of the measurement error model. For example, if h(⋅ ) is set as a linear function, model (5) gives a linear relationship between the response and surrogate measurements:

$$\displaystyle{S_{ij} =\gamma _{0} +\gamma _{1}Y _{ij} +\gamma _{ 2}^{\mathrm{T}}\mathbf{X}_{ ij} +\gamma _{ 3}^{\mathrm{T}}\mathbf{Z}_{ ij} + e_{ij},}$$

where parameters γ 0, γ 1, γ 2, and γ 3 control the dependence of surrogate measurement S ij on the response and covariate variables; in the instance where both γ 2 and γ 3 are zero vectors, surrogate measurement S ij is not affected by the measurements of the covariates and depends on the true response variable Y ij only. More complex relationships can be delineated by employing nonlinear function forms for h(⋅ ). In our following simulation studies and data analysis, linear, exponential, and logarithmic functions are considered for h(⋅ ).

We call (5) additive error models, and (6) multiplicative error models to indicate how noise terms e ij act relative to the mean structure of S ij . Commonly, noise terms e ij are assumed to be independent of each other, of the true responses as well as of the covariates. Let \(f(e_{ij};\boldsymbol{\sigma }_{e})\) denote the probability density function of e ij , where \(\boldsymbol{\sigma }_{e}\) is an associated parameter vector. With model (5), the e ij are often assumed to be normally distributed, while for model (6), a log normal or a Gamma distribution may be considered.

3 Asymptotic Bias Analysis

In this section we investigate asymptotic biases caused by response error under the two situations: (1) response error is totally ignored in estimation procedures, and (2) an intuitively compelling correction method is applied to adjust for measurement error in response.

3.1 Naive Analysis of Ignoring Measurement Error

We consider a naive analysis which fits the GLMM (1) to the observed raw data (hereafter referred to as NAI1), i.e., we assume that the S ij are linked with covariates via the same random effects model. Let \(\boldsymbol{\theta }^{{\ast}} = (\boldsymbol{\beta }^{{\ast}\mathrm{T}},\boldsymbol{\sigma }_{b}^{{\ast}\mathrm{T}},\phi ^{{\ast}})^{\mathrm{T}}\) denote the corresponding parameter vector, and the corresponding working likelihood contributed from cluster i is given by

$$\displaystyle{\mathcal{L}_{i}^{w}(\boldsymbol{\theta }^{{\ast}}) =\int \prod _{ j=1}^{m}f_{ y\vert x,z,b}(s_{ij}\vert \mathbf{x}_{ij},\mathbf{z}_{ij},\mathbf{b}_{i}^{{\ast}};\boldsymbol{\theta }^{{\ast}})f_{ b}(\mathbf{b}_{i}^{{\ast}};\boldsymbol{\sigma }_{ b}^{{\ast}})d\mathbf{b}_{ i}^{{\ast}}.}$$

Maximizing \(\sum _{i=1}^{n}\log \mathcal{L}_{i}^{w}(\boldsymbol{\theta }^{{\ast}})\) with respect to \(\boldsymbol{\theta }^{{\ast}}\) gives an estimator, say \(\hat{\boldsymbol{\theta }}^{{\ast}}\), of \(\boldsymbol{\theta }^{{\ast}}\).

Adapting the arguments of White [14] it can be shown that under certain regularity conditions, as n → ∞, \(\hat{\boldsymbol{\theta }}^{{\ast}}\) converges in probability to a limit that is the solution to a set of estimating equations

$$\displaystyle\begin{array}{rcl} \mathrm{E}_{\mathrm{true}}\left \{\sum _{i=1}^{n}\partial \log \mathcal{L}_{ i}^{w}(\boldsymbol{\theta }^{{\ast}})/\partial \boldsymbol{\theta }^{{\ast}}\right \} = \mathbf{0},& &{}\end{array}$$
(8)

where the expectation is taken with respect to the true joint distribution of the associated random variables. The evaluation of (8) involves integration over the nonlinear error functions which are often intractable.

To gain insights into the impact of ignoring error in response, we consider a LMM

$$\displaystyle\begin{array}{rcl} Y _{ij}& =& \beta _{0} + (\beta _{1} + b_{i})X_{ij} +\epsilon _{ij},{}\end{array}$$
(9)

where β 0 and β 1 are regression parameters, the ε ij are independent of each other and of other variables, ε ij  ∼ N(0, ϕ) with variance ϕ, and b i  ∼ Normal(0, σ b 2) with variance σ b 2. We consider the additive error model (5), where the e ij are independent of each other and of other variables, e ij  ∼ N(0, σ e 2), and the mean error structures are, respectively, specified as one of the following two cases.

Case 1

Linear measurement error.

Commonly seen in epidemiologic studies, this structure specifies a linear form for the measurement error

$$\displaystyle{h(Y _{ij},\mathbf{X}_{ij},\mathbf{Z}_{ij};\boldsymbol{\gamma }) =\gamma _{0} +\gamma _{1}Y _{ij},}$$

where \(\boldsymbol{\gamma }= (\gamma _{0},\gamma _{1})\), γ 0 represents a systematic error of the measuring device at Y ij  = 0, and γ 1 is a scale factor. It can be easily shown that simple relationship between the true and working parameters is

$$\displaystyle{\beta _{0}^{{\ast}} =\gamma _{ 0} +\gamma _{1}\beta _{0},\ \beta _{1}^{{\ast}} =\gamma _{ 1}\beta _{1},\ \sigma _{b}^{{\ast}2} =\gamma _{ 1}^{2}\sigma _{ b}^{2},}$$

and

$$\displaystyle{\phi ^{{\ast}} =\gamma _{ 1}^{2}\phi +\sigma _{ e}^{2}.}$$

These results suggest that estimation of fix effect β 1 and variance component σ b 2 is generally attenuated or inflated by factor γ 1, a factor which governs the difference between the true response Y ij and surrogate measurement S ij . When γ 1 equals 1, even if there is systematic measurement error involved with measuring Y ij (i.e., γ 0 ≠ 0), disregarding error in Y ij does not bias point estimates of fix effect β 1 and variance component σ b 2, but may reduce estimation precision.

Case 2

Exponential measurement error.

The second error structure specifies an exponential form for the measurement error

$$\displaystyle{h(Y _{ij},\mathbf{X}_{ij},\mathbf{Z}_{ij};\gamma ) =\exp (\gamma Y _{ij}),}$$

which may be useful to feature transformed response variables that are not measured precisely.

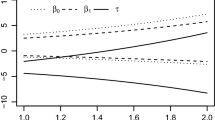
The bias in the naive estimator for fixed effect β 1 does not have an analytic form when the response is subject to nonlinear measurement error. To illustrate the induced bias in estimation of β 1 with response error ignored, we undertake a numerical study. The covariates X ij are independently generated from a normal distribution N(0, 1). We fix the values of β 0 and ϕ at − 1 and 0. 01, respectively, and consider values of σ b 2 to be 0. 01, 0. 25, and 1, respectively. The error parameters are, respectively, specified as γ = 0. 5 and 1, and σ e 2 = 0. 01, 0. 25, and 0. 75.

As shown in Fig. 1, the relationship between the naive limit β 1 ∗ and the value of β 1 is nonlinear. For instance, when γ = 0. 5, the naive estimate is attenuated for small values of β 1 but is inflated for large values of β 1. In general, the direction and magnitude of the bias induced by nonlinear response error depend on the function form of h(⋅ ) as well as the magnitude of the parameters in the measurement error process.

Fig. 1
figure 1

Bias in β 1 ∗ from the completely naive approach induced by an exponential error model. The dashed, two-dash, and dotted lines correspond to σ b 2 = 0. 01, 0. 25, and 1, respectively

Full size image

3.2 Analysis of Transformed Data

With the response process modeled by an LMM, Buonaccorsi [1] considered an intuitively tempting method to correct for response error in estimation. The idea is to employ a two-step approach to correct for response error effects. In the first step, keeping the covariates fixed, we use the mean function h(⋅ ) of the measurement error model and find its inverse function h −1(⋅ ), and then calculate a pseudo-response

$$\displaystyle{\tilde{Y }_{ij} = h^{-1}(S_{ ij};\boldsymbol{\gamma }).}$$

In the second step, we perform standard statistical analysis with \(\tilde{Y }_{ij}\) taken as a response variable. This approach (hereafter referred to as NAI2) is generally preferred over NAI1, as it reduces a certain amount of bias induced by response measurement error. However, this method does not completely remove the biases induced from response error.

To evaluate the performance of using pseudo-response in estimation procedures, we may follow the same spirit of Sect. 3.1 to conduct bias analysis. As it is difficult to obtain analytic results for general models, here we perform empirical studies by employing the same response model (9) and the measurement error model for Case 2 as in Sect. 3.1.

Fig. 2
figure 2

Bias in \(\tilde{\beta }_{1}\) from NAI2 analyses with response subject to exponential error. The dashed, two-dash, and dotted lines are for σ b 2 = 0. 01, 0. 25, and 1, respectively

Full size image

It is seen that as expected, the asymptotic bias, displayed in Fig. 2, is smaller than that from the NAI1 analysis. This confirms that the NAI2 method outperforms the NAI1 method. However, the NAI2 method does not completely remove the bias induced in the response error. The asymptotic bias involved in the NAI2 method is affected by the size of the covariate effect as well as the degree of response error. The asymptotic bias increases as the size of β 1 increases. Furthermore, the values of the error parameters γ and σ e 2 have significant impact on the bias; the size of the bias tends to increase as σ e 2 increases.

4 Inference Methods

The analytic and numerical results in Sect. 3 demonstrate that disregarding response error may yield biased estimation results. To account for the response error effects, in this section we develop valid inference methods for the response model parameter vector \(\boldsymbol{\theta }\). Our development accommodates different scenarios pertaining to the knowledge of response measurement error. Let \(\boldsymbol{\eta }\) denote the parameter vector associated with a parametric model of the response measurement error process. Estimation of \(\boldsymbol{\theta }\) may suffer from nonidentifiability issues in the presence of measurement error in the variables. To circumvent this potential problem, we consider three useful situations: (i) \(\boldsymbol{\eta }\) is known, (ii) \(\boldsymbol{\eta }\) is unknown but a validation subsample is available, and (iii) \(\boldsymbol{\eta }\) is unknown but replicates for the surrogates are available.

The first situation highlights the idea of addressing the difference between the surrogate measurements and the response variables without worrying about model nonidentifiability issues. The second and third scenarios reflect useful practical settings where error model parameter \(\boldsymbol{\eta }\) is often unknown, but estimable from additional data sources such as a validation subsample or replicated surrogate measurements. For each of these three situations, we propose strategies for estimating the response model parameters and derive the asymptotic properties of the resulting estimators.

4.1 \(\boldsymbol{\eta }\) Is Known

In some applications, the value of \(\boldsymbol{\eta }\) is known to be \(\boldsymbol{\eta }_{0}\), say, from a priori study, or specified by the analyst for sensitivity analyses. Inference about \(\boldsymbol{\theta }\) is then carried out based on the marginal likelihood of the observed data:

$$\displaystyle{\mathcal{L}(\boldsymbol{\theta },\boldsymbol{\eta }_{0}) =\prod _{ i=1}^{n}\mathcal{L}_{ i}(\boldsymbol{\theta },\boldsymbol{\eta }_{0})}$$

where

$$\displaystyle\begin{array}{rcl} \mathcal{L}_{i}(\boldsymbol{\theta },\boldsymbol{\eta })& =& \int \Bigg\{\prod _{j=1}^{m_{i} }\int f_{s\vert y,x,z}(s_{ij}\vert y_{ij},\mathbf{x}_{ij},\mathbf{z}_{ij};\boldsymbol{\eta }) {}\\ & & \times \;f_{y\vert x,z,b}(y_{ij}\vert \mathbf{x}_{ij},\mathbf{z}_{ij},\mathbf{b}_{i};\boldsymbol{\theta })dy_{ij}\Bigg\}f_{b}(\mathbf{b}_{i};\boldsymbol{\sigma }_{b})d\mathbf{b}_{i}, {}\\ \end{array}$$

which requires the conditional independence assumption

$$\displaystyle{ f_{s\vert y,x,z,b}(s_{ij}\vert y_{ij},\mathbf{x}_{ij},\mathbf{z}_{ij},\mathbf{b}_{i};\boldsymbol{\eta }) = f_{s\vert y,x,z}(s_{ij}\vert y_{ij},\mathbf{x}_{ij},\mathbf{z}_{ij};\boldsymbol{\eta }); }$$
(10)

\(f_{s\vert y,x,z,b}(s_{ij}\vert y_{ij},\mathbf{x}_{ij},\mathbf{z}_{ij},\mathbf{b}_{i};\boldsymbol{\eta })\) and \(f_{s\vert y,x,z}(s_{ij}\vert y_{ij},\mathbf{x}_{ij},\mathbf{z}_{ij};\boldsymbol{\eta })\) represent the conditional probability density function of S ij given {Y ij , X ij , Z ij , b i } and {Y ij , X ij , Z ij }, respectively.

Maximizing \(\sum _{i=1}^{n}\log \mathcal{L}_{i}(\boldsymbol{\theta },\boldsymbol{\eta }_{0})\) with respect to the parameter \(\boldsymbol{\theta }\) gives the maximum likelihood estimator \(\hat{\boldsymbol{\theta }}\) of \(\boldsymbol{\theta }\). Let \(\mathbf{U}_{i}(\boldsymbol{\theta },\boldsymbol{\eta }_{0}) = \partial \log \mathcal{L}_{i}(\boldsymbol{\theta },\boldsymbol{\eta }_{0})/\partial \boldsymbol{\theta }\). From standard likelihood theory, under regularity conditions, \(\hat{\boldsymbol{\theta }}\) is a consistent estimator for \(\boldsymbol{\theta }\). As n → ∞, \(n^{1/2}(\hat{\boldsymbol{\theta }}-\boldsymbol{\theta })\) is asymptotically normally distributed with mean 0 and variance \(\boldsymbol{\mathcal{I}}^{-1}\), where \(\boldsymbol{\mathcal{I}} = E\{ - \partial \mathbf{U}_{i}(\boldsymbol{\theta },\boldsymbol{\eta }_{0})/\partial \boldsymbol{\theta }^{\mathrm{T}}\}\). By the Bartlett identity and the Law of Large Numbers, \(\boldsymbol{\mathcal{I}}\) can be consistently estimated by \(n^{-1}\sum _{i=1}^{n}\mathbf{U}_{i}(\hat{\boldsymbol{\theta }},\boldsymbol{\eta }_{0})\mathbf{U}_{i}^{\mathrm{T}}(\hat{\boldsymbol{\theta }},\boldsymbol{\eta }_{0})\).

4.2 \(\boldsymbol{\eta }\) Is Estimated from Validation Data

In many applications, \(\boldsymbol{\eta }\) is often unknown and must be estimated from additional data sources, such as a validation subsample or replicates of measurements of Y ij . Here we consider the case that a validation subsample is available, and in the next section we discuss the situation with replicated measurements.

Assume that the validation subsample is randomly selected, and let δ ij  = 1 if Y ij is available and δ ij  = 0 otherwise. Specifically, if δ ij  = 1, then measurements {y ij , s ij , x ij , z ij } are available; when δ ij  = 0, measurements {s ij , x ij , z ij } are available. Let \(N_{v} =\sum _{ i=1}^{n}\sum _{j=1}^{m_{i}}\delta _{ij}\) be the number of the measurements in the validation subsample. The full marginal likelihood of the main data and the validation data contributed from cluster i is given by

$$\displaystyle\begin{array}{rcl} \mathcal{L}_{Fi}(\boldsymbol{\theta },\boldsymbol{\eta })& =& \int \Bigg[\prod _{j=1}^{m_{i} }\left \{f_{s\vert x,z,b}(s_{ij}\vert \mathbf{x}_{ij},\mathbf{z}_{ij},\mathbf{b}_{i};\boldsymbol{\theta },\boldsymbol{\eta })\right \}^{1-\delta _{ij} } \\ & & \times \;\left \{f_{s,y\vert x,z,b}(s_{ij},y_{ij}\vert \mathbf{x}_{ij},\mathbf{z}_{ij},\mathbf{b}_{i};\boldsymbol{\theta },\boldsymbol{\eta })\right \}^{\delta _{ij}}\Bigg]f_{b}(\mathbf{b}_{i};\boldsymbol{\sigma }_{b})d\mathbf{b}_{i},{}\end{array}$$
(11)

where \(f_{s,y\vert x,z,b}(s_{ij},y_{ij}\vert \mathbf{x}_{ij},\mathbf{z}_{ij},\mathbf{b}_{i};\boldsymbol{\theta },\boldsymbol{\eta })\) represents the conditional probability density functions of {S ij , Y ij }, given the covariates {x ij , z ij } and random effects b i .

Under the conditional independence assumption (10), we obtain

$$\displaystyle\begin{array}{rcl} f_{s\vert x,z,b}(s_{ij}\vert \mathbf{x}_{ij},\mathbf{z}_{ij},\mathbf{b}_{i};\boldsymbol{\theta },\boldsymbol{\eta }) =\int f_{s\vert y,x,z}(s_{ij}\vert y_{ij},\mathbf{x}_{ij},\mathbf{z}_{ij};\boldsymbol{\eta })f_{y\vert x,z,b}(y_{ij}\vert \mathbf{x}_{ij},\mathbf{z}_{ij},\mathbf{b}_{i};\boldsymbol{\theta })dy_{ij},& & {}\\ \end{array}$$

and

$$\displaystyle\begin{array}{rcl} f_{s,y\vert x,z,b}(s_{ij},y_{ij}\vert \mathbf{x}_{ij},\mathbf{z}_{ij},\mathbf{b}_{i};\boldsymbol{\theta },\boldsymbol{\eta }) = f_{s\vert y,x,z}(s_{ij}\vert y_{ij},\mathbf{x}_{ij},\mathbf{z}_{ij};\boldsymbol{\eta })f_{y\vert x,z,b}(y_{ij}\vert \mathbf{x}_{ij},\mathbf{z}_{ij},\mathbf{b}_{i};\boldsymbol{\theta }),& & {}\\ \end{array}$$

where \(f_{s\vert y,x,z}(s_{ij}\vert y_{ij},\mathbf{x}_{ij},\mathbf{z}_{ij};\boldsymbol{\eta })\) is the conditional probability density function determined by the measurement error model such as (5) or (6), and f y | x, z, b (y ij  | x ij , \(\mathbf{z}_{ij},\mathbf{b}_{i};\boldsymbol{\theta })\) is the conditional probability density function specified by the GLMM (1) in combination with (2).

Let

$$\displaystyle\begin{array}{rcl} \mathcal{L}_{\theta i}(\boldsymbol{\theta },\boldsymbol{\eta })& =& \int \Bigg[\prod _{j=1}^{m_{i} }\left \{f_{s\vert x,z,b}(s_{ij}\vert \mathbf{x}_{ij},\mathbf{z}_{ij},\mathbf{b}_{i};\boldsymbol{\theta },\boldsymbol{\eta })\right \}^{1-\delta _{ij} } {}\\ & & \times \;\left \{f_{y\vert x,z,b}(y_{ij}\vert \mathbf{x}_{ij},\mathbf{z}_{ij},\mathbf{b}_{i};\boldsymbol{\theta })\right \}^{\delta _{ij}}\Bigg]f_{b}(\mathbf{b}_{i};\boldsymbol{\sigma }_{b})d\mathbf{b}_{i}, {}\\ \end{array}$$

and

$$\displaystyle{\mathcal{L}_{\eta i}(\boldsymbol{\eta }) =\prod _{ j=1}^{m_{i} }\left \{f_{s\vert y,x,z}(s_{ij}\vert y_{ij},\mathbf{x}_{ij},\mathbf{z}_{ij};\boldsymbol{\eta })\right \}^{\delta _{ij}},}$$

then \(\mathcal{L}_{Fi}(\boldsymbol{\theta },\boldsymbol{\eta }) = \mathcal{L}_{\theta i}(\boldsymbol{\theta },\boldsymbol{\eta })\;\mathcal{L}_{\eta i}(\boldsymbol{\eta })\).

Inference about \(\{\boldsymbol{\theta },\boldsymbol{\eta }\}\) can, in principle, be conducted by maximizing \(\prod _{i=1}^{n}\mathcal{L}_{Fi}(\boldsymbol{\theta },\boldsymbol{\eta })\), or \(\sum _{i=1}^{n}\log \mathcal{L}_{Fi}(\boldsymbol{\theta },\boldsymbol{\eta })\), with respect to \(\{\boldsymbol{\theta },\boldsymbol{\eta }\}\). When the dimension of \(\{\boldsymbol{\theta },\boldsymbol{\eta }\}\) is large, direct maximization of \(\sum _{i=1}^{n}\log \mathcal{L}_{Fi}(\boldsymbol{\theta },\boldsymbol{\eta })\) with respect to \(\boldsymbol{\theta }\) and \(\boldsymbol{\eta }\) can be computationally demanding. We propose to use a two-stage estimation procedure as an alternative to the joint maximization procedure.

Let \(\mathbf{U}_{i}^{{\ast}}(\boldsymbol{\theta },\boldsymbol{\eta }) = \partial \log \mathcal{L}_{\theta i}(\boldsymbol{\theta },\boldsymbol{\eta })/\partial \boldsymbol{\theta }\) and \(\mathbf{Q}_{i}(\boldsymbol{\eta }) = \partial \log \mathcal{L}_{\eta i}(\boldsymbol{\eta })/\partial \boldsymbol{\eta }\). In the first stage, estimator for \(\boldsymbol{\eta }\), denoted by \(\hat{\boldsymbol{\eta }}\), is obtained by solving

$$\displaystyle\begin{array}{rcl} \sum _{i=1}^{n}\mathbf{Q}_{ i}(\boldsymbol{\eta }) = \mathbf{0}.& & {}\\ \end{array}$$

In the second stage, replace \(\boldsymbol{\eta }\) with \(\hat{\boldsymbol{\eta }}\) and solve

$$\displaystyle\begin{array}{rcl} \sum _{i=1}^{n}\mathbf{U}_{ i}^{{\ast}}(\boldsymbol{\theta },\hat{\boldsymbol{\eta }}) = \mathbf{0}& &{}\end{array}$$
(12)

for \(\boldsymbol{\theta }\). Let \(\hat{\boldsymbol{\theta }}_{p}\) denote the solution to (12).

Assume that the size of the validation sample is increasing with the sample size n on the same scale, i.e., as n → ∞ and N v ∕n → ρ for a positive constant ρ. Then under regularity conditions, \(\sqrt{n}(\hat{\boldsymbol{\theta }}_{p}-\boldsymbol{\theta })\) is asymptotically normally distributed with mean 0 and variance given by

$$\displaystyle\begin{array}{rcl} \varSigma ^{{\ast}}& =& \left [-E\{\partial \mathbf{U}_{ i}^{{\ast}}(\boldsymbol{\theta },\boldsymbol{\eta })/\partial \boldsymbol{\theta }^{\mathrm{T}}\}\right ]^{-1} + \left [E\{\partial \mathbf{U}_{ i}^{{\ast}}(\boldsymbol{\theta },\boldsymbol{\eta })/\partial \boldsymbol{\theta }^{\mathrm{T}}\}\right ]^{-1}E\{\partial \mathbf{U}_{ i}^{{\ast}}(\boldsymbol{\theta },\boldsymbol{\eta })/\partial \boldsymbol{\eta }^{\mathrm{T}}\} {}\\ & & \times \;\left [E\{\partial \mathbf{Q}_{i}(\boldsymbol{\eta })/\partial \boldsymbol{\eta }^{\mathrm{T}}\}\right ]^{-1}\left [E\{\partial \mathbf{U}_{ i}^{{\ast}}(\boldsymbol{\theta },\boldsymbol{\eta })/\partial \boldsymbol{\eta }^{\mathrm{T}}\}\right ]^{\mathrm{T}}\left [E\{\partial \mathbf{U}_{ i}^{{\ast}}(\boldsymbol{\theta },\boldsymbol{\eta })/\partial \boldsymbol{\theta }^{\mathrm{T}}\}\right ]^{-1}. {}\\ \end{array}$$

The proof is outlined in the Appendix. An estimate of \(\boldsymbol{\varSigma }^{{\ast}}\) can be obtained by replacing \(E\{\partial \mathbf{U}_{i}^{{\ast}}(\boldsymbol{\theta },\boldsymbol{\eta })/\partial \boldsymbol{\theta }^{\mathrm{T}}\}\), \(E\{\partial \mathbf{U}_{i}^{{\ast}}(\boldsymbol{\theta },\boldsymbol{\eta })/\partial \boldsymbol{\eta }^{\mathrm{T}}\}\), and \(E\{\partial \mathbf{Q}_{i}(\boldsymbol{\eta })/\partial \boldsymbol{\eta }^{\mathrm{T}}\}\) with their empirical counterparts \(n^{-1}\sum _{i=1}^{n}\partial \mathbf{U}_{i}^{{\ast}}(\hat{\boldsymbol{\theta }}_{p},\hat{\boldsymbol{\eta }})/\partial \boldsymbol{\theta }^{\mathrm{T}}\), \(n^{-1}\sum _{i=1}^{n}\partial \mathbf{U}_{i}^{{\ast}}(\hat{\boldsymbol{\theta }}_{p},\) \(\hat{\boldsymbol{\eta }})/\partial \boldsymbol{\eta }^{\mathrm{T}}\), and \(n^{-1}\sum _{i=1}^{n}\partial \mathbf{Q}_{i}(\hat{\boldsymbol{\eta }})/\partial \boldsymbol{\eta }^{\mathrm{T}}\), respectively.

4.3 Inference with Replicates

In this section we discuss inferential procedures for the setting with replicates of the surrogate measurements for Y ij . Suppose the response variable for each subject in a cluster is measured repeatedly, and let S ijr denote the rth observed measurement for subject j in cluster i, r = 1, …, d ij , where the replicate number d ij can vary from subject to subject. For r ≠ r′, S ijr and S ijr′ are assumed to be conditionally independent, given {Y i , X i , Z i , b i }. The marginal likelihood contributed from cluster i is given by

$$\displaystyle\begin{array}{rcl} \mathcal{L}_{Ri}(\boldsymbol{\theta },\boldsymbol{\eta })& =& \int f_{b}(\mathbf{b}_{i};\boldsymbol{\sigma }_{b})\prod _{j=1}^{m_{i} }\bigg\{\int f_{y\vert x,z,b}(y_{ij}\vert \mathbf{x}_{ij},\mathbf{z}_{ij},\mathbf{b}_{i};\boldsymbol{\theta }) {}\\ & & \times \;\prod _{r=1}^{d_{ij} }f_{s\vert y,x,z,b}(s_{ijr}\vert y_{ij},\mathbf{x}_{ij},\mathbf{z}_{ij},\mathbf{b}_{i};\boldsymbol{\eta })dy_{ij}\bigg\}d\mathbf{b}_{i}. {}\\ \end{array}$$

Unlike the two-stage estimation procedure for the case with validation data, estimation for \(\boldsymbol{\theta }\) and \(\boldsymbol{\eta }\) generally cannot be separated from each other, because information on the underlying true responses and the measurement process is mixed together. A joint estimation procedure for \(\{\boldsymbol{\theta },\boldsymbol{\eta }\}\) by maximizing \(\prod _{i=1}^{n}\mathcal{L}_{Ri}(\boldsymbol{\theta },\boldsymbol{\eta })\) is particularly required.

Specifically, let

$$\displaystyle{\mathcal{U}_{i}(\boldsymbol{\theta },\boldsymbol{\eta }) = \partial \log \mathcal{L}_{Ri}(\boldsymbol{\theta },\boldsymbol{\eta })/\partial \boldsymbol{\theta },\ \ \mbox{ and}\ \ \mathcal{Q}_{i}(\boldsymbol{\theta },\boldsymbol{\eta }) = \partial \log \mathcal{L}_{Ri}(\boldsymbol{\theta },\boldsymbol{\eta })/\partial \boldsymbol{\eta }}$$

be the score functions. Define

$$\displaystyle{\varPsi _{Ri}(\boldsymbol{\theta },\boldsymbol{\eta }) = \left (\begin{matrix}\scriptstyle \mathcal{Q}_{i}(\boldsymbol{\theta },\boldsymbol{\eta }) \\ \scriptstyle \mathcal{U}_{i}(\boldsymbol{\theta },\boldsymbol{\eta })\end{matrix}\right ).}$$

The maximum likelihood estimators for \(\boldsymbol{\theta }\) and \(\boldsymbol{\eta }\) is obtained by solving

$$\displaystyle{\sum _{i=1}^{n}\varPsi _{ Ri}(\boldsymbol{\theta },\boldsymbol{\eta }) = \mathbf{0};}$$

we let \((\hat{\boldsymbol{\theta }}_{R},\hat{\boldsymbol{\eta }}_{R})\) denote the solution.

Under suitable regularity conditions, \(n^{1/2}\left (\begin{matrix}\scriptstyle \hat{\boldsymbol{\theta }}_{R}-\boldsymbol{\theta } \\ \scriptstyle \hat{\boldsymbol{\eta }}_{R}-\boldsymbol{\eta }\end{matrix}\right )\) is asymptotically normally distributed with mean 0 and covariance matrix \([E\{\varPsi _{Ri}(\boldsymbol{\theta },\boldsymbol{\eta })\varPsi _{Ri}^{\mathrm{T}}(\boldsymbol{\theta },\boldsymbol{\eta })\}]^{-1}.\)

4.4 Numerical Approximation

To implement the proposed methods, numerical approximations are often needed because integrals involved in the likelihood formulations do not have analytic forms in general. With low dimensional integrals, Gaussian–Hermite quadratures may be invoked to handle integrals without a closed form. For example, the integral with an integrand of form exp(−u 2)f(u) is approximated by a sum

$$\displaystyle{\int _{-\infty }^{\infty }\exp (-u^{2})f(u)du \approx \sum _{ k=1}^{K}w_{ k}\,f(t_{k}),}$$

where f(⋅ ) is a given function, K is the number of selected points, and t k and w k are the value and the weight of the kth designated point, respectively. The approximation accuracy relies on the order of the quadrature approximations. We found in our simulation that a quadrature approximation with order 5 performs adequately well for a single integral; as the number of random components increases, more quadrature points are required in order to obtain a good approximation. When f(⋅ ) is a symmetric or nearly symmetric function, the approximation is generally good, even when the number of quadrature points is chosen to be small.

Computation quickly becomes infeasible as the number of nested random components grows [9]. The convergence of an optimization procedure can be very slow if the dimension of the random components is high. One approach to deal with such integrals is to linearize the model with respect to the random effects, e.g., using a first-order population-averaged approximation to the marginal distribution by expanding the conditional distribution about the average random effect [12]. Alternatively, Laplace’s approximation can be useful to obtain an approximate likelihood function with a closed form [12, 15]. The basic form of linearization using Laplace’s approximation is a second-order Taylor series expansion of the integrand f(u) and is given by \(\int _{\mathbb{R}^{d}}f(\mathbf{u})d\mathbf{u} \approx (2\pi )^{d/2}f(\mathbf{u}_{0})\left \vert -\partial ^{2}\log f(\mathbf{u}_{0})/\partial \mathbf{u}\partial \mathbf{u}^{\mathrm{T}}\right \vert ^{-1/2},\) where d is the dimension of u, and u 0 is the mode of f(u), i.e., the solution to ∂logf(u)∕∂ u = 0. To construct Laplace’s approximation, the first two derivatives of logf(u) are basically required.

5 Simulation Studies

We conduct simulation studies to assess the performance of the proposed likelihood-based methods. We consider the setting with n = 100 and m i  = 5 for i = 1, …, n. The covariates X ij are simulated from the standard normal distribution, and random effects b i are generated from a normal distribution with mean 0 and variance σ b 2 = 0. 04. The response measurements are generated from the model

$$\displaystyle{Y _{ij} =\beta _{0} +\beta _{1}X_{ij} + b_{i}X_{ij} +\epsilon _{ij},}$$

where ε ij  ∼ N(0, ϕ), and the parameter values are set as β 0 = −1, β 1 = log(0. 5), and ϕ = 0. 04.

We consider two models for the measurement error process. That is, surrogate measurements S ij are simulated from one of the two measurement error models:

  • (M1). S ij  = exp(γ Y ij ) + e ij ,

  • (M2). S ij  = γ 0 +γ 1 Y ij + e ij ,

where e ij is independent of Y i and X i , and follows a normal distribution with mean 0 and variance σ e 2 = 0. 04. For error model (M1), the error parameters are specified as γ = 0. 5. For error model (M2), the parameters are specified as γ 0 = 0. 5 and γ 1 = 0. 5.

Let \(\boldsymbol{\eta }\) denote the vector of associated parameters for the measurement error model. Specifically, in error model (M1), \(\boldsymbol{\eta }= (\gamma,\sigma _{e}^{2})^{\mathrm{T}}\); while in error model (M2), \(\boldsymbol{\eta }= (\gamma _{0},\gamma _{1},\sigma _{e}^{2})^{\mathrm{T}}\). We evaluate the proposed methods under two scenarios regarding the knowledge of \(\boldsymbol{\eta }\): (i) \(\boldsymbol{\eta }\) is treated as known, and (ii) \(\boldsymbol{\eta }\) is estimated from internal validation data. For scenario (ii), we obtain a validation subsample by randomly selecting one subject from each cluster. We use Gaussian quadrature of order 15 in the numerical approximation for the likelihood-based approaches. Two thousand simulations are run for each parameter configuration.

We conduct three analyses for each simulated data set: the two naive approaches described in Sects. 3.1 and 3.2 and the proposed methods described in Sect. 4. We report the simulation results based on four measures: relative bias in percent (Bias%), sample standard deviation of the estimates (SD), average of model-based standard errors (ASE), and coverage probability of the 95 % confidence interval (CP%).

Table 1 reports the results for the exponential measurement error model (M1). As expected, the NAI1 approach produces very biased (attenuated) estimates of the fixed-effect parameter β 1, and the coverage rates of the 95 % confidence interval are close to 0. The NAI2 approach, which analyzes transformed surrogate responses, produces slightly better estimates of β 1. The magnitude of the relative bias, although smaller than that from NAI1, is still substantial. In contrast, the proposed likelihood approaches give consistent estimates for β 1 in both scenarios, and the coverage rates of its 95 % confidence intervals are close to the nominal value.

Table 1 Simulation results for cases with measurement error model (M1) (2000 simulations)
Full size table
Table 2 Simulation results for cases with linear measurement error model (M2) (2000 simulations)
Full size table

Table 2 reports the results for the linear measurement error model (M2). Again the estimates for β 1 from the NAI1 approach are biased, and the values are scaled approximately by a factor of γ 1, which is in agreement with the analytical result shown in Sect. 3. The NAI2 approach yields good estimates for β 0, β 1, and σ b 2 with small finite sample biases. The NAI2 estimates for ϕ, however, are very biased, resulting in coverage rates of corresponding confidence intervals far from the nominal value of 95 %. In contrast, the proposed likelihood-based approach gives consistent estimators for the fixed-effect and variance component, and the associated standard errors are similar to the empirical standard deviations. As a result, the coverage rates of the 95 % confidence intervals are close to the nominal value.

6 Application

We illustrate our proposed methods by analyzing the data from the Framingham Heart Study. The data set includes exams #2 and #3 for n = 1615 male subjects aged 31–65 [3]. Two systolic blood pressure (SBP) readings were taken during each exam. One of the clinical interests is to understand the relationship between SBP and potential risk factors such as baseline smoking status and age [6, 8, 11]. The risk factors, however, may not have linear effects on SBP directly.

Preliminary exploration shows that SBP measurements are skewed, and using a square-root transformation to (T ij − 50) is reasonably satisfactory for obtaining a symmetric data distribution, where T ij represents the true SBP measurement for subject i at time j, where j = 1 corresponds to exam #2, and j = 2 for exam #3, and i = 1, …, n. We now let Y ij denote such a transformed variable, i.e., \(Y _{ij} = \sqrt{T_{ij } - 50}\). We assume that the Y ij follow the model

$$\displaystyle\begin{array}{rcl} Y _{ij} =\beta _{0} +\beta _{\mathrm{age}}X_{ij1} +\beta _{\mathrm{smoke}}X_{ij2} +\beta _{\mathrm{exam}}X_{ij3} + b_{i} +\epsilon _{ij},\;\;\;j = 1,2,\;i = 1,\ldots,n,& & {}\\ \end{array}$$

where X ij1 is the baseline age of subject i at exam #2, X ij2 is the indicator variable for baseline smoking status of subject i at exam #1, X ij3 is 1 if j = 2 and 0 otherwise, and b i and ε ij are assumed to be independently and normally distributed with means 0 and variances given by σ b 2 and ϕ, respectively.

Because a subject’s SBP changes over time, the two individual SBP readings at each exam are regarded as replicated surrogates. Several measurement error models for SBP reading have been proposed by different researchers [2, 7, 13]. Let T ijr ∗ be the rth observed SBP reading for subject i at time j, i = 1, …, n, j = 1, 2, r = 1, 2. We consider an error model log(T ijr ∗− 50) = log(T ij − 50) + e ijr , suggested by Wang et al. [13], where the e ijr are assumed to be independent of each other and of other variables, and are normally distributed with mean 0 and variance σ e 2. Let S ijr denote log(T ijr ∗− 50), then the measurement error model is equivalently given by

$$\displaystyle\begin{array}{rcl} S_{ijr} = 2\log (Y _{ij}) + e_{ijr}.& & {}\\ \end{array}$$

Table 3 reports results from analyses using the proposed method and the two naive approaches. The estimated regression coefficients β age, β smoke, and β exam from the proposed method are 0.027, −0.120, and −0.087, respectively. At the 5 % significance level, age is significantly associated with increasing blood pressure. The negative coefficient for smoking status may suggest an effect of smoking on decreasing blood pressure. As expected, the results from the NAI2 approach are similar to those from the proposed method due to the small value of the measurement error variance. The NAI1 estimates, however, are not comparable to those from the NAI2 and the proposed method, possibly in part due to a different scale of the response variable.

Table 3 Analysis of data from the Framingham Heart Study
Full size table

7 Discussion

In this paper, we exploit analysis of response-error-contaminated clustered data within the framework of generalized linear mixed models. Although in some situations ignoring error in response does not alter point estimates of regression parameters, ignoring error in response does affect inference results for general circumstances. Error in response can produce seriously biased results.

In this paper we perform asymptotic bias analysis to assess the impact of ignoring error in response. We investigate the performance of a partial-error-correction method that was intuitively used in the literature [1]. To fully account for error effects, we develop valid inferential procedures for various practical settings which pertain to the information on response error. Simulation studies demonstrate satisfactory performance of the proposed methods under various settings.