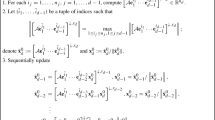Abstract
It is known that many tensor data have symmetric or partially symmetric structure and structural tensors have structure preserving Candecomp/Parafac (CP) decompositions. However, the well-known alternating least squares (ALS) method cannot realize structure preserving CP decompositions of tensors. Hence, in this paper, we consider numerical problems of structure preserving rank-R approximation and structure preserving CP decomposition of partially symmetric tensors. For the problem of structure preserving rank-R approximation, we derive the gradient formula of the objective function, obtain BFGS iterative formulas, propose a BFGS algorithm for positive partially symmetric rank-R approximation, and discuss the convergence of the algorithm. For the problem of structure preserving CP decomposition, we give a necessary condition for partially symmetric tensors with even orders to have positive partially symmetric CP decompositions, and design a general partially symmetric rank-R approximation algorithm. Finally, some numerical examples are given. Through numerical examples, we find that if a tensor has a positive partially symmetric CP decomposition then its partially symmetric rank CP decomposition must be a positive CP decomposition. In addition, we compare the BFGS algorithm proposed in this paper with the standard CP-ALS method. Numerical examples show that the BFGS algorithm has better stability and faster computing speed than CP-ALS algorithm.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Tensor Candecomp/Parafac(CP) decomposition and tensor rank are the basic problems in tensor research and have lots of important applications in data analysis [1, 2], signal processing [3, 4] and others [5, 6]. Although the tensor decomposition problem is NP hard [7], there are many researchers still doing it without bored and tired. The decomposition of a tensor into an outer product of vectors and the corresponding notations were first proposed and studied by Frank L. Hitchcock in [8, 9]. The same decomposition was rediscovered in 1970s [20] in order to extend the data analysis model to multidimensional arrays.
Symmetric tensors are a class of tensors with many different decomposition properties and special applications [10,11,12], so many scholars have conducted in-depth research on symmetric tensors. Comon et al. [13] proved that any symmetric tensor can be decomposed into a linear combination of rank-1 tensor. Brachat et al. [14] presented an algebraic method for symmetric tensor decompositions, based on linear algebra computation with Hankel matrices by extending Sylvester’s theorem to multiple variables in 2010. Kolda [15] considered real-valued decomposition of symmetric tensor, both nonnegative and sparse and presented a numerical optimization algorithm based on gradient in 2015. In 2017, Nie [16] devised a combination of polynomial optimization and numerical approaches for solving complex-valued symmetric tensor decompositions. In 2022, Liu [17] proposed an alternating gradient descent algorithm for solving symmetric tensor CP decomposition by minimizing a multiconvex optimization problem.
Partially symmetric tensor can be used to solve practical engineering problems, such as elastic material analysis [18] and quantum information theory [19]. Carroll and Chang [20] first considered the CP decomposition of partially symmetric tensors and proposed an alternating method of ignoring the symmetry, the decomposition obtained by this method does not have the property of structure preserving unless the decomposition satisfies the uniqueness condition [21]. In 2013, Li and Navasca [22] proposed the so called partial column-wise least squares method to obtain the CP decomposition of the partially symmetric tensor of the third and fourth order. Ni and Li [23] proved that any partially symmetric tensor has a partially symmetric CP decomposition and presented a semi-definite relaxation algorithm. However, the semi-definite relaxation is hard to calculate a partially symmetric CP decomposition if the tensor has higher order and higher dimension, since the number of moments will increase sharply with the increase of tensor order and dimension.
Motivated by the above, we consider the numerical algorithm of structure preserving rank-R approximation of partially symmetric tensors. We deduce the gradient formula of the structure preserving rank-R approximation loss function, propose a gradient descent algorithm and a BFGS algorithm, and analyze the convergence of the BFGS algorithm. The BFGS algorithm can be used to the structure preserving CP decomposition of partially symmetric tensors, completely symmetric tensors and non-symmetric tensors, respectively. Numerical examples show that the BFGS algorithm has good numerical performance.
The paper is structured as follows. Section 2 introduces some basic concepts and related properties, including matrix and tensor product, inner product and Frobenius norm of tensor, as well as partially symmetric tensor, etc. Section 3 deduces the gradient of the partially symmetric rank-R approximation loss function. In Sect. 4, we propose the BFGS algorithm and discuss its convergence. In Sect. 5, We derive the discrimination of partially symmetric tensors with the positive decomposition. Finally, numerical experiments are given in Sect. 6.
Notation. \({\mathbb {N}}_{+}\), \({\mathbb {R}}\) and \({\mathbb {C}}\) denote the set of positive integers, real field and complex field, respectively. A uppercase letter in calligraphic font denotes a tensor, e.g., \({\mathcal {T}}\). A uppercase letter represents a matrix, e.g., U. A boldface lowercase letter represents a vector, e.g., \({\textbf{v}}\). A lowercase letter represents a scalar, e.g., x. The entry with row index i and column index j in a matrix U, i.e., \((U)_{ij}\), is symbolized by \(u_{ij}\) ( also \(({\textbf{v}})_i = v_i\) and \(({\mathcal {T}})_{i_1i_2\cdots i_N} = t_{i_1i_2\cdots i_N}\) ). Let \(s>0\) be an integer, denote \(\left[ s\right] :=\{1,2,\cdots ,s\}\) as an integer set. \({\mathfrak {S}}_t\) denotes the set of all permutations of \(\{1,2,\cdots ,m_t\}\), \(m_t\) is a positive integer, \(t\in [s]\).
2 Preliminaries
2.1 Matrix and tensor products
A tensor can be regarded as a multiway array, which is a generalization of matrices. A tensor is represented with calligraphic script uppercase letters in this paper, e.g., \({\mathcal {T}}\). In this subsection, some basic concepts and products of matrix and tensor will be reviewed. For more details, please refer to the literature [24].
The Kronecker product of matrices \(A \in {{{\mathbb {R}}}^{I\times J}}\) and \( B \in {{{\mathbb {R}}}^{K\times L}}\), denoted as \(A \otimes B\), is defined as
The Khatri-Rao product of two matrices \(A\in {{\mathbb {R}}^{I\times K}}\) and \(B\in {{\mathbb {R}}^{J\times K}}\) is defined as
If \({\textbf{a}}\) and \({\textbf{b}}\) are vectors, then the Khatri-Rao and Kronecker products are identical, i.e., \({\textbf{a}}\otimes {\textbf{b}}={\textbf{a}}\odot {\textbf{b}}\).
The Hadamard product of two same-sized matrices \(A,\ B\in {{\mathbb {R}}^{I\times J}}\), denoted as \(A*B\in {{\mathbb {R}}^{I\times J}}\), is defined as
We use ”\(\circ \)” to represent the outer product of two arbitrary tensors \({\mathcal {X}}\in {\mathbb {R}}^{I_1\times I_2\times \cdots \times I_m}\), \({\mathcal {Y}}\in {\mathbb {R}}^{J_1\times J_2\times \cdots \times J_n}\)
Invoking the definition of tensor outer product as described in (2.1), we can get that for vectors \({{\textbf{x}}_k}\in {\mathbb {R}}^{I_k}\), for \(k\in [m]\), their tensor outer product \({\textbf{x}}_1\circ {\textbf{x}}_2\circ \cdots \circ {\textbf{x}}_m\in {\mathbb {R}}^{I_1\times I_2\times \cdots \times I_m}\) is an mth-order rank-1 tensor such that
In particular, if \({\textbf{x}}_1={\textbf{x}}_2=\cdots {\textbf{x}}_m={\textbf{x}}\in {\mathbb {R}}^n\), then \({\textbf{x}}^{\circ m}\equiv \overbrace{{\textbf{x}}\circ {\textbf{x}}\circ \cdots \circ {\textbf{x}}}^m\) is an mth-order n-dimensional symmetric rank-1 tensor and is denoted as \({\textbf{x}}^m\) for simplicity.
Definition 2.1
Let \({\mathcal {T}}\in {\mathbb {R}}^{I_1\times I_2\times \cdots \times I_m}\) be a tensor and vectors \({{\textbf{x}}_k}\in {\mathbb {R}}^{I_k}\) for \(k\in [m]\). Define the contraction product of tensor \({\mathcal {T}}\) and a rank-1 tensor as follows
Generally, the inner product of two tensors \({\mathcal {X}},{\mathcal {Y}}\in {\mathbb {R}}^{I_1\times I_2\times \cdots \times I_m}\), denoted as \({\mathcal {X}}\cdot {\mathcal {Y}}\) or \(\langle {\mathcal {X}},{\mathcal {Y}}\rangle \), is defined as
The Frobenius norm of a tensor \({\mathcal {X}}\in {\mathbb {R}}^{I_1\times I_2\times \cdots \times I_m}\) is defined as
It follows immediately that \(\left<{\mathcal {X}},{\mathcal {X}}\right>={\Vert {{\mathcal {X}}}\Vert }^2_{F}\).
The mode-k matricization of a tensor \({\mathcal {T}}\in {\mathbb {R}}^{I_1\times I_2\times \cdots \times I_m}\) is denoted as \(T_{\left( k\right) }\) and rearrange its elements into a matrix of size \(I_k\times \prod _{i\ne k}I_i\). Element \(\left( i_1,i_2,\cdots ,i_m\right) \) maps to matrix entry \(\left( i_k,j\right) \), where
Let \({\mathcal {T}}\in {\mathbb {R}}^{I_1\times I_2\times \cdots \times I_m}\) be an mth-order tensor. The CP decomposition of \({\mathcal {T}}\) is
where \(A_k=({\textbf{a}}_1^{(k)}\ {\textbf{a}}_2^{(k)}\ \cdots \ {\textbf{a}}_R^{(k)})\in {\mathbb {R}}^{I_k\times R}\), \(k\in [m]\) are called factor matrices. The mode-k matricization of tensor \({\mathcal {T}}=[\![A_1,A_2,\cdots ,A_m]\!]\), \(A_k\in {\mathbb {R}}^{I_k\times R}\), for \(k\in [m]\) can be written in the form of factor matrix,
2.2 Partially symmetric tensor
Partially symmetric tensor is the main content of this paper, so its basic concepts and some properties are indispensable. Detailed introduction can be referred to the literature [23, 25,26,27].
Definition 2.2
[23] Let \({\textbf{m}}=\left( m_1,m_2,\cdots ,m_s\right) ,\ {\textbf{n}}=\left( n_1,n_2,\cdots ,n_s\right) \in {\mathbb {N}}_{+}^s\). An \({\textbf{m}}\)th-order \({\textbf{n}}\)-dimensional tensor \({\mathcal {T}}\) is an array over the field \({\mathbb {F}}\) indexed by integer tuples \(\left( i_1,\cdots ,i_{m_1},j_1,\cdots ,j_{m_2},\cdots ,l_1,\cdots ,l_{m_s}\right) \), i.e.,
with \(i_1,\cdots ,i_{m_1}\in {\left[ n_1\right] }\), \({j_1,\cdots ,j_{m_2}\in {\left[ n_2\right] }}\), \(\cdots \), \({l_1,\cdots ,l_{m_s}\in {\left[ n_s\right] }}\).
The space of all tensors over the filed \({\mathbb {F}}\) is denoted as \(T\left[ {\textbf{m}}\right] {\mathbb {F}}\left[ {\textbf{n}}\right] \). \({\mathcal {T}}\) is called a square tensor, if all dimensions are equal, that is to say \(n_1=n_2=\cdots =n_s\).
Definition 2.3
[25] Let \({\textbf{m}}=\left( m_1,m_2,\cdots ,m_s\right) ,\ {\textbf{n}}=\left( n_1,n_2,\cdots ,n_s\right) \in {\mathbb {N}}_{+}^s\). A tensor \({\mathcal {S}}\in {T\left[ {\textbf{m}}\right] {\mathbb {F}}\left[ {\textbf{n}}\right] }\) is called partially symmetric if
for every permutation \(\sigma _t\in {\mathfrak {S}}_t\), where \({\mathfrak {S}}_t\) is the set of all permutations of \(\left\{ 1,2,\cdots ,m_t\right\} \), \(t\in {\left[ s\right] }\).
The space of all \({\textbf{m}}\)th-order \({\textbf{n}}\)-dimensional partially symmetric tensors over the field \({\mathbb {F}}\) is denoted by \({S[{\textbf{m}}]{\mathbb {F}}[{\textbf{n}}]}\).
Definition 2.4
[23] Let vectors \({\textbf{u}}^{\left( t\right) }_k\in {{\mathbb {F}}}^{n_t}\) for all \(t\in \left[ s\right] \). The result of the tensor outer product \({\left( {\textbf{u}}^{\left( 1\right) }_k\right) }^{m_1}\circ {\left( {\textbf{u}}^{\left( 2\right) }_k\right) }^{m_2}\circ {\cdots } \circ {\left( {\textbf{u}}^{\left( s\right) }_k\right) }^{m_s}\) is a rank-1 partially symmetric tensor. A tensor \({\mathcal {S}}\in {S\left[ {\textbf{m}}\right] {\mathbb {F}}\left[ {\textbf{n}}\right] }\) is said to have a partially symmetric CP decomposition if the tensor \({\mathcal {S}}\) has a decomposition as
If \(m_1,m_2,\cdots ,m_s=1\), then the tensor \({\mathcal {T}}\in {T[{\textbf{m}}]{\mathbb {F}}[{\textbf{n}}]}\) is an sth-order \(n_1\times n_2\times \cdots \times n_s\)-dimensional tensor, the partially symmetric CP decomposition of \({\mathcal {T}}\) is an usual nonsymmetric CP decomposition. If \(s=1\) and \(n_1=n_2=\cdots =n_s=n\), let \(m_1=m\), then \({\mathcal {T}}\in {T[m]{\mathbb {F}}[n]}\) is an mth-order n-dimensional symmetric tensor.
Theorem 2.1
[23] Let \({\textbf{m}}=\left( m_1,m_2,\cdots ,m_s\right) ,\ {\textbf{n}}=\left( n_1,n_2,\cdots ,n_s\right) \in {\mathbb {N}}_{+}^s\), and \({\mathcal {S}}\in S\left[ {\textbf{m}}\right] {\mathbb {F}}\left[ {\textbf{n}}\right] \) be a partially symmetric tensor. Then there exist \(\lambda _k\in {\mathbb {F}}\), \({\textbf{u}}^{(t)}_k\in {{\mathbb {F}}}^{n_t}\), \(\Vert {{\textbf{u}}^{(t)}_k}\Vert _2=1\) for \(k\in [R]\) and \(t\in [s]\) such that
i.e., any partially symmetric tensor (over any field) has a partially symmetric CP decomposition.
If \({\mathcal {S}}\in S[{\textbf{m}}]{\mathbb {R}}[{\textbf{n}}]\) has a decomposition as (2.3) with \(\lambda _k\ge 0\) for all \(k\in [R]\), then we say that \({\mathcal {S}}\) has a positive partially symmetric CP decomposition. According to Theorem 2.1, there is the following corollary.
Corollary 2.1
If there is \(i\in [s]\) such that \(m_i\) is an odd number, then, any nonzero tensor \({\mathcal {S}}\in {S[{\textbf{m}}]{\mathbb {R}}[{\textbf{n}}]}\) has a positive partially symmetric CP decomposition. However, \({\mathcal {S}}\) may not have positive partially symmetric CP decomposition, if \(m_1, \cdots , m_s\) are even.
Proof
If there is \(i\in \left[ s\right] \) such that \(m_i\) is an odd number, without loss of generality, let \(m_1\) be an odd number. Then, the \(m_1\)th real root of \(\lambda _k\) always exists for \(k\in [R]\), so we can rewrite the item \(\lambda _k\left( {\textbf{u}}_k^{(1)}\right) ^{m_1}\) as
Then,
That is, \({\mathcal {S}}\in {S\left[ {{\textbf{m}}}\right] {\mathbb {R}}\left[ {{\textbf{n}}}\right] }\) has a positive partially symmetric CP decomposition. However, if all orders are even, then \(m_t\)th real root does not exist if \(\lambda _k<0\), for \(t\in [s]\), so the scalar cannot be absorbed. In this case, \({\mathcal {S}}\) may not have positive partially symmetric CP decomposition. This completes the proof. \(\square \)
If \({\mathcal {S}}\) has a positive partially symmetric CP decomposition as in (2.3), then we can write \(\lambda _k \left( {\textbf{u}}^{(t)}_k\right) ^{m_t} = \left( (\lambda _k)^{1/m_t} {\textbf{u}}^{(t)}_k\right) ^{m_t}\) for some \(t\in [s]\). In this case, the decomposition (2.3) can be rewritten as follows
Let \(U_t=({\textbf{u}}_1^{(t)},{\textbf{u}}_2^{(t)},\cdots ,{\textbf{u}}_R^{(t)})\in {\mathbb {R}}^{n_t\times R}\) for \(t\in [s]\). We call \(\{U_1,U_2,\cdots ,U_s\}\) as a tuple of factor matrices of partially symmetric tensor \({\mathcal {S}}\). The partially symmetric CP decomposition (2.4) can also be written as
3 Positive partially symmetric rank-R approximation
Now, we study the positive partially symmetric rank-R approximation of partially symmetric tensors. Let s, R be two positive integers and \({\textbf{m}}=\left( m_1,m_2,\cdots ,m_s\right) ,{\textbf{n}}=\left( n_1,n_2,\cdots ,n_s\right) \in {\mathbb {N}}_{+}^{s}\). Given a real partially symmetric tensor \({\mathcal {S}}\in S\left[ {\textbf{m}}\right] {\mathbb {R}}\left[ {\textbf{n}}\right] \), find positive scalars \(\lambda _k > 0\) and unit-norm vectors \({\textbf{u}}_k^{(t)}\in {\mathbb {R}}^{n_t}\) for \(t\in [s]\) and \(k\in [R]\) such that the rank-R tensor
minimizes the function
The positive partially symmetric rank-R approximation problem of tensors \({\mathcal {S}}\) is equivalent to solving the following optimization problem
Since \({\lambda }_k>0\) for all \(k\in [R]\), we can rewrite \(\hat{{\mathcal {S}}}\) as
Then \({{\textbf{u}}}^{\left( t\right) }_k={\tilde{{\textbf{u}}}^{\left( t\right) }_k}/{\Vert {\tilde{{\textbf{u}}}^{(t)}_k}\Vert _2}\) and \({\lambda }_k=\prod \nolimits _{t=1}^s{{\Vert {\tilde{{\textbf{u}}}^{(t)}_k}\Vert }_2^{m_t}}\), for all \(k\in [R]\) and \(t\in [s]\).
The right hand side of (3.1) may also be written as the form of a tuple of factor matrices
where \(U_t=\left( \tilde{{\textbf{u}}}_1^{(t)}, \tilde{{\textbf{u}}}_2^{(t)}, \cdots , \tilde{{\textbf{u}}}_R^{(t)}\right) \in {\mathbb {R}}^{n_t\times R}\) is a matrix for all \(t\in [s]\).
Let \({\textbf{U}} \in {\mathbb {R}}^{(n_1+\cdots +n_s)\times r}\) be a block-matrix vector as
Then the constrained optimization problem (P1) is turned to an unconstrained optimization
3.1 Gradient calculation of \(f_{{\mathcal {S}}}({{\textbf{U}}})\)
Lemma 3.1
Let s and R be two positive integers, \({\textbf{m}}=(m_1,m_2,\cdots ,m_s),{\textbf{n}}=(n_1,n_2,\cdots ,n_s)\in {\mathbb {N}}_{+}^s\) and \({\mathcal {S}}\in S[{\textbf{m}}]{\mathbb {R}}[{\textbf{n}}]\) be a partially symmetric tensor. Let
Then
Proof
Assume that \({\mathcal {A}}\in S[m]{\mathbb {R}}[n]\) be a symmetric tensor of m-order. Then,
Define a function \(F(\hat{{\mathcal {S}}})=\langle {\mathcal {S}},\hat{{\mathcal {S}}}\rangle \). Then,
According to the formula (3.3), we have that
This completes proof. \(\square \)
Theorem 3.1
Let \({\textbf{m}}=(m_1,m_2,\cdots ,m_s),\ {\textbf{n}}=(n_1,n_2,\cdots ,n_s) \in {\mathbb {N}}_{+}^s\), \(M_t:=m_1+\cdots +m_t\), \(t\in [s]\). Let \({\mathcal {S}}\in {S[{\textbf{m}}]{\mathbb {R}}[{\textbf{n}}]}\) be a given partially symmetric tensor, \(U_t=({\textbf{u}}_1^{(t)},{\textbf{u}}_2^{(t)},\cdots , {\textbf{u}}_R^{(t)})\in {{\mathbb {R}}}^{{n_t}\times R}\) be a matrix for all \(k\in [R]\), \(t\in [s]\) and \({\textbf{U}}=(U_1^T, U_2^T, \cdots , U_s^T)^T\) be a block-matrix vector. Then the first order partial derivative of the function \(f_{\mathcal {S}}({\textbf{U}})\) defined in (3.2) with respect to \(U_t\) is
where \(S_{(M_t)}\) is the mode-\(M_t\) matricization of the tensor \({\mathcal {S}}\) and
Proof
According to the definition of derivative, the first order partial derivative of the function with respect to \(U_t\) is
Let \(\hat{{\mathcal {S}}}=[\![U_1^{\times m_1},U_2^{\times m_2},\cdots ,U_s^{\times m_s}]\!].\) Then
From the Lemma 3.1, for every \(k\in [R]\), it is followed that
According to definition of the mode-k matricization, we have that
Thus,
Substitute (3.4) into the above equation, we get that
This completes the proof. \(\square \)
If the gradient is calculated directly according to the formula (3.5), it will cost a lot of computational expenses. We can save the computational expenses by the following method. The first item \(S_{(M_t)}W_t\) can be obtained by MTTKRP, which is a function in the tensor toolbox [29] to efficiently calculate matricized tensor times Khatri–Rao product. The second item can also avoid forming \(W_t\) since \(W_t^T W_t\) is given by
The following is the algorithm for calculating gradient value of \(f_{\mathcal {S}}({\textbf{U}})\) defined as (3.2) at a given point.

3.2 Gradient descent method
We introduce two linear search methods. Armijo inexact search rule adopts the backtracking strategy to obtain the step size. In other words, the step size is picked as \({\alpha }_k={\beta }{\gamma }^{m_k}\), where \(m_k\) is the smallest nonnegative integer satisfying the following condition
where \(\beta >0,\ \sigma ,\ \gamma \in \left( 0,1\right) \).
Another inexact search rule choosing a step size \(\alpha _k>0\) is Armijo-Wolfe conditions [28],
where \(0<c_1<c_2<1\) are the parameters of line search algorithm, the above two condition are called the sufficient decrease condition and curvature condition respectively.
Therefore, the iterative scheme is
where \(\alpha _k\) is obtained from the above Armijo or Armijo-Wolfe rule, \({{\textbf{d}}}^k\) is the search direction of the k-th iteration. If \({{\textbf{d}}}^k=-\nabla f({\textbf{u}}^k)\), the iteration method is called gradient descent method.
The termination condition of optimization algorithm is that norm of gradient is less than a given criteria, i.e.,
For partially symmetric rank-R approximation problem of some partially symmetric tensors, the iterative formula of gradient descent method is that
where \({\textbf{G}}^k=-\nabla f_{{\mathcal {S}}}({\textbf{U}}^k)\), \(\alpha _k\) satisfies the Armijo or Armijo-Wolfe rule.
The following is gradient descent algorithm with Armijo rule (3.6) for the partially symmetric rank-R approximation of a partially symmetric tensor.

4 BFGS method
We now review the standard BFGS method with Armijo-Wolfe line search for solving the optimization problem \(\min \nolimits _{{\textbf{x}}\in {\mathbb {R}}^n}f({\textbf{x}})\). For more details, please refer to [28]. The iterative formula of BFGS method for solving the problem \(\min \nolimits _{{\textbf{x}}\in {\mathbb {R}}^n}f({\textbf{x}})\) is
where \({\textbf{g}}^k=\nabla f({\textbf{x}}^k)\), \(\alpha _k\) is step size satisfying Armijo-Wolfe rule. The initial point \({\textbf{x}}^0\) of the iterative algorithm is usually given randomly; \(H^0\) and \(B^0\) must be positive definite matrices, usually the identity matrix.
Let \({\textbf{y}}^k={\textbf{g}}^{k+1}-{\textbf{g}}^{k}\) and \({\textbf{s}}^k={\textbf{x}}^{k+1}-{\textbf{x}}^{k}\). The updated formula of \(B^k\) is that
The updated formula of \(H^k\) is that
4.1 The BFGS method for partially symmetric rank-R approximation
Following the standard BFGS method, we will give the tensor BFGS method to solve the partially symmetric rank-R approximation of partially symmetric tensor. Let \({\mathcal {S}}\in S[{\textbf{m}}]{\mathbb {R}}[{\textbf{n}}]\) be a partially symmetric tensor, \({\textbf{U}}=(U^T_1,\cdots ,U_s^T)^T\) be a block-matrix vector, \(U_t\in {\mathbb {R}}^{n_t\times r}\) for \(t\in [s]\) and \(n:=n_1+\cdots +n_s\). The function \(f_{\mathcal {S}}({\textbf{U}})\) is defined as (3.2), then the gradient \(\nabla f_{{\mathcal {S}}}({\textbf{U}})\) of is \(f_{\mathcal {S}}({\textbf{U}})\) that
the Hessian is that
which is a fourth-order tensor.
In order to obtain the BFGS iterative formula for tensor, we define a multiplication of two fourth-order tensors and a product between a fourth-order tensor and a matrix. For any two tensors \({\mathcal {A}},\ {\mathcal {B}}\in {\mathbb {R}}^{K\times L\times K\times L}\), define \({\mathcal {C}}={\mathcal {A}}\oslash {\mathcal {B}}\in {\mathbb {R}}^{K\times L\times K\times L}\) as
For any \({\mathcal {T}}\in {\mathbb {R}}^{K\times L\times K\times L}\) and \(A\in {\mathbb {R}}^{K\times L}\), define \(B={\mathcal {T}} A \in {\mathbb {R}}^{K\times L}\) as
In the sense of the multiplication of two fourth-order tensors, we define the fourth-order identity tensor \({\mathcal {I}}\in {\mathbb {R}}^{K\times L\times K\times L}\) as
According to the definition (4.3) and (4.2), for any matrix \(A\in {\mathbb {R}}^{K\times L}\), we have \({\mathcal {I}}A=A\). The tensor \({\mathcal {A}}\in {\mathbb {R}}^{K\times L\times K\times L}\) is an invertible tensor, if there is a same-sized tensor \({\mathcal {B}}\) such that \({\mathcal {A}}\oslash {\mathcal {B}}={\mathcal {I}}\) and \({\mathcal {B}}\oslash {\mathcal {A}}={\mathcal {I}}\), and if so, then \({\mathcal {B}}\) is called the inverse of \({\mathcal {A}}\). The inverse of \({\mathcal {A}}\) is denoted by \({\mathcal {A}}^{-1}\).
Lemma 4.1
Let fourth-order tensor \({\mathcal {T}}\in {\mathbb {R}}^{K\times L\times K\times L}\) be invertible and its elements satisfy \({\mathcal {T}}_{k_1l_1k_2l_2}={\mathcal {T}}_{k_2l_2k_1l_1}\), and \(A, B, C\in {\mathbb {R}}^{K\times L}\). Then
-
(1)
\(\langle {\mathcal {T}}^{-1}A,{\mathcal {T}}B\rangle =\langle A,B\rangle .\)
-
(2)
\((A\circ B)C=A\langle B,C\rangle .\)
Proof
According to the multiplication defined as (4.2),
Since \({\mathcal {T}}_{k_1l_1k_2l_2}={\mathcal {T}}_{k_2l_2k_1l_1}\), we have that
Therefore, \(\langle {\mathcal {T}}^{-1}A,{\mathcal {T}}B\rangle =\langle A,B\rangle .\) According to the multiplication defined as (4.2) and tensor outer product defined as (2.1),
Hence, \((A\circ B)C = A\langle B,C\rangle \). The proof is completed. \(\square \)
Let \(f_{{\mathcal {S}}}({\textbf{U}})\) be defined as (3.2), then the iterative formula of BFGS algorithm with Armijo-Wolfe line search for solving the optimization problem \(\min _{{\textbf{U}}} f_{{\mathcal {S}}}({\textbf{U}})\) is
where \({\textbf{G}}^k\) is gradient value of \(f_{{\mathcal {S}}}({\textbf{U}})\) at \({\textbf{U}}^k\), i.e., \({\textbf{G}}^k=\nabla f_{{\mathcal {S}}}({\textbf{U}}^k)\), the step size \(\alpha _k\) satisfies Armijo-Wolfe rule.
The updated formula of \({\mathcal {B}}^k\) is that
where \({\textbf{Y}}^k=\nabla f_{{\mathcal {S}}}({\textbf{U}}^{k+1})-\nabla f_{{\mathcal {S}}}({\textbf{U}}^{k})\), \({\textbf{S}}^k={\textbf{U}}^{k+1}-{\textbf{U}}^{k}\).
Lemma 4.2
Let \({\mathcal {B}}^{k+1}\) be defined as (4.4). Then, the inverse of \({\mathcal {B}}^{k+1}\) can be given by
Proof
In order to prove that \({\mathcal {H}}^{k+1}\) is the inverse of \({\mathcal {B}}^{k+1}\), we just need to prove that, for any block-matrix \({\textbf{X}}\), \({\mathcal {B}}^{k+1}({\mathcal {H}}^{K+1}{\textbf{X}})={\textbf{X}}\). Let \(\langle {\textbf{S}}^k,{\textbf{Y}}^k\rangle = \frac{1}{\mu }\), \(\langle {\mathcal {B}}^k{\textbf{S}}^k,{\textbf{S}}^k\rangle =\frac{1}{\nu }\). From the formula (4.4), we have
According to the Lemma 4.1,
By putting (4.7) into (4.6) and using the Lemma 4.1, we get \({\mathcal {B}}^{k+1}({\mathcal {H}}^{K+1}{\textbf{X}})={\textbf{X}}\). The proof is completed. \(\Box \) \(\square \)
Now, we will give the BFGS algorithm with Armijo-Wolfe step size (3.7) for the positive partially symmetric rank-R approximation of a partially symmetric tensor as follows. The initial factor matrix \({\textbf{U}}^1\) is obtained randomly and \({\mathcal {H}}^1\) is usually selected as fourth-order identity tensor \({\mathcal {I}}\) defined as (4.3).

4.2 Convergence analysis of BFGS algorithm
In this subsection, the super-linear convergence of algorithm will be discussed. The proof of following results refers to [28]. First, we give the relevant assumptions.
Assumption 4.1
Let \(s,r>0\) be two integers and \({\textbf{m}}=(m_1,m_2,\cdots ,m_s),\ {\textbf{n}}=(n_1,n_2,\cdots ,n_s)\in {\mathbb {N}}^s_{+}\). Let \({\mathcal {S}}\in S[{\textbf{m}}]{\mathbb {R}}[{\textbf{n}}]\) be a partially symmetric tensor, \(n=n_1+\cdots +n_s\). The function \(f_{{\mathcal {S}}}({\textbf{U}})\) is defined as (3.2), where the block-matrix vector \({\textbf{U}}=(U_1^T,U_2^T,\cdots ,U_s^T)^T\in {\mathbb {R}}^{n\times r}\), \(U_t\in {\mathbb {R}}^{n_t\times r}\) for all \(t\in [s]\).
-
1)
\(\langle \nabla ^2 f_{{\mathcal {S}}} (\mathbf {{\textbf{U}}}^{*})\mathbf {{\textbf{W}}},\mathbf {{\textbf{W}}}\rangle >0\) for any \(\mathbf {{\textbf{W}}}\in {\mathbb {R}}^{n\times r}\), where \(\mathbf {{\textbf{U}}}^{*}\) is a local minimum point of \(f_{{\mathcal {S}}}(\mathbf {{\textbf{U}}})\);
-
2)
there is a neighborhood \(N({\textbf{U}}^{*})\) of \({\textbf{U}}^{*}\) and a constant \(L>0\) such that for any \({\textbf{U}},\ {\textbf{V}}\in N({\textbf{U}}^{*})\)
$$\begin{aligned} \Vert {\nabla }^2f_{{\mathcal {S}}}({\textbf{U}})-{\nabla }^2f_{{\mathcal {S}}}({\textbf{V}})\Vert _F\le {L}\Vert {\textbf{U}}-{\textbf{V}}\Vert _F. \end{aligned}$$
Lemma 4.3
If the function \(f_{{\mathcal {S}}}({\textbf{U}})\) satisfies the second condition of Assumption 4.1, then for any \({\textbf{U}},{\textbf{V}},{\textbf{W}}\in {\mathbb {R}}^{n\times r}\),
Forthermore, if \({\nabla }^2f_{{\mathcal {S}}}({\textbf{U}})\) is invertible and for every \(\varepsilon \in (0,\frac{1}{L\Vert ({\nabla }^2f_{{\mathcal {S}}}({\textbf{U}}))^{-1}\Vert _F})\), for any \({\textbf{V}}\) and \({\textbf{W}}\) that satisfy \(\Vert {\textbf{U}}-{\textbf{W}}\Vert _F <\varepsilon \) and \(\Vert {\textbf{U}}-{\textbf{V}}\Vert _F <\varepsilon , \) respectively, then there are constants \(\beta>\alpha >0\) related to \({\textbf{U}}\) such that
Proof
For any \({\textbf{U}},{\textbf{V}},{\textbf{W}}\in {\mathbb {R}}^{n\times r}\), according to the Cauchy-Schwarz inequality,
For every given \(\varepsilon \in (0,\frac{1}{L\Vert [{\nabla }^2f_{{\mathcal {S}}}({\textbf{U}})]^{-1}\Vert _F})\), any \({\textbf{U}}\) and \({\textbf{V}}\) satisfying
we have that
Let \(\beta =\Vert \nabla ^2f_{{\mathcal {S}}}({\textbf{U}})\Vert _F+L\varepsilon \), then the second inequality of (4.9) holds. Using the properties of the norm, we have that
Let \(\alpha =(\Vert 1/\Vert {(\nabla ^2f_{{\mathcal {S}}}({\textbf{U}}))}^{-1}\Vert _F-L\varepsilon )\), then The first inequality of (4.9) holds. The proof is completed. \(\square \)
Theorem 4.1
Assume that the function \(f_{{\mathcal {S}}}({\textbf{U}})\) satisfies the Assumption 4.1, \(\{{\mathcal {B}}^k\}\) and \(\{{\textbf{U}}^k\}\) are obtained by Algorithm 3 without line search (that is, the step size \(\alpha _k\) is uniformly 1), and \(\{{\textbf{U}}^k\}\) converges to a local minimum point \({\textbf{U}}^{*}\) of \(f_{{\mathcal {S}}}({\textbf{U}})\). Then the point sequence \(\{{\textbf{U}}^k\}\) super-linear converges to \({\textbf{U}}^{*}\) if and only if
Proof
(\(\Leftarrow \)) First we prove the sufficiency. Let \({\textbf{S}}^k={\textbf{U}}^{k+1}-{\textbf{U}}^k\). Then
According to the triangle inequality and Lemma 4.3, for any \( k\ge 0\), we have that
If (4.10) holds, substituting (4.10) and the assumption \(\lim \limits _{k\rightarrow \infty }{{\textbf{U}}^k}={\textbf{U}}^{*}\) into (4.11), we get
Because \({\nabla }^2f_{{\mathcal {S}}}({\textbf{U}}^{*})\) is invertible and \({\textbf{U}}^k\rightarrow {\textbf{U}}^{*}\), according to Lemma 4.3, there exist a real number \(\alpha >0\) and an integer \(k_0>0\), for any integer \( k\ge {k_0}\), such that
Thus
Since the left limit of the above inequality is zero by (4.12), so the right limit of the above inequality is also zero, i.e.,
It follows that
which means that \(\{{\textbf{U}}^k\}\) super-linear converges to \({\textbf{U}}^{*}\).
(\(\Rightarrow \)) Next we prove the necessity. By Lemma 4.3, there exist a real number \(\beta >0\) and an integer \(k_0>0\), for any integer \( k\ge {k_0}\), such that
Because \(\{{\textbf{U}}^k\}\) super-linear converges \({\textbf{U}}^{*}\), we have that
Then
Thus,the equation (4.10) holds. This completes the proof. \(\square \)
Based on the Theorem 4.1, we give a theorem of super-linear convergence of the Algorithm 3.
Theorem 4.2
Let \(\{{\mathcal {B}}^k\}\) and \(\{{\textbf{U}}^k\}\) be obtained by Algorithm 3. Suppose \(f_{{\mathcal {S}}}({\textbf{U}})\) satisfies the Assumption 4.1, \(\{{\textbf{U}}^k\}\) converges to local minimum point \({\textbf{U}}^{*}\), and
Then, \(\{{\textbf{U}}^k\}\) converges to \({\textbf{U}}^{*}\) super-linearly if and only if step size \(\{\alpha _k\}\) converges to 1.
Proof
First, we prove the sufficiency. From the trigonometric inequality, we get
If (4.13) holds, and \(\{\alpha _k\}\) converges to 1, then the limit on the right side of the above inequality is equal to 0 when \(k\rightarrow \infty \). It follows that
By the Theorem 4.1 and (4.14), we can get that \(\{{\textbf{U}}^k\}\) superlinearly converges to \({\textbf{U}}^{*}\).
Next, we prove the necessity. If \(\{{\textbf{U}}^k\}\) converges to \({\textbf{U}}^{*}\) super-linearly, by the Theorem 4.1, it is followed that (4.14) holds. Since \({\mathcal {B}}^k({\textbf{U}}^{k+1}-{\textbf{U}}^k)=-\alpha _k\nabla f_{{\mathcal {S}}}({\textbf{U}}^k)\), by (4.13), we have that
Hence,
By Assumption 4.1 and Lemma 4.3, there exist a real number \(\alpha >0\) and an integer \(k_0>0\), for any integer \( k\ge {k_0}\), such that
So
By (4.15) and (4.16), we have that
Since again \(\{{\textbf{U}}^k\}\) super-linearly converges to \({\textbf{U}}^{*}\), so
Hence \(\lim \limits _{k\rightarrow \infty }\alpha |\alpha _k-1|=0\), i.e., \(\lim \limits _{k\rightarrow \infty }\alpha _k=1\). This completes the proof. \(\square \)
5 Discrimination of positive partially symmetric CP decompositions
Let \({\mathcal {S}}\in S[{\textbf{m}}]{\mathbb {R}}[{\textbf{n}}]\). When all orders \(m_1,m_2,\cdots ,m_s\) are even, according to the Theorem 2.1, the tensor \({\mathcal {S}}\) may not have positive partially symmetric CP decomposition. In this case, we cannot obtain its partially symmetric CP decomposition by Algorithm 3. Therefore, we discuss how to identify whether even order partially symmetric tensors have positive partially symmetric CP decompositions in real number field.
Theorem 5.1
Let \({\textbf{m}}=(m_1,m_2,\cdots ,m_s)\), \({\textbf{n}}=(n_1,n_2,\cdots ,n_s)\), and \({\mathcal {S}}\in S[{\textbf{m}}]{\mathbb {R}}[{\textbf{n}}]\) be a partially symmetric tensor. For any vectors \({\textbf{x}}^{(i)}\in {\mathbb {R}}^{n_i}\) and \({\textbf{y}}^{(j)}\in {\mathbb {R}}^{n_j}\), \(i,j\in [s]\), denote
where \(k\in \{0,1,\cdots ,m_t\}.\) Then,
Proof
Let \(I_k:=\{{\textbf{i}}_t=(i_{t,1},i_{t,2},\cdots ,i_{t,m_t})|i_{t,1},\cdots , i_{t,m_t}\in [n_t]\}\), \(t\in [s]\). For any vectors \({\textbf{x}}^{(i)}\in {\mathbb {R}}^{n_i}\) and \({\textbf{y}}^{(j)}\in {\mathbb {R}}^{n_j}\), \(i,j\in [s]\),
For \(k=0,1,2,\cdots ,m_t\), it is obtained that
Hence,
This completes the proof. \(\square \)
Theorem 5.2
Let \({\mathcal {S}}_1\), \({\mathcal {S}}_2\in S[{\textbf{m}}]{\mathbb {R}}[{\textbf{n}}]\) be two partially symmetric tensors. Assume that all orders \(m_1,m_2,\cdots ,m_s\) are even. Then \(\langle {\mathcal {S}}_1,{\mathcal {S}}_2\rangle \ge 0\) if \({\mathcal {S}}_1\) and \({\mathcal {S}}_2\) both have positive partially symmetric CP decomposition.
Proof
Since \({\mathcal {S}}_1,{\mathcal {S}}_2\in S[{\textbf{m}}]{\mathbb {R}}[{\textbf{n}}]\), and they have positive partially symmetric CP decomposition. Hence, \({\mathcal {S}}_1\) and \({\mathcal {S}}_2\) can be represented as the following form
where \({\textbf{u}}_t^{(k)},{\textbf{v}}_t^{(l)}\in {\mathbb {R}}^{n_t}\), \(k\in [R_1],l\in [R_2], t\in [s]\).
Then, the inner product of \({\mathcal {S}}_1\) and \({\mathcal {S}}_2\) is
Since orders \(m_1,m_2,\cdots ,m_s\) are even, \(\left( \langle {\textbf{u}}^{(k)}_t,{\textbf{v}}^{(l)}_t\rangle \right) ^{m_t}\ge 0\), for all \(k\in [R_1],l\in [R_2], t\in [s]\). Hence, it is followed that \(\langle {\mathcal {S}}_1,{\mathcal {S}}_2\rangle \ge 0\). The proof is completed. \(\square \)
Assume that \(\{U_1,U_2,\cdots ,U_s\}\) is a tuple of factor matrices of \(\hat{{\mathcal {S}}}\in S[{\textbf{m}}]{\mathbb {R}}[{\textbf{n}}]\), i.e.,
In the next, we see the object function \(F_{{\mathcal {S}}}(\hat{{\mathcal {S}}})=\Vert {\mathcal {S}}-\hat{{\mathcal {S}}}\Vert _F^2\) as a function of factor matrix \(U_t, t\in [s]\), i.e.,
For convenience, we denote
Next, in order to study the convexity of the function \(F_{{\mathcal {S}}}(U_t)\), we derive a second-order Taylor formula of \(F_{{\mathcal {S}}}(U_t)\).
Theorem 5.3
Let \({\mathcal {S}}\in S[{\textbf{m}}]{\mathbb {R}}[{\textbf{n}}]\) be a partially symmetric tensor and \(F_{{\mathcal {S}}}(U_t)\) is defined as (5.1). Let
Then, the second-order Taylor formula of the function \(F_{{\mathcal {S}}}(U_t)\) is as follows
Proof
From (5.1), \(F_{{\mathcal {S}}}{(U_t+\varDelta U_t)}=\Vert {\mathcal {S}}-\hat{{\mathcal {S}}}[{\left( U_t+\varDelta U_t\right) }^{\times m_t}]\Vert _F^2\). Then,
Now, we compute the first degree term and the second degree term of \(\triangle U_t\) in the right hand side of (5.5). Since,
According to the Theorem 5.1, we can get that
Since,
And, for all \(k,l\in [R]\) and \(t\in [s]\),
Let
Then, by (5.7) and (5.8), we have that
Hence, by (5.6) and (5.9), the first degree term and the second degree term of \(\varDelta U_t\) in the right hand side of (5.5) are as follows, respectively.
This completes the proof. \(\square \)
It is well known that (1) if \(U_t\) is a stationary point of function \(F_{{\mathcal {S}}}(U_t)\), then \(L_1=0\) for any \(\varDelta U_t\); (2) the function \(F_{{\mathcal {S}}}(U_t)\) is convex at the point \(U_t\) if and only if \(L_2\ge 0\) for any \(\varDelta U_t\). From this, we will discuss the discrimination of partially symmetric tensors with the positive decomposition.
Theorem 5.4
Assume that orders \(m_1,\cdots ,m_s\) are even and \({\mathcal {S}}\in S[{\textbf{m}}]{\mathbb {R}}[{\textbf{n}}]\) has positive partially symmetric CP decomposition. Then, zero tensor \({\mathcal {O}}\in S[{\textbf{m}}]{\mathbb {R}}[{\textbf{n}}]\) is the global minimum point of the function \(F_{-{\mathcal {S}}}(\hat{{\mathcal {S}}})\), and the global minimum value is equal to \(F_{-{\mathcal {S}}}({\mathcal {O}})=\Vert {\mathcal {S}}\Vert _F^2\).
Proof
Since \(F_{-{\mathcal {S}}}(U_t)=\Vert {\mathcal {S}}+\hat{{\mathcal {S}}}\Vert _F^2\). By Theorem 5.3, \(L_1\) and \(L_2\) of \(F_{-{\mathcal {S}}}(U_t)\) are as follows
Since \({\mathcal {S}}\) has positive partially symmetric CP decomposition, and orders \(m_1\), \(m_2,\cdots ,m_s\) are even. According to Theorem 5.2, if \(U_i\ne {\textbf{0}}\) for all \(i\in [s],\ i\ne t\), then \(\langle {\mathcal {S}}, \hat{{\mathcal {S}}}[{\varDelta U_t}^{\times 2},U_t^{\times (m_t-2)}]\rangle \) is nonnegative and \(\langle \hat{{\mathcal {S}}},\hat{{\mathcal {S}}}[{\varDelta U_t}^{\times 2},U_t^{\times (m_t-2)}]\rangle \) is positive if \(U_t\not = {\textbf{0}} \). Hence, \(L_2\) is positive at \(U_t\) for any \(\varDelta U_t\), i.e., the function \(F_{-{\mathcal {S}}}(U_t)\) is convex for every \(t\in [s]\) if \(U_i\ne {\textbf{0}}\) for all \(i\in [s],\ i\ne t\). Since \(\hat{{\mathcal {S}}}={\mathcal {O}}\) if and only if there exists \(U_i={\textbf{0}}\) for some \(i\in [s]\). Hence, \(\hat{{\mathcal {S}}}={\mathcal {O}}\) is the global minimum point of the function \(F_{-{\mathcal {S}}}(\hat{{\mathcal {S}}})\) and the global minimum value is \(F_{-{\mathcal {S}}}({\mathcal {O}})=\Vert {\mathcal {S}}\Vert _F^2\). This completes the proof. \(\square \)
Assume that \({\mathcal {S}}\in S[{\textbf{m}}]{\mathbb {R}}[{\textbf{n}}]\) be a partially symmetric tensor and its orders are even. From the Theorem 5.4, \(U_t=\textbf{0}\) is the global minimum point of the function \(F_{-{\mathcal {S}}}(U_t)\), and the global minimum value is equal to \(\Vert {\mathcal {S}}\Vert _F^2\), if partially symmetric tensor \({\mathcal {S}}\) has positive CP decomposition. According to Theorem 5.4, we have the corollary in the following.
Corollary 5.1
Assume that \({\mathcal {S}}\in S[{\textbf{m}}]{\mathbb {R}}[{\textbf{n}}]\) and its orders are even. The function \(F_{-{\mathcal {S}}}(\hat{{\mathcal {S}}})\) is defined as in (5.1). Then, the partially symmetric tensor \({\mathcal {S}}\) has no positive partially symmetric CP decomposition, if zero tensor \({\mathcal {O}}\) is not the global minimum point of the function \(F_{-{\mathcal {S}}}(\hat{{\mathcal {S}}})\).
Proof
These results can be obtained directly form Theorem 5.4. \(\square \)
When dealing with partially symmetric rank-R approximation of \({\mathcal {S}}\in S[{\textbf{m}}]{\mathbb {R}}[{\textbf{n}}]\) with even orders, i.e., \(m_t\) for all \(t\in [s]\) are even, we construct a new tensor \(\tilde{{\mathcal {S}}}\in S[1,{\textbf{m}}]{\mathbb {R}}[1,{\textbf{n}}]\) satisfying
We compute the partially symmetric rank-R approximation of \(\tilde{{\mathcal {S}}}\) by the Algorithm 3 as
where \(\tilde{U}_t=\left( \tilde{{\textbf{u}}}_t^{(1)},\tilde{{\textbf{u}}}_t^{(2)},\cdots ,\tilde{{\textbf{u}}}_t^{(R)}\right) \), \(t\in [s]\). Compute \({\textbf{u}}^{(t)}_k\) and \(\lambda _k\), \(t\in [s]\), \(k\in [R]\) by the following formula
So, we obtain that
That is, the general partially symmetric rank-R approximation of \({\mathcal {S}}\) is
We give an algorithm to calculate general partially symmetric rank-R approximation of partially symmetric tensors with BFGS algorithm as follows.

6 Numerical examples
We give some examples in this section. All experiments on a laptop with an Intel(R) Core(TM) i7-8550U CPU and 8.00 GB of RAM, using MATLAB 2018b on a Microsoft Win 10. All tensor computations use the tensor toolbox for MATLAB, Version [29].
Example 6.1
(A random tensor) Consider a partially symmetric CP decomposition of a tensor \({\mathcal {S}}\in S[2,2]{\mathbb {R}}[3,2]\). It is obtained randomly as follows
Firstly, we discuss whether there is a positive partially symmetric CP decomposition of tensor \({\mathcal {S}}\). We compute the minimum value of \(F_{-{\mathcal {S}}}(\hat{{\mathcal {S}}})\) defined as in (5.1) for all \(R=1,2\cdots ,6\) by Algorithm 3 and obtain the minimum values min \(F_{-{\mathcal {S}}}(\hat{{\mathcal {S}}})\), norms of the minimum points \(\Vert \hat{{\mathcal {S}}}\Vert _F\) and running time as in Table 1. From the datum in Table 1, it can be seen that the minimum points \(\hat{{\mathcal {S}}}\) are not zero tensor. Hence, tensor \({\mathcal {S}}\) has no positive partially symmetric CP decomposition by Corollary 5.1.
Secondly, we compute the positive partially symmetric rank-R approximation of \({\mathcal {S}}\) by the Algorithm 3 for all \(R=1,2\cdots ,6\). We obtain in the minimum values min \(F_{{\mathcal {S}}}(\hat{{\mathcal {S}}})\) and running time as in Table 2. It can be seen from Table 2 that the minimum values of the objective function are always greater than 14.
Finally, we consider the general partially symmetric CP decomposition of tensor \({\mathcal {S}}\). We compute the partially symmetric rank-R approximation of the tensor \({{\mathcal {S}}}\) by the Algorithm 4 for \(R=1,2,\cdots ,6\) and obtain the minimum values min \(F_{{\mathcal {S}}}(\hat{{\mathcal {S}}})\) and running time as in Table 3.
Therefore, we obtain a general partially symmetric CP decomposition of the tensor \({\mathcal {S}}\) with \(R=6\) as
where \(\lambda _k\in {\mathbb {R}}\), \({\textbf{u}}_k\in {\mathbb {R}}^3\) and \({\textbf{v}}_k\in {\mathbb {R}}^2\) for \(k=1,2,\cdots ,6\) are as in the Table 4
Example 6.2
(Comparison of convergence speed between the gradient descent method and the BFGS method) Partially symmetric tensor \({\mathcal {S}}\in S[1,2]{\mathbb {R}}[n_1,n_2]\) is given by \( {\mathcal {S}}=[\![U_1,U_2^{\times 2}]\!] \), where \(U_1\in {\mathbb {R}}^{n_1\times R}\), \(U_2\in {\mathbb {R}}^{n_2\times R}\) are randomly obtained. We use Algorithm 2 and Algorithm 3 to calculate the rank-R approximation of tensor \({\mathcal {S}}\), that is, its structure preserving CP decomposition. The termination condition of both methods are that the norm of gradient is less \(10^{-5}\), or the number of iteration reaches 5000. We calculate four types of tensors: \((n_1, n_2, R)=(5,5,3)\), (5, 5, 5), (10, 10, 5), (10, 10, 10). For each type, we calculate 10 times. The results of numerical calculation are shown in Table 5, where ‘Iter’ denotes the average number of iterations, ‘Time’ denotes average running time and ‘Error’ denotes average value of \(\Vert {\mathcal {S}}-\hat{{\mathcal {S}}}\Vert _F\), respectively. Form Table 5, we see that the running time of BFGS method is less than that of gradient descent method.
Example 6.3
(Rank partially symmetric CP decomposition) Assume orders \({\textbf{m}}\) of \({\mathcal {S}}\in S[{\textbf{m}}]{\mathbb {R}}[{\textbf{n}}]\) are even. If the tensor \({\mathcal {S}}\) has a positive partially symmetric CP decomposition, must its rank partially symmetric CP decomposition be a positive CP decomposition? Here, we assume that the tensor \({\mathcal {S}}\in S[2,2,2]{\mathbb {R}}[3,4,5]\) has the following form
where \({\textbf{u}}_k\in {\mathbb {R}}^{3}\), \({\textbf{v}}_k\in {\mathbb {R}}^{4}\) and \({\textbf{w}}_k\in {\mathbb {R}}^{5}\) are generated randomly unit vectors for all \(k\in [r]\).
Let \(r=5\). The tensor \({\mathcal {S}}\) is obtained randomly as in Table 6.
We first compute the partially symmetric rank of \({\mathcal {S}}\) by Algorithm 4. We compute the general partially symmetric rank-R approximation by the Algorithm 4 for \(R=1,2,\cdots ,5\) as in Table 7. It is clear that the partially symmetric rank of tensor \({\mathcal {S}}\) is equal to 5.
Furthermore, we obtain a general partially symmetric rank decomposition of the tensor \({\mathcal {S}}\) with \(R=5\) as in Table 8. It is observed that the rank partially symmetric CP decomposition is also a positive CP decomposition. When we take \(r=10\) or 15, the results are the same. Hence, we have the result that if a tensor \({\mathcal {S}}\) has a positive partially symmetric CP decomposition, then its rank partially symmetric CP decomposition must be a positive CP decomposition.
Example 6.4
(Comparison with ALS method) Given a random nonsymmetric tensor \({\mathcal {S}}\in S[1,1,1]{{\mathbb {R}}}[3,4,5]\) as in the following. We compare the compute efficient of the ALS method and the BFGS method.
We compute the CP-rank \( \textrm{rank} ({\mathcal {S}})=7\) by Algorithm 3. Hence, we take \(R=7\) to compute its CP decomposition ten times by the ALS method and the BFGS method, respectively. For each time, the initial point is obtained randomly. For the ALS method, the program code “cp_als” comes from the tensor toolbox [29]. The termination condition of both algorithms is that the iterative steps reaches 10,000 or the absolute error \(\Vert {\mathcal {S}}-\hat{{\mathcal {S}}}\Vert _F\) is less than \(10^{-5}\). We obtain the number of iteration ‘it-number’, running time and the absolute error \(\Vert {{\mathcal {S}}-\hat{{\mathcal {S}}}}\Vert _F\) in Table 9. The average running time of Algorithm 3 and ALS algorithm is 1.4743 seconds and 8.8574 seconds, respectively. The numerical results show that the BFGS method is more effective than the ALS method in terms of calculation accuracy and calculation speed.
Example 6.5
(Comparison with ALS method) We compare the stability and computing speed of the BFGS algorithm and the ALS algorithm. The BFGS algorithm is the structure preserving CP decomposition method proposed in this paper, while the ALS algorithm is the usual CP decomposition method and does not have the structure preserving property. In the numerical example, partially symmetric tensors have the following form
where \({\textbf{u}}_k\in {\mathbb {R}}^{n_1}\) and \({\textbf{v}}_k\in {\mathbb {R}}^{n_2}\) and \({\textbf{w}}_k\in {\mathbb {R}}^{n_3}\) are generated randomly, for all \(k\in [R]\).
For each parameter tuple \(({\textbf{m}}, {\textbf{n}}, R)\), we randomly generate tensor \({\mathcal {S}}\) ten times, and use Algorithm 3 and the ALS algorithm to calculate their CP decomposition respectively, where the program code “cp_als” comes from the tensor toolbox [29]. The termination condition of both algorithms is that the iterative steps reaches 10,000 or the relative error \(\Vert {\mathcal {S}}-\hat{{\mathcal {S}}}\Vert _F/\Vert {\mathcal {S}}\Vert _F\) is less than \(10^{-5}\). We say a run is successful, if the relative error is less than \(10^{-5}\). We obtain the total running time and success times of each tuple \(({\textbf{m}}, {\textbf{n}}, R)\) in Table 10. The numerical results show that the BFGS method is more stable and faster than the ALS method.
7 Conclusion
In this paper, we study the numerical problem of structure preserving rank-R approximation and structure preserving CP decomposition of partially symmetric tensors. For the problem of structure preserving rank-R approximation, we deduce the gradient formula of the objective function, obtain the BFGS iterative formula with tensor form, propose a BFGS algorithm for positive partially symmetric rank-R approximation, and discuss the convergence of the algorithm. For the problem of structure preserving CP decomposition, we give a necessary condition for partially symmetric tensors with even orders to have positive partially symmetric CP decomposition, and design a general partially symmetric rank-R algorithm to obtain structure preserving CP decomposition. Finally, some numerical examples are given. We compute the partially symmetric CP decomposition of the random partially symmetric tensors. By some numerical examples, we find that if a tensor has a positive partially symmetric CP decomposition then its partially symmetric rank CP decomposition must be a positive CP decomposition. Meanwhile, in some numerical examples, we compare the BFGS algorithm proposed in this paper with the standard CP-ALS method.
When \(m_1, m_2, \ldots , m_s\) are all even numbers, it is difficult to judge and obtain the positive partially symmetric CP decomposition of \({\mathcal {S}}\). In particular, when \(m_1=m_2=\ldots =m_s=2\), the tensor \({\mathcal {S}}\) can be regarded as a real Hermitian tensor, and \({\mathcal {S}}\) has real Hermitian separability if and only if \({\mathcal {S}}\) has a positive partially symmetric CP decomposition, see reference [30].
Data Availability
We do not analyse or generate any datasets, because our work proceeds within a theoretical and mathematical approach.
References
Feng, J., Yang, L., Zhu, Q., Choo, K.: Privacy preserving tensor decomposition over encrypted data in a federated cloud environment. IEEE T. Depend. Secure. 17, 857–868 (2020)
Song, Q., Ge, H., Caverlee, J., Xu, X.: Tensor completion algorithms in big data analytics. ACM T. Knowl. Discov. D. 13, 1–48 (2019)
Cichocki, A., Mandic, D.P., Lathauwer, L.D., Zhou, G., Zhao, Q., Caiafa, C.F.: Tensor decompositions for signal processing applications: From two-way to multiway component analysis. IEEE Signal Proc. Mag. 32, 145–163 (2015)
Sidiropoulos, N., Lathauwer, L.D., Fu, X., Huang, K., Papalexakis, E.E., Faloutsos, C.: Tensor decomposition for signal processing and machine learning. IEEE Trans. Signal Proces. 65, 3551–3582 (2017)
Veganzones, M.A., Cohen, J.E., Cabral, F.R., Chanussot, J., Comon, P.: Nonnegative tensor CP decomposition of hyperspectral data. IEEE T. Geosci. Remote. 54, 2577–2588 (2016)
Xu, Y., Wu, Z., Chanussot, J., Comon, P., Wei, Z.: Nonlocal coupled tensor CP decomposition for hyperspectral and multispectral image fusion. IEEE T. Geosci. Remote. 58, 348–362 (2020)
Hillar, C., Lim, L.-H.: Most tensor problems are NP-hard. J. ACM. 60(6) (2013)
Hitchcock, F.L.: The expression of a tensor or a polyadic as a sum of products. J. Math. Phys. 6, 164–189 (1927)
Hitchcock, F.L.: Multiple invariants and generalized rank of a p-way matrix or tensor. J. Math. Phys. 7, 39–79 (1927)
Boyer, R., Lathauwer, L.D., Meraim, K.A.: Higher order tensor-based method for delayed exponential fitting. IEEE T. Signal Proces. 55, 2795–2809 (2007)
Singh, S., Vidal, G.: Global symmetries in tensor network states: symmetric tensors versus minimal bond dimension. Phys. Rev. B. 88, 115–147 (2013)
Uemura, W., Sugino, O.: Symmetric tensor decomposition description of fermionic many-body wave functions. Phys. Rev. Lett. 109, 253001 (2012)
Comon, P., Golub, G.H., Lim, L.-H., Mourrain, B.: Symmetric tensors and symmetric tensor rank. SIAM J. Matrix Anal. Appl. 30, 1254–1279 (2008)
Brachat, J., Comom, P., Mourrain, B., Tsigaridas, E.: Symmetric tensor decomposition. Linear Algebra Appl. 433, 1851–1872 (2010)
Kolda, T.G.: Numerical optimization for symmetric tensor decomposition. Math. Program. 151, 225–248 (2015)
Nie, J.: Generating polynomials and symmetric tensor decompositions. Found. Comput. Math. 17, 423–465 (2017)
Liu, H.: Symmetric tensor decomposition by alternating gradient descent. Numer. Linear Algera Appl. 29, e2406 (2022)
Li, S., Li, C., Li, Y.: M-eigenvalue inclusion intervals for a fourth-order partially symmetric tensor. J. Comput. Appl. Math. 356, 391–401 (2019)
Ballico, E., Bernardi, A., Christandl, M., Gesmundo, F.: On the partially symmetric rank of tensor products of \(w\)-states and other symmetric tensors. Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur 30, 93–124 (2019)
Carroll, J.D., Chang, J.J.: Analysis of individual differences in multidimensional scaling via an n-way generalization of “eckart-young’’ decomposition. Psychometrika 35, 283–319 (1970)
Sidiropoulos, N., Bro, R.: On the uniqueness of multilinear decomposition of n-way arrays. J. Chemometr. 14, 229–239 (2000)
Li, N., Navasca, C., Glenn, C.: Iterative methods for symmetric outer product tensor decomposition. Electron. Trans. Numer. Anal. 44, 124–139 (2015)
Ni, G., Li, Y.: A semidefinite relaxation method for partially symmetric tensor decomposition. Math. Oper. Res. (2022). https://doi.org/10.1287/moor.2021.1231
Kolda, T.G., Bader, B.W.: Tensor decompositions and applications. SIAM Rev. 51, 455–500 (2009)
Wang, X., Che, M., Wei, Y.: Best rank-one approximation of fourth-order partially symmetric tensors by neural network. Numer. Math. Theor. Meth. Appl. 11, 673–700 (2018)
Gesmundo, F., Oneto, A., Ventura, E.: Partially symmetric variants of Comon’s problem via simultaneous rank. SIAM J. Matrix Anal. Appl. 40, 1453–1477 (2019)
Landsberg, J.: Tensors: Geometry and Applications. Graduate Student Mathematics, vol. 128. American Mathematical Society, Providence (2011)
Nocedal, J., Wright, S.J.: Numerical Optimization. Springer Series in Operations Research and Financial Engineering, 2nd edn. Springer, New York (2006)
Bader, B. W., Kolda, T. G.: Matlab tensor toolbox version 2.5. http://www.sandia.gov/~tgkolda/TensorToolbox/ (2012)
Nie, J., Yang, Z.: Hermitian tensor decompositions. SIAM J. Matrix Anal. Appl. 41(3), 1115–1144 (2020)
Acknowledgements
The authors would like to thank two anonymous referees for their valuable suggestions, which helped us to improve this manuscript. This work is supported by the National Natural Science Foundation of China (No. 11871472).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Chen, C., Ni, G. & Yang, B. Partially symmetric tensor structure preserving rank-R approximation via BFGS algorithm. Comput Optim Appl 85, 621–652 (2023). https://doi.org/10.1007/s10589-023-00471-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-023-00471-6