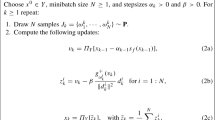1 Introduction

In various practical scenarios, derivative-free algorithms are the single way to solve optimization problems for which no derivative information can be computed or approximated. Among the various classes of such schemes, direct search is one of the most popular, due to its simplicity, robustness, and ease of parallelization. Direct-search methods [2, 10, 22] explore the objective function along suitably chosen sets of directions, called polling directions. When there are no constraints on the problem variables and the objective function is smooth, those directions must provide a suitable angle approximation to the unknown negative gradient, and this is guaranteed by assuming that the polling vectors positively span the whole space (by means of nonnegative linear combinations). In the presence of constraints, such directions must conform to the shape of the feasible region in the vicinity of the current feasible point, and are typically given by the positive generators of some approximate tangent cone identified by nearby active constraints. When the feasible region is polyhedral, it is possible to decrease a smooth objective function value along such directions without violating the constraints, provided a sufficiently small step is taken.

Bound constraints are a classical example of such a polyhedral setting. Direct-search methods tailored to these constraints have been introduced by Lewis and Torczon [26], where polling directions can (and must) be chosen among the coordinate directions and their negatives, which naturally conform to the geometry of such a feasible region. A number of other methods have been proposed and analyzed based on these polling directions (see [15, 17, 30] and [21, Chapter 4]).

In the general linearly constrained case, polling directions have to be computed as positive generators of cones tangent to a set of constraints that are nearly active (see [23, 27]). The identification of the nearly active constraints can be tightened to the size of the step taken along the directions [23], and global convergence is guaranteed to a true stationary point as the step size goes to zero. In the presence of constraint linear dependence, the computation of these positive generators is problematic and may require enumerative techniques [1, 25, 34], although the practical performance of the corresponding methods does not seem much affected. Direct-search methods for linearly constrained problems have been successfully combined with global exploration strategies by means of a search step [11, 37, 38].

Several strategies for the specific treatment of linear equality constraints have also been proposed. For example, one can remove these constraints through a change of variables [3, 14]. Another possibility is to design an algorithm that explores the null space of the linear equality constraints, which is also equivalent to solving the problem in a lower-dimensional, unconstrained subspace [25, 29]. Such techniques may lead to a less separable problem, possibly harder to solve.

All aforementioned strategies involve the deterministic generation of the polling directions. Recently, it has been shown in [19] that the random generation of the polling directions outperforms the classical choice of deterministic positive spanning sets for unconstrained optimization (whose cardinality is at least \(n+1\), where n is the dimension of the problem). Inspired by the concept of probabilistic trust-region models [6], the authors in [19] introduced the concept of probabilistic descent, which essentially imposes on the random polling directions the existence of a direction that makes an acute angle with the negative gradient with a probability sufficiently large conditioning on the history of the iterations. This approach has been proved globally convergent with probability one. Moreover, a complexity bound of the order \(n \epsilon ^{-2}\) has been shown (with overwhelmingly high probability) for the number of function evaluations needed to reach a gradient of norm below a positive threshold \(\epsilon \), which contrasts with the \(n^2 \epsilon ^{-2}\) bound of the deterministic case [39] (for which the factor of \(n^2\) cannot be improved [12]). A numerical comparison between deterministic and random generation of the polling directions also showed a substantial advantage for the latter: using only two directions led to the best observed performance, as well as an improved complexity bound [19].

In this paper, motivated by these results for unconstrained optimization, we introduce the notions of deterministic and probabilistic feasible descent for the linearly constrained setting, essentially by considering the projection of the negative gradient on an approximate tangent cone identified by nearby active constraints. For the deterministic case, we establish a complexity bound for direct search (with sufficient decrease) applied to linearly constrained problems with smooth objectives—left open in the literature until now. We then prove that direct search based on probabilistic feasible descent enjoys global convergence with probability one, and derive a complexity bound with overwhelmingly high probability. In the spirit of [19], we aim at identifying randomized polling techniques for which the evaluation complexity bound improves over the deterministic setting. To this end, two strategies are investigated: one where the directions are a random subset of the positive generators of the approximate tangent cone; and another where one first decomposes the approximate tangent cone into a subspace and a cone orthogonal to the subspace. In the latter case, the subspace component (if nonzero) is handled by generating random directions in it, and the cone component is treated by considering a random subset of its positive generators. From a general complexity point of view, both techniques can be as expensive as the deterministic choices in the general case. However, our numerical experiments reveal that direct-search schemes based on the aforementioned techniques can outperform relevant instances of deterministic direct search. Throughout the paper, we particularize our results for the cases where there are only bounds on the variables or there are only linear equality constraints: in these cases, the good practical behavior of probabilistic descent is predicted by the complexity analysis.

We organize our paper as follows. In Sect. 2, we describe the problem at hand as well as the direct-search framework under consideration. In Sect. 3, we motivate the concept of feasible descent and use this notion to derive the already known global convergence of [23]—although not providing a new result, such an analysis is crucial for the rest of the paper. It allows us to establish right away (see Sect. 4) the complexity of a class of direct-search methods based on sufficient decrease for linearly constrained optimization, establishing bounds for the worst-case effort when measured in terms of number of iterations and function evaluations. In Sect. 5, we introduce the concept of probabilistic feasible descent and prove almost-sure global convergence for direct-search methods based on it. The corresponding worst-case complexity bounds are established in Sect. 6. In Sect. 7, we discuss how to take advantage of subspace information in the random generation of the polling directions. Then, we report in Sect. 8 a numerical comparison between direct-search schemes based on probabilistic and deterministic feasible descent, which enlightens the potential of random polling directions. Finally, conclusions are drawn in Sect. 9.

We will use the following notation. Throughout the document, any set of vectors \(V = \{v_1,\dots ,v_m\} \subset \mathbb {R}^n\) will be identified with the matrix \(\left[ v_1 \cdots v_m \right] \in \mathbb {R}^{n \times m}\). We will thus allow ourselves to write \(v \in V\) even though we may manipulate V as a matrix. \({{\,\mathrm{Cone}\,}}(V)\) will denote the conic hull of V, i.e., the set of nonnegative combinations of vectors in V. Given a closed convex cone K in \(\mathbb {R}^n\), \(P_K[x]\) will denote the uniquely defined projection of the vector x onto the cone K (with the convention \(P_{\emptyset }[x]=0\) for all x). The polar cone of K is the set \(\{x: y^\top x \le 0, \forall y \in K\}\), and will be denoted by \(K^{\circ }\). For every space considered, the norm \(\Vert \cdot \Vert \) will be the Euclidean one. The notation \(\mathcal {O}(A)\) will stand for a scalar times A, with this scalar depending solely on the problem considered or constants from the algorithm. The dependence on the problem dimension n will explicitly appear in A when considered appropriate.

2 Direct search for linearly constrained problems

In this paper, we consider optimization problems given in the following form:

$$\begin{aligned} \begin{array}{ll} \displaystyle \min _{x \in \mathbb {R}^n} &{}f(x) \\ \mathrm {s.t.} &{} A x = b, \\ &{} \ell \le A_{\mathcal {I}} x \le u, \\ \end{array} \end{aligned}$$
(2.1)

where \(f: \mathbb {R}^n \rightarrow \mathbb {R}\) is a continuously differentiable function, \(A \in \mathbb {R}^{m \times n}\), \(A_{\mathcal {I}} \in \mathbb {R}^{m_{\mathcal {I}} \times n}\), \(b \in \mathbb {R}^m\), and \((\ell ,u) \in \left( \mathbb {R}\cup \left\{ -\infty ,\infty \right\} \right) ^{m_{\mathcal {I}}}\), with \(\ell < u\). We consider that the matrix A can be empty (i.e., m can be zero), in order to encompass unconstrained and bound-constrained problems into this general formulation (when \(m_{\mathcal {I}} = n\) and \(A_{\mathcal {I}}=I_n\)). Whenever \(m \ge 1\), we consider that the matrix A is of full row rank.

We define the feasible region as

$$\begin{aligned} \mathcal {F} = \left\{ x \in \mathbb {R}^n: \ Ax=b,\ \ell \le A_{\mathcal {I}} x \le u \right\} . \end{aligned}$$

The algorithmic analysis in this paper requires a measure of first-order criticality for Problem (2.1). Given \(x \in \mathcal {F}\), we will work with

$$\begin{aligned} \chi (x) {\mathop {=}\limits ^{\mathrm {def}}} \max _{\begin{array}{c} x + d \in \mathcal {F} \\ \Vert d\Vert \le 1 \end{array}} d^\top \left[ -\nabla f(x)\right] . \end{aligned}$$
(2.2)

The criticality measure \(\chi \left( \cdot \right) \) is a non-negative, continuous function. For any \(x \in \mathcal {F}\), \(\chi (x)\) equals zero if and only if x is a KKT first-order stationary point of Problem (2.1) (see [40]). It has been successfully used to derive convergence analyses of direct-search schemes applied to linearly constrained problems [22]. Given an orthonormal basis \(W \in \mathbb {R}^{n \times (n-m)}\) for the null space of A, this measure can be reformulated as

$$\begin{aligned} \chi (x) = \max _{\begin{array}{c} x + W{\tilde{d}} \in \mathcal {F} \\ \left\| W{\tilde{d}}\right\| \le 1 \end{array}} {\tilde{d}}^\top [-W^\top \nabla f(x)] = \max _{\begin{array}{c} x + W{\tilde{d}} \in \mathcal {F} \\ \Vert {\tilde{d}}\Vert \le 1 \end{array}} {\tilde{d}}^\top [-W^\top \nabla f(x)] \end{aligned}$$
(2.3)

for any \(x \in \mathcal {F}\).

Algorithm 2.1 presents the basic direct-search method under analysis in this paper, which is inspired by the unconstrained case [19, Algorithm 2.1]. The main difference, due to the presence of constraints, is that we enforce feasibility of the iterates. We suppose that a feasible initial point is provided by the user. At every iteration, using a finite number of polling directions, the algorithm attempts to compute a new feasible iterate that reduces the objective function value by a sufficient amount (measured by the value of a forcing function\(\rho \) on the step size \(\alpha _k\)).

figure a

We consider that the method runs under the following assumptions, as we did for the unconstrained setting (see [19, Assumptions 2.2, 2.3 and 4.1]).

Assumption 2.1

For each \(k\ge 0\), \(D_k\) is a finite set of normalized vectors.

Similarly to the unconstrained case [19], Assumption 2.1 aims at simplifying the constants in the derivation of the complexity bounds. However, all global convergence limits and worst-case complexity orders remain true when the norms of polling directions are only assumed to be above and below certain positive constants.

Assumption 2.2

The forcing function \(\rho \) is positive, non-decreasing, and \(\rho (\alpha )=o(\alpha )\) when \(\alpha \rightarrow 0^+\). There exist constants \({\bar{\theta }}\) and \({\bar{\gamma }}\) satisfying \(0<{\bar{\theta }} <1 \le {\bar{\gamma }} \) such that, for each \(\alpha >0\), \(\rho (\theta \alpha ) \le {\bar{\theta }}\rho (\alpha )\) and \(\rho (\gamma \alpha ) \le {\bar{\gamma }}\rho (\alpha )\), where \(\theta \) and \(\gamma \) are given in Algorithm 2.1.

Typical examples of forcing functions satisfying Assumption 2.2 include monomials of the form \(\rho (\alpha ) = c\,\alpha ^q\), with \(c>0\) and \(q>1\). The case \(q=2\) gives rise to optimal worst-case complexity bounds [39].

The directions used by the algorithm should promote feasible displacements. As the feasible region is polyhedral, this can be achieved by selecting polling directions from cones tangent to the feasible set. However, our algorithm is not of active-set type, and thus the iterates may get very close to the boundary but never lie at the boundary. In such a case, when no constraint is active, tangent cones promote all directions equally, not reflecting the proximity to the boundary. A possible fix is then to consider tangent cones corresponding to nearby active constraints, as in [23, 25].

In this paper, we will make use of concepts and properties from [23, 27], where the problem has been stated using a linear inequality formulation. To be able to apply them to Problem (2.1), where the variables are also subject to the equality constraints \(Ax=b\), we first consider the feasible region \(\mathcal {F}\) reduced to the nullspace of A, denoted by \(\tilde{\mathcal {F}}\). By writing \(x={\bar{x}}+W{\tilde{x}}\) for a fix \({\bar{x}}\) such that \(A{\bar{x}}=b\), one has

$$\begin{aligned} \tilde{\mathcal {F}} = \left\{ {\tilde{x}} \in \mathbb {R}^{n-m}: \ell -A_{\mathcal {I}}{\bar{x}} \le A_{\mathcal {I}}W {\tilde{x}} \le u-A_{\mathcal {I}} {\bar{x}} \right\} , \end{aligned}$$
(2.4)

where, again, W is an orthonormal basis for \({{\,\mathrm{null}\,}}(A)\). Then, we define two index sets corresponding to approximate active inequality constraints/bounds, namely

$$\begin{aligned} \forall x={\bar{x}}+W{\tilde{x}},\qquad \left\{ \begin{array}{l} I_u(x,\alpha ) = \left\{ i: \left| u_i-[A_{\mathcal {I}} {\bar{x}}]_i - [A_{\mathcal {I}}W{\tilde{x}}]_i \right| \le \alpha \Vert W^\top A_{\mathcal {I}}^\top e_i\Vert \right\} \\ \\ I_\ell (x,\alpha ) = \left\{ i: \left| \ell _i-[A_{\mathcal {I}} {\bar{x}}]_i - [A_{\mathcal {I}}W{\tilde{x}}]_i \right| \le \alpha \Vert W^\top A_{\mathcal {I}}^\top e_i\Vert \right\} , \end{array} \right. \nonumber \\ \end{aligned}$$
(2.5)

where \(e_1,\dots ,e_{m_{\mathcal {I}}}\) are the coordinate vectors in \(\mathbb {R}^{m_{\mathcal {I}}}\) and \(\alpha \) is the step size in the algorithm. The indices in these sets contain the inequality constraints/bounds such that the Euclidean distance from x to the corresponding boundary is less than or equal to \(\alpha \). Note that one can assume without loss of generality that \(\Vert W^\top A_{\mathcal {I}}^\top e_i\Vert \ne 0\), otherwise given that we assume that \(\mathcal {F}\) is nonempty, the inequality constraints/bounds \(\ell _i \le [A_{\mathcal {I}}x]_i \le u_i\) would be redundant.

We can now consider an approximate tangent cone \(T(x,\alpha )\) as if the inequality constraints/ bounds in \(I_u(x,\alpha ) \cup I_l(x,\alpha )\) were active. This corresponds to considering a normal cone \(N(x,\alpha )\) defined as

$$\begin{aligned} N(x,\alpha ) = {{\,\mathrm{Cone}\,}}\left( \left\{ W^\top A_{\mathcal {I}}^\top e_i \right\} _{i \in I_u(x,\alpha )} \cup \left\{ -W^\top A_{\mathcal {I}}^\top e_i \right\} _{i \in I_\ell (x,\alpha )} \right) . \end{aligned}$$
(2.6)

We then choose \(T(x,\alpha )=N(x,\alpha )^{\circ }\).Footnote 1

The feasible directions we are looking for are given by \(W{\tilde{d}}\) with \({\tilde{d}} \in T(x,\alpha )\), as supported by the lemma below.

Lemma 2.1

Let \(x \in \mathcal {F}\), \(\alpha > 0\), and \({\tilde{d}} \in T(x,\alpha )\). If \(\Vert {\tilde{d}}\Vert \le \alpha \), then \(x + W{\tilde{d}} \in \mathcal {F}\).

Proof

First, we observe that \(x + W{\tilde{d}} \in \mathcal {F}\) is equivalent to \({\tilde{x}} + {\tilde{d}} \in \tilde{\mathcal {F}}\). Then, we apply [23, Proposition 2.2] to the reduced formulation (2.4). \(\square \)

This result also holds for displacements of norm \(\alpha \) in the full space as \(\Vert W{\tilde{d}}\Vert = \Vert {\tilde{d}}\Vert \). Hence, by considering steps of the form \(\alpha W{\tilde{d}}\) with \({\tilde{d}} \in T(x,\alpha )\) and \(\Vert {\tilde{d}}\Vert =1\), we are ensured to remain in the feasible region.

We point out that the previous definitions and the resulting analysis can be extended by replacing \(\alpha \) in the definition of the nearby active inequality constraints/bounds by a quantity of the order of \(\alpha \) (that goes to zero when \(\alpha \) does); see [23]. For matters of simplicity of the presentation, we will only work with \(\alpha \), which was also the practical choice suggested in [25].

3 Feasible descent and deterministic global convergence

In the absence of constraints, all that is required for the set of polling directions is the existence of a sufficiently good descent direction within the set; in other words, we require

$$\begin{aligned} {{\,\mathrm{cm}\,}}(D,-\nabla f(x)) \ge \kappa \quad \text{ with } \; {{\,\mathrm{cm}\,}}(D,v) = \max _{d\in D}\frac{d^{\top }v}{\Vert d\Vert \Vert v\Vert }, \end{aligned}$$

for some \(\kappa > 0\). The quantity \({{\,\mathrm{cm}\,}}(D,v)\) is the cosine measure of D given v, introduced in [19] as an extension of the cosine measure of D [22] (and both measures are bounded away from zero for positive spanning sets D). To generalize this concept for Problem (2.1), where the variables are subject to inequality constraints/bounds and equalities, we first consider the feasible region \(\mathcal {F}\) in its reduced version (2.4), so that we can apply in the reduced space the concepts and properties of [23, 27] where the problem has been stated using a linear inequality formulation.

Let \({\tilde{\nabla }} f(x)\) be the gradient of f reduced to the null space of the matrix A defining the equality constraints, namely \({\tilde{\nabla }} f(x) = W^\top \nabla f(x)\). Given an approximate tangent cone \(T(x, \alpha )\) and a set of directions \({\tilde{D}}\subset T(x, \alpha )\), we will use

$$\begin{aligned} {{\,\mathrm{cm}\,}}_{T(x,\alpha )}({\tilde{D}},-{\tilde{\nabla }} f(x)) {\mathop {=}\limits ^{\mathrm {def}}} \max _{{\tilde{d}} \in {\tilde{D}} }\frac{{\tilde{d}}^{\top } (- {\tilde{\nabla }} f(x))}{\big \Vert {\tilde{d}}\big \Vert \big \Vert P_{T(x,\alpha )}[- {\tilde{\nabla }} f(x)]\big \Vert } \end{aligned}$$
(3.1)

as the cosine measure of \({\tilde{D}}\) given \(-{\tilde{\nabla }} f(x)\). If \(P_{T(x,\alpha )}[- {\tilde{\nabla }} f(x)] = 0\), then we define the quantity in (3.1) as equal to 1. This cosine measure given a vector is motivated by the analysis given in [23] for the cosine measure (see Condition 1 and Proposition A.1 therein). As a way to motivate the introduction of the projection in (3.1), note that when \(\Vert P_{T(x,\alpha )}[- {\tilde{\nabla }} f(x)]\big \Vert \) is arbitrarily small compared with \(\Vert {\tilde{\nabla }} f(x)\Vert \), \({{\,\mathrm{cm}\,}}({\tilde{D}}, -{\tilde{\nabla }} f(x))\) may be undesirably small but \({{\,\mathrm{cm}\,}}_{T(x,\alpha )}({\tilde{D}},-{\tilde{\nabla }} f(x))\) can be close to 1. In particular, \({{\,\mathrm{cm}\,}}_{T(x,\alpha )}({\tilde{D}},-{\tilde{\nabla }} f(x))\) is close to 1 if \({\tilde{D}}\) contains a vector that is nearly in the direction of \(-{\tilde{\nabla }} f(x)\).

Given a finite set \({\mathbf {C}}\) of cones, where each cone \(C \in {\mathbf {C}}\) is positively generated from a set of vectors G(C), one has

$$\begin{aligned} \lambda ({\mathbf {C}}) = \min _{C \in {\mathbf {C}}}\left\{ \ \inf _{\begin{array}{c} u \in \mathbb {R}^{n-m} \\ P_{C}[u] \ne 0 \end{array}} \max _{v \in G(C)} \frac{v^\top u}{\Vert v\Vert \Vert P_C[u]\Vert }\ \right\} > 0. \end{aligned}$$
(3.2)

For any \(C \in {\mathbf {C}}\), one can prove that the infimum is finite and positive through a simple geometric argument, based on the fact that G(C) positively generates C (see, e.g., [27, Proposition 10.3]). Thus, if \({\tilde{D}}\) positively generates \(T(x,\alpha )\),

$$\begin{aligned} {{\,\mathrm{cm}\,}}_{T(x,\alpha )}({\tilde{D}}) {\mathop {=}\limits ^{\mathrm {def}}} \inf _{\begin{array}{c} u \in \mathbb {R}^{n-m} \\ P_{T(x,\alpha )}[u] \ne 0 \end{array}} \max _{{\tilde{d}}\in {\tilde{D}}}\frac{{\tilde{d}}^{\top }u}{\Vert {\tilde{d}}\Vert \left\| P_{T(x,\alpha )}[u]\right\| } \ge \kappa _{\min } > 0, \end{aligned}$$

where \(\kappa _{\min } = \lambda ({\mathbf {T}})\) and \({\mathbf {T}}\) is formed by all possible tangent cones \(T(x,\varepsilon )\) (with some associated sets of positive generators), for all possible values of \(x \in \mathcal {F}\) and \(\varepsilon > 0\). Note that \({\mathbf {T}}\) is necessarily finite given that the number of constraints is. This guarantees that the cosine measure (3.1) of such a \({\tilde{D}}\) given \(-{\tilde{\nabla }} f(x)\) will necessarily be bounded away from zero.

We can now naturally impose a lower bound on (3.1) to guarantee the existence of a feasible descent direction in a given \({\tilde{D}}\). However, we will do it in the full space \(\mathbb {R}^n\) by considering directions of the form \(d=W{\tilde{d}}\) for \({\tilde{d}} \in {\tilde{D}}\).

Definition 3.1

Let \(x \in \mathcal {F}\) and \(\alpha > 0\). Let D be a set of vectors in \(\mathbb {R}^n\) of the form \(\{d=W{\tilde{d}}, {\tilde{d}} \in {\tilde{D}}\}\) for some \({\tilde{D}} \subset T(x,\alpha ) \subset \mathbb {R}^{n-m}\). Given \(\kappa \in (0,1)\), the set D is called a \(\kappa \)-feasible descent set in the approximate tangent cone \(WT(x,\alpha )\) if

$$\begin{aligned} {{\,\mathrm{cm}\,}}_{WT(x,\alpha )}(D,-\nabla f(x)) {\mathop {=}\limits ^{\mathrm {def}}} \max _{d\in D}\frac{d^{\top } (- \nabla f(x))}{\Vert d\Vert \Vert P_{WT(x,\alpha )}[- \nabla f(x)]\Vert } \ge \kappa , \end{aligned}$$
(3.3)

where W is an orthonormal basis of the null space of A, and we assume by convention that the above quotient is equal to 1 if \(\left\| P_{WT(x,\alpha )}[-\nabla f(x)]\right\| =0\).

In fact, using both \(P_{WT(x,\alpha )}[-\nabla f(x)] = P_{WT(x,\alpha )}[-WW^\top \nabla f(x)] = WP_{T(x,\alpha )}[-W^\top \nabla f(x)]\) and the fact that the Euclidean norm is preserved under multiplication by W, we note that

$$\begin{aligned} {{\,\mathrm{cm}\,}}_{WT(x,\alpha )}(D,-\nabla f(x)) = {{\,\mathrm{cm}\,}}_{T(x,\alpha )}({\tilde{D}},-W^\top \nabla f(x)), \end{aligned}$$
(3.4)

which helps passing from the full to the reduced space. Definition 3.1 characterizes the polling directions of interest to the algorithm. Indeed, if D is a \(\kappa \)-feasible descent set, it contains at least one descent direction at x feasible for a displacement of length \(\alpha \) (see Lemma 2.1). Furthermore, the size of \(\kappa \) controls how much away from the projected gradient such a direction is.

In the remaining of the section, we will show that the algorithm is globally convergent to a first-order stationary point. There will be no novelty here as the result is the same as in [23], but there is a subtlety as we weaken the assumption in [23] when using polling directions from a feasible descent set instead of a set of positive generators. This relaxation will be instrumental when later we derive results based on probabilistic feasible descent, generalizing [19] from unconstrained to linearly constrained optimization.

Assumption 3.1

The function f is bounded below on the feasible region \(\mathcal {F}\) by a constant \(f_{\mathrm {low}}>-\infty \).

It is well known that under the boundedness below of f the step size converges to zero for direct-search methods based on sufficient decrease [22]. This type of reasoning carries naturally from unconstrained to constrained optimization as long as the iterates remain feasible, and it is essentially based on the sufficient decrease condition imposed on successful iterates. We present the result in the stronger form of a convergence of a series, as the series limit will be later needed for complexity purposes. The proof is given in [19] for the unconstrained case but it applies verbatim to the feasible constrained setting.

Lemma 3.1

Consider a run of Algorithm 2.1 applied to Problem (2.1) under Assumptions 2.1, 2.2, and 3.1. Then, \(\sum _{k=0}^\infty \rho (\alpha _k) < \infty \) (thus \(\lim _{k \rightarrow \infty } \alpha _k = 0\)).

Lemma 3.1 is central to the analysis (and to defining practical stopping criteria) of direct-search schemes. It is usually combined with a bound of the criticality measure in terms of the step size. For stating such a bound we need the following assumption, standard in the analysis of direct search based on sufficient decrease for smooth problems.

Assumption 3.2

The function f is continuously differentiable with Lipschitz continuous gradient in an open set containing \(\mathcal {F}\) (and let \(\nu >0\) be a Lipschitz constant of \(\nabla f\)).

Assumptions 3.1 and 3.2 were already made in the unconstrained setting [19, Assumption 2.1]. In addition to those, the treatment of linear constraints also requires the following property (see, e.g., [23]):

Assumption 3.3

The gradient of f is bounded in norm in the feasible set, i.e., there exists \(B_g >0\) such that \(\Vert \nabla f(x)\Vert \le B_g\) for all \(x \in \mathcal {F}\).

The next lemma shows that the criticality measure is of the order of the step size for unsuccessful iterations under our assumption of feasible descent. It is a straightforward extension of what can be proved using positive generators [23], yet this particular result will become fundamental in the probabilistic setting.

Lemma 3.2

Consider a run of Algorithm 2.1 applied to Problem (2.1) under Assumptions 2.1 and 3.2. Let \(D_k\) be a \(\kappa \)-feasible descent set in the approximate tangent cone \(WT(x_k,\alpha _k)\). Then, denoting \(T_k = T(x_k,\alpha _k)\) and \(g_k = \nabla f(x_k)\), if the kth iteration is unsuccessful,

$$\begin{aligned} \left\| P_{T_k}[ -W^\top g_k] \right\| \le \frac{1}{\kappa }\left( \frac{\nu }{2}\alpha _k + \frac{\rho (\alpha _k)}{\alpha _k} \right) . \end{aligned}$$
(3.5)

Proof

The result clearly holds whenever the left-hand side in (3.5) is equal to zero, therefore we will assume for the rest of the proof that \(P_{T_k} [ -W^\top g_k ] \ne 0\) (\(T_k\) is thus non-empty). From (3.4) we know that \({{\,\mathrm{cm}\,}}_{T_k}({\tilde{D}}_k,-W^\top g_k) \ge \kappa \), and thus there exists a \({\tilde{d}}_k \in {\tilde{D}}_k\) such that

$$\begin{aligned} \frac{{\tilde{d}}_k^\top [-W^\top g_k]}{\Vert {\tilde{d}}_k\Vert \left\| P_{T_k}\left[ -W^\top g_k\right] \right\| } \ge \kappa . \end{aligned}$$

On the other hand, from Lemma 2.1 and Assumption 2.1, we also have \(x_k+\alpha _k W {\tilde{d}}_k \in \mathcal {F}\). Hence, using the fact that k is the index of an unsuccessful iteration, followed by a Taylor expansion,

$$\begin{aligned} -\rho (\alpha _k) \le f(x_k+\alpha _k W {\tilde{d}}_k)-f(x_k)\le & {} \alpha _k {\tilde{d}}_k^\top W^\top g_k + \frac{\nu }{2}\alpha _k^2 \\\le & {} -\kappa \alpha _k \Vert {\tilde{d}}_k\Vert \Vert P_{T_k}[-W^\top g_k]\Vert + \frac{\nu }{2}\alpha _k^2, \end{aligned}$$

which leads to (3.5). \(\square \)

In order to state a result involving the criticality measure \(\chi (x_k)\), one also needs to bound the projection of the reduced gradient onto the polar of \( T(x_k,\alpha _k)\). As in [23], one uses the following uniform bound (derived from polyhedral geometry) on the normal component of a feasible vector.

Lemma 3.3

[23, Proposition B.1] Let \(x \in \mathcal {F}\) and \(\alpha > 0\). Then, for any vector \({\tilde{d}}\) such that \(x+ W{\tilde{d}} \in \mathcal {F}\), one has

$$\begin{aligned} \left\| P_{N(x,\alpha )}[{\tilde{d}}] \right\| \le \frac{\alpha }{\eta _{\min }}, \end{aligned}$$
(3.6)

where \(\eta _{\min } = \lambda ({\mathbf {N}})\) and \({\mathbf {N}}\) is formed by all possible approximate normal cones \(N(x,\varepsilon )\) (generated positively by the vectors in (2.6)) for all possible values of \(x \in \mathcal {F}\) and \(\varepsilon > 0\).

We remark that the definition of \(\eta _{\min }\) is independent of x and \(\alpha \).

Lemma 3.4

Consider a run of Algorithm 2.1 applied to Problem (2.1) under Assumptions 2.1, 3.2, and 3.3. Let \(D_k\) be a \(\kappa \)-feasible descent set in the approximate tangent cone \(WT(x_k,\alpha _k)\). Then, if the kth iteration is unsuccessful,

$$\begin{aligned} \chi (x_k) \le \left[ \frac{\nu }{2 \kappa } + \frac{B_g}{\eta _{\min }}\right] \alpha _k + \frac{\rho (\alpha _k)}{\kappa \alpha _k}. \end{aligned}$$
(3.7)

Proof

We make use of the classical Moreau decomposition [33], which states that any vector \(v \in \mathbb {R}^{n-m}\) can be decomposed as \(v = P_{T_k}[v] + P_{N_k}[v]\) with \(N_k=N(x_k,\alpha _k)\) and \(P_{T_k}[v]^\top P_{N_k}[v]=0\), and write

$$\begin{aligned} \chi (x_k)= & {} \max _{\begin{array}{c} x_k+ W {\tilde{d}} \in \mathcal {F} \\ \Vert {\tilde{d}}\Vert \le 1 \end{array}} \left( {\tilde{d}}^\top P_{T_k}[ -W^\top g_k] + \left( P_{T_k}[{\tilde{d}}] + P_{N_k}[{\tilde{d}}] \right) ^\top P_{N_k}[-W^\top g_k] \right) \\\le & {} \max _{\begin{array}{c} x_k + W {\tilde{d}} \in \mathcal {F} \\ \Vert {\tilde{d}}\Vert \le 1 \end{array}} \left( {\tilde{d}}^\top P_{T_k}[ -W^\top g_k] + P_{N_k}[{\tilde{d}}]^\top P_{N_k}[-W^\top g_k] \right) \\\le & {} \max _{\begin{array}{c} x_k + W {\tilde{d}} \in \mathcal {F}\\ \Vert {\tilde{d}}\Vert \le 1 \end{array}} \left( \Vert {\tilde{d}}\Vert \Vert P_{T_k}[ -W^\top g_k ] \Vert + \Vert P_{N_k}[{\tilde{d}}] \Vert \Vert P_{N_k}[ -W^\top g_k ] \Vert \right) . \end{aligned}$$

We bound the first term in the maximum using \(\Vert {\tilde{d}}\Vert \le 1\) and Lemma 3.2. For the second term, we apply Lemma 3.3 together with Assumption 3.3, leading to

$$\begin{aligned} \Vert P_{N_k}[{\tilde{d}}]\Vert \Vert P_{N_k}[ -W^\top g_k ] \Vert \le \frac{\alpha _k}{\eta _{\min }} B_g, \end{aligned}$$

yielding the desired conclusion. \(\square \)

The use of feasible descent sets (generated, for instance, through the techniques described in “Appendix A”) enables us to establish a global convergence result. Indeed, one can easily show from Lemma 3.1 that there must exist an infinite sequence of unsuccessful iterations with step size converging to zero, to which one then applies Lemma 3.4 and concludes the following result.

Theorem 3.1

Consider a run of Algorithm 2.1 applied to Problem (2.1) under Assumptions 2.1, 2.2, 3.1, 3.2, and 3.3. Suppose that for all k, \(D_k\) is a \(\kappa \)-feasible descent set in the approximate tangent cone \(WT(x_k,\alpha _k)\). Then,

$$\begin{aligned} \liminf _{k \rightarrow \infty } \chi (x_k) = 0. \end{aligned}$$
(3.8)

4 Complexity in the deterministic case

In this section, our goal is to provide an upper bound on the number of iterations and function evaluations sufficient to achieve

$$\begin{aligned} \min _{0 \le l \le k} \chi (x_l) \le \epsilon , \end{aligned}$$
(4.1)

for a given threshold \(\epsilon > 0\). Such complexity bounds have already been obtained for derivative-based methods addressing linearly constrained problems. In particular, it was shown that adaptive cubic regularization methods take \(\mathcal {O}(\epsilon ^{-1.5})\) iterations to satisfy (4.1) in the presence of second-order derivatives [8]. Higher-order regularization algorithms require \(\mathcal {O}(\epsilon ^{-(q+1)/q})\) iterations, provided derivatives up to the qth order are used [7]. A short-step gradient algorithm was also proposed in [9] to address general equality-constrained problems: it requires \(\mathcal {O}(\epsilon ^{-2})\) iterations to reduce the corresponding criticality measure below \(\epsilon \).

In the case of direct search based on sufficient decrease for linearly constrained problems, a worst-case complexity bound on the number of iterations can be derived based on the simple evidence that the methods share the iteration mechanism of the unconstrained case [39]. Indeed, since Algorithm 2.1 maintains feasibility, the sufficient decrease condition for accepting new iterates is precisely the same as for unconstrained optimization. Moreover, Lemma 3.4 gives us a bound on the criticality measure for unsuccessful iterations that only differs (from the unconstrained case) in the multiplicative constants. As a result, we can state the complexity for the linearly constrained case in Theorem 4.1. We will assume there that \(\rho (\alpha ) = c \,\alpha ^2/2\), as \(q=2\) is the power q in \(\rho (\alpha ) = \text{ constant } \times \alpha ^q\) that leads to the least negative power of \(\epsilon \) in the complexity bounds for the unconstrained case [39].

Theorem 4.1

Consider a run of Algorithm 2.1 applied to Problem (2.1) under the assumptions of Theorem 3.1. Suppose that \(D_k\) is a \(\kappa \)-feasible descent set in the approximate tangent cone \(WT(x_k,\alpha _k)\) for all k. Suppose further that \(\rho (\alpha )=c \, \alpha ^2/2\) for some \(c>0\). Then, the first index \(k_\epsilon \) satisfying (4.1) is such that

$$\begin{aligned} k_\epsilon \le \left\lceil E_1\epsilon ^{-2}+E_2 \right\rceil , \end{aligned}$$

where

$$\begin{aligned}&E_1=\left( 1-\log _{\theta }(\gamma )\right) \frac{f(x_{k_0})-f_{\mathrm {low}}}{0.5\theta ^2 L_1^2}-\log _{\theta }(\exp (1)), \\&E_2=\log _{\theta }\left( \frac{\theta L_1\exp (1)}{\alpha _{k_0}}\right) +\frac{f(x_0)-f_{\mathrm {low}}}{0.5\alpha _0^2}, \\&L_1=\min (1,L_2^{-1}), \quad L_2 = \mathcal {C} = \frac{\nu +c}{2\kappa }+\frac{B_g}{\eta _{\min }}. \end{aligned}$$

and \(k_0\) is the index of the first unsuccessful iteration (assumed \(\le k_\epsilon \)). The constants \(\mathcal {C},\kappa ,\eta _{\min }\) depend on \(n,m,m_{\mathcal {I}}\): \(\mathcal {C}=\mathcal {C}_{n,m,m_{\mathcal {I}}}\), \(\kappa =\kappa _{n,m,m_{\mathcal {I}}}\), \(\eta _{\min }=\eta _{n,m,m_{\mathcal {I}}}\).

We refer the reader to [39, Proofs of Theorems 3.1 and 3.2] for the proof, a verbatim copy of what works here (up to the multiplicative constants), as long as we replace \(\Vert g_k\Vert \) by \(\chi (x_k)\).

Under the assumptions of Theorem 4.1, the number of iterations \(k_\epsilon \) and the number of function evaluations \(k^f_\epsilon \) sufficient to meet (4.1) satisfy

$$\begin{aligned} k_\epsilon \le \mathcal {O} \left( \mathcal {C}_{n,m,m_{\mathcal {I}}}^2 \epsilon ^{-2} \right) , \quad k^f_\epsilon \le \mathcal {O} \left( r_{n,m,m_{\mathcal {I}}} \mathcal {C}_{n,m,m_{\mathcal {I}}}^2 \epsilon ^{-2} \right) , \end{aligned}$$
(4.2)

where \(r_{n,m,m_{\mathcal {I}}}\) is a uniform upper bound on \(|D_k|\). The dependence of \(\kappa _{n,m,m_{\mathcal {I}}}\) and \(\eta _{n,m,m_{\mathcal {I}}}\) (and consequently of \(\mathcal {C}_{n,m,m_{\mathcal {I}}}\) which is \(\mathcal {O}(\max \{\kappa _{n,m,m_{\mathcal {I}}}^{-2},\eta _{n,m,m_{\mathcal {I}}}^{-2}\})\)) in terms of the numbers of variables n, equality constraints m, and inequality constraints/bounds \(m_{\mathcal {I}}\) is not straightforward. Indeed, those quantities depend on the polyhedral structure of the feasible region, and can significantly differ from one problem to another. Regarding \(r_{n,m,m_{\mathcal {I}}}\), one can say that \(r_{n,m,m_{\mathcal {I}}}\le 2n\) in the presence of a non-degenerate condition such as the one of Proposition A.1 (see the sentence after this proposition in “Appendix A”). In the general, possibly degenerate case, the combinatorial aspect of the faces of the polyhedral may lead to an \(r_{n,m,m_{\mathcal {I}}}\) that depends exponentially on n (see [34]).

4.1 Only bounds

When only bounds are enforced on the variables (\(m=0\), \(m_{\mathcal {I}}=n\), \(A_{\mathcal {I}}=W=I_n\)), the numbers \(\kappa ,\eta ,r\) depend only on n, and the set \(D_{\oplus }=[I_n \; -\!I_n]\) formed by the coordinate directions and their negatives is the preferred choice for the polling directions. In fact, given \(x \in \mathcal {F}\) and \(\alpha > 0\), the cone \(T(x,\alpha )\) defined in Sect. 2 is always generated by a set \(G \subset D_{\oplus }\), while its polar \(N(x,\alpha )\) will be generated by \(D_{\oplus } \setminus G\). The set of all possible occurrences for \(T(x,\alpha )\) and \(N(x,\alpha )\) thus coincide, and it can be shown (see [26] and [22, Proposition 8.1]) that \(\kappa _n \ge \kappa _{\min } = 1/\sqrt{n}\) as well as \(\eta _n = \eta _{\min } = 1/\sqrt{n}\). In particular, \(D_{\oplus }\) is a \((1/\sqrt{n})\)-feasible descent set in the approximate tangent cone \(WT(x,\alpha )\) for all possible values of x and \(\alpha \). Since \(r_n \le 2 n\), one concludes from (4.2) that \(\mathcal {O}(n^2 \epsilon ^{-2})\) evaluations are taken in the worst case, matching the known bound for unconstrained optimization.

4.2 Only linear equalities

When there are no inequality constraints/bounds on the variables and only equalities (\(m > 0\)), the approximate normal cones \(N(x,\alpha )\) are empty and \(T(x,\alpha )=\mathbb {R}^{n-m}\), for any feasible x and any \(\alpha >0\). Thus, \(\kappa _{n,m} \ge 1/\sqrt{n-m}\) and by convention \(\eta _{n,m} = \infty \) (or \(B_g/\eta _{n,m}\) could be replaced by zero). Since \(r_{n,m} \le 2(n-m)\), one concludes from (4.2) that \(\mathcal {O}((n-m)^2 \epsilon ^{-2})\) evaluations are taken in the worst case. A similar bound [39] would be obtained by first rewriting the problem in the reduced space and then considering the application of deterministic direct search (based on sufficient decrease) on the unconstrained reduced problem—and we remark that the factor of \((n-m)^2\) cannot be improved [12] using positive spanning vectors.

5 Probabilistic feasible descent and almost-sure global convergence

We now consider that the polling directions are independently randomly generated from some distribution in \(\mathbb {R}^n\). Algorithm 2.1 will then represent a realization of the corresponding generated stochastic process. We will use \(X_k,G_k,{\mathfrak {D}}_k,A_k\) to represent the random variables corresponding to the kth iterate, gradient, set of polling directions, and step size, whose realizations are respectively denoted by \(x_k,g_k=\nabla f(x_k),D_k,\alpha _k\) (as in the previous sections of the paper).

The first step towards the analysis of the corresponding randomized algorithm is to pose the feasible descent property in a probabilistic form. This is done below in Definition 5.1, generalizing the definition of probabilistic descent given in [19] for the unconstrained case.

Definition 5.1

Given \(\kappa ,p \in (0,1)\), the sequence \(\{{\mathfrak {D}}_{k}\}\) in Algorithm 2.1 is said to be p-probabilistically \(\kappa \)-feasible descent, or \((p,\kappa )\)-feasible descent in short, if

$$\begin{aligned} \mathbb {P}\left( {{\,\mathrm{cm}\,}}_{WT(x_0,\alpha _0)}\left( {\mathfrak {D}}_0,-G_0\right) \ge \kappa \right) \ge p, \end{aligned}$$
(5.1)

and, for each \(k \ge 1\),

$$\begin{aligned} \mathbb {P}\left( {{\,\mathrm{cm}\,}}_{WT(X_k,A_k)}\left( {\mathfrak {D}}_k,-G_k\right) \ge \kappa | {\mathfrak {D}}_0,\dots ,{\mathfrak {D}}_{k-1}\right) \ge p. \end{aligned}$$
(5.2)

Observe that at iteration \(k \ge 1\), the probability (5.2) involves conditioning on the \(\sigma \)-algebra generated by \({\mathfrak {D}}_0,\dots ,{\mathfrak {D}}_{k-1}\), expressing that the feasible descent property is to be ensured with probability at least p regardless of the outcome of iterations 0 to \(k-1\).

As in the deterministic case of Sect. 3, the results from Lemmas 3.1 and 3.4 will form the necessary tools to establish global convergence with probability one. Lemma 3.1 states that for every realization of Algorithm 2.1, thus for every realization of the random sequence \(\{{\mathfrak {D}}_k\}\), the step size sequence converges to zero. We rewrite below Lemma 3.4 in its reciprocal form.

Lemma 5.1

Consider Algorithm 2.1 applied to Problem (2.1), and under Assumptions 2.1, 3.2, and 3.3. The kth iteration in Algorithm 2.1 is successful if

$$\begin{aligned} {{\,\mathrm{cm}\,}}_{WT(x_k,\alpha _k)}\left( D_k,-g_k\right) \ge \kappa \quad and \quad \alpha _k < \varphi (\kappa \chi (x_k)), \end{aligned}$$
(5.3)

where

$$\begin{aligned} \varphi (t) {\mathop {=}\limits ^{\mathrm {def}}} \inf \left\{ \alpha : \alpha > 0, \frac{\rho (\alpha )}{\alpha }+ \left[ \frac{\nu }{2}+\frac{\kappa B_g}{\eta }\right] \alpha \ge t \right\} . \end{aligned}$$
(5.4)

Note that this is [19, Lemma 2.1] but with \({{\,\mathrm{cm}\,}}_{WT(x_k,\alpha _k)}(D_k,-g_k)\) and \(\chi (x_k)\) in the respective places of \({{\,\mathrm{cm}\,}}(D_k,-g_k)\) and \(\Vert g_k\Vert \).

For any \(k \ge 0\), let

$$\begin{aligned} Y_k = {\left\{ \begin{array}{ll} 1 &{}\text{ if } \text{ iteration } k \text{ is } \text{ successful, }\\ 0 &{}\text{ otherwise } \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} Z_k = {\left\{ \begin{array}{ll} 1 &{}\text{ if } {{\,\mathrm{cm}\,}}_{WT(X_k,A_k)}\left( {\mathfrak {D}}_k,-G_k\right) \ge \kappa , \\ 0 &{}\text{ otherwise }, \end{array}\right. } \end{aligned}$$

with \(y_k,z_k\) denoting their respective realizations. One can see from Theorem 4.1 that, if the feasible descent property is satisfied at each iteration, that is \(z_k =1\) for each k, then Algorithm 2.1 is guaranteed to converge in the sense that \(\liminf _{k \rightarrow \infty } \chi (x_k) = 0\). Conversely, if \(\liminf _{k \rightarrow \infty } \chi (x_k) >0\), then it is reasonable to infer that \(z_k=1\) did not happen sufficiently often during the iterations. This is the intuition behind the following lemma, for which no a priori property on the sequence \(\{{\mathfrak {D}}_k\}\) is assumed.

Lemma 5.2

Under the assumptions of Lemmas 3.1 and 5.1, it holds for the stochastic processes \(\{\chi (X_k)\}\) and \(\{Z_k\}\) that

$$\begin{aligned} \left\{ \liminf _{k \rightarrow \infty } \chi (X_k) > 0 \right\} \subset \left\{ \sum _{k=0}^{\infty } \left[ Z_k\ln \gamma + (1-Z_k)\ln \theta \right] = -\infty \right\} . \end{aligned}$$
(5.5)

Proof

The proof is identical to that of [19, Lemma 3.3], using \(\chi (x_k)\) instead of \(\Vert g_k\Vert \). \(\square \)

Our goal is then to refute with probability one the occurrence of the event on the right-hand side of (5.5). To this end, we ask the algorithm to always increase the step size in successful iterations (\(\gamma > 1\)), and we suppose that the sequence \(\{{\mathfrak {D}}_k\}\) is \((p_0,\kappa )\)-feasible descent, with

$$\begin{aligned} p_0 = \frac{\ln \theta }{\ln (\gamma ^{-1}\theta )}. \end{aligned}$$
(5.6)

Under this condition, one can proceed as in [6, Theorem 4.1] to show that the random process

$$\begin{aligned} \sum _{l=0}^k [Z_l \ln \gamma + (1-Z_l)\ln \theta ] \end{aligned}$$

is a submartingale with bounded increments. Such sequences have a zero probability of diverging to \(-\infty \) ( [6, Theorem 4.2]), thus the right-hand event in (5.5) also happens with probability zero. This finally leads to the following almost-sure global convergence result.

Theorem 5.1

Consider Algorithm 2.1 applied to Problem (2.1), with \(\gamma > 1\), and under Assumptions 2.1, 2.2, 3.1, 3.2, and 3.3. If \(\{{\mathfrak {D}}_k\}\) is \((p_0,\kappa )\)-feasible descent, then

$$\begin{aligned} \mathbb {P}\left( \liminf _{k \rightarrow \infty } \chi (X_k) = 0\ \right) = 1. \end{aligned}$$
(5.7)

The minimum probability \(p_0\) is essential for applying the martingale arguments that ensure convergence. Note that it depends solely on the constants \(\theta \) and \(\gamma \) in a way directly connected to the updating rules of the step size.

6 Complexity in the probabilistic case

The derivation of an upper bound for the effort taken by the probabilistic variant to reduce the criticality measure below a tolerance also follows closely its counterpart for unconstrained optimization [19]. As in the deterministic case, we focus on the most favorable forcing function \(\rho (\alpha ) = c\,\alpha ^2/2\), which renders the function \(\varphi (t)\) defined in (5.4) linear in t,

$$\begin{aligned} \varphi (t) = \left[ \frac{\nu +c}{2}+\frac{B_g\kappa }{\eta }\right] ^{-1} t. \end{aligned}$$

A complexity bound for probabilistic direct search is given in Theorem 6.1 below for the linearly constrained case, generalizing the one proved in [19, Corollary 4.9] for unconstrained optimization. The proof is exactly the same but with \({{\,\mathrm{cm}\,}}_{WT(X_k,A_k)}(D_k,-G_k)\) and \(\chi (X_k)\) in the respective places of \({{\,\mathrm{cm}\,}}(D_k,-G_k)\) and \(\Vert G_k\Vert \). Let us quickly recall the road map of the proof. First, a bound is derived on \(\mathbb {P}\left( \min _{0 \le l \le k} \chi (X_l) \le \epsilon \right) \) in terms of a probability involving \(\sum _{l=0}^{k-1} Z_l\) [19, Lemma 4.4]. Assuming that the set of polling directions is \((p,\kappa )\)-feasible descent with \(p > p_0\), a Chernoff-type bound is then obtained for the tail distribution of such a sum, yielding a lower bound on \(\mathbb {P}\left( \min _{0 \le l \le k} \chi (X_l) \le \epsilon \right) \) [19, Theorem 4.6]. By expressing the event \(\min _{0 \le l \le k} \chi (X_l) \le \epsilon \) as \(K_\epsilon \le k\), where \(K_\epsilon \) is the random variable counting the number of iterations performed until the satisfaction of the approximate optimality criterion (4.1), one reaches an upper bound on \(K_\epsilon \) of the order of \(\epsilon ^{-2}\), holding with overwhelming probability (more precisely, with probability at least \(1-\exp (\mathcal {O}(\epsilon ^{-2}))\); see [19, Theorem 4.8 and Corollary 4.9]). We point out that in the linearly constrained setting the probability p of feasible descent may depend on n, m, and \(m_{\mathcal {I}}\), and hence we will write \(p=p_{n,m,m_{\mathcal {I}}}\).

Theorem 6.1

Consider Algorithm 2.1 applied to Problem (2.1), with \(\gamma > 1\), and under the assumptions of Theorem 5.1. Suppose that \(\{{\mathfrak {D}}_k\}\) is \((p, \kappa )\)-feasible descent with \(p > p_0\), with \(p_0\) being defined by (5.6). Suppose also that \(\rho (\alpha ) = c \, \alpha ^2/2\) and that \(\epsilon > 0\) satisfies

$$\begin{aligned} \epsilon \le \frac{\mathcal {C}\alpha _0}{2\gamma }. \end{aligned}$$

Then, the first index \(K_\epsilon \) for which (4.1) holds satisfies

$$\begin{aligned} \mathbb {P}\left( K_\epsilon \le \left\lceil \frac{\beta \mathcal {C}^2}{c(p-p_0)}\epsilon ^{-2} \right\rceil \right) \ge 1-\exp \left[ -\frac{\beta (p-p_0)\mathcal {C}^2}{8c p}\epsilon ^{-2}\right] , \end{aligned}$$
(6.1)

where \(\beta = \frac{2\gamma ^2}{c(1-\theta )^2}\left[ \frac{c}{2}\gamma ^{-2}\alpha _0^2 + f_0 - f_{\mathrm {low}}\right] \) is an upper bound on \(\sum _{k=0}^{\infty } \alpha _k^2\) (see [19, Lemma 4.1]). The constants \(\mathcal {C},\kappa ,p\) depend on \(n,m,m_{\mathcal {I}}\): \(\mathcal {C}=\mathcal {C}_{n,m,m_{\mathcal {I}}}\), \(\kappa =\kappa _{n,m,m_{\mathcal {I}}}\), \(p=p_{n,m,m_{\mathcal {I}}}\).

Let \(K^f_\epsilon \) be the random variable counting the number of function evaluations performed until satisfaction of the approximate optimality criterion (4.1). From Theorem 6.1, we have:

$$\begin{aligned} \mathbb {P}\left( K^f_\epsilon \le r_{n,m,m_{\mathcal {I}}} \left\lceil \frac{\beta \mathcal {C}_{n,m,m_{\mathcal {I}}}^2}{c(p_{n,m,m_{\mathcal {I}}}-p_0)}\epsilon ^{-2} \right\rceil \right) \ge 1-\exp \left[ -\frac{\beta (p_{n,m,m_{\mathcal {I}}}-p_0) \mathcal {C}_{n,m,m_{\mathcal {I}}}^2}{8c\,p_{n,m,m_{\mathcal {I}}}}\epsilon ^{-2}\right] .\nonumber \\ \end{aligned}$$
(6.2)

As \(\mathcal {C}^2_{n,m,m_{\mathcal {I}}} = \mathcal {O}(\max \{\kappa _{n,m,m_{\mathcal {I}}}^{-2},\eta _{n,m,m_{\mathcal {I}}}^{-2}\})\), and emphasizing the dependence on the numbers of variables n, equality constraints m, and linear inequality/bounds \(m_{\mathcal {I}}\), one can finally assure with overwhelming probability that

$$\begin{aligned} K^f_\epsilon \le \mathcal {O} \left( \frac{r_{n,m,m_{\mathcal {I}}} \max \{\kappa _{n,m,m_{\mathcal {I}}}^{-2},\eta _{n,m,m_{\mathcal {I}}}^{-2}\}}{p_{n,m,m_{\mathcal {I}}}-p_0} \epsilon ^{-2} \right) . \end{aligned}$$
(6.3)

6.1 Only bounds

When there are only bounds on the variables (\(m=0\), \(m_{\mathcal {I}}=n\), \(A_{\mathcal {I}}=W=I_n\)), we can show that probabilistic direct search does not necessarily yield a better complexity bound than its deterministic counterpart. Without loss of generality, we reason around the worst case \(T(x_k,\alpha _k) = \mathbb {R}^n\), and use a certain subset of positive generators of \(T(x_k,\alpha _k)\), randomly selected for polling at each iteration. More precisely, suppose that instead of selecting the entire set \(D_{\oplus }\), we restrict ourselves to a subset of uniformly chosen \(\lceil 2n p\rceil \) elements, with p being a constant in \((p_0,1)\). Then the corresponding sequence of polling directions is \((p,1/\sqrt{n})\)-feasible descent (this follows an argument included in the proof of Proposition 7.1; see (B.8) in “Appendix B”). The complexity result (6.2) can then be refined by setting \(r_n = \lceil 2n p \rceil \), \(\kappa _n \ge \kappa _{\min } = 1/\sqrt{n}\), and \(\eta _n = \kappa _{\min } = 1/\sqrt{n}\), leading to

$$\begin{aligned}&\mathbb {P}\left( K^f_\epsilon \le \lceil 2n p \rceil \left\lceil \frac{\bar{\mathcal {C}} n\epsilon ^{-2}}{p-p_0} \right\rceil \right) \nonumber \\&\quad \ge 1-\exp \left[ - \frac{\bar{\mathcal {C}}(p-p_0)\epsilon ^{-2}}{8p}\right] , \end{aligned}$$
(6.4)

for some positive constant \(\bar{\mathcal {C}}\) independent of n. This bound on \(K^f_\epsilon \) is thus \(\mathcal {O}(n^2\epsilon ^{-2})\) (with overwhelming probability), showing that such a random strategy does not lead to an improvement over the deterministic setting. To achieve such an improvement, we will need to uniformly generate directions on the unit sphere of the subspaces contained in \(T(x_k,\alpha _k)\), and this will be described in Sect. 7.

6.2 Only linear equalities

As in the bound-constrained case, one can also here randomly select the polling directions from \([W \; -\!W]\) (of cardinal \(2(n-m)\)), leading to a complexity bound of \(\mathcal {O}((n-m)^2 \epsilon ^{-2})\) with overwhelming probability. However, if instead we uniformly randomly generate on the unit sphere of \(\mathbb {R}^{n-m}\) (and post multiply by W), the complexity bound reduces to \(\mathcal {O}((n-m)\epsilon ^{-2})\), a fact that translates directly from unconstrained optimization [19] (see also the argument given in Sect. 7 as this corresponds to explore the null space of A).

7 Randomly generating directions while exploring subspaces

A random generation procedure for the polling directions in the approximate tangent cone should explore possible subspace information contained in the cone. In fact, if a subspace is contained in the cone, one can generate the polling directions as in the unconstrained case (with as few as two directions within the subspace), leading to significant gains in numerical efficiency as we will see in Sect. 8.

In this section, we will see that such a procedure still yields a condition sufficient for global convergence and worst-case complexity. For this purpose, consider the kth iteration of Algorithm 2.1. To simplify the presentation, we will set \({\tilde{n}}=n-m\) for the dimension of the reduced space, \({\tilde{g}}_k=W^\top g_k\) for the reduced gradient, and \(T_k\) for the approximate tangent cone. Let \(S_k\) be a linear subspace included in \(T_k\) and let \(T^c_k = T_k\cap S_k^\perp \) be the portion of \(T_k\) orthogonal to \(S_k\). Any set of positive generators for \(T_k\) can be transformed into a set \(V_k=[V^s_k\ V^c_k]\), with \(V_k\),\(V^s_k\),\(V^c_k\) being sets of positive generators for \(T_k\),\(S_k\),\(T^c_k\), respectively (details on how to compute \(S_k\) and \(V^c_k\) are given in the next section). Proposition 7.1 describes a procedure to compute a probabilistically feasible descent set of directions by generating random directions on the unit sphere of \(S_k\) and by randomly selecting positive generators from \(V_k^c\) (the latter corresponding to the technique mentioned in Sect. 6 for the bound-constrained case). The proof of the proposition is quite technical, thus we defer it to “Appendix B”.

Proposition 7.1

Consider an iteration of Algorithm 2.1 and let \(T_k\) be the associated approximate tangent cone. Suppose that \(T_k\) contains a linear subspace \(S_k\) and let \(T^c_k = T_k \cap S^\perp _k\). Let \(V^c_k\) be a set of positive generators for \(T^c_k\).

Let \(U^s_k\) be a set of \(r_s\) vectors generated on the unit sphere of \(S_k\), where

$$\begin{aligned} r_s = \left\lfloor \log _2\left( 1-\frac{\ln \theta }{\ln \gamma } \right) \right\rfloor + 1. \end{aligned}$$
(7.1)

and \(U^c_k\) be a set of \(\left\lceil p_c |V^c_k| \right\rceil \) vectors chosen uniformly at random within \(V^c_k\) such that

$$\begin{aligned} p_0< p_c < 1. \end{aligned}$$
(7.2)

Then, there exist \(\kappa \in (0,1)\) and \(p \in (p_0,1)\), with \(p_0\) given in (5.6), such that

$$\begin{aligned} \mathbb {P}\left( {{\,\mathrm{cm}\,}}_{T_k}([U^s_k\ U^c_k],-{\tilde{G}}_k) \ge \kappa {|} \sigma _{k-1} \right) \ge p, \end{aligned}$$

where \(\sigma _{k-1}\) represents the \(\sigma \)-algebra generated by \({\mathfrak {D}}_0,\dots ,{\mathfrak {D}}_{k-1}\).

The constant \(\kappa \) depends on \(n,m,m_{\mathcal {I}}\): \(\kappa =\kappa _{n,m,m_{\mathcal {I}}}\), while p depends solely on \(\theta ,\gamma , p_c\).

In the procedure presented in Proposition 7.1, we conventionally set \(U_k^s = \emptyset \) when \(S_k\) is zero, and \(U_k^c = \emptyset \) when \(T_k^c\) is zero. As a corollary of Proposition 7.1, the sequence of polling directions \(\left\{ {\mathfrak {D}}_k = W [ U^s_k\ U^c_k]\right\} \) corresponding to the subspace exploration is \((p,\kappa )\)-feasible descent. By Theorem 5.1, such a technique guarantees almost-sure convergence, and it also falls into the assumptions of Theorem 6.1. We can thus obtain a general complexity bound in terms of iterations and evaluations, but we can also go further than Sect. 6 and show improvement for specific instances of linearly constrained problems.

7.1 Improving the complexity when there are only bounds

Suppose that the cones \(T_k\) always include an \((n-n_b)\)-dimensional subspace with \(n_b \ge 1\) (this is the case if only \(n_b < n\) problem variables are actually subject to bounds). Then, usingFootnote 2\(|V^c_k| \le n_b\), the number of polling directions to be generated per iteration varies between \(r_s\) and \(r_s+p_c n_b\), where \(r_s\) given in (7.1) does not depend on n nor on \(n_b\), and \(p_c\) is a constant in \((p_0,1)\). This implies that we can replace r by \(r_s+n_b\), \(\kappa \) by \(t/\sqrt{n}\) with \(t \in (0,1]\) independent of n (see “Appendix B”) and \(\eta \) by \(1/\sqrt{n}\) so that (6.2) becomes

$$\begin{aligned}&\mathbb {P}\left( K^f_\epsilon \le \left( \left\lfloor \log _2\left( 1-\frac{\ln \theta }{\ln \gamma } \right) \right\rfloor + 1 + n_b \right) \left\lceil \frac{\bar{\mathcal {C}} n\epsilon ^{-2}}{p-p_0} \right\rceil \right) \nonumber \\&\quad \ge 1-\exp \left[ - \frac{\bar{\mathcal {C}}(p-p_0)\epsilon ^{-2}}{8p}\right] \end{aligned}$$
(7.3)

for some positive constant \(\bar{\mathcal {C}}\) independent of \(n_b\) and n. The resulting bound is \(\mathcal {O}\left( n_b n \epsilon ^{-2}\right) \). If \(n_b\) is substantially smaller than n, then this bound represents an improvement over those obtained in Sects. 4 and 6, reflecting that a problem with a small number of bounds on the variables is close to being unconstrained.

7.2 Improving the complexity when there are only linear equalities

In this setting, our subspace generation technique is essentially the same as the one for unconstrained optimization [19]. We can see that (6.2) renders an improvement from the bound \(\mathcal {O}((n-m)^2 \epsilon ^{-2})\) of Sect. 6 to \(\mathcal {O}((n-m) \epsilon ^{-2})\) (also with overwhelming probability), which is coherent with the bound for the unconstrained case obtained in [19].

8 Numerical results

This section is meant to illustrate the practical potential of our probabilistic strategies through a comparison of several polling techniques with probabilistic and deterministic properties. We implemented Algorithm 2.1 in MATLAB with the following choices of polling directions. The first choice corresponds to randomly selecting a subset of the positive generators of the approximate tangent cone (dspfd-1, see Sect. 6). In the second one, we first try to identify a subspace of the cone, ignore the corresponding positive generators, and then randomly generate directions in that subspace (dspfd-2, see Sect. 7). Finally, we tested a version based on the complete set of positive generators, but randomly ordering them at each iteration (dspfd-0)—such a variant can be analyzed in the classic deterministic way despite the random order. The three variants require the computation of a set of positive generators for the approximate tangent cone, a process we describe in “Appendix A”. For variant dspfd-2, subspaces are detected by identifying opposite vectors in the set of positive generators: this forms our set \(V^s_k\) (following the notation of Sect. 7), and we obtain \(V^c_k\) by orthogonalizing the remaining positive generators with respect to those in \(V^s_k\). Such a technique always identifies the largest subspace when there are either only bounds or only linear constraints, and benefits in the general case from the construction described in Proposition A.1. To determine the approximate active linear inequalities or bounds in (2.5), we used \(\min \{10^{-3},\alpha _k\}\) instead of \(\alpha _k\)—as we pointed out in Sect. 3, our analysis can be trivially extended to this setting. The forcing function was \(\rho (\alpha ) = 10^{-4}\alpha ^2\).

8.1 Comparison of deterministic and probabilistic descent strategies

Our first set of experiments aims at comparing our techniques with a classical deterministic direct-search instance. To this end, we use the built-in MATLAB patternsearch function [36]. This algorithm is a direct-search-type method that accepts a point as the new iterate if it satisfies a simple decrease condition, i.e., provided the function value is reduced. The options of this function can be set so that it uses a so-called Generating Set Search strategy inspired from [22]: columns of \(D_\oplus \) are used for bound-constrained problems, while for linearly constrained problems the algorithm attempts to compute positive generators of an approximate tangent cone based on the technique of Proposition A.1 (with no provision for degeneracy).

For all methods including the MATLAB one, we chose \(\alpha _0 = 1\), \(\gamma =2\), and \(\theta =1/2\). Those were the reference values of [19], and as they yield \(p_0=1/2\) we thus expect this parameter configuration to allow us to observe in practice the improvement suggested by the complexity analysis. We adopted the patternsearch default settings by allowing infeasible points to be evaluated as long as the constraint violation does not exceed \(10^{-3}\) (times the norm of the corresponding row of \(A_{\mathcal {I}}\)). All methods rely upon the built-in MATLAB null function to compute the orthogonal basis W when needed. We ran all algorithms on a benchmark of problems from the CUTEst collection [18], stopping whenever a budget of 2000n function evaluations was consumed or the step size fell below \(10^{-6}\alpha _0\) (for our methods based on random directions, ten runs were performed and the mean of the results was used). For each problem, this provided a best obtained value \(f_{best}\). Given a tolerance \(\varepsilon \in (0,1)\), we then looked at the number of function evaluations needed by each method to reach an iterate \(x_k\) such that

$$\begin{aligned} f(x_k) - f_{best} < \varepsilon \,\left( f(x_0) - f_{best} \right) , \end{aligned}$$
(8.1)

where the run was considered as a failure if the method stopped before (8.1) was satisfied. Performance profiles [13, 32] were built to compare the algorithms, using the number of function evaluations (normalized for each problem in order to remove the dependence on the dimension) as a performance indicator.

Bound-constrained problems We first present results on 63 problems from the CUTEst collection that only enforce bound constraints on the variables, with dimensions varying between 2 and 20 (see Table 1 in “Appendix C” for a complete list). Figure 1 presents the results obtained while comparing our three variants with the built-in patternsearch function. One observes that the dspfd-2 variant has the highest percentage of problems on which it is the most efficient (i.e., the highest curve leaving the y-axis). In terms of robustness (large value of the ratio of function calls), the dspfd methods outperform patternsearch, with dspfd-0 and dspfd-2 emerging as the best variants.

Fig. 1
figure 1

Performance of three variants of Algorithm 2.1 and MATLAB patternsearch on bound-constrained problems

Full size image
Fig. 2
figure 2

Performance of three variants of Algorithm 2.1 and MATLAB patternsearch on larger bound-constrained problems

Full size image

To further study the impact of the random generation, we selected 31 problems among the 63 for which we could increase their dimensions, so that all problems had at least 10 variables, with fifteen of them having between 20 and 52 variables. We again refer to Appendix and Table 2 for the problem list. Figure 2 presents the corresponding profiles. One sees that the performance of dspfd-0 and of the MATLAB function has significantly deteriorated, as they both take a high number of directions per iteration. On the contrary, dspfd-1 and dspfd-2, having a lower iteration cost thanks to randomness, present better profiles, and clearly outperform the strategies with deterministic guarantees. These results concur with those of Sect. 7, as they show the superiority of dspfd-2 when the size of the problem is significantly higher than the number of nearby bounds.

Linearly constrained problems Our second experiment considers a benchmark of 106 CUTEst problems for which at least one linear constraint (other than a bound) is present. The dimensions vary from 2 to 96, while the number of linear inequalities (when present) lies between 1 and 2000 (with only 14 problems with more than 100 of those constraints). Those problems are given in “Appendix C”, in Tables 3 and 4.

Fig. 3
figure 3

Performance of three variants of Algorithm 2.1 and MATLAB patternsearch on problems subject to general linear constraints

Full size image

Figure 3 presents the results of our approaches and of the MATLAB function on those problems. Variant dspfd-2 significantly outperforms the other variants, in both efficiency and robustness. The other dspfd variants seem more expensive in that they rely on a possibly larger set of tangent cone generators; yet, they manage to compete with patternsearch in terms of robustness.

Fig. 4
figure 4

Performance of three variants of Algorithm 2.1 and MATLAB patternsearch on problems with at least one linear inequality constraint

Full size image

We further present the results for two sub-classes of these problems. Figure 4 restricts the profiles to the 48 CUTEst problems for which at least one linear inequality constraint was enforced on the variables. The MATLAB routine performs quite well on these problems; still, dspfd-2 is competitive and more robust. Figure 5 focuses on the 61 problems for which at least one equality constraint is present (and note that 3 problems have both linear equalities and inequalities). In this context, the dspfd-2 profile highlights the potential benefit of randomly generating in subspaces. Although not plotted here, this conclusion is even more visible for the 13 problems with only linear equality constraints where dspfd-2 is by far the best method, which does not come as a surprise given what was reported for the unconstrained case [19].

Fig. 5
figure 5

Performance of three variants of Algorithm 2.1 and MATLAB patternsearch on problems with at least one linear equality constraint

Full size image

We have also run variant dspfd-0 with \(\gamma _2=1\) (i.e., no step-size increase at successful iterations), and although this has led to an improvement of efficiency for bound-constrained problems, the relative position of the profiles did not seem much affected in the general linearly constrained setting. We recall that dspfd-0 configures a case of deterministic direct search from the viewpoint of the choice of the polling directions, and that it is known that insisting on always increasing the step size upon a success is not the best approach at least in the unconstrained case.

8.2 Comparison with well-established solvers

In this section, we propose a preliminary comparison of the variant dspfd-2 with the solvers NOMAD [4, 24] (version 3.9.1 with the provided MATLAB interface) and PSwarm [38] (version 2.1). For both NOMAD and PSwarm, we disabled the use of models to yield a fairer comparison with our method. No search step was performed in NOMAD, but this step is maintained in PSwarm as it is intrinsically part of the algorithm. The various parameters in both codes were set to their default values, except for the maximum number of evaluations allowed (set to 2000n as before). The linear constraints were reformulated as one-side inequality constraints (addressed through the extreme barrier approach in NOMAD). For the dspfd-2 method, we kept the settings of Sect. 8.1 except for the relative feasibility tolerance, that was decreased from \(10^{-3}\) to \(10^{-15}\), a value closer to those adopted by NOMAD and PSwarm. We will again use performance profiles to present our results. Those profiles were built based on the convergence criterion (8.1), using the means over 10 runs of the three algorithms corresponding to different random seeds. We emphasize that our implementation is not as sophisticated as that of NOMAD and PSwarm, therefore we do not expect to be overwhelmingly superior to those methods. Nonetheless, we believe that our results can illustrate the potential of our algorithmic paradigm.

Bound-constrained problems Figure 6 presents the results obtained on the 31 bound-constrained problems with the largest dimensions. The PSwarm algorithm is the most efficient method, and finds points with significantly lower function values on most problems. This appears to be a feature of the population-based technique of this algorithm: during the search step, the method can compute several evaluations at carefully randomly generated points, that are projected so as to satisfy the bound constraints. In that sense, the randomness within PSwarm is helpful in finding good function values quickly. The NOMAD method is able to solve more problems within the considered budget, and its lack of efficiency for a small ratio of function evaluations is consistent with the performance of dspfd-0 in the previous section: one poll step might be expensive because it relies on a (deterministic) descent set. We point out that NOMAD handles bound constraints explicitly, and even in a large number they do not seem detrimental to its performance. The dspfd-2 variant of our algorithm falls in between those two methods. We note that it is comparable to PSwarm for small ratios of function evaluations, because random directions appear to lead to better values. It is also comparable to NOMAD for large ratios, which can be explained by the fact that our scheme can use deterministically descent sets in the worst situation, that is, when a significant number of bound constraints become approximately active. This observation is in agreement with Sect. 8.1, where we observed that using coordinate directions (or a subset thereof) can lead to good performance.

Fig. 6
figure 6

Performance of Algorithm 2.1 (version 2) versus NOMAD and PSwarm on the largest tested bound-constrained problems. PSwarm was tested with a search step

Full size image

Linearly constrained problems Figure 7 summarizes the performance of the three algorithms on the 106 CUTEst problems with general linear constraints. The performance of NOMAD on such problems is clearly below the ones of the other two algorithms. NOMAD is not equipped with dedicated strategies to handle linear constraints, particularly linear equalities, and we believe that this is the main explanation for this bad performance. We have indeed observed that the method tends to stall on these problems, especially in the presence of a large number of constraints. Moreover, on seven of the problems having more than 500 linear inequalities, the NOMAD algorithm was not able to complete a run due to memory requirements. The PSwarm algorithm is outperforming both NOMAD and dspfd-2, which we again attribute to the benefits of the search step. We note that in the presence of linear constraints, the initial feasible population is generated by an ellipsoid strategy (see [38] for details). We have observed failure of this ellipsoid procedure on seven of the problems in our benchmark with linear inequality constraints (other than bounds).

Fig. 7
figure 7

Performance of Algorithm 2.1 (version 2) versus NOMAD and PSwarm on problems subject to general linear constraints. PSwarm was tested with a search step

Full size image
Fig. 8
figure 8

Performance of Algorithm 2.1 (version 2) versus NOMAD and PSwarm on problems with at least one linear inequality constraint. PSwarm was tested with a search step

Full size image

As in Sect. 8.1, we then looked at the results on specific subsets of the problems included to compute Fig. 7. The profiles are similar if we consider only problems involving at least one linear equality (with PSwarm standing out as the best method), and thus not reported. On the other hand, the results while considering the 48 problems having at least one linear inequality exhibit a different pattern, and the corresponding profiles are given in Fig. 8. We note that our approach dspfd-2 yields a much improved profile compared to Fig. 7, especially for small ratios. This behavior is likely a consequence of our use of the double description algorithm (see “Appendix A”), that efficiently computes cone generators even with a large number of constraints. We believe that our probabilistic strategy brings an additional benefit: the method only considers a subset of those generators for polling, which is even more economical. Even though our strategy does not fully outperform PSwarm, it is certainly competitive on this particular set of experiments (and, again, without a search step). This suggests that our approach could be particularly beneficial in the presence of linear inequality constraints.

9 Conclusions

We have shown how to prove global convergence with probability one for direct-search methods applied to linearly constrained optimization when the polling directions are randomly generated. We have also derived a worst-case analysis for the number of iterations and function evaluations. Such worst-case complexity bounds are established with overwhelming probability and are of the order of \(\epsilon ^{-2}\), where \(\epsilon > 0\) is the threshold of criticality. It was instrumental for such probabilistic analyses to extend the concept of probabilistic descent from unconstrained to linearly constrained optimization. We have also refined such bounds in terms of the problem dimension and number of constraints for two specific subclasses of problems, where it is easier to exhibit an improvement over deterministic direct search. The numerical behavior of probabilistic strategies was found coherent with those findings, as we observed that simple direct-search frameworks with probabilistic polling techniques can perform better than variants based on deterministic guarantees. The performance of our algorithm, especially when compared to the well-established solvers tested, is encouraging for further algorithmic developments.

A natural extension of the presented work is the treatment of general, nonlinear constraints. One possibility is to apply the augmented Lagrangian method, where a sequence of subproblems containing all the possible original linear constraints is solved by direct search, as it was done in [28] for the deterministic case. Although it is unclear at the moment whether the extension of the probabilistic analysis would be straightforward, it represents an interesting perspective of the present work. Other avenues may include linearizing constraints [31], using a barrier approach to penalize infeasibility [5], or making use of a merit function [20]. Adapting the random generation techniques of the polling directions to any of these settings would also represent a continuation of our research.