1 Introduction

In designing interplanetary and deep-space missions, issues such as feasibility and cost efficiency of a large number of mission scenarios have to be addressed. On the other hand, these facets of any mission design problem are inherently coupled with the spacecraft’s trajectory (Sarli and Kawakatsu 2017). Developments in electric propulsion technology and optimization methods have led to a paradigm shift in mission design evident by missions such as Deep Space-1 in 1998 (Rayman et al. 2000), Hayabusa in 2003 (Kawaguchi et al. 2005), SMART-1 in 2003 (Kugelberg et al. 2004), and Dawn in 2007 (Rayman et al. 2006).

Electric propulsion systems (Racca 2003) produce a small amount of thrust and result in challenging optimal control problems (OCPs) (Betts 1998), which are solved by indirect (Conway 2011; Saghamanesh and Novinzadeh 2014; Taheri et al. 2016; Taheri and Junkins 2019), direct (Enright and Conway 1992; Sentinella and Casalino 2009), and hybrid (Dellnitz et al. 2009) optimization methods. The focus of this paper is on the indirect optimization method, but we employ a hybrid solution strategy (not to be confused with the hybrid method) in order to solve the resulting OCPs. In addition to the use of electric propulsion systems, an important step in designing deep-space trajectories is to leverage planetary gravity-assist (GA) maneuvers in order to reduce the time of flight and fuel consumption (Yam et al. 2004; Longuski and Williams 1991). For instance, Galileo spacecraft (Lieske 1996) used an Earth–Venus–Earth–Earth–Jupiter sequence, which consists of three GA maneuvers.

In reality, GA maneuvers are continuous events and high-fidelity tools such as Mystic (Whiffen 2006) and Copernicus (Ocampo 2003) model such as continuous maneuvers. However, these high-fidelity trajectory optimization tools are usually used at later mission design stages, whereas the majority of preliminary studies are performed using low- to medium-fidelity optimization tools (Whiffen and Lam 2006). A rather comprehensive comparison of the capabilities of various trajectory optimization tools is conducted in Polsgrove et al. (2006).

In preliminary studies, it is a common practice to use impulsive planetary GA model (as opposed to a continuous multi-body model) where each GA maneuver is modeled as an instantaneous change (delta-v) to the heliocentric velocity vector. Indirect optimization methods encounter difficulties when GA maneuvers are modeled, and numerical continuation and homotopy methods have found widespread applications in order to alleviate the difficulties when indirect methods are used (Bertrand and Epenoy 2002). Some solution methods take alternative approaches, for instance, by finding the unknown co-states by particle swarm optimization (PSO) algorithms (Jiang et al. 2012), or by forming an auxiliary unconstrained optimization problem (Hans and Renjith 1996), by adjoint variable solutions (Martell and Lawton1995), or by smoothing the control input using a hyperbolic tangent smoothing method (Taheri and Junkins 2018). The homotopy approach proposed by Jiang et al. (2012) has presented a suite of practical techniques to alleviate some of the numerical difficulties associated with solving OCP problems. These practical approaches have been improved by Saghamanesh and Baoyin (2018a). In a recent work, Saghamanesh and Baoyin (2018b) and Saghamanesh et al. (2019) demonstrated the utility of their method to solve direct-type (i.e., no GA maneuver) fuel-optimal low-thrust trajectory optimization problems using an ephemeris planetary model and taking into account accurate modeling of perturbations.

Typical mission design process starts with simple models (i.e., 2-body gravity models). Extensive trade studies are performed to determine the best launch dates, flight time, and mission options (i.e., gravity-assist sequence). A useful tool could be one in which the important perturbations are modeled in the dynamics and are incorporated within the indirect optimization method, while the parameters of the mission (e.g., event times such as departure, gravity-assist and final times) are fixed. Such a tool allows us to obtain more realistic solutions. The current study investigates and demonstrates the utility of the method developed in Saghamanesh and Baoyin (2018a) to more challenging problems, namely low-thrust trajectory optimization with one GA opportunity.

We incorporate and investigate the impact of important disturbances on a fuel-optimal low-thrust rendezvous-type trajectory optimization from the Earth to Jupiter with an Earth-GA maneuver. The dynamic model includes perturbations due to: (1) gravitational force of all planets in the Solar system, (2) Solar radiation pressure, and (3) non-spherical gravity model of the Earth and all of the planets in the Solar system (i.e., perturbation due to second zonal harmonic \( J_{2} \) of each planet). In addition, planetary ephemeris data (JPL’s Horizon database) are used during the numerical integration of the dynamics. Herein, the above model is referred to as the high-fidelity ephemeris model. For low-thrust trajectory design tasks to a massive body such as Jupiter, incorporation of perturbations is known to lead to significant improvements in fuel consumption and time of flight compared to a GA trajectory in the two-body (2B) dynamic model (Saghamanesh and Baoyin 2018c). The errors caused by the 2B model in the estimation of the variation of the impulsive planetary GA are studied in Negri et al. (2017).

In addition to the complications arising from a GA maneuver, inclusion of the enumerated disturbances compounds the OCP since a multi-point boundary-value problem (MPBVP) has to be solved. Therefore, we make use of the robust dual-step optimization strategy developed in Saghamanesh and Baoyin (2018a). GA maneuvers increase the dimension of the design variables. The high-dimensional design space is parameterized using a hyper-sphere in an abstract angular space. Another contribution of the paper is that we present a new parameterization and provide the complete set of mapping relations from the abstract high-dimensional sphere to the physical design space.

The application of the proposed methodology is shown for two types of trajectories: (1) without Earth GA and (2) with an Earth GA. Each case is further studied when the 2B and/or high-fidelity ephemeris model are used. The Earth–Earth–Jupiter (denoted as E–E–J for brevity) represents a specially challenging case since the Earth is a dominant source of gravitational perturbation during the early phase of trajectory. To further verify the performance of the proposed algorithm, the results are compared against two sets of solutions obtained in Yam et al. (2004) and Guo et al. (2011). The results are interesting and of significant practical utility and demonstrate the capability of the robust dual-step methodology to satisfy the prescribed constraints with remarkable accuracies as are shown herein.

2 System description

There are several choices of coordinates and/or elements to formulate low-thrust trajectories as is investigated in Batliss (1971); however, the derivations can be achieved in a more straightforward manner compared to the other sets of coordinates/elements when Cartesian coordinates are used for modeling the state dynamics and perturbations. In a high-fidelity ephemeris model, it is important to consider perturbing accelerations due to: (1) other planets of the Solar system, \( {\boldsymbol{\mathcal{F}}}_{\rm p} \) (Vallado 2001), (2) oblateness effects of planets, \( {\boldsymbol{\mathcal{F}}}_{J2.} \) (Li et al. 2018), and (3) Solar radiation pressure, \( {\boldsymbol{\mathcal{F}}}_{s} \) (McInnes 2013). Let \( \varvec{r} \) denote the position vector, these perturbing accelerations can be modeled (Saghamanesh et al. 2019) as

$$ \begin{aligned} {\boldsymbol{\mathcal{F}}}_{\rm p} & = - \frac{{\mu_{\rm pl} }}{{\left\| {\varvec{r} - \varvec{r}_{\rm pl} } \right\|^{3} }}\left( {\varvec{r} - \varvec{r}_{\rm pl} } \right) - \frac{{\mu_{\rm pl} }}{{\left\| {\varvec{r}_{\rm pl} } \right\|^{3} }}\varvec{r}_{\rm pl} , \\ {\boldsymbol{\mathcal{F}}}_{J2.} & = - \frac{{\mu_{\rm pl} r_{0}^{2} J_{2} }}{{2r^{5} }}\left( {3\varvec{r} + 6r\sin \varphi \frac{\partial z}{{\partial \varvec{r}}} - 15\varvec{r}\sin^{2} \varphi } \right) , { } \\ {\boldsymbol{\mathcal{F}}}_{s} & = \beta \frac{\varvec{r}}{{mr^{3} }}; \quad \beta = \frac{{\sigma^{*} }}{\sigma }, \\ \end{aligned} $$
(1)

where \( \varvec{r}_{\rm pl} \) and \( \mu_{\rm pl} \) denote the position vector and the gravitational parameter of a planet in the Heliocentric Ecliptic Reference Frame (HERF), \( \partial z/\partial \varvec{r} = \left[ {0,0,1} \right]^{\rm T} \), \( \varphi \) denotes the planet-centric latitude, \( \sigma = m/A \) denotes a constant flight loading, \( A \) is the unit area, \( \sigma^{*} = 1.53 \) (g m−2), and \( \beta \) denotes the Solar radiation pressure. For each planet, \( {\boldsymbol{\mathcal{F}}}_{\rm p} \) and \( {\boldsymbol{\mathcal{F}}}_{J2.} \) have to be considered. The state dynamics, thus, become

$$ \dot{\varvec{r}} = \varvec{v},\quad \dot{\varvec{v}} = - \frac{\mu }{{r^{3} }}\varvec{r} + \frac{{T_{\hbox{max} } u}}{m}\varvec{\alpha}+ \sum {{\boldsymbol{\mathcal{F}}}_{\rm p} } + \sum {{\boldsymbol{\mathcal{F}}}_{J2.} } + {\boldsymbol{\mathcal{F}}}_{s} ,\quad \dot{m} = - \frac{{T_{\hbox{max} } }}{c}u, $$
(2)

where \( \varvec{v} \in {\mathbb{R}}^{3} \) denotes the spacecraft velocity vector and \( m \) is the instantaneous spacecraft mass. The summations are performed over the planets of the Solar system. The thrust vector of the spacecraft is parameterized as \( \varvec{T} = uT_{ \hbox{max} }\varvec{\alpha} \), in which \( T_{ \hbox{max} } \), \( u \in \left[ {0,1} \right] \), and \( \varvec{\alpha} \) denote maximum thrust magnitude, the engine throttle magnitude, and the thrust steering unit vector, respectively. The effective exhaust velocity (a constant value) of the propulsion system is \( c = I_{\text{sp}} g_{0} \) where \( \mu, I_{\text{sp}} \) and \( g_{0} \) denote the Sun’s gravitational parameter, the thruster specific impulse, and the Earth’s sea-level gravitational acceleration.

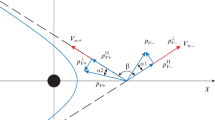
A GA impulse model is adopted in which the spacecraft position vector, \( \varvec{r} \), is equal to the position vector of the planet, \( \varvec{r}_{\rm pl} \), at the time of GA maneuver, \( t_{\rm G} \). Thus, we have

$$ \left\{ \begin{array}{*{20}l} t_{\rm G}^{ - } = t_{\rm G}^{ + } = t_{\rm G} \hfill \\ \varvec{r}\left( {t_{\rm G}^{ - } } \right) = \varvec{r}\left( {t_{\rm G}^{ + } } \right) = \varvec{r}_{\rm pl} \left( {t_{\rm G} } \right) \hfill \\ \end{array} \right., $$
(3)

where superscripts ‘−’ and ‘+’ denote the time instants immediately before and after the GA maneuver. The spacecraft velocities can be written as

$$ \left\{ \begin{array}{*{20}l} \varvec{v}(t_{\rm G}^{ - } ) = \varvec{v}_{\rm pl} (t_{\rm G} ) + \varvec{v}_{\infty }^{ - } \hfill \\ \varvec{v}(t_{\rm G}^{ + } ) = \varvec{v}_{\rm pl} (t_{\rm G} ) + \varvec{v}_{\infty }^{ + } \hfill \\ \end{array} \right.;\quad \left\| {\varvec{v}_{\infty }^{ - } } \right\| = \left\| {\varvec{v}_{\infty }^{ + } } \right\| = v_{\infty }, $$
(4)

where \( \varvec{v}_{\infty }^{ \pm } \) and \( \varvec{v}_{\rm pl} \left( {t_{\rm G} } \right) \) denote GA hyperbolic excess velocity vectors (‘\( - \)’ for incoming and ‘+’ for outgoing) and the velocity vector of the planet at \( t_{\rm G} \), and \( r_{\rm p} \) denotes the hyperbolic periapsis radius associated with the GA orbit as

$$ r_{\rm p} = \frac{{\mu_{\rm pl} }}{{v_{\infty }^{ - } v_{\infty }^{ + } }}\left( {\frac{1}{\sin (\delta /2)} - 1} {} \right), $$
(5)

where \( \delta \) denotes the GA turn angle and \( \delta_{ \hbox{max} } \) is limited by \( r_{ \hbox{min} } \) as the minimum acceptable GA radius:

$$ \left\{ \begin{array}{*{20}l} \delta = \arccos \left( {\frac{{\varvec{v}_{\infty }^{ - } .\varvec{v}_{\infty }^{ + } }}{{v_{\infty }^{2} }}} \right) \hfill \\ \delta_{\hbox{max} } = 2\arcsin \left( {\frac{1}{{1 + \frac{{r_{\hbox{min} } }}{{\mu_{\rm pl} }}v_{\infty }^{2} }}} \right) \hfill \\ \end{array} \right.{ , }\quad \delta \le \delta_{\hbox{max} } . $$
(6)

The GA frame is defined by three orthogonal unit vectors as follows:

$$ \hat{i} = \frac{{\varvec{v}_{\infty }^{ - } }}{{v_{\infty } }},\quad \hat{k} = \frac{{\varvec{v}_{\rm pl} (t_{\rm G} ) \times \varvec{v}_{\infty }^{ - } }}{{\left\| {\varvec{v}_{\rm pl} (t_{\rm G} ) \times \varvec{v}_{\infty }^{ - } } \right\|}},\quad \hat{j} = \hat{k} \times \hat{i},\quad \delta \in [0,\delta_{\hbox{max} } ]. $$
(7)

Ultimately, the net change in the velocity vector due to a GA maneuver can be derived as

$$ \Delta \varvec{v}_{\rm G} = \varvec{v}(t_{\rm G}^{ + } ) - \varvec{v}(t_{\rm G}^{ - } ) = v_{\infty } (\cos \delta \,\hat{i} + \sin \delta \sin \alpha \,\hat{j} + \sin \delta \cos \alpha \,\hat{k}). $$
(8)

where \( \alpha \) and \( \delta \) are used to parameterize the velocity vector in the GA frame.

3 Low-thrust trajectory optimization description

In this section, fundamental components of the problem are reviewed briefly. For fuel-optimal trajectories, the performance index is written in two different Lagrange forms as

$$ J = \int\limits_{{t_{0} }}^{{t_{\rm f} }} {\frac{{T_{\hbox{max} } }}{c}u{\text{d}}t} \Rightarrow J_{a} = \lambda_{0} \int\limits_{{t_{0} }}^{{t_{\rm f} }} {\frac{{T_{\hbox{max} } }}{c}[u - \varepsilon u(1 - u)]{\text{d}}t}, $$
(9)

where a quadratic term is introduced to \( J \) and the resulting expression is further multiplied by a constant auxiliary multiplier \( \left( {\lambda_{0} \in \left( {0,1} \right]} \right) \) to form the auxiliary homotopy performance index, \( J_{\text{a}} \) according to Jiang et al. (2012) and Saghamanesh and Baoyin (2018a). These modifications are introduced to achieve two specific goals: (1) to alleviate the difficulties associated with bang–bang controls (by a homotopic method) that are attributes of fuel-optimal solutions, and (2) to make use of the homogeneity of the set of resulting equations, which allows us to bound the search space. In the auxiliary performance index, \( \varepsilon \) is a continuation parameter where \( \varepsilon = 1 \) and \( \varepsilon = 0 \) correspond to the energy- and fuel-optimal problems, respectively.

The procedure for deriving parts of the optimality conditions is straightforward (Saghamanesh and Baoyin 2018a), and only the final relations are presented. Let \( \varvec{\lambda}= \left[ {\lambda_{0} ,\varvec{\lambda}_{\varvec{r}}^{\rm T} ,\varvec{\lambda}_{\varvec{v}}^{\rm T} , \lambda_{m} } \right]^{\rm T} \) denote the vector of co-states (note that \( \lambda_{0} \) is one of the unknown parameters, but it is constant in the homotopic process). Application of Pontryagin’s minimum principle along with Lawden’s primer vector theory leads to the following extremal controls (Saghamanesh and Baoyin 2018a)

$$ \varvec{\alpha}= - \frac{{\varvec{\lambda}_{\varvec{v}} }}{{\left\| {\varvec{\lambda}_{\varvec{v}} } \right\|}} \, ,\quad u = \left\{ {\begin{array}{*{20}l} {0 \, \rho > \varepsilon } \hfill \\ {1 \, \rho < - \varepsilon } \hfill \\ {\frac{1}{2} - \frac{\rho }{2\varepsilon } \, \left| \rho \right| \le \varepsilon } \hfill \\ \end{array} } \right. \, ,\quad \rho = 1 - \frac{{c\left\| {\varvec{\lambda}_{\varvec{v}} } \right\|}}{{m\lambda_{0} }} - \frac{{\lambda_{m} }}{{\lambda_{0} }}, $$
(10)

where \( \rho \) is the so-called switching function. Co-state dynamics \( \dot{\varvec{\lambda}} = - \left[ {\partial H/\partial \varvec{x}} \right]^{\rm T} \) can be derived by Euler–Lagrange conditions (Bryson 2018) as follows:

$$ \begin{aligned} \dot{\varvec{\lambda}}_{\varvec{r}} & = \frac{\mu }{{r^{3} }}\varvec{\lambda}_{\varvec{v}} - \frac{{3\mu\varvec{\lambda}_{\varvec{v}} . \, \varvec{r}}}{{r^{5} }}\varvec{r} - \sum {\left( {\frac{{3\mu_{\rm pl}\varvec{\lambda}_{\varvec{v}} .(\varvec{r} - \varvec{r}_{\rm pl} )}}{{\left\| {\varvec{r} - \varvec{r}_{\rm pl} } \right\|^{5} }}(\varvec{r} - \varvec{r}_{\rm pl} ) - \frac{{\mu_{\rm pl}\varvec{\lambda}_{\varvec{v}} }}{{\left\| {\varvec{r} - \varvec{r}_{\rm pl} } \right\|^{3} }}} \right) - \beta \left( {\frac{{\varvec{\lambda}_{\varvec{v}} }}{{mr^{3} }} - \frac{{3\varvec{\lambda}_{\varvec{v}} . \, \varvec{r}}}{{r^{5} }}\varvec{r}} \right)} \\ & \quad - \sum {\left[ {\frac{{15\mu_{\rm pl} r_{0}^{2} J_{2} }}{2}\left( {\frac{{\sin^{2} \varphi }}{{r^{5} }}\varvec{\lambda}_{\varvec{v}} - \frac{{7\sin^{2} \varphi (\varvec{\lambda}_{\varvec{v}} . \, \varvec{r})}}{{r^{7} }}\varvec{r} + \frac{{2\sin \varphi (\varvec{\lambda}_{\varvec{v}} . \, \varvec{r})}}{{r^{6} }}\frac{\partial z}{{\partial \varvec{r}}}} \right)} \right.} \\ & \quad \left. { - \frac{{\mu_{\rm pl} r_{0}^{2} J_{2} }}{2}\left( {\frac{{3\varvec{\lambda}_{\varvec{v}} }}{{r^{5} }} - \frac{{15(\varvec{\lambda}_{\varvec{v}} . \, \varvec{r})}}{{r^{7} }}\varvec{r}} \right) - 3\mu_{\rm pl} r_{0}^{2} J_{2} \left( {\varvec{\lambda}_{\varvec{v}} .\frac{\partial z}{{\partial \varvec{r}}}} \right)\left( { - \frac{5\sin \varphi }{{r^{6} }}\varvec{r} + \frac{1}{{r^{5} }}\frac{\partial z}{{\partial \varvec{r}}}} \right)} \right], \\ \dot{\varvec{\lambda}}_{\varvec{v}} & = -\varvec{\lambda}_{\varvec{r}} , \\ \dot{\lambda }_{m} & = - \frac{{T_{\hbox{max} } u}}{{m^{2} }}\left\| {\varvec{\lambda}_{\varvec{v}} } \right\| - \beta \frac{{\varvec{\lambda}_{\varvec{v}} . \, \varvec{r}}}{{m^{2} r^{3} }}. \\ \end{aligned} $$
(11)

3.1 Constraints

In this paper, a fuel-optimal rendezvous-type trajectory from the Earth to Jupiter with one Earth-GA maneuver is considered. The initial time \( t_{0} \) and the final time \( t_{\rm f} \) are fixed. The boundary conditions (subscripts ‘E’ and ‘J’ for Earth and Jupiter) are given by

$$ \varvec{\psi}(t_{0} ) = \left[ {\begin{array}{*{20}c} {\varvec{r}(t_{0} ) - \varvec{r}_{\rm E} } \\ \begin{array}{*{20}l} \varvec{v}(t_{0} ) - \varvec{v}_{\rm E} \hfill \\ m(t_{0} ) - 1 \hfill \\ \end{array} \\ \end{array} } \right] = {\mathbf{0 }},\quad\varvec{\psi}(t_{\rm f} ) = \left[ {\begin{array}{*{20}c} {\varvec{r}(t_{\rm f} ) - \varvec{r}_{\rm J} } \\ \begin{array}{*{20}l} \varvec{v}(t_{\rm f} ) - \varvec{v}_{\rm J} \\\varvec{\lambda}_{m} (t_{\rm f} ) \\ \end{array} \\ \end{array} } \right] = {\mathbf{0 }}, $$
(12)

where \( \lambda_{m} \left( {t_{\rm f} } \right) = 0 \) is due to transversality condition since the final mass is free, and that the spacecraft mass is normalized such that \( m\left( {t_{0} } \right) = 1 \). The position and velocity vectors of the spacecraft \( \varvec{r}(t_{\rm G} ) \) and \( \varvec{v}(t_{\rm G} ) \) are equal to the GA planet’s position vector \( \varvec{r}_{\rm pl} \), and the relations given in Eq. (4) hold.

The GA maneuver introduces four equality constraints and one inequality constraint written as

$$ \varvec{\psi}(t_{\rm G} ) = \left[ {\begin{array}{*{20}c} {\varvec{r}(t_{\rm G} ) - \varvec{r}_{\rm pl} (t_{\rm G} )} \\ {\left\| {\varvec{v}_{\infty }^{ - } } \right\| - \left\| {\varvec{v}_{\infty }^{ + } } \right\|} \\ \end{array} } \right]{ = }{\mathbf{0}}\text{,}\quad \sigma_{\rm G} = 1 - \frac{{r_{\rm p} }}{{r_{\hbox{min} } }} \le 0. $$
(13)

In addition, rigid conditions should be added because of the inequality constraint as

$$ \kappa \cdot \sigma_{\rm G} = 0,\quad \kappa \ge 0. $$
(14)

Two additional inner conditions have to be included if/when a GA maneuver exists (Jiang et al. 2012). The GA transversal conditions constitute the first set of inner conditions written as

$$ \left\{ \begin{array}{*{20}l}\varvec{\lambda}_{\varvec{r}} \left( {t_{\rm G}^{ + } } \right) =\varvec{\lambda}_{\varvec{r}} \left( {t_{\rm G}^{ - } } \right) - {{\boldsymbol{\mathsf{Z}}}}_{1 \sim 3} , \hfill \\\varvec{\lambda}_{\varvec{v}} \left( {t_{\rm G}^{ + } } \right) = {{\boldsymbol{\mathsf{Z}}}}_{4} \varvec{u}^{ + } + \frac{1}{{r_{\hbox{min} } }}\kappa \varvec{B},\hfill \\\varvec{\lambda}_{\varvec{v}} \left( {t_{\rm G}^{ - } } \right) = {{\boldsymbol{\mathsf{Z}}}}_{4} \varvec{u}^{ - } - \frac{1}{{r_{\hbox{min} } }}\kappa \varvec{A}, \hfill \\ \end{array} \right.;\quad \left\{ \begin{array}{*{20}l} \varvec{A} = \frac{{r_{\rm p} }}{{v_{\infty }^{ - } }}\left[ {\frac{1}{{4\sin^{2} {\delta \mathord{\left/ {\vphantom {\delta 2}} \right. \kern-0pt} 2}\left( {1 - \sin {\delta \mathord{\left/ {\vphantom {\delta 2}} \right. \kern-0pt} 2}} \right)}}\left( {\varvec{u}^{ + } - \cos \delta \varvec{u}^{ - } } \right) - \varvec{u}^{ - } } \right], \hfill \\ \varvec{B} = \frac{{r_{\rm p} }}{{v_{\infty }^{ + } }}\left[ {\frac{1}{{4\sin^{2} {\delta \mathord{\left/ {\vphantom {\delta 2}} \right. \kern-0pt} 2}\left( {1 - \sin {\delta \mathord{\left/ {\vphantom {\delta 2}} \right. \kern-0pt} 2}} \right)}}\left( {\varvec{u}^{ - } - \cos \delta \varvec{u}^{ + } } \right) - \varvec{u}^{ + } } \right], \hfill \\ \end{array} \right.. $$
(15)

where \( {{\boldsymbol{\mathsf{Z}}}}_{1\sim4} \) is a 4-D multiplier and \( \kappa \) is a positive scalar multiplier and \( \varvec{u}^{ \pm } = \varvec{v}_{\infty }^{ \pm } /v_{\infty } \). The velocity vector of the spacecraft and its co-state vector are different at time instances \( t_{\rm G}^{ - } \) and \( t_{\rm G}^{ + } \). Hence, the Hamiltonian values would differ before and after the moment of GA. Consequently, the GA stationarity condition constitutes a second inner condition, which should be satisfied in an extremal solution and can be written as follows:

$$ H\left( {t_{\rm G}^{ - } } \right) - H\left( {t_{\rm G}^{ + } } \right) - {{\boldsymbol{\mathsf{Z}}}}_{1\sim3} \cdot \varvec{v}_{\rm pl} \left( {t_{\rm G} } \right) + {\mathbf{Z}}_{4} \left( {\varvec{u}^{ + } - \varvec{u}^{ - } } \right) \cdot \varvec{a}_{\rm pl} \left( {t_{\rm G} } \right) - \frac{1}{{r_{\hbox{min} } }}\kappa \varvec{C} = 0, $$
(16)

where \( \varvec{a}_{\rm pl} \left( {t_{\rm G} } \right) \) is the acceleration of the GA planet at \( t_{\rm G} \), and \( \varvec{C} \) are defined as

$$ \varvec{C} = r_{\rm p} \left\{ { - \frac{1}{{4\sin^{2} {\delta \mathord{\left/ {\vphantom {\delta 2}} \right. \kern-0pt} 2}\left( {1 - \sin {\delta \mathord{\left/ {\vphantom {\delta 2}} \right. \kern-0pt} 2}} \right)}}\left[ {\frac{1}{{v_{\infty }^{ + } }}} \right.} \right.\left. {\left. {\left( {\varvec{u}^{ - } - \cos \delta \varvec{u}^{ + } } \right) + \frac{1}{{v_{\infty }^{ - } }}\left( {\varvec{u}^{ + } - \cos \delta \varvec{u}^{ - } } \right)} \right]} \right\}.\varvec{a}_{\rm pl} \left( {t_{\rm G} } \right), $$
(17)
$$ \varvec{a}_{\rm pl} \left( {t_{\rm G} } \right) = - \frac{\mu }{{r_{\rm pl}^{3} (t_{\rm G} )}}\varvec{r}_{\rm pl} (t_{\rm G} ), $$
(18)

where \( \alpha \) and \( \delta \) are used to parameterize the velocity vector in the GA frame.

4 Multiple-point boundary-value problem

The optimal control problem is transformed into a MPBVP, which includes: the final constraints, \( \varvec{\psi}\left( {t_{\rm f} } \right) \), Eq. (12), the intermediate GA constraints, Eq. (13), the GA transversal conditions, \( \varvec{\lambda}_{\varvec{v}} \left( {t_{\rm G}^{ - } } \right) \), from Eq. (15), the GA stationarity condition, Eq. (16), and the rigid conditions, Eq. (14). Let \( \varvec{\varGamma}\left( {t_{0} ,\varepsilon } \right) = \left[ {\lambda_{0} ,\varvec{\lambda}_{r}^{\rm T} ,\varvec{\lambda}_{v}^{\rm T} ,\lambda_{m} ,\varvec{Z}_{1\sim4}^{\rm T} ,\kappa } \right]^{\rm T} \in {\mathbb{R}}^{13} \) denote the vector of unknown co-states and constant Lagrange multipliers, and let \( {\varvec{\Theta}}\left( \varepsilon \right) = \left[ {\varvec{\varGamma}^{\varvec{{}}} ,\Delta \varvec{v}^{\rm T} } \right]^{\rm T} \in {\mathbb{R}}^{16} \) denote the vector of total unknowns that characterizes a solution completely. A shooting equation, \( \varPhi \), given in Eq. (19) characterizes the problem. We mention that a normalization technique used in Jiang et al. (2012) and Saghamanesh and Baoyin (2018a) can be employed throughout the optimization algorithm (Saghamanesh and Baoyin 2018a), which maps the designs variables to the surface of a hyper-sphere surface of dimension 13. As a consequence of normalization, a scalar equality constraint \( \varvec{\varGamma}\left( {t_{0} ,\varepsilon } \right) - 1 = 0 \) should be introduced to the shooting problem (last relation).

$$ \varPhi \left( \varTheta \right) = \left[ \begin{array}{*{20}l}\varvec{\psi}(t_{\rm f} ) \\ \varvec{r}(t_{\rm G} ) - \varvec{r}_{\rm pl} (t_{\rm G} ) \\ v_{\infty }^{ - } - v_{\infty }^{ + } \\\varvec{\lambda}_{\varvec{v}} \left( {t_{\rm G}^{ - } } \right) - {{\boldsymbol{\mathsf{Z}}}}_{4} \varvec{u}^{ - } + \frac{1}{{r_{\hbox{min} } }}\kappa \varvec{A} \\ {\text{Eq}} .\,(15) \\ \sigma_{\rm G} \\ \left\| {\varvec{\varGamma}(t_{0} ,\varepsilon )} \right\| - 1 \\ \end{array} \right] = {\mathbf{0}}. $$
(19)

It is also possible to remove the scalar equality constraint entirely by parameterizing the elements of the 13-D hyper-sphere, \( \varvec{\varGamma}\left( {t_{0} ,\varepsilon } \right) \), throughout the algorithm as is demonstrated herein, which improves the convergence. The high-dimensional design space is parameterized using a high-dimensional sphere in an abstract angular space. The mapping relations from the abstract high-dimensional sphere to the physical design space are given in this paper. These mapping relations are especially effective when GA with a high-dimension design space is parameterized.

We introduce a 15-D vector of search variables\( \varvec{X}\left( \varepsilon \right) = \left[ {x_{1} , \ldots ,x_{15} } \right] \) (where \( x_{i} \in \left[ {0,1} \right] \) for \( i = 1, \ldots ,15 \)). These search variables are used to construct some intermediate angle variables. Eventually, the angle variables form the 13 elements of the \( \varvec{\varGamma} \) vector such that the \( \left\| \varvec{\varGamma}\left( {t_{0} ,\varepsilon } \right) \right\| - 1 = 0 \) constraint is satisfied automatically during the optimization process. First, the 12-D angle variables \( \varvec{\varphi } = \left[ {\varphi_{1} , \ldots ,\varphi_{12} } \right]^{\varvec{T}} \) are obtained from 12-D \( x_{1 - 12} \left( \varepsilon \right) \) as follows:

$$ \left\{ \begin{array}{*{20}l} \varphi_{1,2,3} { = }\frac{\pi }{2}x_{1,2,3} \in \left[ {0,\frac{\pi }{2}} \right] \hfill \\ \varphi_{4,5} { = }\pi (x_{4,5} { - }\frac{1}{2}) \in \left[ { - \frac{\pi }{2},\frac{\pi }{2}} \right] \hfill \\ \varphi_{6,7} { = 2}\pi x_{6,7} \in \left[ {0,2\pi } \right] \hfill \\ \varphi_{8} { = }\pi (x_{8} { - }\frac{1}{2}) \in \left[ { - \frac{\pi }{2},\frac{\pi }{2}} \right] \hfill \\ \end{array} \right. \, ;\quad \left\{ \begin{array}{*{20}l} \varphi_{9} { = }\frac{\pi }{2}x_{9} \in \left[ {0,\frac{\pi }{2}} \right] \hfill \\ \varphi_{10} { = 2}\pi x_{10} \in \left[ {0,2\pi } \right] \, \hfill \\ \varphi_{11,12} { = }\frac{\pi }{2}x_{11,12} \in \left[ {0,\frac{\pi }{2}} \right] \hfill \\ \end{array} \right.. $$
(20)

Then, here we have introduced the relations between the 8-D unknown co-states \( \varvec{\lambda}= \left[ {\lambda_{0} ,\varvec{\lambda}_{\varvec{r}}^{\rm T} ,\varvec{\lambda}_{\varvec{v}}^{\rm T} , \lambda_{m} } \right]^{\rm T} \) and the 5-D GA numerical multipliers, \( \left[ {\varvec{Z}_{1\sim4} ,\kappa } \right] \) as follows:

$$ \begin{aligned} & \lambda_{0} = \sin \varphi_{1} , \\ & \lambda_{m} (t_{0} ,\varepsilon ) = \cos \varphi_{1} \sin \varphi_{2} \cos \varphi_{12} , \\ &\varvec{\lambda}_{\varvec{r}} (t_{0} ,\varepsilon ) = \cos \varphi_{1} \cos \varphi_{2} \cos \varphi_{3} \cos \varphi_{12} [\cos \varphi_{4} \cos \varphi_{6} \, \cos \varphi_{4} \sin \varphi_{6} \, \sin \varphi_{4} ]^{\rm T} , \\ &\varvec{\lambda}_{\varvec{v}} (t_{0} ,\varepsilon ) = \cos \varphi_{1} \cos \varphi_{2} \sin \varphi_{3} \cos \varphi_{12} [\cos \varphi_{5} \cos \varphi_{7} \, \cos \varphi_{5} \sin \varphi_{7} \, \sin \varphi_{5} ]^{\rm T} , \\ \end{aligned} $$
(21)
$$ \begin{aligned} {{\boldsymbol{\mathsf{Z}}}}_{1} & = \cos \varphi_{1} \sin \varphi_{8} \sin \varphi_{12} , \\ {{\boldsymbol{\mathsf{Z}}}}_{2\sim4} & = \cos \varphi_{1} \cos \varphi_{8} \cos \varphi_{9} \sin \varphi_{12} [\cos \varphi_{10} \cos \varphi_{11} \, \cos \varphi_{10} \sin \varphi_{11} \, \sin \varphi_{10} ]^{\rm T} , \\ \end{aligned} $$
(22)
$$ \kappa = \cos \varphi_{1} \cos \varphi_{8} \sin \varphi_{9} \sin \varphi_{12} , $$
(23)

where \( \varvec{\lambda}_{\varvec{r}} \), \( \varvec{\lambda}_{\varvec{v}} \), and \( \varvec{Z}_{1\sim4} \) are restricted within the domain \( \left[ { - 1, 1} \right] \) and \( \lambda_{0} \), \( \lambda_{m} \), and \( \kappa \) are restricted within the domain \( \left[ {0, 1} \right] \) throughout the optimization algorithm. Note that this parameterization is different from the one given in Jiang et al. (2012).

In addition, the 3-D GA velocity increment vector becomes [see Eq. (8)]

$$ \Delta v_{\rm G} = x_{15} \sqrt {\frac{{\mu_{\rm pl} }}{{r_{\hbox{min} } }}} \left[ {\cos \delta \cos \alpha ,\,\sin \delta \cos \alpha ,\,\sin \alpha } \right]^{\rm T} , $$
(24)

where

$$ \alpha = \pi \left( {x_{13} - 0.5} \right) \in \left[ { - \frac{\pi }{2},\frac{\pi }{2}} \right],\quad \delta = 2\pi x_{14} \in \left[ {0,2\pi } \right]. $$
(25)

Altogether, there are 15-D search variables, \( \varvec{X}\left( \varepsilon \right) \), but they are related to the actual 16 unknowns of the original MPBVP, \( {\varvec{\Theta}}\left( \varepsilon \right) \in {\mathbb{R}}^{16} \). An ideal scenario is to fix the initial time, \( t_{0} \), the final time \( t_{\rm f} \), and especially the GA time, \( t_{\rm G} \). The reason behind fixing these three times is that any change in the results can be solely attributed to a combination of performance of the robust dual-step optimization algorithm and the use of a high-fidelity ephemeris model. However, when all of these times instants are fixed, the resulting OCP is more challenging. Note that when GA time, \( t_{\rm G} \), is fixed, the GA stationarity condition Eq. (16) has to be removed from the shooting function since it does not hold.

5 Solution methodology

The first step of the optimization makes use of a PSO algorithm to perform a broad search, whereas the second step improves upon the solution of the first step through a gradient-based algorithm. A brief review of the involved steps of the dual-step optimization algorithm (Saghamanesh and Baoyin 2018a) is presented:

  • Energy-optimal step (\( \varepsilon = 1 \)) that consists of two parts: (1) we employ a PSO algorithm with the goal or objective of finding a minimum to a cost defined in Eq. (26), and (2) optimization based on an indirect method (using MATLAB’s fsolve function) to solve the shooting problem defined in Eq. (19) starting from the solution of the first part. PSO is applied to determine an approximate energy-optimal solution.

    $$ I\left( {\varvec{X}(1)} \right) = \left\| {\varPhi \left( {\varvec{\lambda}(t_{0} ,1)} \right)} \right\|^{2} + \, \lambda_{0} \int\limits_{{t_{0} }}^{{t_{\rm f} }} {\frac{{T_{\hbox{max} } }}{c}[u - \varepsilon u(1 - u)]{\text{ d}}t} , $$
    (26)

    where \( \varvec{X}\left( \varepsilon \right) \) denotes the 15-D vector of search variables.

  • Fuel-optimal solution is achieved through a homotopic method. A one-parameter family of neighboring OCPs is constructed to guide the energy-optimal solution to a fuel-optimal one. The optimal (denoted by superscript ‘*’) search-variables vector \( \varvec{X}^{\varvec{*}} \left( 1 \right) \) are iterated as is outlined in Saghamanesh and Baoyin (2018a).

The key point in the algorithm proposed by Saghamanesh and Baoyin (2018a), that enhances convergence, is that the 15-D search-variables vector \( \varvec{X}\left( \varepsilon \right) \) and the 8-D unknown co-states \( \varvec{\lambda}= \left[ {\lambda_{0} ,\varvec{\lambda}_{\varvec{r}}^{\rm T} ,\varvec{\lambda}_{\varvec{v}}^{\rm T} , \lambda_{m} } \right]^{\rm T} \) are efficiently restricted within domain \( \left[ { - 1,1} \right] \), and the switching function remains bounded in close proximity to the domain \( \left[ { - 1,1} \right] \). In fact, these domains are mapped from an unbounded domain \( \left[ { - \infty ,\infty } \right] \) to the domain \( \left[ { - 1,1} \right] \). Consequently, the optimal solution is rapidly designed to obtain the global robust convergence to satisfy all constraints without any ambiguity. The fitting process of all iterations robustly finds the unknown variables with the percent of converged solutions to maximum, and the penalty terms are quickly satisfied with predetermined high accuracy, from the energy- to fuel-optimal solutions, especially close to zero point as a critical point (Saghamanesh and Baoyin 2018a). A fixed step-size fourth-order Runge–Kutta method is used as the integrator throughout the computational process.

6 Numerical simulations

An interplanetary trajectory from the Earth to Jupiter is considered with an Earth-GA maneuver en route to the Jupiter, i.e., an E–E–J sequence. Two dynamic models are considered: (1) a 2B dynamic model and (2) a high-fidelity ephemeris dynamic model that takes into account all of the sources of perturbations modeled in Sect. 2. The particular mission we have chosen has also been already solved in a 2B model by Yam et al. (2004) using program GALLOP, and by Guo et al. (2011) using a homotopic method. We compare our results against the reported solutions of these two papers. The optimization solution is significantly challenging: (1) when Earth-GA scenario in full ephemeris model is implemented, (2) when the flight time is long, and (3) when the high-energy transfer between Earth and Jupiter is considered.

Similar to Yam et al. (2004), we assume that there exists a launcher with an upper stage (rocket engine with a specific impulse of \( I_{{{\text{sp}},{\text{chemical}}}} = 404 \) (s)), which is capable of injecting a spacecraft with an initial mass of 20,000 (kg) to a parabolic escape trajectory, i.e., \( v_{\infty } = 0 \). For \( v_{\infty } > 0 \), the launcher injects less mass on the escape hyperbola. At the launch time, the magnitude of the hyperbolic excess velocity is a design variable and influences both the trajectory and the final mass considerably as is shown herein. The spacecraft launch hyperbolic excess velocity vector \( \varvec{v}_{\infty i} \) is calculated as follows:

$$ \varvec{v}_{{\infty_{i} }} = v_{{\infty_{i} }} \varvec{u}_{\infty } ;\quad \varvec{u}_{\infty } = \pm \frac{{\varvec{v}_{\rm E} (t_{0} )}}{{\left\| {\varvec{v}_{\rm E} (t_{0} )} \right\|}}, $$
(27)

where \( \varvec{v}_{\rm E} \) is the Earth velocity vector and the positive direction is used for an E–E–J scenario. Furthermore, Tsiolkovsky rocket equation can be used to determine the initial spacecraft mass immediately after performing the impulsive maneuver as

$$ m_{0} (v_{{\infty_{i} }} ) = m_{0} \exp \left( { - \frac{{\Delta v_{i} }}{{v_{\text{ex,chemical}} }}} \right),\quad \Delta v_{i} = v_{\text{LEO}} \left( {\sqrt {2 + \left( {\frac{{v_{{\infty_{i} }} }}{{v_{\text{LEO}} }}} \right)^{2} } - 1} \right), $$
(28)

where \( m_{0} = 20,000 \) (kg) denotes the initial spacecraft mass, when \( v_{\infty i} = 0 \), and \( v_{{{\text{ex}},{\text{chemical}}}} = I_{{{\text{sp}},{\text{chemical}}}} g_{0} \) denotes the effective exhaust velocity of the rocket engine. Besides, \( \Delta v_{i} \) denotes the launch hyperbolic velocity required to inject the spacecraft into the hyperbolic interplanetary trajectory where \( v_{\text{LEO}} \) is the low-Earth orbit circular velocity. Therefore, the initial and final conditions, Eqs. (12), have to be updated as follows:

$$ \varvec{\psi}_{i} = \left[ {\begin{array}{*{20}c} {\varvec{r}_{i} (t_{0} ) - \varvec{r}_{\rm E} } \\ \begin{array}{*{20}l} \varvec{v}_{i} (t_{0} ) - \varvec{v}_{\rm E} - v_{{\infty_{i} }} \varvec{u}_{\infty } \hfill \\ \, m_{i} (t_{0} ) - m_{0} (v_{{\infty_{i} }} ) \hfill \\ \end{array} \\ \end{array} } \right] = {\mathbf{0 }}, \,\varvec{\psi}_{\rm f} = \left[ {\begin{array}{*{20}c} {\varvec{r}_{i} (t_{\rm f} ) - \varvec{r}_{\rm J} (t_{\rm f} )} \\ \begin{array}{*{20}l} \varvec{v}_{i} (t_{\rm f} ) - \varvec{v}_{\rm J} (t_{\rm f} ) \\ \lambda_{{m_{i} }} (t_{\rm f} ) \\ \end{array} \\ \end{array} } \right] = {\mathbf{0 }}. $$
(29)

Due to Eq. (28) and the upper stage parameters of the heavy lifter with chemical propulsion system, Fig. 1 depicts the variation of the injected spacecraft mass versus different values of the launch hyperbolic excess velocity, \( v_{{\infty_{i} }} \in \left[ {0,10} \right] \) (km/s). The parameters of the problem that are used for numerical simulations are listed in Table 1. These parameters are chosen according to Yam et al. (2004) and Guo et al. (2011). The state vectors of the planets, the gravitational constant (µ), and the radius of the sphere of influence (SOI) of the planets, the Sun, and the Moon are extracted from JPL/HORIZON.Footnote 1

Fig. 1
figure 1

Variation of initial mass versus different values of launch hyperbolic excess velocity magnitude

Full size image
Table 1 Parameters and boundary values for E–E–J mission
Full size table

Table 2 provides a summary of the fuel-optimal solutions for seven different discrete values of launch hyperbolic excess velocity, \( v_{\infty i} \) (km/s), for both the 2B and high-fidelity ephemeris models. The minimum launch hyperbolic excess velocity required for the considered mission is 0.2 and 0.71 (km/s) for the 2B and high-fidelity ephemeris models, respectively. Furthermore, the optimal spacecraft final mass in the 2B model is 16,194.92 (kg) and corresponds to \( v_{\infty i} = 0.71 \) (km/s), whereas for a \( v_{\infty i} = 1.0 \) (km/s), the optimal spacecraft final mass value is 15,816.01 (kg) in the high-fidelity model. The minimum propellant consumption of the spacecraft trajectory in the 2B and high-fidelity ephemeris models is 3,172.9 and 3,439.76, respectively. The 2B and high-fidelity ephemeris fuel-optimal GA maneuvers have turn angles, \( \delta = 62.45^\circ \) and \( \delta = 61.88^\circ \), respectively. Furthermore, Table 2 illustrates that all fuel-optimal trajectory solutions in both the 2B and high-fidelity ephemeris models with different \( v_{\infty i} \) have happened at \( r_{\rm p} = r_{\hbox{min} } \) since the turn angle \( \delta \) has approached its maximum turn angle, \( \delta_{\hbox{max} } \). To demonstrate the accuracy of the method, sum of the residuals of the shooting function associated with the resulting MPBVP, \( \varvec{\sigma}_{\varPhi } \), is shown in Table 2. Such small errors correspond to remarkable accuracies in satisfying position and velocity level constraints. Accordingly, for example, final errors for the fuel-optimal solution in the high-fidelity ephemeris model are \( \Delta r_{\rm f} = 9.329 \times 10^{ - 5} \,\left( {\text{km}} \right) \) and \( \Delta v_{\rm f} = 1.545 \times 10^{ - 13} \,\left( {{\text{km}}/{\text{s}}} \right) \).

Table 2 Comparison of the fuel-optimal solutions versus seven selected values of launch hyperbolic excess velocity for both models
Full size table

Table 3 summarizes the GA fuel-optimal co-states and numerical results for both dynamic models to make the results reproducible. The 8-D fuel-optimal (\( \varepsilon = 0 \)) unknown co-states are presented for 2B and full ephemeris models. The GA point numerical results are illustrated including the GA hyperbolic excess velocity vectors \( \varvec{v}_{\infty }^{ \pm } \), the GA velocity increment \( \Delta \varvec{v}_{\rm G} \), and the 5-D GA numerical multipliers \( \left[ {\varvec{Z}_{1\sim4}\varvec{\kappa}} \right] \). The 6-D unknown co-states, \( \varvec{\lambda}\left( {t,\varepsilon } \right) = \left[ {\varvec{\lambda}_{\varvec{r}} ;\varvec{\lambda}_{\varvec{v}} } \right] \), and the 4-D GA numerical multipliers \( \left[ {\varvec{Z}_{1\sim4} } \right] \) are restricted in domain \( \left[ { - 1,1} \right] \); and the homotopy multiplier, \( \gamma_{0} \), the mass co-state, \( \lambda_{m} \), and the numerical multiplier, \( {\kappa} \), are restricted in domain \( \left[ {0,1} \right] \), respectively, throughout the continuation procedure.

Table 3 GA fuel-optimal (\( \varepsilon = 0 \)) co-states and numerical results for both dynamic models
Full size table

Figure 2 depicts the time history of the magnitudes of the planetary gravity perturbations along the high-fidelity GA trajectory with \( v_{\infty i} = 1 \) (km/s). The blue and red color lines correspond to segments before and after the Earth-GA maneuver, respectively. Prior to the Earth-GA moment, the main sources of perturbations are due to the Earth’s gravity potentials and Earth’s moon. During the Earth-GA maneuver, Earth and moon become the main source of perturbations. The influence of the gravity potential of Jupiter grows over time and gets large as the spacecraft enters the Jupiter’s SOI. Figure 3 shows the Solar radiation pressure perturbations for both constant and instantaneous spacecraft mass before and after the Earth-GA maneuver. With respect to the physical quantity contained in Eq. (1), the Solar radiation pressure perturbation in the case of the constant spacecraft mass is always smaller than the instantaneous spacecraft mass.

Fig. 2
figure 2

Magnitude of planetary gravity perturbations versus time

Full size image
Fig. 3
figure 3

Solar radiation pressure perturbation for variable and constant spacecraft mass

Full size image

Figure 4 shows the time history of the magnitude of the perturbing acceleration due to second zonal harmonic, \( J_{2} \), for both Earth and Jupiter before and after the Earth-GA maneuver. As expected, the influence of the non-spherical perturbation appears solely in the Earth and Jupiter’s SOI, especially when the spacecraft is in vicinity of the Earth and Jupiter. Obviously, some of the perturbations are small and ignorable, but the developed tool gives us an important flexibility since we can remove or add any of the considered perturbations and further investigate the contribution and impact of any of the modeled disturbances on the final result. What makes this tool appealing is that high-resolution, accurate solutions are achievable since we have used the indirect optimization method for formulating and solving the resulting OCPs.

Fig. 4
figure 4

Time history of magnitude of the accelerations due to J2 for Earth and Jupiter

Full size image

Figure 5 depicts time histories of the optimal thrust magnitude profile and the corresponding switching functions for both of the dynamic models. The SF profiles in Fig. 5 remain bounded in close proximity to the domain \( \left[ { - 1,1} \right] \), and it shows that there are six thrust switches in the 2B and high-fidelity models. Another point worthy of mentioning is that as expected, the switching function has a discontinuity in both models.

Fig. 5
figure 5

E–E–J mission, time histories of thrust, and switching functions for both dynamic models

Full size image

Figure 6 shows the fuel-optimal co-state vectors \( \varvec{\lambda}^{*} \left( {t,\varepsilon = 0} \right) = \left[ {\varvec{\lambda}_{\varvec{r}} ,\varvec{\lambda}_{\varvec{v}} } \right] \) in both the 2B and full ephemeris models. In addition, the fuel-optimal co-states are restricted within domain \( \left[ { - 1,1} \right] \) throughout the iterations, which is an advantage of the method developed in Saghamanesh and Baoyin (2018a) and used in the current paper. On the contrary, without using normalization, unknown co-states should, frequently, be searched over a large domain [− 100000, 100000], which makes the process of continuing from energy- to fuel-optimal solution significantly challenging. The corresponding auxiliary multiplier, \( \lambda_{0} \), for the 2B and full ephemeris models is 0.933882435 and 0.991005017, respectively.

Fig. 6
figure 6

Time histories of fuel-optimal co-state vectors for both dynamic models

Full size image

Table 4 provides a summary of the results of this study against those reported in the literature. The optimal launch hyperbolic excess velocity, \( v_{\infty i} \), and the GA hyperbolic excess velocity, \( \varvec{v}_{\infty }^{ \pm } \), are different compared with the values of the existing solutions in the 2B model with an Earth-GA trajectory in the 2B model. First, we compare the optimal direct transfer trajectories (the last two columns). In order to compare our solution with that of Yam et al. (2004), we used a 2B model by turning off the perturbations in our model. Our method has found a solution with \( v_{\infty i} = 0.6 \) (km/s) that puts a larger initial mass on the escape hyperbola. Even though the propellant consumption is greater than the solution in Yam et al. (2004), the final delivered mass has been improved by 191.8 kg (a 1.4% improvement, which is not huge). Obviously, this improvement is solely due the hyperbolic excess velocity and the fact that an indirect optimization method is used, which results in a high-resolution solution. The time of transfer is not optimized, but such direct trajectories are longer compared to a solution with a GA maneuver with the Earth.

Table 4 Comparison of the fuel-optimal results with existing solutions
Full size table

For a GA trajectory, we look at the solutions when a 2B model is used (columns 4–6). For the same value of \( v_{\infty i} = 0.71 \) (km/s), our method results in the best solution although the margin of improvement is nearly negligible. As is well known and evident in the results, the value of final mass is significantly improved compared to a direct trajectory and also the time of flight is reduced by almost 1 year. We proceed by considering the difference between the results when a high-fidelity ephemeris model is used with the same \( v_{\infty i} = 0.71 \) (km/s) (columns 3 and 4). The difference in the fuel consumption between the high-fidelity and 2B models is equal to 418.2 (kg). The 2B model results in a trajectory that may appear to consume close to half a ton less propellant than an optimized solution in a high-fidelity ephemeris model. Obviously, the 2B model over-predicts the performance and may lead to erroneous mission design conclusions. Finally, the best solution using a high-fidelity model corresponds to \( v_{\infty i} = 1 \) (km/s). The optimal Earth \( v_{\infty } \) increases from 0.71 to 7.4461 km/s and from 1 to 7.5104 km/s during the E–E transfer in 441 days for the 2B and high-fidelity ephemeris models, respectively.

Figure 7 plots the fuel-optimal direct and GA trajectories using the high-fidelity ephemeris and 2B models. Solid line and dash-dot line styles denote the portion of trajectories before and after the Earth-GA event, respectively. A distinct difference between the trajectories is the direct transfer to the Jupiter using the 2B model, which takes a longer time of flight of 2020 days. The challenging part of the problem is that the Earth’s gravity is constantly affecting the trajectory during the first 441 days and becomes dominant at the time of GA. In addition, the last 417 days of flight occurs within Jupiter’s SOI, which influences the trajectory significantly. Nevertheless, the proposed methodology shows robustness while taking all of the considered perturbations into account.

Fig. 7
figure 7

E–E–J GA transfer, fuel-optimal low-thrust trajectories for both dynamic models; and E–J 2B fuel-optimal direct transfer

Full size image

7 Concluding remarks

In this study, contribution of three sources of perturbations is studied on designing a fuel-optimal low-thrust gravity-assist trajectory from the Earth to Jupiter with a gravity-assist maneuver with the Earth. These disturbances constitute a high-fidelity ephemeris dynamic model, which consists of (1) gravitational perturbations due to all planets in the Solar system, (2) disturbance due to Solar radiation pressure, and (3) non-spherical perturbations of all of the planets (i.e., perturbation due to second zonal harmonic \( J_{2} \)). A two-step robust homotopic method is used to solve the resulting multi-point boundary-value problem with remarkable accuracies in satisfying the constraints.

A fixed-time rendezvous trajectory (i.e., launch, gravity-assist, and capture times are fixed) is considered so that any changes in the results can be attributed solely to the use of the high-fidelity ephemeris model and the application of the robust two-step hybrid optimization method. In addition to the gravity-assist trajectory, a fixed-time direct trajectory from the Earth to Jupiter is also studied. A comprehensive comparison of the results using two-body and high-fidelity ephemeris models are conducted for different values of escape hyperbolic excess velocities. For the same initial mass of 19820 kg, the results indicate that for the same value of hyperbolic excess velocity (0.7 km/s), an optimized solution obtained using a high-fidelity ephemeris model may consume as much as half a ton more propellant than a trajectory obtained using a two-body model! This difference is considerable and shows the necessity to have a tool that allows us to obtain more realistic results. While not a new finding, the results indicate that it is possible to improve the final mass by a different hyperbolic excess velocity value.