Selection and trajectory design to mission secondary targets

Abstract

Recently, with new trajectory design techniques and use of low-thrust propulsion systems, missions have become more efficient and cheaper with respect to propellant. As a way to increase the mission’s value and scientific return, secondary targets close to the main trajectory are often added with a small change in the transfer trajectory. As a result of their large number, importance and facility to perform a flyby, asteroids are commonly used as such targets. This work uses the Primer Vector theory to define the direction and magnitude of the thrust for a minimum fuel consumption problem. The design of a low-thrust trajectory with a midcourse asteroid flyby is not only challenging for the low-thrust problem solution, but also with respect to the selection of a target and its flyby point. Currently more than 700,000 minor bodies have been identified, which generates a very large number of possible flyby points. This work uses a combination of reachability, reference orbit, and linear theory to select appropriate candidates, drastically reducing the simulation time, to be later included in the main trajectory and optimized. Two test cases are presented using the aforementioned selection process and optimization to add and design a secondary flyby to a mission with the primary objective of 3200 Phaethon flyby and 25143 Itokawa rendezvous.

1 Introduction

Though there have been only a few asteroid dedicated missions, some past missions, e.g. Galileo and Rosetta, increased the mission’s value by adding a secondary asteroid objective on the proximity of the main trajectory. With a small propellant addition, a flyby was obtained by performing a small change on the original trajectory. In such cases, asteroid selection and trajectory planning is a challenging task due to the large number of variables and unknowns present in the problem. This study presents a method for trajectory design, based on optimal control, and target selection for the case of a mission using low-thrust propulsion system. The objective is to perform the smallest possible change on the main trajectory to allow the flyby of a neighboring asteroid, while maintaining the initial and final conditions required for achieving the mission’s main target.

Minimization of the fuel consumption for interplanetary trajectories is usually the main driver of a preliminary trajectory design. By saving fuel, it is possible to add payload, decrease the launch cost, and often increase the mission lifetime. Another important parameter when dealing with a midcourse asteroid flyby missions is the selection of the target and its flyby time. Currently the minor bodies database includes more than 700,000 items, this allied with a phase-fix requirement for the flyby generate millions of possibilities for the midcourse.

With the rapid increase in computational performance, trajectory design of low-thrust missions have relied mainly on solutions provided by direct methods that rely on non-linear programing (Sims et al. 2006; McConaghy et al. 2003) performing extensive searches. Indirect methods, however, have also been proved useful for mission design of low-thrust trajectories (Russell 2007; Ranieri and Ocampo 2005) by solving a system of non-linear equations given by the two-point boundary value problem (Press et al. 1997). Among the different solution methods, the Primer Vector theory, a derivation using optimal control, is of special interest for space trajectories dealing with minimum mass optimization. The Primer Vector defines an analytical relation between the control variables that can be easily implemented into the spacecraft equations of motion. This theory provides a comprehensive method to define the direction and magnitude of the thrust that minimizes the propellant consumption. Particularly for space trajectory design, solutions of indirect methods are very sensitive to the initial estimation and a good convergence is sometimes difficult to obtain. In this particular situation, however, this difficulty is overcome by the fact that the modified trajectory lies close to the original reference trajectory, which is a good initial estimation. This implies that it is necessary to know the costates of the reference trajectory, which can be done in two ways. First, by optimizing the reference trajectory through the Primer Vector, which can be done without prior knowledge of the solution or use a direct method solution as initial estimation. Second, as done here, if a trajectory is already optimized without its costates, they can be estimated using a combination of linear low-thrust approximation, to define small variations on the states, with the second-order form of the state and costate evolution equations, to obtain the costates (as described in Sect. 4). Indirect methods are, in general, faster than direct methods especially if analytical derivatives are provided, this is an important characteristic for problem settings such as this where many cases need to be analyzed.

The asteroid selection for a midcourse flyby is challenging: high number of possible targets, no predefined specific asteroid or group of asteroids, and flyby time has to be taken into account (not a phase-free problem). In this work the flyby time is narrowed to a small range considering the proximity of possible flyby points to the reference trajectory. However, other system requirements can play an important role in selecting the flyby time, such as the optical navigation time, communication link (distance from the Earth) and power requirements (distance from the Sun). The target has to be close to the main reference trajectory at a specific time and require little propellant to modify the trajectory. The fundamental assumption in this part is that, in order to use a small quantity of fuel, the flyby target or point has to be close to the trajectory. This implies that the point lies inside the linear region of the reference trajectory. Therefore, at some level first order evaluations are adequate to prune the asteroid candidates

This paper will address the aforementioned problem by outlining key theories and detailing a method for the asteroid selection and its subsequent trajectory design. In Sect. 2, the equations of motion of a low-thrust propelled spacecraft in the two-body problem are derived. In Sect. 3, the optimal control is defined using calculus of variations and Pontryagin maximum principle. Section 4 details the asteroid selection process based on reachability, reference orbit, and linear theory. In Sect. 5, the solution method for the entire problem is described from selection to optimization. Section 6 presents a test case used for demonstrating the methodology described in this work, followed by Sect. 7 that presents the conclusion of this work.

2 Equations of motion

For the trajectory design performed in this work, the main forces acting on the spacecraft are considered to be the gravitational forces of the main bodies and the on-board thrust provided by the propulsion system. The equations of motion used for the test case presented here are inertial, Sun-centered for a spacecraft with a low-thrust propulsion system. Therefore, only the gravity of the primary body is considered to be acting on the spacecraft. Nevertheless, the procedure can be used also in the rotating frame with multiple bodies, the changes will come in the derivation of the equations of motion and on the optimal control law. The problem is then subject to a dynamical system described by 7 state variables as:

$$\begin{aligned} \mathbf{x }= & {} {}^t\left[ \mathbf{r },\mathbf{v },m\right] ; \quad \mathbf{p }={}^t\left[ {\mathbf{u }},T\right] ; \end{aligned}$$

(1)

$$\begin{aligned} {\dot{\mathbf{x}}}= & {} f\left( {\mathbf{x }},\mathbf{p },t\right) =\left[ \begin{array}{c} {\dot{\mathbf{r}}} \\ {\dot{\mathbf{v}}} \\ {\dot{m}} \end{array} \right] = \left[ \begin{array}{c} \mathbf{v } \\ -\mu \frac{{\mathbf{r }}}{\left| {\mathbf{r }}\right| ^{3}} + \frac{{\mathbf{u }}T}{m}\\ -\frac{T}{c} \end{array} \right] \end{aligned}$$

(2)

where ${\mathbf{x }}$ is a $7\times 1$ state vector, ${\mathbf{p }}$ is a $4\times 1$ control vector, $\mathbf{r }$ is a $3\times 1$ position vector, $\mathbf{v }$ is a $3\times 1$ velocity vector, m is the mass, $\mathbf{u }$ is a $3\times 1$ unit vector that defines the thrust direction, $\mu$ is the central body gravitational parameter, T is the thrust magnitude and $c = g_0 I_{SP}$ is the propulsion exhaust velocity with $g_0$ the gravity acceleration at sea level and $I_{SP}$ the engine specific impulse.

The control variables are the thrust direction, $\mathbf{u }$, and magnitude, T, which are constrained by the following relations:

$$\begin{aligned} 1={}^t\mathbf{u }\mathbf{u } \quad \text {and} \quad 0\le T \le T_{max} \end{aligned}$$

(3)

3 Optimal control

In this section, the control profile is defined for a minimum mass problem with the control variables T and u. The objective or cost function is used for the minimum mass problem is defined by a Mayer function as

$$\begin{aligned} J=-m_f \end{aligned}$$

(4)

Therefore, the performance index J is being minimized and as a result of the negative sign, the final mass $m_f$ is maximized. Considering the minimum mass cost function and the dynamics, the system’s Hamiltonian can be derived as

(5)

(6)

where 0 represents the integral part of the cost function, in this case zero, $\varvec{\uplambda }$ is the costates vector for each of its associated states $\mathbf{r }$, $\mathbf{v }$ and m.

The optimal control theory uses calculus of variation to identify the control relation with the problem states that minimizes a particular cost function for an unconstrained system. The theory also defines the conditions to be met by the states in order to achieve a particular initial, final or midcourse condition. During the derivation of these relations linear assumptions are made which as a result are valid only in neighboring conditions of the states. This in turn guarantees only a local optimum as opposed to a global optimum. The final form of the optimal relation between the control variables and the states derived by the optimal control theory is (Kirk 2004)

$$\begin{aligned} \frac{\partial H}{\partial \varvec{\uplambda }}= & {} -{}^t\varvec{\dot{\uplambda }}\end{aligned}$$

(7)

$$\begin{aligned} \frac{\partial H}{\partial \mathbf{p }}= & {} 0 \end{aligned}$$

(8)

Using the Hamiltonian associated with the minimum mass cost function, the optimal control conditions are

$$\begin{aligned}&\frac{\partial H}{\partial \mathbf{u }}={}^t\varvec{\uplambda }_v\frac{T}{m}=0 \end{aligned}$$

(9)

(10)

The above conditions are not straightforward. Moreover, they are only valid for unconstrained states and controls which is not the case here, since the thrust magnitude is bounded between zero and $T_{\max }$.

The Pontryagin’s Maximum Principle (Pontryagin 1987) comes primarily from a geometric interpretation of the system phase space and its relation with the control variables. The principle provides more stringent conditions for the control, allowing a better definition of the control profile. It is especially useful when the problem raises constraints on the states and/or on the controls. As in the optimal control theory, the Pontryagin’s Maximum Principle also makes use of linear assumptions during its derivation; therefore, the optimal conditions are also valid only locally. The final form of the Pontryagin’s Maximum Principle defining the optimal control profile is

$$\begin{aligned} H\left[ \mathbf{x }^*,\mathbf{p }^*+\delta \mathbf{p },\varvec{\uplambda }^*,t\right] \ge H\left[ \mathbf{x }^*,\mathbf{p }^*,\varvec{\uplambda }^*,t\right] \end{aligned}$$

(11)

where the asterisk represents the optimal condition and $\varvec{\uplambda }$ is the costates vector.

Once again the Hamiltonian calculated for the minimum mass cost can be applied to the above relation, which results in the minimum value for the Hamiltonian generated by the controls. From Eq. 5, it is clear that the Hamiltonian will decrease by taking $\mathbf{u }$ parallel and in opposite direction of $\varvec{\uplambda }_v$,

$$\begin{aligned} \varvec{u}=-\frac{\varvec{\uplambda }_v}{\left| \varvec{\uplambda }_v\right| } \end{aligned}$$

(12)

As $\mathbf{u }$ is a unit vector, it has to be divided by the magnitude of $\varvec{\uplambda }_v$. The second relation for the control T comes from Eq. 5, by substituting Eq. 12 on it one gets

(13)

Note that now the $\varvec{\uplambda }_v$ in parenthesis is the norm and the value of T that minimizes H depend on the value of the expression multiplying it,

$$\begin{aligned} T=\left\{ \begin{array}{cc} 0 &{} \text {if} \quad S<0\\ 0<T<T_{max} &{} \text {if} \quad S=0\\ T_{max} &{} \text {if} \quad S>0 \end{array} \right. \end{aligned}$$

(14)

where is generally called switching function. As described in Russell (2007), $S=0$ characterizes a ”singular arc” that, even though it does exist for finite durations, is rare for practical applications. Therefore, in this work a bang-bang solution will be used defined by: $S\le 0$ and $S>0$.

3.1 Primer vector control law

In 1963, Lawden derived the necessary conditions for an optimal impulsive trajectory utilizing the optimal control theory by examining the limiting conditions on an optimal finite thrust solution. Such conditions are known as Lawden’s necessary conditions for an optimal impulsive trajectory. In impulsive trajectories, T is not limited, therefore, Eq. 14 is not applicable. However, Eq. 12 concerning the direction is still valid.

So important is the costate associated with the velocity, $\varvec{\uplambda }_v$, that Lawden named the relation $-\varvec{\uplambda }_v$ primer vector in allusion to the burning cord of a primer charge for a cannon. His results were complemented over the years by other researchers, some important steps were taken by Lion and Handelsman (1968), Jezewski and Rozendaal (1968), and Jezewski and Faust (1971).

Since then, the primer vector control law has been applied to different types of space problems using constant specific impulse (Ranieri and Ocampo 2005), variable specific impulse (Senent et al. 2005) in both inertial frame (Russell 2007) and rotational frame (Petropoulos and Russell 2008). Some of the trajectory design applications include problems with modulated impulse (Vadali et al. 2000) and solar sailing (Colasurdo and Casalino 2003) for mission analysis of three-body problems (Kluever and Pierson 1995), spiral escapes (Ranieri and Ocampo 2005) and gravity assist trajectories (Casalino et al. 1999).

3.2 Minimum mass control profile

Using the Primer Vector control law, Eqs. 12 and 14, in the dynamical system of Eq. 2, we obtain the equations of motion for a spacecraft whose thrust direction and magnitude are already locally optimized for a minimum mass usage of propellant,

$$\begin{aligned} {\dot{\mathbf{y}}}= & {} f\left( {\mathbf{y }}\right) =\left[ \begin{array}{c} {\dot{\mathbf{r}}} \\ {\dot{\mathbf{v}}} \\ \dot{m} \\ \varvec{\dot{\uplambda }}_r \\ \varvec{\dot{\uplambda }}_v \\ \dot{\uplambda }_m \end{array} \right] = \left[ \begin{array}{c} \mathbf{v } \\ -\mu \frac{\mathbf{r }}{\left| \mathbf{r }\right| ^3} -\frac{\varvec{\uplambda }_v}{\left| \varvec{\uplambda }_v\right| } \frac{T}{m}\\ -\frac{T}{c} \\ -{}^t\mathbf {G}\varvec{\uplambda }_v \\ -\varvec{\uplambda }_r \\ - \frac{\uplambda _v T}{m^2} \end{array} \right] \end{aligned}$$

(15)

(16)

Finally, the optimized minimum mass trajectory can be propagated by integrating Eq. 15 with the thrust magnitude provided by the relation at Eq. 16. In order to integrate the above system, the initial conditions are necessary. The initial states come naturally from the mission’s starting time and departure planet, yet the initial costates are not clear and sometimes difficult to estimate.

3.3 Analytical derivatives

The cost function gradient is necessary for the solution of indirect and direct optimal control problems (gradient based methods). Analytical derivatives improve the quality and speed of the solutions as opposed to numerically estimated derivatives. However, it should be noted that multicomplex variables and the complex-step method have been shown to obtain similar accuracy; these methods are particularly useful in cases where analytical derivatives are hard to obtain or impossible to be derive (Lantoine et al. 2012; Martins et al. 2003). In particular for indirect methods, analytical derivatives provide a good option for the high sensibility found in this method. As pointed out in Russell (2007) and Zhang et al. (2015), the use of analytical derivatives in multiple-revolution solutions is particularly important due to the high sensitivity to small initial perturbations. The derivatives have to take into account the low-thrust arcs, the coast arcs and the switch between them.

We start this derivation by the general form of the state transition matrix, $\varvec{\varPhi }$ (Russell 2007). It is important to point out that since the low-thrust is considered in $\varvec{\varPhi }$, it is no longer calculated for an elliptical orbit.

$$\begin{aligned} \varvec{\varPhi }(t,t_0)= & {} \frac{\partial \mathbf{y }(t)}{\partial \mathbf{y }(t_0)}\end{aligned}$$

(17)

$$\begin{aligned} \dot{\varvec{\varPhi }}(t,t_0)= & {} \left. \frac{\partial f}{\partial \mathbf{y }}\right| _t\varvec{\varPhi }(t,t_0) \end{aligned}$$

(18)

where,

$$\begin{aligned} \varvec{\varPhi }(t_0,t_0)= & {} \mathbf {I}\end{aligned}$$

(19)

$$\begin{aligned} \frac{\partial f}{\partial \mathbf{y }}= & {} \left[ \begin{array}{cccccc} \mathbf {O} &{} \mathbf {I} &{} \mathbf {O} &{} \mathbf {O} &{} \mathbf {O} &{} \mathbf {O} \\ \mathbf {G} &{} \mathbf {O} &{} \frac{\varvec{\uplambda }_v}{\left| \varvec{\uplambda }_v\right| } \frac{T}{m^2} &{} \mathbf {O} &{}-\frac{T}{m}\left( \frac{\mathbf {I}}{\left| \varvec{\uplambda }_v\right| }-\frac{{}^t\varvec{\uplambda }_v\varvec{\uplambda }_v}{\left| \varvec{\uplambda }_v\right| ^3}\right) &{} \mathbf {O} \\ \mathbf {O} &{} \mathbf {O} &{} 0 &{} \mathbf {O} &{} \mathbf {O} &{} 0 \\ -\frac{\partial {}^t\mathbf {G}\varvec{\uplambda }_v}{\partial \mathbf{r }} &{} \mathbf {O} &{} \mathbf {O} &{} \mathbf {O} &{} -{}^t\mathbf {G} &{} \mathbf {O} \\ \mathbf {O} &{} \mathbf {O} &{} \mathbf {O} &{} -\mathbf {I} &{} \mathbf {O} &{} \mathbf {O} \\ \mathbf {O} &{} \mathbf {O} &{} \frac{2\left| \varvec{\uplambda }_v\right| T}{m^3} &{} \mathbf {O} &{} \frac{-{}^t\varvec{\uplambda }_v T}{\varvec{\uplambda }_v m^2} &{} 0 \end{array} \right] \end{aligned}$$

(20)

Based on the above, the state transition matrix can be obtained for coast or thrust arcs at any time interval by integrating Eq. 18. Next, it is necessary to connect the different coast and low-thrust arcs in order to calculate $\varvec{\varPhi }$ from beginning to end. The switch points between the propelled and coast legs constitute discontinuities on $\varvec{\varPhi }$, a simple solution is to calculate $\varvec{\varPhi }$ in between the discontinuities (each leg) and connect then by a new matrix, $\varvec{\varPsi }$, that handles the discontinuities at the switching point. Therefore, for N discontinuities,

$$\begin{aligned} \frac{\partial \mathbf{y }(t)}{\partial \mathbf{y }(t_0)}= \varvec{\varPhi }(t_f,t_{N+}) \varvec{\varPsi }_N \varvec{\varPhi }(t_{N-},t_{(N-1)+}) \varvec{\varPsi }_{N-1}\cdots \varvec{\varPsi }_2 \varvec{\varPhi }(t_{2-},t_{1+}) \varvec{\varPsi }_1 \varvec{\varPhi }(t_{1-},t_0) \end{aligned}$$

(21)

where, the discontinuity and the switching points are calculated as the partial derivative of the states after, $t_{n+}$, and before, $t_{n-}$, the switch,

$$\begin{aligned} \varvec{\varPsi }_n=\frac{\partial \mathbf{y }(t_{n+})}{\partial \mathbf{y }(t_{n-})}= \varvec{I}+\left( \left. {\dot{\mathbf{y}}}\right| _{n+}-\left. {\dot{\mathbf{y}}}\right| _{n-}\right) \left. \left( \frac{\frac{\partial S}{\partial \mathbf{y }}}{\dot{S}}\right) \right| _{n-} \end{aligned}$$

(22)

Finally, the gradient of the cost function can be obtained by calculating the state transition matrix (integrating Eq. 17) and extracting its relevant terms. The integration is done with an event-based numerical integration with variable step to identify the thrust switch points and obtain the trajectory’s ${\varvec{\varPhi }}$s. Section 5.1 details the calculation of the coast function’s gradient.

4 Asteroid target selection

Potentially, millions of midcourse flyby points need to be considered in the target selection because of the large number of possible candidates (>700,000) combined with different flyby times. The large number of candidates makes the computational time to optimize all these points prohibitive; therefore, a strategy needs to be considered to decrease the optimization candidates’ number. It is important to point out that a simple distance evaluation does not provide a good result because it does not consider: the plane change, different points on the reference orbit for the transfer maneuver, and it fails to provide a good initial estimation for the optimization on both the states and costates.

The fundamental assumption here is based on the fact that the auxiliary trajectory will not deviate much from the reference trajectory due to a limit on the propellant use and the constraints related to the initial and final conditions. Therefore, the flyby point will not be far from the reference trajectory and, due to this, the selected flyby point will lie inside the reference trajectory’s linear region. This assumption allows the use of the linear theory in the selection process.

The asteroid selection for the midcourse flyby point is divided into 5 steps, with the fifth being the optimization itself, pertaining to 3 large areas: selection by parameter, selection by linear approximation and selection by non-linear optimization. The asteroid database considered in this study was provided by The Minor Planet Center (2013). The flowchart of the step sequence can be seen on Fig. 1 and the following sections describe in detail each step.

Fig. 1

Asteroid selection flowchart

4.1 Selection by parameter—step 1: maximum and minimum distances

In the first step the reference orbit is taken into account. Considering its initial conditions and engine characteristics, it is propagated with a constant tangential thrust in the direction of the velocity vector for the duration of the trajectory’s time of flight. The maximum distance achieved from the orbit’s center defines the farthest point that the spacecraft can reach from the reference orbit. It is important to point out that it has been proved on Campagnola et al. (2014b) that the tangential acceleration (along the velocity vector) does not maximize the semi-major axis, but it constitutes a good approximation because it maximizes the spacecraft’s instantaneous increase in two-body orbital energy. This approximation is considered enough for this work since this limit is an over estimation; in the midcourse flyby case, it is not enough for the spacecraft to reach the point it is also necessary to return and reach the orbit’s final conditions, i.e. main trajectory objective. The asteroids with the perihelion larger than the maximum reachable point, defined by the tangential thrust propagation, are excluded.

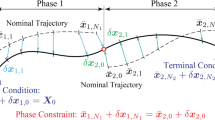
Next, the asteroids orbits are precomputed, using a simple Keplerian propagation, for the duration of the mission; as the arrival time is a constraint, the time of flight is fixed. The time step, $\Delta t$, can be selected by the user considering that a small time step will generate more points to be analyzed, which makes the analysis more robust but slower. However, it is necessary to guarantee that the points distributed along the reference trajectory, based on the defined time step, does not exclude better solutions that would lie in between them. Inside the linear regime, it is possible to derive a fast evaluation based on the distance from the spacecraft to the asteroid, $\Delta \mathbf{r } = \mathbf{r }^{ast}-\mathbf{r }^{s/c}$, that would result in a theoretical minimum allowed time step, $\Delta t_{\min }$, that guarantees a non exclusive solution. For each asteroid, we start by selecting the two neighboring points along the reference trajectory that connected form a line which crosses the asteroid’s orbit, $\mathbf{x }\left( t_{n-1}\right) =[\mathbf{r }_{n-1},\mathbf{v }_{n-1},m_{n-1}]^t$ and $\mathbf{x }\left( t_{n}\right) =[\mathbf{r }_{n},\mathbf{v }_{n},m_{n}]^t$. Figure 2 presents the aforementioned points in the linear regime. Note that, considering a linear motion between the points, there is no acceleration, $\ddot{\mathbf{r }}_{s/c} = \ddot{\mathbf{r }}_{ast} = 0$, and the velocities are simply defined by $\mathbf{v }_n = {\dot{\mathbf{r}}}_n+\mathbf{v }_{n-1}$. Therefore, the following relation holds for both $t_{n-1}$ and $t_n$

$$\begin{aligned} \left\{ \begin{array}{l} \Delta \ddot{\mathbf{r }} = \ddot{\mathbf{r }}_{n}^{ast} - \ddot{\mathbf{r }}_{n}^{s/c} = 0 \\ \Delta {\dot{\mathbf{r}}} = {\dot{\mathbf{r}}}_{n}^{ast} - {\dot{\mathbf{r}}}_{n}^{s/c} = {\dot{\mathbf{r}}}_{n}^{s/c}+\mathbf{v }_{n-1}^{s/c} - {\dot{\mathbf{r}}}_{n}^{ast}-\mathbf{v }_{n-1}^{ast} \\ \Delta \mathbf{r } = \mathbf{r }_{n}^{s/c}+\mathbf{v }_{n}^{s/c}\Delta t_{min}+\mathbf{r }_{n-1}^{s/c} -\mathbf{r }_{n}^{ast}-\mathbf{v }_{n}^{ast} \Delta t_{min}-\mathbf{r }_{n-1}^{ast} \end{array} \right. \end{aligned}$$

(23)

where, the superscripts s / c and ast refer to the spacecraft and asteroid, respectively.

The last line of Eq. 23 defines the distance between the orbits of the spacecraft and asteroid should have for the theoretical $\Delta t_{min}$,

$$\begin{aligned} \Delta t_{min} = \frac{\Delta \mathbf{r }-\mathbf{r }_{n}^{s/c}-\mathbf{r }_{n-1}^{s/c} +\mathbf{r }_{n}^{ast}+\mathbf{r }_{n-1}^{ast}}{\mathbf{v }_{n}^{s/c}-\mathbf{v }_{n}^{ast}} \end{aligned}$$

(24)

and if

$$\begin{aligned} \Delta t < \Delta t_{min} \end{aligned}$$

(25)

This means that there would be no points in between $\varvec{x}_{n-1}$ and $\varvec{x}_{n}$ that would be closer to the asteroid if $\Delta t$ where smaller. The case $\Delta t > \Delta t_{min}$ implies that there is a $\Delta t^*$ that results in points $\varvec{x}_{n-1}$ and $\varvec{x}_n$ which are closer to the asteroid, $\Delta \varvec{r}^* < \Delta \varvec{r}$.

Therefore, by defining an initial guess for the time step, $\Delta t$, it is possible to evaluate using Eqs. 24 and 25 if the selected time step is sufficient or it should be decreased. In case it should be decreased, the calculation of $\Delta t_{min}$ needs to be redone and the newly obtained $\Delta t_{min}$ compared with the new $\Delta t$. Note that this check needs to be done for all asteroids with the worst case, i.e. smaller $\Delta t_{min}$, selected to be compared in Eq. 25.

Fig. 2

Step size limit

With the precomputed asteroid trajectory, the points on the asteroid orbit can be compared once again with the maximum reachable distance and, also, with the minimal reachable distance, which can be calculated in the same way as the maximum distance but with the tangential thrust in opposite direction to the velocity vector. The maximum and minimum reachable distances define a two-dimensional corridor in which the points have to lie within. After, all the remaining points are changed coordinates from the Keplerian to the Cartesian system for the next steps.

As a final selection on this step, the general reachability for each individual point of the trajectory is considered. The reachable limit can be defined in two ways, by a fixed value which is estimated to be more than the linear region, to include all the feasible points, or by calculating the linear reachability as derived in Campagnola (2015).

Given a set of reachable positions $\varvec{r}_{n+1}=\varvec{r}(t_{n+1})$ starting from a given position in the reference trajectory, $\varvec{r}_n=\varvec{r}(t_n)$, for all possible controls (bounded by $|\varvec{u}T|\le Tmax$), the reachability can be computed for each state, $\sigma _{(i)}$, based on the linearized dynamics. The set is approximated by a supporting polyhedron, with 2M polygons, which is expressed as a set of inequalities for $\varvec{r}_{n+1}$

$$\begin{aligned} -T_{max} \sigma _{(i)} \le {}^t \varvec{\upsilon }_{(i)}\varvec{r}_{n+1} \le T_{max} \sigma _{(i)}, \quad i = 1,\ldots ,M \end{aligned}$$

(26)

Here, $\upsilon _{(i)}$ are the normal to the supporting planes tangent to the reachable set and $\sigma _{(i)}$ are the distances from the origin to the planes. They can be computed as,

$$\begin{aligned} \sigma _{(i)} = \int _{t_n}^{t_{n+1}} \left| {}^t\varvec{\varPhi }_{rv}(\tau ,t_{n+1}) \varvec{\upsilon }_{(i)}\right| \, d\tau \end{aligned}$$

(27)

where, $\varvec{\varPhi }_{rv}$ is the $3\times 3$ sub-matrix of the state transition matrix.

To check whether a point belongs to the set, one only needs to verify if the inequalities are satisfied. Note that in the linearized dynamics, the reachable set is compact, convex, and symmetric about the origin. In this work the support planes are chosen in the direction of each state, thus defining a cube region for the position and velocity,

$$\begin{aligned} \left\{ \begin{array}{l} \varvec{\upsilon }_{(1)} = {}^t\left[ \begin{array}{ccc} 1 &{} 0 &{} 0 \end{array} \right] \\ \varvec{\upsilon }_{(2)} = {}^t\left[ \begin{array}{ccc} 0 &{} 1 &{} 0 \end{array} \right] \\ \varvec{\upsilon }_{(3)} = {}^t\left[ \begin{array}{ccc} 0 &{} 0 &{} 1 \end{array} \right] \\ \varvec{\upsilon }_{(4)} = {}^t\left[ \begin{array}{ccc} 1 &{} 0 &{} 0 \end{array} \right] \\ \varvec{\upsilon }_{(5)} = {}^t\left[ \begin{array}{ccc} 0 &{} 1 &{} 0 \end{array} \right] \\ \varvec{\upsilon }_{(6)} = {}^t\left[ \begin{array}{ccc} 0 &{} 0 &{} 1 \end{array} \right] \\ \end{array} \right. \end{aligned}$$

(28)

The calculation is performed forward and backward, since after the flyby the spacecraft still needs to reach the final point. With this, both solutions are intersected to generate the final reachable range.

4.2 Selection by linear approximation—step 2: point-by-point impulsive analysis

With the reference orbit state transition matrix (Sect. 3.3) it is possible to calculate for each point an impulsive approximation to reach the target. The calculation with $\varvec{\varPhi }$ is faster than a Lambert solution, thus it allows the calculation of several points in a short time. The impulses will not be compared with a maximum $\Delta v$, but instead will be evaluated with respect to their associated $\Delta t$ to check if the time available is enough to provide the necessary velocity change.

The Tsiolkovsky rocket equation (Eq. 29) will be used to estimate the $\Delta t$ combined with the mass variation (third line of Eq. 15) and the mass dynamics (Eq. 30) as,

$$\begin{aligned} \Delta v= & {} c \ln \left[ \frac{m_n}{m_{n+1}}\right] \end{aligned}$$

(29)

$$\begin{aligned} m_n= & {} m_{n-1}-\dot{m} \Delta t \end{aligned}$$

(30)

$$\begin{aligned} \Delta t= & {} \frac{c}{T_{max}} m_n \left( 1-e^{-\Delta v/c}\right) \end{aligned}$$

(31)

It is important to point out that Eq. 31 uses $T_{max}$ that makes the time variation smaller, which overestimates the points selected; it includes more points that would not be selected if the optimized T was known. Also, it uses the rocket equation that is a chemical evaluation of propulsion instead the of low-thrust, which once again provides a smaller value of the time variation than the low-thrust propulsion system would be able to achieve; once again, an overestimation on the points selected.

For this evaluation three impulses are considered: the first at the initial point, $\Delta v_{o}$, second somewhere in the trajectory in between beginning and end, $\Delta v_{i}$, and third at the final point, $\Delta v_{f}$, see Fig. 3.

Fig. 3

Trajectory representation

The calculation considers a time free point, therefore, the distance between reference orbit and target is considered not necessarily in the correct time. In this way, the calculation is done for all points of the orbit, i.e. the calculation of the second impulse is done for every point of the trajectory. This is a very fast process since the necessary $\varvec{\varPhi }$s were already pre-calculated. This allows the selection of the combination of points, [o, i, f], that results in the lowest possible $\Delta t$, which improves solutions with plane changes. It is noted that this 3 impulse approach is not necessarily optimal for a plane changing trajectory, but it is a reasonable approximation since the calculation is performed in the linear regime, which means that the variation between optimal and sub-optimal solutions will be small. As the trajectory in the midcourse is a flyby, only the impulses at o and f will be considered for the time check. This of course means that the correction maneuver at the midcourse point is not taken into account in the evaluation. This will result in possible infeasible points to be considered, but, on the other hand, it ensures that the feasible points are included.

In order to calculate the necessary velocity changes, we make use of a subset of the state transition matrix that includes position and velocity, $\varvec{\varPhi }'$, evaluated at neighboring points $(n+1)$ and n, Eq. 32

$$\begin{aligned} \left[ \begin{array}{c} \delta \mathbf{r }_{n+1}\\ \delta \mathbf{v }_{n+1} \end{array}\right]= & {} \varvec{\varPhi }'_{(n+1)n}\left[ \begin{array}{c} \delta \mathbf{r }_{n}\\ \delta \mathbf{v }_{n} \end{array}\right] \end{aligned}$$

(32)

$$\begin{aligned} \left[ \begin{array}{c} \delta \mathbf{v }_{n}\\ \delta \mathbf{v }_{n+1} \end{array}\right]= & {} \left. \left[ \begin{array}{cc} -\varvec{\varPhi }_{rv}^{'-1} \varvec{\varPhi }'_{rr} &{} \varvec{\varPhi }_{rv}^{'-1} \\ \varvec{\varPhi }'_{vr}-\varvec{\varPhi }'_{vv} \varvec{\varPhi }_{rv}^{'-1}\varvec{\varPhi }'_{rr} &{} \varvec{\varPhi }'_{vv} \varvec{\varPhi }_{rv}^{'-1} \end{array}\right] \right| _{(n+1)n} \left[ \begin{array}{c} \delta \mathbf{r }_{n}\\ \delta \mathbf{r }_{n+1} \end{array}\right] \end{aligned}$$

(33)

With Eq.33 it is possible to calculate the $\Delta v$ at the points (n) and $(n+1)$

$$\begin{aligned} \left[ \begin{array}{c} \Delta \mathbf{v }_{n}\\ \Delta \mathbf{v }_{n+1} \end{array}\right] = \left. \left[ \begin{array}{cc} \varvec{\varPhi }_{rv}^{'-1} \varvec{\varPhi }'_{rr} &{} \mathbf {I} \\ \varvec{\varPhi }'_{vr}-\varvec{\varPhi }'_{vv} \varvec{\varPhi }_{rv}^{'-1}\varvec{\varPhi }'_{rr} &{} \mathbf {O} \end{array}\right] \right| _{(n+1)n} \left[ \begin{array}{c} \delta \mathbf{r }_{n}\\ \delta \mathbf{v }_{n} \end{array}\right] +\left. \left[ \begin{array}{cc} \varvec{\varPhi }_{rv}^{'-1} &{} \mathbf {O} \\ -\varvec{\varPhi }'_{vv} \varvec{\varPhi }_{rv}^{'-1} &{} \mathbf {I} \end{array}\right] \right| _{(n+1)n} \left[ \begin{array}{c} \delta \mathbf{r }_{n+1}\\ \delta \mathbf{v }_{n+1} \end{array}\right] \end{aligned}$$

(34)

where, for the flyby case considered here,

$$\begin{aligned} \left[ \begin{array}{c} \delta \mathbf{r }_{o}\\ \delta \mathbf{v }_{o} \end{array}\right] = \left[ \begin{array}{c} 0\\ 0 \end{array}\right] ; \quad \left[ \begin{array}{c} \delta \mathbf{r }_{m}\\ \delta \mathbf{v }_{m} \end{array}\right] = \left[ \begin{array}{c} \delta \varvec{r}\\ 0 \end{array}\right] = \left[ \begin{array}{c} \varvec{r}_{ast}-\varvec{r}_{S/C}\\ 0 \end{array}\right] ; \quad \left[ \begin{array}{c} \delta \mathbf{r }_{f}\\ \delta \mathbf{v }_{f} \end{array}\right] = \left[ \begin{array}{c} 0\\ 0 \end{array}\right] \end{aligned}$$

(35)

Therefore,

$$\begin{aligned} \left[ \begin{array}{c} \Delta \mathbf{v }_{o}\\ \Delta \mathbf{v }_{i}^- \end{array}\right] = \left. \left[ \begin{array}{c} \varvec{\varPhi }_{rv}^{'-1}\\ -\varvec{\varPhi }'_{vv} \varvec{\varPhi }_{rv}^{'-1} \end{array}\right] \right| _{io} \left[ \begin{array}{c} \varvec{r}_{ast}-\varvec{r}_{S/C} \end{array}\right] \end{aligned}$$

(36)

and

$$\begin{aligned} \left[ \begin{array}{c} \Delta \mathbf{v }_{i}^+\\ \Delta \mathbf{v }_{f} \end{array}\right] = \left. \left[ \begin{array}{c} \varvec{\varPhi }_{rv}^{'-1} \varvec{\varPhi }'_{rr}\\ \varvec{\varPhi }'_{vr}-\varvec{\varPhi }'_{vv} \varvec{\varPhi }_{rv}^{'-1}\varvec{\varPhi }'_{rr} \end{array}\right] \right| _{fi} \left[ \begin{array}{c} \varvec{r}_{ast}-\varvec{r}_{S/C} \end{array}\right] \end{aligned}$$

(37)

which results in $\Delta v_{o}$ for the trajectory’s beginning and $\Delta v_{f}$ for the last point. These are calculated for all possible combinations of m and the selected point is the one that results on $min(\Delta v_{o}+\Delta v_{f})$. To account for approximation errors a margin is added to the time, $t_{margin}$.

The point is then selected if,

$$\begin{aligned} \left\{ \begin{array}{l} \Delta t_{mo}< t_m-t_o \\ \Delta t_{fm} < t_f-t_m \end{array} \right. \end{aligned}$$

(38)

where, $t_m$ and $t_o$ are the actual times of the trajectory’s beginning and $\Delta t_{mo}$, and $\Delta t_{fm}$ are the time variation calculated using Eq. 31.

4.3 Selection by linear approximation—step 3: low-thrust linear approximation

This step uses a linear approximation to the low-thrust problem to check if the low-thrust propulsion system can perform the flyby from both extremities, two legs originating from o and f. This approach does not match the velocity from the two legs at the flyby point, just the position. The velocity cannot be be computed at the midcourse because, since it is an unpowered flyby, $\delta v_m$ is not available. This approach includes solutions that cannot be fully optimized due to the velocity mismatch at the flyby point; therefore, it results in a small overestimation of the points, however, once again, it ensures that the feasible points remain in the selection. Note that this step is more precise than the previous one; in principle step 3 could replace step 2 at the cost of more simulation time. Although very fast, for a large number of points, step 3 still uses a considerable amount of time when compared with the simple matrix multiplication used in step 2.

The low-thrust linear calculation works in a similar way as in step 2, but instead of a single impulse in each leg the trajectory contains several small impulses across the leg that results in an approximation for the low-thrust solution (Sims et al. 2006). Based on the work of Campagnola (2014a), the low-thrust approximation is here modified for the flyby case. The cost function to be minimized is

$$\begin{aligned} \sum \left| \Delta \varvec{v} \right| =\int _{t_o}^{t_m} \left| \varvec{u}'(t)\right| \, dt + \int _{t_m}^{t_f} \left| \varvec{u}'(t)\right| \, dt \end{aligned}$$

(39)

with, $\left| \varvec{u}'(t)\right| =\left| \varvec{u}(t)T(t)/m(t)\right| <T_{max}/m(t)$ $\in$ $\left[ t_o \quad t_f\right]$.

As in Campagnola (2014a) the trajectory is discretized, as already done previously on step 1, and the impulses are given in the middle of two consecutive nodes: $t_i$ for the time, $\varvec{x}_i=\varvec{x}(t_i)$ for the position and velocity states, and $\varvec{u}'_i=\varvec{u}'_i(t_i)$ for the control that defines the thrust law as

$$\begin{aligned} \varvec{u}'\left( t\right) =\sum _{i=1}^{N_{mo}} \varvec{u}'_i rect\left( \frac{t_i}{\Delta t}\right) + \sum _{i=1}^{N_{fm}} \varvec{u}'_i rect\left( \frac{t_i}{\Delta t}\right) \end{aligned}$$

(40)

where, N is the number of discretized points in each arc and rect(t) is the rectangular function. The velocity variation in each node is

$$\begin{aligned} \Delta \varvec{v}_i = \int _{t_i-\delta t /2}^{t_i+\delta t /2} \varvec{u}'(t) \, dt = \varvec{u}'_i \Delta t \end{aligned}$$

(41)

where, $\Delta t$ is the time variation from each node. Since the control is constant for each interval Eq. 39 can be rewritten as

$$\begin{aligned} \sum \left| \Delta \varvec{v} \right| = \sum _{i=1}^{N_{mo}} u'_i \Delta t + \sum _{i=1}^{N_{fm}} u'_i \Delta t = \sum _{i=1}^{N_{mo}} \left| \Delta \varvec{v}_i\right| + \sum _{i=1}^{N_{fm}} \left| \Delta \varvec{v}_i\right| \end{aligned}$$

(42)

The $\Delta v$ in each node is calculated by Eq. 34 and the control can be computed as

$$\begin{aligned} \varvec{u}'_i = \alpha _i \frac{\Delta \varvec{v}_i}{\Delta t} \end{aligned}$$

(43)

where, $\alpha$ is a scaling factor that reinforces the constraint $\left| \varvec{u}'(t)\right| <T_{max}$,

$$\begin{aligned} \alpha _i = \min \left( 1, \frac{u_{max} \Delta t}{\left| \Delta \varvec{v}_i\right| }\right) \end{aligned}$$

(44)

Since the final velocity change is not considered the calculation is aways performed from the node, i, to the flyby point, m. This implies in a forward evaluation from o to m and a backward evaluation from f to m. Every consecutive state can be calculated as

(45)

The propagation continues until an $\alpha =1$ is found, which means that from that point all the necessary $\Delta v$ can be provided to reach the final point. On the other hand, if $\alpha =1$ is not found it means that no feasible solution exists. Note that $\alpha$ in Eq. 44 considers that no thrust has been used in the reference trajectory. This is not always true depending on the reference trajectory and the state transition matrix already carries in it the control contribution. Once again this is over estimation of the available thrust, but it guarantees that feasible solutions are not excluded.

4.4 Selection by non-linear optimization—step 4: state and costate estimation

Step 4 provides a good estimation for the position, velocity, and control to be applied to the midcourse optimization on the next step. Recalling Sect. 3, the optimized solution or the initial guess for the optimization requires the full $\mathbf{y }$ which also includes the mass and costates. The $\varvec{\uplambda }_{r}$ and $\varvec{\uplambda }_{v}$ can be estimated by using the second-order form of the state and costate evolution equations in state space form (a detailed derivation is presented in Sarli and Kawakatsu (2015b)). Reference Restrepo and Russell (2016) outlines the quality and speed of this approximation applied in an indirect method.

$$\begin{aligned}&\displaystyle \left\{ \begin{array}{l} \ddot{\varvec{\uplambda }}_{v}(t)=\mathbf {G}(\mathbf{r })\varvec{\uplambda }_{v}(t) \\ \delta \ddot{\mathbf{r }}(t)= \mathbf {G}(\mathbf{r })\delta \mathbf{r }(t) \end{array} \right. \end{aligned}$$

(46)

$$\begin{aligned}&\displaystyle \left[ \begin{array}{c} \dot{\varvec{\uplambda }}_{r}(t)\\ \dot{\varvec{\uplambda }}_{v}(t) \end{array}\right] =-\left[ \begin{array}{cc} \mathbf {O} &{} {}^t\mathbf {G}\\ \mathbf {O} &{} \mathbf {I} \end{array}\right] \left[ \begin{array}{c} \varvec{\uplambda }_{r}(t)\\ \varvec{\uplambda }_{v}(t) \end{array}\right] \end{aligned}$$

(47)

Combining both equations and performing some mathematical manipulation, it results in

$$\begin{aligned} \delta \dot{\varvec{r}}(t)=-\dot{\varvec{\uplambda }}_{v}(t); \quad \delta \dot{\varvec{v}}(t)= \dot{\varvec{\uplambda }}_{r}(t) \end{aligned}$$

(48)

If the initial conditions of states and associated costates are the same, $\delta {\varvec{r}}_0=-{\varvec{\uplambda }}_{v0}$ and $\delta {\varvec{v}}_0={\varvec{\uplambda }}_{r0}$, then

$$\begin{aligned} \delta {\varvec{r}}(t)=-{\varvec{\uplambda }}_{v}(t); \quad \delta {\varvec{v}}(t)= {\varvec{\uplambda }}_{r}(t) \end{aligned}$$

(49)

The two remaining variables to be found are m and . The mass can be easily estimated by the resulting control profile, $u'(t)$, of step 3,

$$\begin{aligned} m(t) = m(t_0) - \frac{u'(t)}{c} \Delta t(t); \qquad \text {where} \quad \Delta t(t) = \sum _{i=1}^{N=t} \Delta t_i \end{aligned}$$

(50)

and, finally, is a simple quadrature that results from Eq. 49 applied in the last line of Eq. 15

$$\begin{aligned} \dot{\uplambda }_m(t) = -\frac{u'(t)}{m(t)^2} \left| \delta \mathbf{r }(t)\right| \end{aligned}$$

(51)

The problem is reduced to a reasonable number of points with a good initial estimation for all the states and costates. As a result of the accurate initial guess the optimization can be performed fast, converging in just a few iterations for the feasible points.

4.5 Selection by non-linear optimization—step 5: trajectory optimization

The trajectory optimization with a midcourse condition, asteroid flyby, is the final and conclusive step where the points selected in step 3 combined with the initial guess calculated at step 4 are evaluated in a non-linear indirect method optimization. The solution consists in finding the initial costates that when propagated result in the desired final and midcourse conditions, only the initial costates are needed since the initial states are known. The problem to be solved is then to find the solution of a set of non-linear equations refereed to as Two Point boundary Value Problem, here with the flyby represented as the additional midcourse constraints (Sect. 5.1). The next Sect. 5, details the methods used in the solution of this optimization. The problem is solved using the ”feasible point” mode with the sequential quadratic programming software SNOPT (Gill et al. 2002). Through the solution process all variables are transformed to non-dimensional units to improve the convergence.

5 Solution method

This section presents details of the solution method used in step 5, the trajectory optimization with midcourse flyby. In order to improve the convergence two main strategies are used: indirect multiple shooting and analytical gradient for the cost function. These two are incorporated in the solution of the set of non-linear equations, Two Point boundary Value Problem (TPBVP), that here include the extra equations needed to comply with the midcourse constraints, midcourse asteroid flyby.

5.1 Two point boundary value problem with midcourse constraint

As outlined before on Sect. 3.2, with Eqs. 15 and 16 the optimal control problem is solved. What remains is to find the initial costates such that a propagation with them will result in the desired conditions, or problem’s constraints. To find the missing initial costates the problem is reduced to a set of non-linear equations, originated from the transversality conditions, and solved.

The equations for the TPBVP are derived as follows. First, recalling Eqs. 53 and 54 from Kirk (2004) we have a fixed initial and final time problem, $\delta t=0$, with fixed final conditions, $\delta w=0$.

$$\begin{aligned} \left. \left\{ \left( \bar{q}-\bar{q}_{\dot{w}}\dot{w}\right) \delta t\right\} \right| _{t_0}^{t_f}= & {} 0 \end{aligned}$$

(52)

$$\begin{aligned} \left. \left\{ \bar{q}_{\dot{w}}\delta w \right\} \right| _{t_0}^{t_f}= & {} 0 \end{aligned}$$

(53)

$$\begin{aligned} \bar{q}_{w}-\frac{d\bar{q}_{\dot{w}}}{dt}= & {} 0 \end{aligned}$$

(54)

where q represents a generic function of the path conditions (Lagrange function) and w a generic vector form of the problem’s states and costates.

Also, regarding the midcourse constraint, the flyby point is fixed on time and position, requiring that all the states are continuous at the midcourse point, which, in turn, provides the following conditions at the midcourse point (Bryson and Ho 1975),

$$\begin{aligned} \left\{ \begin{array}{lcl} -\varvec{\uplambda }_{r}(t^-_m) + \varvec{\uplambda }_{r}(t^+_m) + \varvec{\nu } =0 &{} \Rightarrow &{} \varvec{\uplambda }_{r}(t^-_m) = \varvec{\uplambda }_{r}(t^+_m) + \varvec{\nu }\\ -\varvec{\uplambda }_{v}(t^-_m) + \varvec{\uplambda }_{v}(t^+_m) =0 &{} \Rightarrow &{} \varvec{\uplambda }_{v}(t^-_m) = \varvec{\uplambda }_{v}(t^+_m)\\ -{\uplambda }_{m}(t^-_m) + {\uplambda }_{m}(t^+_m) =0 &{} \Rightarrow &{} {\uplambda }_{m}(t^-_m) = {\uplambda }_{m}(t^+_m) \end{array} \right. \end{aligned}$$

(55)

Note that the constant $\nu$ becomes a problem unknown to relate $\varvec{\uplambda }_{r}(t_m)$ before and after the midcourse; however, in this case this unknown can be replaced by $\varvec{\uplambda }_{r}(t^+_m)$ itself without loss of generality. This implies that $\varvec{\uplambda }_{r}$ presents a discontinuity at the midcourse and based on Eq. 15 this can generate a discontinuity on $\dot{\varvec{\uplambda }}_{v}$, the integration $\varvec{\uplambda }_{v}$ generates a ramp along the discontinuity, and by extension a ramp in the control. As there is no discontinuity on the control evolution, it is assumed that the spacecraft can follow the ramp change since the the frequencies of the attitude change and orbit translation are orders of magnitude apart for interplanetary transfer problems.

Considering the above conditions and constraints, the TPBVP is defined as

$$\begin{aligned} \mathbf U = \left( \begin{array}{l} \varvec{\uplambda }_{ro} \\ \varvec{\uplambda }_{vo} \\ \varvec{\uplambda }_{rm}^+ \\ \end{array} \right) ; \quad \mathbf C = \left( \begin{array}{l} \mathbf{r }_m - \mathbf{R }_m \\ \mathbf{r }_f - \mathbf{R }_f \\ \mathbf{v }_f - \mathbf{V }_f \\ \end{array} \right) \end{aligned}$$

(56)

where, U $9\times 1$ is a vector of the problem’s unknowns, C $9\times 1$ is a vector of the problem’s constraints, $\mathbf{R }_m$ is the desired midcourse position at $t_m$, $\mathbf{R }_f$ is the desired final position, and $\mathbf{V }_f$ is the desired final velocity. Note that $\uplambda _{m0}=-1$, as it monotonically decreases, the final condition is known.

5.2 Indirect multiple shooting

The convergence of an optimal problem in the indirect method frame is very sensitive to the initial conditions and small control perturbations; therefore, convergence for this type of problems is difficult. In order to improve the solution, a multiple shooting strategy is used, which attempts to limit the sensitivity issue by splitting the integration interval to reduce the propagation error. The implementation of this strategy is particularly important for problems that require one or more revolution, without it even a good initial guess can fail to converge due to a very sensitive variation in the costates. Moreover, the multiple shooting combined with the initial guess provided at step 4, allows the optimization to achieve convergence with a small number of iteration steps for feasible solutions.

In essence the multiple shooting strategy breaks the problem into Q segments (been Q defined by the user) that have to be patched in the optimized solution. This, in turn, adds constraints and unknowns to the TPBVP,

(57)

where, Q is the extra number of segments that the problem has been broken, being the midcourse point m somewhere in i. This process adds $Q\times 14$ unknowns and constraints to the problem.

Fig. 4

Earth-to-Phaethon flyby ballistic trajectory, extracted from Sarli et al. (2015a), a ballistic transfer, b transfer orbit resonance

Fig. 5

Phaethon flyby ballistic and optimized low-thrust reference trajectories, a ballistic, b low-thrust

5.3 Analytical gradient

The analytical gradient improves the convergence accuracy and speed, it is calculated based on the state transition matrix, Eq. 17. The gradient, including the multiple shooting, is calculated as

$$\begin{aligned} \nabla \mathbf C = \frac{\partial \mathbf C }{\partial \mathbf U }= \left[ \begin{array}{ccccccccc} -\varvec{\varPhi }_0 &{} \mathbf I &{} &{} &{} &{} &{} &{} &{}\\ &{} -\varvec{\varPhi }_{1} &{} \mathbf I &{} &{} &{} &{} &{} &{}\\ &{} &{} -\varvec{\varPhi }_{2} &{} \mathbf I &{} &{} &{} &{} &{}\\ &{} &{} &{} \ddots &{} &{} &{} &{} &{}\\ &{} &{} &{} &{} \mathbf A &{} \mathbf B &{} &{} &{}\\ &{} &{} &{} &{} &{} \mathbf C &{} \mathbf I &{} &{}\\ &{} &{} &{} &{} &{} &{} \ddots &{} &{} \\ &{} &{} &{} &{} &{} &{} &{}-\varvec{\varPhi }_{Q-1} &{}\mathbf I \\ &{} &{} &{} &{} &{} &{} &{} &{} -\varvec{\varPhi }_{Q} \end{array} \right] \end{aligned}$$

(58)

where, the subscript in $\varvec{\varPhi }$ denotes the leg of the trajectory with m being the initial point of the midcourse leg, the blank space on the matrix represents zeros, and

$$\begin{aligned} \mathbf{A }= & {} -\left[ \frac{\partial \left[ \begin{array}{ccccc} \mathbf{r }_{f}&\mathbf{v }_{f}&m_{f}&\varvec{\uplambda }_{vf}&{\uplambda }_{mf} \end{array}\right] }{\partial \mathbf{y }_{o}}\right] _{Q_i=m-1}\nonumber \\ \mathbf{B }= & {} \left[ \begin{array}{c} \mathbf{O }_{3\times 11} \\ \mathbf{I }_{4\times 11} \\ \mathbf{O }_{4\times 7} \quad \mathbf I _{4\times 4} \end{array}\right] \nonumber \\ \mathbf{C }= & {} -\left[ \frac{\partial \mathbf{y }_{f} }{\partial \left[ \begin{array}{ccccc} \mathbf{v }_{o}&\mathbf m _{o}&\varvec{\uplambda }_{ro}&{\uplambda }_{vo}&{\uplambda }_{mo} \end{array}\right] }\right] _{Q_i=m} \end{aligned}$$

(59)

Table 1 Spacecraft’s engine characteristics

Table 2 Trajectories’ constraints

Fig. 6

Itokawa rendezvous ballistic and optimized low-thrust reference trajectories, a ballistic, b low-thrust

Note the discontinuity caused by the midcourse since the costates associated with the position, Eq. 55, do not need to be continuous and the position at the midcourse, $\mathbf{r }_m$, is not an unknown.

Table 3 Selected points at each step for the Phaethon case

Table 4 Selected points at each step for the Itokawa case

Table 5 Simulation time

6 Test case

This section applies the selection and optimization method described in the previous sections to two test cases, the first case is the Phaethon flyby with a launch window that is significant for the DESTINY extended mission (Kawakatsu and Itawa 2012), and the second case is a Itokawa rendezvous with the dates of the successful asteroid sample return HAYABUSA (2015). These cases were selected due to their importance, for a future mission or historically from a past mission, and because they are representative of two intrinsically different mission types: a flyby and a rendezvous.

The Phaethon flyby case has a launch date on 2023 and a ballistic trajectory with an Earth resonance close to 1:1. This particular solution is extracted from the catalog made on Sarli et al. (2015a), see Fig. 4a, b. From all the possible trajectories in 2023, the selected ballistic trajectory has the lowest departure $v_{\infty }$, Fig. 5a. To make the problem more interesting the ballistic trajectory’s initial and final conditions are used to design a low-thrust trajectory, Fig.  5b, based on the theory presented in Sect. 5, but without considering the midcourse. Table 1 presents the spacecraft’s engine characteristics based on the DESTINY mission (Kawakatsu and Itawa 2012) and the first column of Table 2 shows the low-thrust reference trajectory’ initial and final constraints.

The Itokawa rendezvous case has a launch date on 9 May 2003 and rendezvous with the Itokawa asteroid on 15 September 2005. The ballistic trajectory is the same used on the test case of Sarli and Kawakatsu (2015b), Fig. 6a. Once again adding another degree of complexity for the solution, this trajectory’s initial and final conditions are used to design a low-thrust trajectory (Sect.  5), Fig. 6b, with no midcourse present. The engine characteristics used in this problem are also from the DESTINY mission (Kawakatsu and Itawa 2012), presented in Table 1. The second column of Table 2 shows the low-thrust reference trajectory’ initial and final constraints. Both reference trajectories had their optimal solutions compared against an optimization using a modified Sims–Flanagan direct method that accommodates a continuous thrust arc in each segment (Yam and Kawakatsu 2015). The solutions with indirect and direct methods presented a good agreement.

Note that the low-thrust trajectories contain multiple thrusting arcs, inclination plan change, and have more than one revolution around the Sun; these characteristics make the selection process and optimization more challenging. Both low-thrust trajectories are taken as reference orbits for the selection process described in Sect. 4. Tables 3 and 4 show, respectively, the selection results for Phaethon and Itokawa cases highlighting the reference trajectory with each possible target point at each step represented by $\times$. Note that some asteroids can have more than one possible flyby point. A check was performed to confirm that no potential point is excluded in the selection process, the first 10 points excluded in steps 2, 3 and 4 are included in the optimization. As expected, these excluded points did not converge, which suggests that no feasible point was excluded during the selection process. The points of the step 1 are not considered in this evaluation because the exclusion is based solely in the reachability defined by the engine characteristics.

Fig. 7

Optimized low-thrust Phaethon flyby with midcourse asteroid flyby, a Earth-(411270) 2006 QJ65-Phaethon, b Earth-2009 ET-Phaethon, c Earth-(375400) 2000 ED14-Phaethon, d Earth-2011 EK-Phaethon, e Earth-(420841) 2007 DJ-Phaethon

Fig. 8

Optimized low-thrust Itokawa rendezvous with midcourse asteroid flyby, a Earth-(374110) 1998 HK49-Itokawa, b Earth-(136795) 1997 BQ-Itokawa, c Earth-(395828) 2005 GB34-Itokawa, d Earth-(373447) 1992 SZ-Itokawa, e Earth-(431966) 2007 YQ56-Itokawa

Phaethon case presents 166 possible asteroids to fly by in 578 flyby points, while Itokawa case presents 256 different asteroids in 1362 flyby points. The simulation time for each step of the selection is presented in Table 5, where step 1 includes the precomputed database time. The simulations were performed in a MATLAB environment in a desktop machine with a dual processor, 16 cores, 2.40 GHz and 16.0 GB of RAM memory. A considerable improvement on the simulation time is expected if the process is made with native code. Finally, Fig. 7 presents the top 5 optimization results that have the highest final mass for the Phaethon case and Fig. 8 presents the top 5 optimization results that have the highest final mass for the Itokawa case. A list with the 166 asteroid targets for Phaethon and 256 for Itokawa is available as a supplementary resource linked to the online version of the paper, the midcourse asteroids solutions are ranked based on the highest final mass.

7 Conclusion

In this work a method for selecting and optimizing a midcourse flyby asteroid based on a reference trajectory was presented. Using optimal control, linear theory and reachability, a process was derived which allows the asteroid selection in a short time. The selection also provides a good initial guess for the posterior low-thrust trajectory optimization that, as a result of a good initial guess, converges in only a few iterations for feasible results. Finally, two test cases were used to demonstrate the applicability and gain a better understanding of the advantages of the selection and optimization methods.

The results show a fast selection and optimization for several midcourse asteroid flyby in both cases: a final Phaethon flyby and a Itokawa rendezvous. These test cases are of special interest because, not only they take into account realistic scenarios and engine characteristics, but also the reference trajectories have multiple revolutions, with multiple thrust and coast arcs, and a plane change. All these posed challenges for the trajectory selection and optimization methods, which were successfully completed for both test cases.

Additional flybys could be added by performing a distributions of the selected targets of interest in the optimization step (respecting the flyby times) and solving a Two Point Boundary Value Problem with multiple midcourse constraints. However, this would not be an automated process requiring from the user to rank the importance of target in order to select the flyby sequence or sequences that is of interest for the mission. Then, the different combination of targets and flyby scenarios would need to be optimized separately. Same rational can be done for the addition of gravity assist maneuvers to the problem that would also require the implementation of the patched conic approximation for the swing-by event and the transcription of its associated state transition matrix. With the addition that in the target selection part, the gravity assist maneuver considers that the midcourse provides an instantaneous velocity change (calculated by the patched conic approximation).

Finally, the calculations were not made in native code and a future work could include the implementation of the code in such environment with a considerable gain in time expected.