Resonant Laplace-Lagrange theory for extrasolar systems in mean-motion resonance

Abstract

Extrasolar systems with planets on eccentric orbits close to or in mean-motion resonances are common. The classical low-order resonant Hamiltonian expansion is unfit to describe the long-term evolution of these systems. We extend the Lagrange-Laplace secular approximation for coplanar systems with two planets by including (near-)resonant harmonics and realize an expansion at high order in the eccentricities of the resonant Hamiltonian both at orders one and two in the masses. We show that the expansion at first order in the masses gives a qualitative good approximation of the dynamics of resonant extrasolar systems with moderate eccentricities, while the second order is needed to reproduce more accurately their orbital evolutions. The resonant approach is also required to correct the secular frequencies of the motion given by the Laplace-Lagrange secular theory in the vicinity of a mean-motion resonance. The dynamical evolutions of four (near-)resonant extrasolar systems are discussed, namely GJ 876 (2:1 resonance), HD 60532 (3:1), HD 108874 and GJ 3293 (close to 4:1).

1 Introduction

The search for exoplanets around nearby stars has produced a tremendous amount of observational data, pointing out the peculiar character of the Solar system. To date, more than 600 multiple planet systems have been found and the number of discovered planets with unexpected orbital properties (such as highly eccentric orbits, mutually inclined planetary orbits, hot Jupiters, compact multiple systems) constantly increases. Extrasolar systems that reside in or near mean-motion resonances are commonly detected with significantly high eccentricities. Therefore, the classical approach based on low-order expansions in eccentricities conceived for the Solar system is at least questionable when applied to extrasolar systems.

In the non-resonant scenario, the long-term evolution of a planetary system is described by the secular theory which consists in an averaging of the Hamiltonian over the fast angles (related to the mean anomalies). The classical procedure, denoted “averaging by scissors,” removes from the Hamiltonian all the terms including the fast angles. Thus, the fast actions are fixed and so are the semi-major axes. This Hamiltonian is named approximation at order one in the masses, and the linearized equations of motion correspond to the Laplace-Lagrange secular theory. This approach is adequate for the quasi-circular planetary orbits of the Solar system. Pushing the expansions at higher-order terms in the eccentricities (up to order 12) in Libert and Henrard (2005, 2007), the authors have shown that the high-order expansion accurately reproduces the long-term dynamics of extrasolar systems with eccentric orbits and which are far away from mean-motion resonance.

Instead, if the ratio between the mean-motion frequencies is close to the ${k_1^*}:{k_2^*}$ commensurability, the impact of the harmonics $(k_1^* \lambda _1 -k_2^* \lambda _2)$ on the long-term evolution of the system should be included in the Hamiltonian formulation. Still, in view of the exponential decay of the Fourier expansion with $|{\mathbf {k}}|_1=|k_1|+|k_2|$, only low-order mean-motion resonances must be considered. The effect of near resonances on the long-term evolution of a planetary system is taken into account by considering the so-called Hamiltonian at order two in the masses, where the integrable approximation describes an invariant torus (up to order two in the masses) instead of the classical circular orbits. The gain obtained with this approximation in the context of the planetary motion of the Solar system has been deeply studied in Laskar (1988). Also, the second-order approximation plays a crucial role in the applicability of the celebrated theorems of Kolmogorov and Nekhoroshev to the planetary case since it allows to tackle analytically the problem of the stability of the Solar system, see, e.g., Robutel (1995), Celletti and Chierchia (2005), Gabern (2005), Locatelli and Giorgilli (2007), Giorgilli et al. (2009, 2017), Sansottera et al. (2013, 2011), and Sansottera et al. (2015). Regarding extrasolar systems, in Libert and Sansottera (2013), we have considered a secular Hamiltonian at order two in the masses and showed that this secular Hamiltonian provides a good approximation of the dynamics for extrasolar systems which are near a mean-motion resonance, but not really close to or in a mean-motion resonance. Furthermore, the canonical transformation used for the approximation at second order in the masses allowed to evaluate the proximity of the system to a mean-motion resonance. In particular, we defined an heuristic criterion based on the computation of a $\delta$-parameter which allows to discriminate between the different regimes (see Sect. 3.3 and also Libert and Sansottera (2013) for more details).

Coming to the resonant case, several alternatives have been proposed to study analytically the dynamics of resonant extrasolar systems. Instead of expanding the disturbing function in series of the eccentricities following the classical approach, Beaugé and Michtchenko (2003) have introduced an analytic expansion based on a linear regression, which is convenient for the high-eccentricity planetary three-body problem. Other works (e.g., Alves et al. (2015)) avoid the use of expansions and consider the adiabatic regime, eliminating all the short-period terms by directly performing a numerical averaging of the Hamiltonian. For systems with small planetary eccentricities, the classical low-order expansion in eccentricities is suitable, as highlighted for instance in Callegari et al. (2004) for the near resonance between Uranus and Neptune and in Callegari et al. (2006) for a 3:2 resonance among planets around the pulsar PSRB1257+12. The limitations of an expansion at first order in the masses and truncated at order four in the eccentricities have been studied in Veras (2007), making reference to the GJ 876 extrasolar system. Finally, an integrable approximation for first-order mean-motion resonance (i.e., a $k:k-1$ resonance) has been developed in Batygin and Morbidelli (2013) in order to address resonant encounters during divergent migration.

In the present work, we are interested in the dynamics of systems which are really close to or in a mean-motion resonance. Our strategy is to reconstruct their evolution using a resonant Hamiltonian expanded at high orders, hence including appropriate resonant combinations of the fast angles. In other words, our goal is to extend the classical Laplace-Lagrange secular theory to the resonant case. We aim to see whether it is worth pushing the expansion of the resonant Hamiltonian to high order in eccentricities and to the order two in the masses for describing the evolutions of resonant exoplanets with moderate eccentricity.

The problem tackled here is challenging: the convergence domain of the Laplace-Lagrange expansion of the disturbing function is limited, as demonstrated by Sundman (1916) (see also Ferraz-Mello (1994)). Considering only the secular terms of the expansion, Libert and Henrard (2005, 2007) observed a numerical convergence of the secular expansion (convergence au sens des astronomes, see Poincaré (1893)) and showed that the approximation is accurate even for moderate to high planetary eccentricities. However, here we must consider also the contribution of the resonant combinations, making this approach potentially doubtful for extrasolar systems. As a result, we think that establishing the extent of validity of the classical approaches, along the lines of classical Celestial Mechanics, is pivotal and deserves to be investigated.

The paper is organized as follows. In Sect. 2, we introduce the planar Poincaré variables and outline the expansion of the Hamiltonian. The resonant Hamiltonians, both at orders one and two in the masses, are presented in Sect. 3, while Sect. 4 is dedicated to the application of our analytical approach to several (near-)resonant extrasolar systems, where representative planes of the dynamics and the proximity to periodic orbits family are also discussed. Finally, our findings are summarized in Sect. 5.

2 Hamiltonian expansion

We consider a system consisting of a central star of mass $m_0$ and two coplanar planets of masses $m_1$ and $m_2$. The indices 1 and 2 refer to the inner and outer planets, respectively. The Hamiltonian formulation of the planetary three-body problem in canonical heliocentric variables (see, e.g., Laskar (1989)) with coordinates ${\mathbf {r}}_j$ and momenta ${\tilde{{\mathbf {r}}}}_j$, for $j = 1,\, 2$, has four degrees of freedom and reads

$$\begin{aligned} F({\mathbf {r}},{{\tilde{{\mathbf {r}}}}})= T^{(0)}({{\tilde{{\mathbf {r}}}}})+U^{(0)}({\mathbf {r}})+ T^{(1)}({{\tilde{{\mathbf {r}}}}})+U^{(1)}({\mathbf {r}}), \end{aligned}$$

(1)

where

$$\begin{aligned} T^{(0)}({\tilde{\mathbf{r}}})&=\frac{1}{2}\sum _{j=1}^2 \Vert {\tilde{\mathbf{r}}}_j\Vert ^2 \left( \frac{1}{m_0}+\frac{1}{m_j} \right) , \qquad&T^{(1)}({\tilde{\mathbf{r}}})&= \frac{{\tilde{\mathbf{r}}}_1 \cdot {\tilde{\mathbf{r}}}_2}{m_0},\\ U^{(0)}(\mathbf{r})&=-{\mathcal {G}}\sum _{j=1}^2 \frac{m_0m_j}{\Vert {\mathbf{r}}_j\Vert }, \qquad&U^{(1)}(\mathbf{r})&= -\,{\mathcal {G}}\frac{m_1m_2}{\Vert {\mathbf{r}}_1-{\mathbf{r}}_2\Vert }. \end{aligned}$$

When adopting the planar Poincaré canonical variables, i.e.,

$$\begin{aligned} \Lambda _j= & {} \frac{m_0\, m_j}{m_0+m_j}\sqrt{{\mathcal {G}}(m_0+m_j) a_j}, \qquad \qquad \lambda _j = M_j+\omega _j, \nonumber \\ \xi _j= & {} \sqrt{ 2\Lambda _j}\, \sqrt{1-\sqrt{1-e_j^2}}\,\cos \omega _j, \qquad \qquad \eta _j = -\sqrt{2\Lambda _j}\, \sqrt{1-\sqrt{1-e_j^2}}\, \sin \omega _j, \end{aligned}$$

(2)

for $j=1\,,\,2\,$, where $a_j\,,\> e_j\,,\> M_j$ and $\omega _j$ are the semi-major axis, the eccentricity, the mean anomaly and the longitude of the pericenter of the j-th planet, respectively, we have

$$\begin{aligned} F(\varvec{\Lambda }, \varvec{\lambda }, \varvec{\xi }, \varvec{\eta })= F^{(0)}(\varvec{\Lambda })+F^{(1)}(\varvec{\Lambda }, \varvec{\lambda }, \varvec{\xi },\varvec{\eta }), \end{aligned}$$

(3)

where $F^{(0)}=T^{(0)}+U^{(0)}$ is the Keplerian part and $F^{(1)}=T^{(1)}+U^{(1)}$ is the perturbation (see, e.g., Laskar (1989)). The ratio between the two parts is of order ${\mathcal {O}}(\mu )$ with $\mu =\max \{m_1/m_0,m_2/m_0\}$, so the variables $(\varvec{\Lambda },\varvec{\lambda })$ are referred to as the fast variables and $(\varvec{\xi },\varvec{\eta })$ as the secular variables. Following Libert and Sansottera (2013), we realize an expansion of the Hamiltonian in Taylor-Fourier series of the Poincaré variables.

To do so, we first realize a translation, ${\mathcal {T}}_{F}$, in the fast actions

$$\begin{aligned} {\mathbf {L}}=\varvec{\Lambda }-\varvec{\Lambda }^*, \end{aligned}$$

where $\varvec{\Lambda }^*$ is a fixed value.¹ The Hamiltonian (3) is then expanded in Taylor series of ${\mathbf {L}}$, $\varvec{\xi }$ and $\varvec{\eta }$ around the origin, as well as in Fourier series of $\varvec{\lambda }$, and we obtain

$$\begin{aligned} {\mathcal {H}}^{({\mathcal {T}})}={\mathbf {n}}^*\cdot {\mathbf {L}}+\sum _{j_1=2}^{\infty } h_{j_1,0}^{\mathrm{(Kep)}}({\mathbf {L}})+ \mu \sum _{j_1=0}^{\infty }\sum _{j_2=0}^{\infty } h^{({\mathcal {T}})}_{j_1,j_2}({\mathbf {L}},\varvec{\lambda },\varvec{\xi },\varvec{\eta }), \end{aligned}$$

(4)

with $n_j^* = \sqrt{(m_0+m_j)/a_j^3}$ for $j=1,2\,$, and where the terms $h_{j_1,0}^{\mathrm{(Kep)}}$ are homogeneous polynomials of degree $j_1$ in the fast actions ${\mathbf {L}}$, while the functions $h^{({\mathcal {T}})}_{j_1,j_2}$ are homogeneous polynomials of degree $j_1$ in the fast actions ${\mathbf {L}}$, degree $j_2$ in the secular variables $(\varvec{\xi },\varvec{\eta })$ and trigonometric polynomials in the angles $\varvec{\lambda }$. A detailed treatment can be found in Duriez (1989a, b), Laskar (1989) and Laskar and Robutel (1995) where the low-order analytical expressions of the crucial terms are given in Sect. 7. The computations have been done via algebraic manipulation, using a package developed on purpose named X $\varrho \acute{o} \nu$ o $\varsigma$ (see Giorgilli and Sansottera (2011)).

The expansion is truncated as follows. We include in the Keplerian part terms up to degree 2 in the fast actions ${\mathbf {L}}$, while in the perturbation we consider the terms which are: (i) up to degree 1 in ${\mathbf {L}}$; (ii) up to degree 12 in the secular variables $(\varvec{\xi },\varvec{\eta })$; and (iii) up to trigonometric degree 24 in the fast angles $\varvec{\lambda }$.

3 Resonant approximation of the Hamiltonian

In the present work, we are interested in the dynamics of systems that are really close to or in a mean-motion resonance. The averaging procedures, both at first and second orders in the masses, must be adapted so as to take into account the strong influence of the mean-motion resonance. The main issue concerns the presence of small divisors that prevents the convergence of the averaging procedure on a domain that contains the initial data. We explore here two different approaches, considering resonant Hamiltonians at order one and two in the masses.

3.1 Resonant Hamiltonian at order one in the masses

The classical “averaging by scissors” method can be simply modified by including appropriate resonant combinations of the fast angles into the Laplace-Lagrange secular expansion. The resonant combination to take into account is related to the nearest mean-motion resonance and can be determined from the vector ${\mathbf {n}}^*$, for example, by means of continued fraction approximations, or by exploiting the $\delta$-parameter (see Sect. 3.3). Precisely, having fixed a resonant harmonic ${\mathbf {k}}^*\cdot \varvec{\lambda }$, the resonant Hamiltonian at order one in the masses writes

$$\begin{aligned} {\mathcal {H}}_{\mathrm{res}}^{({\mathcal {O}}1)} = {\overline{{\mathcal {H}}}}^{({\mathcal {T}})} + {\widetilde{{\mathcal {H}}}}^{({\mathcal {T}})}, \end{aligned}$$

(5)

with

$$\begin{aligned} {\overline{{\mathcal {H}}}}^{({\mathcal {T}})} = \frac{1}{4\pi ^2} \int _{0}^{2\pi }\int _{0}^{2\pi } {\mathcal {H}}^{({\mathcal {T}})} \,\mathrm{d}\lambda _1\,\mathrm{d}\lambda _2 \quad \text {and}\quad {\widetilde{{\mathcal {H}}}}^{({\mathcal {T}})} = \mu \sum _{j_1=0}^{\infty }\sum _{j_2=0}^{\infty } h^{({\mathcal {T}})}_{j_1,j_2}({\mathbf {L}},{\mathbf {k}}^*\cdot \varvec{\lambda },\varvec{\xi },\varvec{\eta }). \end{aligned}$$

The first term, ${\overline{{\mathcal {H}}}}^{({\mathcal {T}})}$, is the classical averaging of the Hamiltonian over the fast angles, $\varvec{\lambda }$. In the second one, ${\widetilde{{\mathcal {H}}}}^{({\mathcal {T}})}$, all the terms corresponding to the resonant harmonic ${\mathbf {k}}^*\cdot \varvec{\lambda }$ and its multiples are collected. Although they depend on the fast angles, due to the (near-)resonance relation, they are slow terms and have to be taken into account in the study of the long-term evolution.

3.2 Resonant Hamiltonian at order two in the masses

The secular approximation at order two in the masses is based on a “Kolmogorov-like” normalization step aiming at removing the fast angles from terms that are at most linear in the fast actions ${\mathbf {L}}$. Again, we modify the standard approach by putting the resonant combinations of the fast angles, the harmonics ${\mathbf {k}}^*\cdot \varvec{\lambda }$, in the normal form, thus removing them from the generating function.

We briefly summarize the averaging procedure here; more details can be found in, e.g., Locatelli and Giorgilli (2007), Sansottera et al. (2013) and Libert and Sansottera (2013). We adopt the standard Lie series algorithm (see, e.g., Henrard (1973) and Giorgilli (1995)) to transform the Hamiltonian (4) into ${\widehat{{\mathcal {H}}}}^{({\mathcal {O}}2)}=\exp {\mathcal {L}}_{\mu \,\chi _{1}^{({\mathcal {O}}2)}}\,{\mathcal {H}}^{({\mathcal {T}})}$. The generating function $\mu \, \chi _1^{({\mathcal {O}}2)}(\varvec{\lambda },\varvec{\xi },\varvec{\eta })$ is determined by solving the homological equation

$$\begin{aligned} \sum _{j=1}^{2}n^*_j \frac{\partial \,\chi _{1}^{({\mathcal {O}} 2)}}{\partial \lambda _j} +\sum _{j_2=0}^{K_S}\left\lceil h_{0,j_2}^{({\mathcal {T}})} \right\rceil _{\varvec{\lambda };K_F} (\varvec{\lambda },\varvec{\xi },\varvec{\eta })=\sum _{j_2=0}^{K_S}\left\lceil h_{0,j_2}^{({\mathcal {T}})} \right\rceil _{\varvec{\lambda };K_F} ({\mathbf {k}}^*\cdot \varvec{\lambda },\varvec{\xi },\varvec{\eta }), \end{aligned}$$

(6)

where $\lceil f \rceil _{\varvec{\lambda };K_F}$ denotes the Fourier expansion of a function f including only the harmonics satisfying $0<|{\mathbf {k}}|_1\le K_F$. The parameters $K_S$ and $K_F$ are tailored according to the considered mean-motion resonance, and the actual choice is detailed in Sect. 4 for each system studied here. The transformed Hamiltonian $\widehat{\mathcal H}^{({\mathcal {O}} 2)}$ can be written in the same form as (4), replacing $h^{({\mathcal {T}})}_{j_1,j_2}$ with ${\hat{h}}^{({\mathcal {O}} 2)}_{j_1,j_2}$. Here and in the following, with a common little abuse of notation, we denote the new variables with the same names as the old ones in order to not unnecessarily burden the notation.

To compute the resonant Hamiltonian to the second order in the masses, ${\mathcal {H}}^{({\mathcal {O}}2)}=\exp {\mathcal {L}}_{\mu \,\chi _{2}^{({\mathcal {O}}2)}}\,{\widehat{{\mathcal {H}}}}^{({\mathcal {O}}2)}$, we solve the following homological equation to determine the generating function $\mu \,\chi _{2}^{({\mathcal {O}}2)}({\mathbf {L}},\varvec{\lambda },\varvec{\xi },\varvec{\eta })$, which is linear in ${\mathbf {L}}$,

$$\begin{aligned}&\sum _{j=1}^{2}n^*_j \frac{\partial \,\chi _{2}^{({\mathcal {O}}2)}}{\partial \lambda _j} +\sum _{j_2=0}^{K_S}\left\lceil {\hat{h}}_{1,j_2}^{({\mathcal {O}}2)} \right\rceil _{\varvec{\lambda };K_F} ({\mathbf {L}},\varvec{\lambda },\varvec{\xi },\varvec{\eta }) =\sum _{j_2=0}^{K_S}\left\lceil {\hat{h}}_{1,j_2}^{({\mathcal {O}}2)} \right\rceil _{\varvec{\lambda };K_F} ({\mathbf {L}},{\mathbf {k}}^*\cdot \varvec{\lambda },\varvec{\xi },\varvec{\eta }). \nonumber \\ \end{aligned}$$

(7)

The resonant Hamiltonian ${\mathcal {H}}^{({\mathcal {O}} 2)}$ writes

$$\begin{aligned} {\mathcal {H}}^{({\mathcal {O}}2)}({\mathbf {L}},\varvec{\lambda },\varvec{\xi },\varvec{\eta })= & {} {\mathbf {n}}^*\cdot {\mathbf {L}}+ \sum _{j_1=2}^\infty h_{j_1,0}^{(\mathrm{Kep})}({\mathbf {L}}) + \mu \sum _{j_1=0}^\infty \sum _{j_2=0}^\infty h_{j_1,j_2}^{({\mathcal {O}}2)}({\mathbf {L}},\varvec{\lambda },\varvec{\xi },\varvec{\eta };\mu )+{\mathcal {O}}(\mu ^3). \nonumber \\ \end{aligned}$$

(8)

Note that we denote again by $({\mathbf {L}},\varvec{\lambda },\varvec{\xi },\varvec{\eta })$ the new coordinates. The composition of the Lie series with generating functions $\mu \,\chi _{1}^{({\mathcal {O}}2)}$ and $\mu \,\chi _{2}^{({\mathcal {O}}2)}$ will be denoted by ${\mathcal {T}}_{{\mathcal {O}}2}$, precisely

$$\begin{aligned} {\mathcal {T}}_{{\mathcal {O}}2}({\mathbf {L}},\varvec{\lambda },\varvec{\xi },\varvec{\eta }) = \exp {\mathcal {L}}_{\mu \,\chi _{2}^{({\mathcal {O}}2)}} \circ \exp {\mathcal {L}}_{\mu \,\chi _{1}^{({\mathcal {O}}2)}}({\mathbf {L}},\varvec{\lambda },\varvec{\xi },\varvec{\eta }). \end{aligned}$$

(9)

Finally, since we aim for a second-order approximation, we neglect the terms of order ${\mathcal {O}}(\mu ^3)$ and, likewise we do in the first-order approximation, we select the secular and resonant terms as in (5), namely

$$\begin{aligned} {\mathcal {H}}_{\mathrm{res}}^{({\mathcal {O}}2)} = {\overline{{\mathcal {H}}}}^{({\mathcal {O}}2)} + {\widetilde{{\mathcal {H}}}}^{({\mathcal {O}}2)}. \end{aligned}$$

(10)

Similarly to the resonant approximation at order one in the masses, ${\overline{{\mathcal {H}}}}^{({\mathcal {O}}2)}$ denotes the Hamiltonian ${\mathcal {H}}^{({\mathcal {O}}2)}$ averaged over the fast angles, $\varvec{\lambda }$, while ${\widetilde{{\mathcal {H}}}}^{({\mathcal {O}}2)}$ contains the terms corresponding to the resonant harmonic ${\mathbf {k}}^*\cdot \varvec{\lambda }$ and its multiples. Let us stress the crucial difference between the first- and second-order approximations: the second-order one takes into account the effect of low-order harmonics in both expressions ${\overline{{\mathcal {H}}}}^{({\mathcal {O}}2)}$ and ${\widetilde{{\mathcal {H}}}}^{({\mathcal {O}}2)}$.

To illustrate the averaging procedure described here, the expressions of the resonant Hamiltonians at order one and two in the masses are given in “Appendix A” for GJ 876 system (see Subsect. 4.2 for a complete description of the system). All the terms are reported up to order one in the fast actions ${\mathbf {L}}$, degree 6 in the fast angles $\varvec{\lambda }$ and order two in the secular variables $(\varvec{\xi }, \varvec{\eta })$.

3.3 The $\delta$-parameter: proximity to a mean-motion resonance

In Libert and Sansottera (2013), we introduced an heuristic criterion to evaluate the proximity of planetary systems to mean-motion resonance, by exploiting the canonical change of coordinates used for the approximation at order two in the masses. We report here the definition of the $\delta$-parameter that will be used in the analysis of the selected planetary systems and refer to Libert and Sansottera (2013) for a detailed discussion.

The first-order terms of the near the identity change of variables, ${\mathcal {T}}_{{\mathcal {O}}2}$, are

$$\begin{aligned} \xi _j'&=\xi _j\,\left( 1-\frac{1}{\xi _j}\frac{\partial \,\mu \,\chi _1^{({\mathcal {O}}2)}}{\partial \eta _j}\right) ,\\ \eta _j'&=\eta _j\,\left( 1-\frac{1}{\eta _j}\frac{\partial \,\mu \,\chi _1^{({\mathcal {O}}2)}}{\partial \xi _j}\right) , \end{aligned}$$

for $j=1\,,\,2\,$. Considering the coefficients of the functions

$$\begin{aligned} \delta \xi _j = \frac{1}{\xi _j}\frac{\partial \,\mu \,\chi _1^{({\mathcal {O}}2)}}{\partial \eta _j} \qquad \hbox {and}\qquad \delta \eta _j = \frac{1}{\eta _j}\frac{\partial \,\mu \,\chi _1^{({\mathcal {O}}2)}}{\partial \xi _j}, \end{aligned}$$

(11)

we identify the most important (near) mean-motion resonance terms corresponding to the harmonic ${\mathbf {k}}\cdot \varvec{\lambda }$. Given a polydisk of radius $\varvec{\varrho }$ around the origin, $\Delta _{\varvec{\varrho }}$, and adopting the weighted Fourier norm, we define the quantities

$$\begin{aligned} \delta \xi _j^* = \max _{{\mathbf {k}}}(\Vert \delta \xi ^{({\mathbf {k}})}_j\Vert _{\varvec{\varrho }}) \qquad \hbox {and}\qquad \delta \eta _j^* = \max _{{\mathbf {k}}}(\Vert \delta \eta ^{({\mathbf {k}})}_j\Vert _{\varvec{\varrho }}) \end{aligned}$$

needed for the computation of the $\delta$-parameter given by $\delta =\max (\delta _1, \delta _2)\,$ where $\delta _j = \min (\delta \xi _j^*, \delta \eta _j^*)$ for $j=1,2$. The $\delta$-parameter is a measure of the change from the original secular variables to the averaged ones. The actual computation of the $\delta$-parameter is quite cumbersome, but is more reliable than just looking at the semi-major axes ratio, since it holds information about the nonlinear character of the system.

In particular, in Libert and Sansottera (2013), we defined an heuristic criterion based on the computation of the $\delta$-parameter to discriminate between three different regimes: (i) if $\delta <2.6\times 10^{-3}$, the system is far from the mean-motion resonance, so the first-order secular approximation describes the long-term evolution of the system with great accuracy; (ii) if $2.6\times 10^{-3}<\delta \le 2.6\times 10^{-2}$, a secular Hamiltonian at order two in the masses is required to describe the long-term evolution; and (iii) if $\delta >2.6\times 10^{-2}$, the system is too close to a mean-motion resonance and a secular approximation is not enough to describe the long-term evolution.

3.4 Resonant variables

The resonant Hamiltonians at order one and two in the masses, ${\mathcal {H}}_{\mathrm{res}}^{({\mathcal {O}}1)}$ and ${\mathcal {H}}_{\mathrm{res}}^{({\mathcal {O}}2)}$, respectively, reduce the problem to two degrees of freedom. To highlight this point, we introduce the canonical resonant variables associated with a ${k_1^*}:{k_2^*}$ mean-motion resonance (see for instance Beaugé and Michtchenko (2003)). The canonical change of coordinate ${\mathcal {T}}_{\mathcal {R}}$ is given by

$$\begin{aligned} \begin{aligned} J_1&=L_1+ \frac{k_2^*}{{k_1^*}-{k_2^*}} (I_1+I_2), \quad \lambda _1, \\ J_2&=L_2- \frac{k_1^*}{{k_1^*}-{k_2^*}} (I_1+I_2), \quad \lambda _2, \\ I_1&= \sqrt{2\Lambda _1} \sqrt{1-\sqrt{1-e_1^2}}, \qquad \sigma _1=-\frac{k_2^*}{{k_1^*}-{k_2^*}}\lambda _1+ \frac{k_1^*}{{k_1^*}-{k_2^*}}\lambda _2-\omega _1, \\ I_2&= \sqrt{2\Lambda _2} \sqrt{1-\sqrt{1-e_2^2}}, \qquad \sigma _2=-\frac{k_2^*}{{k_1^*}-{k_2^*}}\lambda _1+ \frac{k_1^*}{{k_1^*}-{k_2^*}}\lambda _2-\omega _2. \end{aligned} \end{aligned}$$

(12)

The resonant Hamiltonians (5) and (10) contain two types of terms only: (i) secular terms which have no dependency in the fast angles; and (ii) resonant terms depending on the fast angles through the resonant angles $\sigma _1$ and $\sigma _2$. As a result, $J_1$ and $J_2$ are constants of motions and the resonant Hamiltonians have only two degrees of freedom $(I_1,\sigma _1)$ and $(I_2,\sigma _2)$. In the next section, we investigate the limitations and/or improvements of the analytical expansion detailed here in modeling the long-time dynamics of extrasolar systems really close to or in a mean-motion resonance.

4 Application to (near-)resonant extrasolar systems

We selected eight extrasolar systems in the vicinity of a low-order mean-motion resonance for which a full parameterization has been derived, namely GJ 876 (Laughlin and Chambers (2001)), HD 128311 (Vogt et al. (2005)), HD 73526 (Wittenmyer et al. (2014)) and HD 82943 (Tan et al. (2013)) for the 2:1 mean-motion resonance, HD 45364 (Correia et al. (2009)) for the 3:2 resonance, HD 60532 (Laskar and Correia (2009)) for the 3:1 resonance, and HD 108874 (Wright et al. (2009)) and GJ 3293 (Astudillo-Defru et al. (2015)) for the 4:1 resonance.

As previously explained, the convergence of the Laplace-Lagrange expansion of the disturbing function is not guaranteed for high planetary eccentricities. Despite the high eccentricities of the planets, the expansion made of the secular terms only, when pushed to high order in eccentricities, can represent the orbits of non-resonant extrasolar systems with enough accuracy, as shown by, e.g., Libert and Henrard (2005) for the expansion at first order in the masses and Libert and Sansottera (2013) for the second-order expansion. However, in the Hamiltonians (5) and (10), additional resonant terms are present and could restrain the convergence domain.

To check the validity of the expansion for the eight extrasolar systems considered here, we have computed the boundaries of the domain of convergence of the Laplace-Lagrange expansion of the disturbing function, as given by the Sundman’s criterion (Sundman (1916), see also Ferraz-Mello (1994)). The criterion for the absolute convergence of the planar Laplace-Lagrange expansion is

$$\begin{aligned} a_1F_1(e_1)<a_2F_0(e_2) \end{aligned}$$

(13)

with real functions $F_1(g)=\sqrt{1+g^2}\cosh {w}+g+\sinh {w}$ and $F_0(g)=\sqrt{1+g^2}\cosh {w}-g-\sinh {w}$, where $w=g \cosh {w}$.

Fig. 1

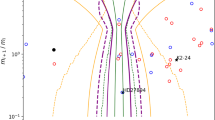
Sundman’s convergence domain for the selected extrasolar systems. The lines represent the boundary (in eccentricities) delimitation of the convergence domain (below area), for different semi-major axis ratios. Initial parameters of several extrasolar systems are shown, with the planetary semi-major axis ratio given in parenthesis

Table 1 Parameters of GJ 876 (Laughlin and Chambers (2001)), HD 60532 (Laskar and Correia (2009)), HD 108874 (Wright et al. (2009)) and GJ 3293 (Astudillo-Defru et al. (2015)) extrasolar systems

The boundaries of the convergence domain in $(e_1,e_2)$ space given by the Sundman’s criterion are shown in Fig. 1 for several semi-major axes ratios. The selected extrasolar systems are indicated on the graph with the value of their semi-major axes ratio in parenthesis. The convergence domain of each system is the domain below the curve corresponding to the semi-major axes ratio of the system. We observe that the eccentricities of HD 60532 and HD 108874 systems are located well inside the convergence domain, while GJ 876 and GJ 3293 systems are slightly above the boundary curve. On the contrary, the four remaining systems, HD 128311, HD 73526, HD 82943 and HD 45364, have eccentricities too large to be located inside their Sundman’s convergence domain, and the use of the expansion is not appropriate. In the following, we will then focus on the long-term evolutions of the four systems fulfilling the Sundman’s criterion. Their physical and orbital parameters are given in Table 1. The last column of Table 1 gives an indication of the proximity of the system to the mean-motion resonance (see Sect. 3.3). The value of the $\delta$-parameter clearly shows that GJ 876 and HD 60532 systems are in the third category of systems, asking for a resonant approach, while HD 108874 and GJ 3293 systems are only near the 4:1 resonance, being close to the upper limit of the second regime. Although a secular approach at order two in the masses already gives a good approximation of the dynamical evolution for these last two systems, we aim to see whether the resonant approach yields to further improvements.

4.1 Validation of the resonant approximations

To assess the validity of the resonant Hamiltonians in describing the long-term evolution of the planetary orbits, we will compare the Runge-Kutta integration of the equations of motion associated with the Hamiltonians (5) and (10) with the direct numerical integration of the full problem (adopting the ${\mathcal {S}}{\mathcal {B}}{\mathcal {A}}{\mathcal {B}}3$ symplectic scheme, see Laskar and Robutel (2001)).

We introduce the compact notations ${\mathcal {C}}^{({\mathcal {O}}1)}$ and ${\mathcal {C}}^{({\mathcal {O}}2)}$ for the composition of the canonical transformations defined in Sect. 2, namely

$$\begin{aligned} {\mathcal {C}}^{({\mathcal {O}}1)}={\mathcal {T}}_{F}\circ {\mathcal {T}}_{{\mathcal {R}}} \quad \text {and}\quad {\mathcal {C}}^{({\mathcal {O}}2)}={\mathcal {T}}_{F}\circ {\mathcal {T}}_{{\mathcal {O}}2}\circ {\mathcal {T}}_{{\mathcal {R}}}. \end{aligned}$$

(14)

Given initial values of the orbital elements $\big ({\mathbf {a}}(0),\varvec{\lambda }(0),{\mathbf {e}}(0),\varvec{\omega }(0)\big )$, we compute their evolution by exploiting the resonant Hamiltonian at order two in the masses as follows

(15)

where $(\varvec{\Lambda },\varvec{\lambda },\varvec{\xi },\varvec{\eta }) = {\mathcal {E}}^{-1}({\mathbf {a}}(0),\varvec{\lambda }(0),{\mathbf {e}}(0),\varvec{\omega }(0))$ is the non-canonical change of coordinates (2). Of course, the same scheme holds for the resonant Hamiltonian at order one in the masses with the change of ${\mathcal {C}}^{({\mathcal {O}}1)}$ in place of ${\mathcal {C}}^{({\mathcal {O}}2)}$.

In the following sections, we detail the comparison of the long-term evolutions of the eccentricities and possibly resonant angles given by our analytical approach and by direct numerical integration for each of the four considered extrasolar systems.

Fig. 2

Evolution of the eccentricities (left panels) and resonant angles (right panels) for GJ 876 system, given by (i) direct numerical integration (green curves); (ii) second-order resonant approximation (red curves); (iii) first-order resonant approximation (blue curves)

4.2 GJ 876

One of the first detected resonant extrasolar systems was GJ 876 system locked in a 2:1 mean-motion resonance (Marcy et al. (2001); Laughlin and Chambers (2001)). The dynamical evolution of the two-planet system was carefully studied in Beaugé and Michtchenko (2003), where they used an analytical expansion specifically devised for high-eccentricity planetary three-body problem. Moreover, Veras (2007) showed the limitations of a resonant Hamiltonian expanded up to order four in the eccentricities. Here, we aim to perform a similar study of GJ 876 system using the resonant Hamiltonian at order two in the masses.²

In Fig. 2, we show the evolution of the eccentricities (left panels) and the resonant angles (right panels) of the two-planet (c–b pair) GJ 876 system, as given by our analytical approach. The parameters $K_S$ and $K_F$ have been fixed so as to include the effects up to the third resonant harmonics, namely $K_S=3$ and $K_F=9$. The blue curves indicate the orbital evolutions obtained with the Hamiltonian expansion at first order in the masses, while the evolution with the second-order expansion is given in red. Figure 2 shows that both resonant angles of GJ 876 planetary system librate, confirming that the system is locked in a 2:1 mean-motion resonance.

The accuracy of our Hamiltonian approximation is verified by comparison with a direct numerical integration of the Newton equations (green curves). We observe in Fig. 2 that the resonant Hamiltonian to first order in the masses, although giving a rather good approximation of the frequencies of the motion, does not reproduce reliably the variation amplitudes of the eccentricities and the resonant angles. On the contrary, the second-order approximation is very efficient and the evolutions given by the analytical approach and the numerical integration do superimpose nearly perfectly.

To analyze more deeply the dynamics of the two-planet GJ 876 system, we reproduce in Fig. 3 (left panel) the level curves of the first-order Hamiltonian in the representative plane $(e_1 \sin {\sigma _1},e_2 \sin {\sigma _2})$, where both resonant angles are fixed to $0^\circ$ in the positive part of the axis and $180^\circ$ in the negative part of the axis, as previously done by Beaugé and Michtchenko (2003). We insist that this plane is neither a phase portrait nor a surface of section, since the problem is four-dimensional. To find the stationary solutions of the (averaged) Hamiltonian, we have computed the curves $\dot{\sigma _1}=0$ and $\dot{\sigma _2}=0$ on the representative plane (green and red curves), since their intersections give the eccentricities of the stationary solutions. The star symbol in Fig. 3 indicates the location of GJ 876 planetary system. We observe that the system lies close to a stationary solution (also often denoted ACR, for apsidal corotation resonance, see, e.g., Beaugé and Michtchenko (2003)), thus in a region where both resonant angles librate.

Fig. 3

Level curves of the first-order resonant Hamiltonian in the plane $(e_1 \sin {\sigma _1},e_2 \sin {\sigma _2})$ for GJ 876 (left panel) and in $(e_1 \sin {2\sigma _1},e_2 \sin {\Delta \omega })$ for HD 60532 (right panel), with the angles fixed to $0^\circ$ in the positive part of the axis and $180^{\circ }$ in the negative part of the axis. The stars indicate the locations of the extrasolar systems. See text for more details

Fig. 4

Family of periodic orbits of the 2:1 mean-motion resonance corresponding to $(\sigma _1,\sigma _2)=(0,0)$ in the $(e_1,e_2)$ plane for the mass ratio of GJ 876, obtained with the first-order resonant approximation. The star indicates the eccentricities of GJ 876 system, demonstrating its proximity to the family of periodic orbits

The stationary solutions of the Hamiltonian averaged over the short periods correspond to periodic orbits of the full problem. Using our first-order approach, we have computed, in Fig. 4, the family of periodic orbits corresponding to $(\sigma _1,\sigma _2)=(0,0)$ in the $(e_1,e_2)$ plane, for the mass ratio of GJ 876. Comparisons can be made with the works of Hadjidemetriou (2002) and Beaugé and Michtchenko (2003), showing the accuracy of the analytical approximation. As expected, we observe the proximity of GJ 876 system to the family of periodic orbits.

It is interesting to note that the approximation to first order in the masses is accurate enough to compute both the dynamics on the representative plane and the family of periodic orbits, giving a good qualitative representation of the dynamics. As a result, we can conclude that, while the resonant Hamiltonian at first order in the masses gives a good indication on the resonant dynamics of GJ 876 system, the second-order correction is needed to reproduce carefully the orbital evolution of the system.

Fig. 5

Same as Fig. 2 for HD 60532 system

4.3 HD 60532

HD 60532 system consists of two giant planets in a 3:1 mean-motion resonance (Desort et al. 2008). Two exhaustive dynamical analyses of the system have been performed by Laskar and Correia (2009) and Alves et al. (2015). Likewise the previous study, the evolutions of the eccentricities and resonant angles are reported in Fig. 5. The parameters $K_S$ and $K_F$ have been fixed so as to include the effects up to the second resonant harmonics, namely $K_S=4$ and $K_F=8$. Figure 5 shows that both the resonant angle $\sigma _1$ and the difference of the longitudes $\Delta \omega$ librate, confirming that the system is locked in a 3:1 mean-motion resonance. This can also be deduced from Fig. 3 (right panel), which shows the level curves of the resonant Hamiltonian at first order in the masses, in the representative plane $(e_1 \sin {2\sigma _1},e_2 \sin {\Delta \omega })$, where both resonant angles are fixed to $0^\circ$ in the positive part of the axis and $180^\circ$ in the negative part of the axis. Again, a perfect agreement with the results presented in Alves et al. (2015) is observed.

The same conclusions can be drawn on the accuracy of the analytical approach, as for GJ 876 system. The resonant Hamiltonian at order one in the masses gives already a good approximation of the long-term evolutions in Fig. 5, while the one at order two reliably reproduces the frequencies of the motion and the variation amplitudes of the orbital elements.

Fig. 6

Same as Fig. 2 for HD 108874 system

4.4 HD 108874

HD 108874 system (e.g., Butler et al. (2003), Vogt et al. (2005), Wright et al. (2009)) is composed of two giant planets very close to the 4:1 mean-motion resonance, as previously deduced from the $\delta$-parameter value of the system (see the discussion at the beginning of Sect. 4). Secular Hamiltonian expansions both at first and second orders in the masses were considered in our previous contribution (Libert and Sansottera 2013), showing a good agreement for the amplitudes of the long-term evolutions of the eccentricities, but not for the secular frequencies of the motion (see the black curves in Fig. 6).

The results obtained with the resonant Hamiltonian formulations are reported in Fig. 6. The parameters $K_S$ and $K_F$ have been fixed so as to include the effects up to the second resonant harmonics, namely $K_S=6$ and $K_F=10$. The resonant angles circulate; thus, HD 108874 planetary system is not locked in a 4:1 mean-motion resonance.³ The difference of the longitudes $\Delta \omega$ librates. We see that a resonant Hamiltonian approach is needed in order to accurately reproduce the long-term dynamics of the system. In particular, the resonant approximation at order two in the masses is the most efficient, and the evolutions given by this analytical approach superimpose with the direct numerical integration. As a result, we conclude that, for systems very close to a mean-motion resonance, the resonant approach is required to reproduce perfectly the secular frequencies of the motion.

4.5 GJ 3293

Astudillo-Defru et al. (2015) reported the detection of two Neptune-like planets around GJ 3293 with periods near the 4:1 commensurability. Let us note that the parameters of GJ 3293 b and c have slightly changed with the discovery of two additional super-Earths in the system (Astudillo-Defru et al. 2017); however, the dynamical analysis of the four-body system is beyond the scope of the present work.

Fig. 7

Same as Fig. 2 for GJ 3293 system

GJ 3293 system behaves similarly to HD 108874, also being very close to the same mean-motion resonance. However, the smaller value of the $\delta$-parameter indicates that the system is less close to the resonance. As a result, a resonant Hamiltonian at order one in the masses already describes accurately the long-term evolutions of the orbits, as illustrated in Fig. 7. Still, looking more closely to the orbital evolutions, we can appreciate the improvements due to the second-order approximation.

5 Conclusions

In the present work, we have analyzed the long-term evolution of four exoplanetary systems by using two different approximations: the resonant Hamiltonians at order one and two in the masses. Both approximations include the (near-)resonant harmonics, extending the classical Lagrange-Laplace secular approximation adopted to describe the long-term evolution of non-resonant systems. This allows us to treat the systems which are really close to or in a mean-motion resonance, and for which the secular approximation failed in Libert and Sansottera (2013). Let us note that we only consider here planetary systems for which the Sundman’s criterion is fulfilled. We assess the proximity of a system to the resonance by using the $\delta$-parameter. This criterion reveals accurate and confirms the need of a resonant Hamiltonian at order two in the masses for high values of the $\delta$-parameter ($\delta >2.6\times 10^{-2}$), while a resonant Hamiltonian at order one in the masses gives a good approximation of the long-term evolution of the system for $2.0\times 10^{-2}<\delta <2.6\times 10^{-2}$.

We considered two systems, HD 108874 and GJ 3293, which are really close to a 4:1 mean-motion resonance, but not in the resonance. For these systems, the resonant Hamiltonian at order one already gives a good approximation, while the resonant Hamiltonian at order two perfectly represents the long-time evolution of these systems.

The second-order approximation, due to the careful treatment of the contribution of low-order fast harmonics, gives a substantial impact when dealing with resonant systems. This was illustrated in the study of GJ 876 and HD 60532 systems, where the difference between resonant approximations at order one and two in the masses is much more noticeable.

Appendix Low-order expansions of \({\mathcal {H}}_{\mathrm{res}}^{({\mathcal {O}}1)}\) and \({\mathcal {H}}_{\mathrm{res}}^{({\mathcal {O}}2)}\) for GJ 876

We report here the low-order expansion of ${\mathcal {H}}_{\mathrm{res}}^{({\mathcal {O}}1)} = {\overline{{\mathcal {H}}}}^{({\mathcal {T}})} + {\widetilde{{\mathcal {H}}}}^{({\mathcal {T}})}$ and ${\mathcal {H}}_{\mathrm{res}}^{({\mathcal {O}}2)} = {\overline{{\mathcal {H}}}}^{({\mathcal {O}}2)} + {\widetilde{{\mathcal {H}}}}^{({\mathcal {O}}2)}$ (see (5) and  (10), respectively) for GJ 876. We refer to Table 1 for the physical and orbital parameters of the system and Subsect. 4.2 for a complete description of the system (Tables 2, 3).

Table 2 Low-order secular contributions of the resonant Hamiltonians at order one and two in the masses, namely ${\overline{{\mathcal {H}}}}^{({\mathcal {T}})}$ and ${\overline{{\mathcal {H}}}}^{({\mathcal {O}}2)}$

Table 3 Low-order resonant contributions of the resonant Hamiltonians at orders one and two in the masses, namely ${\widetilde{{\mathcal {H}}}}^{({\mathcal {T}})}$ and ${\widetilde{{\mathcal {H}}}}^{({\mathcal {O}}2)}$