Spatial unstable periodic quasi-satellite orbits and their applications to spacecraft trajectories

Abstract

This paper explores the rich dynamics of quasi-satellite orbits (QSOs) with out-of-plane motions in the Earth–Moon and Mars–Phobos systems. The first part of the paper computes families of spatial periodic QSOs in the circular restricted three-body problem via bifurcation analyses and presents their orbital characteristics. We pay special attention to unstable families of spatial periodic QSOs of weak instabilities. The second part of the paper presents three applications of the obtained spatial unstable periodic QSOs to space mission trajectories. The first application is concerned with a ballistic landing concept on the surface of Phobos via unstable manifolds emanating from spatial weakly unstable periodic QSOs. The second application identifies stability regions of spatial, long-term stable, quasi-periodic QSOs based on phase-space structures of invariant manifolds emanating from spatial unstable periodic QSOs. The third application proposes a method of designing nearly ballistic, two-impulse transfers from a low Earth orbit to a spatial, long-term stable, quasi-periodic QSO around the Moon in the bicircular restricted four-body problem including solar perturbation.

1 Introduction

Co-orbital orbits such as quasi-satellite orbits (QSOs), tadpole orbits, and horseshoe orbits have attracted interests in Celestial Mechanics as orbits where many asteroids reside (Murray and Dermott 1999). Recently, several studies (Llanos et al. 2013; Capdevila and Howell 2018) investigated the use of co-orbital orbits as novel mission options due to their long-term stable behavior. Future missions such as JAXA’s Martian Moons eXploration (MMX) plan to use QSOs for close observations of Phobos (Kawakatsu et al. 2017).

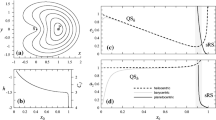
Many researchers (Hénon 1970; Lam and Whiffen 2005; Demeyer and Gurfil 2007; Scott and Spencer 2010; Capdevila et al. 2014) investigated the dynamics of planar QSOs in the planar circular restricted three-body problem (CR3BP), where a Poincaré section is a useful tool to visualize global phase-space structures in the three-dimensional energy surface. Figure 1a shows planar stable and unstable periodic QSOs, which are sometimes called a distant retrograde orbit and a period-three distant retrograde orbit, respectively. Figure 1b shows the corresponding locations of the planar stable and unstable periodic QSOs in the panel (a), and stable and unstable manifolds associated with the planar unstable periodic QSO on the Poincaré section at $y=0$, $v_y>0$ superimposed on regular islands and chaotic sea. As noted in earlier works (Villac 2008; Scott and Spencer 2010; Capdevila et al. 2014), invariant manifolds emanating from a planar unstable periodic QSO form a boundary of the stability region. This significant role of the planar unstable periodic QSO and the associated invariant manifolds may suggest extensions of them to higher-dimensional systems.

Fig. 1

a Planar stable (black) and unstable (gray) periodic QSOs, which are sometimes called a distant retrograde orbit and a period-three distant retrograde orbit, respectively, in the Sun-Jupiter rotating frame (SJrf). b Corresponding locations of the periodic QSOs (triangles of the same colors as in a), and stable (blue) and unstable (red) manifolds emanating from the planar unstable periodic QSO superimposed on regular islands and chaotic sea (black dots) on the Poincaré section at $y=0$, $v_y>0$

QSOs in higher-dimensional systems such as spatial or non-autonomous models have attracted interests and require further investigation. Robin and Markellos (1980), Lara et al. (2007), Vaquero and Howell (2014) revealed families of spatial periodic QSOs directly bifurcated from a planar stable periodic QSO. Lam and Whiffen (2005), Ming and Shijie (2009), Bezrouk and Parker (2017) found spatial, long-term stable, quasi-periodic QSOs via grid searches in some parts of the phase space. Russell (2006) globally searched for periodic orbits including spatial QSOs via a grid search and a differential correction scheme. Lara et al. (2007), Villac (2008) applied the method of fast Lyapunov indicator to identify stability regions of quasi-periodic QSOs. Cabral (2011), Canalias et al. (2017) developed a semi-analytical approach to design spatial, long-term stable, quasi-periodic QSOs. Baresi (2017), Scheeres et al. (2017), Oshima and Yanao (2017) generated quasi-periodic invariant tori around a planar stable periodic QSO.

In this paper, we pay special attention to unstable families of spatial periodic QSOs in the Earth–Moon and Mars–Phobos CR3BPs. Our motivation stems from the significant role of unstable periodic QSOs and associated invariant manifolds mentioned above. We perform bifurcation analyses and present orbital characteristics of bifurcated families and show spatial periodic QSOs of weak instabilities in each system. Based on the obtained families of spatial unstable periodic QSOs, we explore three applications: The first application is concerned with a ballistic landing concept on the surface of Phobos via unstable manifolds emanating from spatial weakly unstable periodic QSOs. The second application identifies stability regions of spatial, long-term stable, quasi-periodic QSOs based on phase-space structures of invariant manifolds emanating from spatial unstable periodic QSOs, which can be regarded as an extension of the stability region in the planar problem in Fig. 1b to the spatial problem. The third application develops a method of designing nearly ballistic, two-impulse transfers from a low Earth orbit to a spatial, long-term stable, quasi-periodic QSO around the Moon in the bicircular restricted four-body problem.

The remainder of this paper is organized as follows. Section 2 introduces mathematical models. Section 3 summarizes a method of bifurcation analyses. Section 4 presents the results of bifurcation analyses and orbital characteristics of each family of spatial periodic QSOs. Section 5 explores three applications of spatial unstable periodic QSOs to spacecraft trajectories.

2 Mathematical models

2.1 Circular restricted three-body problem (CR3BP)

The CR3BP is concerned with the motion of a massless particle, $P_3$, under the gravitational influences of two massive bodies, $P_1$, $P_2$ of masses $m_1$, $m_2$ ($m_1 > m_2$), respectively. The model assumes that $P_1$ and $P_2$ revolve in circular orbits around their barycenter. The equations of motion in the $P_1$–$P_2$ rotating frame are (Szebehely 1967)

$$\begin{aligned} \begin{aligned} \ddot{x}-2{\dot{y}}=-\,{\bar{U}}_{3x}, \\ \ddot{y}+2{\dot{x}}=-\,{\bar{U}}_{3y}, \\ \ddot{z}=-\,{\bar{U}}_{3z}, \\ \end{aligned} \end{aligned}$$

(1)

where

$$\begin{aligned} {\bar{U}}_3(x, y, z) :=-\frac{1}{2}(x^2+y^2)-\frac{1-\mu }{\sqrt{{(x+\mu )}^2+y^2+z^2}}-\frac{\mu }{\sqrt{{(x-1+\mu )}^2+y^2+z^2}}, \nonumber \\ \end{aligned}$$

(2)

and the lower alphabetic subscripts on the right-hand sides in Eq. (1) denote the partial differentiations with respect to the subscripts, and $\mu :=m_2 / (m_1+m_2)$ is the mass parameter.

Equation (1) admits an energy integral of motion

$$\begin{aligned} E = \frac{1}{2}({{\dot{x}}}^2+{{\dot{y}}}^2+{{\dot{z}}}^2)+{\bar{U}}_3, \end{aligned}$$

(3)

and we also conventionally use the Jacobi energy $C :=-\,2E$.

2.2 Bicircular restricted four-body problem (BCR4BP)

The BCR4BP (Simó et al. 1995; Koon et al. 2011) is concerned with the motion of a massless particle, $P_3$, under the gravitational influences of three massive bodies, $P_0$, $P_1$, $P_2$ of masses $m_0$, $m_1$, $m_2$ ($m_0> m_1 > m_2$), respectively. The model assumes that $P_1$ and $P_2$ revolve in circular orbits around their barycenter, and $P_0$ revolves in a circular orbit around the $P_1$–$P_2$ barycenter in the same orbital plane as $P_1$ and $P_2$. In this paper, $P_0$ is the Sun, $P_1$ is the Earth, and $P_2$ is the Moon. The equations of motion in the $P_1$-$P_2$ rotating frame are

$$\begin{aligned} \begin{aligned} \ddot{x}-2{\dot{y}}=-{\bar{U}}_{4x}, \\ \ddot{y}+2{\dot{x}}=-{\bar{U}}_{4y}, \\ \ddot{z}=-{\bar{U}}_{4z}, \\ \end{aligned} \end{aligned}$$

(4)

where

$$\begin{aligned} {\bar{U}}_4(x, y, z, t):= & {} {\bar{U}}_3 - \dfrac{m_s}{\sqrt{(x - a_s \cos {\theta _s})^2 + (y - a_s \sin {\theta _s})^2 + z^2}} \nonumber \\&+ \dfrac{m_s}{a_s^2} (x \cos {\theta _s} + y \sin {\theta _s}), \end{aligned}$$

(5)

and t is time, $m_s$ is the mass of the Sun, $a_s$ is the distance from the Earth–Moon barycenter to the Sun, and the phase angle of the Sun is $\theta _s(t) :=\theta _{s0} + \omega _s t$ where $\theta _{s0}$ is the phase angle at $t=0$; $\omega _s$ is the relative angular velocity of the Sun.

Tables 1 and 2 summarize the physical constants used in this paper. We integrate Eq. (1) or (4) by a variable step Runge–Kutta algorithm of orders 7 and 8 with absolute and relative tolerances of $10^{-12}$. In the remainder, EMrf, MPrf, and SErf abbreviate Earth–Moon, Mars–Phobos, and Sun–Earth rotating frames, respectively.

Table 1 Physical constants in the Earth–Moon CR3BP and the Earth–Moon–Sun BCR4BP (Topputo 2013)

Table 2 Physical constants in the Mars–Phobos CR3BP

3 Bifurcation analysis

The following subsections summarize the procedure of the bifurcation analysis implemented in this study. We confirmed that the method can successfully reproduce the known bifurcated families of libration point orbits in the literature (Doedel et al. 2003; Grebow 2006).

3.1 Continuation

We use the pseudo-arclength continuation scheme (Keller 1977; Doedel et al. 2003) to continue families of periodic orbits. Figure 2 shows a schematic comparison between a parameter continuation and the pseudo-arclength continuation in terms of converged results at the $(i+1)$th step. The parameter continuation scheme, which continuously changes one parameter (energy in the figure for example), may converge into a different family from the original one at a bifurcation as shown in Fig. 2a, or may fail to converge when a fold exists as shown in Fig. 2b. On the other hand, the pseudo-arclength continuation, which continuously changes all the parameters $\varvec{u}$ necessary to define a periodic orbit, can robustly continue along a targeted family against a bifurcation and a fold by taking an initial guess in the tangential direction $\varvec{u}^{i'}$ of the family and then converging perpendicularly.

Fig. 2

A schematic figure comparing converged results of a parameter continuation (red) and a pseudo-arclength continuation (green) in the cases of a a bifurcation and b a fold. The black curves represent families of periodic orbits, the solid arrows show initial guesses, and the dashed arrows represent convergence processes

In order to perform continuation more robustly, we adopt the multiple shooting scheme (Keller 1968). Therefore, the parameters necessary to define a periodic orbit at the ith continuation step are

$$\begin{aligned} \varvec{u}^{i} :=(\varvec{x}^{i}_{j}, T^{i}, \lambda ^{i}), ~~ j=1,\ldots ,N. \end{aligned}$$

(6)

In the remainder of this paper, we omit the superscript when obvious. In this parameterization, $\varvec{x}_j ~ (1\le j \le N)$ is the state at the jth node, N is the total number of nodes, and nodes are equally separated with respect to time. T is the period of an orbit and $\lambda$ is an unfolding parameter to vary the Jacobi energy (Giancotti et al. 2014), both of which are explicitly added to the equations of motion (Doedel et al. 2003) of the CR3BP in Eq. (1) as

$$\begin{aligned} \mathrm{d}x / \mathrm{d}\tau= & {} T v_x + \lambda \partial E / \partial x,\nonumber \\ \mathrm{d}y / \mathrm{d}\tau= & {} T v_y + \lambda \partial E / \partial y, \nonumber \\ \mathrm{d}z / \mathrm{d}\tau= & {} T v_z + \lambda \partial E / \partial z, \nonumber \\ \mathrm{d}v_x / \mathrm{d}\tau= & {} T(2v_y - {\bar{U}}_{3x}) + \lambda \partial E / \partial v_x, \nonumber \\ \mathrm{d}v_y / \mathrm{d}\tau= & {} T(-2v_x - {\bar{U}}_{3y}) + \lambda \partial E / \partial v_y,\nonumber \\ \mathrm{d}v_z / \mathrm{d}\tau= & {} T(- {\bar{U}}_{3z}) + \lambda \partial E / \partial v_z, \end{aligned}$$

(7)

where $\tau :=t/T$ is a scaled time. Note that $\lambda \ne 0$ makes the system nonconservative and prohibits the existence of periodic orbits in the vicinity of the original orbit. Therefore, $\lambda$ must be zero upon the convergence of each continuation step (Muñoz-Almaraz et al. 2003).

We use the MATLAB^®’s fmincon function to solve Eq. (7) under the following constraints by setting a tolerance of $10^{-10}$ for constraint violations in each convergence process:

$$\begin{aligned} \varvec{\zeta }_j:= & {} \varvec{\varphi }(\varvec{x}_j, t_j, t_{j+1}) - \varvec{x}_{j+1}=0, \end{aligned}$$

(8)

$$\begin{aligned} \varvec{\varPsi }:= & {} \varvec{x}_{1} - \varvec{x}_{N}=0, \end{aligned}$$

(9)

$$\begin{aligned} \varvec{\varGamma }:= & {} (\varvec{u}^{i+1} - \varvec{u}^{i}) \cdot \varvec{u}^{i'} - \varDelta s = 0, \end{aligned}$$

(10)

$$\begin{aligned} \varvec{\varTheta }:= & {} (\varvec{x}^{i+1}_{1} - \varvec{x}^{i}_{1}) \cdot \frac{\mathrm{d}\varvec{x}^{i}_{1}}{\mathrm{d}\tau } = 0, \end{aligned}$$

(11)

where $\varvec{\zeta }_j$ is the continuity condition in terms of states (position and velocity) at each node, and $\varvec{\varphi }(\varvec{x}_j, t_j, t_{j+1})$ represents the integration of the state $\varvec{x}_j$ at the jth node from the time $t_j$ to $t_{j+1}$. $\varvec{\varPsi }$ represents the periodicity condition that the states of the first and the final nodes match. $\varvec{\varGamma }$ is the pseudo-arclength condition that the converged direction $\varvec{u}^{i+1}-(\varvec{u}^{i} + \varvec{u}^{i'} \varDelta s)$ is perpendicular to the initial guess $\varvec{u}^{i'} \varDelta s$, where $\varvec{u}^{i'}$ is the unit vector tangentially taken to the path of solutions at $\varvec{u}^{i}$ (Doedel et al. 2003) with the prescribed continuation step $\varDelta s$. $\varvec{\varTheta }$ is the phase condition (Giancotti et al. 2014) to uniquely determine the states of nodes by fixing the phase of the first node.

3.2 Detection of bifurcation points

The monodromy matrix of a periodic orbit $M :=\mathrm{d}\varvec{\varphi }(\varvec{x}, T) / \mathrm{d}\varvec{x}$ has one trivial pair of eigenvalues $D=1$ in the CR3BP (Koon et al. 2011). The emergence of a nontrivial pair of eigenvalues $D=1$ is a signal of a bifurcation into a periodic orbit with the same period as the original family, and that of $D=-1$ indicates a period-doubling bifurcation (Lara et al. 2007; Nagata et al. 2015). We focus on these fundamental bifurcations, while other bifurcations associated with higher-order resonances, such as those investigated in Robin and Markellos (1980), Lara et al. (2007), are out of scope of this paper.

Figure 3 shows the change in real and imaginary parts of six eigenvalues of the monodromy matrix in terms of the Jacobi energy C as a result of continuation of a planar unstable periodic QSO in the Earth–Moon CR3BP. We start continuation from the orbit with the largest Jacobi energy in the figure. The figure indicates that there are seven bifurcation points #1-#7 detected by nontrivial pairs of unity eigenvalues.

Fig. 3

The change in real (red) and imaginary (blue) parts of six eigenvalues D of the monodromy matrix in terms of the Jacobi energy C as a result of continuation of a planar unstable periodic QSO in the Earth–Moon CR3BP. Seven bifurcation points #1-#7 detected by nontrivial pairs of unity eigenvalues are indicated

3.3 Branch switching

At each bifurcation point, we perturb a periodic orbit in the direction of an eigenvector associated with nontrivial unity eigenvalues and converge the perturbed orbit to a bifurcated family by using the multiple shooting scheme. As shown in Fig. 4a, we perturb not only a single point on a periodic orbit, but also multiple points, which correspond to nodes in the multiple shooting scheme, to robustly switch from the original family to a bifurcated one.

Figure 4b shows an example result of branch switching from the bifurcation point #6 in Fig. 3 to a spatial unstable periodic QSO family and subsequent continuation, where the out-of-plane amplitude gradually increases from the planar unstable periodic QSO. Note that Fig. 4b displays several spatial unstable periodic QSOs in the same family.

Fig. 4

a An example of an initial guess for a bifurcated family at the bifurcation point #6 in Fig. 3 perturbed at multiple points (red) in the direction of eigenvectors associated with nontrivial unity eigenvalues of the monodromy matrix. b A family of spatial unstable periodic QSOs computed by branch switching from the bifurcation point #6 in Fig. 3 and subsequent continuation

4 Families of spatial periodic quasi-satellite orbits

This section presents families of spatial periodic QSOs in the Earth–Moon and Mars-Phobos CR3BPs.

4.1 Bifurcation analysis of QSOs in Earth–Moon system

Figure 5 shows the bifurcation diagram of periodic QSOs in the Earth–Moon CR3BP, where families are represented in terms of the Jacobi energy C, the perilune altitude, and the out-of-plane amplitude $A_z$. The color denotes the maximum absolute value of eigenvalues of the monodromy matrix, which indicates the strength of instability. Planar stable and unstable QSOs correspond to the two curves with $A_z=0$ labeled as planar stable and planar unstable, respectively, in Fig. 5, and the seven bifurcation points of the planar unstable family shown in Fig. 3 are indicated. Among the seven bifurcation points, #1 and #4 correspond to bifurcations to the planar stable family.

Fig. 5

Bifurcation diagram of periodic QSOs in the Earth–Moon CR3BP. Families are represented in terms of the Jacobi energy C, the perilune altitude, and the out-of-plane amplitude $A_z$. The color denotes the maximum absolute value of eigenvalues of the monodromy matrix, which indicates the strength of instability. The seven bifurcation points of the planar unstable family shown in Fig. 3 are indicated

We obtained one spatial family from the planar stable family labeled as SQSO in Fig. 5, and five spatial families at the bifurcation points #2, #3, #5, #6, and #7 from the planar unstable one. (We call them the first generation bifurcated families because they directly bifurcate from the planar families.) Figure 5 includes additional nine bifurcated families from the spatial unstable families, which are highly complicated, unstable, and long-period orbits, and are not investigated in this paper. In the computation, we focus on the range $2<C<4$, which is considered to be wide enough, and stop continuation outside the range.

The following subsections show orbital characteristics of the first generation bifurcated families in the Earth–Moon system. We use the notation EM-UQSO-#N for the name of a family bifurcated from a bifurcation point with Nth largest Jacobi energy of a planar unstable periodic QSO.

4.1.1 EM-SQSO

Figure 6a shows the values of Jacobi energy C, the period T, and the perilune altitude of the family EM-SQSO. This family is always linearly stable, being far from the Moon, and exists in the range of relatively small C. Figure 6b shows a sample orbit of this family and the symmetric counterpart with respect to the x-y plane propagated after inverting the signs of z and $v_z$ at the initial condition.

Fig. 6

a The Jacobi energy C, the period T, and the perilune altitude, and b a sample orbit (blue) of EM-SQSO and the symmetric counterpart with respect to the x-y plane (red) propagated after inverting the signs of z and $v_z$ at the initial condition. The sample orbit shown in b corresponds to the red diamond in a

4.1.2 EM-UQSO-#2

Figure 7a shows the values of Jacobi energy C, the period T, and the perilune altitude of the family EM-UQSO-#2. This family emerges from a period-doubling bifurcation. The instability of EM-UQSO-#2 is always weak and the orbit becomes linearly stable at the minimum C where further continuation was impossible in our computation. Figure 7b shows a sample orbit of this family, and there is no symmetric counterpart of this family with respect to the x-y plane.

Fig. 7

a The Jacobi energy C, the period T, and the perilune altitude and b a sample orbit of EM-UQSO-#2. The sample orbit shown in b corresponds to the red diamond in a

4.1.3 EM-UQSO-#3

Figure 8a shows the Jacobi energy C, the period T, and the perilune altitude of the family EM-UQSO-#3. This family emerges from a period-doubling bifurcation. The instability of EM-UQSO-#3 is weak for relatively large C. Figure 8b shows a sample orbit of this family, and there is no symmetric counterpart of this family with respect to the x-y plane.

Fig. 8

a The Jacobi energy C, the period T, and the perilune altitude and b a sample orbit of EM-UQSO-#3. The sample orbit shown in b corresponds to the red diamond in a

4.1.4 EM-UQSO-#5

Figure 9a shows the Jacobi energy C, the period T, and the perilune altitude of the family EM-UQSO-#5, which indicates the existence of a weak instability region. Figure 9b shows a sample orbit of this family and the symmetric counterpart with respect to the x-y plane propagated after inverting the signs of z and $v_z$ at the initial condition.

Fig. 9

a The Jacobi energy C, the period T, and the perilune altitude, and b a sample orbit (blue) of EM-UQSO-#5 and the symmetric counterpart with respect to the x-y plane (red) propagated after inverting the signs of z and $v_z$ at the initial condition. The sample orbit shown in b corresponds to the red diamond in a

4.1.5 EM-UQSO-#6

Figure 10a shows the Jacobi energy C, the period T, and the perilune altitude of the family EM-UQSO-#6. This family is highly unstable for the wide range of parameters. Figure 10b shows a sample orbit of this family and the symmetric counterpart with respect to the x-y plane propagated after inverting the signs of z and $v_z$ at the initial condition.

Fig. 10

a The Jacobi energy C, the period T, and the perilune altitude, and b a sample orbit (blue) of EM-UQSO-#6 and the symmetric counterpart with respect to the x-y plane (red) propagated after inverting the signs of z and $v_z$ at the initial condition. The sample orbit shown in b corresponds to the red diamond in a

4.1.6 EM-UQSO-#7

Figure 11a shows the Jacobi energy C, the period T, and the perilune altitude of the family EM-UQSO-#7. This family emerges from a period-doubling bifurcation. This family is always highly unstable and complicated. Figure 11b shows a sample orbit of this family, and there is no symmetric counterpart of this family with respect to the x-y plane.

Fig. 11

a The Jacobi energy C, the period T, and the perilune altitude and b a sample orbit of EM-UQSO-#7. The sample orbit shown in b corresponds to the red diamond in a

4.2 Bifurcation analysis of QSOs in Mars–Phobos system

We also explore spatial families of QSOs in the Mars–Phobos CR3BP. We use “MP” instead of “EM” for the notation of families. Since MP-SQSO is always far from Phobos and similar to EM-SQSO (see Sect. 4.1.1), we omit to report it. As in the Earth–Moon system, bifurcations to the planar stable family occur at the bifurcation points #1 and #4. In our computation, families corresponding to EM-UQSO-#6 and EM-UQSO-#7 were not found in the Mars–Phobos system. We note that it is difficult to clearly see families in a bifurcation diagram in the Mars–Phobos system because they are localized in the parameter space. Therefore, we separately plot the values of parameters of each family of spatial unstable periodic QSOs in Figs. 12a, 13a, and 14a in the following subsections.

4.2.1 MP-UQSO-#2

Figure 12a shows the Jacobi energy C, the period T, and the periapsis altitude, and (b) shows a sample orbit of the family MP-UQSO-#2. There is no symmetric counterpart of this family with respect to the x-y plane. This family emerges from a period-doubling bifurcation. This family is an analogue of EM-UQSO-#2, sharing similar properties such as the weak instability and the linear stability at the minimum C.

Fig. 12

a The Jacobi energy C, the period T, and the periapsis altitude and b a sample orbit of MP-UQSO-#2. The sample orbit shown in b corresponds to the red diamond in a

4.2.2 MP-UQSO-#3

Figure 13a shows the Jacobi energy C, the period T, and the periapsis altitude, and (b) shows a sample orbit of the family MP-UQSO-#3. There is no symmetric counterpart of this family with respect to the x-y plane. This family emerges from a period-doubling bifurcation. This family is an analogue of EM-UQSO-#3 given the similarities between Figs. 13a and 8a.

Fig. 13

a The Jacobi energy C, the period T, and the periapsis altitude and b a sample orbit of MP-UQSO-#3. The sample orbit shown in b corresponds to the red diamond in a

4.2.3 MP-UQSO-#5

Figure 14a shows the Jacobi energy C, the period T, and the periapsis altitude, and (b) shows a sample orbit of the family MP-UQSO-#5 and the symmetric counterpart with respect to the x-y plane propagated after inverting the signs of z and $v_z$ at the initial condition. Figure 14a only displays orbits of periapsis altitudes higher than $-10$ km, where the negative sign indicates that the orbit is under the surface of Phobos. Note that this family is always very near or under the surface of Phobos at its periapsis. This family is an analogue of EM-UQSO-#5 given the similarities between Figs. 14a and 9a.

Fig. 14

a The Jacobi energy C, the period T, and the periapsis altitude, and b a sample orbit (blue) of MP-UQSO-#5 and the symmetric counterpart with respect to the x-y plane (red) propagated after inverting the signs of z and $v_z$ at the initial condition. The sample orbit shown in b corresponds to the red diamond in a

4.3 Relations to the solutions in the literature

This section discusses relations of the obtained families in Sects. 4.1 and 4.2 to the known solutions in the literature. Vaquero and Howell (2014) found the family EM-SQSO in the CR3BP and Voyatzis and Antoniadou (2018) identified it in the elliptic and general three-body problems. Robin and Markellos (1980), Lara et al. (2007) revealed spatial families directly bifurcated from resonant planar stable periodic QSOs, which are different from the families in this paper because our families bifurcate from the planar unstable family. Russell (2006) globally searched for periodic orbits in the Jupiter-Europa CR3BP by combining a grid search and a differential correction scheme. Though the system was different, the global nature of the search had made it possible to find spatial periodic QSOs corresponding to the families computed in this paper, except for orbits that exhibit the symmetry with respect to the x-z plane but does not exhibit the symmetry with respect to the x-axis due to the limitation of the search space as noted in Russell (2006). The families EM-SQSO and EM-UQSO-#6 of the present study are classified into this exception because the values of y, z, and $v_x$ do not become zero simultaneously. Therefore, EM-UQSO-#6 might be a new family found in the present paper.

5 Applications of spatial unstable periodic QSOs

This section presents three applications of the spatial unstable periodic QSOs obtained by the bifurcation analyses in Sect. 4. The first part is concerned with a ballistic landing concept on the surface of Phobos via unstable manifolds emanating from spatial unstable periodic QSOs. The second part identifies stability regions of spatial, long-term stable, quasi-periodic QSOs based on phase-space structures of invariant manifolds emanating from spatial unstable periodic QSOs. The third part proposes a method of designing nearly ballistic, two-impulse transfer from a low Earth orbit to a spatial, long-term stable, quasi-periodic QSO around the Moon.

5.1 Ballistic landing on Phobos

Wallace et al. (2012) investigated a ballistic landing/takeoff option on/from the surface of Phobos via invariant manifolds emanating from halo orbits around Lagrange points in the Mars-Phobos system. However, they found out that stationkeeping on an unstable halo orbit far from the Earth is difficult because of the requirement of very frequent stationkeeping maneuvers. Therefore, they proposed transfers between a halo orbit and a long-term stable QSO before and after landing and takeoff.

Instead of using halo orbits which have strong instabilities, this study proposes the use of the spatial unstable periodic QSOs obtained by the bifurcation analyses in Sect. 4 and highlights the difference in characteristics between the families. Since the instability of MP-UQSO-#2 and a part of MP-UQSO-#3 is much weaker than that of halo orbits, and they are sufficiently close to the surface of Phobos (but not too close as in MP-UQSO-#5 avoiding the danger of crashing), unstable manifolds emanating from these spatial weakly unstable periodic QSOs could be useful to ballistically land on the surface of Phobos. Note that stable manifolds can be similarly used for ballistic takeoff from the surface of Phobos.

Figure 15 shows the Jacobi energy C, the periapsis altitude, and the out-of-plane amplitude $A_z$ of (a) MP-UQSO-#2 and (b) a part of MP-UQSO-#3 for relatively weak instabilities. The values of the out-of-plane amplitude in Fig. 15 indicate that MP-UQSO-#2 could be more favorable for exploring near-equatorial regions, whereas MP-UQSO-#3 could be advantageous for exploring polar regions. Note that Fig. 15 does not assure that invariant manifolds emanating from the QSOs can reach the surface of Phobos, and the reachability is investigated in the following numerical computations. We preliminarily investigate a concept of ballistic landing on Phobos via unstable manifolds of MP-UQSO-#2 and MP-UQSO-#3 by assuming Phobos as a sphere of 11 km radius and the point-mass gravity field. Note that a more accurate model should be considered for realistic mission analyses.

Fig. 15

The Jacobi energy C, the periapsis altitude, and the out-of-plane amplitude $A_z$ of a MP-UQSO-#2 and b a part of MP-UQSO-#3 of relatively weak instabilities

In the case of MP-UQSO-#2, Fig. 16a shows the values of transfer time from the orbit shown in Fig. 12b to the surface of Phobos and $\varDelta v$ necessary to escape the periodic QSO, which corresponds to the perturbation given to the direction of the unstable eigenvector of the monodromy matrix. We give perturbation with the magnitude $5 \times 10^{-5}$ in dimensionless units only to the velocity components of the normalized unstable eigenvector in the computation of unstable manifolds, which are sometimes called pseudo-unstable manifolds (Davis et al. 2013). Note that Fig. 16a does not include unstable manifolds not reaching the surface of Phobos, many of which escape from the vicinity of Phobos. The color indicates the magnitude of velocity at the surface of Phobos. Transfer time and necessary $\varDelta v$ are small and the landing velocity could be feasible given that the planned landing velocity of OMOTENASHI, the CubeSat lunar landing mission, is around 20 m/s (Hernando-Ayuso et al. 2017). Figure 16b shows the landing trajectory of the largest magnitude of the out-of-plane component |z| at the landing location among the results in Fig. 16a, which however results in the near-equatorial region.

Fig. 16

a Transfer time from the orbit (MP-UQSO-#2) in Fig. 12b to the surface of Phobos and $\varDelta v$ to escape the periodic QSO, colored according to the magnitude of the velocity at the surface. b The landing trajectory (red) of the largest magnitude of the out-of-plane component |z| at the landing location among the results in a, where the black thick curve represents the periodic QSO and the triangle represents the landing location. The diamond in a corresponds to the trajectory in b

Figure 17 shows the results of computing unstable manifolds emanating from the family MP-UQSO-#3 shown in Fig. 13b. The values of transfer time, $\varDelta v$ to escape the periodic QSO, and the landing velocity are similar to those in Fig. 16a. On the other hand, the trajectory lands on the polar region of Phobos. Therefore, the results indicate that the family MP-UQSO-#2 is more favorable for observing and landing on near-equatorial regions, whereas the family MP-UQSO-#3 is advantageous for the exploration of polar regions.

Fig. 17

a Transfer time from the orbit (MP-UQSO-#3) in Fig. 13b to the surface of Phobos and $\varDelta v$ to escape the periodic QSO, colored according to the magnitude of the velocity at the surface. b The landing trajectory (red) of the largest magnitude of the out-of-plane component |z| at the landing location among the results in a, where the black thick curve represents the periodic QSO and the triangle represents the landing location. The diamond in a corresponds to the trajectory in b

5.2 Spatial, long-term stable, quasi-periodic QSOs

This section explores the relationship between phase-space structures of invariant manifolds emanating from spatial unstable periodic QSOs and stability regions of spatial, long-term stable, quasi-periodic QSOs.

5.2.1 Earth–Moon system

Figure 18 shows crossing points of stable and unstable manifolds emanating from the family EM-UQSO-#2 with $C=2.9$ on (a) x-$v_x$ and (b) z-$v_z$ planes of the Poincaré section at $y=0$, $v_y>0$. We set eight initial values (i–viii) on the x-$v_x$ plane as shown in Fig. 18a and locate initial values on grids on the z-$v_z$ plane around the invariant manifolds with $C=2.9$. We propagate the initial conditions and visualize escape time from the vicinity of the Moon (time until reaching $x=0$) in Fig. 19, where the number of each panel (i–viii) corresponds to the number of each initial value on the x-$v_x$ plane in Fig. 18a.

Fig. 18

Crossing points of stable (blue) and unstable (red) manifolds emanating from EM-UQSO-#2 with $C=2.9$ on a x-$v_x$ and b z-$v_z$ planes of the Poincaré section at $y=0$, $v_y>0$. Eight initial values (crosses) on the x-$v_x$ plane for the subsequent propagation are indicated

Figure 19 indicates that stability regions lie around invariant manifolds emanating from the spatial unstable periodic QSO. According to earlier works on libration point orbits by Gómez et al. (2004), Ren and Shan (2012), Anderson et al. (2017), invariant manifolds emanating from a set of unstable periodic QSOs and unstable quasi-periodic QSOs could identify the stability boundary more accurately. Though the computation of unstable quasi-periodic QSOs around the spatial unstable periodic QSOs is out of scope of this paper, our result indicates that invariant manifolds emanating from the spatial unstable periodic QSO could aid the search for spatial, long-term stable, quasi-periodic QSOs.

Fig. 19

Escape time from the vicinity of the Moon resulting from the propagation of initial values on grids on the z-$v_z$ plane. Initial values of x and $v_x$ for each panel (i–viii) are those indicated in each label (i–viii) in Fig. 18a. The upper bound of the color bar corresponds to the maximum propagation time (approximately 6 years), which includes trajectories not escaping within this time. The stable and unstable manifolds are shown in black

Figure 20 shows an example of spatial long-term stable quasi-periodic QSOs computed by propagating the initial condition on the Poincaré section at $y=0$, $v_y>0$, $x=0.75$, $v_x=0$, $z=0.02$, $v_z=0.04$ with $C=2.9$, for approximately 6 years. The initial values of x and $v_x$ are those used in Fig. 19(ii). This kind of QSOs may be useful for observing and exploring the Moon for a long period, and capturing asteroids around the Moon for a long period in ARRM-like missions (Strange et al. 2013).

Fig. 20

A spatial long-term stable quasi-periodic QSO computed by propagating the initial condition on the Poincaré section at $y=0$, $v_y>0$, $x=0.75$, $v_x=0$, $z=0.02$, $v_z=0.04$ with $C=2.9$, for approximately 6 years

Figure 21 shows the Poincaré section of approximately 119-year propagation of the spatial long-term stable quasi-periodic QSO in Fig. 20, superimposed on the stable and unstable manifolds of EM-UQSO-#2 in Fig. 18. We thus confirm that the corresponding trajectory does not escape from the vicinity of the Moon for a long time.

Fig. 21

Poincaré section (gray) of approximately 119-year propagation of the spatial long-term stable quasi-periodic QSO in Fig. 20, superimposed on the stable (blue) and unstable (red) manifolds of EM-UQSO-#2 in Fig. 18 on a x-$v_x$ and b z-$v_z$ planes of the Poincaré section at $y=0$, $v_y>0$

5.2.2 Mars–Phobos system

We also investigate the relationship between the stability regions of spatial, long-term stable, quasi-periodic QSOs and invariant manifolds emanating from the family MP-UQSO-#3 in the Mars–Phobos CR3BP. Figure 22 shows the crossing points of stable and unstable manifolds emanating from the family MP-UQSO-#3 with $C=2.999989$ on (a) x-$v_x$ and (b) z-$v_z$ planes of the Poincaré section at $y=0$, $v_y>0$. Note that the stable and unstable manifolds almost completely overlap.

Fig. 22

Crossing points of stable (blue) and unstable (red) manifolds emanating from MP-UQSO-#3 with $C=2.999989$ on a x-$v_x$ and b z-$v_z$ planes of the Poincaré section at $y=0$, $v_y>0$. Eight initial values (crosses) on the x-$v_x$ plane for the subsequent propagation are indicated in a. The stable and unstable manifolds almost completely overlap in this figure

We set eight initial values (i–viii) on the x-$v_x$ plane as shown in Fig. 22a and distribute initial values on grids on the z-$v_z$ plane around the invariant manifolds with $C=2.999989$. We propagate the initial conditions and visualize escape time from the vicinity of Phobos (time until reaching $x=0.9$) in Fig. 23, where the number of each panel (i–viii) corresponds to the number of each initial value on the x-$v_x$ plane in Fig. 22a. Similarly to Fig. 19, Fig. 23 indicates the existence of stability regions around invariant manifolds emanating from the spatial unstable periodic QSO.

Fig. 23

Escape time from the vicinity of Phobos resulting from the propagation of initial values on grids on the z-$v_z$ plane. Initial values of x and $v_x$ for each panel (i–viii) correspond to those on the x-$v_x$ plane with the same label in Fig. 22a. The upper bound of the color bar corresponds to the maximum propagation time (approximately 25 days), which includes trajectories not escaping within this time. The stable and unstable manifolds are shown in black

Figure 24 shows an example of spatial long-term stable quasi-periodic QSOs computed by propagating the initial condition on the Poincaré section at $y=0$, $v_y>0$, $x=0.99694$, $v_x=0$, $z=-\,0.0016$, $v_z=-\,0.0004$ with $C=2.999989$, for approximately 25 days. The initial values of x and $v_x$ are those used in Fig. 23(ii). This kind of QSOs may be useful for observing and exploring the high-latitude regions of Phobos in MMX-like missions (Kawakatsu et al. 2017).

Fig. 24

A spatial long-term stable quasi-periodic QSO computed by propagating the initial condition on the Poincaré section at $y=0$, $v_y>0$, $x=0.99694$, $v_x=0$, $z=-0.0016$, $v_z=-0.0004$ with $C=2.999989$, for approximately 25 days

Figure 25 shows the Poincaré section of approximately 1.4-year propagation of the spatial long-term stable quasi-periodic QSO in Fig. 24, superimposed on the stable and unstable manifolds of MP-UQSO-#3 in Fig. 22. We confirm that the corresponding trajectory does not escape from the vicinity of Phobos.

Fig. 25

Poincaré section (gray) of approximately 1.4-year propagation of the spatial long-term stable quasi-periodic QSO in Fig. 24, superimposed on the stable (blue) and unstable (red) manifolds of MP-UQSO-#3 in Fig. 22 on a x-$v_x$ and b z-$v_z$ planes of the Poincaré section at $y=0$, $v_y>0$. The stable and unstable manifolds almost completely overlap in this figure

5.3 Design of transfers from low Earth orbits to quasi-periodic QSOs around the Moon

Modern space missions (Lo et al. 1998; Folta et al. 2012) have been utilizing instabilities of dynamics around collinear Lagrange points to reduce insertion maneuvers into libration point orbits. However, stationkeeping maneuvers are necessary to stay around the orbits against the instabilities. Stable orbits usually require substantial insertion maneuvers as shown in Capdevila et al. (2014), Welch et al. (2015) for the cases of stable QSOs, whereas it is possible to ballistically transfer into long-term stable, quasi-periodic orbits by exploiting chaotic tangles of invariant manifolds (Scott and Spencer 2010; Oshima and Yanao 2015). Recently, Parker et al. (2015) developed a method of designing ballistic transfers from low Earth orbits (LEOs) to long-term stable, quasi-periodic QSOs in a high-fidelity ephemeris model. They perturbed x- and z-components of velocity of a reference planar stable periodic QSO (distant retrograde orbit) and found desired transfers such that forward propagation stays around the Moon and backward propagation reaches LEOs. However, it is still difficult to efficiently guess sensitive forward-capture and backward-escape conditions in the high-dimensional phase space. Additionally, it could be also difficult to find long-term stable, quasi-periodic QSOs with relatively large out-of-plane motions by searching only the vicinity of a planar stable periodic QSO.

This study proposes a method of designing nearly ballistic, two-impulse transfers from LEOs to spatial, long-term stable, quasi-periodic QSOs around the Moon in the bicircular restricted four-body problem (BCR4BP). Since our second application in Sect. 5.2 indicates that stability regions of spatial quasi-periodic QSOs exist around invariant manifolds of spatial unstable periodic QSOs, we firstly generate initial guesses of desired transfers as stable manifolds emanating from a spatial unstable periodic QSO. We then extract stable manifolds that can reach the vicinity of the Earth in backward propagation and can jump from the periodic QSO into long-term stable orbits with small $\varDelta v$, i.e., insertion maneuver, in forward propagation. We finally optimize them to minimize total $\varDelta v$, which are the sum of a departure maneuver $\varDelta v_i$ at a LEO and an insertion maneuver $\varDelta v_f$ into a quasi-periodic QSO. The following subsections explain each process of the method in detail and present computational results.

5.3.1 Problem statement

We compute two-impulse transfers from an initial circular LEO of the altitude $h_i=167$ km to a spatial, long-term stable, quasi-periodic QSO around the Moon in the BCR4BP. The first impulse of magnitude $\varDelta v_i$ at initial time $t_i$ injects the spacecraft into a transfer trajectory, and the second impulse of magnitude $\varDelta v_f$ at final time $t_f$ inserts it into a quasi-periodic QSO. We set $\varDelta v_i$ tangential to the local velocity of the initial circular orbit. Therefore,

$$\begin{aligned} \varDelta v_i= & {} \sqrt{({v_x}_i - y_i)^2 + ({v_y}_i + x_i + \mu )^2 + {{v_z}_i}^2} - \sqrt{\dfrac{1-\mu }{r_i}}, \end{aligned}$$

(12)

$$\begin{aligned} \varDelta v_f= & {} \sqrt{({v_x}_f - {v_x}_{QPi})^2 + ({v_y}_f - {v_y}_{QPi})^2 + ({v_z}_f - {v_z}_{QPi})^2}, \end{aligned}$$

(13)

where the subscripts i and f represent initial and final values of a transfer trajectory, respectively, the subscript QPi represents initial values of a quasi-periodic QSO, and $r_i$ is the non-dimensional initial distance from the center of the Earth.

In this formulation, the cost of transfer is $\varDelta v :=\varDelta v_i+\varDelta v_f$ and the transfer time is $t_f-t_i$, with the boundary conditions

$$\begin{aligned} \varvec{\psi _i}:= & {} \begin{bmatrix} (x_i+\mu )^2 + {y_i}^2 + {z_i}^2 - {r_i}^2 \\ (x_i+\mu ) ({v_x}_i - y_i) + y_i ({v_y}_i + x_i + \mu ) + z_i {v_z}_i \\ \end{bmatrix}=\varvec{0}, \end{aligned}$$

(14)

$$\begin{aligned} \varvec{\psi _f}:= & {} \begin{bmatrix} x_f - x_{QPi} \\ y_f - y_{QPi} \\ z_f - z_{QPi} \\ \end{bmatrix}=\varvec{0}, \end{aligned}$$

(15)

and an inequality condition

$$\begin{aligned} \varGamma _f :=\varDelta v_f - \varDelta {v_f}_{ub} < 0, \end{aligned}$$

(16)

where $\varDelta {v_f}_{ub}$ is the prescribed upper bound of the magnitude of $\varDelta v_f$, which is set to 2 m/s in this computation.

Therefore, the optimization problem for this two-impulse transfer is to minimize the cost $\varDelta v$ under the boundary conditions $\varvec{\psi _i}=\varvec{0}$ and $\varvec{\psi _f}=\varvec{0}$, and the inequality condition $\varGamma _f<0$.

5.3.2 Generation of initial guesses

As an example, we choose spatial, weakly unstable, periodic QSOs of $C=2.9$ and $A_z=17,414$ km of EM-UQSO-#2, $C=2.8$ and $A_z=138,328$ km of EM-UQSO-#3, and $C=2.7$ and $A_z=46,235$ km of EM-UQSO-#5, from the large set of the bifurcated solutions in Fig. 5. We parameterize stable manifolds of these periodic QSOs by two parameters: the phase along a periodic orbit, the minimum of which is zero and the maximum of which is the period of the periodic orbit, and the phase angle of the Sun $\theta _s$ at the time when stable manifolds are on the periodic orbit. On a periodic orbit, we give small $\varDelta v$ to initial states of stable manifolds that can reach the vicinity of the Earth in backward propagation, and propagate them forward in time. Both forward and backward propagations are done in the BCR4BP including solar perturbation. Initial guesses for the subsequent optimization are those that can stay around the Moon for sufficiently long time.

We present examples of searching for initial guesses as stable manifolds emanating from the periodic QSOs of EM-UQSO-#2 (Fig. 26), EM-UQSO-#3 (Fig. 27), and EM-UQSO-#5 (Fig. 28), respectively. Figures 26a, 27a, and 28a show transfer times and the Jacobi energies at perigees of stable manifolds emanating from the periodic QSOs of EM-UQSO-#2, EM-UQSO-#3, and EM-UQSO-#5, respectively, that can reach 36,000 km altitude from the Earth, colored according to the perigee altitude. In this computation, the maximum propagation time of the stable manifolds is 200 days. The red diamonds represent good initial guesses that can reach 1,000 km altitude from the Earth surface and can stay around the Moon for longer than 1 year after executing $\varDelta v=$1 m/s on the periodic orbit. Note that the transfer times span a wide range, from approximately 100 days to 200 days, due to the sensitive dependence on initial conditions in the BCR4BP. Figures 26b, 27b, and 28b visualize escape time from the vicinity of the Moon for one of the good initial guesses (red diamonds) in Figs. 26a, 27a, and 28a, respectively, parameterized by azimuth ($\theta$) and elevation ($\psi$) angles of $\varDelta v$, where

$$\begin{aligned} \begin{aligned} \varDelta v_x&=|\varDelta v| \cos {\psi } \cos {\theta }, \\ \varDelta v_y&=|\varDelta v| \cos {\psi } \sin {\theta }, \\ \varDelta v_z&=|\varDelta v| \sin {\psi }, \\ 0&\le \theta \le 2\pi , \\ -0.5\pi&\le \psi \le 0.5\pi . \end{aligned} \end{aligned}$$

(17)

The figures indicate that numerous transfers from LEOs to quasi-periodic QSOs are possible with a small insertion maneuver $\varDelta v=$1 m/s. We also note that invariant manifolds of spatial unstable periodic QSOs are still good indicators of spatial, long-term stable, quasi-periodic QSOs even in the BCR4BP perturbed by the Sun. We target long-term stable orbits achieved by $\varDelta v=$1 m/s in Figs. 26b, 27b, and 28b (yellow) in the subsequent optimization as final destinations of transfer trajectories. As mentioned in Sect. 5.2.1, direct identifications of high-dimensional dynamical objects in the BCR4BP may help deeper understandings of the generating mechanism of the stability regions in future works.

Fig. 26

a Transfer times and the Jacobi energies at perigees ($C_{\mathrm{perigee}}$) of stable manifolds emanating from the periodic QSO of EM-UQSO-#2 that can reach 36,000 km altitude from the Earth surface, colored according to the perigee altitude. The red diamonds represent good initial guesses that can reach 1,000 km altitude from the Earth surface and can stay around the Moon for longer than 1 year after executing $\varDelta v=$1 m/s on the periodic QSO. b Escape time from the vicinity of the Moon for one of the good initial guesses of transfer time of 186.58 days and $C_{\mathrm{perigee}}=0.88$ in a in terms of azimuth ($\theta$) and elevation ($\psi$) angles of $\varDelta v$

Fig. 27

a Transfer times and the Jacobi energies at perigees ($C_{\mathrm{perigee}}$) of stable manifolds emanating from the periodic QSO of EM-UQSO-#3 that can reach 36,000 km altitude from the Earth surface, colored according to the perigee altitude. The red diamonds represent good initial guesses that can reach 1,000 km altitude from the Earth surface and can stay around the Moon for longer than 1 year after executing $\varDelta v=$1 m/s on the periodic QSO. b Escape time from the vicinity of the Moon for one of the good initial guesses of transfer time of 177.82 days and $C_{\mathrm{perigee}}=0.72$ in a in terms of azimuth ($\theta$) and elevation ($\psi$) angles of $\varDelta v$

Fig. 28

a Transfer times and the Jacobi energies at perigees ($C_{\mathrm{perigee}}$) of stable manifolds emanating from the periodic QSO of EM-UQSO-#5 that can reach 36,000 km altitude from the Earth surface, colored according to the perigee altitude. The red diamonds represent good initial guesses that can reach 1,000 km altitude from the Earth surface and can stay around the Moon for longer than 1 year after executing $\varDelta v=$1 m/s on the periodic QSO. b Escape time from the vicinity of the Moon for one of the good initial guesses of transfer time of 162.81 days and $C_{\mathrm{perigee}}=2.32$ in a in terms of azimuth ($\theta$) and elevation ($\psi$) angles of $\varDelta v$

5.3.3 Optimization

We optimize the good initial guesses found in Sect. 5.3.2 by a direct transcription and multiple shooting procedure (Enright and Conway 1992), which translates an optimal control problem into a nonlinear programming (NLP) problem. The method divides a trajectory into $N-1$ segments by N nodes of equal time intervals, and introduces NLP variables

$$\begin{aligned} \varvec{y} :=\{\varvec{x}_j, t_1\},\qquad j = 1, \ldots , N, \end{aligned}$$

(18)

where $t_1$ is the departure time on a LEO, and $\varvec{x}_j :=(x_j, y_j, z_j, {v_x}_j, {v_y}_j, {v_z}_j)$ is the state on a jth node at time $t_j=t_1+\frac{j-1}{N-1}(t_N-t_1)$, and $t_N$ is the arrival time at the quasi-periodic QSO, which is fixed to the initial time of the quasi-periodic QSO.

The objective function is

$$\begin{aligned} J(\varvec{y}) :=\varDelta v_1 + \varDelta v_N, \end{aligned}$$

(19)

where Eqs. (12) and (13) are evaluated on the initial and final nodes for $\varDelta v_1$ and $\varDelta v_N$, respectively.

The boundary conditions are

$$\begin{aligned} \varvec{\psi _1}=\varvec{0}, \quad \varvec{\psi _N}=\varvec{0}, \end{aligned}$$

(20)

where Eqs. (14) and (15) are evaluated on the initial and final nodes for $\varvec{\psi _1}$ and $\varvec{\psi _N}$, respectively.

The state $\varvec{x}_j$ on a jth node ($1 \le j \le N-1$) is propagated in the BCR4BP given by Eq. (4) for the fixed time span $[t_j, t_{j+1}]$. For the continuity of a trajectory, the defect

$$\begin{aligned} \varvec{\zeta }_j :=\varvec{\varphi }(\varvec{x}_j, t_j, t_{j+1}) - \varvec{x}_{j+1}, \qquad j = 1, \ldots , N-1 \end{aligned}$$

(21)

must vanish.

Table 3 An example of optimal solutions originated from EM-UQSO-#2

Table 4 An example of optimal solutions originated from EM-UQSO-#3

Table 5 An example of optimal solutions originated from EM-UQSO-#5

The inequality condition in terms of $\varDelta v_f$ is

$$\begin{aligned} \varGamma _N<0, \end{aligned}$$

(22)

where Eq. (16) is evaluated on the final node for $\varGamma _N$.

To avoid impacts on the surfaces of the Earth or the Moon of radius $R_e$ or $R_m$ (see Table 1), we impose inequality conditions on each node

$$\begin{aligned} \varvec{\eta }_j :=\begin{bmatrix} {R_e}^2 - \{(x_j+\mu )^2 + {y_j}^2 + {z_j}^2)\} \\ {R_m}^2 - \{(x_j -1+\mu )^2 + {y_j}^2 + {z_j}^2)\} \\ \end{bmatrix}<\varvec{0}, \qquad j = 1, \ldots , N. \end{aligned}$$

(23)

For the sake of consistency in terms of time, an inequality condition $\chi :=t_1 - t_N < 0$ is also respected.

As a summary, the NLP problem is formulated to minimize the scalar objective function $J(\varvec{y})$, subject to the nonlinear $(6N-1)$-dimensional equality constraints $\varvec{c(y)}$ and $(2N+2)$-dimensional inequality constraints $\varvec{g(y)}$, which are the functions of the $(6N+1)$-dimensional NLP variables $\varvec{y}$, as

$$\begin{aligned} \mathrm {Minimize} \quad {J({\varvec{{y}}})} \qquad \mathrm {subject ~ to} \nonumber \\ \varvec{c(y)} :=\{\varvec{\zeta }_j, \varvec{\psi }_1, \varvec{\psi }_N\}=\varvec{0},\qquad j = 1, \ldots , N-1, \nonumber \\ \varvec{g(y)} :=\{\varGamma _N, \varvec{\eta }_j, \chi \}<\varvec{0},\qquad j = 1, \ldots , N. \end{aligned}$$

(24)

Fig. 29

The trajectory in a x-y-z space, b x-y-z space amplifying around the Moon, c x-y plane, and d the change in the Jacobi energy in the Earth–Moon rotating frame, and the trajectory in e x-y-z space and f x-y plane in the Sun–Earth rotating frame of the optimal solution in Table 3 originated from EM-UQSO-#2. The black trajectory represents a transfer trajectory, the gray trajectory is a quasi-periodic QSO propagated for 6 years after the insertion maneuver $\varDelta v_f$, and the dashed circle represents the lunar orbit. Perigee and perilune altitudes of the transfer trajectory (above (a)) and the quasi-periodic QSO (above (b)) are shown

Fig. 30

The trajectory in a x-y-z space, b x-y-z space amplifying around the Moon, c x-y plane, and d the change in the Jacobi energy in the Earth–Moon rotating frame, and the trajectory in e x-y-z space and f x-y plane in the Sun–Earth rotating frame of the optimal solution in Table 4 originated from EM-UQSO-#3. The black trajectory represents a transfer trajectory, the gray trajectory is a quasi-periodic QSO propagated for 6 years after the insertion maneuver $\varDelta v_f$, and the dashed circle represents the lunar orbit. Perigee and perilune altitudes of the transfer trajectory (above (a)) and the quasi-periodic QSO (above (b)) are shown

Fig. 31

The trajectory in a x-y-z space, b x-y-z space amplifying around the Moon, c x-y plane, and d the change in the Jacobi energy in the Earth–Moon rotating frame, and the trajectory in e x-y-z space and f x-y plane in the Sun–Earth rotating frame of the optimal solution in Table 5 originated from EM-UQSO-#5. The black trajectory represents a transfer trajectory, the gray trajectory is a quasi-periodic QSO propagated for 6 years after the insertion maneuver $\varDelta v_f$, and the dashed circle represents the lunar orbit. Perigee and perilune altitudes of the transfer trajectory (above a) and the quasi-periodic QSO (above b) are shown

5.3.4 Result

We solve the NLP problem (24) using the MATLAB^®’s constrained optimization solver fmincon by setting tolerances of $10^{-10}$ for constraint violations and for function evaluations. Tables 3, 4, and 5 summarize examples of optimal solutions originated from the stable manifolds of EM-UQSO-#2, EM-UQSO-#3, and EM-UQSO-#5, respectively. Due to the small insertion maneuvers ($\varDelta v_f$), total $\varDelta v$s of the obtained optimal solutions are much smaller than those of low-energy transfers from LEOs to low lunar orbits in Topputo (2013), Oshima et al. (2019). Total $\varDelta v$s are comparable to those of ballistic transfers from LEOs to unstable halo orbits in Parker and Anderson (2014) (see Table 3-20 in the reference), but stationkeeping efforts of the arrival orbits against instabilities could be smaller in our solutions due to the long-term stability of the quasi-periodic QSOs. Transfer times are longer than many of those in the same reference.

Figure 29 shows the trajectory in the Earth–Moon rotating frame ((a), (b), (c)), (d) the change in the Jacobi energy, and the trajectory in the Sun–Earth rotating frame ((e) and (f)) of the optimal solution in Table 3 originated from EM-UQSO-#2. The black trajectory represents a transfer trajectory and the gray trajectory is a quasi-periodic QSO propagated for 6 years after the insertion maneuver $\varDelta v_f$. The relatively small out-of-plane amplitude of the quasi-periodic QSO results in the nearly planar transfer. The change in the Jacobi energy indicates the significance of solar perturbation for the transfer phase. Since the apogee of the transfer trajectory is located in the second quadrant in the Earth-centered Sun–Earth rotating frame (see the panel (f)), the solar tidal force accelerates the trajectory and pumps up the perigee altitude (Yamakawa 1993).

Figure 30 shows the trajectory in the Earth–Moon rotating frame ((a), (b), (c)), (d) the change in the Jacobi energy, and the trajectory in the Sun–Earth rotating frame ((e) and (f)) of the optimal solution in Table 4 originated from EM-UQSO-#3. The transfer trajectory has larger out-of-plane motion due to larger out-of-plane amplitude of the quasi-periodic QSO than that in Fig. 29. The high perilune altitude of the transfer trajectory avoids the risk of critical operations for low-altitude lunar flyby as noted in Parker et al. (2015). According to the panels (d), (e), and (f), the transfer trajectory exploits solar perturbation similarly to Fig. 29.

Figure 31 shows the trajectory in the Earth–Moon rotating frame ((a), (b), (c)), (d) the change in the Jacobi energy, and the trajectory in the Sun–Earth rotating frame ((e) and (f)) of the optimal solution in Table 5 originated from EM-UQSO-#5. The out-of-plane amplitudes of the transfer trajectory and the quasi-periodic QSO are similar to those in Fig. 30. The transfer trajectory exploits not only solar perturbation, but also high- and low-altitude lunar flybys, which reduce the departure maneuver $\varDelta v_i$. The large amplitudes in x and y directions of the quasi-periodic QSO could be useful for explorations of triangular Lagrange points $L_4$ and $L_5$.

6 Conclusion

The first part of this paper computed families of spatial periodic QSOs via bifurcation analyses in the Earth–Moon and Mars-Phobos circular restricted three-body problems. In each problem, we showed spatial weakly unstable periodic QSOs of the families UQSO-#2, UQSO-#3, and UQSO-#5. The second part of this paper presented three applications of the spatial unstable periodic QSOs. The first application was concerned with a ballistic landing concept on the surface of Phobos via unstable manifolds emanating from periodic QSOs of MP-UQSO-#2 and MP-UQSO-#3. Our preliminary results indicated that MP-UQSO-#2 is favorable for landing on near-equatorial regions, whereas MP-UQSO-#3 is advantageous for the exploration of polar regions. The second application identified stability regions of spatial, long-term stable, quasi-periodic QSOs based on phase-space structures of invariant manifolds emanating from spatial unstable periodic QSOs. Such long-term stable orbits could be useful for observations and explorations of high-latitude regions of celestial bodies. The third application designed nearly ballistic, two-impulse transfers from a low Earth orbit to a spatial, long-term stable, quasi-periodic QSO around the Moon in the bicircular restricted four-body problem including solar perturbation. The method exploited the result of the second application to find initial guesses of small insertion $\varDelta v$ into quasi-periodic QSOs, based on stable manifolds emanating from spatial unstable periodic QSOs. We presented examples of nearly ballistic, two-impulse optimal transfers from low Earth orbits to different families of spatial, long-term stable, quasi-periodic QSOs, which could be useful in the missions, such as CubeSat missions, where $\varDelta v$ is of much higher priority than transfer time.