Long-term behavior of the spatial orbit near the Moon in restricted three-body problem

Abstract

In the Earth-Moon-spacecraft circular restricted three-body problem (CRTBP), the evaluation of the orbits near the Moon can distinctly reflect the complexity of the dynamical system. In this paper, the long-term behavior of the spatial orbit near the Moon is investigated in the CRTBP. The Poincare section, where the section points are defined as the lunar apsides, is an effective tool. The distribution of the long-term capture solutions and the orbital elements of the section points display the long-term behavior of the spatial lunar orbits from the qualitative and quantitative angles, respectively. As two kinds of important long-term lunar orbits, the quasi-periodic and periodic orbits are also investigated. Using the continuation scheme, we obtain the spatial lunar periodic orbit families. The characters of the periodic orbit families are discussed in detail. In addition, some applications of the spatial lunar periodic orbits are given. The method to investigate the long-term behavior of the spatial lunar orbits we present is simple and direct. We can easily locate the lunar quasi-periodic orbit and obtain the spatial periodic orbit family.

1 Introduction

In the Earth-Moon-spacecraft circular restricted three-body problem (CRTBP), the dynamics in the vicinity of the Moon is a hot topic in the astrodynamics. In the vicinity of the Moon, the lunar gravity is dominant, but the effect of the larger primary body, Earth, is also significant. Therefore, compared with the other regions in the restricted problem, the dynamical circumstance near the Moon is more complicated, which leads to many complex phenomena, such as the gravitational capture, chaotic orbits and the quasi-periodic and periodic orbits near the libration points. Many scholars have investigated this problem and tried to discover the mechanism behind the complex phenomena. Besides, many studies focused on the applications of the dynamics to the space missions, which are markedly different from the results of the traditional two-body model.

To investigate the dynamics in the vicinity of the smaller primary, many methods have been developed. Poincare section is an effective tool to study the long-term behavior of the orbits. By the means of chaos dynamics and the Poincare section, Astakhov et al. (2004) proposed a new dynamical model to capture irregular moons which identifies chaos as the essential feature responsible for initial temporary gravitational trapping within a planet’s Hill sphere. Periapsis Poincare maps were first defined and introduced by Villac and Scheeres (2003) to relate a trajectory escaping the vicinity of smaller primary back to its previous periapsis in the planar Hill problem. Davis and Howell (2012) investigated the evolution of various orbits over both short- and long-term propagations in the vicinity of smaller primary using the periapsis Poincare maps. Haapala and Howell (2014) presented a method to represent the information in higher-dimensional Poincare maps using a planar visualization. In addition, the manifolds associated with the $L_{1}$ and $L_{2}$ periodic orbits have also been used to predict the long-term behavior of the orbits in the CRTBP (Gómez et al. 2001). Jorba and Masdemont (1999) devised an effective computation of the center manifold of the collinear points to give an overall qualitative description of the dynamics of these libration orbits. Koon et al. (2000) discussed and showed the existence of the heteroclinic connections between periodic orbits using the complex manifolds structure.

Due to the complex dynamical circumstance in the vicinity of the Moon, the lunar orbits are not the conics of the two-body model any more. The evaluation of orbits near the smaller primary can reflect the dynamical complexity of the CRTBP distinctly. Hénon (1969, 1970, 1973, 2003, 2005) published a series of articles to investigate the existence and stability of the periodic and non-periodic orbits about the smaller primary in the Hill restricted three-body problem (HRTBP). Russell (2006) performed a grid search to find planar and spatial periodic orbits in the restricted three-body problem using the dimensioned parameters associated with the Jupiter-Europa system. Besides, the periodic and quasi-periodic orbits near the $L_{1}$ and $L_{2}$ are also investigated by many scholars, such as the Halo orbits (Farquhar 1966), the Lyapunov orbits (Szebehely 1967), the Lissajous orbits (Howell and Pernicka 1988), the vertical orbits and the butterfly orbits (Grebow et al. 2006). These orbits not only enrich the types of the orbits in the CRTBP, but also are valuable for the space missions, for example, the Genesis Discovery mission (Howell et al. 1997), the Solar and Heliospheric Observatory (SOHO) mission (Simo et al. 1986) and the Lunar Communications and Navigation Systems (LCNS) group (Grebow et al. 2006).

The investigation of the long-term behavior of the trajectories near the smaller primary can provide a better understanding of the complex dynamical circumstance. Davis and Howell (2010) investigated the long-term evolution of planar trajectories in the vicinity of smaller primary in detail using the periapsis Poincare maps. After that, Davis and Howell (2012) discussed the out-of-plane long-term trajectory evolution using the same method. However, the distribution and the orbital characters of the long-term capture solutions near the smaller primary were not investigated systematically in the previous literatures (to the best of the authors’ knowledge). To solve this problem, in this paper, taking the Earth-Moon system as the example, we will investigate the long-term behavior of the spatial orbits in the vicinity of the Moon under the CRTBP and discuss their distribution and orbital characters in detail. As mentioned before, Poincare section is an effective tool to study the long-term behavior of the orbits. Therefore, firstly, we introduce how to define and obtain the Poincare section using the numerical calculation. Then, via the distributions of the long-term lunar capture solutions and the orbital elements of the section points, the long-term behaviors of the spatial lunar orbits with different parameters are discussed. In addition, the spatial quasi-periodic and periodic lunar orbits will also be investigated in this paper. The section points in the long-term lunar capture solutions can be applied to locate the quasi-periodic orbits. Then, using the differential correction and continuation scheme, we can obtain the spatial lunar periodic orbits and periodic orbit families, respectively. After that, the characters of the periodic orbit families, such as the stability, inclination and period, are analyzed in detail. At last, some applications of the spatial lunar periodic orbits are given.

According to the above analysis, this paper can be divided into 5 parts. The CRTBP is introduced as the basic theory of this paper in Sect. 2. The Poincare section and long-term lunar capture will be presented in Sect. 3 to investigate the long-term behavior of the spatial orbits near the Moon. In Sect. 4, the spatial quasi-periodic and periodic orbits will be obtained and analyzed. Section 5 is the applications of the spatial lunar periodic orbits. In Sect. 6, we will give our conclusions of this paper.

2 Circular restricted three-body problem

In this paper, we will use the circular restricted three-body problem (CRTBP), which describes the motion of a massless particle in the gravitational force field created by two primary bodies in circular motion around their barycenter of mass. In this paper, the two primary bodies are the Earth and the Moon, denoted by $m_{1}$ and $m_{2}$, respectively. The mass of the spacecraft is supposed to be negligible.

In the rotating centrobaric reference system and with the usual units of longitude, mass and time, the Earth is placed at ($- \mu, 0, 0$) and the Moon is placed at ($1 - \mu, 0, 0$), where the mass ratio $\mu = m_{2} / (m_{1} + m_{2}) = 0.01215$. The equation of motion of the spacecraft in the dimensionless Earth-Moon rotating frame can be expressed as (Szebehely 1967)

$$\begin{aligned}& \begin{aligned} &\ddot{x} - 2\dot{y} = \bar{U}_{x} \\ &\ddot{y} + 2\dot{x} = \bar{U}_{y} \\ &\ddot{z} = \bar{U}_{z}, \end{aligned} \end{aligned}$$

(1)

where

$$ \bar{U}(x,y,z) = \frac{1}{2}\bigl(x^{2} + y^{2}\bigr) + \frac{1 - \mu}{r_{1}} + \frac{\mu}{r_{2}} + \frac{1}{2}\mu (1 - \mu ) $$

(2)

and

$$ \begin{aligned} &r_{1}^{2} = (x + \mu )^{2} + y^{2} + z^{2} \\ &r_{2}^{2} = (x - 1 + \mu )^{2} + y^{2} + z^{2}. \end{aligned} $$

(3)

The equations of the motion of the spacecraft are Hamiltonian and independent of the time. The system has the well-known Jacobi constant (or Jacobi integral)

$$ C(x,y,z,\dot{x},\dot{y},\dot{z}) = - \bigl(\dot{x}^{2} + \dot{y}^{2} + \dot{z}^{2}\bigr) + 2\bar{U}(x,y,z). $$

(4)

For the given Jacobi constant $\bar{C}$, the region

$$M = \biggl\{ (x,y,z)\big|\bar{U}(x,y,z) \ge \frac{1}{2}\bar{C}\biggr\} $$

is the region of possible motion for spacecraft, known historically as the Hill’s region. The boundary of the $M$ is known as the zero velocity surfaces (ZVSs). Based on Eq. (4), the spacecraft can only move on the side of this surface for which the kinetic energy is positive. The other side of the surface, where the kinetic energy is negative, is defined as the forbidden region. The Hill region near the Moon and the Earth are defined as the lunar region and the Earth region, respectively (Koon et al. 2006).

These occur when the spacecraft moves in a circular orbit with the same frequency as the primaries, so that it is stationary in the rotating frame. Numerical calculation sheds light on that there are five equilibrium points or libration points. We label these points $L_{i}$, $i = 1, \ldots, 5$. Since $L_{1}$, $L_{2}$ and $L_{3}$ lie along the $x$-axis, they are called the collinear points. $L_{4}$ and $L_{5}$ lie at the vertices of two equilateral triangles with common base extending from the Earth to the Moon, so they called the equilateral points. Let $C_{i}$ be the Jacobi energy of the spacecraft at $L_{i}$, then we can calculate the following values, $C_{1} \approx 3.20034$, $C_{2} \approx 3.18416$, $C_{3} \approx 3.02415$, and $C_{4} = C_{5} = 3$.

3 Poincare section and long-term lunar capture

In this section, we investigate the long-term behavior of spatial orbits near the Moon by the distribution of the long-term capture solutions and the orbital elements of the section points.

3.1 Poincare section

As we know, the lunar gravitation is dominant in the vicinity of the Moon, therefore we can regard the CRTBP near the Moon as a nearly-integrable system, seen as a perturbation of the two-body integrable system. According to the KAM theory, there are invariant tori in the nearly-integrable system, i.e. the KAM tori (Arnold et al. 2006). The orbits in the KAM tori are the periodic orbits or the quasi-periodic orbits around the Moon, which we call the regular orbits. The long-term behaviors of regular orbits are predictable. In the CRTBP, the spacecraft in the regular orbits can be long-term captured by the Moon. The regions outside the KAM tori are the chaotic areas, where the randomicity of the orbits are high. The orbits in the chaotic areas more easily escape from the Moon or collide with the Moon after long-term propagation. But Howell et al. (2012) found that some chaotic orbits can also remain bounded for long time period.

Based on the above discussion, the regular orbits in the KAM tori and some chaotic orbits outside the KAM tori can be retained in vicinity of the Moon in long term, which we call the long-term lunar capture orbits. In this paper, the long-term lunar capture orbits are the emphasis of our investigation. The Poincare section is a valuable tool to gain insight into the complicated dynamics in the CR3BP and study the long-term behavior of the lunar orbits.

Qi and Xu (2014) applied the Poincare section to investigate the distribution of the KAM tori near the Moon in the planar CRTBP. In this paper, we extend this method to the spatial problem to investigate the distribution of the long-term lunar capture. Given the constraint on the value of Jacobi constant $C^{*}$, the section surface is defined by

$$S\bigl(C^{*}\bigr) = \bigl\{ (x,y,z)|C(x,y,z,\dot{x},\dot{y},\dot{z}) = C^{*}, \mathbf{r}_{2} \bot \mathbf{v} \bigr\} $$

where $\mathbf{r}_{2} = (x - 1 + \mu, y,z)^{T}$ is the vector from the center of the Moon to the spacecraft and $\mathbf{v} = (\dot{x}, \dot{y},\dot{z})^{T}$ is the velocity vector of the spacecraft in the rotating frame. Therefore, the section points are the lunar apsides. The section surface is described in the 3-dimensional position phase space.

For the spatial CRTBP, the phase space is 6-dimensional. The use of the Poincare section allows us to restrict the problem to the surface of section and, hence, reduce the problem by one dimension. As mentioned earlier, there exists the Jacobi constant $C$ in the problem that allows us to reduce the problem by one additional dimension. The Poincare section is then computed at a given value of the constant $C$ and is 4-dimensional. However, the section surface defined above is described in the 3-dimensional position phase space. Apparently, this image surface cannot represent full information of the 4-dimensional Poincare section. For the section points, their spatial positions are described in the 3-dimensional position phase space. Their magnitude of the velocity can be determined by the given value of the Jacobi constant $C$. Therefore, the unknown information of the section point is the direction of the velocity in spatial. To solve this problem, Haapala and Howell (2014) explored a planar visualization method to represent the information of the four-dimensional Poincare maps. However, we do not adopt their method, because we think that 3-dimensional position phase space can enough figure the distribution of the long-term lunar capture orbits.

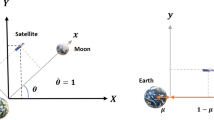
Next we introduce how to obtain the Poincare section using the numerical integration. Based on the definition of the Poincare section, the section points (or the lunar apsides) are generated by propagating initial conditions and displaying intersections of the resulting trajectories with the section surface. Therefore, firstly, we should determine the initial conditions of the numerical integration. The initial point includes the full six Cartesian states (three position coordinates and three velocity coordinates) in the Earth-Moon rotating frame. Using the experience of the classical orbital elements, we can also propose some elements to represent the position $\boldsymbol{p}$ and the velocity $\mathbf{v}$ of any section point in the Moon-centric rotating frame. For example, let the angles $i_{m}$, $\varOmega_{m}$ and $\omega_{m}$ be the inclination, the right ascension of the ascending node (RAAN) and the argument of the initial point in the Moon-centric rotating frame, respectively, the initial point (the position $\boldsymbol{p}$ and the velocity $\mathbf{v}$) can be determined by them in Fig. 1. The $x_{m}$ axis of the Moon-centric rotating frame is along the direction from the Earth to the Moon. In this figure, the position $\boldsymbol{p}$ can be obtained by the distance $r_{p}$ and the matrix $\mathbf{R}$:

$$ \mathbf{p} = \mathbf{R} \left [ \textstyle\begin{array}{c} r_{p} \\ 0 \\ 0 \end{array}\displaystyle \right ], $$

(5)

where $\mathbf{R}$ is the transition matrix from the Moon-centric apsis coordinate frame to the Moon-centric rotating frame:

$$\begin{aligned} \mathbf{R} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \cos \omega_{m}\cos \varOmega_{m} - \sin \omega_{m}\cos i_{m}\sin \varOmega_{m} & - \sin \omega_{m}\cos \varOmega_{m} - \cos \omega_{m}\cos i_{m}\sin \varOmega_{m} & \sin i_{m}\sin \varOmega_{m} \\ \cos \omega_{m}\sin \varOmega_{m} + \sin \omega_{m}\cos i_{m}\cos \varOmega_{m} & - \sin \omega_{m}\sin \varOmega_{m} + \cos \omega_{m}\cos i_{m}\cos \varOmega_{m} & - \sin i_{m}\cos \varOmega_{m} \\ \sin \omega_{m}\sin i_{m} & \cos \omega_{m}\sin i_{m} & \cos i_{m} \end{array}\displaystyle \right ]. \end{aligned}$$

Fig. 1

The initial point described by the elements in the Moon-centric rotating frame

For the given value of the Jacobi constant $C$, we can obtain the magnitude of the velocity of the initial point:

$$ v = \sqrt{ - C + 2\bar{U}(x,y,z)}. $$

(6)

where the calculation of the effective potential $\bar{U}$ needs the position coordinate of the initial point in the Earth-Moon rotating frame

$$ (x, y, z)^{T} = \mathbf{p} + (1 - \mu, 0, 0)^{T} $$

(7)

Since the section points are the lunar apsides, the velocity $\mathbf{v}$ of the section point in the Moon-centric rotating frame is given by

$$ \mathbf{v} = \mathbf{R} \left [ \textstyle\begin{array}{c} 0 \\ v \\ 0 \end{array}\displaystyle \right ], $$

(8)

where the magnitude of the velocity $v$ can be obtained from Eq. (6).

Because the velocity of the initial point in the Earth-Moon rotating frame is consistent with that in the Moon-centric rotating frame, we can obtain the full six states of the initial point by Eqs. (7) and (8). The initial point is described by four parameters: the distance $r_{p}$, the angles $i_{m}$, $\omega_{m}$ and $\varOmega_{m}$. The ranges of $i_{m}$, $\omega_{m}$ and $\varOmega_{m}$ are from $0^{\circ}$ to $180^{\circ}$, from $0^{\circ}$ to $360^{\circ}$, and from $0^{\circ}$ to $360^{\circ}$, respectively. When $0^{\circ} \le i_{m} \le 90^{\circ}$, the direction of motion of the initial point is defined as the prograde motion. When $90^{\circ} \le i_{m} \le 180^{\circ}$, the direction of motion of the initial point is defined as the retrograde motion. When $i_{m} = 90^{\circ}$, the direction of motion of the initial point can be either prograde or retrograde.

Fixed the Jacobi constant $C$ and the angles $i_{m}$ and $\varOmega_{m}$, $r_{p}$ is divided into 20 equal parts from 1838 km to 41738 km, and $\omega_{m}$ is divided into 20 equal parts from $0^{\circ}$ to $360^{\circ}$. Then, we can obtain 400 initial points. In the Earth-Moon rotating frame, these initial points are located on a series of coplanar concentric circles around the Moon and their directions of velocity are along the tangent of the circles. The corresponding trajectories can be generated by forward integration from these initial points. The integral time is 200 unit times, approximately 861 days. During the numerical integral, the orbits colliding with the Moon are regarded as the infeasible orbits and excluded (the radius of the Moon is 1738 km). The section points are the intersections of the trajectories with the section surface. Figure 2(a) shows the Poincare section in the Earth-Moon rotating frame when $C = 3.07$, $i_{m} = 120^{\circ}$ and $\varOmega_{m} = 45^{\circ}$. The long-term lunar capture solutions can be extracted from the 3-dimensional cloud of the propagated points via the following extract method.

Fig. 2

The Poincare section (a) and the long-term capture solutions (b)

Firstly, the long-term capture trajectories should retain in the vicinity of the Moon in long term. In this paper, we apply the definition of the sphere of the lunar influence proposed by Yamakawa (1992), which considersthat the radius of the sphere of the lunar influence is 100000 km. Therefore, we demand that the section points of the long-term capture trajectories should be confined to the sphere of the lunar influence during the integral time.

Besides, the relative stable and regular shape is another requirement for the long-term capture trajectory. The classical orbital elements with respect to the Moon can provide a more intuitive understanding of the shape of the orbits that remain a long-term orbiting the Moon, especially the inclination (relative to the Earth-Moon orbital plane) and the eccentricity. To make sure spacecraft captured by the Moon, we demand the osculating eccentricities of all section points of the long-term capture solution less than 1. The distribution of the osculating inclinations of the section points in the long-term capture trajectory should be stable and concentrated. Then, we demand their variation range less than $90^{\circ}$.

The extract method is based on the above requirements of distance, eccentricity and inclination of the section points. Using this extract method, we can classify the long-term lunar capture solutions in the 3-dimensional cloud of the propagated points. Figure 2(b) displays the long-term capture solutions extracted from the section points of Fig. 2(a). The colored points denote the section points in the long-term capture trajectories, and the different colors denote different long-term capture trajectories. Figure 3 shows the osculating eccentricity and inclination of the section points based on the 400 trajectories. The red points display the elements of the long-term capture trajectories. The green points display the elements of the escaping chaotic orbits. The blank trajectories are the orbits colliding with the Moon. Of particular note is that, because of the large scale of the eccentricities (from 0 to 1000) of the escaping chaotic orbits, we just show their enlarged views (from 0 to 2) in Fig. 3.

Fig. 3

Eccentricity and inclination of the section points

3.2 Long-term lunar capture

In last subsection, we introduced how to obtain the Poincare section and extract the long-term capture solutions using the numerical method. We find that the Poincare sections are influenced by three parameters in our calculation, including the Jacobi constant $C$ and the angles $i_{m}$ and $\varOmega_{m}$. In this subsection, we will discuss the influences of $C$ and $i_{m}$ in detail to investigate the long-term behavior of the spatial orbits in the vicinity of the Moon.

We still use the numerical methodology to analyze the influences of the parameters. The first one is the Jacobi constant $C$. In our numerical calculation, we obtain 400 trajectories for each case. Figure 4 shows the Poincare sections for different $C$ when $i_{m} = 30^{\circ}$ and $\varOmega_{m} = 0^{\circ}$. Since $i_{m} < 90^{\circ}$, the directions of motion of the initial points are the prograde motion. The colored points denote the section points of the long-term capture trajectories. The black points denote the section points of the escaping chaotic trajectories. When $C = 3.21$, the lunar region is completely disconnected with the Earth region. In this case, the section points can only exist in the vicinity of the Moon and there are numerous long-term capture trajectories on the section surface. When $C = 3.20$, the region around $L_{1}$ opens up, permitting the spacecraft to move between the regions around the Moon and the Earth, but $L_{2}$ is still located in the forbidden region. In this case, we find that the section points of the 400 trajectories do not flow to the Earth region through the gateway at $L_{1}$, and there are still abundant long-term capture trajectories on the section surface. When $C = 3.18416 \approx C_{2}$, the gateway at $L_{2}$ is opening. In this case, many section points flow to the Earth region through the gateway at $L_{1}$. The long-term capture trajectories disappear rapidly in the lunar region and few long-term capture solutions are retained on the image surface. When $C = 3.17$, the regions around $L_{1}$ and $L_{2}$ have opened up. The section points become more spread out and overflow through the gateways at $L_{1}$ and $L_{2}$ in abundance. Almost all of the long-term capture solutions of 400 trajectories around the Moon cease to exist.

Fig. 4

Poincare sections of the prograde motion for different $C$

The quantitative results can prove the observation about the 3-dimensional cloud of the section points. The amounts of long-term capture trajectories of Fig. 4 are illustrated in Table 1.

Table 1 Amount of long-term capture trajectories of Fig. 4

Figure 5 shows the osculating eccentricity and the inclination of the section points based on the results of Fig. 4. As mentioned before, because of the large scale of the eccentricity (from 0 to 1000) of the escaping chaotic orbits, we show their enlarged views in Fig. 5 to facilitate analysis. As we can see from the figures, when $C = 3.20$ and 3.21, all feasible orbits of 400 trajectories are long-term capture trajectories. The eccentricities are smaller than 1. The inclinations are stable and concentrated. When $C = 3.18416$, most of the feasible orbits are escaping chaotic trajectories. Their maximum eccentricities are larger than 1 and the distribution of the inclinations is chaotic. Only the long-term capture trajectories possess the regular orbital elements. Actually, before escaping from the sphere of lunar influence, many escaping chaotic orbits have revolved round the Moon for a long time. Therefore, most of the eccentricities of them are densely clustered within the region less than 1 in the figures. When $C = 3.17$, all the feasible orbits of 400 trajectories escape from the Moon. The distributions of the eccentricity and inclination are disorderly and unsystematic.

Fig. 5

Eccentricity and inclination of the section points for different $C$

Figure 6 shows the Poincare sections for different $C$ when $i_{m} = 150^{\circ}$ and $\varOmega_{m} = 0^{\circ}$. Since $i_{m} > 90^{\circ}$, the directions of motion of the initial points are the retrograde motion. When $C = 3.17$, the regions around $L_{1}$ and $L_{2}$ have opened up. However, the section points of 400 trajectories are compact and focus on the Moon rather than spread out like the prograde motion. There exist abundant long-term capture solutions around the Moon. When $C = 3.12$, the structure of the section points expands outward and few section points overflow from the lunar region. But there are still abundant long-term capture solutions in the section surface. When $C = 3.07$, the section points become more spread out. The compact structures of the long-term capture trajectories are gradually eroded. When $C = 3.02$, we find that long-term capture solutions have been destroyed heavily, especially those near the Moon. The long-term capture trajectories are sparsely distributed.

Fig. 6

Poincare sections of the retrograde motion for different $C$

The amounts of long-term capture trajectories of Fig. 6 are illustrated in Table 2. Figure 7 shows the osculating eccentricity and inclination of the section points using the results of Fig. 6. When $C = 3.17$, all feasible orbits for 400 trajectories are long-term capture trajectories. The eccentricities are smaller than 1. The inclinations are stable and concentrated. When $C = 3.12$, most of the feasible orbits for 400 trajectories are long-term capture solutions. Few escaping chaotic orbits exist. When $C = 3.07$ and 3.02, the amount of the escaping chaotic orbits increase gradually.

Fig. 7

Eccentricity and inclination of the section points for different $C$

Table 2 Amount of long-term capture trajectories of Fig. 6

Synthesizing above analysis, we find that both for the prograde motion and retrograde motion, the structures of the long-term capture solutions in the vicinity of the Moon are gradually destroyed with the decrease of the Jacobi constant $C$. This trend is not difficult to understand, because for the given $i_{m}$ and $\varOmega_{m}$, the smaller $C$ the larger velocity is, which means the spacecraft is easier to escape from the lunar region. Therefore, we conclude that in the vicinity of the Moon, the spatial orbit with smaller $C$ is more likely to escape from the lunar region after long-term propagation, both for prograde and retrograde motion. That is to say, the long-term behavior of the spatial lunar orbit with smaller $C$ is more instable and inscrutable in the vicinity of the Moon. In addition, we discover that when $C$ is small, the long-term capture trajectories can be maintained in the retrograde motion but disappear rapidly in the prograde motion. This phenomenon is similar to the result in the planar case discovered by Qi and Xu (2014). We think that it is also due to the rotation of the Earth-Moon system.

Next we discuss the influence of the angle $i_{m}$. Since the planar problem has been discussed by Davis and Howell (2010), we just analyze the out-of-plane ($0^{\circ} < i_{m} < 180^{\circ}$) problem. Figure 8 shows the Poincare sections for different $i_{m}$ (the prograde motion) when $C = 3.21$ and $\varOmega_{m} = 0^{\circ}$. As we can see from the figure, when $i_{m}$ increases from $10^{\circ}$ to $60^{\circ}$, the distribution of the section points of 400 trajectories extends along the vertical direction, but the structures of long-term capture trajectories are still compact and exist around the Moon in abundance. However, when $i_{m} = 90^{\circ}$, the section points and the long-term capture trajectories of 400 trajectories disappear heavily. Since the lunar region is isolated by the forbidden region, the section points can only exist in the lunar region. Therefore, the disappearing points belong to the trajectories impacting with the Moon. Also note that because only a finite number of initial points are considered in the numerical methodology, the number of the long-term capture trajectories displayed in the figure is less than the actual fact. Hence, in fact, there is more than one long-term capture trajectory when $i_{m} = 90^{\circ}$. But the trend of the long-term capture solutions shown in Fig. 8 is true.

Fig. 8

Poincare sections of the prograde motion for different $i_{m}$

The amounts of long-term capture trajectories of Fig. 8 are illustrated in Table 3. Figure 9 shows the osculating eccentricity and inclination of the section points based on results of Fig. 8. When $i_{m} = 10^{\circ}$, $30^{\circ}$ and $60^{\circ}$, all of the feasible orbits of 400 trajectories can achieve long-term lunar capture. The distribution of the eccentricities and inclinations are concentrated and stable. When $i_{m} = 90^{\circ}$, most of the orbits impact the Moon. Only a long-term capture trajectory exists for 400 trajectories.

Fig. 9

Eccentricity and inclination of the section points for different $i_{m}$

Table 3 Amount of long-term capture trajectories of Fig. 8

Figure 10 displays the Poincare sections for different $i_{m}$ (the retrograde motion) when $C = 3.12$ and $\varOmega_{m} = 0^{\circ}$. From the figure, abundant section points overflow from the vicinity of the Moon when $i_{m} = 90^{\circ}$. The long-term capture trajectories are all destroyed for 400 trajectories. When $i_{m}$ increases to $120^{\circ}$, a large number of section points focus on the Moon, and many long-term capture solutions exist on the section surface. When $i_{m}$ increases from $120^{\circ}$ to $170^{\circ}$, the structure of the section points is compressed along the $z$ axis. Abundant long-term capture trajectories are distributed around the Moon in more closely form.

Fig. 10

Poincare sections of the retrograde motion for different $i_{m}$

The amounts of long-term capture trajectories of Fig. 10 are illustrated in Table 4. Figure 11 shows the osculating eccentricity and inclination of the section points based on results of Fig. 10. When $i_{m} = 90^{\circ}$, all of the 400 trajectories cannot achieve long-term lunar capture. When $i_{m}$ increases from $120^{\circ}$ to $170^{\circ}$, the amount of the escaping chaotic orbits decrease dramatically. Most of the feasible orbits for 400 trajectories are the long-term capture trajectories. The distribution of the eccentricities and inclinations are stable and concentrated.

Fig. 11

Eccentricity and inclination of the section points for different $i_{m}$

Table 4 Amount of long-term capture trajectories of Fig. 10

According to the above results, we find that for the given $C$ and $\varOmega_{m}$, generally, more long-term capture trajectories exist in the vicinity of the Moon if $i_{m}$ is closer to $0^{\circ}$ or $180^{\circ}$, but the long-term capture solutions are destroyed heavily if $i_{m}$ is closer to $90^{\circ}$. Therefore, we conclude that in the vicinity of the Moon, if the orbit plane of the spacecraft is closer to the Earth-Moon orbital plane, the spatial lunar orbit is more likely to be captured and retained in the lunar region for long term period, but if the orbit plane of the spacecraft is more perpendicular to the Earth-Moon orbital plane, the spatial lunar orbits is more likely to impact the Moon or escape from the lunar region after long-term propagation.

4 Quasi-periodic and periodic orbits around the Moon

The quasi-periodic and periodic orbits are two sorts of important orbits in the study of the long-term behavior of the spatial lunar orbits. In this section, we will investigate the spatial quasi-periodic and periodic orbits.

4.1 Spatial quasi-periodic and periodic orbits

In the Sect. 3.2, we located the long-term capture solutions using the section points. As mentioned before, those long-term capture trajectories include the regular orbits (quasi-periodic and periodic orbits) and some long-term capture chaotic orbits. Because of the regular structures of the quasi-periodic orbits, we think that the orbital elements of quasi-periodic orbits possess more stable and concentrated distribution than the long-term capture chaotic orbits. Based on this fact, we can choose the quasi-periodic orbits from the long-term capture solutions. Of particular note is that, if we want to obtain the quasi-periodic orbit, the information of the point on the section surface is insufficient. The section points just represent the position of the 3-dimensional position phase, but the velocity direction is unavailable. To solve this problem, we need to store the velocity direction of the section point in the numerical integration, even though this information is not displayed on the Poincare section. Figure 12 shows the quasi-periodic orbits based on the section points and the corresponding velocity direction. The black points are the section points in the quasi-periodic orbits.

Fig. 12

Quasi-periodic orbits and corresponding section points

In the planar case, the orbits in the KAM tori are the quasi-periodic orbits, and there is a periodic orbit with the same Jacobi constant in the center of KAM tori. Therefore, the section point of the KAM torus can be regarded as the initial point. Then using the differential correction, we can obtain the section point of the periodic orbit in the center of the KAM torus. Figure 13(a) shows the section points of a KAM torus and the corresponding quasi-periodic orbit. Via the differential correction, the corresponding periodic orbit and its section points can be obtained, denoted by the blue line and the red points in the Fig. 13(b), respectively.

Fig. 13

Planar quasi-periodic orbit and corresponding periodic orbit

The example of the planar case inspires us to find the spatial periodic orbits using the differential correction and the section points. However, the complex distribution of the section points in spatial is a challenge to determine the initial point. Our solution is choosing the points of the quasi-periodic orbit where $z = 0$ and $\dot{z} > 0$ as the initial points of the differential correction. The distribution of the intersection points of the quasi-periodic orbit with the x-y plane is a regular pattern due to the regular structure of the quasi-periodic orbit in phase space. Figure 14(a) displays a prograde quasi-periodic orbit with $C = C_{2}$. As we can see, the intersection points of the quasi-periodic orbit where $z = 0$ and $\dot{z} > 0$, denoted by the black points, present a well-regulated distribution.

Fig. 14

Quasi-periodic orbit (a) and corresponding periodic orbit (b)

Using the intersection points of the quasi-periodic orbit where $z = 0$ and $\dot{z} > 0$ as the initial points, we can perform the differential correction to obtain the intersection point of the periodic orbit with the x-y plane. Then the corresponding periodic orbit can be located. The detailed numerical method is shown as follows.

• (1) The variables of the differential correction: The intersection point of the quasi-periodic orbit where $z = 0$ and $\dot{z} > 0$ is chosen as the initial point $p_{0}$, including six Cartesian states in the Earth-Moon rotating frame: $x_{0},y_{0},z_{0},\dot{x}_{0},\dot{y}_{0},\dot{z}_{0}$, where $z_{0} = 0$ and $\dot{z}_{0} > 0$. We demand the $k$-th iteration point $p_{k}$ ($k = 1,2,\ldots$) stay on the x-y plane, i.e. $z_{k} = 0$. Besides, we assume that the Jacobi constant $C$ is invariable in each iteration. Then, $\dot{z}_{k}$ can be represented by $C$ and other states: $\dot{z}_{k} = \sqrt{ - C + 2\bar{U}(x_{k},y_{k},0) - \dot{x}_{k}^{2} - \dot{y}_{k}^{2}}$. Hence, the pending states in the correction process are actually only four variables: $x,y,\dot{x},\dot{y}$. Besides, the period of the periodic orbit $T$ also need to be corrected. In summary, the reduced variables in the differential correction can be denoted by $X = (x,y,\dot{x},\dot{y},T)$.

• (2) The initial guess and the constraint: Take Fig. 14(a) for example, there exist some groups of the intersection points based on the relative distance. We choose one of them as the target set, where the arrival times of the intersection points are different. Choose one point in the target set arbitrarily as the initial guess of the states $p_{i}:x_{i},y_{i},0,\dot{x}_{i},\dot{y}_{i},\dot{z}_{i}$. The minimum time interval between the initial point and other points in the target set is designated as the initial guess of period $T_{i}$. Then we can obtain the full initial guess of the correction process: $X_{i} = (x_{i},y_{i},\dot{x}_{i},\dot{y}_{i},T_{i})$. The constraint of the differential correction is obviously to enforce the periodicity of the orbit, i.e., the orbit starting from the initial point at moment 0 can return back the initial point at the moment $T$.

• (3) Perform the differential correction process and modify the initial point step by step until the periodicity of the orbit is satisfied.

Figure 14(b) shows the periodic orbit we obtained. The eigenvalues of the monodromy matrix reflect the stability of the periodic orbit. We can calculate that there are six eigenvalues of the monodromy matrix of the periodic orbit: $\lambda_{1,2} = 0.5441 \pm 0.8390i$, $\lambda_{3} = 1.0006$, $\lambda_{4} = 1 / \lambda_{3} = 0.9994$, $\lambda_{5} = \lambda_{6} = 1$. According to the Floquet theory, if the modulus of at least one eigenvalues are larger than 1, then the periodic orbit is unstable (Koon et al. 2006). Therefore, the periodic orbit we obtained is unstable due to $\lambda_{3} > 1$. The eigenvector corresponding to $\lambda_{3}$ is the unstable direction. However, the numerical integration shows that the unstable manifold can still remain near the periodic orbit after 10 periods (the period $T$ is about 71.17 days) even though the orbit is unstable. Therefore, we need an index to quantify the degree of the stability or instability. In this paper, we adopt the stability index $\nu$ presented by Grebow et al. (2006) to evaluate the stability of the periodic orbit.

$$ \nu = \frac{1}{2}\biggl(\lambda_{\max} + \frac{1}{\lambda_{\max}} \biggr) $$

(9)

where $\lambda_{\max}$ is the maximum magnitude eigenvalue of the monodromy matrix. A stability index of one indicates a linear stable orbit, whereas stability indices with magnitude greater than one reflect instability. Of course, a larger stability index indicates a more divergent mode that departs from the vicinity of the orbit very quickly. We can compute the stability index of the periodic orbit in Fig. 14 $\nu = 1.0000001799$, very close to 1.

4.2 Spatial periodic orbit family

In the differential correction process, we assume the Jacobi constant $C$ invariable. Therefore, $C$ can be regard as the family parameter of the periodic orbit family. Based on the Jacobi constant $C$, we can employ the continuation scheme to obtain the complete periodic orbit family from a periodic orbit. The idea of the continuation scheme is shown as follows.

• (1) Assuming that a spatial periodic orbit with the Jacobi constant $\bar{C}$ has been obtained, we regard it as the initial normal orbit. The initial point is chosen as the intersection point of the initial normal orbit where $z = 0$ and $\dot{z} > 0$, and the period of the initial normal orbit is the initial guess of the period in the continuation process.

• (2) Let the Jacobi constant increases to $C = \bar{C} + \Delta C$. Using the differential correction mentioned in Sect. 4.2, we can obtain the periodic orbit with the Jacobi constant $C$.

• (3) The Jacobi constant $C$ can continue to change by $\Delta C$, then a new periodic orbit is obtained using steps (1) and (2). At last, we can obtain a family of the periodic orbits from the initial normal orbit by the change of $C$.

Note that $\Delta C$ can be either a positive value or a negative value, but the absolute value of it cannot be large in order to guarantee the convergence in the continuation scheme.

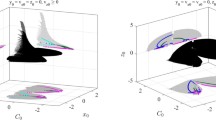
Six periodic orbits extracted from a prograde periodic orbit family are shown in Fig. 15. The Jacobi constants $C$ of the six periodic orbits from ($a$) to ($f$) are 3.20893, 3.206, 3.20, 3.18, 3.16 and 3.14, respectively. From Fig. 15, we find that with the decrease of the Jacobi constant $C$, the planar periodic orbit is gradually lifted up until it becomes the vertical orbit. The inclination of the periodic orbit increases from $0^{\circ}$ to approximately $90^{\circ}$.

Fig. 15

Six periodic orbits of a prograde periodic orbit family

Figure 16 shows six periodic orbits of a retrograde periodic orbit family. The Jacobi constants $C$ of the six periodic orbits from ($a$) to ($f$) are 3.1064, 3.11, 3.119, 3.14, 3.15 and 3.17, respectively. From the figure, we find that with the increase of the Jacobi constant $C$, the planar periodic orbit is gradually lifted up until it becomes the vertical orbit. The inclinations of the periodic orbits decrease from $180^{\circ}$ to approximately $90^{\circ}$.

Fig. 16

Six periodic orbits of a retrograde periodic orbit family

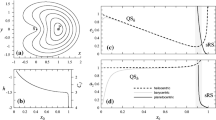
The stability indices $\nu$ of the prograde periodic orbit family with different Jacobi constants $C$ are displayed in Fig. 17(a). As we can see from the figure, when $C$ is larger than 3.18, $\nu$ remains one, so the corresponding periodic orbit is linear stable; when $C$ is smaller than 3.18, $\nu$ is larger than one and $\nu$ increases with the decrease of $C$, so the corresponding periodic orbit has smaller stability. Although some periodic orbits are unstable, we find that the stability indices $\nu$ are quite small, less than 4.

Fig. 17

$\nu$ and inclination of prograde periodic orbits with different $C$

Since the periodic orbits are obtained in the CRTBP rather than the two-body model, the inclination of the periodic orbit is time-depended. Hence, there exist a maximum and a minimum of the inclination during a period. Figure 17(b) shows the plot of the maxima and minima of the inclinations of the prograde periodic orbit family versus the Jacobi constant $C$. In this figure, the upper and the lower triangles denote the minima and maxima of the inclinations during a period, respectively. According to this figure, both of the maximum and minimum of the inclination gradually increase from $0^{\circ}$ to approximately $90^{\circ}$ with the decrease of $C$. Comparing the analysis about Fig. 17(a), we conclude that for the prograde periodic orbit family, the larger inclination the smaller stability of the periodic orbit.

The stability indices $\nu$ of the retrograde periodic orbit family with different Jacobi constants $C$ are displayed in Fig. 18(a). Different from the prograde periodic orbit family, we find that when $C$ is larger than 3.1064, $\nu$ is larger than one and $\nu$ increases with the increase of $C$, so the corresponding periodic orbit possesses the smaller stability. Besides, the stability indices $\nu$ are very small, less than 2.5. Figure 18(b) shows the plot of the maxima and minima of the inclinations of the retrograde periodic orbit family versus the Jacobi constant $C$. According to this figure, both of the maximum and minimum of the inclination of the periodic orbit gradually decrease from $180^{\circ}$ to approximately $90^{\circ}$ with the increase of $C$. Comparing the discussion of Fig. 18(a), we conclude that for the retrograde periodic orbit family, the smaller inclination the smaller stability of the periodic orbit.

Fig. 18

$\nu$ and inclination of the retrograde periodic orbits versus $C$

Synthesizing above analysis, we find that, both for the prograde and retrograde periodic orbit family, the periodic orbit is more stable if the its orbit plane is closer to the Earth-Moon orbital plane; whereas the periodic orbit has smaller stability if its orbital plane is more perpendicular to the Earth-Moon orbital plane. This quantitative conclusion is analogous to the qualitative observation about the angle $i_{m}$ in Sect. 3.2.

Figure 19 displays the plots of the period $T$ versus the Jacobi constant $C$ for the prograde and retrograde periodic orbit families. As we can see from the figures, if $C$ is smaller, $T$ is larger, both for the prograde and retrograde periodic orbit families.

Fig. 19

$T$ versus $C$ for the prograde and retrograde periodic orbit families

5 Applications of the spatial periodic orbits

In this section, we introduce some applications of the spatial periodic orbit around the Moon.

5.1 Formation-flying around the Moon

As mentioned before, the stability index $\nu$ indicates the degree of the stability of the periodic orbit. Generally, the stability index is directly correlated to the station-keeping costs and is inversely related to transfer costs (Grebow et al. 2006). Because the stability indices of the periodic orbit families we obtained in Sect. 4.2 are quite small, those periodic orbits likely have the advantage in the station-keeping costs. Therefore, those periodic orbits can be applied to the long-term lunar exploration or communication. For example, if we want to perform the all-time exploration for the lunar north and south poles, it must guarantee that at least one spacecraft is visible to each pole, i.e. its elevation with respect to the north or south poles is larger than $0^{\circ}$. As we can see from Fig. 20, when the $z$-component of the spacecraft is less than the radius of the Moon $R_{m} = 1738~\mbox{km}$, it will be invisible both for the north and south poles. Therefore, two spacecraft are not enough for the all-time mission, and the formation-flying needs at least three spacecraft.

Fig. 20

Elevations with respect to the lunar north and south poles

We choose a prograde periodic orbit with $C = 3.139$ as the orbit of the lunar formation-flying. The calculation shows that the stability index of orbit is about 3.97, very small. The inclination of the periodic is $83.55^{\circ}\sim 90.50^{\circ}$ and the period is about 26.84 days. Figure 21 displays the architecture of the formation-flying we design for the all-time lunar mission. In this architecture, three spacecraft are arranged in the periodic orbit. Figure 22 displays the elevations of three spacecraft with respect to the north and south poles in a period. In this figure, the black bold lines denote the maximum of the elevations of three spacecraft at every moment. The result shows that the range of maximum of the elevations with respect to the north pole is from $24.67^{\circ}$ to $89.83^{\circ}$. The average maximum of the elevations with respect to the north pole is $60.29^{\circ}$, denoted by the bold dash line. The range of maximum of the elevation with respect to the south pole is from $24.34^{\circ}$ to $89.70^{\circ}$. The average maximum of the elevation with respect to the south pole is $60.35^{\circ}$, denoted by the bold dash line. Therefore, in each moment, there exists at least one spacecraft visible to each pole. Besides, according to Fig. 21(c), the period orbit does not cross the Moon shadow, which can also guarantee the all-time communication with the Earth.

Fig. 21

Architecture of the formation-flying for the all-time lunar mission

Fig. 22

Elevations of three spacecraft in a period

5.2 Earth-Moon transfer

On the other hand, the small stability index $\nu$ results in more transfer costs between the Earth parking orbit and spatial periodic orbit around the Moon.

For the Earth-Moon transfer in this paper, the initial point is located in the low Earth orbit (LEO) of height 167 km, and the end point of the transfer is a perilune of the spatial periodic orbit around the Moon. Figure 23 displays the interior transfer we design in the Earth-Moon rotating frame. The target orbit of the transfer is a prograde lunar periodic orbit. The inclination is $58.38^{\circ}\sim 63.99^{\circ}$ and the period is about 25.71 days. Three tangential maneuvers are performed at the initial point, the patch point (apogee) and the end point. After the first maneuver, the spacecraft is inserted into the Earth escape orbit (the red line in Fig. 23). After the second the maneuver at the apogee, the spacecraft is inserted into the $L_{1}$ transit orbit (the blue line in Fig. 23) and flies to the Moon. After the third maneuver, the spacecraft is captured by the Moon and inserted into the spatial periodic orbit (the green line in Fig. 23). The total transfer cost $\Delta V$ required is 3847.8 m/s, including 3114.9 m/s, 701.09 m/s and 31.85 m/s at three maneuver points, successively. The time-of-flight from the initial point to the end point is approximately 43.83 days. Of particular note is that the design of the Earth-Moon transfer is not the emphasis of this paper, therefore, the transfer orbits we design are not the optimal results. As for construction of the optimal transfer trajectory, it will be our future work.

Fig. 23

Earth-Moon transfer in the rotating frame

6 Conclusions

In this paper, the long-term behavior of the spatial orbits near the Moon was investigated in the Earth-Moon-spacecraft CRTBP. Using the numerical methodology, we obtained the Poincare section, where the section points are defined as the lunar apsides. The distribution of the long-term capture solutions and the orbital elements of the section points illustrated the long-term behavior of the spatial orbits near the Moon from the qualitative and quantitative angles, respectively. We found that in the vicinity of the Moon, the long-term behavior of the spatial lunar orbit with smaller Jacobi constant $C$ is more instable and inscrutable. Besides, the spatial orbit near the Moon is more likely to retain in the vicinity of the Moon in long term if the orbit plane is closer to the Earth-Moon orbital plane, but the spatial lunar orbit is more likely to impact the Moon or escape from the lunar region after long-term propagation if the orbit plane is more perpendicular to the Earth-Moon orbital plane.

The spatial lunar quasi-periodic and periodic orbits were also investigated. The section points in the long-term capture trajectories were applied to locate the quasi-periodic orbits. Then, using the differential correction and continuation scheme, we obtained the spatial lunar periodic orbits and periodic orbit families, respectively. The characters of the periodic orbit families, such as the stability, inclination and period, were discussed in detail. The analysis showed that the stability indices $\nu$ of the periodic orbits obtained from the quasi-periodic orbits were very small, but their stabilities were influenced by their inclinations. Besides, the smaller Jacobi constant the larger period is. At last, some applications of the spatial lunar periodic orbits were given. The lunar formation-flying for the all-time lunar north and south poles exploration was designed. The Earth-Moon transfer was constructed in the CRTBP.

The method to investigate the long-term behavior of the spatial orbits near the Moon by the section points and the orbital elements we presented in this paper is simple and direct. We can easily locate the lunar quasi-periodic orbit and obtain the spatial lunar periodic orbit family.