Spatial collinear restricted four-body problem with repulsive Manev potential

Abstract

We outline some aspects of the dynamics of an infinitesimal mass under the Newtonian attraction of three point masses in a symmetric collinear relative equilibria configuration when a repulsive Manev potential ($-1/r +e/r^{2}$), $e>0$, is applied to the central mass. We investigate the relative equilibria of the infinitesimal mass and their linear stability as a function of the mass parameter $\beta$, the ratio of mass of the central body to the mass of one of two remaining bodies, and e. We also prove the nonexistence of binary collisions between the central body and the infinitesimal mass.

1 Introduction and statement of the problem

A quasi-homogeneous potential of the form $-(a/r + e/r^{2})$, where r is the distance between particles, and a, e are real constants, was considered by Newton in his work Philosophiae Naturalis Principia Mathematica (Book I, Article IX, Proposition XLIV, Theorem XIV, Corollary 2). The reason to add the term $e/r^{2}$ was the impossibility to explain the Moon’s apsidal motion within the framework of the inverse-square force law. Nevertheless, the model was abandoned in favor of the classical potential. Many years later Manev Maneff (1924) proposed a similar corrective term in order to maintain dynamical astronomy within the framework of classical mechanics and offering at the same time equally good justifications of the observed phenomena as in the relativity theory. For instance, when a and e are positive, the corrective term provides a justification of the perihelion advance of Mercury.

Our aim is to study the dynamics of a few-body celestial system considering the gravitational field of a charged, nonrotating, spherically symmetric body of mass M, also known as Reissner–Nordström metric, that is, a Manev potential with positive e. Such kinds of potentials are relevant in astronomical and astrophysical context when the big body, like a star, owns a net electric charges. See the introduction in Iorio (2012) and the references therein for more details.

We consider the motion of an infinitesimal mass P under the gravitational attraction of three point masses, $P_{0}, P_{1}, P_{2}$ called primaries, see Maranhão and Llibre (1999) for the Newtonian case. Assume that the gravitational attraction of the primary $P_{0}$ is generated by a Manev potential ($-1/r +e/r^{2}$), with parameter $e>0$, and that the gravitational attraction due to $P_{1}$ and $P_{2}$ is Newtonian ($-1/r$). We also shall assume that the primaries are in a collinear central configuration, that is, bodies $P_{1}$ and $P_{2}$ have the same mass $m_{1}=m_{2}=m$, and are located symmetrically with respect to the central body $P_{0}$, of mass $m_{0}=\beta m$, which is at the center of masses of the system. $P_{0}$ will also be called the central body, and $P_{1}$ and $P_{2}$ the peripherals, as in the Maxwell’s ring model. In an inertial reference system the peripheral bodies move in a circular orbit around $P_{0}$ with angular velocity $\omega$.

In Fakis and Kalvouridis (2013) the authors study numerically some aspects of the dynamics of a small body under the action of Maxwell-type N-body system with a spheroidal central body. They modeled the nonsphericity by a corrective term that coincide with Manev potential [our setup with two peripherals equals to the case $n=2$ in Fakis and Kalvouridis (2013)]. See also Elipe et al. (2007), Arribas et al. (2003) and Arribas et al. (2007). In Alavi and Razmi (2015), such a correction term in a Newtonian potential, with $e>0$ (that represents a repulsive centripetal force), is used in disk galaxies evolution. Also, in Mioc and Stoica (1997) the Manev-type potential is considered in the frame of a two-body problem.

When $e>0$ one effect of the repulsive term $e/r^{2}$ is the existence of equilibrium points out of the plane of motion of the primaries which increases the dynamical richness of the problem. We study analytically the existence and the linear stability of the equilibrium points of the problem. The existence of out-of-plane equilibrium points is one novelty with respect to restricted problems with Newtonian potentials. Another problem in which out-of-plane equilibrium points appear is the symmetric collinear restricted four-body problem with radiation pressure [see Arribas et al. (2016b)]. For the interested reader about problems where both gravitational and radiation forces are considered see Arribas et al. (2016a) and the references therein.

We begin taking a synodic reference frame Oxyz with origin at the central body $P_{0}$ where the Ox axis coincides with the line joining the primaries. We choose the units of distance, mass and time such that the distance between the two peripherals is one and $Gm=1$, where G is the gravitational constant. Then, the coordinates of the primaries $P_{0}, P_{1}, P_{2}$ in our synodic reference frame are, respectively, (0, 0, 0), (1 / 2, 0, 0) and $(-1/2,0,0)$.

According to Fakis and Kalvouridis (2013) and Elipe et al. (2007), the condition to keep the peripherals on their circular orbit of radius 1 / 2 and angular velocity $\omega$ is that $\omega ^2=\varDelta$, where

$$\begin{aligned} \varDelta =\varDelta (\beta , e)= 2(1+4 \beta - 16 e \beta ). \end{aligned}$$

(1)

The function $\varDelta$ has to be positive. Thus, the parameter e must satisfy the following sharp bound,

$$\begin{aligned} e < e_{0}:=\frac{1+4 \beta }{16 \beta }, \end{aligned}$$

(2)

for each fixed $\beta >0$. We will say that a value of $e>0$ is admissible if it follows inequality (2) for a fixed value of $\beta$.

The equations of motion of an infinitesimal mass P in a rotating coordinate system Oxyz, in which the peripherals are fixed in the Ox axis, are given by the following differential equations

$$\begin{aligned} \begin{aligned} \ddot{x}- 2 \dot{y}&=\varOmega _{x},\\ \ddot{y}+ 2 \dot{x}&=\varOmega _{y},\\ \ddot{z}&=\varOmega _{z}, \end{aligned} \end{aligned}$$

(3)

where the function $\varOmega$ is defined by

$$\begin{aligned} \varOmega = \varOmega (x, y, z)= \frac{1}{2}(x^{2}+y^{2})+ \frac{1}{\varDelta }\left[ \beta \left( \frac{1}{r_{0}}- \frac{e}{r_{0}^{2}}\right) + \frac{1}{r_{1}}+ \frac{1}{r_{2}}\right] , \end{aligned}$$

(4)

with

$$\begin{aligned} \begin{array}{ll} r_{0} = \sqrt{x^{2}+y^{2}+z^{2}}, &{}\quad \begin{array}{l} r_{1} = \sqrt{(x-1/2)^2+y^{2}+z^{2}}, \\ r_{2} = \sqrt{(x+1/2)^2+y^{2}+z^{2}}. \end{array} \end{array} \end{aligned}$$

(5)

See Fakis and Kalvouridis (2013) and Elipe et al. (2007) for details.

The phase space associated with system (3) (as a first-order differential system) is given by

$$\begin{aligned} \mathcal {M}= \Big \{ (x,y,z,\dot{x},\dot{y},\dot{z}) \in \left( \mathbb {R}^3 \setminus \{(0,0,0), (1/2 , 0,0), (-1/2, 0, 0)\}\right) \times \mathbb {R}^3\Big \}. \end{aligned}$$

Our goal in this paper is to study important aspects of the dynamics of the spatial restricted four-body problem with repulsive Manev potential (Manev R4BP in short) from an analytical point of view. Initially we prove that, due to the repulsive force emanating from the central body, it is not possible to have a binary collision between the infinitesimal mass and the central body in the Manev R4BP (see Sect. 2). In Sect. 3 we observe that any equilibrium must lie on the coordinates axes. Using this information we are able to determine the type of equilibrium points and the number of them as function of the parameters $\beta$ and e. Bifurcation parameters are characterized. After that, in Sect. 4, we analyze the Hill’s regions as a function of the parameters using the Jacobi integral. In Sect. 5 several general results concerning the stability are proved analytically, and the study is completed numerically in some cases. Finally, in Sect. 6 the dynamics of the particular one-dimensional case with $x=y=\dot{x}= \dot{y}=0$ is studied. We also study numerically the linear stability of the family of periodic orbits that emanates from the equilibrium point of this subproblem.

2 Main features

The problem has two invariant subspaces, the plane $z=\dot{z}=0$, named Planar Manev R4BP and the z axis, named Rectilinear Manev R4BP. These two subproblems can be studied separately. We will see in Sect. 6 that the Rectilinear Manev R4BP is integrable.

Furthermore, we can also consider the following three limit problems:

• For $\beta =0$, we obtain the classical circular restricted three-body problem (CR3BP) with two equal masses. This is also known as the Copenhagen problem [see for example Szebehely (1967)].

• For $e=0$, we obtain a Newtonian restricted four-body problem (R4BP) where the primaries are in collinear configuration, and two of them (the exterior ones) have equal masses [see for example Papadakis (2007)].

• We can also consider the case when $\beta \rightarrow \infty$. In this case, the two peripherals disappear and the potential $\varSigma$ associated is

  $$\begin{aligned} \varSigma =\frac{1}{2}(x^{2}+y^{2})+ \frac{1}{8(1-4e)}\left( \frac{1}{r_{0}}-\frac{e}{r_{0}^{2}}\right) , \end{aligned}$$

  which can be viewed as a perturbed central force field.

System (3) admits the following time-reversible symmetries:

$$\begin{aligned} \begin{aligned}&S_{1}: \, (x, y, z, \dot{x}, \dot{y}, \dot{z}, t) \rightarrow (-x, y, z, \dot{x}, -\dot{y}, -\dot{z}, -t).\\&S_{2}: \, (x, y, z, \dot{x}, \dot{y}, \dot{z}, t) \rightarrow (x, -y, -z, -\dot{x}, \dot{y}, \dot{z}, -t). \\&S_{3}: \, (x, y, z, \dot{x}, \dot{y}, \dot{z}, t) \rightarrow (-x, y, -z, \dot{x}, -\dot{y}, \dot{z}, -t). \end{aligned} \end{aligned}$$

(6)

In particular, if $\gamma (t)\in \mathcal {M}$ is a solution, then $\tilde{\gamma }(t)= S_{j}(\gamma (-t))$, for $j=1,2,3$ is also a solution. Of course, the composition of these symmetries give us new symmetries.

Similarly to the classical circular R3BP, system (3) possesses the first integral, known as Jacobi constant, given by

$$\begin{aligned} C=2 \varOmega (x, y, z)-( \dot{x}^2 + \dot{y}^2+ \dot{z}^2). \end{aligned}$$

(7)

Finally, due to the repulsive term emanating from the central body, it is not possible to have a binary collision between the infinitesimal mass and the central body in the Manev R4BP. This is consequence of the following result.

Theorem 1

  For any $\beta > 0$ and an admissible e, a solution of Manev R4BP (3) must satisfy

$$\begin{aligned} \liminf _{t\rightarrow \pm \infty } r_{0}(t) >0, \end{aligned}$$

where $r_{0}$ is given in (5).

Proof

Consider $\gamma (t)$ a solution of the Manev R4BP. Then by (7), there exists a constant $C \in \mathbb {R}$ such that $C(\gamma (t))=C$, $\forall \; t$. Suppose that $\liminf _{t\rightarrow \infty } r_{0}(t) =0$ (analogously when $t\rightarrow -\infty$). Then, there exists a sequence $t_n\underset{n\nearrow \infty }{\longrightarrow }\infty$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty } C(\gamma (t_n)) = -\infty \end{aligned}$$

which is a contradiction.

3 Equilibrium points

The equilibrium points of (3) correspond to the points $(x,y,z,0,0,0) \in \mathcal {M}$ such that

$$\begin{aligned} \begin{aligned}&x- \frac{1}{\varDelta }\left[ \beta \left( \frac{1}{r_{0}^3}-\frac{2e}{r_{0}^4}\right) x+ \frac{(x-1/2)}{r_{1}^3}+ \frac{(x+1/2)}{r_{2}^3} \right] = 0,\\&y\left( 1- \frac{1}{\varDelta }\left[ \beta \left( \frac{1}{r_{0}^3}-\frac{2 e}{r_{0}^4}\right) + \frac{1}{r_{1}^3}+\frac{1}{r_{2}^3}\right] \right) = 0,\\&z\left( \beta \left( \frac{1}{r_{0}^3}-\frac{2 e}{r_{0}^4}\right) +\frac{1}{r_{1}^3}+\frac{1}{r_{2}^3}\right) = 0. \end{aligned} \end{aligned}$$

(8)

Since any equilibrium point is determined by the position (x, y, z) of the infinitesimal mass, from now we represent the equilibrium points of (3) only by the position vector.

Theorem 2

For any $\beta > 0$ and an admissible e, the equilibrium points of the Manev R4BP must lie on the coordinates axes.

Proof

Let (x, y, z) be the position vector of an equilibrium point. Because of symmetries (6) we only need to study the case $x \ge 0$, $y \ge 0$ and $z \ge 0$. System (8) can be written as

$$\begin{aligned} 2\varDelta \,x \; Q= & {} \frac{1}{r_{2}^3}-\frac{1}{r_{1}^3},\\ y \; Q= & {} 0,\\ \varDelta \,z \,(1-Q)= & {} 0, \end{aligned}$$

where $Q=1- \frac{1}{\varDelta }\left[ \beta \left( \frac{1}{r_{0}^3}-\frac{2 e}{r_{0}^4}\right) + \frac{1}{r_{1}^3}+\frac{1}{r_{2}^3}\right]$. From the third equation we have two possibilities:

• (i) Suppose that $z=0$. If $y=0$, the solutions are on the x axis. Suppose that $y\ne 0$. Then, $Q=0$, and therefore $r_{1}=r_{2}$, which implies that $x=0$, so the equilibrium points are on the y axis.

• (ii) Suppose now that $z\ne 0$. Then, $Q=1$, $y=0$ and

  $$\begin{aligned} x= \frac{1}{2 \varDelta } \left( \frac{1}{r_{2}^3}- \frac{1}{r_{1}^3}\right) . \end{aligned}$$

  Since we are looking for solutions $x\ge 0$, we have that $r_{2}\le r_{1}$, and using (5), $(x+1/2)^2+z^{2} \le (x-1/2)^2+z^{2}$, which means that $x=0$, and the solutions are on the z axis.

Next our purpose is to characterize the localization and number of equilibrium points for a fixed value of $\beta > 0$ and admissible e. As we have mentioned, using symmetries (6), for any equilibrium point, there exists the symmetric one with respect to the origin in the same axis. We will denote the equilibrium points as $L_{\xi }^{\pm }$, $\xi \in \{x,y,z\}$, depending on the axis and the sign of the position coordinate.

In what follows, there are some quantities and expressions that appear repeatedly. We summarize in the next table the most used ones where they appear for the first time (Table 1).

Table 1 Notations and quantities most used

3.1 Equilibrium points on the z axis

From (8), an equilibrium point on the positive z axis, $L_{z}^{+}$, is a solution $z>0$ of

$$\begin{aligned} \beta \left( \frac{1}{z^{3}}-\frac{2 e}{z^{4}}\right) + \frac{2}{(1/4+ z^{2})^{3/2}}= 0. \end{aligned}$$

(9)

Proposition 1

For any $\beta > 0$ and an admissible e, there exists a unique equilibrium point on the positive z axis, $L_{z}^{+}=(0, 0, \overline{z})$. Furthermore, $\min \{e,\beta e\}< \overline{z} < 2 e$.

Proof

Consider the auxiliary functions

$$\begin{aligned} h_{1}(z)=\beta \left( \frac{1}{z^{3}}-\frac{2 e}{z^{4}}\right) , \quad \hbox { and } \quad h_{2}(z)=-\frac{2}{(1/4+ z^{2})^{3/2}}. \end{aligned}$$

Then, an equilibrium point on the positive z axis is a solution of the equation $h_{1}(z)= h_{2}(z)$. On the one hand, we have that $\lim _{z\rightarrow 0^{+}}h_{1}(z)=-\infty$, $h_{1}(z)<0$ and $h_{1}'(z)>0$ for $0<z<2e$, and $h_{1}(z)>0$ for $z>2e$. On the other hand, $h_{2}'(z)>0$ for $z>0$. Then, it is straightforward that there exists a unique positive solution of $h_{1}(z)=h_{2}(z)$.

To obtain the upper and lower bounds of the solution, notice that $h_{2}(0)=-16$ and

$$\begin{aligned} h_{1}(e)= & {} \dfrac{-\beta }{e^3}< -16 \Leftrightarrow e< \dfrac{1}{2}\root 3 \of {\dfrac{\beta }{2}}, \\ h_{2}(e)= & {} \dfrac{\beta -2}{\beta ^3e^3}< -16 \Leftrightarrow e < \dfrac{1}{2\beta }\root 3 \of {\dfrac{2-\beta }{2}}. \end{aligned}$$

For $\beta \ge 1$, we have that $e_{0} < \frac{1}{2}\root 3 \of {\frac{\beta }{2}}$, whereas for $\beta < 1$, we have that $e_{0} < \frac{1}{2\beta }\root 3 \of {\frac{2-\beta }{2}}$. Using the fact that $e < e_{0}$ (recall (2)), the claim is proved.

Remark 1

For any $\beta >0$ and admissible e, let $L_{z}^{+}$ the equilibrium point given in Proposition 1. Then,

$$\begin{aligned} \lim _{e\rightarrow 0} \overline{z} =0, \quad \lim _{\beta \rightarrow 0} \overline{z} = 0, \quad \hbox {and} \quad \lim _{\beta \rightarrow \infty } \overline{z} = 2e. \end{aligned}$$

The first limit is obtained from the upper and lower bounds of $\overline{z}$. To obtain the second limit, notice that using (9), we can write (for any fixed value of e) $\beta$ as a function of $\overline{z}$ as

$$\begin{aligned} \beta = \dfrac{2\overline{z}^{4}}{(2e-\overline{z})(1/4+\overline{z}^{2})^{3/2}}. \end{aligned}$$

Using Taylor expansion we get $\beta = \frac{8}{e}\overline{z}^{4} + O(\overline{z}^{5})$. Finally the third limit is obtained directly dividing Eq. (9) by $\beta$.

In the first two cases, this means that there exist no equilibrium points on the z axis both in the collinear R4BP and in the circular R3BP, as it is well known. In the circular R3BP, the limit of $L_z^{\pm }$ as $\beta \rightarrow 0$ corresponds to the equilibrium point known as $L_{2}$.

3.2 Equilibrium points on the y axis

From (8), an equilibrium point on the positive y axis, $L_{y}^{+}$, is a solution $y>0$ of

$$\begin{aligned} 1-\frac{1}{\varDelta }\left[ \beta \left( \frac{1}{y^{3}}-\frac{2 e}{y^4}\right) +\displaystyle \frac{2}{\left( \frac{1}{4}+y^{2}\right) ^{3/2}}\right] =0, \end{aligned}$$

(10)

where $\varDelta$ is given in (1).

In order to calculate the equilibrium points we use the auxiliary functions

$$\begin{aligned} f_{1}(s) = \varDelta s^{3}+\dfrac{2\beta e}{s}, \quad \hbox { and } \quad f_{2}(s) = \beta +\dfrac{2s^{3}}{\left( 1/4+s^{2}\right) ^{3/2}}, \end{aligned}$$

(11)

defined for $s>0$ (or $s\ge 0$ when it is possible). Some properties of the function $f_{1}$ will be used in different proofs, so we resume them in the next lemma.

Lemma 1

For any fixed value of $\beta >0$, the function $f_{1}(s)$, $s>0$, defined in (11) has the following properties:

• (i) It has only one critical point, which is a minimum, at

  $$\begin{aligned} s^{*}=s^{*}(e)=\left( \dfrac{2\beta e}{3\varDelta }\right) ^{1/4}, \qquad 0< e < e_{0}, \end{aligned}$$

  where $e_{0}$ is given in (2).

• (ii) $s^{*}(e)$ is an increasing function and $s^{*}(3e_{0}/4)=1/2$.

• (iii) $f_{1}(s^{*}(e))=4\varDelta ^{1/4}\left( \frac{2\beta e}{3}\right) ^{3/4}$ has only one critical point, which is a maximum, at $3e_{0}/4$.

The proof is straightforward calculations.

Proposition 2

For any $\beta > 0$ and an admissible e, there exist exactly two equilibrium points on the positive y axis, $L_{y_{i}}^{+}=(0, \overline{y}_i, 0)$, $i=1,2$. Furthermore,

$$\begin{aligned} \overline{y}_{1}\le \min \{s^{*},1/2\}, \qquad \max \{1/2,s^{*}\} \le \overline{y}_{2}\le \left( \dfrac{2+\beta }{\varDelta }\right) ^{1/3}, \end{aligned}$$

where $s^{*}$ is given in Lemma 1.

Proof

A solution of Eq. (10) on the positive y axis is a solution of $f_{1}(y)=f_{2}(y)$ for $y>0$.

On the one hand, recall the properties of $f_{1}$ given in Lemma 1. On the other hand $f_{2}(0)=\beta$, $\lim _{y\rightarrow +\infty } f_{2}(y)=2+\beta$ and $f_{2}'(y)>0$ for $y>0$. We claim that for any $\beta >0$ and admissible e, $f_{1}(s^{*})<f_{2}(s^{*})$. Then it follows that the equation has exactly two solutions.

Furthermore, using the claim and that $f_{1}(1/2) < f_{2}(1/2)$, we obtain the upper bound of $\overline{y}_{1}$ and the lower bound of $\overline{y}_{2}$. To obtain the upper bound of $\overline{y}_{2}$ we use the fact that $\overline{y}_{2}$ is smaller than the solution of the equation $\varDelta s^{3} =s+2$.

To prove the claim, for any fixed value of $\beta >0$ consider the functions $g_i(e) = f_i(s^{*}(e))$, $i=1,2$. We want to see that $g_1(e) < g_2(e)$ for all $e\in (0,e_{0})$. On the one hand, using Lemma 1, $g_1(e)$ has a maximum at $3e_{0}/4$ and $g_1(3e_{0}/4)=\frac{1}{4}+\beta$, On the other hand, $g_2'(e)>0$, $g_2(0)=\beta$ and $g_2(e_{0}/4)=\frac{1}{4}+\beta$. Then the claim follows.

Remark 2

For any $\beta >0$ and admissible e, let $L_{y_{i}}^{+}$, $i=1,2$, be the equilibrium points given in Proposition 2. Then, from the upper bound of $\overline{y}_{1}$ we have that

$$\begin{aligned} \lim _{e\rightarrow 0} \overline{y}_{1} =0, \quad \hbox {and} \quad \lim _{\beta \rightarrow 0} \overline{y}_{1} = 0. \end{aligned}$$

Furthermore, it is not difficult to see from Eq. (10) that

$$\begin{aligned} \lim _{e\rightarrow 0}\overline{y}_{2} = \overline{y}_{2}^0(\beta ) \; \hbox { exists, and } \; \lim _{\beta \rightarrow 0}\overline{y}_{2}=\sqrt{3}/2, \end{aligned}$$

where

$$\begin{aligned} \overline{y}_{2}^0(\beta )=\dfrac{1}{2} + \dfrac{-1+2\sqrt{2}}{24}\dfrac{1}{\beta }+\dfrac{6-5\sqrt{2}}{288}\dfrac{1}{\beta ^2}- \dfrac{104+37\sqrt{2}}{41472}\dfrac{1}{\beta ^3}+O(1/\beta ^4). \end{aligned}$$

This agrees with the fact that there exists only one equilibrium point on the y axis both in the collinear R4BP and in the circular R3BP. In the circular R3BP, when $\beta \rightarrow 0$, the limit of $L_{y_{1}}^{\pm }$ corresponds to the equilibrium point known as $L_{2}$, located at the origin, and the limit of $L_{y_{2}}^{\pm }$ corresponds to the triangular equilibrium points $L_{4,5}$, which are in equilateral configuration with the peripherals.

In particular, in the Manev R4BP we can find a value of an admissible e for all $\beta$ such that $L_{y_{2}}^{\pm }$ are in an equilateral configuration with the secondaries.

Proposition 3

For any value of $\beta$, there exists an admissible value of e, $e = \frac{9-\sqrt{3}}{32}$, such that each equilibrium point $L_{y_{2}}^{\pm }$ forms an equilateral triangle with the two peripheral bodies.

Proof

We look for values of e for which $f_{1}(\sqrt{3}/2)=f_{2}(\sqrt{3}/2)$ for all $\beta >0$. Simplifying we get that

$$\begin{aligned} 3\dfrac{\sqrt{3}}{4}+3\sqrt{3}\beta -\dfrac{32}{3}\sqrt{3}\beta e = \beta +\dfrac{3}{4}\sqrt{3}. \end{aligned}$$

The above equation is independent of $\beta$, and it is satisfied for $e = \dfrac{9-\sqrt{3}}{32} < e_{0}$ for all $\beta$.

Remark 3

When $\beta \rightarrow \infty$, the perturbed central force problem obtained has two equilibrium points on the positive y axis.

From (10), the equilibrium points for the problem when $\beta \rightarrow \infty$ must satisfy the equation

$$\begin{aligned} 8(1-4e)y^4-y+2e=(1-2y)((4e-1)(4y^{3}+2y^{2}+y)+2e)=0, \end{aligned}$$

which has two positive solutions for each admissible value of e, one of them equals to 1 / 2.

In Fig. 1 left, some families of the equilibrium points $L_{y_{i}}^{+}$, $i=1,2$, for different values of $\beta$ are plotted. The equilateral triangular equilibrium point is marked with a dot. The families of equilibrium points in the limit case $\beta \rightarrow \infty$ are shown in the right plot.

Fig. 1

Left Evolution of the coordinates $\overline{y}_{1}$ (in red) and $\overline{y}_{2}$ (in blue) as a function of e for different values of $\beta$. The circle corresponds to the value for which $L_{y_{2}}^{+}$ forms an equilateral configuration for all values of $\beta$ (see Proposition 3). Right Families of equilibrium points for the limit problem when $\beta \rightarrow \infty$

3.3 Equilibrium points on the x axis

From (8), an equilibrium point on the positive x axis, $L_x^{+}$, is a solution of

$$\begin{aligned} x- \frac{1}{\varDelta }\left[ \beta \left( \frac{1}{x^{2}}- \frac{2e}{x^{3}}\right) + \frac{x-1/2}{|x-1/2|^3}+\frac{1}{(x+1/2)^2}\right] = 0. \end{aligned}$$

For $x>1/2$ we have that the previous equation writes as

$$\begin{aligned} x- \frac{1}{\varDelta }\left[ \beta \left( \frac{1}{x^{2}}- \frac{2e}{x^{3}}\right) + \frac{2(x^{2}+1/4)}{(x^{2}-1/4)^2}\right] = 0, \end{aligned}$$

(12)

whereas for $x<1/2$ we obtain

$$\begin{aligned} x- \frac{1}{\varDelta }\left[ \beta \left( \frac{1}{x^{2}}- \frac{2e}{x^{3}}\right) - \frac{2x}{(x^{2}-1/4)^2}\right] = 0. \end{aligned}$$

(13)

In order to calculate the equilibrium points we use the auxiliary function $f_{1}$ introduced in (11) and:

$$\begin{aligned} f_{3}(s) = \beta - \dfrac{2s^{3}}{(s^{2}-1/4)^2}, \quad \hbox { and } \quad f_{4}(s) = \beta + \dfrac{2s^{2}(s^{2}+1/4)}{(s^{2}-1/4)^2}. \end{aligned}$$

(14)

Proposition 4

For any $\beta > 0$ and an admissible e, there exists exactly one equilibrium point on the positive x axis with $x>1/2$, $L_{x_{1}}^{+}=(\overline{x}_{1}, 0, 0)$. Furthermore, $\overline{x}_{1}\ge \max \{1/2,s^{*}\},$ where $s^{*}$ is given in Lemma 1.

Proof

Equation (12) is equivalent to $f_{1}(x) = f_{4}(x)$. On the one hand, $f_{4}$ is a decreasing function, $\lim _{x\rightarrow 1/2^{+}}f_{4}(x)=+\infty$ and $\lim _{x\rightarrow +\infty }f_{4}(x)=\beta +2$. On the other hand, using Lemma 1 and $f_{1}(1/2)=\beta +1/4$, it is clear that both functions intersect only once for $x>1/2$. Finally, using that $f_{1}(s^{*})< f_{1}(1/2) < f_{4}(x)$ for any $x>1/2$, we obtain the lower bound.

Remark 4

For any $\beta >0$ and admissible e, let $L_{x_{1}}^{+}$ the equilibrium point given in Proposition 4. Then

$$\begin{aligned} \lim _{e\rightarrow 0}\overline{x}_{1} = \overline{x}_{1}^0(\beta ) \; \hbox { exists, and } \; \lim _{\beta \rightarrow 0} \overline{x}_{1} = \overline{x}_{1_{0}}, \end{aligned}$$

where $\overline{x}_{1_{0}}$ does no depend on e and coincides with the x coordinate of the equilibrium point $L_{1}$ of the R3BP with equal masses.

When $e\rightarrow 0$, we can write the equation $f_{1}(s)=f_{4}(s)$ as

$$\begin{aligned} \dfrac{2(1+4\beta )}{\beta } s^{3}= 1 + \dfrac{2}{\beta } \dfrac{s^{2}(s^{2}+1/4)}{(s^{2}-1/4)^2}, \end{aligned}$$

which clearly has one solution for $s>1/2$. It corresponds to the equilibrium point on the right-hand side of the collinear R4BP.

When $\beta \rightarrow 0$ the equation $f_{1}(s)=f_{4}(s)$ transforms into

$$\begin{aligned} 2s^{3}=\dfrac{2s^{2}(s^{2}+1/4)}{(s^{2}-1/4)^2}. \end{aligned}$$

Removing the solution $s=0$, we get $s^{5}-s^{3}/2-s^{2}+s/16-1/4=0$ that corresponds, after the displacement $s\rightarrow x+1/2$, to the Euler’s quintic

$$\begin{aligned} x^{5}+\dfrac{5}{2}x^4+2x^{3}-\dfrac{1}{2}x^{2}-x-\dfrac{1}{2}=0 \end{aligned}$$

of the Copenhagen R3BP. Thus, the equilibrium point $(\overline{x}_{1_{0}},0,0)$ coincides with the equilibrium point $L_{1}$ of the R3BP.

Fig. 2

Left Evolution of the coordinates $\overline{x}_{1}$ (in red) and $\overline{x}_{2,3}$ (in blue) as functions of e, for different values of $\beta$. The circle corresponds to the value for which $L_{x_{1}}^{+}$ coincides with the point $L_{1}$ of the R3BP for all values of $\beta >0$ (see Proposition 5). Right Difference $\overline{x}_{2} - s^{*}$ as a function of e, for the values of $\beta$ shown

Similarly to the case of the equilibrium points on the y axis, there exists an admissible value of e such that for all values of $\beta$, the equilibrium point $L_{x_{1}}^{+}$ coincides with the equilibrium point $L_{1}$ of the R3BP (see Fig. 2).

Proposition 5

There exists an admissible value of e, such that be the equilibrium point $L_{x_{1}}^{+}=(\overline{x}_{1_{0}},0,0)$ for all $\beta >0$, where $\overline{x}_{1_{0}}$ is given in Remark 4.

Proof

Recall that $\overline{x}_{1}$ is the only positive solution of the equation $f_{1}(s)=f_{4}(s)$ given by (11) and (14). This equation can be written as

$$\begin{aligned} 2s^{2} \left( s- \dfrac{s^{2}+1/4}{(s^{2}-1/4)^2}\right) + \dfrac{\beta }{s} (8(1-4e)s^4-s+2e)=0. \end{aligned}$$

Substituting $s=\overline{x}_{1_{0}}$ in the above equation, the first term vanishes and we get that

$$\begin{aligned} 8(1-4e)\overline{x}_{1_{0}}^4-\overline{x}_{1_{0}} + 2e =0. \end{aligned}$$

Solving for e,

$$\begin{aligned} e= \dfrac{\overline{x}_{1_{0}} (4\overline{x}_{1_{0}}^2+2\overline{x}_{1_{0}} +1)}{2 (2\overline{x}_{1_{0}}+1)(4\overline{x}_{1_{0}}^2+1)}< \dfrac{1}{4}, \end{aligned}$$

which is an admissible value.

The approximate value of e for which $L_{x_{1}}^{\pm }=(\pm \overline{x}_{1_{0}},0,0)$ is $e\simeq 0.239087978$. See Fig. 2.

Next, we study the number of equilibrium points on the x axis for $0<x<1/2$.

Proposition 6

For any $\beta > 0$, there exists a value $e^{*}= e^{*}(\beta )$ such that the number of the equilibrium points along the x axis for $0<x<1/2$ is

• 0 if $e \in (e^{*},e_{0})$,

• 1 if $e= e^{*}$,

• 2 if $e < e^{*}$.

Furthermore, $e^{*} < 3e_{0}/4$, where $e_{0}$ is given in (2).

Proof

From Eq. (13), the number of equilibrium points with $0<x<1/2$ is equivalent to the number of solutions of

$$\begin{aligned} f_{1}(x) = f_{3}(x) \quad \text {for} \quad 0<x<\frac{1}{2}, \end{aligned}$$

where $f_{1}$ and $f_{3}$ are given in (11) and (14).

Fix a value of $\beta >0$. Recall that $f_{1}$ has a unique minimum at $s^{*}=s^{*}(e)$ (see Lemma 1). Notice also that $f_{3}$ does not depend on e, is a decreasing function, $f_{3}(0)=\beta$ and $\lim _{x\rightarrow 1/2^{-}}f_{3}(x)=-\infty$. Then, on one hand if $e>3e_{0}/4$, $s^{*}(e)>1/2$, $f_{1}(1/2)=\beta +1/4$ and the two functions do not intersect. On the other hand, $\lim _{e\rightarrow 0}f_{1}(s^{*}(e))=0$, so that for small values of e, $f_{1}(s^{*}) < f_{3}(s^{*})$ and the two functions intersect twice.

Finally, by continuity, there exists a value of e such that $f_{1}$ and $f_{3}$ coincide tangentially only once.

For the values of $e \in (0,e^{*}]$ we denote the equilibrium points $L_{x_{i}}^{\pm }=(\pm \overline{x}_{i},0,0)$, $i=2,3$, where $0<\overline{x}_{3}\le \overline{x}_{2}<1/2$, and the equality holds when $e=e^{*}$. From the properties shown in the previous proposition the following result can be proved.

Proposition 7

For any $\beta$, let $e^{*}$ and $s^{*}$ be as in Proposition 6 and Lemma 1, respectively. Then, for any $e< e^{*}$, the equilibrium point $L_{x_{3}}^{+}$ satisfies that $0<\overline{x}_{3} < s^{*}$.

In Fig. 2 left, some families of the equilibrium points $L_{x_{i}}^{+}$, $i=1,2,3$, for different values of $\beta$ are plotted. The common equilibrium point $L_{x_{1}}^{+}$ is marked with a dot. The families of equilibrium points in the limit case $\beta \rightarrow \infty$ are the same as in Fig. 1 right.

As we have seen, $\overline{x}_{3}< s^{*} < \overline{x}_{1}$ for all admissible values of $\beta$ and e, though $\overline{x}_{2}$ is greater or less than $s^{*}$ depending on $\beta$ and e. In Fig. 2 left, we show $\overline{x}_{2} - s^{*}$ as a function of e for different values of $\beta$.

Remark 5

For any $\beta >0$ and admissible $e\le e^{*}$, let $L_{x_{i}}^{+}$, $i=2,3$ the equilibrium points given in Proposition 6. Then

$$\begin{aligned} \lim _{e\rightarrow 0} \overline{x}_{3} =0, \quad \hbox {and} \quad \lim _{\beta \rightarrow 0} \overline{x}_{3} = 0. \end{aligned}$$

Furthermore, it is not difficult to see from Eq. (13) that

$$\begin{aligned} \lim _{e\rightarrow 0}\overline{x}_{2} = \overline{x}_{2}^0(\beta ) \; \hbox { exists, and } \; \lim _{\beta \rightarrow 0}\overline{x}_{2}=0. \end{aligned}$$

Therefore, in the collinear R4BP there exist two equilibrium points on the positive x axis, one located between the central body and the peripheral ($L_{x_{2}}^{+}$), and the other one on the right-hand side of the peripheral ($L_{x_{1}}^{+}$). In the circular R3BP, when $\beta \rightarrow 0$, the limit of $L_{x_{i}}^{\pm }$, $i=2,3$ corresponds to the equilibrium point $L_{2}$, located at the origin.

Remark 6

When $\beta \rightarrow \infty$, the perturbed central force problem obtained has two equilibrium points on the positive x axis.

From (8), the equilibrium points for the problem when $\beta \rightarrow \infty$ must satisfy the equation

$$\begin{aligned} 8(1-4e)x^4-x+2e=(1-2x)((4e-1)(4x^{3}+2x^{2}+x)+2e)=0, \end{aligned}$$

which has two positive solutions. Notice that they are the same solutions as in Remark 3.

4 Hill’s regions

In this section we describe the geometry of the Hill’s region of the Manev R4BP,

$$\begin{aligned} \mathcal {R}_C=\{(x,y,z) \in \mathbb {R}^3\setminus \{(0,0,0), (1/2 , 0,0), (-1/2, 0, 0)\} \ / \ 2\varOmega (x,y,z) \ge C \}, \end{aligned}$$

that is, the regions in the configuration space where the motion of the particle takes place for a fixed value of the Jacobi constant C (given in (7)). The zero-velocity surface is defined as the boundary of the Hill’s region, that is,

$$\begin{aligned} \mathcal {Z}_C=\{(x,y,z) \in \mathbb {R}^3\setminus \{(0,0,0), (1/2 , 0,0), (-1/2, 0, 0)\} \ / \ 2 \varOmega (x,y,z) = C \}. \end{aligned}$$

Following the arguments used in Theorem 1, it is clear that for any value of the Jacobi constant C, there exists $\delta$ such that $2\varOmega (x,y,z)-C\le 0$ for $r_{0}\le \delta$. Therefore, at any value of the Jacobi constant, there exists a neighborhood of the central body that it is not contained in the Hill’s region $\mathcal {R}_C$.

It is well known that the equilibrium points of the problem correspond to the bifurcation values of the zero-velocity surfaces. That is, when varying C, the topology of the Hill’s regions $\mathcal {R}_C$ changes when the equilibrium points appear. For C big enough, the Hill’s region has three disjoint components: one contained in the exterior of a sphere $r_{0}>R$ (for a certain R), and two around each peripheral. When C decreases, the components merge and there appear channels connecting different regions. These connections depend on the order in which the equilibrium points appear. In Fig. 3, we plot the variation of the value of the Jacobi constant at each equilibrium point $L_{\xi }\in \{L_{\xi }^{\pm }, \ \xi =x,y,z\}$ for two different values of $\beta$. As we can see, the order in which the equilibrium points are born (with respect to C) depends on $\beta$.

Fig. 3

Evolution of Jacobi constant along the equilibrium points for $\beta =1$ (left) and $\beta =100$ (right)

In Figs. 4 and 5 we plot the projections onto the coordinate planes of the Hill’s regions for $\beta =1$ and $\beta =100$, respectively, and $e=0.1$ (in both cases) and five different values of the Jacobi constant close to the values of some equilibrium points, in decreasing order. When $\beta =1$ and $e=0.1$, $C(L_{x_{1}}^{\pm })> C(L_{y_{1}}^{\pm })> C(L_z^{\pm }) > C(L_{y_{2}}^{\pm })$ (notice that $L_{x_{i}}^{\pm }$, $i=2,3$ do not exist in this case). Therefore, after the apparition of $L_{x_{1}}^{\pm }$ the regions around the peripherals can connect with the exterior region and a particle can escape. To connect both peripherals directly (that is, from the neighborhood of one peripheral to the other one passing close to the central body) it is necessary that $C<C(L_{y_{1}}^{\pm })$ (see third column in Fig. 4). When $\beta =100$ and $e=0.1$, $C(L_{x_{3}}^{\pm })> C(L_{y_{1}}^{\pm })> C(L_z^{\pm })> C(L_{x_{2}}^{\pm })>C(L_{x_{1}}^{\pm })>C(L_{y_{2}}^{\pm })$. Then, after the apparition of $L_{x_{2}}^{\pm }$ it is possible to connect both peripherals directly (see third column in Fig. 5), and the motion is still bounded until $L_{x_{1}}^{\pm }$ appear.

Fig. 4

For $\beta =1$ and $e=0.1$, projections of the Hill’s regions into the xy (first row), xz (second row) and yz (third row) planes, respectively. The values of the Jacobi constant are: a $C=2.0358$, b $C=1.86917$, c $C=1.83383$, d $C=1.5208$, e $C=1$

Fig. 5

For $\beta =100$ and $e=0.1$, projections of the Hill’s regions into the xy (first row), xz (second row) and yz (third row) planes, respectively. The values of the Jacobi constant are: a $C=1.09442$, b $C=1.05276$, c $C=0.983845$, d $C=0.95$, e $C=0.9$

5 Stability of the equilibrium solutions

Next, we will focus on the study of the linear stability of the equilibrium points. In any dynamical system, the periodic orbits play an important role in the description of the local dynamics of the model. One way to find periodic orbits is through the equilibrium points. It is well known that when the Lyapunov Center Theorem applies, there exist families of periodic orbits emanating from the equilibrium point. On the other hand, when the equilibrium points are unstable, there exist stable/unstable manifolds (and in some cases, the periodic orbits can be also unstable, so they will have their own stable/unstable manifolds associated with them). The (heteroclinic) connections of these invariant manifolds, when they exist, can be used to obtain orbits starting around one equilibrium point, and ending in a different one.

System (3) can be written in Hamiltonian form with Hamiltonian

$$\begin{aligned} H= H(x, y, z, X, Y, Z)= \frac{1}{2}(X^2+Y^2+Z^2)+(y X- x Y)- V(x, y,z), \end{aligned}$$

where the function V is given by

$$\begin{aligned} V= V(x, y,z)= \frac{1}{\varDelta }\left[ \beta \left( \frac{1}{r_{0}}- \frac{e}{r_{0}^{2}}\right) + \frac{1}{r_{1}}+ \frac{1}{r_{2}}\right] . \end{aligned}$$

The linearization of the Hamiltonian system is given by the matrix

$$\begin{aligned} A = A(x,y,z) = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0\\ -1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1\\ V_{xx} &{}\quad V_{xy} &{}\quad V_{xz} &{}\quad 0 &{}\quad 1 &{}\quad 0\\ V_{xy} &{}\quad V_{yy} &{}\quad V_{yz} &{}\quad -1 &{}\quad 0 &{}\quad 0\\ V_{xz} &{}\quad V_{yz} &{}\quad V_{zz} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \end{array}\right) , \end{aligned}$$

where

$$\begin{aligned} V_{xx}= & {} \dfrac{-1}{\varDelta } \left[ \beta \left( \frac{1}{r_{0}^3}-\frac{2e}{r_{0}^4}\right) + \frac{1}{r_{1}^3}+\frac{1}{r_{2}^3}\right] +\dfrac{1}{\varDelta } \left[ \beta \left( \frac{3}{r_{0}^5}-\frac{8 e}{r_{0}^6}\right) x^{2}\right. \nonumber \\&\quad \left. +3\left( \frac{(x-1/2)^2}{r_{1}^5}+ \frac{(x+1/2)^2}{r_{2}^5}\right) \right] ,\nonumber \\ V_{xy}= & {} \dfrac{y}{\varDelta } \left[ \beta x \left( \frac{3}{r_{0}^5}-\frac{8 e}{r_{0}^6}\right) + 3 \left( \frac{x-1/2}{r_{1}^5}+ \frac{x+1/2}{r_{2}^5}\right) \right] ,\nonumber \\ V_{xz}= & {} \dfrac{z}{\varDelta } \left[ \beta x \left( \frac{3}{r_{0}^5}-\frac{8 e}{r_{0}^6}\right) + 3 \left( \frac{x-1/2}{r_{1}^5}+ \frac{x+1/2}{r_{2}^5}\right) \right] ,\nonumber \\ V_{yy}= & {} \dfrac{-1}{\varDelta } \left[ \beta \left( \frac{1}{r_{0}^3}-\frac{2 e}{r_{0}^4}\right) + \frac{1}{r_{1}^3}+\frac{1}{r_{2}^3}\right] + \dfrac{y^{2}}{\varDelta } \left[ \beta \left( \frac{3}{r_{0}^5}-\frac{8 e}{r_{0}^6}\right) + 3\left( \frac{1}{r_{1}^5}+\frac{1}{r_{2}^5}\right) \right] ,\nonumber \\ V_{yz}= & {} \dfrac{zy}{\varDelta } \left[ \beta \left( \frac{3}{r_{0}^5}-\frac{8 e}{r_{0}^6}\right) + 3 \left( \frac{1}{r_{1}^5}+ \frac{1}{r_{2}^5}\right) \right] ,\nonumber \\ V_{zz}= & {} \dfrac{-1}{\varDelta }\left[ \beta \left( \frac{1}{r_{0}^3}-\frac{2 e}{r_{0}^4}\right) + \frac{1}{r_{1}^3}+\frac{1}{r_{2}^3}\right] + \dfrac{z^{2}}{\varDelta }\left[ \beta \left( \frac{3}{r_{0}^5}-\frac{8e}{r_{0}^6}\right) + 3 \left( \frac{1}{r_{1}^5}+ \frac{1}{r_{2}^5}\right) \right] .\nonumber \\ \end{aligned}$$

(15)

Next, we study the eigenvalues and eigenvectors of the matrix A evaluated on each equilibrium point. Due to the symmetries, we will only study the stability of the equilibrium points $L_{\xi }^{+}$, $\xi \in \{x_{i},y_{j},z\}$, $i=1,2,3$, $j=1,2$.

5.1 Stability of the equilibrium points on the z axis

Consider the equilibrium point $L_{z}^{+}=(0,0,\overline{z})$ (see Proposition 1). Using the fact that $\overline{z}$ must satisfy relation (9), it is not difficult to see that

$$\begin{aligned} \begin{aligned} V_{xy}(L_{z}^{+})&=V_{xz}(L_{z}^{+})=V_{yy}(L_{z}^{+})=V_{yz}(L_{z}^{+})=0,\\ V_{xx}(L_{z}^{+})&=\dfrac{3}{2\varDelta } \dfrac{1}{(1/4+\overline{z}^{2})^{5/2}},\\ V_{zz}(L_{z}^{+})&=\dfrac{\beta }{\varDelta \overline{z}^{4} (1/4+\overline{z}^{2})} \left( \dfrac{3}{4} \overline{z}- 2 e-2 e \overline{z}^{2}\right) . \end{aligned} \end{aligned}$$

(16)

Proposition 8

For any $\beta >0$ and an admissible e, let $\gamma =V_{xx}(L_{z}^{+})$ be as in (16). Then, the eigenvalues associated with the equilibrium point $L_{z}^{+}$ are $\pm \lambda _3 = \pm w \mathrm {i}$, $w>0$, and

• $\pm \lambda _{1,2} = \pm a \pm b \mathrm {i}$, $a>0$, $b>0$, if $\gamma \in (0,8)$;

• $\pm \lambda _{1,2}=\pm \sqrt{3}$, if $\gamma =8$;

• $\pm \lambda _{1,2} \in {\mathbb R}$, if $\gamma >8$.

Proof

Using (16), the eigenvalues of the matrix $A(L_{z}^{+})$ are $\pm \lambda _3=\pm \sqrt{V_{zz}(L_{z}^{+})}$ and the solutions $\pm \lambda _{1,2}$ of

$$\begin{aligned} p(\lambda )= \lambda ^4-(\gamma -2) \lambda ^2+ 1+\gamma , \end{aligned}$$

where $\gamma =V_{xx}(L_{z}^{+})>0$.

On the one hand, using the fact that $\overline{z} < 2e$ (see Proposition 1), we have that

$$\begin{aligned} \frac{3}{4} \overline{z}- 2 e - 2 e \overline{z}^{2}< \frac{3}{4} \overline{z}- 2 e<\frac{3}{4} 2 e- 2 e=-\frac{1}{2}e<0. \end{aligned}$$

Therefore, $V_{zz}(L_{z}^{+})<0$ and two of the eigenvalues are pure imaginary.

On the other hand, the solutions of $p(\lambda )=0$ are

$$\begin{aligned} \lambda _{\pm }^2= \frac{1}{2}\left( \gamma -2 \pm \sqrt{\gamma (\gamma -8)}\right) . \end{aligned}$$

This completes the proof.

Notice that for any fixed value of $\beta$, $\lim \nolimits _{e\rightarrow e_{0}} V_{xx}(L_{z}^{+}) =+\infty$ and for $\beta >1/2$, $\lim \nolimits _{e\rightarrow 0} V_{xx}(L_{z}^{+}) <8$. Then for any fixed value of $\beta >1/2$ there are values of e where $V_{xx}(L_{z}^{+})$ is less, equal or greater than eight. In Fig. 6 we show the variation of $V_{xx}(L_{z}^{+})$ as a function of e for different values of $\beta$.

Fig. 6

Evolution of the $V_{xx}(L_{z}^{+})$ as a function of e for different values of $\beta \in [1,100]$

5.2 Stability of planar equilibrium points

Consider the equilibrium points $L_{x_{i}}^{+}=(\overline{x}_{i},0,0)$, $i=1,2,3$, and $L_{y_{j}}^{+}=(0,\overline{y}_{j}, 0)$, $j=1,2$ (see Propositions 4, 6, 2, respectively). From the expressions of second derivatives (15), we have that

$$\begin{aligned} V_{xz}(L_{\xi }^{+})=V_{yz}(L_{\xi }^{+})=V_{xy}(L_{\xi }^{+})=0, \end{aligned}$$

and

$$\begin{aligned} V_{zz}(L_{\xi }^{+}) = -\frac{1}{\varDelta }\left[ \beta \left( \frac{1}{r_{0}^3}-\frac{2 e}{r_{0}^4}\right) + \frac{1}{r_{1}^3}+ \frac{1}{r_{2}^3}\right] , \end{aligned}$$

where $\xi \in \{x_{i},y_{j}\}$, $i=1,2,3$, $j=1,2$. Then, the eigenvalues of the matrix $A(L_{\xi }^{+})$ can be written as

$$\begin{aligned} \begin{aligned} {\pm } \lambda _1&= \pm \frac{1}{\sqrt{2}} \left( \varGamma + \sqrt{\varLambda }\right) ^{1/2},\\ \pm \lambda _2&= \pm \frac{1}{\sqrt{2}} \left( \varGamma - \sqrt{\varLambda }\right) ^{1/2},\\ \pm \lambda _3&= \pm \sqrt{V_{zz}}, \end{aligned} \end{aligned}$$

(17)

where

$$\begin{aligned} \varLambda = (V_{xx}-V_{yy})^2-8(V_{xx}+V_{yy}), \qquad \varGamma =V_{xx}+V_{yy}-2, \end{aligned}$$

(18)

and the derivatives are evaluated at the corresponding equilibrium point. Notice that

$$\begin{aligned} \varLambda < \varGamma ^2 \Leftrightarrow (1+V_{xx}) (1+ V_{yy}) > 0. \end{aligned}$$

(19)

5.2.1 Stability of the equilibrium points on the y axis

We consider the points $L_{y_{j}}^{+}$, $j=1,2$. From Eq. (10) we have that

$$\begin{aligned} 1-\frac{1}{\varDelta }\left[ \beta \left( \frac{1}{\overline{y}_{j}^3}-\frac{2 e}{\overline{y}_{j}^4}\right) +\displaystyle \frac{2}{\left( \frac{1}{4}+\overline{y}_{j}^2\right) ^{3/2}}\right] =0. \end{aligned}$$

Introducing this relation in (15), we have that,

$$\begin{aligned} V_{xx}(L_{y_{j}}^{+})= & {} -1 + \dfrac{3}{2\varDelta } \dfrac{1}{(\overline{y}_{j}^2+1/4)^{5/2}},\nonumber \\ V_{yy}(L_{y_{j}}^{+})= & {} 2 - \dfrac{2\beta e}{\varDelta \overline{y}_{j}^4} - \dfrac{3}{2\varDelta }\dfrac{1}{(\overline{y}_{j}^2+1/4)^{5/2}},\\ V_{zz}(L_{y_{j}}^{+})= & {} -1.\nonumber \end{aligned}$$

(20)

Notice that $\varGamma$ can be written as

$$\begin{aligned} \varGamma = -1 - \dfrac{2\beta e}{\varDelta \overline{y}_{j}^4}<0, \end{aligned}$$

(21)

for $j=1,2$.

The next result proves that the equilibrium point $L_{y_{1}}^{+}$ is a center $\times$ center $\times$ saddle.

Proposition 9

For any $\beta >0$ and admissible e, the eigenvalues associated with the equilibrium point $L_{y_{1}}^{+}$ are

$$\begin{aligned} \pm \lambda _{1} \in \mathbb {R}, \quad \pm \lambda _{2}=\pm w\,\mathrm {i}, \;w>0, \quad \pm \lambda _3=\pm \mathrm {i}. \end{aligned}$$

Proof

From (17) and (20), $\lambda _3=i$. On the one hand, it is also clear that $1+V_{xx} >0$. On the other hand, using the fact that $\overline{y}_{1}< s^{*}$ (see Proposition 2), we get $1+V_{yy} < 0$. Then, from (19), $\varGamma ^2 < \varLambda$. Since $\varGamma <0$, we have that $0<\varGamma + \sqrt{\varLambda }$ and $\varGamma - \sqrt{\varLambda } <0$. Thus, $\pm \lambda _1$ are real and $\pm \lambda _2$ are pure imaginary.

With respect to the equilibrium point $L_{y_{2}}^{+}$, the sign of $\varLambda$ depends on $\beta$ and e. Next results give a region in the $(\beta , e)$ plane where $\varLambda (L_{y_{2}}^{+})>0$.

Proposition 10

Let $L_{y_{2}}^{+}$ be given in Proposition (2), and $e_{0}$ and $\varLambda$ be defined in (2) and (18), respectively. For any $\beta >9\sqrt{2}-1/4$ and $0<e< e_{0}-\dfrac{9\sqrt{2}}{4\beta }$, $\varLambda (L_{y_{2}}^{+})>0$.

Proof

From (18) and (20), and using that $\overline{y}_{2} > 1/2$ we have that

$$\begin{aligned} \varLambda (L_{y_{2}}^{+}) \ge 1-\dfrac{18}{\varDelta (\overline{y}_{2}^2+1/4)^{5/2}} \ge 1- \dfrac{36\sqrt{2}}{1+4\beta -16\beta e}. \end{aligned}$$

The expression on the right is positive for $e< e_{0}-\dfrac{9\sqrt{2}}{4\beta }$, which is a positive bound only for $\beta > 9\sqrt{2}-1/4$.

We have explored numerically how $\varLambda (L_{y_{2}}^{+})$ varies with respect to both parameters. In Fig. 7 we show the region in the $(\beta ,e)$ plane for which $\varLambda (L_{y_{2}}^{+})$ is positive or negative. We see that for $\beta >9\sqrt{2}-1/4$ and any admissible value of e, $\varLambda (L_{y_{2}}^{+})>0$. In fact, the region obtained in Proposition 10 is smaller than the region where $\varLambda (L_{y_{2}}^{+})>0$.

Fig. 7

For the equilibrium point $L_{y_{2}}^{+}$ the regions in the $(\beta ,e)$ plane in which $\varLambda <0$ and $\varLambda >0$. The curve plotted corresponds to $e=e_{0}-\frac{9\sqrt{2}}{4\beta }$ (see Proposition 10)

When $\varLambda (L_{y_{2}}^{+})>0$, using (21), the equilibrium point $L_{y_{2}}^{+}$ has at least two pure imaginary eigenvalues,

$$\begin{aligned} \pm \lambda _{2}=\pm w\,\mathrm {i}, \;w>0, \quad \pm \lambda _3=\pm \mathrm {i}, \end{aligned}$$

and the third eigenvalue can be real or pure imaginary depending on the sign of $\varGamma +\sqrt{\varLambda }$. Numerically we have observed that the equilibrium point is linearly stable, that is, center $\times$ center $\times$ center for the values explored ($\beta \le 1000$).

5.2.2 Stability of the equilibrium points on the x axis

We consider the points $L_{x_{i}}^{+}$, $i=1,2,3$. Using (8), we have that

$$\begin{aligned} 1-\dfrac{1}{\varDelta \overline{x}_{i}} \left( \dfrac{\overline{x}_{i}-1/2}{r_{1}^3}+\dfrac{\overline{x}_{i}+1/2}{r_{2}^3} \right) = \dfrac{\beta }{\varDelta }\left( \dfrac{1}{\overline{x}_{i}^3}-\dfrac{2e}{\overline{x}_{i}^4}\right) , \end{aligned}$$

where $r_{1}=|\overline{x}_{i}-1/2|$ and $r_{2}=\overline{x}_{i}+1/2$, $i=1,2,3$. Using the above relation, it is not difficult to see that

$$\begin{aligned} \begin{aligned} V_{yy}(L_{x_{i}}^{+})&= -1 + \dfrac{1}{2 \varDelta \overline{x}_{i}}\left( \dfrac{1}{r_{2}^3}-\dfrac{1}{r_{1}^3} \right) ,\\ V_{xx}(L_{x_{i}}^{+})&= -2V_{yy}(L_{x_{i}}^{+})-\dfrac{2\beta e}{\varDelta \overline{x}_{i}^4},\\ V_{zz}(L_{x_{i}}^{+})&= V_{yy}(L_{x_{i}}^{+}). \end{aligned} \end{aligned}$$

(22)

Using that $\overline{x}_{1} > 1/2$ and $\overline{x}_{i} < 1/2$, $i=2,3$

$$\begin{aligned} V_{yy}(L_{x_{1}}^{+})= & {} -1-\dfrac{1}{2\varDelta \overline{x}_{1}}\dfrac{3\overline{x}_{1}^2+1/4}{(\overline{x}_{1}^2-1/4)^3},\nonumber \\ V_{yy}(L_{x_{i}}^{+})= & {} -1-\dfrac{1}{\varDelta }\dfrac{\overline{x}_{i}^2+3/4}{(1/4-\overline{x}_{i}^2)^3}, \quad i=2,3. \end{aligned}$$

(23)

Lemma 2

For any $\beta >0$ and admissible e, let $\varLambda$ be defined in (18). Then $\varLambda (L_{x_{i}}^{+}) >0$, for $i=1,2,3$.

Proof

Using (22), we can write $\varLambda$ as a quadratic polynomial in the variable $V_{yy}$:

$$\begin{aligned} \varLambda = 9 V_{yy}^2+ 4(2+3\alpha _i) V_{ yy}+ 4 \alpha _i (\alpha _i+4), \end{aligned}$$

where $V_{yy}=V_{yy}(L_{x_{i}}^{+})$, $\alpha _i= \frac{\beta e}{\varDelta \overline{x}_{i}^4}$, and its roots are

$$\begin{aligned} V_{yy}^{\pm }= \frac{-2}{9}\left( 3 \alpha _i+2\pm 2\sqrt{1-6 \alpha _i}\right) , \end{aligned}$$

$i=1,2,3$. If the roots $V_{yy}^{\pm }$ are complex, $\varLambda >0$ for any value of $V_{yy}$. If the roots are real, using that $\alpha _i >0$, $V_{yy}^-> -1 > V_{yy}^{+}$ the claim follows.

We want to study whether eigenvalues (17) are real or complex. Clearly $V_{zz}(L_{x_{i}}^{+})<0$, $i=1,2,3$, so that

$$\begin{aligned} \pm \lambda _3 = \pm w\,\mathrm {i}, \qquad \hbox {for some} \; w>0, \end{aligned}$$

at the three equilibrium points. Using Lemma 2, it is only necessary to study the sign of $\varGamma ^2-\varLambda$ and $\varGamma$.

Lemma 3

For any $\beta >0$ and admissible e, let $\varLambda$ and $\varGamma$ be defined in (18). Then $\varGamma ^2(L_{x_{1}}^{+})< \varLambda (L_{x_{1}}^{+})$.

Proof

Using (19) and the fact that $V_{yy} < -1$, it is enough to study the sign of $1+V_{xx}$. From (22) and (23) we have that

$$\begin{aligned} 1+V_{xx}(L_{x_{1}}^{+}) > 3-\dfrac{2\beta e}{\varDelta \overline{x}_{1}^4}, \end{aligned}$$

and using that $\overline{x}_{1} > s^{*}$ (see Lemma (1) and Proposition 4), we get $1+V_{xx}(L_{x_{1}}^{+})>0$.

From the above results, it follows that the equilibrium point $L_{x_{1}}^{+}$ is a center $\times$ center $\times$ saddle.

Proposition 11

For any $\beta >0$ and admissible e, the eigenvalues given in (17) associated with the equilibrium point $L_{x_{1}}^{+}$ are

$$\begin{aligned} \pm \lambda _{1} \in \mathbb {R}, \quad \pm \lambda _{2}=\pm \sigma \,\mathrm {i}, \;\sigma>0, \quad \pm \lambda _3=\pm w\,\mathrm {i}, \; w>0. \end{aligned}$$

We can prove similar results for $L_{x_{2}}^{+}$ for some values of $\beta$ and e.

Lemma 4

For any $\beta >0$ and admissible e, let $\varLambda$ and $\varGamma$ be defined in (18). Let $f_{1}$ and $f_{3}$ the functions given in (11) and (14), and $s^{*}$ given in Proposition 4. Then, for any fixed value of $\beta$:

• 1. There exists one value $\overline{e} \in (0,e_{0})$ solution of $f_{1}(s^{*})=f_{3}(s^{*})$.

• 2. For $e\in (0,\overline{e})$, $\overline{x}_{2} > s^{*}$ and $\varGamma ^2 (L_{x_{2}}^{+})< \varLambda (L_{x_{2}}^{+})$.

Proof

The first two claims follow directly from the behavior of the functions $f_{1}$ and $f_{3}$. The third claim follows from the fact that $1+V_{xx}(L_{x_{2}}^{+})>0$ as in Lemma 3.

When the hypothesis of Lemma 4 applies, $L_{x_{2}}^{+}$ is also a center $\times$ center $\times$ saddle, and we obtain the following proposition. Numerically, for values $\beta \le 100$, we have observed that $\varGamma ^2(L_{x_{2}}^{+})< \varLambda (L_{x_{2}}^{+})$ for all values of e, but we have not been able to prove it.

Proposition 12

For any $\beta >0$ and admissible $e<\overline{e}$, where $\overline{e}$ is given in Lemma 4, the eigenvalues given in (17) associated with the equilibrium point $L_{x_{2}}^{+}$ are

$$\begin{aligned} \pm \lambda _{1} \in \mathbb {R}, \quad \pm \lambda _{2}=\pm \sigma \,\mathrm {i}, \;\sigma>0, \quad \pm \lambda _3=\pm w\,\mathrm {i}, \; w>0. \end{aligned}$$

Finally, we have not been able to study analytically the sign of $1+V_{xx}(L_{x_{3}}^{+})$. Numerically, for values $\beta \le 100$, we have observed that it is negative, so that $\varGamma ^2(L_{x_{3}}^{+})- \varLambda (L_{x_{3}}^{+})>0$. Furthermore $\varGamma ^2(L_{x_{3}}^{+})<0$ so the equilibrium point is linearly stable.

6 Global dynamics of the rectilinear Manev R4BP

As we said in Sect. 2, the $(z,\dot{z})$ plane is an invariant plane of the Manev R4BP. Equation (3) reduces to the first-order system

$$\begin{aligned} \dot{z}= & {} Z,\nonumber \\ \dot{Z}= & {} -\frac{z}{\varDelta } \left[ \beta \left( \frac{1}{|z|^3}- \frac{2e}{z^{4}}\right) + \frac{2}{(1/4+z^{2})^{3/2}}\right] . \end{aligned}$$

(24)

Furthermore, due to the symmetry $(z,Z) \rightarrow (-z,-Z)$, it is enough to study the problem for $z>0$. We consider in this section the rectilinear Manev R4BP, that is, the subproblem given by (24) for $z>0$.

The problem can be written in Hamiltonian form with Hamiltonian function associated

$$\begin{aligned} H= H(z, Z)= \frac{1}{2} Z^2 + V(z), \end{aligned}$$

(25)

where the potential $V(z)=-\varOmega (0,0,z)$ [see (4)], can be written for $z>0$ as

$$\begin{aligned} V(z)= -\frac{1}{\varDelta } \left[ \beta \left( \frac{1}{z}- \frac{e}{z^{2}}\right) + \frac{2}{(1/4+z^{2})^{1/2}}\right] . \end{aligned}$$

V(z) possesses a unique critical point, which is a local minimum, that coincides with the equilibrium point $\overline{z}$ [see Eq. (9)]. The constant value of $H=h$, called energy, is related to Jacobi constant (7) by $H=-C/2$. Clearly, the energy of the equilibrium point $L_{z}^{+}$ is negative.

Analogously to the 2-body problem, we will say that a solution of (24), (z(t), Z(t)), is hyperbolic if comes from (and arrive at) infinity with positive velocity, and it is parabolic if come from (and arrive at) infinity with zero velocity. Next result states that the solutions of the rectilinear Manev R4BP are similar to the solutions of the one-dimensional two-body problem: periodic (bounded), parabolic and hyperbolic orbits.

Theorem 3

For any $\beta >0$ and admissible e, let $L_{z}^{+}=(0,0,\overline{z})$ be the equilibrium point of the Manev R4BP given in Proposition 1. Let H be Hamiltonian (25) and $\overline{h}=H(\overline{z},0)$. If (z(t), Z(t)) is a solution of the rectilinear Manev R4BP problem with $h=H(z(t),Z(t))$, then

• (i) it is periodic, if and only if, $\overline{h}< h < 0$,

• (ii) it is parabolic, if and only if, $h=0$,

• (iii) it is hyperbolic, if and only if, $h>0$.

Proof

Since this restricted problem is given by an autonomous Hamiltonian with one-degree of freedom, any solution of system of (24) lies on a level curve of $H=h$. Clearly, $H \ge V(\overline{z})=\overline{h}$.

For $h \in (\overline{h}, 0)$, the level curve $H= h$ in the (z, Z) plane cuts the positive z axis in two points. Using the symmetry $(z, Z)\rightarrow (z, -Z)$, the crossings are perpendicular, so the level curve is symmetric with respect to the z axis, and the solution is periodic. If $h= 0$, the level curve is $Z^2=-2V(z)$, which corresponds to the parabolic solution. Finally, if $h>0$, the level curve is $2h-2V(z)=Z^2 \longrightarrow 2h$ when $z\nearrow \infty$. That correspond to the hyperbolic orbits.

The phase portrait of the rectilinear Manev R4BP is shown (for a specific values of $\beta$ and e) in Fig. 8. Notice that, as stated in Theorem 1, solutions cannot accumulate at $z=0$.

Fig. 8

Phase portrait of Hamiltonian system (24) for $\beta =1$ and $e=\frac{1}{4}$

Recall that we have seen that the equilibrium point $L_{z}^{+}$ of the Manev R4BP has a center in the z direction (see Sect. 5.1). The Lyapunov Center Theorem ensures that if the ratios between the associated eigenvalues of $L_{z}^{+}$ are not integers, there exists a family of periodic orbits emanating from the equilibrium point. Theorem 3 shows that this family of periodic orbits (p.o.) exists for all values of $\beta$ and admissible e (vertical p.o. from now on).

It would be interesting to explore the existence of orbits connecting the vertical periodic orbits with planar orbits (in the (x, y) plane). For this reason, we explore numerically the linear stability of the family of vertical p.o. as periodic orbits of the whole Manev R4BP for different values of $\beta$ and e.

Fixed a p.o., its linear stability is given by the eigenvalues of monodromy matrix, which due to the Hamiltonian structure of the Manev R4BP are $1,1,\lambda _1,1/\lambda _1, \lambda _2,1/\lambda _2$. The stability parameters associated are defined as $s_{i}=\lambda _{i}+1/\lambda _{i}$, $i=1,2$. If $s_{i}$ is real and $|s_{i}|>2$, then $\lambda _{i}$ is real; if $s_{i}$ is real and $|s_{i}|\le 2$, then $\lambda _{i}$ is complex of modulus 1; if $s_{i}$ is complex with $Im(s_{i})\ne 0$, then $\lambda _{i}$ is complex of modulus different from 1.

If both stability parameters are real with modulus less (or equal) than 2, then the p.o. is linearly stable and it has associated a center manifold of dimension 5. If both stability parameters are real, one of modulus greater than 2, the other with modulus less than 2, the p.o. has associated stable $W^{s}$ and unstable $W^{u}$ invariant manifolds of dimension 2 each one, and a center manifold of dimension 3. When both stability parameters are real with modulus greater than 2, or both are complex nonreal, the p.o. has associated stable $W^{s}$ and unstable $W^{u}$ invariant manifolds of dimension 3 each one. See  Perko (1996), for example.

Fixed a value of $\beta$ and e we compute the stability parameters along the family of vertical p.o. We look for orbits that are not linearly stable, so the existence of stable/unstable manifolds allows the possibility for connecting orbits with planar ones. The exploration of the existence of such orbits will be the aim of a future work. Here we present the results about the linear stability of the vertical p.o. for different values of the parameters.

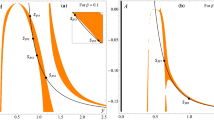
In Fig. 9 we show the behavior of $s_{1}$ and $s_{2}$ for $\beta =1,100$ and $e=0.1, 0.25$. For other values we have obtained similar results. In all the cases explored only two scenarios appear: both stability parameters are real with modulus greater than two (so the four eigenvalues are real), or both stability parameters are complex nonreal (so the four eigenvalues are complex). In all the plots, the red (continuous line) $S^1$-shaped curves corresponds to the value of $Re(s_{1})$ when the stability parameters are complex nonreal, whereas the blue curves (dashed line) corresponds to the case when both $s_{i}$ are real. As $\beta$ gets bigger, the set of values of C such that both $s_{i}$ are real shrinks, and their values get closer to $\pm 2$, but always $|s_{i}|>2$.

Fig. 9

Stability parameters $s_{i}$, $i=1,2$ for the families of vertical p.o. for different values of $\beta$ and e. Continuous lines (in red) correspond to $s_{i}$, $i=1,2$ when they are real. Dashed lines (in blue) correspond to $s_{i}$, $i=1,2$ complex; in that case only $Re(s_{1})$ is plotted. First row: $\beta =1$ and $e=0.1$ (left) and $e=0.25$ (right). Second row: $\beta =100$ and $e=0.1$ (left) and $e=0.25$ (right)

Therefore, all the p.o. explored are unstable and there exist invariant manifolds associated with them. This opens a door to the existence of orbits connecting the vertical p.o. with planar ones. Looking at the stability of the equilibrium points, the best candidates to start with are $L_{x_{1}}^{\pm }$ and $L_{y_{1}}^{\pm }$. Both equilibrium points are of type center $\times$ center $\times$ saddle. Therefore, when the Lyapunov Center Theorem applies, there exist families of p.o. that will inherit the instability of the equilibrium points. Considering suitable values of the Jacobi constant (so the Hill’s regions are open), the exploration of the intersections of the stable and unstable of the corresponding p.o. will show if connections between the p.o. along the z axis and p.o. around the planar equilibrium points can exist.

7 Conclusions

We have studied a spatial R4BP where the gravitational attraction of the central mass is given by a Manev potential ($-1/r +e/r^{2}$), $e>0$, and the other two masses are equal with Newtonian potential ($-1/r$), called Spatial Manev R4BP. The problem depends on two parameters, the ratio of mass of the central body to the mass of one of two other bodies, $\beta$ and the Manev perturbation, e. For instance, due to the repulsive term emanating from the central body, we have proved that it is not possible to have a binary collision between the infinitesimal mass and the central body.

In the present work we have focused on the existence and stability of equilibrium points. An important property is the apparition of equilibrium points in the z axis which are unstable from a global point of view. Moreover, the restriction of the Manev R4BP to this axis is an integrable problem, and a family of periodic orbits emanate from each equilibrium point. We have seen numerically that these periodic orbits inherit their instability.

There are always four equilibrium points on the y axis, and there exist 2, 4 or 6 equilibrium points on the x axis, depending on $\beta$ and e. Two of the equilibrium points on the y axis and two on the x axis are always of type center $\times$ center $\times$ saddle. That means that, when the Lyapunov Center Theorem applies, there exist families of periodic orbits emanating from each equilibrium point, which will be unstable (at least close to the equilibrium points). The invariant manifolds associated with all these periodic orbits can be explored in order to find connections between neighborhoods of the planar equilibrium points and the equilibrium points along the z axis. The existence of such a kind of connections will be the core of future work.