Dynamics of a small body under the action of a Maxwell ring-type N-body system with a spheroidal central body

Abstract

This study outlines some aspects of the dynamics of a small body under the action of a Maxwell-type N-body system with a spheroidal central body. The non-sphericity of the central primary is described by means of a corrective term in the Newton’s law of gravitation and is taken into account during the derivation of the equations of motion of the small body, improving in this way, previous treatments. Based on this new consideration we investigate the equilibrium locations of the small body and their parametric dependence, as well as the zero-velocity curves and surfaces for the planar motion, and the evolution of the regions where this motion is permitted when the Jacobian constant varies.

1 Introduction

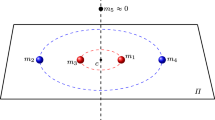
The N-body problem is one of the most important issues in Astronomy and has frequently inspired researchers in order to raise new problems. In the relevant literature there are many pertinent cases, one of which is the so-called restricted N-body regular polygon problem (or Maxwell-type configuration), where ${\upnu }=\text{ N }-1$ of the bodies-members of the system are spherical, homogeneous with equal masses $m$, and are located at the vertices of an imaginary regular $\nu$-gon, while the $\text{ N }\mathrm{th}$ body has a different mass $m_{0}$ and is located at the center of mass of the system (Fig. 1). The relative equilibrium of such formations has been studied, among others, by Elmabsout (1994) and Bang and Elmabsout (2004), while it has been proved (Salo and Yoder 1988; Vanderbei and Kolemen 2007) that this configuration may exist for $\upnu >6$. A similar investigation was made by Vanderbei (2008) who assumed an oblate central mass. A small body, natural or artificial, moves in the vicinity of such a system under the influence of all the primaries yet having no effect on their motion. The problem has been treated by many investigators over the last few years and is also referred to as the ring problem of $(\text{ N }+1)$ bodies (Scheeres 1992; Kalvouridis 1999, 2008; Hadjifotinou and Kalvouridis 2005; Pinotsis 2005; Croustalloudi and Kalvouridis 2007; Barrio et al. 2008, 2009; Papadakis 2009; Bountis and Papadakis 2009; Barrabes et al. 2010; Garcia-Azpeitia and Ize 2011; etc). The initial statement of the problem was based on the assumption that all big bodies create Newtonian force fields. Newton’s theory dominated for many centuries, and still does, since it has been able to explain the motion of the bodies in a very simple way. However, some physical phenomena, such as the motion of the apsidal line of the Moon, which were already known at that time, could hardly be explained within this framework. Newton himself knew that his theory could not give a precise and convincing answer to this problem and for this reason he proposed in the “margin” of his famous and classic work Philosophiae Naturalis Principia Mathematica (Book I, Article IX, Proposition XLIV, Theorem XIV, Corollary 2) an improvement of his universal law of gravity, by inserting a corrective term of the form $1/{\mathrm{r}}^{3}$. Many years later, Maneff (1924) proposed a similar corrective term [see for a very well-documented and detailed historical review, the work of Haranas et al. (2011)]. This corrective term was adjusted by some authors to provide a justification of the perihelion advance of Mercury, or to explain some relativistic effects without using the theory of relativity. In 2004, an improved and interesting version of the gravitational ring $(\text{ N }+1)$-body problem was presented by Arribas and Elipe. It was based on the assumption that the central body of the primaries’ configuration is a spheroid. This fact resulted in a corrective term which was inserted directly in the force function of the system and could also reflect some special physical properties of this body like radiation emission. A little later, Elipe et al. (2007) studied the periodic motions of the particle in such a dynamical system. Here, this corrective term is taken into account during the derivation of the equations of motion of the small body. We improve in this way the expression of the force function of the dynamical system. Although this small difference in the consideration of the problem does not create crucial changes to some dynamical aspects of the problem when the parameter measuring the oblateness is positive (oblate body), it may do so when this parameter is negative (prolate body). In Section 2 below, we give a short outline of the followed process for the derivation of the equations of motion. Based on the new consideration our treatment mainly focuses on the equilibrium locations of the small body and on the regions where planar solutions may exist, mainly when the oblateness parameter is negative. The first issue is discussed in Section 3, where we display the bifurcation diagrams which describe the transitions from a planar equilibrium state to another, as well as the parametric variation of these equilibria. The second issue is discussed in Sections 4 and 5, where we focus on the case of negative oblateness parameter. The areas where the planar motion of the particle is permitted are determined by means of the zero-velocity curves. We describe the evolution of these regions when the Jacobian constant varies and we investigate the areas where the moving particle is trapped.

Fig. 1

The configuration of the problem with the two coordinate systems employed; the inertial frame $\text{ O }\xi \eta \zeta$ and the synodic Oxyz. S is the small body and $P_{i},\text{ i }=0,1,2,\ldots \nu$ are the primaries

2 Equations of motion

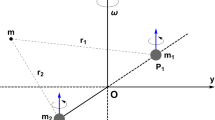
We use an inertial coordinate system $O\xi \eta \zeta$ where plane $O\xi \eta$ coincides with the plane of the primaries and a synodic one Oxyz centered at the mass center of the primaries formation (Fig. 1), the plane Oxy of which coincides with $O\xi \eta$ plane. We assume that the primaries are in relative equilibrium and rotate around the perpendicular axis $O\zeta \equiv Oz$ with constant angular velocity $\omega$. We take the line which connects the central primary $P_{0}$ with a peripheral one, let us say $P_{1}$, as the $x$-axis of the synodic system. The force exerted from the central primary on a peripheral one, let us say $P_{1}$, is

$$\begin{aligned} \overrightarrow{F_{1,0}}=\left[ {\frac{k^{2}m_{0}m}{(P_{1}P_{0} )^{3}}+2\frac{k^{2}Bm_{0} m}{(P_{1} P_{0} )^{4}}}\right] \overrightarrow{P_{1} P_{0} }=-\left[ {\frac{k^{2}\beta m^{2}}{d^{2}}+2\frac{k^{2}\beta Bm^{2}}{d^{3}}}\right] \vec {i} \end{aligned}$$

where $d=\frac{a}{2\sin (\pi /\nu )}$ is the distance $P_{1}P_{0},\,a$ is the side of the regular $\nu$-gon, $k^{2}$ is the Gaussian constant, $\beta =m_{0}/m$ is the ratio of the central mass to a peripheral one (mass parameter) and $B$ is the coefficient of the corrective term. In order that this term is consistent with the Newtonian one, $B$ must be expressed in length units. Here, we express it as the product of a dimensionless coefficient $e$ (oblateness parameter) and the physical quantity a (which is expressed in length units), that is $B=ea$. This choice relates to the normalization process of the physical quantities as it will be seen later in this paragraph. The forces exerted on $P_{1}$ from each of the $\nu -1$ remaining peripheral bodies are given by the relations

$$\begin{aligned} \overrightarrow{F_{1,i}}=\frac{k^{2}m^{2}\sin ^{2}(\pi /\nu )}{a^{2}\sin ^{2}\left[ {(\nu -i+1)(\pi /\nu )} \right] }\overrightarrow{p_{i}} \end{aligned}$$

where $\overrightarrow{p_{i}},i=2,3,\ldots ,\nu$ are the unit vectors along these directions. The projection of these forces on the $x$-axis must satisfy the relation,

$$\begin{aligned} \frac{k^{2}}{a^{2}}m \Lambda +\frac{k^{2}\beta m M^{2}}{a^{2}}+2\frac{k^{2}\beta emM^{3}}{a^{2}}=\omega ^{2}\frac{a}{M}, \end{aligned}$$

(1)

where

$$\begin{aligned} \Lambda =\sum _{i=2}^{\nu } {\frac{\sin ^{2}(\pi /\nu )}{\sin \left[ {(i-1)(\pi /{\nu )}}\right] }}, M=a/d=2\sin (\pi /\nu ) \end{aligned}$$

From (1) we obtain,

$$\begin{aligned} \frac{k^{2}m}{a^{3}\omega ^{2}}=\frac{1}{\Delta } \end{aligned}$$

(2)

where

$$\begin{aligned} \Delta =M(\Lambda +\beta M^{2}+2\beta eM^{3}) \end{aligned}$$

The expression of $\Delta$ depends on all three parameters $\nu ,\,\beta$ and $e$, a fact that is reflected on all dynamical aspects of the system and, because of (2), it must always be positive.

The motion of the small body S in the inertial coordinate system $O\xi \eta \zeta$ is then described by the following equations in matrix form,

$$\begin{aligned} \left[ {{\ddot{\xi }}{\ddot{\eta }}{\ddot{\zeta }}} \right] ^{T}=k^{2}m\left[ {{\begin{array}{lll} {-\frac{\beta \xi }{r_{o/A}^{3}}-\frac{2ea\beta \xi }{r_{o/A}^{4} }+\sum \limits _{i=1}^\nu {\frac{\xi _{i} -\xi }{r_{i/A}^3 }} } \\ {-\frac{\beta \eta }{r_{o/A}^3}-\frac{2ea\beta \eta }{r_{o/A}^{4} }+\sum \limits _{i=1}^\nu {\frac{\eta _{i} -\eta }{r_{i/A}^3 }} } \\ {-\frac{\beta \zeta }{r_{o/A}^{3}}-\frac{2ea\beta \zeta }{r_{o/A}^{4} }+\sum \limits _{i=1}^\nu {\frac{-\zeta }{r_{i/A}^{3}}}} \\ \end{array}}}\right] \end{aligned}$$

(3)

where

$$\begin{aligned} r_{o/A}^2 =\xi ^{2}+\eta ^{2}+\zeta ^{2}, r_{i/A}^2 =(\xi _{i} -\xi )^{2}+(\eta _{i} -\eta )^{2}+\zeta ^{2}, i=1,{\ldots } \nu \end{aligned}$$

are the distances of the particle from the primaries and symbol $A$ denotes the inertial frame. We normalize all physical quantities of (3) by using the transformation (Kalvouridis 1999),

$$\begin{aligned} \xi ^{*}=\xi /a,\quad \eta ^{*}=\eta /a,\quad \zeta ^{*}=\zeta /a, \quad m_{o} =\beta m, \quad t^{*}=\omega t=t \end{aligned}$$

The asterisk denotes the dimensionless quantities and in the final form we omit it. Without loss of generality we assume that $\omega =1$. By transforming the normalized equations in the synodic system, we obtain the following system of second-order differential equations,

$$\begin{aligned} \ddot{x}-2\dot{y}=\frac{\partial U}{\partial x}=U_{x},\quad \ddot{y}+2\dot{x}=\frac{\partial U}{\partial y}=U_{y},\quad \ddot{z}=\frac{\partial U}{\partial z}=U_{z} \end{aligned}$$

(4)

where

$$\begin{aligned} U(x,y,z)=\frac{1}{2}(x^{2}+y^{2})+\frac{1}{\Delta }\left[ {\beta \left( {\frac{1}{r_{0} }+\frac{e}{r_{0}^2}} \right) +\sum _{i=1}^\nu {\frac{1}{r_{i}}}} \right] \\ r_{0} =\left( {x^{2}+y^{2}+z^{2}} \right) ^{1/2}, \quad r_i =[(x-x_i )^{2}+(y-y_i )^{2}+z^{2}]^{1/2}\nonumber \end{aligned}$$

(5)

From Eqs. (4) we obtain a Jacobian-type integral of motion,

$$\begin{aligned} \dot{x}^{2}+\dot{y}^{2}+\dot{z}^{2}=2U(x,y,z)-C \end{aligned}$$

(6)

3 Equilibrium points and equilibrium zones: parametric evolution

The equilibrium positions of the small body are the solutions of the nonlinear algebraic system

$$\begin{aligned} \frac{\partial U}{\partial x}=U_{x} =0, \frac{\partial U}{\partial y}=U_{y} =0, \frac{\partial U}{\partial z}=U_{z}=0 \end{aligned}$$

(7)

and are obtained numerically. Among the existing numerical methods we have chosen to apply the well-known Newton–Raphson method which is simple, and adequately efficient.

In the gravitational case of the ring problem, Kalvouridis (1999) proved that all equilibrium positions lie on the xy-plane of the synodic system. In this case, the three quantities $\Lambda ,\, \mathrm{M}$ and $\Delta$, are positive, since the two parameters $\nu$ and $\beta$ are always positive. This means that the last Eq. of (7)

$$\begin{aligned} U_{z} =\frac{-z}{\Delta }\left( {\frac{\beta }{r_{o}^{3}} + \frac{2e\beta }{r_{o}^{4}}+\sum _{i=1}^\nu {\frac{1}{r_{i}^{3}}}} \right) =0, \end{aligned}$$

in the case of $e=0$, is satisfied only if $z=0$. The equilibrium positions can be grouped on either five $(\text{ A }_{1},\, \text{ A }_{2},\, \text{ B },\,\text{ C }_{2},\, \text{ C }_{1})$ or three $(\text{ A }_{1},\, \text{ C }_{2}$ and $\text{ C }_{1})$ equilibrium zones, each one with $\nu$ equidistant equilibria. All the equilibria which belong to a particular zone are “dynamically equivalent” positions in the sense that they are characterized by the same Jacobian constant and have the same status of stability. For each $\nu$ there is a unique marginal value $\beta =l_{\nu }$ at which a transition (bifurcation) from five to three equilibrium zones occurs (Croustalloudi and Kalvouridis 2007).

In a similar way we can prove that if $e>0$, then all the equilibrium points lie on the xy-plane. The equilibria are distributed on either five or three equilibrium zones as in the previous purely gravitational case. However, this transition occurs along a bifurcation curve which is different for each $\nu$. We must stress that, for the considered problem the symmetric distribution of the equilibrium points is preserved regardless of the value of parameter $e$. Figure 2 shows the evolution of the bifurcation curve in the (e, $\beta$) plane for $\nu =7$. In the area below this curve (area I) there are five equilibrium zones, while in the area above it (area II) there are only three equilibrium zones. As $\nu$ increases, the corresponding bifurcation curves are displaced towards the upper part of the diagram and thus towards larger values of $\beta$.

Fig. 2

Bifurcation curve for $\nu =7$

In the diagrams of Fig. 3 we show the variations with $e>0$ of the distance (rad) of the equilibrium zones from the origin (Fig. 3a) as well as, of the Jacobian constant $C$ of these zones respectively (Fig. 3b), for a sample case where $\nu =7$ and $\beta =2$. As it is seen, the distances of the three zones $\text{ A }_{1},\, \text{ C }_{2}$ and $C_{1}$ slightly change when parameter $e$ increases. Regarding B and $\text{ A }_{2}$ zones, their distances vary in such a way, that the two curves finally meet at a point. This occurs at a value of $e$ which, together with the considered value of $\beta$, gives a point on the bifurcation curve of Fig. 2 drawn for $\nu =7$. A similar situation is observed in Fig. 3b, where the curves showing the variation of the Jacobian constant of all zones evolve almost linearly. The curves of the $\text{ A }_{1},\, \text{ C }_{2}$ and $\text{ C }_{1}$ zones are characterized by almost the same constant slope and follow a decreasing path as parameter $e$ increases. The curves of the $\text{ A }_{2}$ and B zones approach each other until a particular value of $e$, where these two curves meet (Fig. 3b). This meeting point is the same as the one discussed in the previous diagram of Fig. 3a.

Fig. 3

Variations of equilibrium zones for $\nu =7, \,\beta =2$. a Variation of their distances with $e$, b variation of their Jacobian constants with $e$

When $e<0$, and by taking relation (2) into account, we must exclude those values of $e$ which make $\Delta$ negative or zero. Therefore the values of $e$ must satisfy the relation,

$$\begin{aligned} e>-\frac{\Lambda +\beta M^{2}}{2\beta M^{3}} \end{aligned}$$

(8)

In this case, besides the equilibrium zones known from the gravitational case, two new equilibrium zones which lie on the same plane Oxy, namely $\text{ E }_{1}$ and $\text{ E }_{2}$, may appear. These locations evolve inside the circle of the peripheral primaries and very close to the central primary (Fig. 4). The equilibria of $\text{ E }_{1}$ zone lie on the radii, where the equilibria that belong to $\text{ A }_{1}$ and $\text{ C }_{1}$ zones also appear (collinear equilibria), while those of $\text{ E }_{2}$ zone lie on the same radii, where the equilibria of $\text{ A }_{2}$, B and $\text{ C }_{2}$ are traced (triangular equilibria).

Fig. 4

Distribution of the planar equilibrium locations. The large black dots show the positions of the primaries, while the tiny triangles, squares and circles show the positions of the equilibria

Figure 5 is a bifurcation diagram showing the number of the existing equilibrium zones on the xy-plane for $\upnu =7$ and for various values of $e$ and $\beta$. There are three bifurcation curves, $\text{ BC }_{0},\, \text{ BC }_{1}$ and $\text{ BC }_{3}$ which intersect, converge or coincide in some parts of the diagram, this way dividing the area $(e, \beta )$ into five sub-regions. We have found that there are some general rules which govern the number and the type of the existing equilibrium zones in these sub-regions. These are summarized as follows:

• On the left side of $\text{ BC }_{0}$, B and $\text{ A }_{2}$ zones appear.

• On the left side of $\text{ BC }_{1},\, \mathrm{E}_{1}$ and $\mathrm{A}_{1}$ zones disappear.

• On the left side of $\text{ BC }_{2},\, \mathrm{A}_{2}$ and $\mathrm{E}_{2}$ zones do not exist.

Provided that in region II five equilibrium zones exist, namely, $\text{ C }_{2},\, \mathrm{E}_{2},\, \text{ E }_{1},\, \text{ A }_{1},\, \text{ C }_{1}$ zones, then according to these rules, in region I there are seven zones, namely, $\text{ C }_{2},\, \mathrm{B},\, \mathrm{A}_{2}, \,\mathrm{E}_{2},\, \text{ E }_{1},\, \text{ A }_{1}$ and $\text{ C }_{1}$, in region IV five equilibrium zones exist, namely, $\text{ C }_{2},\, \mathrm{B},\, \mathrm{A}_{2},\, \mathrm{E}_{2}$ and $C_{1}$ zones and in region III there are three zones, namely $C_{2},\, \mathrm{E}_{2}$ and $\text{ C }_{1}$. Finally, in region V the existing zones are three; $\text{ C }_{2},\, \mathrm{B}$ and $\text{ C }_{1}$. The bifurcation diagram is very useful and must be plotted for a particular configuration $(\nu )$ during the exploration of the equilibrium points and before the investigation of any other dynamical aspect of the problem.

Fig. 5

$\upnu =7$. The three bifurcation curves $\text{ BC }_{0},\text{ BC }_{1}$ and $\text{ BC }_{2}$ and the five regions (I–V) with the number of the existing equilibrium zones on the xy-plane

Figures 6a, b show respectively the variations of the distances (rad) from the origin and of the Jacobian constants $C$ of the equilibrium zones with $e$ respectively for a configuration with $\nu =7, \beta =2$. It is observed that $\text{ C }_{1,} \text{ B }$, and $\text{ C }_{2}$ zones retain virtually invariable distances from the origin for the considered interval of values of $e$ (Fig. 6a). This does not happen with the remaining four zones which converge to a point. Beyond this point only the three previously mentioned zones $\text{ C }_{1,}\text{ B }$, and $\text{ C }_{2}$ exist. A similar situation is observed in Fig. 6b, where the three curves showing the variation of the Jacobian constants C of $\text{ C }_{1,} \text{ B }$, and $\text{ C }_{2}$ zones have an increasing slope, which means that as the absolute value of $e$ increases their Jacobian constants increase too. The curves corresponding to the remaining four zones converge to a point and then disappear. This change is due to the fact that when $e$ takes small absolute values, then the considered set of parameters $(e, \beta )$ gives a point in region I of the bifurcation diagram (Fig. 5), where all seven equilibrium zones exist. However, by continuously increasing the absolute value of $e$, the set of parameters $(e, \beta )$ lead to a point in region V of the same diagram.

Fig. 6

Regular polygon configuration with $\upnu =7, \beta =2$. a Variation of the distances of the equilibrium zones with $e$, b variation of the Jacobian constants of the equilibrium zones with $e$

In addition to the planar equilibria when $e<0$ and provided that condition (8) is satisfied, two out-of-plane equilibria $\text{ L }_{-Z}$ and $\text{ L }_{+Z}$ appear on the $z$-axis of the synodic system and in symmetric positions with respect to the xy-plane.

Figures 7a, b show respectively the variation of the distance (rad) from the origin and of the Jacobian constant $C$ respectively, with $e$ for $\nu =7$ of the out-of-plane equilibria for two values of $\beta$ ($\beta =2$ and $\beta =5$). In Fig. 7a, we observe that as $e$ decreases, the distance of these points from the origin increases and the two curves drawn for $\beta =2$ and $\beta =5$, decline. In Fig. 7b we observe that for very small absolute values of $e$, the out-of-plane equilibria are characterized by very large values of the Jacobian constant. As this absolute value increases there is an abrupt decrement of the curves and after that, the Jacobian value remains almost constant. Both curves drawn for $\beta =2$ and $\beta =5$ evolve very close to each other. This means that the Jacobian constant $C$ displays nearly identical variety patterns every time we have relatively small mass parameters.

Fig. 7

$\upnu =7, \beta =2$ and $\beta =5$. a $e$-rad curves, b $e$-C curves

We have numerically investigated the linear stability of the equilibria by computing the roots of the characteristic polynomial of their variational equations for $\nu \le 36, \beta \in \left[ {1.0,500.} \right] , e\in \left[ {-0.3,0.8} \right]$ (considering only the triads $\nu ,\,\beta ,e$ for which $\Delta >0$) and we have found that for these values the existing equilibria are unstable.

4 Zero-velocity curves and surfaces in the planar motion

By means of relation (6) and by assuming particle motions on the xy-plane, we draw the networks of zero-velocity curves which for each value of $C$, separate the regions of this plane where motion is permitted (positive kinetic energy) from those where this motion is forbidden (negative kinetic energy). By considering a third axis which counts the values of the Jacobian constant $C$, we obtain, for each zero-velocity diagram, a corresponding three-dimensional plot like the one shown in Fig. 8b, called zero-velocity surface of particle planar motion. The gravitational case has been studied in a previous paper by Kalvouridis (1999). In the 3D plot, a “chimney” evolves around each primary. The particle is permitted to move inside the “chimney” and under the zero-velocity surface. The “chimneys” around the peripheral primaries are exactly the same in size since these primaries are assumed to have equal masses. However, the size of the central “chimney” depends on the value of parameter $\beta$. If $\beta >1$, then the central “chimney” is larger than a peripheral one. Similar pictures are obtained if we consider that for the central primary $e>0$. In the latter case, the size of the central “chimney” is influenced by both parameters $\beta$ and $e$.

Fig. 8

a Networks of zero-velocity curves, b zero-velocity surface for $\beta =2$ and $e=-0.05$, c detail of the “folding” in the neighborhood of the central primary

The situation changes when $e<0$. Then a “folding” of the central “chimney” that surrounds the central primary, starts to form (Fig. 8b, c). As a consequence, a closed area of non-permitted motion in the immediate vicinity of $\text{ P }_{0}$ is created (dark area around the central primary of Fig. 8a). This region is surrounded by another narrow annular region of permitted motion.

5 Evolution of particle motion regions

For a particular set of parameters, the way that the regions of permitted motion on the xy-plane evolve, depends on the $C_{Li}$ values of the Jacobian constants of the equilibria. At these values, bifurcations of the topology occur and, as a result, the evolution of permitted motion regions is directly related to the $C_{Li}$ sequence. Trapping regions of the small particle, that is regions where its motion is bound, are formed for certain values of the Jacobian constant (Kalvouridis 1999). A similar evolution occurs when $e>0$. However, changes happen when $e<0$. Figure 9 shows the evolution of the areas where planar motion is permitted in an application with $\nu =7,\, \beta =2$ and $e= -0.05$. Then,

$$\begin{aligned} C_{E1}\approx C_{E2}> C_{B}> C_{A1 }> C_{A2}> C_{C1}> C_{C2} \end{aligned}$$

When $C> C_{E1}\approx C_{E2}$ (Fig. 9a), there are only: (1) $\nu$ closed areas of permitted motion which evolve around the $\nu$ peripheral primaries and constitute areas of trapped motion and (2) another larger limit curve which surrounds all the $\nu$ closed areas, beyond which the motion of the particle is free on the xy-plane. In this case there is no closed curve around the central primary where motion is permitted. At $C=C_{E1}\approx C_{E2}$ we have the first bifurcation point since, for lower values of $C$, two new closed zero-velocity curves which surround the central primary appear. Initially, these curves which form a narrow ring area that surrounds the central primary, are very close to each other (Fig. 9b and embedded detail). However, as $C$ decreases $(C_{E1}\approx C_{E2}>C>C_{B})$ this ring area enlarges (Fig. 9c). The particle is trapped either inside this ring area, or inside the closed areas around the peripheral primaries (white areas), while it is free to move outside the external closed zero-velocity curve which surrounds all the primaries.

Fig. 9

Evolution of the regions of permitted motion (white areas) for $\nu =7,\, \beta =2,\, e=-0.05$, a $C=12$, b $C=11.9$, c $C=7.85$, d $C=7.57197553$, e $C=7.54$, f $C= 7.50317263$, g $C=7.45$, h $C= 7.41838529$, i $C=7.37392456$, j $C=7.2$, k $C= 7.1$

When $C=C_{\mathrm{B}}$, the closed areas around the peripheral primaries touch each other at $\upnu$ points which coincide with the points of the B zone (Fig. 9d). Then, for $C_{\mathrm{B}}>C>C_{A1}$, a united closed area of permitted motion is created (Fig. 9e). Therefore, for these values of C, two trapping regions exist.

Another bifurcation in the evolution of the zero-velocity curves occurs when $C=C_{\mathrm{A}1}$ (Fig. 9f). For lower values of $C(C_{\mathrm{A}1 }>C>C_{\mathrm{A}2})\nu$ channels of communication between the two previously described trapping regions are created (see the white area in Fig. 9g) and $\nu$ isolated “islands” of non-permitted motion in the vicinity of the peripheral primaries are formed. However, the particle, as we have previously mentioned, is free to move outside the external limiting zero-velocity curve. For $C=C_{\mathrm{A}2}$ these “islands” are reduced to points which coincide with the equilibria of the $\mathrm{A}_{2}$ zone, while for even lower values of $C (C_{\mathrm{A}2}>C >C_{C1})$ a new united large, closed area of permitted motion is created around all the primaries (Fig. 9h). This area encircles a very small closed region which evolves around the central primary. When $C=C_{C1}$, the $\nu$ parts of the colored forbidden area touch each other at the equilibria of the $\text{ C }_{1}$ zone. From this point on, $\nu$ channels of intercommunication between the internal area of permitted motion and the external one are created (Fig. 9i). As $C$ decreases $(C_{C1}>C>C_{C2})$, the $\nu$ “islands” of non-permitted motion shrink until, at $C=C_{C2}$, they disappear. Finally, for even lower values $C\le C_{C2}$, the motion of the particle is free in the xy-plane, except in a very small closed area around the central primary (Fig. 9k).

6 Conclusions and remarks

We have reprocessed the ring ($\text{ N }+1$)-body problem with a spheroidal central mass and we have studied some aspects of the dynamics of the small body in such a system. Examining the corrective term that describes the influence of the oblateness from a fresh perspective, we have presented some results which mainly concern the case where the oblateness parameter $e$ is negative (prolate body). We have observed that the folding of the central “chimney” in the zero-velocity surfaces towards its interior occurs immediately after $e$ becomes negative and for very high values of the Jacobian constant. As a consequence, when $C$ decreases, the zero-velocity curves on the xy-plane which evolve near the central primary form a small, almost circular area inside which the motion of the particle is forbidden. This area is surrounded by a narrow, almost circular ring-type area where motion is both permitted and trapped. Regarding the equilibrium positions of the particle, two new equilibrium zones ($\text{ E }_{1}$ and $\text{ E }_{2}$), as well as two out-of-plane equilibria appear. These zones may be seven, five or three according to the values of $\beta$ and $e$. The relative bifurcation diagram, consists of three bifurcation curves which intersect and divide the $(\beta ,e)$-plane into five regions. Within each region a different number of equilibrium zones or even different zones exist. Regarding the permitted motion regions, as well as the trapping ones, their evolution depends on the $\beta$ and $e$ and consequently on the number and the types of the existing equilibrium zones for a particular pair $( \beta , e)$. It also depends on the Jacobian constants $C_{\mathrm{Li}}$ of the existing zones and is directly related to the sequence of $\text{ C }_{\mathrm{Li}}$. At the values $C=C_{\mathrm{Li}}$, bifurcations of the topology occur which directly influence the number of the trapping regions.

Closing this article we would like to express our intention to enrich the information concerning this dynamical system by investigating various types of particle planar and three-dimensional motions, such as simple and multiple periodic ones, symmetric and asymmetric orbits, etc.