Study of lunar gravity assist orbits in the restricted four-body problem

Abstract

In this paper, the lunar gravity assist (LGA) orbits starting from the Earth are investigated in the Sun–Earth–Moon–spacecraft restricted four-body problem (RFBP). First of all, the sphere of influence of the Earth–Moon system (SOIEM) is derived. Numerical calculation displays that inside the SOIEM, the effect of the Sun on the LGA orbits is quite small, but outside the SOIEM, the Sun perturbation can remarkably influence the trend of the LGA orbit. To analyze the effect of the Sun, the RFBP outside the SOIEM is approximately replaced by a planar circular restricted three-body problem, where, in the latter case, the Sun and the Earth–Moon barycenter act as primaries. The stable manifolds associated with the libration point orbit and their Poincaré sections on the SOIEM are applied to investigating the LGA orbit. According to our research, the patched LGA orbits on the Poincaré sections can efficiently distinguish the transit LGA orbits from the non-transit LGA orbits under the RFBP. The former orbits can pass through the region around libration point away from the SOIEM, but the latter orbits will bounce back to the SOIEM. Besides, the stable transit probability is defined and analyzed. According to the variant requirement of the space mission, the results obtained can help us select the LGA orbit and the launch window.

1 Introduction

In the Earth–Moon system, the lunar gravity assist (LGA) has a significant effect on the path of a spacecraft flying close to the Moon. This phenomenon has been applied to many space missions and studied by numerous researchers (Dunham and Davis 1985; Kawaguchi et al. 1995; Wilson and Howell 1998; Penzo 1998; Ocampo 2003; Qi and Xu 2015). However, the previous studies about the LGA orbits were confined to the patched conic model or the Earth–Moon–spacecraft restricted three-body problem (RTBP). The influence of the Sun on the LGA orbits was often neglected. In this paper, we intend to investigate the LGA orbits in the Sun–Earth–Moon–spacecraft restricted four-body problem (RFBP). In general, the general RFBP system is time dependent; hence, some mature theories established in the autonomous CRTBP system, such as the libration point orbit and the invariant manifolds, will be discarded in the RFBP. One of the techniques used to approximate the four-body dynamics, or in general the n-body problem, is the coupled restricted three-body problem approximation: Partial orbits from different restricted problems are connected into a single trajectory, yielding energy efficient transfers to the Moon (Koon et al. 2001), interplanetary transfers (Dellnitz et al. 2006) or very complicated itineraries (Gomez et al. 2004). Parker (2006) used the coupled three-body model to systematically construct families of ballistic lunar transfers. The three-body sphere of influence (3BSOI) was proposed to assess which restricted three-body model should be adopted. Another technique used to approximate the four-body dynamics is the bicircular model (BCM). Taking the Sun–Earth–Moon system as an example, the BCM assumes that the Earth and the Moon are revolving in circular orbits around the Earth–Moon barycenter (EMB); meanwhile, the Sun and the EMB are also assumed in the circular orbits around their common center of mass. Castelli (2012) investigated the role played by a couple of the planar circular restricted three-body problem in the approximation of the BCM. The two restricted three-body problems are the Earth–Moon CR3BP and the Sun–EMB CR3BP, where, in the latter case, the Sun and the EMB act as primaries. The comparison of the mentioned systems leads to the definition of regions of prevalence in the space where one of the restricted problems performs, at least locally, the best approximation of the BCM and therefore it should be preferred in designing the trajectory. Using the Lagrangian coherent structures (LCSs) as substitutes, Qi et al. (2012) proposed the time-dependent invariant manifolds to design the Earth–Moon transfer based on the Sun–Earth–Moon BCM. Yagasaki (2004) constructed an Earth-to-Moon transfer with low cost and moderate flight time under the framework of the BCM. The design problem of transfers connecting low Earth orbits with halo orbits around libration points of the Earth–Moon CRTBP using impulsive maneuvers was treated under the Sun–Earth–Moon BCM by Zanzottera et al. (2012). Oshima and Yanao (2014) studied the mechanism of gravity assist in the Sun–Earth–Moon–spacecraft system based on the BCM and the bielliptic model, respectively. Qi et al. (2014) investigated the gravitational lunar capture by the minimum capture eccentricity under Sun–Earth–Moon BCM. Besides, Scheeres (1998) derived a restricted Hill four-body problem and applied it to analyzing the parameter values in the neighborhood of the Earth–Moon–Sun system.

In this paper, the undertaken model considered here for the restricted four-body dynamics is the Sun–Earth–Moon planar bicircular model (PBCM). In addition, among the LGA orbits, the orbits starting from the region near the Earth are most interesting and useful for us. Therefore, the goal of this paper is to investigate the kinetic characters of this kind of LGA orbits under the Sun–Earth–Moon PBCM. According to the Sun–Earth–Moon PBCM, when the spacecraft is near the EMB, the influences of the Earth and the Moon on the LGA orbit are dominant, but the effect of the Sun may be relatively slight. Hence, first of all, we can approximately analyze the LGA orbits based on the Earth–Moon PCRTBP or patched conic approach. When the spacecraft is far away from the EMB, the influence of the Sun on the LGA orbit will increase and the gravities from the Earth and the Moon can be concentrated at the EMB approximately. Under this circumstance, the PBCM can be regarded as the Sun–EMB PCRTBP approximately. Based on the Sun–EMB PCRTBP, we can preliminarily apply the mature theory of the invariant manifolds to analyzing the LGA orbits. Finally, using the results of the patched model, the LGA orbits under the complete PBCM will be investigated.

According to the discussion above, this paper is divided into five parts. In Sect. 2, we introduce the dynamical models of our study, including the PCRTBP and the PBCM. In Sect. 3, the LGA orbits, the sphere of the influence of the Earth–Moon system and the influence of the Sun on the LGA orbits are investigated. In Sect. 4, the invariant manifolds and their Poincaré sections are introduced under the framework of the Sun–EMB PCRTBP. In Sect. 5, the LGA orbits based on the PBCM are analyzed. The patched LGA orbits and the stable transit probability are proposed and discussed. Finally, the conclusions of this paper are presented in Sect. 6.

2 Dynamical models

In this section, the PCRTBP and the PBCM are introduced as the dynamical models of our study.

2.1 Planar circular restricted three-body problem

In this paper, the planar circular restricted three-body problem (PCRTBP) is one of the dynamical models we will use. The definition of this well-known model will not be repeated here. The readers can refer to the book of Szebehely (1967) for the details of this model and the definition of the normalized distance, mass and time units. We assume that $m_4$, $m_1$, $m_2$ and $m_3$ represent the mass of the Sun, the Earth, the Moon and the spacecraft, respectively. Two specific realizations of the PCR3BP are considered here. The first one is the Earth–Moon–spacecraft PCRTBP (see Fig. 1a). In the dimensionless Earth–Moon rotating coordinates, the origin is taken at the Earth–Moon barycenter (EMB) and the mass parameter of the system $\mu = \mu _{\mathrm{EM}} ={m_2 }/{(m_1 +m_2 )}=0.01215$. Hence, the Earth is placed at $(-\mu _{\mathrm{EM}},0)$ and the Moon is placed at $(1-\mu _{\mathrm{EM}},0)$. The second one is the Sun–EMB–spacecraft PCRTBP (see Fig. 1b). In the dimensionless Sun–EMB rotating coordinates, the origin is taken at the Sun–EMB barycenter (SEB) and the mass parameter of the system $\mu =\mu _\mathrm{SE} ={(m_1 +m_2 )}/{(m_1 +m_2 +m_4 )}=3.04042\times 10^{-6}$. Correspondingly, the Sun is placed at $(-\mu _\mathrm{SE},0)$ and the EMB is placed at $(1-\mu _\mathrm{SE},0)$.

Fig. 1

The Earth–Moon–spacecraft PCRTBP (a) and the Sun–EMB–spacecraft PCRTBP (b) in the dimensionless rotating coordinates

Fig. 2

PBCM in the dimensionless Earth–Moon rotating coordinates

For the general PCRTBP, the equations of motion of the massless body in dimensionless rotating coordinates in the plane of the primaries can be expressed by (Szebehely 1967)

$$\begin{aligned} \ddot{x}-2\dot{y}= & {} \frac{\partial \Omega _3}{\partial x} \nonumber \\ \ddot{y}+2\dot{x}= & {} \frac{\partial \Omega _3}{\partial y}, \end{aligned}$$

(1)

where $\Omega _3$ is the effective potential

$$\begin{aligned} \Omega _3(x,y)=\frac{1}{2}(x^2 +y^2 )+\frac{1-\mu }{r_{p1} }+\frac{\mu }{r_{p2} }+\frac{1}{2}\mu (1-\mu ). \end{aligned}$$

(2)

$r_{p1}$ and $r_{p2}$ denote the instantaneous distances of the massless body from the larger and the smaller primary, respectively.

$$\begin{aligned} r_{p1}= & {} \sqrt{(x+\mu )^{2}+y^2 } \nonumber \\ r_{p2}= & {} \sqrt{(x-1+\mu )^{2}+y^2 }. \end{aligned}$$

(3)

The dynamical system above is independent of the time and has the well-known Jacobi constant (or Jacobi integrals).

$$\begin{aligned} C(x,y,\dot{x},\dot{y})=-(\dot{x}^2 +\dot{y}^2 )+2\Omega _3(x,y). \end{aligned}$$

(4)

Let $C_i$ be the Jacobi constant of the spacecraft at the libration point $L_i$, $i=1,\ldots ,5$. Specifically, for the Sun–EMB PCRTBP, we can calculate $C_1 \approx 3.00090098$, $C_2 \approx 3.00089693$, $C_3 \approx 3.00060808$, and $C_4 =C_5 =3$.

2.2 Planar bicircular model

The planar bicircular model (PBCM) in the restricted four-body problem (RFBP) is other undertaken dynamical model in this paper. In this subsection, we will introduce this model in two different rotating coordinates.

Firstly, we describe the PBCM in the dimensionless Earth–Moon rotating coordinates (see Fig. 2). The equations of motion of the spacecraft in the PBCM are (Topputo 2013)

$$\begin{aligned} \ddot{x}_{\mathrm{EM}} -2\dot{y}_{\mathrm{EM}}= & {} \frac{\partial \Omega _4^{\mathrm{EM}}}{\partial x_{\mathrm{EM}} } \nonumber \\ \ddot{y}_{\mathrm{EM}} +2\dot{x}_{\mathrm{EM}}= & {} \frac{\partial \Omega _4^{\mathrm{EM}}}{\partial y_{\mathrm{EM}} }, \end{aligned}$$

(5)

where $\Omega _4^{\mathrm{EM}}$ is a modified, time-dependent effective potential

$$\begin{aligned} \Omega _4^{\mathrm{EM}} (x_{\mathrm{EM}} ,y_{\mathrm{EM}} ,t)= & {} \Omega _3^{\mathrm{EM}} (x_{\mathrm{EM}} ,y_{\mathrm{EM}} )+\frac{m_s }{r_1 (t)} \nonumber \\&-\frac{m_s }{\rho ^{2}}[x_{\mathrm{EM}} \cos (\omega _s t)+y_{\mathrm{EM}} \sin (\omega _s t)]. \end{aligned}$$

(6)

In Eq. (6), t is the dimensionless time, $m_s =m_4 /(m_1 +m_2 )$ is the scaled mass of the Sun and equals $3.28900541\times 10^{5}$, $\rho$ is the distance between the Sun and the EMB and equals $3.88811\times 10^{2}$, and $\omega _s$ is the angular velocity of the Sun in the Earth–Moon dimensionless rotating coordinates and equals $-9.25195985\times 10^{\hbox {-}1}$. $\omega _s t$ is the phase angle of the Sun, and the present location of the Sun is $(\rho \cos (\omega _s t),\,\rho \sin (\omega _s t))$. Therefore, under the framework of the PBCM, the influence of the Sun is periodic, and the period is ${-2\pi }/{\omega _s }$. The distance between the Sun and the spacecraft is

$$\begin{aligned} r_1 (t)=\sqrt{(x_{\mathrm{EM}} -\rho \cos (\omega _s t))^{2}+(y_{\mathrm{EM}} -\rho \sin (\omega _s t))^{2}}. \end{aligned}$$

Fig. 3

PBCM in the dimensionless Sun–EMB rotating coordinates

Secondly, we introduce the PBCM in the dimensionless Sun–EMB rotating coordinates (see Fig. 3). The equations of motion of the spacecraft in the PBCM are

$$\begin{aligned} \ddot{x}_\mathrm{SE} -2\dot{y}_\mathrm{SE}= & {} \frac{\partial \Omega _4^{\mathrm{SE}} }{\partial x_\mathrm{SE} } \nonumber \\ \ddot{y}_\mathrm{SE} +2\dot{x}_\mathrm{SE}= & {} \frac{\partial \Omega _4^{\mathrm{SE}} }{\partial y_\mathrm{SE} }, \end{aligned}$$

(7)

where $\Omega _4^{\mathrm{SE}}$ is a modified, time-dependent effective potential

$$\begin{aligned} \Omega _4^{\mathrm{SE}} (x_\mathrm{SE} ,y_\mathrm{SE} ,t_\mathrm{SE} )=\Omega _3^{\mathrm{SE}} (x_\mathrm{SE} ,y_\mathrm{SE} )+\Phi (x_\mathrm{SE} ,y_\mathrm{SE} ,t_\mathrm{SE} ), \end{aligned}$$

(8)

and

$$\begin{aligned} \Phi (x_\mathrm{SE} ,y_\mathrm{SE} ,t_\mathrm{SE} )=\mu _\mathrm{SE} \left[ \frac{\mu _{\mathrm{EM}} }{r_m (x_\mathrm{SE} ,y_\mathrm{SE},t_\mathrm{SE} )}+\frac{1-\mu _{\mathrm{EM}} }{r_e (x_\mathrm{SE} ,y_\mathrm{SE} ,t_\mathrm{SE} )}-\frac{1}{r_2 (x_\mathrm{SE} ,y_\mathrm{SE} )}\right] . \end{aligned}$$

(9)

$\Phi$ denotes the difference between the PBCM and the Sun–EMB PCRTBP, which will be used to derive the sphere of influence of the Earth–Moon system (SOIEM) in Sect. 3.2. $\omega _e$ is the angular velocity of the Earth or Moon in the Sun–EMB rotating frame and equals $1/{(\omega _s +1)}-1=12.368266$. Therefore, $\omega _e t_\mathrm{SE}$ is the phase angle between the Earth–Moon line and the Sun–EMB line, and the present location of the Moon and the Earth in the Sun–EMB rotating coordinates is, respectively, $(1-\mu _\mathrm{SE} +\frac{1-\mu _{\mathrm{EM}} }{\rho }\cos (\omega _e t_\mathrm{SE} )$, $\frac{1-\mu _{\mathrm{EM}} }{\rho }\cos (\omega _e t_\mathrm{SE} ))$ and $(1-\mu _\mathrm{SE} -\frac{\mu _{\mathrm{EM}} }{\rho }\cos (\omega _e t_\mathrm{SE} ),-\frac{\mu _{\mathrm{EM}} }{\rho }\cos (\omega _e t_\mathrm{SE} ))$.

For the sack of space, the algorithm of the transformation between the Earth–Moon rotating frame and the Sun–EMB rotating frame will not be described in this paper. The detailed algorithm can be found in the book of Koon et al. (2006). Based on the models we introduced above, we will investigate the LGA orbits using the numerical simulations. In this paper, we adopt a variable-step Runge–Kutta integrator of order 4–5 with absolute and relative tolerances set to $10^{-14}$.

3 Lunar gravity assist orbit

In this section, we will introduce the basic theories of the LGA and the LGA orbits starting from the region near the Earth. Then, the sphere of influence of the Earth–Moon system (SOIEM) and the influence of the Sun on the LGA orbit will be investigated under the framework of the PBCM.

3.1 Lunar gravity assist

According to the Earth–Moon PCRTBP, the total energy of the spacecraft with respect to the EMB inertial frame, E, can be expressed by (Qi and Xu 2015)

$$\begin{aligned} E=\frac{1}{2}\left[ {(\dot{x}_{\mathrm{EM}}^2 +\dot{y}_{\mathrm{EM}}^2 )+(x_{\mathrm{EM}}^2 +y_{\mathrm{EM}}^2 )} \right] -\dot{x}_{\mathrm{EM}} y_{\mathrm{EM}} +x_{\mathrm{EM}} \dot{y}_{\mathrm{EM}} -\frac{1-\mu _{\mathrm{EM}}}{r_e}-\frac{\mu _{\mathrm{EM}}}{r_m}. \end{aligned}$$

(10)

Thus, the derivative of E with respect to t is

$$\begin{aligned} \frac{\mathrm{d}E}{\mathrm{d}t}=\frac{\partial \Omega _3^{\mathrm{EM}}}{\partial x_{\mathrm{EM}} }y_{\mathrm{EM}} -\frac{\partial \Omega _3^{\mathrm{EM}} }{\partial y_{\mathrm{EM}}} x_{\mathrm{EM}} =\mu _{\mathrm{EM}}(1-\mu _{\mathrm{EM}}) y_{\mathrm{EM}}\left( \frac{1}{r_e^3 }-\frac{1}{r_m^3 }\right) . \end{aligned}$$

(11)

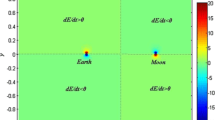
Figure 4 illustrates the distribution of ${\mathrm{d}E}/{\mathrm{d}t}$ in the Earth–Moon rotating frame based on the calculation of Eq. (11), and the right picture displays the details in the region near the Moon. As we can see from the figure, the energy E significantly changes in the region near the Moon. Therefore, the lunar flyby can remarkably influence the orbit, which is a useful technique in the mission design (Qi and Xu 2015).

Fig. 4

Distribution of ${\mathrm{d}E}/{\mathrm{d}t}$ near the Moon in the Earth–Moon rotating coordinates

Fig. 5

Four kinds of LGA orbits: a the E-increasing prograde LGA orbit, b the E-increasing retrograde LGA orbit, c the E-decreasing prograde LGA orbit, and d the E-decreasing retrograde LGA orbit

Fig. 6

Distributions of the feasible perilunes of the LGA orbits in different e and motions

In the Earth–Moon rotating frame, if the motion of the perilune of the LGA orbit is clockwise, the LGA orbit is defined as the retrograde LGA orbit. On the contrary, if the motion of the perilune of the LGA orbit is anticlockwise, the LGA orbit is defined as the prograde LGA orbit. Figure 5a–d displays four kinds of LGA orbits: the E-increasing prograde LGA orbit, the E-increasing retrograde LGA orbit, the E-decreasing prograde LGA orbit and the E-decreasing retrograde LGA orbit, respectively. The middle column of the figures shows the details of the lunar flyby. The right column of the figures displays the corresponding time history data of E for the LGA orbits. As we can see from the figures, the energy Es of the LGA orbits change dramatically during the lunar flyby.

The state of the perilune can be described by three variables as follows:

D::

the distance between the perilune and the center of the Moon.

$\psi _0 :$ :

the angle between the perilune and the Earth–Moon line, counterclockwise measured.

e::

the instantaneous eccentricity of the spacecraft with respect to the Moon at the perilune.

For the perilune of the LGA orbit in this paper, we require e to be larger than 1 in the derivation, i.e., the instantaneous orbit with respect to the Moon at the perilune is a hyperbolic orbit. Besides, D should be larger than the radius of the Moon to avoid the collision. Once parameters D, $\psi _0$ and e and the direction of motion are given, the LGA orbit is uniquely specified according to the Earth–Moon PCRTBP.

In this paper, we focus on a special kind of LGA orbit from the perspective of the practical space mission. We require that the height of the perigee of the LGA orbit, h, cannot be larger than 10,000 km. Besides, we require that E of the spacecraft must increase after the lunar flyby. This kind of LGA orbits, such as the orbits in Fig. 5a, b, can be applied to the deep-space mission starting from the low Earth orbit. The LGA orbits satisfying the two requirements above can be obtained by appropriately selecting their perilunes.

Firstly, according to the research of Qi and Xu (2015), the perilune of the E-increasing LGA orbit must be located in the region with $180^{\circ }<\psi _0 <360^{\circ }$. Secondly, for the given perilune, h can be calculated approximately using the patched conic approach (Qi and Xu 2015); hence, the feasible perilunes also need to satisfy the requirement of h. For example, taking into account two requirements of the perilune above, Figure 6 shows the distributions of the feasible perilunes of the LGA orbits when e equals 1.5 and 1.7. Here, h of the orbit colliding with the Earth is set as 0. In the following investigation, the perilune of the feasible LGA orbit can be obtained in the same way.

3.2 Sphere of influence of the Earth–Moon system

In the last subsection, the LGA orbit is studied under the framework of the Earth–Moon PCRTBP and the patched conic model. However, if the undertaken model is the PBCM, the LGA orbit will be quite different from that in the two models above. Since the PBCM is time dependent, the moment of the perilune can affect the LGA orbit. For example, the LGA orbits with the fixed state variables of perilune at the different moments of the perilune are displayed in Fig. 7, where (a) and (b) are the prograde LGA orbits and the retrograde LGA orbits, respectively. The blue solid lines represent the LGA orbits based on the Earth–Moon PCRTBP, and the red dash lines denote the LGA orbits under the framework of the PBCM. As we can see, when the spacecraft is near the EMB, the LGA orbits in two kinds of models are close, which means that the influence of the Sun is quite slight. But when the distance between the spacecraft and the EMB enlarges, the differences between the LGA orbits based on the PBCM increase gradually. The influence of the Sun becomes more and more important. In this situation, we assume that the gravities from the Earth and the Moon can be concentrated at the EMB. Therefore, the PBCM can be regarded as the Sun–EMB CRTBP approximately. Under the Sun–EMB CRTBP, we can apply the mature theory of the invariant manifolds to analyzing the LGA orbits based on the PBCM.

Fig. 7

Influence of the moment of the perilune: a prograde LGA orbits and b retrograde LGA orbit

Based on the discussion above, the first issue we should solve is to search an appropriate region where the PBCM can be regarded as the Sun–EMB PCRTBP approximately. According to the Sun–EMB PCRTBP, the Jacobi constant C is the invariant. But according to the PBCM, C defined by Eq. (4) is time variant. When the value of C changes greatly, we think that the difference between the PBCM and the Sun–EMB PCRTBP cannot be ignored. Only when the variation of C is quite small can we substitute the Sun–EMB PCRTBP for the PBCM. Therefore, the variation of C can be regarded as an index to evaluate the difference between the PBCM and the Sun–EMB CRTBP. The smaller variation of C, the Sun–EMB PCRTBP is more approximate to the PBCM.

According to Eqs. (4) and (7), the derivative of C with respective to the time $t_\mathrm{SE}$ based on the PBCM can be expressed by

$$\begin{aligned} \frac{\hbox {d}C}{\hbox {d}t_\mathrm{SE}}= & {} -2\left( \dot{x}_\mathrm{SE} \ddot{x}_\mathrm{SE} +\dot{y}_\mathrm{SE} \ddot{y}_\mathrm{SE} \right) +2\frac{\hbox {d}\Omega _3^{\mathrm{SE}}}{\hbox {d}t_\mathrm{SE}}\nonumber \\= & {} -2\dot{x}_\mathrm{SE} \left( 2\dot{y}_\mathrm{SE} +\frac{\partial \Omega _4^{\mathrm{SE}} }{\partial x_\mathrm{SE} }\right) -2\dot{y}_\mathrm{SE} \left( -2\dot{x}_\mathrm{SE} +\frac{\partial \Omega _4^{\mathrm{SE}}}{\partial y_\mathrm{SE}}\right) +2\frac{\hbox {d}\Omega _3^{\mathrm{SE}} }{\hbox {d}t_\mathrm{SE}}\nonumber \\= & {} -2\left( \dot{x}_\mathrm{SE} \frac{\partial \Omega _4^{\mathrm{SE}} }{\partial x_\mathrm{SE} }+\dot{y}_\mathrm{SE} \frac{\partial \Omega _4^{\mathrm{SE}} }{\partial y_\mathrm{SE}}\right) +2\frac{\hbox {d}\Omega _3^{\mathrm{SE}}}{\hbox {d}t_\mathrm{SE}}. \end{aligned}$$

(12)

Based on Eq. (8),

$$\begin{aligned} \frac{\mathrm{d}\Omega _4^{\mathrm{SE}} }{\mathrm{d}t_\mathrm{SE}}= & {} \frac{\mathrm{d}\Omega _3^{\mathrm{SE}} }{dt_\mathrm{SE} }+\frac{\hbox {d}\Phi }{\mathrm{d}t_\mathrm{SE} } \nonumber \\= & {} \dot{x}_\mathrm{SE} \frac{\partial \Omega _4^{\mathrm{SE}} }{\partial x_\mathrm{SE} }+\dot{y}_\mathrm{SE} \frac{\partial \Omega _4^{\mathrm{SE}} }{\partial y_\mathrm{SE} }+\frac{\partial \Omega _4^{\mathrm{SE}} }{\partial t_\mathrm{SE}}. \end{aligned}$$

(13)

Therefore,

$$\begin{aligned} \frac{\mathrm{d}C}{\mathrm{d}t_\mathrm{SE}}= & {} -2\left( \frac{d\Omega _3^{\mathrm{SE}} }{\hbox {d}t_\mathrm{SE} }+\frac{d\Phi }{dt_\mathrm{SE} }-\frac{\partial \Omega _4^{\mathrm{SE}} }{\partial t_\mathrm{SE}}\right) +2\frac{\hbox {d}\Omega _3^{\mathrm{SE}} }{\hbox {d}t_\mathrm{SE} } \nonumber \\= & {} -2\left( \frac{\hbox {d}\Phi }{\hbox {d}t_\mathrm{SE} }-\frac{\partial \Omega _4^{\mathrm{SE}}}{\partial t_\mathrm{SE} }\right) =-2\left( \frac{d\Phi }{dt_\mathrm{SE} }-\frac{\partial \Phi }{\partial t_\mathrm{SE}}\right) . \end{aligned}$$

(14)

Taking the integral for both sides over the time $t_\mathrm{SE}$, we can derive

$$\begin{aligned} \int _C^{C^{*}} {\mathrm{d}C}=-2\int _\Phi ^{\Phi ^{*}} {\mathrm{d}\Phi } +2 \int _t^{t^{*}} {\frac{\partial \Phi }{\partial t_\mathrm{SE} }\mathrm{d}t_\mathrm{SE}} \end{aligned}$$

(15)

or

$$\begin{aligned} C^{*}-C=2\Phi -2\Phi ^{*}+2\int _t^{t^{*}}{\frac{\partial \Phi }{\partial t_\mathrm{SE}}\mathrm{d}t_\mathrm{SE}}. \end{aligned}$$

(16)

Circi and Teofilatto (2001) pointed out that the integral in Eq. (16) depends on the actual trajectory, not only on the initial/final point, and hence it cannot be estimated a priori. Of course, the faster the spacecraft crosses the lunar region of influence the smaller the value of the integral is. If the spacecraft reaches its perilune soon (so the local eccentricity turns out to be bigger than 1), the integral in Eq. (16) can be neglected. For the LGA orbits we investigate in this paper, e of the perilune has been required to be larger than 1 in Sect. 3.1. Hence, the integral in Eq. (16) can be removed. Then, Eq. (16) can be rewritten

$$\begin{aligned} C^{*}-C=2\Phi -2\Phi ^{*}. \end{aligned}$$

(17)

The gravities of the Earth and the Moon are more approximate to the gravity of the EMB, if the spacecraft is farther away from the EMB. Based on Eq. (9), if we let $C^{*}$ denote the Jacobi constant located at infinite, the corresponding $\Phi ^{*}$ tends to 0. Then, at a certain position of the LGA orbit, the relationship of the Jacobi constant C and the corresponding $\Phi$ can be obtained by

$$\begin{aligned} C^{*}-C=2 \Phi \end{aligned}$$

(18)

As mentioned before, if the difference between C and $C^{*}$ is quite small, the PBCM can be regarded as the Sun–EMB CRTBP in the corresponding region. Consequently, we present a criterion to estimate difference between C and $C^{*}$ as follows.

$$\begin{aligned} \left| {\frac{C^{*}-C}{C^{*}}} \right| \le 10^{-5},\hbox { i.e., }\left| {\frac{2\Phi }{C^{*}}} \right| \le 10^{-5}, \end{aligned}$$

(19)

where $\Phi$ is time variant in the Sun–EMB rotating frame. However, in the Earth–Moon rotating frame, $\Phi$ is time independent and only depends on the position. Hence, we can describe the regions satisfying above criterion in the Earth–Moon rotating frame. In Eq. (19), $C^{*}$ depends on the LGA orbit, but for the LGA orbits investigated in this paper, we can estimate $C^{*}$ in the range of $[C_4 ,C_1 ]\approx [3,3.0009]$. Therefore, we might as well let $C^{*}$ equal 3. Figure 8 shows the distribution of ${2\Phi }/3$ in the Earth–Moon rotating frame. There are two circular dash lines centered at the EMB in this figure. The radius of the inner one is $1-\mu _{\mathrm{EM}}$ (379,734.2 km), i.e., the distance between the Moon and the EMB. The radius of the outer one is 200,000 km larger than that of the inner one, i.e., 579,734.2 km.

Fig. 8

Distribution of ${2\Phi }/3$ in the Earth–Moon rotating frame

In this paper, the regions dissatisfying the criterion of Eq. (19) are defined as the regions of influence of the Earth–Moon system, where the gravities from the Earth and the Moon cannot be concentrated at the EMB approximately. The dark red and the dark blue regions in Fig. 8 are the regions of influence of the Earth–Moon system. Apparently, these regions are not a circular region. However, it should be noted that in the Sun–EMB rotating frame, the regions of influence of the Earth–Moon system rotate about the EMB, i.e., the dark red and the dark blue regions in Fig. 8 rotate about the origin (EMB). Hence, the circular region covered by the rotating dark red and the dark blue regions about the origin are defined as the sphere of influence of the Earth–Moon system (SOIEM). We find that the dark red and the dark blue regions are all located inside the outer circular dash line. That is to say that the variation of C is quite slight when the spacecraft is located outside the outer circular dash line. Hence, in this paper, the sphere centered at the EMB with the radius of 579734.2 km is considered to be the SOIEM for the LGA orbits. Outside the SOIEM, we can substitute the Sun–EMB PCRTBP for the PBCM to analyze the LGA orbits. Figure 9 displays six prograde LGA orbits in the Sun–EMB rotating frame. The inner circle is the Moon’s orbit and the outer circle is the SOIEM. The red lines denote the LGA orbits based on the PBCM, and the blue lines represent the LGA orbits based on the Sun–EMB PCRTBP. We find that outside the SOIEM, the six blue orbits are very close to the corresponding red orbits, which testifies the adequacy of the SOIEM.

Fig. 9

Comparisons between the LGA orbits based on the Sun–EMB PCRTBP and the PBCM

Fig. 10

Definitions of $\alpha$ and $\beta$

Figure 10 displays a LGA orbit in the Sun–EMB rotating frame. When the LGA orbit flies out of the SOIEM, there exists a intersection point (denoted by the red dot), which can be located by the phase angle $\alpha$, counterclockwise measured. The direction of motion of the LGA orbit at the intersection point can be indicated by the angle $\beta$, clockwise measured. Therefore, $(\alpha ,\beta )$ reflects the geometric property of the LGA orbit on the SOIEM. According to the definitions above, the range of $\alpha$ is $[{0, 360}^{\circ }]$, and the range of $\beta$ is $[{0, 180}^{\circ }]$.

3.3 Influence of the Sun

Comparing the PBCM with the Earth–Moon PCRTBP, the only difference between them is that the influence of Sun is included in the PBCM. Therefore, if the influence of the Sun on the LGA orbits can be analyzed in detail, the characters of the LGA orbits based on the PBCM will be clear. According to the analysis in the last subsection, the influence of the Sun on the LGA orbits can be divided into two portions by the SOIEM.

For the portion of the LGA orbit outside the SOIEM, we intend to investigate the influence of the Sun in the next two sections in detail, so in this subsection, only an example is given to show the effect of the Sun on the LGA orbits. Figure 11 displays a cluster prograde LGA orbits with the same state variables of perilune ($D=2164.4\hbox { km}$, $\psi _0=213.96^{\circ }$ and $e =1.3291$) at different moments of the perilune t. Since t is various, the influence of the Sun on the LGA orbits is also different. As we can see from the figure, the influence of the Sun is remarkable, especially for the portion outside the SOIEM: Some LGA orbits fly away from the SOIEM along different directions, but some return to the SOIEM. This phenomenon is explained in Sect. 5.

Besides, we find that for the given LGA orbit (the state variables of the perilune are fixed except the moment of the perilune), when the moment of perilune t changes at regular intervals in the period $[0,{-2\pi }/{\omega _s}]$, $\alpha$ correspondingly changes at regular intervals in the period $[0,2\pi ]$. And there exists an exactly corresponding relationship between t and $\alpha$. Therefore, for the given LGA orbits, we can substitute $\alpha$ for t as a state variable of the perilune. This substitution will be used directly in the following parts and not be explained again.

Fig. 11

Influence of the Sun on the LGA orbits

For the portion of the LGA orbit inside the SOIEM, we discuss the influence of the Sun by the numerical methodology. As mentioned in the last subsection, we consider that inside the SOIEM, the influence of the Sun on the LGA orbits is slight, such as the examples in Fig. 7. In this subsection, we quantitatively analyze the influence of the Sun.

Fig. 12

h versus $\alpha$

First of all, we discuss the effect of Sun on the perigee of the LGA orbits. According to the LGA orbits in Fig. 11, the plot of height of the perigee h versus $\alpha$ is displayed in Fig. 12. As we can see from the figure, except the orbits colliding with the Earth, the amplitude of h is less than 300 km. The influence of the Sun on the perigee is quite small.

Since SOIEM is the interface to distinguish the influence of the Sun, it is significant to investigate the influence of the Sun at the intersection points between the LGA orbits and the SOIEM. Besides, for the portion of the LGA orbits inside the SOIEM, the intersection points are farthest away from the EMB, so the influence of the Sun is greatest at that point. If the influence of the Sun at the intersection points is in an acceptable range, we can conclude that the influence of the Sun on the LGA orbits inside the SOIEM is quite small.

The orbital state of the intersection points in Fig. 11, such as the angle $\beta$ and Jacobi constant C, can be calculated. Figure 13a, b shows the plots of $\beta$ versus $\alpha$ and C versus $\alpha$, respectively. In a period of $\alpha$, we find that the amplitude of $\beta$, $\Delta \beta$, is smaller than $1^{\circ }$. The change of C is also quite small, and the amplitude $\Delta C<2\times 10^{-5}$.

Fig. 13

a $\beta$ versus $\alpha$ and b C versus $\alpha$

In order to examine the influence of the Sun at the intersection points, we can calculate more $\Delta \beta$ and $\Delta C$ for different LGA orbits. For the sake of space, we only display the results of the LGA orbits with $e = 1.5$ in Figs. 14 and 15. It is noted that only the perilunes of the LGA orbits with $C<C_1 \approx 3.0009$ at the intersection points are displayed in Figs. 14 and 15, because the trends of the LGA orbits with $C\ge C_1$ are predictable: They cannot fly away from the Earth–Moon system and will return to the SOIEM. From Figs. 14 and 15, we find that for the feasible LGA orbits with $e =1.5$, $\Delta \beta <1^{\circ }$ and $\Delta C<4\times 10^{-5}$. Therefore, we conclude that inside the SOIEM, the influence of the Sun on the feasible LGA orbits is slight. The changes of $\beta$ and C for different $\alpha$ at the intersection points are quite small. This conclusion is used in Sect. 5.

Fig. 14

$\Delta \beta$ and $\Delta C$ for the prograde LGA orbits with $e = 1.5$

Fig. 15

$\Delta \beta$ and $\Delta C$ for the retrograde LGA orbits with $e = 1.5$

4 Sun–EMB stable manifolds and Poincaré section

In the last subsection, we mentioned that outside the SOIEM, the PBCM can be regarded as the Sun–EMB CRTBP approximately to analyze the LGA orbits. In this section, we will review some theories based on the Sun–EMB PCRTBP.

The Lyapunov periodic orbit (LPO) around $L_1$ or $L_2$ is an important result of the PCRTBP (Szebehely 1967). The LPOs based on Sun–EMB PCRTBP with different C are displayed in the Sun–EMB rotating frame in Fig. 16. The inner circle is the Moon orbit and the outer circle is the SOIEM. With the decrease of C, the scale of the LPO increases. As we can see from Fig. 16, some LPOs can enter the SOIEM. However, according to the analysis in Sect. 3.2, C of the LPO inside the SOIEM will be distinctly changed by the Earth–Moon system, which leads to the destruction of the LPO. Therefore, there exists a critical C for $L_1$ or $L_2$ under the PBCM: If C is smaller than this value, the corresponding LPO will enter the SOIEM and be heavily destroyed. In this paper, $\tilde{C}_1$ and $\tilde{C}_2$ denote the critical C of $L_1$ and $L_2$, respectively. Numerical calculation shows $\tilde{C}_1 =3.00034839$ and $\tilde{C}_2 =3.00035320$.

Fig. 16

LPOs with different C in the Sun–EMB rotating frame

The stable manifold associated with the LPO is another important theory of the PCRTBP (Koon et al. 2006). As mentioned before, the Earth–Moon system can remarkably change the Jacobi constant of the Sun–EMB PCRTBP inside the SOIEM. Therefore, the investigation of the stable manifolds also should be limited in the region outside the SOIEM. Taking the SOIEM as the section surface, we can obtain the intersection points between the stable manifolds and the SOIEM. The information of section points can be denoted by the angles $\alpha$ and $\beta$, i.e., the Poincaré section of the stable manifolds can be described in the coordinates of $(\alpha ,\beta )$. Since the Poincaré section can reduce the dimension of the stable manifolds, it is an effective tool for us to understand the geometric properties of the PCRTBP system. Figure 17a, b displays the stable manifolds associated with the LPOs outside the SOIEM when $C = 3.00085$ and 3.00080, respectively. The red lines and the blue lines denote the stable manifolds associated with the LPO around $L_1$ and $L_2$, respectively. Figure 18a, b is the Poincaré sections corresponding to Fig. 17a, b in the coordinates of $(\alpha ,\beta )$. In the Poincaré sections, the red section points and the blue section points stem from the stable manifolds associated with the LPO around $L_1$ and $L_2$, respectively. Note that, in the calculation of the stable manifolds, if the number of revolution that the spacecraft performs about the EMB along the stable manifold is equal or greater than 1, the corresponding manifold will be discarded, because the flight time of this kind of trajectory is too long to be acceptable in practice.

Fig. 17

Stable manifolds associated with the LPOs outside the SOIEM when a $C = 3.00085$ and b $C = 3.00080$

Fig. 18

Poincaré sections with a $C = 3.00085$ and b $C = 3.00080$ in the coordinates of $(\alpha ,\beta )$

In Fig. 17a, when $C = 3.00085$, since the tubes of stable manifolds are narrow, the entire stable manifolds can intersect the SOIEM on their first pass, yielding the closed Poincaré sections in Fig. 18a. However, in Fig. 17b, when C decreases to 3.00080, the scale of the stable manifold tubes is wide enough that not all of the stable manifolds can intersect the SOIEM on their first pass. Hence, the Poincaré sections intersect the axis $\beta =0^{\circ }$ and become open (see Fig. 18b). Some fractions of stable manifolds pass over the SOIEM and intersect the SOIEM in the region of the section points belonging to other libration point. Therefore, some isolated section points (the red points in Fig. 18b) belonging to $L_1$ appear at the left side near the open Poincaré sections belonging to $L_2$; meanwhile, some isolated section points (the blue points in Fig. 18b) belonging to $L_2$ also appear at the left side near the open Poincaré sections belonging to $L_1$. In this paper, the closed or open Poincaré sections, stemming from the intersection between the SOIEM and the stable manifolds on their first pass, are defined as the primary sections. The isolated Poincaré sections, stemming from the intersection between the SOIEM and some stable manifolds overflying the SOIEM on their first pass, are defined as the subordinate sections.

According to the discussion above, we infer that only when the primary sections are open will the subordinate sections appear. Numerical computation indicates that $C=3.00083000$ is the critical value to determine the primary sections of $L_1$ closed or open: If C is larger than this value, the primary section of $L_1$ is closed; otherwise, the primary section is opened. In this paper, $C_1^*$ denotes this critical value of $L_1$. In the same way, the critical value of $L_2$ can also be calculated $C_2^*=3.00082863$. Figure 19 shows the critical primary sections of $L_1$ (the red section) and $L_2$ (the blue section).

Fig. 19

Critical primary sections of $L_1$ (the red section) and $L_2$ (the blue section)

Fig. 20

Distribution of the Poincaré sections with different C in the coordinates of $(\alpha ,\beta )$

Fig. 21

Contour map of the Poincaré sections with different C

Furthermore, we can obtain the Poincaré sections of the stable manifolds with different C using the numerical method. Figure 20 is the distribution of the Poincaré sections with different C in the coordinates of $(\alpha ,\beta )$, where the different colors denote the different values of C. Based on the previous discussion, the left dark red region belongs to the primary sections of $L_1$, while the right dark red region belongs to the primary sections of $L_2$. Besides, due to the periodicity of the angle $\alpha$, the leftmost red region also belongs to the primary sections of $L_2$. The subordinate sections of $L_1$ are located at the left side closed to the primary sections of $L_2$, and the subordinate sections of $L_2$ are located at the left side closed to the primary sections of $L_1$. Figure 21 is the contour map of the Poincaré sections with different C, where we can observe the positions of the subordinate sections more clearly. We find that the subordinate sections are very close to left side of the primary sections, and some subordinate sections are even mingled with the primary sections with different C. Therefore, if the orbit is located in those jumbled regions, the motion will be quite sensitive to the initial condition. The small deviation will bring about the motion in different directions (toward $L_1$ or $L_2$). Therefore, those regions are regarded as the chaotic areas, which demonstrate the dynamical complexity of the PCRTBP.

5 LGA orbit based on the PBCM

In this section, the stable manifolds and the Poincaré sections of the Sun–EMB PCRTBP will be applied to investigating the LGA orbits based on the PBCM. In addition, the patched LGA orbits and the stable transit probability will be presented and studied.

Fig. 22

Integrated picture of the prograde LGA orbit on the SOIEM

5.1 LGA orbit and stable manifolds

As mentioned previously, outside the SOIEM, the stable manifolds can be applied to investigating the character of the LGA orbits and predicting their motion. In this subsection, we take two kinds of LGA orbits (the prograde and retrograde LGA orbits) as example to introduce how to apply the stable manifolds to the LGA orbits based on the PBCM.

Firstly, we investigate a prograde LGA orbit based on the PBCM. The state variables of the perilune are fixed: $D= 1796.7\,\hbox {km}$, $\psi _0 =206.6131^{\circ }$ and $e= 1.2967$. The influence of the Sun on $\beta$ of the prograde LGA orbit illustrates in Fig. 22: The black solid line overlapping the distribution of the Poincaré sections denotes the change curve of $\beta$ versus $\alpha$. As we can see from the figure, the change of $\beta$ is very small, which is in accord with the discussion in Sect. 3.3. The numerical calculation indicates that $\beta$ remains around $58.22^{\circ }$, and the amplitude $\Delta \beta <1^{\circ }$. Then, we display the influence of the Sun on C of the LGA orbits on the SOIEM. The lower part of Fig. 22 illustrates the change curve of C versus $\alpha$. The black horizontal line corresponds to the mean value of C, $\bar{{C}}=3.000804$. The numerical calculation indicates that the amplitude of C is quite small: $\Delta C=2.0135\times 10^{-5}$. Therefore, even for different $\alpha$, we assume that the Jacobi constants of the LGA orbits on the SOIEM equal $\bar{{C}}$. The Poincaré sections of the stable manifolds with $C=\bar{{C}}$ are indicated by the black points in Fig. 22. Since $\bar{{C}}<C_2^*$, we can obtain two open primary sections and two branches of subordinate sections. Hence, there exist six intersection points between the curve of $\beta$ and the Poincaré sections: four intersection points on the primary sections and two intersection points on the subordinate sections. If all of the Jacobi constants of the LGA orbits on the SOIEM strictly equal $\bar{{C}}$, the six values of $\alpha$ corresponding to the above intersection points can be regarded as the phase angles where the LGA orbits are spliced with the stable manifolds on the SOIEM. Unfortunately, as we can see from Fig. 22, C changes for different $\alpha$, i.e., the six values of $\alpha$ are not the real patched angles. However, because $\Delta C$ is quite small, we consider that the real patched angles are located in the neighborhood of the six values of $\alpha$. Therefore, the six values of $\alpha$ can be regarded as the initial guesses for searching the real patched angles. In order to improve the efficiency of the searching problem, we can use the curve of C versus $\alpha$ to determine the orientations of the real patched angles relative to the initial points. For example, in Fig. 22, we can easily obtain six values of C corresponding to the six initial value of $\alpha$ using the curve of C versus $\alpha$. If the value of C is smaller than $\bar{{C}}$, the real patched angle $\alpha$ will be located at the C-decreasing side of the corresponding intersection point in the distribution of the Poincaré section (the upper part of Fig. 22). On the contrary, if the value of C is larger than $\bar{{C}}$, the real patched angle $\alpha$ will be located at the C-increasing side of the corresponding intersection point in the distribution of the Poincaré section. In the lower part of Fig. 22, the red arrows indicate the orientations of the real patched angles relative to the corresponding initial values of $\alpha$. The relative orientations can improve the efficiency of the searching problem.

In Fig. 22, the information of the LGA orbit on the SOIEM, such as the change curve of $\beta$ versus $\alpha$ and the change curve of C versus $\alpha$, is handily integrated into the distribution of the Poincaré sections. Therefore, Fig. 22 is named the integrated picture of the prograde LGA orbit on the SOIEM. Using the information of this integrated picture comprehensively, we propose a simple and intuitive method to search patched points of the prograde LGA orbits and the stable manifolds.

Figure 23 displays the six real patched points obtained by the searching problem. The two patched points on the primary section of $L_1$ are, successively, defined as Point 1 and Point 2 in the anticlockwise direction. The two patched points on the primary section of $L_2$ are, successively, defined as Point 3 and Point 4 in the anticlockwise direction. The patched points on the subordinate sections of $L_1$ and $L_2$ are defined as the Point 6 and Point 5, respectively. As we can see, Points 1 and 5 and Points 3 and 6 are located in the chaotic areas.

Fig. 23

Six real patched points in the coordinates of $(\alpha ,\beta )$

Figure 24 shows the patched LGA orbits corresponding to the six patched points in Fig. 23, where the red lines denote the LGA orbit based on the PBCM and the blue lines represent the stable manifolds based on the Sun–EMB PCRTBP. Figure 24a displays the patched LGA orbits corresponding to the Points 2 and 4, which are named after Orbits 2 and 4, respectively. Similarly, in Fig. 24b, the patched LGA orbits corresponding to the Points 1, 3, 5 and 6 are named after Orbits 1, 3, 5 and 6, respectively. As we can see from the figures, Orbits 2 and 4, Orbits 1 and 3 and Orbits 5 and 6 seem symmetrical about the EMB. Besides, we find that although Point 1 and Point 5 are very close, Orbit 1 and Orbit 5 are quite different and move toward different directions. The same situation occurs when it comes to Orbit 3 and Orbit 6. Therefore, we conclude that the motions of Orbits 1, 3, 5 and 6 in the chaotic areas are more sensitive to the initial condition than those of Orbits 2 and 4.

Fig. 24

Patched LGA orbits corresponding to the six patch points in Fig. 23

Next, we analyze the roles of the patched orbits for the LGA orbits based on the PBCM. Figure 23 shows that the patched LGA orbits between Point 1 and Point 2 are located inside the stable manifolds tube of $L_1$, and the patched LGA orbits between Point 3 and Point 4 are located inside the stable manifolds tube of $L_2$. According to the theory of the stable manifolds (Koon et al. 2006), the patched LGA orbits between Point 1 and Point 2 are the transit orbits through $L_1$, and the patched LGA orbits between Point 3 and Point 4 are the transit orbits through $L_2$. Based on the analysis in Sect. 3.2, the PBCM can be regarded as the Sun–EMB CRTBP approximately outside the SOIEM. Therefore, we speculate that the conclusions above based on the patched model can still be applicable in the complete PBCM, i.e., under the complete PBCM, the LGA orbits between Point 1 and Point 2 are the transit orbits passing through $L_1$, and the LGA orbits between Point 3 and Point 4 are the transit orbits passing through $L_2$. In Fig. 25a, the blue orbits are Orbits 1–4, and the green orbits are the LGA orbits based on the complete PBCM. As we can see from the figure, the LGA orbits between Orbit 1 and Orbit 2 can transit the region near $L_1$ and fly to the interior region of the Sun; meanwhile, the LGA orbits between Orbit 3 and Orbit 4 can transit the region near $L_2$ and fly to the exterior region of the Sun. Those results are in accord with our speculation.

Besides, based on the theory of stable manifolds, the orbits outside the stable manifolds tube are the non-transit orbits. However, because of the existence of the subordinate sections, not all the patched LGA orbits between Point 4 and Point 1 or the patched LGA orbits between Point 2 and Point 3 are located outside the stable manifolds tubes. Some orbits located in the chaotic areas are inside the manifolds tubes. We speculate that the conclusions above based on the patched model can still be applicable in the complete PBCM, i.e., under the complete PBCM, not all the LGA orbits between Point 4 and Point 1 or the LGA orbits between Point 2 and Point 3 are the non-transit orbits, and some located in the chaotic areas will be the transit orbits. Figure 25b displays the LGA orbits between Orbit 4 and Orbit 1 and the LGA orbits between Orbit 2 and Orbit 3 based on the complete PBCM. Similarly, in this figure, the blue lines denote Orbits 1–4. The red lines and the green lines represent the non-transit orbits and transit orbits, respectively. In this figure, we find that most of the LGA orbits between Orbit 4 and Orbit 1 or between Orbit 2 and Orbit 3 are the non-transit orbits and can return to the SOIEM. But there are still a few transit orbits, which can pass through the regions near $L_1$ or $L_2$. Those transit orbits are close to Orbit 1 or Orbit 3, located in the chaotic areas.

Fig. 25

Roles of the patched LGA orbits for the LGA orbits based on the PBCM

Figure 26 illustrates the motion of the LGA orbits in the chaotic areas in detail, where the red lines and green lines are the non-transit orbits and transit orbits, respectively. Figure 26a shows the LGA orbits located in the chaotic areas near Orbits 1 and 5. From this picture, we find that there exist some transit orbits passing through the regions of $L_2$ in the small neighborhood of Orbit 5. Meanwhile, in the small neighborhood of Orbit 1, few LGA orbits can pass through regions of $L_1$. Since the transit orbits and the non-transit orbits are concentrated in a narrow region, the motion will be quite sensitive to the initial condition. The small deviation will bring about the motion in different directions. The same conclusions are also applicable to the LGA orbit in the chaotic areas near Orbits 3 and 6 (see Fig. 26b).

Fig. 26

LGA orbits in the chaotic areas

Fig. 27

Integrated picture of the retrograde LGA orbit on the SOIEM

Secondly, we investigate a retrograde LGA orbit based on the PBCM. The state variables of the perilune are fixed: $D= 3343.1\hbox { km}$, $\psi _0 =322.8968^{\circ }$ and $e = 1.4603$. Similarly, we apply the integrated picture of the retrograde LGA orbit on the SOIEM to searching the patched points (see Fig. 27). In the distribution of the Poincaré sections, the black solid line denotes the change curve of $\beta$ versus $\alpha$. The numerical calculation indicates that $\beta$ remains around $55.67^{\circ }$ and the amplitude $\Delta \beta \approx 1^{\circ }$. The lower part of Fig. 27 illustrates the change curve of C versus $\alpha$. The black horizontal line corresponds to the mean value of C, $\bar{{C}}= 3.000872$. The numerical calculation indicates that the amplitude of C is also quite small, $\Delta C=1.8928\times 10^{-5}$. The Poincaré sections of the stable manifolds with $C=\bar{{C}}$ are denoted by the black points in Fig. 27. Since $\bar{{C}}>C_1^*$, we can obtain two closed primary sections in the figure. Hence, there exist four intersection points between the curve of $\beta$ and the primary sections. In the lower picture of Fig. 27, the red arrows indicate the orientations of the real patched angles relative to the corresponding initial values of $\alpha$. Using the method we propose, the four patched points can be obtained by the searching problem easily, which are denoted by the white dot in Fig. 27.

Figure 28 shows the patched LGA orbits corresponding to the four patched points in Fig. 27, where the red lines denote the LGA orbit based on the PBCM and the blue lines denote the stable manifolds based on the Sun–EMB PCRTBP.

Fig. 28

Patched LGA orbits corresponding to the four patched points in Fig. 27

The roles of the patched orbits for the LGA orbits based on the PBCM are displayed in Fig. 29. In this figure, the blue lines denote Orbits 1–4. Since there are no subordinate sections, the patched LGA orbits between Points 4 and 1 and the patched LGA orbits between Points 2 and 4 are rigorously outside the stable manifolds tube, belonging to the non-transit orbits of the patched model. Figure 29 indicates that the corresponding LGA orbits based on the complete PBCM are still the non-transit orbits (denoted by the red lines). On the other hand, the patched LGA orbits between Points 1 and 2 and the patched LGA orbits between Points 2 and 3 are inside the stable manifolds tube, belonging to the transit orbits based on the patched model. Figure 29 indicates that the corresponding LGA orbits (denoted by the green) based on the complete PBCM can still transit the regions near $L_1$ or $L_2$.

Fig. 29

Roles of the patched LGA orbits for the LGA orbits based on the PBCM

Based on the two examples above, we find that the Poincaré section of the stable manifolds is an effective tool to analyze the motion of the LGA orbits based on the PBCM. The patched trajectories can efficiently distinguish the transit LGA orbits from the non-transit LGA orbits based on the PBCM. The LGA orbits inside the primary sections are the transit orbits. If there are no the subordinate sections, the LGA orbits outside the primary sections are the non-transit orbits. If there exist the subordinate sections, most of the LGA orbits outside the primary sections are the non-transit orbits, and only in the narrow region near the subordinate sections, the LGA orbits are the transit orbits. Based on the results above, we can easily select the LGA orbit according to the requirement of the actual space mission. For example, for the Earth–Moon transfer, we should select the non-transit LGA orbits outside the primary sections. For the interplanetary missions, we recommend using the transit LGA orbits inside the primary sections.

5.2 Stable transit probability

In this subsection, we investigate the transit LGA orbits based on the PBCM. According to the research in the last subsection, the LGA orbits inside the primary section are transit orbits and their directions of the transit are certain and straightforward. Some LGA orbits near the subordinate sections are the transit orbits, but they are distributed in the narrow chaotic areas. Their motions are quite sensitive to the initial condition. Besides, we find that the flight time of the transit LGA orbits near the subordinate sections is apparently longer than that of the transit LGA orbits inside the primary sections. In summary, the transit LGA orbits inside the primary sections possess substantial advantages over those near the subordinate sections. Hence, in this subsection, we focus on the former. The transit LGA orbits inside the primary sections are defined as the stable transit LGA orbits.

For a given LGA orbit (the state variables of the perilune are fixed except the moment of the perilune), its probability to become a stable transit LGA orbit during a Sun–Earth–Moon period can be expressed by

$$\begin{aligned} \hbox {Stable Transit Probability}=\frac{\hbox {Stable Transit Window}}{\hbox {Sun}{\text {--}}\hbox {Earth}{\text {--}}\hbox {Moon}\,\hbox {Period}}. \end{aligned}$$

In this paper, the stable transit probability is denoted as $\eta$. The stable transit window can be measured by the total width of the primary sections in the coordinates of $(\alpha ,\beta )$. The Sun–Earth–Moon period just equals to the period of $\alpha$. Therefore, we can obtain the approximate expression of $\eta$ as follows.

$$\begin{aligned} \eta =\frac{\alpha _2 -\alpha _1 +\bmod (\alpha _4 -\alpha _3 ,360^{\circ })}{360^{\circ }}, \end{aligned}$$

(20)

where $\alpha _i ,\,i=1,2,3,4$, denote the phase angles of the patched points in the primary sections. For example, Fig. 30a, b displays the distributions of the stable transit window for the prograde LGA orbits and the retrograde LGA orbits in the last subsection, respectively.

Fig. 30

Stable transit windows for (a) the prograde LGA orbits and (b) the retrograde LGA orbits

Based on Eq. (20), we can calculate the distribution of $\eta$ for different perilunes of the LGA orbits in the Earth–Moon rotating coordinates. Figure 31 shows the distributions of $\eta$ for the prograde LGA orbits and the retrograde LGA orbits when e equals to 1.5 and 1.7. As we can see from the figures, in the Earth–Moon rotating coordinates, $\eta$ increases from 0 to 1 in the anticlockwise (or prograde) direction for the prograde LGA orbits, but for the retrograde LGA orbits, $\eta$ increases from 0 to 1 in the clockwise (or retrograde) direction. It should be noted that in the numerical calculation, according to the distribution of the Poincaré section (see Fig. 30), if C of the LGA orbits on the SOIEM is larger than 3.0009, we define $\eta =0$; if C of the LGA orbits on the SOIEM is smaller than 3.0000, we define $\eta =1$. The distributions of $\eta$ can help us choose the appropriate perilune of the LGA orbit based on the launch window of the deep-space mission.

Fig. 31

Distributions of $\eta$ for the prograde LGA orbits and the retrograde LGA orbits when $e =1.5$ and 1.7

6 Conclusion

In this paper, the lunar gravity assist (LGA) orbits starting from the Earth were treated under the framework of the Sun–Earth–Moon PBCM.

First of all, using the Jacobi constant C of the Sun–EMB PCRTBP, we derived the SOIEM, which is centered at the EMB with the radius of 579734.2 km. The numerical calculation indicated that inside the SOIEM, the influence of the Sun on the LGA orbits is quite slight. Even on the SOIEM, the influence of the Sun on the LGA orbits is small. For example, when $e=1.5$, $\Delta \beta <1^{\circ }$ and $\Delta C<4\times 10^{-5}$.

However, outside the SOIEM, the influence of the Sun on the LGA orbits cannot be neglected. We can substitute the Sun–EMB PCRTBP for the PBCM approximately to analyze the LGA orbits. According to the Sun–EMB PCRTBP, the stable manifolds associated with the LPOs and their Poincaré sections on the SOIEM were investigated. Based on our research, we found that when C is larger than 3.00083000, the Poincaré sections of $L_1$ and $L_2$ are two closed primary sections; when C is smaller than 3.00082863, the Poincaré sections of $L_1$ and $L_2$ include two open primary sections and two branches of isolated subordinate sections. The subordinate sections are located in the chaotic areas.

Using the integrated picture of the LGA orbit on the SOIEM, we proposed a simple and intuitive method to obtain the patched LGA orbits: The portions inside the SOIEM are the LGA orbits based on the PBCM; the portions outside the SOIEM are the stable manifolds based on the Sun–EMB PCRTBP. According to our study, these patched LGA orbits can efficiently predict the trends of the LGA orbits based on the PBCM. The LGA orbits inside the primary sections are the transit orbits. If there are no the subordinate sections, the LGA orbits outside the primary sections are non-transit orbits. If there exist the subordinate sections, most of the LGA orbits outside the primary sections are the non-transit orbits, and only in the narrow region near the subordinate sections, the LGA orbits are the transit orbits. Finally, based on the results above, we proposed the stable transit probability $\eta$ and obtained the distribution of $\eta$ for different perilunes of the LGA orbits by numerical method.

According to variant deep-space mission, such as the Earth–Moon transfer and the interplanetary missions, the results of this paper can be applied to selecting the LGA orbit and the launch window.