Dispersive Fluxes Within and Over a Real Urban Canopy: A Large-Eddy Simulation Study

Abstract

Large-eddy simulations (LES) are conducted to study the transport of momentum and passive scalar within and over a real urban canopy in the City of Boston, USA. This urban canopy is characterized by complex building layouts, densities and orientations with high-rise buildings. Special attention is given to the magnitude, variability and structure of dispersive momentum and scalar fluxes and their relative importance to turbulent momentum and scalar fluxes. We first evaluate the LES model by comparing the simulated flow statistics over an urban-like canopy to data reported in previous studies. In simulations over the considered real urban canopy, we observe that the dispersive momentum and scalar fluxes can be important beyond 2–5 times the mean building height, which is a commonly used definition for the urban roughness sublayer height. Above the mean building height where the dispersive fluxes become weakly dependent on the grid spacing, the dispersive momentum flux contributes about 10–15% to the sum of turbulent and dispersive momentum fluxes and does not decrease monotonically with increasing height. The dispersive momentum and scalar fluxes are sensitive to the time and spatial averaging. We further find that the constituents of dispersive fluxes are spatially heterogeneous and enhanced by the presence of high-rise buildings. This work suggests the need to parameterize both turbulent and dispersive fluxes over real urban canopies in mesoscale and large-scale models.

1 Introduction

The world’s urban population has seen unprecedented growth over the last decade, and 68% of people are expected to live in cities by 2050 (United Nations 2018). As a result, urban systems have received significant attention in many fields, including meteorology. Studies on urban weather and air quality forecasting, the dispersion of air pollutants and the impact of new construction projects on urban climate are urgently needed to develop sustainable and resilient cities and improve the quality of life of urban dwellers (Britter and Hanna 2003; Fernando et al. 2001, 2010; Barlow et al. 2017). Advancing the current understanding and modelling capabilities of momentum and scalar transport in the so-called urban roughness sublayer (RSL) is critical to address these issues. The urban RSL is the lowest part of the urban atmospheric boundary layer, where the atmospheric flow is directly affected by the presence of roughness elements (such as buildings, trees and cars). Flow and transport in the urban RSL are complex and highly heterogeneous precisely due to the interactions between the turbulence and the varying arrangement and morphology of the roughness elements (Wang et al. 2014; Auvinen et al. 2020; Cheng et al. 2021; Torres et al. 2021). A commonly used definition for the urban RSL height is about 2–5 times the mean building height (Oke et al. 2017).

Most urban parameterizations represent the complexities of urban RSL via one-dimensional approaches. One-dimensional approaches such as Monin–Obukhov similarity theory (Monin and Obukhov 1954; Obukhov 1971) relying on horizontal homogeneity have been shown to be inapplicable in the urban RSL (Rotach 1999; Roth 2000). Hence, better models that account for the inherently complex urban topology are strongly needed (Britter and Hanna 2003). By averaging the conservation equations over time and space, often called the double-averaging procedure (Xie and Fuka 2018; Schmid et al. 2019), terms that result from spatial heterogeneities in the time-averaged flow need to be considered (Mahrt 1987, 2010). These terms have different names in different fields. For example, in canopy studies, they are called dispersive fluxes (Raupach and Shaw 1982) while in the global atmospheric modelling literature, they are often called mesoscale fluxes (Avissar and Chen 1993; Chen and Avissar 1994). In studies of land surface heterogeneity, similar terms have been called heterogeneity-induced fluxes (Maronga and Raasch 2013; Zhou et al. 2018). But these fluxes all represent the spatial variabilities in the time-averaged flow fields within a certain domain (or over a certain scale) or unresolved, time-lasting advection fluxes generated by a priori unresolved spatial heterogeneities (Calaf et al. 2020). Throughout this paper, they will be called dispersive fluxes. These dispersive fluxes, especially the dispersive scalar fluxes, remain poorly understood, which motivates this study.

The study of dispersive fluxes originates from vegetation canopies (Finnigan 2000; Raupach and Shaw 1982) and gradually moves to other types of canopies. However, their relative importance to turbulent fluxes remains debated and whether they need to be parameterized in large-scale models is unclear. Using wind tunnel measurements, studies showed that the dispersive momentum fluxes are negligible throughout the depth of densely placed plant or urban-like canopy (Raupach et al. 1986; Raupach 1994; Kaimal and Finnigan 1994; Cheng and Castro 2002). In contrast, other investigations have shown that dispersive fluxes play an important role in the description of spatially averaged flow statistics (Bohm et al. 2000; Poggi et al. 2004; Martilli and Santiago 2007; Niroobakhsh et al. 2022). For example, Mignot et al. (2009) found that dispersive fluxes were about 6% of the total fluxes in gravel bed channel flows. However, Bailey and Stoll (2013) showed that the dispersive momentum flux was more than 20% of the turbulent momentum flux in sparse, vegetative canopies. In urban canopy studies, due to the complex pressure field and velocity variations, the dispersive fluxes are formed around canopy edges, and they can be large in the entry region and at the canopy top (Moltchanov et al. 2015). Li and Bou-Zeid (2019) confirmed the significance of dispersive fluxes over urban canopies and studied the effect of changing urban geometry on dispersive fluxes. They showed that the dispersive momentum flux can be about 50% of the total flux, especially for the most eccentric urban geometry. Studies of flow over real urban canopies also confirm the importance of dispersive momentum fluxes (Giometto et al. 2016; Cheng et al. 2021), but little is known about the dispersive scalar flux. Thus, it may be summarized that the importance of dispersive fluxes is highly dependent on a range of morphological factors, including but not limited to canopy densities and heights (Kanda et al. 2013; Sützl et al. 2021). Moreover, the sensitivities of dispersive fluxes to time/spatial averaging scales and grid resolution remain poorly understood, especially over real canopies. For example, previous studies emphasized that a much longer averaging time is needed to compute dispersive fluxes compared to the computation of turbulent fluxes due to the presence of slowly evolving mean circulations (Coceal et al. 2006; Leonardi et al. 2015). However, it is still unknown how the dispersive fluxes over real urban canopies depend on the averaging time and spatial scales.

Research on dispersive fluxes in urban RSL has been often carried out over simplified urban-like configurations, mostly in the form of staggered/aligned cube-, cuboid- or rod-like obstacles (Cheng and Castro 2002; Rasheed and Robinson 2013; Leonardi et al. 2015; Blunn et al. 2022; Sützl et al. 2021). These studies examined the dispersive fluxes under various geometric factors such as aspect ratios, orientations and packing densities (Coceal et al. 2006; Kanda 2006; Cheng et al. 2007; Bou-Zeid et al. 2009; Herpin et al. 2018; Li and Bou-Zeid 2019). These studies were justified on the grounds that it is better to understand flows over simple configurations before introducing other forms of complexities such as variable roughness heights, orientations and/or shapes (Sützl et al. 2021). However, flows over urban-like canopies are different from those over real urban canopies because of the intrinsic surface heterogeneity and the varied aerodynamic properties of individual roughness elements in the real world (Kanda et al. 2013; Giometto et al. 2016; Auvinen et al. 2020). Moreover, the increase in urban population necessitates the construction of high-rise buildings either in isolation or as clusters in many cities. The effects of the wakes behind these high-rise buildings and their interactions with lower buildings were the focus of recent wind tunnel studies (Park et al. 2015; Aristodemou et al. 2018; Hertwig et al. 2019; Mo et al. 2021), which provide a strong motivation to investigate urban RSL flows over real urban canopies characterized by high-rise buildings.

To study real urban canopies, experimental or numerical approaches can be employed. However, experimental studies of turbulence in the RSL over real urban canopies (Grimmond and Oke 1999; Eliasson et al. 2006; Christen et al. 2007, 2009; Ramamurthy et al. 2007; Wang et al. 2014; Ramamurthy and Pardyjak 2015; Mo et al. 2021) are often hindered by the limitations associated with performing thorough measurements in the field (i.e. measurements are only taken at a few points in space). As a result, spatially averaged quantities are often unknown and need to be approximated (Christen et al. 2009). Fortunately, state-of-the-art modelling techniques such as large-eddy simulation (LES) offer the opportunities to comprehensively examine the spatiotemporal variability of RSL flows over real urban canopies. Using LES over real canopies, Kanda et al. (2013) found that the standard deviation of building heights and the maximum building height, in addition to the mean building height, were also relevant for the parameterization of spatially averaged flow statistics. Several other LES studies also feature real urban canopies (e.g. Xie and Castro 2009; Giometto et al. 2016, 2017; Efthimiou et al. 2017; Auvinen et al. 2020), but the range of building heights in these studies is often limited. For example, the maximum building height is three times the mean building height in Auvinen et al. (2020) and four times in Giometto et al. (2016, 2017).

In view of these knowledge gaps, this study aims to use LES to simulate flows within and over a real urban canopy in the City of Boston, Massachusetts, USA, which is characterized by a wide range of building heights with maximum building height of about twelve times the mean building height. As a preliminary step towards developing parameterizations for dispersive fluxes, we study the temporally and spatially averaged flow fields and the dispersive fluxes, including their sensitivities to the temporal and spatial averaging scales as well as the grid resolution. We further quantify the spatial structure of dispersive fluxes using quadrant analysis, which is commonly used to study turbulent fluxes. The paper is organized as follows: the concept of dispersive fluxes and the quadrant analysis approach are introduced in Sect. 2; Sect. 3 describes the LES model and its evaluation; Sect. 4 presents the results, and conclusions are drawn in Sect. 5.

2 Theoretical Background

2.1 The Double-Averaging Procedure

Due to the spatial heterogeneity of RSL flows and the need to evaluate spatially averaged quantities, the double-averaging (DA) procedure is often employed (Schmid et al. 2019). The ‘double-averaging’ procedure bears its name from the fact that the averaging operation is conducted along both space and time. The spatial averaging in the DA procedure can be carried out using the intrinsic averaging operation (Nikora et al. 2007), where the averaging volume (a horizontal slab of arbitrarily small thickness $\Delta z$) includes the ambient air only, or the extrinsic averaging (Yuan and Piomelli 2014), where the averaging is performed over the whole horizontal slab (i.e. including the air volume within the buildings). The intrinsic averaging operation is widely used in the literature to characterize flow fields over vegetation canopies (Wilson and Shaw 1977; Raupach and Shaw 1982), over gravel beds (Nikora et al. 2007) and rigid canopies (Raupach et al. 1991; Coceal et al. 2006; Xie et al. 2008). Here, we consider the intrinsic spatial averaging of a temporally averaged variable $X$, defined as:

$$\langle \overline{X }\rangle =\frac{1}{{V}_{f}}\iiint \overline{X }\left(x,y,z\right) \alpha \left(x,y,z\right) {\text{d}}x{\text{d}}y{\text{d}}z,$$

(1)

where $X$ is a flow quantity (such as velocity and scalar concentration), ${V}_{f}$ is the fluid volume and $\alpha$ is 1 when the space corresponds to the outdoor air and 0 otherwise. The overbar and angular brackets denote time and spatial averaging, respectively. This approach will be used to compute flow statistics including the dispersive fluxes.

2.2 Dispersive Fluxes

Dispersive fluxes, initially introduced by Wilson and Shaw (1977) and Raupach and Shaw (1982), appear as an additional term that represent a contribution to momentum transfer in the doubly averaged momentum equation. As an illustration, upon applying time and spatial averaging to the product between the vertical velocity $w$ and any flow quantity $X$, one obtains $\langle \overline{wX }\rangle = \langle \overline{w }\rangle \langle \overline{X }\rangle +\langle \overline{w{^{\prime}}X{^{\prime}}}\rangle + \langle {\overline{w} }^{{{\prime\prime}}}{\overline{X} }^{{{\prime\prime}}}\rangle$ (Mahrt 1987). Here, prime and double prime denote temporal and spatial deviations, respectively. Namely, ${X}^{{{\prime}}}=X- \overline{X }$ is the temporal fluctuation of $X$ (i.e. deviations from the temporally averaged $\overline{X }$) and ${\overline{X} }^{{{\prime\prime}}}= \overline{X }- \langle \overline{X }\rangle$ is the spatial deviation of $\overline{X }$ from the spatially averaged $\langle \overline{X }\rangle$. The left-hand side of the equation is the temporally and spatially averaged vertical flux of $X$, while the terms on the right-hand side of the equation represent the mean or resolved flux, the turbulent flux and the dispersive flux, respectively. The mean flux is due to time-averaged structures that are larger than the size of the spatial averaging scale. The turbulent flux arises from the temporal correlations in the instantaneous field at any given point, which can be estimated using the temporal eddy covariance method (i.e. $\overline{w{^{\prime}}X{^{\prime}}} = \overline{wX }- \overline{w } \overline{X }$). In contrast, the dispersive fluxes are the result of the spatial correlations of quantities averaged in time but varying with space, calculated as $\langle {\overline{w} }^{{{\prime\prime}}}{\overline{X} }^{{{\prime\prime}}}\rangle = \langle \overline{w }\overline{X }\rangle - \langle \overline{w }\rangle \langle \overline{X }\rangle$.

2.3 Quadrant Analysis

The classical quadrant analysis provides information on the relationship between the temporal fluctuations of velocity components $u{^{\prime}}$ and $w{^{\prime}}$ (for momentum transport), as well as $w{^{\prime}}$ and $s{^{\prime}}$ (for scalar transport) (Wallace 2016). Here $u$ refers to the streamwise velocity and $s$ refers to the scalar concentration. Correlation between these fluctuations reveals the presence of turbulent coherent structures that are categorized into outward interaction, sweep, inward interaction and ejection, according to the sign of the fluctuating quantities (Shaw et al. 1983; Katul et al. 1997; Li and Bou-Zeid 2011; Wang et al. 2014). In this study, dispersive fluxes are investigated by applying quadrant analysis to the spatial deviations of time-averaged velocity components ($\overline{w }{^{\prime\prime}}$ and $\overline{u }{^{\prime\prime}}$) and scalar concentration $\overline{s }{^{\prime\prime}}$. As a result, the quadrant analysis applied here aims to reveal the spatially persistent structures of the time-averaged flow. This technique has been used to study dispersive fluxes in flows over urban-like canopies (Li and Bou-Zeid 2019), rough beds (Pokrajac et al. 2007), rod canopies (Poggi and Katul 2008) and plant canopies (Christen and Vogt 2004). Quadrants for $\overline{w }{^{\prime\prime}}\overline{u }{^{\prime\prime}}$ and $\overline{w }{^{\prime\prime}}\overline{s }{^{\prime\prime}}$ in the (${\overline{w} }^{{{\prime\prime}}}$, $u{^{\prime\prime}}$)-plane and (${\overline{w} }^{{{\prime\prime}}}$, $s{^{\prime\prime}}$)-plane are defined as follows (Poggi and Katul 2008):

• Quadrant 1 (${Q}_{1}$): ${\overline{w} }^{{{\prime\prime}}}> 0$, ${\overline{u} }^{{{\prime\prime}}}>0$ or ${\overline{s} }^{{{\prime\prime}}}<0$—outward interactions (O),

• Quadrant 2 (${Q}_{2}$): ${\overline{w}}^{{{\prime\prime}}}< 0$, ${\overline{u} }^{{{\prime\prime}}}>0$ or ${\overline{s} }^{{{\prime\prime}}}<0$—sweeps (S),

• Quadrant 3 (${Q}_{3}$): ${\overline{w} }^{{{\prime\prime}}}< 0$, ${\overline{u} }^{{{\prime\prime}}}<0$ or ${\overline{s} }^{{{\prime\prime}}}>0$—inward interactions (I),

• Quadrant 4 (${Q}_{4}$): ${\overline{w} }^{{{\prime\prime}}}> 0$, ${\overline{u} }^{{{\prime\prime}}}<0$ or ${\overline{s} }^{{{\prime\prime}}}>0$—ejections (E).

Furthermore, a threshold ${T}_{h}$ is defined to separate large, important persistent structures from the less important ones, as follows: $\left|{\overline{w} }^{{{\prime\prime}}}{\overline{u} }^{{{\prime\prime}}}\right|={T}_{h}|\langle {\overline{w} }^{{{\prime\prime}}}{\overline{u} }^{{{\prime\prime}}}\rangle |$. Higher values of ${T}_{h}$ identify structures with larger absolute values of ${\overline{w} }^{{{\prime\prime}}}{\overline{u} }^{{{\prime\prime}}}$ relative to the absolute value of dispersive flux $\langle {\overline{w} }^{{{\prime\prime}}}{\overline{u} }^{{{\prime\prime}}}\rangle$. With this threshold, the dispersive flux fraction from each quadrant, denoted as ${F}_{i,{T}_{h}}$, is defined as:

$${F}_{i,{T}_{h}}=\frac{{[{\overline{w} }^{{{\prime\prime}}}{\overline{u} }^{{{\prime\prime}}}]}_{i,{T}_{h}}}{\langle {\overline{w} }^{{{\prime\prime}}}{\overline{u} }^{{{\prime\prime}}}\rangle },$$

(2)

where the subscript $i$ is the quadrant number and:

$${\left[{\overline{w} }^{{{\prime\prime}}}{\overline{u} }^{{{\prime\prime}}}\right]}_{i,{T}_{h}}= \frac{1}{{{V}}_{f}}\iiint {\overline{w} }^{{{\prime\prime}}}{\overline{u} }^{{\prime\prime}}(x,y,z) {I}_{i,{T}_{h}}\left(x,y,z\right) {\text{d}}x{\text{d}}y{\text{d}}z ,$$

(3)

is a conditional average with an indicator function ${I}_{i,{T}_{h}}$ defined as

$${I}_{i,{T}_{h}}=\left\{\begin{array}{c}1, {\text{if}} \, {\text{the}} \, {\text{point}} \left({\overline{w} }^{{\prime\prime}}, {\overline{u} }^{{\prime\prime}}\right) \text{lies in quadrant} \, {Q}_{i} \, {\text{and}} \left|{\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}\right|{>T}_{h}\langle {|\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}|\rangle \\ 0, {\text{otherwise}}.\end{array}\right.$$

From the above definition of dispersive flux fraction ${F}_{i,{T}_{h}}$, we obtain:

$$\sum_{i=1}^{4}{F}_{i,0}=1,$$

(4)

The space occupied by quadrant ${Q}_{i}$ is called the space fraction ${S}_{i,{T}_{h}}$, defined as:

$${S}_{i,{T}_{h}}=\frac{1}{{{V}}_{f}}\iiint {I}_{i,{T}_{h}}\left(x,y,z\right) {\text{d}}x{\text{d}}y{\text{d}}z.$$

(5)

The dispersive flux fraction ${F}_{i,{T}_{h}}$ in Eq. 2 and the space fraction ${S}_{i,{T}_{h}}$ in Eq. 5 for scalar are defined similarly by replacing ${\overline{u} }^{{\prime\prime}}$ with ${\overline{s} }^{{\prime\prime}}$.

3 Methodology

3.1 Large-Eddy Simulation Framework

The LES has become an indispensable tool for studying the atmospheric boundary layer. It resolves the large turbulent motions that are mostly responsible for momentum and scalar transfer and thus only requires a parameterization for the effect of small-scale turbulence. For this study, the PALM model system in revision 4901 (Maronga et al. 2015, 2020) is used. The PALM model system has been widely used to study urban flows over both idealized (Letzel et al. 2008; Park et al. 2012; Gronemeier and Suhring 2019; Nazarian et al. 2020; Blunn et al. 2022) and real urban canopies (Kanda et al. 2013; Park et al. 2015; Gronemeier et al. 2017; Auvinen et al. 2020; Kurppa et al. 2020) and has been validated extensively (Fröhlich and Matzarakis 2020; Gronemeier et al. 2021; Resler et al. 2021).

The PALM solver numerically integrates the filtered, Navier–Stokes equations for incompressible and Newtonian fluids in the Boussinesq approximations form. For this study, a neutrally stratified environment is assumed, and Coriolis-related terms are negligible. To close the system of filtered equations, PALM employs the 1.5-order subgrid-scale model of Deardorff (1980). Temporal discretization is done with the third-order Runge–Kutta scheme and a predictor–corrector approach, where the divergence generated by the predictor step is corrected via the solution of the Poisson equation for the pressure field. The Poisson equation is solved using an iterative multigrid scheme (Hackbusch 1985), while the fifth-order Wicker–Skamarock and the second-order central difference schemes are employed to discretize the advection and diffusion schemes. The domain is spatially discretized using the finite difference approach on Arakawa staggered C-grid (Arakawa and Lamb 1977). For more details, we refer readers to Maronga et al. (2015, 2020).

3.2 Evaluation of the PALM Model for Idealized Urban Canopy Flows

Before investigating flows over real urban canopies, it is important to evaluate the predictive capabilities of the PALM model. For this purpose, we adopt a simple configuration with staggered array of cubes (see Fig. 1), similar to that used in previous work such as Coceal et al. (2006), Li and Bou-Zeid (2019) and Tian et al. (2021). We choose this simple configuration because it has been well studied so our results can be compared to previously reported experimental and numerical data. The flow is driven by a negative pressure gradient, whose magnitude and direction are adjusted such that $\langle \overline{u }\left(z= \delta \right)\rangle \approx 3.5$ m ${\text{s}}^{-1}$ where $\delta =9H$ is the boundary-layer height and $H=12.48$ m is the height of cubes. The dimension of the computational domain is $3\delta \times 1.5\delta \times \delta$ with ${N}_{x}=216$, ${N}_{y}=108$ and ${N}_{z}=72$, where ${N}_{x}, {N}_{y}, {N}_{z}$ are the number of grid points in the streamwise, spanwise and vertical direction, respectively. A horizontal and vertical grid spacing of $\Delta = H/8$ is used, which is justified based on the grid spacing comparison ($\Delta =H/8$, $H/16$, $H/32$) performed by Xie and Castro (2006) for staggered cube array. They showed that LES of turbulent flows over urban-like canopy has a weak dependence on grid spacing because the total surface drag is mostly pressure drag (i.e. drag caused by the presence of the cube) and the scale of turbulence production processes is comparable to the cube size. Also, our computational domain and grid spacing are similar to those used in Li and Bou-Zeid (2019). No slip wall boundary conditions are used at the floor or cube surfaces. Between the surface (including vertical walls) and the first computational grid-level, a constant flux layer with momentum roughness length ${z}_{0} = 0.01$ m is used. Periodic boundary conditions are imposed in the lateral directions to simulate an infinite array of cubes while the top boundary is impermeable with zero stress. The Reynolds number based on friction velocity ${u}_{*}$, height $H$ and air kinematic viscosity $\nu$ (assuming $\nu =1.47 \times {10}^{-5} {\text{m}}^{2} {\text{s}}^{-1}$) is $1.53 \times {10}^{5}.$ The friction velocity ${u}_{*}$ is evaluated from the total surface drag per unit floor area ${\tau }_{*}$, i.e. ${u}_{*}=\sqrt{{\tau }_{*}/\rho }=0.18 {\text{m}} {\text{s}}^{-1}$, where $\rho$ is the air density ($1 {\text{kg}} {\text{m}}^{-3}$) and ${\tau }_{*}$ is the sum of ground floor drag and the total cube (form and skin friction) drag (Kanda et al. 2013).

Fig. 1

Plan view of canopy configurations used for PALM evaluation where P0–P3 are at the ‘top’, ‘behind’, ‘in front’ and ‘in between’ the cubes. The computational domain consists of 5 by 4 cubes and only a subsection (or a repeating unit) of the domain is shown here

The simulation is initially run for $200 T$ where $T=H/{u}_{*}$ in order to reach a statistical steady state. This duration is the same as the one reported in Li and Bou-Zeid (2019), but longer than the one reported in Coceal et al. (2007a, b). The simulation is then continued for another $200 T$ to compute the flow statistics. Figure 2 presents the vertical profiles of the mean streamwise velocity normalized by the friction velocity at four positions (P0 to P3, as indicated in Fig. 1). Note that the result at each position is the average of 20 (5 times 4) profiles because the computational domain consists of 5 by 4 cubes. Previously reported LES results of Tian et al. (2021) and direct numerical simulation (DNS) results of Coceal et al. (2007b) are shown for comparison. Moreover, two experimental datasets generated by Particle image velocimetry (PIV) (Blackman and Perret 2016; Blackman et al. 2017) and laser Doppler velocimetry (LDV) (Castro et al. 2006) are shown. The LES runs of Tian et al. (2021) were carried out at a finer grid resolution of $H/32$ for $z \le 1.5H$ with a refinement of $H/64$ on all surfaces and down to $H/128$ at the top of all cubes. PIV datasets were extracted at positions P0 to P3 without spatial averaging and normalized by the friction velocity obtained from drag force measurements. All datasets (numerical and experimental) presented for comparison in this study are extracted from figures presented in Tian et al. (2021). As shown in Fig. 2, the PALM results (black solid lines) are in good agreement with LES data from Tian et al. (2021), DNS data from Coceal et al. (2007b) and wind tunnel measurements performed by Castro et al. (2006) at the four positions. The PALM results also agree with observations of Blackman et al. (2017) using PIV within the canopy. As reported in Tian et al. (2021), the discrepancies with the PIV measurements of Blackman et al. (2017) above the canopy may be caused by the differences in the boundary-layer height $\delta$. Close inspection of the simulated streamwise velocity profiles indicates that there is an inflection point at $z = H$ over P1, P2 and P3 (see Fig. 2a–c). The actual values of the velocity gradient at the inflection point vary from point to point (it is the largest at P1), which highlights the spatial variation in the local shear layer at the top of the cubes.

Fig. 2

Vertical profiles of the mean streamwise velocity component normalized by the friction velocity ${u}_{*}$ at position a P1, b P2, c P3 and d P0. Black solid line: PALM computations; blue solid line: LES data from Tian et al. (2021); red dashed line: DNS data from Coceal et al. (2007b); black circles: wind tunnel data from Castro et al. (2006); green circles: PIV data from Blackman et al. (2017)

Figure 3a, c, e shows the vertical profiles of turbulent momentum flux (including the subgrid-scale contribution) at three positions. The turbulent momentum flux from $z/H=0.3$ to the top of the canopy at positions P1 and P2 agrees quite well with LES data from Tian et al. (2021), DNS data from Coceal et al. (2007b) and wind tunnel measurements performed by Castro et al. (2006) (see Fig. 3a, c). For all positions, the maximum turbulent momentum flux is located near $z = H$ in both simulations and experiments. At position P1 (at the back of the cube), the numerical simulations underestimate this maximum in comparison with the experimental data of Castro et al. (2006), but overestimate this maximum when compared to the PIV data (see Fig. 3a). Consistent with this, the simulated peak values for the standard deviation of vertical velocity ${\sigma }_{w}$ lie between the two experimental datasets (see Fig. 3b). These discrepancies were also found in Tian et al. (2021) and Reynolds and Castro (2008). The first cause of these deviations, as proposed by Reynolds and Castro (2008), is the difference in the ratio of $H/\delta$. The datasets in Fig. 3 have different values of $H/\delta$. We note that our $H/\delta =11{\%}$ is close to the $H/\delta =12.5{\%}$ used in Tian et al. (2021) and Coceal et al. (2007b), and $H/\delta =13{\%}$ in Castro et al. (2006). This value differs from $H/\delta =4.5{\%}$ used in Blackman et al. (2017). The second cause of these discrepancies is the resolution as the peak value is smoothed out when a coarse resolution is used (Scarano and Riethmuller 2000). Note that the vertical resolution of the PALM run ($\Delta /H = 0.125$) is coarser than both the numerical simulations of Tian et al. (2021) and Coceal et al. (2007b), and the experimental datasets of Castro et al. (2006) and Blackman et al. (2017). At position P2, the vertical profiles of the turbulent momentum flux and ${\sigma }_{w}$ again fall between the two experimental datasets. At position P3, the only available numerical simulation result is the LES data from Tian et al. (2021) and the only available experimental dataset is the PIV from Blackman et al. (2017). The simulated turbulent momentum flux and ${\sigma }_{w}$ agree with the LES data from Tian et al. (2021) over $0.3 \le z/H \le 1.5$. However, the simulated turbulent momentum flux only agrees with the PIV data over $z/H \ge 0.6$ and the simulated ${\sigma }_{w}$ deviates strongly from the PIV data.

Fig. 3

Vertical profiles of normalized turbulent momentum flux and standard deviation of vertical velocity at position a, b P1; c, d P2; and e, f P3. Black solid line: PALM computations; blue solid line: LES data from Tian et al. (2021); red dashed line: DNS data from Coceal et al. (2007b); black circles: wind tunnel data from Castro et al. (2006); green circles: PIV data from Blackman et al. (2017)

Figure 4 presents the standard deviations of streamwise velocity (${\sigma }_{u}$) and spanwise velocity (${\sigma }_{v}$). In general, larger discrepancies exist between the numerical simulations and the experimental data at all positions when compared to the results shown in Fig. 3. This is because the standard deviations of horizontal velocity components, especially ${\sigma }_{v}$, are notoriously difficult to measure and simulate (Tian et al. 2021). The resolution of the simulation also plays an important role. At position P1, the ${\sigma }_{u}$ simulated by PALM model agrees with the LES data from Tian et al. (2021) and experimental datasets from Castro et al. (2006) and Blackman et al. (2017) around the canopy top, but deviates elsewhere (see Fig. 4a). Interestingly, the PALM results seem to agree better with the wind tunnel data than the other two simulations within the canopy, but are worse above the canopy at position P1. At positions P2 and P3, the ${\sigma }_{u}$ from the PALM model deviates from the LES data of Tian et al. (2021), but agrees better with wind tunnel data from Castro et al. (2006), especially above the canopy.

Fig. 4

Vertical profiles of the standard deviation of the streamwise and spanwise velocity component at position a, b P1; c, d P2; and e, f P3. Black solid line: PALM computations; blue solid line: LES data from Tian et al. (2021); red dashed line: DNS data from Coceal et al. (2007b); black circles: wind tunnel data from Castro et al. (2006); green circles: PIV data from Blackman et al. (2017)

In summary, the PALM model results of both first- and second-order moments show overall good agreement with previous numerical and experimental data. In the following, we use it to study RSL flows over a real urban canopy.

3.3 Description of the Urban Building Height Dataset

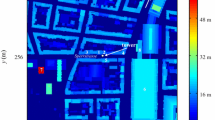
We begin our investigation of RSL flows over real urban canopies with a description of the building height distribution in our study area (see Fig. 5), which is a $2.4\times 2.4 {\text{k}}{\text{m}}^{2}$ area around Fenway–Kenmore square in the City of Boston, Massachusetts, USA. This area features a dense arrangement of residential blocks, an irregular distribution of narrow street canyons, a park in the north-west region and the Charles River in the north. The north-eastern region is a business district with many high-rise buildings of height above 100 m (e.g. the Prudential centre which is 227 m high), while the south-western region is the home to several hospitals (Boston children hospital, Beth Israel Medical centre, Brigham and Women’s hospital) and universities (Harvard school of public health, Emmanuel college, Simmons university and Massachusetts College of Pharmacy and Health Sciences) with moderately tall buildings of about 60–80 m in height. Within the study area, the mean building height $H$ is 19 m, the standard deviation ${\upsigma }_{H}$ is 17 m, and the plan area fraction ${\uplambda }_{p}={A}_{p}/{A}_{\text{total}}=0.25$, where ${A}_{p}$ is the planar area of urban buildings at the ground level and ${A}_{\text{total}}$ is the total planar area of the domain. Note that in previous studies like Auvinen et al. (2020), the building height distribution is almost symmetric with ${\upsigma }_{H}/H=0.4-0.6$ while Giometto et al. (2016, 2017) studied a building height distribution which was trimodal with ${\upsigma }_{H}/H=0.42$. In our study, the distribution is distinctly skewed with ${\upsigma }_{H}/H=0.89$. We do not include vegetation, which is justified by its small plan area fraction (Giometto et al. 2016).

Fig. 5

a Map of the building heights in the study area, with the Charles River in the north, the Boston children hospital (about 75 m) in the south-west, and the Prudential centre (maximum building height of 227 m) in the north-east. b Normalized fraction of building heights

3.4 Simulation Set-up

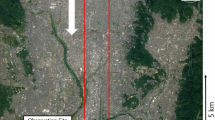
For the simulation, we adopt a set-up similar to that of Auvinen et al. (2020) and Resler et al. (2021) as shown in Fig. 6. To save computational resources, the self-nesting feature of PALM is utilized (Hellsten et al. 2021). Here self-nesting means that a finer resolution domain (also called child domain) is defined inside a larger but coarser resolution domain (or parent domain). These two model domains run simultaneously with one-way nesting. That is, the simulation in the child domain receives its boundary conditions from the parent domain, but does not affect the simulation in the parent domain. The parent domain is ${L}_{x}^{\text{p}}=13.82$ km, ${L}_{y}^{\text{p}}=3.45$ km and ${L}_{z}^{\text{p}}= 1.15$ km while the child domain is ${L}_{x}^{\text{c}}=2.88$ km, ${L}_{y}^{\text{c}}= 2.88$ km and ${L}_{z}^{\text{c}}=0.57$ km in the streamwise, spanwise and vertical directions, respectively. The superscripts ‘p’ and ‘c’ denote the parent and child domains, respectively. The child domain starts from $x = 9.40$ km and $y = 0.29$ km in the parent domain. The parent domain is discretized with an isotropic grid spacing of 8 m (i.e. $\Delta {z}^{\text{p}}=8$ m) while the child domain has a grid spacing of 4 m (i.e. $\Delta {z}^{\text{c}}=4$ m). The sensitivity of the flow statistics to the resolution of the child domain is presented in Sect. 4.2.3.

Fig. 6

Model set-up. The solid black line shows the horizontal extent of the parent domain while the red solid line on the right is the child domain and the region where all statistics are computed. The horizontal extent of the precursor simulation domain, used to initialize both domains, is shown in the bottom left corner of the parent domain in blue. The left corner of the parent domain features the recycling region. The black arrow at the top left corner indicates the wind direction

For the parent domain, a cyclic boundary condition is applied at the spanwise boundaries while non-cyclic conditions are set at the streamwise boundaries. This is different from many other studies where cyclic boundary conditions were used for all lateral boundaries (Kanda et al. 2013; Giometto et al. 2016, 2017; Inagaki et al. 2017; Gronemeier et al. 2021). The use of non-cyclic boundary conditions along the streamwise direction ensures that the building-induced turbulence is not recycled into the analysis region, which is especially important when dealing with horizontally inhomogeneous surface morphologies such as the one considered herein. The inlet boundary condition is created to mimic a fully developed, homogeneous, neutral boundary layer, which is not affected by buildings downstream. This is achieved with the turbulence recycling technique based on the method by Lund et al. (1998) with modification of Kataoka and Mizuno (2002). This technique has been applied to spatially developing LES of many engineering and environmental flows (Wu 2017; Wang et al. 2021).

The implementation of this boundary condition on the parent domain in PALM is presented in Maronga et al. (2015) and it is discussed here with modified notation to make this paper self-contained. The inlet boundary value of a prognostic variable $\phi = \phi (x,y,z,t)$, where $\phi \in \{u,v,w,s, e\}$, is constructed from its temporally and horizontally averaged vertical profiles $\langle \overline{\phi }\rangle \left(z\right)$ and the fluctuating components ${\phi }^{{\prime}}\left(x,y,z,t\right)$ through ${\phi }_{\text{inlet}}\left(x,y,z,t\right){|}_{x= {x}_{\text{inlet}}}= \langle \overline{\phi }\rangle \left(z\right)+{\phi }^{{\prime}}\left(x,y,z,t\right)$. The fluctuating component ${\phi }^{{\prime}}$ is computed from a specified recycling $y- z$ plane at a given streamwise coordinate ${x}_{\text{recycle}}=5$ km, placed far downstream from the inlet to avoid the feedback of disturbances between the inlet and the recycling plane. ${\phi }^{{\prime}}$ is obtained as: ${\phi }^{{\prime}}= {\phi }_{\text{recycle}}\left(x,y,z,t\right){|}_{x= {x}_{\text{recycle}}}- {\langle \phi \rangle }_{y}{|}_{x= {x}_{\text{recycle}}}$, where ${\langle \phi \rangle }_{y}{|}_{x= {x}_{\text{recycle}}}$ is the spanwise mean at ${x}_{\text{recycle}}=5 {\text{km}}$. Only fluctuations at $z<0.75{ L}_{z}^{\text{p}}$ are recycled while fluctuations at $z>0.75 { L}_{z}^{\text{p}}$ are damped to zero to prevent the growth of the boundary layer; hence, $\delta$ is $0.75 { L}_{z}^{\text{p}}$. The boundary-layer height of the parent domain is $\delta /H=45$, which almost satisfies the $\delta /H\gtrsim 50$ requirement (Jimenez 2004). The temporally and horizontally averaged vertical profile $\langle \overline{\phi }\rangle \left(z\right)$ for the prognostic variable is held fixed at the inlet and is generated from a precomputed simulation, called a precursor run. The domain of the precursor run can be seen in the bottom left corner of Fig. 6 with dimension $3.45$ km $\times 1.1$ km $\times 1.1$ km in the streamwise, spanwise and vertical directions, respectively. The precursor run has the same resolution as the parent domain, but with periodic lateral boundary conditions, and free-slip and no-slip conditions at the top and bottom, respectively. The precursor run is driven by a constant initial streamwise velocity of 3.5 m ${\text{s}}^{-1}$ and zero spanwise velocity. It is then computed for $390 {T}_{\text{precursor}}$, where ${T}_{\text{precursor}}={L}_{z}/\langle \overline{u }\left(z= \delta \right)\rangle$. The temporally and horizontally averaged vertical profiles are obtained from the last 150 ${T}_{\text{precursor}}$. The wind direction is held constant for the precursor and parent runs and is from west to east.

A long section of the parent domain before the urban canopy is constructed for two reasons. First, it helps in the development and evolution of large-scale motions and very large-scale motions that are seen in boundary-layer flows (Balakumar and Adrian 2007; Chung and McKeon 2010; Hutchins et al. 2012). The presence and relevance of these large-scale streamwise structures have been extensively studied (Hutchins and Marusic 2007; Mathis et al. 2009; Anderson 2016). Studies have shown that these structures affect the RSL flows via amplitude modulation, and they are considered a universal trait of boundary-layer flows under neutral conditions (Anderson 2016). The sizes of these large-scale structures are usually in the range $10\updelta {-} 20\delta$ in the streamwise direction (Fang and Porté-Agel 2015). Here, the size of our computational domain in the streamwise direction is about $18\delta$ and hence might accommodate these large-scale structures. Second, the recycling region needs to avoid the disturbances that travel upstream from the edge of the urban canopy. These disturbances can give rise to a weak perturbation at the recycling region, which can be transported to the inlet because of turbulence recycling mentioned earlier. As a result, we limit this effect by increasing the distance between the recycling region and the edge of the urban canopy. Moreover, the turbulence recycling technique is prone to numerically amplify long streamwise disturbances when neutral stratification with no spanwise velocity component is used, causing large-scale structures at the recycling plane to become correlated with those at the inlet (Fishpool et al. 2009). These numerical streak-like artefacts can be eliminated either by introducing a small flow angle to the simulation (Auvinen et al. 2020; Karttunen et al. 2020) or using a shifting method (Munters et al. 2016) to the parent run. In the shifting approach, the velocity at the recycling plane is first shifted uniformly in the spanwise direction by a constant distance ${d}_{s}$ before it is reintroduced at the inlet. The parameter ${d}_{s}$ should be chosen in a way to avoid reintroducing the same turbulent structure in the same spanwise location after a few flowthroughs. This approach was shown to be effective in breaking up these persistent streaks for developing urban boundary layers (Munters et al. 2016; Gronemeier et al. 2021; Hellsten et al. 2021). We apply the shifting method (using ${d}_{s}=380$ m) to the parent run.

The simulation is initialized by repetitively copying the precursor run flow solution to the parent and child domains (Maronga et al. 2015). The no-slip wall boundary condition is imposed on all surfaces (including the roofs, ground and building walls) while free-slip conditions are applied to the top of the parent domain. To account for the effects of low vegetation and other structural details, a momentum roughness length ${z}_{0} = 0.01$ m is used, which agrees the recommendation of Basu and Lacser (2017) that ${z}_{0}\le 0.02\times {\min}\left(\Delta z\right)$. The value ${\min}\left({\Delta z}^{\text{c}}\right)=2$ m for this study because the first computational level is positioned at $0.5\Delta {z}^{\text{c}}$ for the staggered grid. We assume a constant flux layer between the surface (including the roofs, ground and building walls) and the first computational grid-level. The boundary condition for passive scalar is a surface flux of ${0.05 \text{kg m}}^{-2} {\text{s}}^{-1}$ imposed on all surfaces (including the roofs, ground and building walls).

After the initialization, the urban simulation runs for a spin-up period of $180 T$ where $T=H/{u}_{*}$ in order to reach a steady state. Here $T$ is interpreted as the eddy turnover time for the largest eddies (Coceal et al. 2006). The friction velocity ${u}_{*}=0.17 \text{m }{\text{s}}^{-1}$ is again computed from the total surface drag (as defined in Sect. 3.2), which is the sum of the friction and pressure drag on the buildings and the friction drag on the ground floor. The pressure drag on the buildings accounts for about 90% of the total surface drag. The simulation is then pursued for another $360 T$ to compute all temporal averaging statistics. Data analyses are conducted only in the child domain where all statistics are computed. The streamwise velocity, vertical velocity, momentum fluxes and velocity variances are normalized with the friction velocity ${u}_{*}$. The scalar concentration is normalized with ${s}_{*}= {\stackrel{-}{w{^{\prime}}s{^{\prime}}}}_{0}/{u}_{*}$ where ${\stackrel{-}{w{^{\prime}}s{^{\prime}}}}_{0}={0.05 \text{kg m}}^{-2} {\text{s}}^{-1}$ is the surface scalar flux. The scalar fluxes are normalized with ${u}_{*}{s}_{*}$. The vertical height is normalized with the mean building height ($H = 19$ m).

4 Results and Discussion

4.1 Instantaneous Velocity and Scalar Concentration

Figures 7 and 8 display the instantaneous streamwise velocity, vertical velocity and scalar concentration. As can be seen, the RSL flow is strongly affected by the heterogeneity of the urban canopy and is characterized by a wide range of length scales. The relatively large ratio between the standard deviation of building heights and the mean building height (${\sigma }_{H}/H=0.89$) causes the flow to alternate between different flow regimes such as skimming and wake interference (see Oke (1988) for the definition of flow regimes). Wake and non-wake regions can clearly be identified in the RSL (see Fig. 7a) (Böhm et al. 2013) while the flow contains high and low momentum streamwise elongated streaks within the inertial sublayer (see Fig. 7b) (Inagaki et al. 2012; Giometto et al. 2016).

Fig. 7

Horizontal slice of the instantaneous snapshot for a streamwise velocity at $z/H = 1$, b streamwise velocity at $z/H = 13$, c vertical velocity at $z/H = 1$ and d logarithm of the scalar concentration at $z/H = 1$. Streamwise and vertical velocity are normalized by the friction velocity ${u}_{*}$ while the scalar concentration is normalized by ${s}_{*}$. The $x$- and $y$- axis are defined in terms of the child domain

Fig. 8

Vertical slice of the instantaneous snapshot for a streamwise velocity, b vertical velocity and c logarithm of the scalar concentration at $y/H = 116$. Streamwise and vertical velocity are normalized by the friction velocity ${u}_{*}$ while the scalar concentration is normalized by ${s}_{*}$.The dashed horizontal line indicates the height $z/H = 1$. The $x$- axis are defined in terms of the child domain

Elongated wakes with a streamwise extent of about $0.5{-}1$ km are found behind high-rise buildings (see Fig. 8a). The vertical velocity shows regions of updrafts mostly at the windward side of the buildings, efficiently transporting passive scalars to the upper part of the RSL while downdrafts are seen at the leeward side of the building (see Figs. 7c and 8b). The presence of high-rise buildings causes strong updrafts at its windward side. The leeward side contains two distinct regions of the building wake: the momentum deficit in the main wake and the recirculation zone in the near wake, consistent with the study of Hertwig et al. (2019). The wake can extend downward and interact with lower buildings (see Fig. 8). The scalar concentration mostly peaks in low-speed regions especially in areas where there are building clusters or at the wake of high-rise buildings (see Fig. 7d), which agrees with Aristodemou et al. (2018). These results are consistent with the literature that shows the importance of high-rise buildings in affecting urban RSL flow structures (Flaherty et al. 2007; Xie and Castro 2009; Cheng et al. 2021; Mo et al. 2021).

4.2 Double-Averaging Flow Statistics in the Roughness Sublayer

The double-averaging (DA) approach described in Sect. 2.1 is used to compute the flow statistics. For the DA profiles presented in this study, the time averaging is performed first, followed by the intrinsic spatial averaging over horizontal slabs of thickness ${\Delta z}^{\text{c}}$ (i.e. using Eq. 1). Figure 9 presents the double-averaging profiles of streamwise velocity, vertical velocity and scalar concentration and their variances below $z/H=30$. The reason we focus on the region below $z/H=30$ is that the dispersive momentum flux does not disappear until $z/H=30$, as shall be seen later.

Fig. 9

Normalized DA profiles of a streamwise velocity, b vertical velocity, c logarithm of the scalar concentration, d variance of streamwise velocity, e variance of vertical velocity and f turbulent kinetic energy $TKE=0.5(\langle \overline{{u }^{{{\prime}}2}}+ \overline{{v }^{{{\prime}}2}}+\overline{{w }^{{{\prime}}2}}\rangle )$. Momentum and $TKE$ profiles are normalized with the friction velocity ${u}_{*}$ while the scalar profile is normalized by with ${s}_{*}$. Solid horizontal line indicates the mean building height $H$ while the dashed horizontal line is the maximum building height ${H}_{{\max}}$

One outstanding feature is that there is no inflection point in the mean streamwise velocity profile. This is in contrast to previous studies on vegetation canopy (Raupach et al. 1996), urban-like canopy flows (Li and Bou-Zeid 2019) and real urban canopy with smaller ${\sigma }_{H}$ (Giometto et al. 2016, 2017; Auvinen et al. 2020). But this is consistent with the profiles presented in Park et al. (2015) and Inagaki et al. (2017) who also studied real urban canopies with large ${\sigma }_{H}$ values. The reason for this is that the irregularity of the building shape and height induces large vortical wakes that interact with downstream elements, causing significant flow penetration into the urban canopy (Britter and Hunt 1979; Belcher et al. 2003). This interaction prevents the formation of inflection points and could introduce high mixing rates (Makedonas et al. 2021). The variance of streamwise velocity has its maximum below $H$ (around $z/H=0.5$) and then decreases with increasing height. The maximum of the vertical velocity at the maximum building height, which corresponds to $z/H=12$, shows the presence of strong updrafts mostly induced by high rise buildings (see Fig. 8b). The variance of the vertical velocity peaks slightly above $H$ (around $z/H=2.5$), which is about five times the height of the maximum peak of $\langle \overline{{u }^{{{\prime}}2}}\rangle$. The maximum turbulent kinetic energy is $4.59{ u}_{*}^{2}$ seen around $z/H=0.5$ (see Fig. 9f) and decreases with increasing height. The DA profile of the logarithm of scalar concentration indicates a strong mixing of passive scalar from urban surfaces where it is released to the atmosphere when compared with the scalar initial profile (not shown).

The mean, turbulent, dispersive fluxes and the ratio of dispersive fluxes to the sum of turbulent and dispersive fluxes for both momentum and scalar are presented in Figs. 10 and 11. Only the resolved parts of the turbulent fluxes are presented. Note that the subgrid-scale flux is less than 6% of sum of resolved and subgrid-scale flux for momentum above $z/H = 0.5$. The mean momentum flux in Fig. 10a is nonzero as buildings significantly slow down the flow, causing strong vertical motions (Mason 1995). Note that the mean momentum or scalar flux is absent in studies that impose cyclic lateral boundary conditions in both streamwise and spanwise directions. A sensitivity test shows that using non-cyclic boundary conditions in the streamwise direction not only creates a mean momentum or scalar flux, but also affects the dispersive fluxes (not shown). While this is an important technical detail to point out, a full investigation of such differences is left for the future. In Fig. 10a, the mean momentum flux peaks at ${H}_{{\max}}$, which agrees with Cheng et al. (2021), while its scalar counterpart peaks at ${0.6 H}_{{\max}}$ (see Fig. 11a). From now on, the mean fluxes will not be discussed further since they are resolved in large-scale meteorological models. The peak turbulent momentum flux, which occurs at $z/H=2$, is more than four times its value in the inertial sublayer (see Fig. 10b). The same behaviour is seen for the turbulent scalar flux, which also peaks at $z/H=2$ (see Fig. 11b).

Fig. 10

Normalized DA profiles of a mean momentum flux, b turbulent momentum flux, c dispersive momentum flux d contribution of dispersive momentum flux to the sum of turbulent and dispersive momentum flux. Momentum profiles in a, b and c are normalized by the friction velocity ${u}_{*}$. Solid horizontal line indicates the mean building height $H$ while the dashed horizontal line is the maximum building height ${H}_{{\max}}$. Grey region in d corresponds to the values of $z/H$ between 2 and 5

Fig. 11

Normalized DA profiles of a mean scalar flux, b turbulent scalar flux, c dispersive scalar flux and d contribution of dispersive scalar flux to the sum of turbulent and dispersive momentum flux. Scalar profiles in a, b and c are normalized by ${u}_{*}{s}_{*}$ Solid horizontal line indicates the mean building height $H$ while the dashed horizontal line is the maximum building height ${H}_{{\max}}$. Grey region in d corresponds to the values of $z/H$ between 2 and 5

The dispersive momentum flux peaks at $z/H=0.5$ with an opposite sign (positive) as the turbulent momentum flux, but becomes negative above ${H}_{{\max}}$ (see Fig. 10c). The positive sign of the dispersive momentum flux below $z={H}_{{\max}}$ deviates from some idealized or realistic urban canopy studies (e.g. Giometto et al. 2016; Coceal et al. 2006), but other idealized studies (such as Nazarian et al. 2020; Blunn et al. 2022) showed that the dispersive momentum flux can be positive below$H$, especially for flows over aligned cubes with large plan area fractions. The magnitude of the strongest dispersive momentum flux is found to be $0.09 {u}_{*}^{2}$. Below this peak value, which occurs at $z/H= 0.5$, the dispersive momentum flux increases with height from the surface. The dispersive momentum flux then decreases until it reaches $0.04 {u}_{*}^{2}$ at $H$. Above $H$, it increases to another peak value at $z/H=5$, with magnitude only slightly smaller than the one at $z/H=0.5$. Further up, the dispersive momentum flux decreases with height from this secondary peak (i.e. $z/H=5$) and becomes negative at around the maximum building height, its magnitude reaching 10% of the peak value at $z/H=15$ and zero at $z/H= 30$. If we use zero dispersive momentum flux as an indicator of the inertial sublayer, then the height of RSL extends to $z/H=30$, which is much higher than other studies with smaller ${\sigma }_{H}$ (Giometto et al. 2016, 2017; Auvinen et al. 2020).

For the dispersive scalar flux, the peak of about $0.35 {u}_{*}{s}_{*}$ is seen at $z/H=0.5$, which is about 35% of the turbulent scalar flux. This is larger than the value (10%) reported by Leonardi et al. (2015) for urban-like canopies. The dispersive scalar flux decreases with height to a negative value at $z/H= 4$ and then increases until it reaches zero at $z/H= 15$ (see Fig. 11c). The main difference observed between the dispersive momentum transport and its scalar counterpart is because of the non-local action of pressure on momentum, which causes the streamwise velocity to decrease at the windward region, but does not influence the transport of scalars (Li and Bou-Zeid 2019). It is clear from these results that the entire building height distribution, including ${\sigma }_{H}$, influences the vertical variations of turbulent and dispersive fluxes.

The reason for the smaller peak of the dispersive momentum flux compared to $0.15 {u}_{*}^{2}$ reported in Giometto et al. (2016) might be caused by the differences in the morphology of the urban canopy. It may also be due to the spatial averaging scale used, which is four times larger than that in Giometto et al. (2016). In Cheng et al. (2021), the dispersive momentum fluxes were calculated locally over small regions with sizes $300 {\text{m}} \times 350$ m. They found that turbulent and dispersive momentum fluxes are comparable below $z/H=4$. Comparing these studies raises an important question: what is the sensitivity of dispersive momentum flux to the spatial averaging scale? We will address this question in Sect. 4.2.2.

Figures 10d and 11d shows the ratio of dispersive fluxes to the sum of turbulent and dispersive fluxes. Below $H$, the contribution of dispersive momentum flux decreases with height from about 75% close to the surface to 10% at $H$. Between $H$ and ${H}_{{\max}}$, its contribution is around 5% to 15% while above ${H}_{{\max}}$, it is around 7%. The largest contribution of dispersive scalar flux is found below $H$ (between 20% and 40% of the sum of turbulent and dispersive scalar fluxes) and the dispersive scalar flux becomes zero above $z/H = 15$ (also around $z/H = 4$ due to a change of the sign of dispersive scalar flux). This result shows that the dispersive (momentum and scalar) flux within the urban RSL can be significant beyond $z/H=2-5$ (represented by the grey area in Figs. 10d and 11d), which is often used as an estimate of the urban RSL height by previous studies with uniform height or relatively smaller ${\sigma }_{H}$ (Coceal et al. 2006; Martilli and Santiago 2007; Giometto et al. 2016; Li and Bou-Zeid 2019). This commonly used urban RSL height ($z/H=2-5$) also roughly corresponds to the typical height of the lowest atmospheric model level (about $30{-}100$ m) in weather and climate models. This emphasizes the need to parameterize dispersive fluxes in large-scale meteorological models, due to their contributions to the unresolved momentum and scalar fluxes, even beyond $z/H=2-5$. The results presented in the remaining part of Sect. 4.2 is normalized with the sum of dispersive and turbulent fluxes to highlight the sensitivity of the contribution of dispersive fluxes to temporal and spatial averaging, as well as the grid resolution.

4.2.1 Temporal Averaging Sensitivity

The strong variability of the building heights can trigger secondary circulations that remain in the urban RSL for a long time. This has been observed by Coceal et al. (2006) and Leonardi et al. (2015) for flow over staggered cubes. These studies showed that dispersive fluxes (momentum and scalar) are important on intermediate timescales and can become very small when averages are performed over long timescales. It is still unknown whether these findings also apply to real urban canopies. To examine the sensitivity of the contribution of dispersive fluxes to temporal averaging, we apply different averaging time intervals. Figure 12 shows that the profiles of dispersive momentum and scalar fluxes are indeed sensitive to the averaging time interval, but converges at about $360 T$. For this reason, intermediate averaging time interval of $360 T$ is used in the present study. Similar argument was made by Li and Bou-Zeid (2019) to estimate dispersive momentum fluxes over urban-like canopies. Due to the limitation in computational resources, it is not possible to see if the profile will further change at timescales longer than $720 T$.

Fig. 12

Normalized dispersive a momentum b scalar fluxes computed using averaging time intervals of $10 T$, $90 T$, $360 T$ and $720 T$. The dispersive momentum and scalar fluxes are normalized by the sum of their turbulent and dispersive fluxes. Solid horizontal line indicates the mean building height $H$ while the dashed horizontal line is the maximum building height ${H}_{{\max}}$

4.2.2 Spatial Averaging Sensitivity

As discussed earlier, both time and spatial averaging are required to compute dispersive fluxes. For urban-like canopies of uniform height, the spatial averaging scale over which the dispersive fluxes are calculated will not significantly affect the magnitude of the dispersive fluxes. This is not the case for real urban canopies since the flow statistics strongly depends on the entire building height distribution. In Sect. 4.2, we observed a smaller peak value of dispersive momentum flux compared to previous studies such as Giometto et al. (2016). Also, locally calculated dispersive momentum fluxes by Cheng et al. (2021) were shown to be of similar magnitude as the turbulent momentum flux below $z/H=4$ and about 20% to 30% of the turbulent momentum flux above this height. As a result, we hypothesized that one cause of these discrepancies is the difference in spatial averaging scale. In Fig. 13, the sensitivity of the dispersive flux to the spatial averaging scale is shown. Since the flow moves from west to east, the partitioning of the child domain into subdomains is done to observe how the dispersive fluxes change as the flow moves downstream. To do so, we include subdomains with different streamwise lengths (${L}_{x}^{c}$) but covering the whole spanwise length (${L}_{y}^{c}$). In the streamwise direction, each subdomain starts from the transition region (i.e. smooth–rough interface) and extends to ${L}_{x}^{c}/4$, ${L}_{x}^{c}/2$ and ${L}_{x}^{c}$ (see Fig. 13). The ${L}_{x}^{c}/2$ subdomain has a mean building height $H=19$ m, maximum building height ${H}_{{\max}}=74$ m, standard deviation of building height ${\sigma }_{H}=13$ m and plan area fraction ${\lambda }_{p}=0.23$ m while the ${L}_{x}^{c}/4$ subdomain has $H=22$ m, ${H}_{{\max}}=74$ m, ${\sigma }_{H}=15$ m and ${\lambda }_{p}=0.27$ m. Figure 13 shows that above $H$, the peak magnitude of the contribution of dispersive momentum flux increases as the streamwise length decreases. Its peak is the largest when the size of the subdomain is close to the transition length scale ${L}_{T}$. The transition length scale ${L}_{T}$ is the length scale the turbulent boundary layer needs to adjust to the urban roughness below it (Belcher et al. 2003). Based on the definition of ${L}_{T}$ (Belcher et al. 2003), we find ${L}_{T}\approx 1$ km and ${L}_{T}/{L}_{x}^{c}=0.3$, which is close to ${L}_{x}^{c}/4$. Note that for the ${L}_{x}^{c}/4$ subdomain, the peak of the dispersive momentum flux is larger than $0.15 {u}_{*}^{2}$ reported in Giometto et al. (2016). For the scalar, only the shape of the profile is affected by the spatial averaging scale.

Fig. 13

Normalized dispersive a momentum fluxes b scalar fluxes for different averaging scales over the real urban canopy (where ${L}_{x}^{c}$ is the streamwise length of the child domain highlighted by dashed lines in Fig. 6). The dispersive momentum and scalar fluxes are normalized by the sum of their turbulent and dispersive fluxes. Solid horizontal line indicates the mean building height $H$ while the dashed horizontal line is the maximum building height ${H}_{{\max}}$

Here it is important to emphasize that the shape of the dispersive momentum and scalar flux profiles depend not only on its streamwise distance from the transition (as demonstrated in this study) or the scale of spatial averaging operation, but also on the urban morphology within the averaging domain. This implies that the plan area fraction ${\lambda }_{p}$, the frontal area fraction ${\lambda }_{f}= {A}_{f}/{A}_{\text{total}}$ (${A}_{f}$ is the product of the building width and height) and the scale of the spatial averaging operation affect the significance of the dispersive momentum and scalar fluxes over real urban canopies. Note that the sensitivity of the dispersive fluxes to variations in ${\lambda }_{f}$ was studied in Li and Bou-Zeid (2019). Despite its relevance for the urban microclimate community, a more detailed investigation on the sensitivity of dispersive fluxes to variations in the aforementioned parameters is beyond the scope of this analysis and is hence left for the future.

4.2.3 Grid Resolution Sensitivity

It is a well-known fact that a decrease in grid resolution increases discretization and subgrid-scale model errors when the LES approach is used (Chow and Moin 2003; Meyers et al. 2007). To explore the sensitivity of dispersive fluxes to changes in the grid resolution, we present the profiles of the contribution of dispersive momentum and scalar fluxes to the sum of turbulent and dispersive fluxes at 2 m, 4 m and 8 m resolutions in Fig. 14. Due to the large computational resources needed for the 2 m resolution simulation, the dispersive fluxes can only be calculated with a smaller temporal averaging interval of $90 T$. For consistency, we compare the dispersive fluxes calculated with a temporal averaging interval of $90 T$ for all grid resolutions. Note that averaging over $90 T$ suffices to converge the dispersive flux profiles, as shown in Fig. 12. The contribution of dispersive momentum flux and its scalar counterpart vary weakly with the grid resolution (see Fig. 14a,b) especially above $H$. Below $H$, the contribution of dispersive momentum flux displays a strong sensitivity to the grid resolution while the contribution of dispersive scalar flux does not. However, the shapes of the profiles and the main conclusions made in previous sections related to the behaviour of dispersive fluxes above the mean building height are not strongly altered by changing the spatial resolution. We note that the dispersive fluxes presented here are for the entire child domain, and thus, the findings might not apply to the dispersive fluxes computed over subdomains.

Fig. 14

Normalized dispersive a momentum fluxes b scalar fluxes for different grid resolutions. The dispersive momentum and scalar fluxes are normalized by the sum of their turbulent and dispersive fluxes. Solid horizontal line indicates the mean building height $H$ while the dashed horizontal line is the maximum building height ${H}_{{\max}}$. Temporal averaging was carried out for $90 T$ for all grid resolutions due to limited computation resources

4.3 Spatial Structure of Dispersive Terms

4.3.1 Spatial Variability of ${\overline{w} }^{{{\prime\prime}}}{\overline{u} }^{{{\prime\prime}}}$ and ${\overline{w} }^{{{\prime\prime}}}{\overline{s} }^{{{\prime\prime}}}$

In addition to the dispersive fluxes (i.e. spatially averaged ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$ and ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$), we examine the spatial variability of ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$ and ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$. A direct comparison between $\stackrel{-}{w{^{\prime}}u{^{\prime}}}$ and ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$ at a given x–z plane is presented in Fig. 15. ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$ spans a broader range of values (about one order of magnitude) than the turbulent momentum flux in the RSL, which agrees with the findings by Giometto et al. (2016). The same is observed for $\stackrel{-}{w{^{\prime}}s{^{\prime}}}$ and ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$. These results emphasize the strong spatial heterogeneity of ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$ and ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$, and show regions in the RSL where their contributions to the total fluxes can be larger than turbulent fluxes. It is also clear that high-rise buildings enhance the values of ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$ at higher altitude ($z/H\ge 3$), especially at the leeward side. Negative values of ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$ are observed at the leeward side of the buildings while positive values are observed at the windward side, especially for regions with high-rise buildings, in agreement with Coceal et al. (2007b) and Blunn et al. (2022). The opposite is seen for ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$, in which positive values are observed at the leeward side of the buildings while negative values at the windward side (see Fig. 15d). This results from the fact that scalar concentration mostly peaks in low-speed regions.

Fig. 15

Colour contour of the spatial variability of dispersive fluxes a $\overline{w{^{\prime}}u{^{\prime}}}$ b $\overline{w }{^{\prime\prime}}\overline{u }{^{\prime\prime}}$ c $\overline{w{^{\prime}}s{^{\prime}}}$ d $\overline{w }{^{\prime\prime}}\overline{s }{^{\prime\prime}}$ at $y/H = 116$. Momentum fluxes are normalized by the friction velocity ${u}_{*}$ while the scalar fluxes are normalized by ${u}_{*}{s}_{*}$. The dashed horizontal line indicates the height $z/H = 1$. The $x$- axis is defined in terms of the child domain

The standard deviations of ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$ and ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$ are presented in Fig. 16. For ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$, the maximum standard deviation occurs at $H$. It increases drastically with increase in height to a peak value of $2.35 {u}_{*}^{2}$ from the surface and gradually decreases to zero at $z/H=15$. The standard deviation of ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$ exhibits a similar profile as ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$, but has a peak value of $8.41 {u}_{*}{s}_{*}$. In general, ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$ and ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$ are spatially heterogeneous within the urban RSL and are clearly enhanced by the presence of high-rise buildings at higher altitude.

Fig. 16

Standard deviations of a $\overline{w }^{{\prime\prime}}\overline{u }^{{\prime\prime}}$ normalized by the friction velocity ${u}_{*}$ b $\overline{w }^{{\prime\prime}}\overline{s }^{{\prime\prime}}$ normalized by ${u}_{*}{s}_{*}$. The solid horizontal line indicates the mean building height $H$ while the dashed horizontal line is the maximum building height ${H}_{\text{max}}$

4.3.2 Quadrant Analysis

Quadrant analysis is used to quantify the spatial structure of ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$ and ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$. Figure 17 shows the quadrant map for ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$ and ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$ with colour bar showing ejection (E), inward interaction (I), sweep (S) and outward interaction (O). Each grid point in the map corresponds to one of the quadrants based on their definition in Sect. 2.3 (also presented in the caption of Fig. 17). At the interface between the smooth surface and the rough urban canopy, the dominant quadrant is outward interaction (${\overline{w} }^{{\prime\prime}}>0$ and ${\overline{u} }^{{\prime\prime}}>0$) at $z/H<10$ while the upper part of this interface (i.e. $z/H>10$) is dominated by ejection (${\overline{w} }^{{\prime\prime}}>0$ and ${\overline{u} }^{{\prime\prime}}<0$). Within the urban canopy, all the quadrants are present, but the dominant one is ejection below $z/H= 15$ while sweep (${\overline{w} }^{{\prime\prime}}<0$ and ${\overline{u} }^{{\prime\prime}}<0$) is dominant at $z/H\ge 20$ (not shown). This is also observed in plant-like canopies (Nepf and Koch 1999; Poggi and Katul 2008). The positive ${\overline{w} }^{{\prime\prime}}$ within the urban canopy and near the ground may be due to the negative pressure gradients introduced by the buildings (Nepf and Koch 1999). At the leeward side of the canopy, the inward interaction is dominant below $z/H= 12$ as result of negative ${\overline{w} }^{{\prime\prime}}$ and ${\overline{u} }^{{\prime\prime}}$. However, in Poggi and Katul (2008), this quadrant was dominant near the top of the rod forming a vertical secondary circulation with the positive ${\overline{w} }^{{\prime\prime}}$ near the ground. The variability of the building height in real urban canopy may have prevented the formation of such vertical secondary circulations at lower altitudes. The quadrant map for ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$ is similar to that for ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$, except that the vertical extent of the outward interaction (${\overline{w} }^{{\prime\prime}}>0$ and ${\overline{s} }^{{\prime\prime}}<0$) at the interface between the smooth surface and rough urban surface extends higher than that in ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$. The dominant quadrant within the urban canopy is also ejection (${\overline{w} }^{{\prime\prime}}>0$ and ${\overline{s} }^{{\prime\prime}}>0$). Sweep (${\overline{w} }^{{\prime\prime}}<0$ and ${\overline{s} }^{{\prime\prime}}<0$) is the dominant quadrant at the leeward end of the canopy for $z/H<5$ while the inward interaction (${\overline{w} }^{{\prime\prime}}<0$ and ${\overline{s} }^{{\prime\prime}}>0$) is dominant for $z/H>5$.

Fig. 17

Quadrant map for a ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$ and b ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$ showing ejection E (${\overline{w} }^{{\prime\prime}}> 0$, ${\overline{u} }^{{\prime\prime}}<0$ or ${\overline{s} }^{{\prime\prime}}>0$), inward interaction I (${\overline{w} }^{{\prime\prime}}< 0$, ${\overline{u} }^{{\prime\prime}}<0$ or ${\overline{s} }^{{\prime\prime}}>0$), sweep S (${\overline{w} }^{{\prime\prime}}< 0$, ${\overline{u} }^{{\prime\prime}}>0$ or ${\overline{s} }^{{\prime\prime}}<0$) and outward interaction O (${\overline{w} }^{{\prime\prime}}> 0$, ${\overline{u} }^{{\prime\prime}}>0$ or ${\overline{s} }^{{\prime\prime}}<0$) persistent structures at $y/H = 116$. The $x$- axis are defined in terms of the child domain

The quadrant map in Fig. 17 only gives information about the quadrant to which each point in space belongs. In comparison, the absolute value of the dispersive flux fraction ${F}_{i,{T}_{h}}$ normalized by $\sum_{i}{|F}_{i,{T}_{h}}|$ (hereafter the magnitude of dispersive flux fraction) and the corresponding space fraction for different thresholds ${T}_{h}$ are presented in Figs. 18 and 19, respectively, for ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$. The results for ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$ are presented in Appendix.

Fig. 18

Absolute value of the dispersive flux fraction ${F}_{i,{T}_{h}}$ normalized by $\sum_{i}{|F}_{i,{T}_{h}}|$ for each quadrant ${Q}_{i}$ (Quadrant 1: Outward interaction (O), Quadrant 2: Sweep (S), Quadrant 3: Inward interaction (I), Quadrant 4: Ejection (E)) and for different thresholds ${T}_{h}$ for ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$. The results at heights $z/H=1, 4, 12$ and 30 are shown

Fig. 19

Space fraction ${S}_{i,{T}_{h}}/{S}_{i,0}$ for each quadrant ${Q}_{i}$ (Quadrant 1: Outward interaction (O), Quadrant 2: Sweep (S), Quadrant 3: Inward interaction (I), Quadrant 4: Ejection (E)) and for different thresholds ${T}_{h}$ for ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$. The results at heights ${z}/{H}=1, 4, 12$ and 30 are shown

The magnitude of dispersive flux fractions decreases with increasing threshold ${T}_{h}$. At $z/H=1$ and $z/H=4$, |${F}_{i,6}|$ values decrease to half or less of |${F}_{i,0}|$ and only |${F}_{{4,10}}|$ values exceeded 0.2, which gives evidence that ejections are the largest structures involved in momentum transport at these two heights. At $z/H=12$, only |${F}_{{3,10}}|$ values exceeded 0.35, which shows that the inward interaction has the largest contribution to momentum transport at this height. The dominance of ejection at $z/H=1$ and $z/H=4$ and inward interactions at $z/H=$ $12$ shows that strong negative values of ${\overline{u} }^{{\prime\prime}}$ are present at these heights. In the inertial sublayer (at $z/H=30$), both |${F}_{{2,0}}|$ and |${F}_{{4,0}}|$ values exceed 0.4. This implies that the ejections (dominant above the interface between the smooth surface and the rough urban canopy) and sweeps (dominant above the rough urban canopy) are the dominant structures at this height, which is consistent with the previous study by Shaw et al. (1983).

In Fig. 19, the space fraction ${S}_{i,{T}_{h}}$ values also decrease with increasing threshold ${T}_{h}$. For ${T}_{h}=0$, 37% of the horizontal plane are occupied by negative regimes (${S}_{{2,0}}$ and ${S}_{{4,0}}$) at $z/H=1$ and $z/H=4$ while 63% are dominated by ‘counter-gradient’ regimes (${S}_{{1,0}}$ and ${S}_{{3,0}}$). Christen and Vogt (2004) showed the quadrant analysis of dispersive fluxes within a cork oak plantation. In contrast to our study, they found out that 64% of the area contributed to negative dispersive fractions (${S}_{{2,0}}$ and ${S}_{{4,0}}$) at $z/H=0.18$. The resolution of our simulation and the limitations of field measurement prevent any form of comparison. Much higher above the urban canopy ($z/H=12$ and $z/H=30$), 68% of the horizontal plane are occupied by negative dispersive fractions (${S}_{{2,0}}$ and ${S}_{{4,0}}$).

In summary, the urban RSL contains persistent structures in all four quadrants, but based on the dispersive flux fraction, ejections and inward interactions dominate within the urban canopy while sweeps and ejections dominate above the urban canopy.

5 Conclusion

In this study, the transport of momentum and passive scalar over and within a real urban RSL is investigated with the PALM model system in LES mode. The model domain features the Fenway–Kenmore square area in the City of Boston, Massachusetts, USA. The LES model is first evaluated with a simple configuration set-up of staggered cubes using previously reported numerical and experimental datasets. We find that the PALM model performs reasonably well in reproducing first- and second-order flow statistics.

The heterogeneous nature of the flow, induced by the complex urban canopy, requires the double-averaging procedure to quantify flow statistics. The focus of this study is on dispersive momentum and scalar fluxes, whose importance remains debated. Due to the large variability of building heights in our study domain, the dispersive momentum flux is found to be significant below and above the maximum building height ${H}_{\text{max}}$ with two peak values at $z/H=0.5$ and $z/H= 5$, while the scalar dispersive flux peaks at the mean building height $H$. The dispersive momentum flux does not become zero until $z/H=30$, suggesting a much higher RSL than found in previous studies.

The double-averaging procedure used in the calculation of dispersive fluxes requires temporal and spatial averaging. The sensitivity of the dispersive fluxes in real urban canopies to both averaging is carried out. Previous studies over urban-like canopies reveal the presence of secondary circulations that are triggered by urban roughness. These circulations cause the dispersive fluxes to be large when averages are performed over short timescales and small for long timescales. In this study, statistical convergence is obtained with time averaging of $360 T$ or $720 T$, where $T$ is the eddy turnover time. However, we caution that the time averaging scale needed to reach statistical convergence for dispersive fluxes may depend on the domain size. Also, the dispersive fluxes are sensitive to changes in spatial averaging scale. We find that the peak of the dispersive momentum flux increases as the spatial scale decreases while the dispersive scalar flux slightly decreases with decreases in the spatial scale, but this conclusion may depend on other parameters such as the distance to the transition from non-urban to urban areas and the plan area fractions within the spatial averaging domain. We also test the sensitivity of dispersive fluxes to the grid spacing. Above the mean building height, the sensitivity of dispersive fluxes to the grid spacing is rather weak. However, below the mean building height, the dispersive momentum flux displays a strong dependency on the grid spacing. In general, our main findings related to the behaviour of dispersive fluxes above the mean building height are not influenced by the grid spacing.

We also examine the spatial variability of ${\overline{w}}^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$ and ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$, including their standard deviations and spatially persistent structures. The ${\overline{w}}^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$ and ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$ show a broader range of values when compared with turbulent fluxes in RSL and are enhanced by the presence of high-rise buildings. The quadrant analysis reveals that ejection and inward interactions are the dominant structures contributing to dispersive momentum transport within the canopy while sweep and ejection are dominant above the canopy. For ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$, ejections and outward interactions are the dominant structure within the urban canopy and inertial sublayer, respectively.

This study highlights the importance of dispersive fluxes over real urban canopies and thus the need to parameterize both turbulent and dispersive fluxes in mesoscale models. Our conclusions are based on assuming neutral stratification and future investigations on the effects of stratification (stable or unstable) are needed.

Appendix: Dispersive Flux Fraction and Spatial Fraction for \({\overline{{\varvec{w}}} }^{{{\prime\prime}}}{\overline{{\varvec{s}}} }^{{{\prime\prime}}}\)

For ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$, the magnitude of dispersive flux fraction decreases with height only for ejection (${F}_{1,{T}_{h}}$) at all thresholds and decreases with increasing thresholds ${T}_{h}$ for all heights, like ${\overline{w} }^{{\prime\prime}}{\overline{u} }^{{\prime\prime}}$ (see Fig. 

Fig. 20

Absolute value of the dispersive flux fraction ${F}_{i,{T}_{h}}$ normalized by $\sum_{i}{|F}_{i,{T}_{h}}|$ for each quadrant ${Q}_{i}$ (Quadrant 1: Outward interaction (O), Quadrant 2: Sweep (S), Quadrant 3: Inward interaction (I), Quadrant 4: Ejection (E)) and for different thresholds ${T}_{h}$ for ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$. The results at heights $z/H=1, 4, 12$ and 30 are shown

20). At $z/H=1$ and $z/H=4$, only |${F}_{{1,4}}|$ values exceeded 0.25, which is evidence that ejections are the largest structures involved in scalar transport. At $z/H=12$, only |${F}_{{4,4}}|$ values exceed 0.35 and at $z/H=30$, only |${F}_{{4,4}}|$ values exceed 0.2, which shows that the outward interaction has the largest contribution to scalar transport at these two heights. The inward interaction (${S}_{{2,0}}$) occupies the largest horizontal plane for all heights (see Fig. 

Fig. 21

Space fraction ${S}_{i,{T}_{h}}/{S}_{i,0}$ for each quadrant ${Q}_{i}$ (Quadrant 1: Outward interaction (O), Quadrant 2: Sweep (S), Quadrant 3: Inward interaction (I), Quadrant 4: Ejection (E)) and for different thresholds ${T}_{h}$ for ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$. The results at heights ${z}/{H}=1, 4, 12$ and 30 are shown

21). In summary, ejections and outward interactions are the dominant structure within the urban canopy and inertial sublayer, respectively, for ${\overline{w} }^{{\prime\prime}}{\overline{s} }^{{\prime\prime}}$.