Abstract
We propose a fractional Adams–Simpson-type method for nonlinear fractional ordinary differential equations with fractional order \(\alpha \in (0,1)\). In our method, a nonuniform mesh is used so that the optimal convergence order can be recovered for non-smooth data. By developing a modified fractional Grönwall inequality, we prove that the method is unconditionally convergent under the local Lipschitz condition of the nonlinear term, and show that with a proper mesh parameter, the method can achieve the optimal convergence order \(3+\alpha \) even if the given data is not smooth. Under very mild conditions, the nonlinear stability of the method is analyzed by using a perturbation technique. The extensions of the method to multi-term nonlinear fractional ordinary differential equations and multi-order nonlinear fractional ordinary differential systems are also discussed. Numerical results confirm the theoretical analysis results and demonstrate the effectiveness of the method for non-smooth data.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Fractional ordinary differential equations (FODEs) appear in many fields of science and engineering, such as viscoelastic materials [2, 3, 35, 52], underground transport [31], anomalous diffusion [6, 16, 34], advection and dispersion of solutes in natural porous or fractured media [4, 5], options pricing model in financial markets [58], and etc. Some FODEs with special form, such as linear equations, can be solved by the Fourier transform method or the Laplace transform method (see [53]). However, analytical solutions of many generalized FODEs, such as nonlinear FODEs, are usually difficult to obtain. Therefore, it is necessary to develop numerical methods for these equations. In this paper, we propose and analyze a high-order numerical method for the following initial value problem of nonlinear FODE:
where \(\phi _{0}\) is an arbitrary real number and the fractional derivative \({_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y \) is defined, in the Caputo sense, by
Existence and uniqueness of solutions for (1.1) have been discussed, e.g. in [19, 53]. For any function \(w\in L_{1}[0,T]\), we define the Riemann-Liouville fractional integral \({_{0}}{{\mathcal {I}}}_{t}^{\alpha }w\) of order \(\alpha \) by
It has been proved in [19] that the problem (1.1), if a continuous solution is admitted, is equivalent to the following Volterra integral problem
Our numerical method for the problem (1.1) is based on the above equivalent problem (1.4). Let N be a positive integer, and let \(\{t_{n}\}_{0}^{N}\) be a general mesh such that
The goal of this paper is to construct high-order schemes of the form:
where \(y_{n}\approx y(t_{n})\) and the kernel \(Q_{k,n}^{(\alpha )}\) represents approximation coefficients generated in the Lagrange interpolation polynomial approximation of the integral operator \({_{0}}{{\mathcal {I}}}_{t}^{\alpha }\) (see Sect. 3 below).
So far, two types of discretization techniques have been used to develop numerical methods for the problem (1.1). The first technique is to directly discretize the fractional derivative (1.2) by using finite difference schemes (see, e.g. [1, 9, 12, 25, 28, 37, 38, 45, 50, 57]). The second technique is to approximate the fractional integral (1.3) and develop the corresponding numerical method of the equivalent Volterra integral problem (1.4). Since our scheme (1.6) follows the second technique, we focus our literature review on works using this technique. Lubich [48, 49] studied a kind of fractional multistep methods of the fractional integral (1.3) based on a discrete convolution form. Brunner and Houwen [7] discussed the linear multistep methods for Volterra integral problems. Lin and Liu [44] analyzed a linear multistep method and proved the stability and convergence of the method. A review on the linear multistep methods of the fractional integral (1.3) can be found in [22]. Kumar and Agrawal [36] proposed a block-by-block method for Volterra integral problem (1.4). Huang et al. [32] derived the error estimate and the convergence order of the block-by-block method under certain assumptions. Following the idea of the block-by-block method in [36], Cao and Xu [10] constructed and analyzed an improved block-by-block method. To treat the nonlinear term and avoid solving nonlinear equations, Diethelm et al. [23, 24] discussed an Adams-type predictor–corrector method for Volterra integral problem (1.4) and gave an error analysis of the method. Li and Tao [41] further studied the error analysis for the Adams-type predictor-corrector method proposed in [23, 24]. Deng [15] and Daftardar-Gejji et al. [13] modified the method discussed in [23, 24] and introduced, respectively, a new predictor–corrector method. Using piecewise quadratic interpolation polynomials, Yan et al. [59] proposed a high order fractional Adams-type predictor–corrector method for solving integral problem (1.4). This method has higher convergence order than the method in [15] and is easier to implement than the methods in [10, 62]. For other studies on Adams-type methods, we refer to [14, 27, 29, 30, 42]. In most of the above numerical methods, the expected convergence order requires that the Caputo derivative \({_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y\) (or f(t, y(t))) be smooth enough. For example, it is required that \({_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y\in {{\mathcal {C}}}^{1}[0,T]\) or \({{\mathcal {C}}}^{2}[0,T]\) in [42], \({_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y\in {{\mathcal {C}}}^{2}[0,T]\) in [13, 15, 24], \({_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y\in {{\mathcal {C}}}^{3}[0,T]\) in [32, 59], \({_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y\in {{\mathcal {C}}}^{4}[0,T]\) in [10]. However, the Caputo derivative \({_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y\) is usually not in \({{\mathcal {C}}}^{1}[0,T]\) and has a weak singularity at \(t=0\), even if the forcing term or the solution y is smooth; see, e.g. [19, 22, 24, 33] or Theorems 2.1 and 2.2 below. Indeed, the low regularity of \({_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y\) will make the numerical methods in the above works unable to produce the expected convergence order.
In order to compensate for the initial weak singularity, several methods have been proposed. One method is to introduce the correction terms by selecting starting values and starting weights (see, e.g. [11, 22, 30, 49, 60]). In this method, as Diethelm et al. [22] pointed out, unsuitable starting values and starting weights may lead to calculation instability. Another method is to use non-polynomial basis function methods to include the correct singularity index (see [8, 26, 61]). In addition to the above two methods, a more easily implemented method is to use nonuniform meshes to keep the error small near \(t=0\) and make up for the loss of accuracy. Based on a class of nonuniform meshes, Liu et al. [46] studied the error estimates of the fractional rectangle, trapezoid and predictor-corrector methods introduced in [42], and showed that the methods can achieve optimal convergence orders between 1 and 2 when \({_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y \not \in {{\mathcal {C}}}^{1}[0,T]\). Liu et al. [47] extended the fractional Adams-type predictor-corrector method proposed in [23, 24] to the graded mesh, which is a very effective nonuniform mesh for dealing with related problems (see [39, 40, 43, 47, 56]), and proved that the optimal convergence order \(1+\alpha \) of this method can be recovered when \({_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y \not \in {{\mathcal {C}}}^{2}[0,T]\). Employing piecewise quadratic interpolation polynomials and the graded mesh, Lyu and Vong [51] proposed a high-order approximation for the fractional integral (1.3). The resulting numerical method for the integral problem (1.4) has the optimal convergence order 3 even if \({_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y \not \in {{\mathcal {C}}}^{1}[0,T]\). We would like to note that nonuniform meshes have also been used to deal with fractional partial differential equations and parabolic equations with non-smooth data in many applications (see, e.g. [12, 39, 40, 43, 56]).
The main purpose of this paper is to develop a higher-order approximation for the fractional integral (1.3) and propose a higher-order Adams-type method of the form (1.6) for the problem (1.1) with non-smooth data. To do this, we follow the idea of the block-by-block methods in [10, 32, 36, 59], but with some necessary modifications. Similar to [51], we use a general nonuniform mesh, including the graded mesh as a special case, to deal with the initial weak singularity, and employ piecewise quadratic interpolation polynomials to approximate the function within the integral, but the specific construction process is different. In addition, our analysis of the local truncation error is also different from [51]. In order to prove the unconditional convergence of the proposed method, we present a modified fractional Grönwall inequality. The convergence result shows that with a proper mesh parameter, the proposed method can achieve the optimal convergence order \(3+\alpha \), even if \({_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y \not \in {{\mathcal {C}}}^{1}[0,T]\). Therefore, our method has a higher convergence order than the methods in [46, 47, 51]. It is also easy to implement because we do not need to solve any nonlinear equation at each time level. Our method can be interpreted as a fractional variant of the classical Adams–Simpson-type method, so we call it the fractional Adams–Simpson-type method.
The outline of the paper is as follows. In Sect. 2, we describe the regularity assumption imposed in this paper. Section 3 is devoted to the construction of the fractional Adams–Simpson-type method. The local truncation error of the method is analyzed in Sect. 4. In Sect. 5, we present the convergence analysis of the method by introducing a modified fractional Grönwall inequality, and give the nonlinear stability analysis of the method by using a perturbation technique. In Sect. 6, we extend the method to multi-term nonlinear fractional ordinary differential equations and multi-order nonlinear fractional ordinary differential systems with non-smooth data. Numerical results are given in Sect. 7 to confirm the theoretical convergence results and demonstrate the computational effectiveness of the method for non-smooth data. The concluding section contains a brief conclusion.
Notation. Throughout the paper, the sums and integrals are always set to zero if the upper index is less than the lower one. The notation C with or without subscript, denotes a positive constant which may differ at different occurrences, but it is always independent of the step size and the time levels.
2 Regularity assumption
Define \(G=\left\{ (t,y)~|~t\in [0,T], ~\left| y-\phi _{0}\right| \le K \right\} \) with some \(K >0\). Assume that \(f\in {{\mathcal {C}}}(G)\) and fulfills a Lipschitz condition with respect to its second variable on G. According to Theorem 6.5 of [18] (also see [19]), there exists a unique solution y on [0, T] for the problem (1.1). The regularity properties of the solution y and its Caputo derivative are given as follows.
Theorem 2.1
(see [24]) (1) Assume \(f\in {{\mathcal {C}}}^{2}(G)\). Define \({\widehat{\nu }}=\lceil \frac{1}{\alpha } \rceil -1\). Then there exist a function \(\psi \in {{\mathcal {C}}}^{1}[0,T]\) and some \(c_{1}, c_{2},\dots , c_{{\widehat{\nu }}}\in {{\mathbb {R}}}\) such that the solution y of (1.1) is of the form
(2) Assume \(f\in {{\mathcal {C}}}^{3}(G)\). Define \({\widehat{\nu }}=\lceil \frac{2}{\alpha } \rceil -1\) and \({\widetilde{\nu }}=\lceil \frac{1}{\alpha } \rceil -1\). Then there exist a function \(\psi \in {{\mathcal {C}}}^{2}[0,T]\) and some \(c_{1}, c_{2},\dots , c_{{\widehat{\nu }}}\in {{\mathbb {R}}}\) and \(d_{1}, d_{2},\dots , d_{{\widetilde{\nu }}}\in {{\mathbb {R}}}\) such that the solution y of (1.1) is of the form
Theorem 2.2
(see [24]) If \(y\in {{\mathcal {C}}}^{m}[0,T]\) for some \(m\in {{\mathbb {N}}}\) and \(0<\alpha <m\), then
with some function \(\psi \in {{\mathcal {C}}}^{m-1}[0,T]\), where \(y^{(l)}\) means the lth derivative of y.
Theorem 2.1 shows that the solution y of (1.1) is usually non-smooth, even if f is smooth on G. We see from Theorem 2.2 that smoothness of the function y will imply non-smoothness of its Caputo derivative unless some special conditions are fulfilled. For more discussions, we refer to [19, 22, 24]. When \(f\in {{\mathcal {C}}}^{m}(G)\) (\(m\ge 3\) or \(m=2\) but \(\alpha \in (0,\frac{1}{2})\)), we have from Theorem 2.1 that, with some \({\widehat{c}}_{1},{\widehat{c}}_{2}, \dots , {\widehat{c}}_{{\widehat{\nu }}}\in {{\mathbb {R}}}\) \(({\widehat{\nu }}>1)\),
which implies that \({_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y\) behaves as \(C(1+t^{\alpha })\). Based on the above observations, we introduce the following assumption for the solution y of the problem (1.1):
Assumption 1
Assume that \(g:={_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y\in {{\mathcal {C}}}^{4}(0,T]\) and there exists a positive constant C such that
where \(\sigma \in (0,1)\) is a real number.
The above assumption admits a certain weak singularity of g at \(t=0\), i.e. g is continuous at \(t=0\), but \(g^{(l)}\) \((l=1,2,3,4)\) blow up at \(t=0\).
3 Fractional Adams–Simpson-type method
Under Assumption 1, many existing numerical methods for the problem (1.1) would produce less accurate numerical solutions when they are directly applied. Next, we will develop a fractional Adams-type method of the form (1.6) on a nonuniform mesh (1.5), which has higher-order convergence under Assumption 1.
Let \(\tau _{n}:=t_{n}-t_{n-1}\) \((1\le n\le N)\) be the step size. Given two nonnegative integers p and q satisfying \(p\le q\), for any function \(w \in L_{1}[0,T]\cap {{\mathcal {C}}}^{p+1}(0,T]\), we let \(L_{p,q}w\) be the Lagrange interpolation polynomial (of degree p) of w with respect to the nodes \((t_{q}, t_{q-1}, \dots ,t_{q-p})\), that is,
where
The corresponding interpolation error is denoted by \(R_{p,q}w(t):=w(t)-L_{p,q}w(t)\). Define
We approximate the integral \({_{0}}{{\mathcal {I}}}_{t}^{\alpha }w(t_{n})\) by
This approximation method can be interpreted as a fractional variant of the classical Adams–Simpson-type method. We call it the fractional Adams–Simpson-type method.
Remark 3.1
The approximation (3.6) is completely different from the block-by-block methods used in [10, 32, 36, 59]. A major difference is the approximation on the last interval. Specifically, our approximation (3.6) does not depend on the value \(w(t_{n})\). This will enable us to avoid solving nonlinear equations when applying the approximation (3.6) to nonlinear problems. Another difference is that our approximation (3.6) is based on the general nonuniform mesh (1.5), which helps to make up for the loss of accuracy for non-smooth data.
In order to give a compact form of (3.6), we define
Then we have
When \(n\ge 3\) and is odd,
When \(n\ge 4\) and is even,
Define
For an odd \(n\ge 7\), we define
For an even \(n\ge 8\), we define
Then a compact form of (3.6) is given by
Applying the above approximation to (1.4), we obtain the scheme (1.6) for solving (1.1). We call this scheme the fractional Adams–Simpson-type scheme.
4 Analysis of the local truncation error
Letting \(t=t_{n}\) in (1.4), we obtain
where \(R_{n}\) is the local truncation error given by
where we have used \(g(t):={_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y(t)=f(t,y(t))\). From the derivation of (3.21), we can see that
where the interpolation error \(R_{p,q}g(t)=g(t)-L_{p,q}g(t)\) is given by the following lemma.
Lemma 4.1
Under Assumption 1, it holds that
Proof
See “Appendix A”. \(\square \)
In order to obtain a better bound of the local truncation error \(R_{n}\) under Assumption 1, it is reasonable to choose a nonuniform mesh (1.5) that concentrates grid points near \(t=0\). Let \(\gamma \ge 1\) be a user-chosen parameter and assume that there are two positive constants \({\underline{\rho }}>0\) and \({\overline{\rho }}>0\), dependent on \(\gamma \) but independent of n, such that the nonuniform mesh (1.5) satisfies
Since \(\tau _{1}=t_{1}\), the property (4.9)-(ii) implies that \(\tau _{1}={{\mathcal {O}}}(N^{-\gamma })\) while for those \(t_{n}\) bounded away from \(t=0\) one has \(\tau _{n}={{\mathcal {O}}}(N^{-1})\). This is necessary to compensate for the initial weak singularity given by (2.5). An example satisfying (4.9) is the graded mesh
which is very efficient for dealing with related problems (see [39, 40, 43, 47, 56]). When \(\gamma = 1\), the graded mesh (4.10) reduces to the uniform mesh.
Theorem 4.1
Assume that the solution y of the problem (1.1) satisfies Assumption 1, and let the mesh assumption (4.9) hold. Then
Proof
It follows from (4.5) and (2.5) that
Therefore, we have from (4.4), (4.13) and (4.9)-(ii) that
By (4.6), (4.9)-(iv) and (2.5), we have that for \(t\in (t_{0}, t_{2})\),
This implies
where we have used \(t_{2}\le {\overline{\rho }}t_{1}\le {\overline{\rho }}^{\gamma +1} N^{-\gamma } \) from (4.9)-(iv) and (4.9)-(ii) to derive the last inequality. This proves (4.11).
In order to prove (4.12), we first consider the case of odd n and \(n\ge 3\). According to (4.4), we decompose \(R_{n}\) into three terms:
where
(i) The estimation of \(R1_{n}\) By (4.7), (4.9)-(i), (4.9)-(iv) and (2.5), we have that for \(t\in (t_{0}, t_{2})\),
and thus
(ii) The estimation of \(R2_{n}\) We have from (4.8) that for \(k\ge 1\),
where
Define \(\Omega _{2k}(t)=(t-t_{2k})(t-t_{2k+1})(t-t_{2k+2})\). According to divided difference theory,
and so
Based on the above expression, we write
where
In order to estimate \(R21_{n}\), we define
It follows from integration by parts that
Since
we have from (2.5) and (4.9)-(i) that the first term of \(R21_{n}\) in (4.31), denoted by \(R21_{1,n}\), is bounded by
A simple calculation shows that
Therefore, we obtain
Define \(\beta =\min \{\frac{\gamma }{2}(\sigma +\alpha ), 2\}\). By (4.9),
For the second term of \(R21_{n}\) in (4.31), denoted by \(R21_{2,n}\), we have
Finally, we obtain from (4.31), (4.34) and (4.36) that
We next estimate \(R22_{n}\). Since for \(t\in (t_{2k}, t_{2k+2})\) and \(m=2k,2k+1,2k+2\) (\(k\ge 1\)),
and
it follows from (4.9)-(i), (4.9)-(ii), (4.9)-(iv) and (2.5) that
where we have used the following estimate:
Consequently, we have from (4.27), (4.37) and (4.40) that
(iii) The estimation of \(R3_{n}\) In order to estimate \(R3_{n}\), we first give a bound of \(R_{2,n-1}g(t)\). By (4.8), (4.9)-(i) and (2.5), we have that for \(t\in (t_{n-1},t_{n})\),
This bound implies
where we have used (4.9)-(i) and (4.9)-(ii) to derive the above last two inequalities.
Finally, we conclude from (4.22), (4.41) and (4.43) that for an odd number n and \(n\ge 3\),
This proves (4.12) for the case of odd n and \(n\ge 3\).
For the case of even n and \(n\ge 4\), the proof of (4.12) is similar and we omit it for the length of the paper. \(\square \)
5 Convergence and stability analysis
5.1 Auxiliary results
We give some auxiliary results, which will be used later.
Lemma 5.1
Let the mesh assumption (4.9)-(i) hold. Then the coefficients \(Q_{k,n}^{(\alpha )}\) defined in Sect. 3 satisfy
Proof
It is clear that
When \(n\ge 3\) and \(k=n-3,n-2,n-1\), we have
We next estimate \(a_{k,q,n}^{(\alpha )}\), where \(n\ge 3,~2\le q\le n-1,~k=q-2,q-1,q\). By the definition of \(a_{k,q,n}^{(\alpha )}\) and (4.9)-(i),
Since \(0<\alpha <1\), we have
This proves
Combining (5.2)–(5.4) and (5.7) with the definition of \(Q_{k,n}^{(\alpha )}\), we immediately get (5.1). \(\square \)
Let \(\textsf{E}(z)\) be the Mittag-Leffler function of order \(\alpha \), defined by
Lemma 5.2
(A fractional Grönwall inequality) Let \(g_{0}\) and \(C_{0}\) be two positive constants, and let the mesh be given by (1.5). Also let \(\{ \theta _{n}\}_{0}^{N}\) be a set function. Assume that
Then \(\theta _{n}\le {{\mathcal {E}}}(\alpha ) g_{0}\), where
Proof
See the proof of Lemma 3.3 of [42] (note that \(\tau _{j}\) in that paper corresponds to \(\tau _{j+1}\) in this paper). \(\square \)
Lemma 5.3
(A modified fractional Grönwall inequality) Let \(g_{0}\), \(C_{0}\) and \(\varepsilon \) be positive constants, and let the mesh be given by (1.5). Also let \(\{ E_{n} \}_{0}^{N}\) be a nonnegative set function. Assume that
-
(i)
for any \(1\le n\le N\), if \(\max _{0\le k\le n-1} E_{k}\le \varepsilon \), one has
$$\begin{aligned} E_{n}\le C_{0} \sum _{k=0}^{n-1}\tau _{k+1}(t_{n}-t_{k})^{\alpha -1}E_{k}+g_{0}; \end{aligned}$$ -
(ii)
\(E_{0}\le g_{0}\) and \({{\mathcal {E}}}(\alpha ) g_{0}\le \varepsilon \), where the function \({{\mathcal {E}}}(\alpha )\) is defined by (5.10).
Then \(E_{n}\le {{\mathcal {E}}}(\alpha ) g_{0}\) for all \(0\le n\le N\).
Proof
By the condition (ii), \(E_{0}\le g_{0}< {{\mathcal {E}}}(\alpha ) g_{0}\le \varepsilon \). We assert that \(\max _{0\le n\le N}E_{n}\le \varepsilon \). Otherwise, there exists \(1\le n\le N\) such that \(\max _{0\le k\le n-1}E_{k}\le \varepsilon \) and \(E_{n}>\varepsilon \). Then for any \(1\le j\le n\), \(\max _{0\le k\le j-1}E_{k}\le \max _{0\le k\le n-1}E_{k}\le \varepsilon \). By the condition (i), we have
Therefore, we get from Lemma 5.2 and the condition (ii) that \(E_{n}\le {{\mathcal {E}}}(\alpha ) g_{0}\le \varepsilon \) which is a contradiction. Since \(\max _{0\le n\le N}E_{n}\le \varepsilon \), the desired result follows from the condition (i) and Lemma 5.2. \(\square \)
5.2 Convergence analysis
Let y be the solution of the problem (1.1). Without loss of generality, we assume that \({\underline{M}}\le y(t)\le {\overline{M}}\) for all \(t\in [0,T]\). For the sake of numerical analysis, we assume that f fulfills the following local Lipschitz condition with respect to its second variable:
Theorem 5.1
Assume that the solution y of the problem (1.1) satisfies Assumption 1, and let the local Lipschitz condition (5.11) and the mesh assumption (4.9) be fulfilled. Let \(y_{n}\) be the numerical solution of the fractional Adams–Simpson-type scheme (1.6). Then there exists a positive constant \(N_{0}\), independent of N and n, such that when \(N\ge N_{0}\),
Proof
Let \(e_{n}=y(t_{n})-y_{n}\). We have from (1.6) and (4.1) that
Taking absolute values and using Theorem 4.1, we deduce
It is clear that \(|e_{0}|=0\). For any \(1\le n\le N\), we assume \(\max _{0\le k\le n-1}|e_{k}|\le 1\). This ensures
and so by the local Lipschitz condition (5.11),
Substituting the above estimate into (5.14) and using (5.1), we obtain
where
Let \({{\mathcal {E}}}(\alpha )\) be defined by (5.10), and let \(N\ge N_{0}\) be sufficiently large such that
This shows that when \(N\ge N_{0}\), the nonnegative set function \(\{ |e_{n}|\}_{0}^{N}\) satisfies the conditions (i) and (ii) of Lemma 5.3 with \(g_{0}\) and \(C_{0}\) being given in (5.18) and \(\varepsilon =1\). Therefore, by Lemma 5.3,
This proves (5.12). \(\square \)
Theorem 5.1 shows that under Assumption 1 and the mesh assumption (4.9), the numerical solution of the fractional Adams–Simpson-type scheme (1.6) converges with the order \(\min \{\gamma (\sigma +\alpha ), 3+\alpha \}\). Especially, the numerical solution can achieve the optimal convergence order \(3+\alpha \) when the mesh parameter \(\gamma \ge (3+\alpha )/(\sigma +\alpha )\). Since a large value of \(\gamma \) will result in a high concentration of the grid points near \(t=0\), the optimal mesh parameter \(\gamma \) is given by \(\gamma _{\textrm{opt}}=(3+\alpha )/(\sigma +\alpha )\).
Remark 5.1
The introduction of Lemma 5.3 (a modified fractional Grönwall inequality) in the proof of Theorem 5.1 makes us naturally get the convergence estimate (5.12).
5.3 Nonlinear stability analysis
Let \(y_{n}\) be the numerical solution of the fractional Adams–Simpson-type scheme (1.6). We have from Theorem 5.1 that for sufficiently large N, the numerical solution \(y_{n}\) is bounded by
where \({\underline{M}}\) and \({\overline{M}}\) are the constants appeared in (5.11).
We first investigate the stability of the numerical solution \(y_{n}\) with respect to the initial value \(\phi _{0}\). Suppose that in (1.6), \(\phi _{0}\) is perturbed and becomes \(\phi _{0}+\epsilon _{0}\). Denote by \({\widetilde{y}}_{n}\) the resulting perturbed solution of (1.6).
Theorem 5.2
Let the local Lipschitz condition (5.11) and the mesh assumption (4.9)-(i) be fulfilled. Let \(y_{n}\) be the solution of the fractional Adams–Simpson-type scheme (1.6), and let N be sufficiently large such that (5.20) is satisfied. Then for sufficiently small \(|\epsilon _{0}|\),
Proof
Let \({\widetilde{z}}_{n}={\widetilde{y}}_{n}-y_{n}\). We have the following perturbed problem:
Taking absolute values, we have
When \(|\epsilon _{0}|\le \frac{1}{2}\), \(|{\widetilde{z}}_{0}|=|\epsilon _{0}|\le \frac{1}{2}\). For any \(1\le n\le N\), we assume \(\max _{0\le k\le n-1}|{\widetilde{z}}_{k}|\le \frac{1}{2}\). Then by (5.20),
and so by (5.1) and the local Lipschitz condition (5.11),
where \(C_{0}=CL\) and \(g_{0}=|\epsilon _{0}|\). Let \({{\mathcal {E}}}(\alpha )\) be defined by (5.10). When \(|\epsilon _{0}|\) is sufficiently small such that
the nonnegative set function \(\{ |{\widetilde{z}}_{n}|\}_{0}^{N}\) satisfies the conditions (i) and (ii) of Lemma 5.3 with \(\varepsilon =\frac{1}{2}\). Therefore, by Lemma 5.3,
This proves (5.21). \(\square \)
Next, we discuss the influence of changes in the given function f on the right-hand side of the equation. Assume that the function f is perturbed and becomes \({\widehat{f}}\). Denote by \({\widehat{y}}_{n}\) the resulting perturbed solution of (1.6). Define
where \({\underline{M}}\) and \({\overline{M}}\) are the constants appeared in (5.11).
Theorem 5.3
Let the local Lipschitz condition (5.11) and the mesh assumption (4.9)-(i) be fulfilled. Let \(y_{n}\) be the solution of the fractional Adams–Simpson-type scheme (1.6), and let N be sufficiently large such that (5.20) is satisfied. Then for sufficiently small \({\overline{\epsilon }}_{f}\),
Proof
Let \({\widehat{z}}_{n}=y_{n}-{\widehat{y}}_{n}\). We have the following perturbed problem:
For any \(1\le n\le N\), we assume \(\max _{0\le k\le n-1}|{\widehat{z}}_{k}|\le \frac{1}{2}\). Then by (5.20),
Taking absolute values in (5.29) and using (5.11), (5.27) and (5.1), we get
Since
we have from (5.31) that
The remaining proof is similar to that of Theorem 5.2. \(\square \)
Remark 5.2
It should be mentioned that the bounds (5.21) and (5.28) on the perturbations only apply provided that \(|\epsilon _{0}|\) and \({\overline{\epsilon }}_{f}\) are sufficiently small. This phenomenon is typical of nonlinear stability analysis (see [55]) and has no counterpart in the linear stability theory (see [54]).
6 Extensions
6.1 Extension to multi-term nonlinear fractional ordinary differential equations
In the previous sections, we have only considered so-called single-term equations, i.e. equations where only one fractional differential operator is involved. However, in certain cases, we need to solve equations containing more than one fractional differential operators. An equation of this type is called a multi-term fractional differential equation (see [17, 18, 20, 21]). Consider the following initial value problem of multi-term nonlinear fractional ordinary differential equation:
Let \(\varphi (t)= \phi _{0} \omega _{\alpha -\beta +1}(t)\). We can transform the above problem into its integral form as
Then we apply (3.21) to discretize each fractional integral in (6.2) and derive the following fractional Adams–Simpson-type scheme for (6.1):
where \(y_{n}\approx y(t_{n})\) and \(\varphi _{n}=\varphi (t_{n})\). Under the mesh assumption (4.9)-(i), we have from Lemma 5.1 that
Define \(g_{\alpha \beta }:={_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y+{_{~0}^{C}}{{\mathcal {D}}}_{t}^{\beta }y\). Let \(R_{\textrm{mt},n}\) be the local truncation error of (6.3). From (6.2) and (6.3), we have \(R_{\textrm{mt},n}=R_{y,n}+R_{f,n}\), where
In order to apply Theorem 4.1 to obtain bounds of \(R_{y,n}\) and \(R_{f,n}\), we introduce the following assumption for the solution y of the problem (6.1):
Assumption 2
-
(i)
Assume that \(y\in C^{4}(0,T]\) and there exists a positive constant C such that
$$\begin{aligned} |y^{(l)}(t)|\le C(1+ t^{\sigma _{y} -l}), \qquad t\in (0,T],~l=0,1,2,3,4, \end{aligned}$$(6.8)where \(\sigma _{y}\in (0,1)\) is a real number.
-
(ii)
Assume that \(g_{\alpha \beta }:={_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y+{_{~0}^{C}}{{\mathcal {D}}}_{t}^{\beta }y\in {{\mathcal {C}}}^{4}(0,T]\) satisfies Assumption 1, where \(\sigma \) is replaced with \(\sigma _{f}\).
By directly applying Theorem 4.1, we can easily obtain the following theorem on bounds of local truncation errors \(R_{y,n}\) and \(R_{f,n}\).
Theorem 6.1
Let the mesh assumption (4.9) hold.
-
(i)
Assume that the solution y of the problem (6.1) satisfies Assumption 2-(i). Then
$$\begin{aligned}{} & {} \left| R_{y,n} \right| \le C N^{-\gamma (\sigma _{y}+\alpha -\beta )}, \qquad n=1,2, \end{aligned}$$(6.9)$$\begin{aligned}{} & {} \left| R_{y,n} \right| \le C N^{-\min \{\gamma (\sigma _{y} +\alpha -\beta ), 3+\alpha -\beta \}},\qquad 3\le n\le N. \end{aligned}$$(6.10) -
(ii)
Assume that the solution y of the problem (6.1) satisfies Assumption 2-(ii). Then
$$\begin{aligned}{} & {} \left| R_{f,n} \right| \le C N^{-\gamma (\sigma _{f}+\alpha )}, \qquad n=1,2, \end{aligned}$$(6.11)$$\begin{aligned}{} & {} \left| R_{f,n} \right| \le C N^{-\min \{\gamma (\sigma _{f} +\alpha ), 3+\alpha \}},\qquad 3\le n\le N. \end{aligned}$$(6.12)
Using Theorem 6.1, we prove the following theorem on the convergence of the fractional Adams–Simpson-type scheme (6.3).
Theorem 6.2
Assume that the solution y of the problem (6.1) satisfies Assumption 2, and let the local Lipschitz condition (5.11) and the mesh assumption (4.9) be fulfilled. Let \(y_{n}\) be the numerical solution of the fractional Adams–Simpson-type scheme (6.3). Then there exists a positive constant \(N_{0}\), independent of N and n, such that when \(N\ge N_{0}\),
Proof
Let \(e_{n}=y(t_{n})-y_{n}\). We have from (6.2) and (6.3) that
Taking absolute values and using Theorem 6.1, we get
Using (6.4) and (6.6), the remaining proof is similar to that of Theorem 5.1. \(\square \)
We now turn to the nonlinear stability analysis of the fractional Adams–Simpson-type scheme (6.3).
Theorem 6.3
Let the local Lipschitz condition (5.11) and the mesh assumption (4.9)-(i) be fulfilled. Let \(y_{n}\) be the solution of the fractional Adams–Simpson-type scheme (6.3), and let N be sufficiently large such that (5.20) is satisfied. Suppose that in (6.3), \(\phi _{0}\) is perturbed and becomes \(\phi _{0}+\epsilon _{0}\), and denote by \({\widetilde{y}}_{n}\) the resulting perturbed solution of (6.3). Then for sufficiently small \(|\epsilon _{0}|\),
Proof
Let \({\widetilde{z}}_{n}={\widetilde{y}}_{n}-y_{n}\). We have the following perturbed problem:
Comparing (6.17) with (5.22), we find out that the first term and the term \(\omega _{\alpha -\beta +1}(t_{n})\epsilon _{0}\) in (6.17) are the only extra terms to (5.22). With the help of the bounds given in (6.4) and (6.6) and the estimate \(|\omega _{\alpha -\beta +1}(t_{n})\epsilon _{0}|\le [ T^{\alpha -\beta }/\Gamma (\alpha -\beta +1)]|\epsilon _{0}|\), we can easily prove (6.16) by using a technique similar to the proof of Theorem 5.2. \(\square \)
Theorem 6.4
Let the local Lipschitz condition (5.11) and the mesh assumption (4.9)-(i) be fulfilled. Let \(y_{n}\) be the solution of the scheme (6.3), and let N be sufficiently large such that (5.20) is satisfied. Assume that the function f in (6.3) is perturbed and becomes \({\widehat{f}}\), and denote by \({\widehat{y}}_{n}\) the resulting perturbed solution of (6.3). Also let \({\overline{\epsilon }}_{f}\) be defined by (5.27). Then for sufficiently small \({\overline{\epsilon }}_{f}\),
Proof
With the help of (6.4) and (6.6), the proof of the theorem is similar to that of Theorem 5.3. \(\square \)
6.2 Extension to multi-order nonlinear fractional ordinary differential systems
The proposed fractional Adams–Simpson-type scheme (1.6) can also be extended to a system of fractional ordinary differential equations where each equation has an order that may or may not coincide with the orders of the other equations. A system of this class is called a multi-order fractional ordinary differential system (see [17, 18]). Consider the following initial value problem of multi-order nonlinear fractional ordinary differential system:
Its integral form is given by
Similar to deriving the scheme (1.6), we get the following fractional Adams–Simpson-type scheme for (6.19):
where \(y_{n}\approx y(t_{n})\) and \(z_{n}\approx z(t_{n})\). Under the mesh assumption (4.9)-(i), we have from Lemma 5.1 that
Define \(g_{y}:={_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y\) and \(g_{z}:={_{~0}^{C}}{{\mathcal {D}}}_{t}^{\beta }z\). Let \(R_{f_{1},n}\) and \(R_{f_{2},n}\) be the local truncation errors of the first and second equations in (6.21). From (6.20) and (6.21), we have
A direct application of Theorem 4.1 leads to the following theorem on the bounds of the local truncation errors \(R_{f_{1},n}\) and \(R_{f_{2},n}\).
Theorem 6.5
Let (y, z) be the solution of problem (6.19), and let the mesh assumption (4.9) hold.
-
(i)
Assume that \(g_{y}:={_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y\) satisfies Assumption 1, where \(\sigma \) is replaced with \(\sigma _{f_{1}}\). Then
$$\begin{aligned}{} & {} \left| R_{f_{1},n} \right| \le C N^{-\gamma (\sigma _{f_{1}}+\alpha )}, \qquad n=1,2, \end{aligned}$$(6.26)$$\begin{aligned}{} & {} \left| R_{f_{1},n} \right| \le C N^{-\min \{\gamma (\sigma _{f_{1}} +\alpha ), 3+\alpha \}},\qquad 3\le n\le N. \end{aligned}$$(6.27) -
(ii)
Assume that \(g_{z}:={_{~0}^{C}}{{\mathcal {D}}}_{t}^{\beta }z\) satisfies Assumption 1, where \(\sigma \) is replaced with \(\sigma _{f_{2}}\). Then
$$\begin{aligned}{} & {} \left| R_{f_{2},n} \right| \le C N^{-\gamma (\sigma _{f_{2}}+\beta )}, \qquad n=1,2, \end{aligned}$$(6.28)$$\begin{aligned}{} & {} \left| R_{f_{2},n} \right| \le C N^{-\min \{\gamma (\sigma _{f_{2}} +\beta ), 3+\beta \}},\qquad 3\le n\le N. \end{aligned}$$(6.29)
Let (y, z) be the solution of the problem (6.19). We assume that \({\underline{M}}\le y(t), z(t)\le {\overline{M}}\) for all \(t\in [0,T]\), and assume that \(f_{1}\) and \(f_{2}\) satisfy the following local Lipschitz conditions:
The following theorem gives the convergence of the fractional Adams–Simpson-type scheme (6.21).
Theorem 6.6
Let (y, z) be the solution of the problem (6.19). Assume that \(g_{y}:={_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y(t)\) and \(g_{z}:={_{~0}^{C}}{{\mathcal {D}}}_{t}^{\beta }z(t)\) satisfy Assumption 1, where \(\sigma \) is replaced with \(\sigma _{f_{1}}\) and \(\sigma _{f_{2}}\) respectively. Let the local Lipschitz condition (6.30) and the mesh assumption (4.9) be fulfilled. Let \((y_{n},z_{n})\) be the numerical solution of the fractional Adams–Simpson-type scheme (6.21). Then there exists a positive constant \(N_{0}\), independent of N and n, such that when \(N\ge N_{0}\),
Proof
Let \(e_{y,n}=y(t_{n})-y_{n}\) and \(e_{z,n}=z(t_{n})-z_{n}\). From (6.20) and (6.21), we have
Using (6.22), (6.23), (6.33) and Theorem 6.5, we can use a technique similar to the proof of Theorem 5.1 to get
This proves (6.31) and (6.32). \(\square \)
We now carry out the nonlinear stability analysis of the fractional Adams–Simpson-type scheme (6.21).
Theorem 6.7
Let the local Lipschitz condition (6.30) and the mesh assumption (4.9)-(i) be fulfilled. Let \((y_{n},z_{n})\) be the solution of the fractional Adams–Simpson-type scheme (6.21), and let N be sufficiently large such that \(y_{n}\) and \(z_{n}\) satisfy (5.20). Suppose that in (6.21), \((\phi _{y,0}, \phi _{z,0})\) are perturbed and become \((\phi _{y,0}+\epsilon _{y,0},\phi _{z,0}+\epsilon _{z,0})\), and denote by \(({\widetilde{y}}_{n},{\widetilde{z}}_{n})\) the resulting perturbed solution of (6.21). Then for sufficiently small \(|\epsilon _{y,0}|\) and \(|\epsilon _{z,0}|\),
Proof
With the help of (6.22) and (6.23), we can easily prove (6.35) for sufficiently small \(|\epsilon _{y,0}|\) and \(|\epsilon _{z,0}|\) by a technique similar to the proof of Theorem 5.2. \(\square \)
Assume that the functions \((f_{1}, f_{2})\) in (6.21) are perturbed and become \(({\widehat{f}}_{1}, {\widehat{f}}_{2})\). Denote by \(({\widehat{y}}_{n}, {\widehat{z}}_{n})\) the resulting perturbed solution of (6.21). Define
where \({\underline{M}}\) and \({\overline{M}}\) are the constants appeared in (6.30).
Theorem 6.8
Let the local Lipschitz condition (6.30) and the mesh assumption (4.9)-(i) be fulfilled. Let \((y_{n},z_{n})\) be the solution of the fractional Adams–Simpson-type scheme (6.21), and let N be sufficiently large such that \(y_{n}\) and \(z_{n}\) satisfy (5.20). Then for sufficiently small \({\overline{\epsilon }}_{f_{1}}\) and \({\overline{\epsilon }}_{f_{2}}\),
Proof
With the help of (6.22) and (6.23), the proof of the theorem is similar to that of Theorem 5.3. \(\square \)
7 Numerical results
In this section, we give numerical results of the proposed fractional Adams–Simpson-type schemes for three model problems. The exact analytical solution of each problem is explicitly known and is mainly used to compare with the numerical solution. In Example 7.1, we check the accuracy and the convergence order of the scheme (1.6) for a nonlinear fractional ordinary differential equation with non-smooth data. In this example, we also numerically compare our scheme (1.6) with the Adams predictor–corrector scheme proposed in [47] (see (1.6) of [47]) and the scheme developed in [51] (see (3.16) of [51]). In Examples 7.2 and 7.3, we test the effectiveness of the schemes (6.3) and (6.21) in solving a multi-term nonlinear fractional ordinary differential equation and a multi-order nonlinear fractional ordinary differential system.
In our computations, we use the graded mesh (4.10) with a given number N of steps and a mesh parameter \(\gamma \ge 1\). For checking the accuracy and the convergence order of the numerical solution \(y_{n}\) of the schemes (1.6) and (6.3) and the schemes given in [47, 51], we record the maximum error \({\textrm{E}}(N)=\max _{0\le n\le N}|y(t_{n})-y_{n}|\) and compute the convergence order \({\textrm{O}}(N)\) by
Similarly, for the numerical solution \((y_{n}, z_{n})\) of the scheme (6.21), we measure its error in the sense of \({\textrm{E}}(N)=\max _{0\le n\le N}\{ |y(t_{n})-y_{n}|, |z(t_{n})-z_{n}| \}\) and compute its convergence order \({\textrm{O}}(N)\) by (7.1).
Example 7.1
Consider the initial value problem of the nonlinear fractional ordinary differential equation:
We choose a suitable F(t) such that the solution y of (7.2) is given by \(y(t)=t^{\alpha }+t^{2\alpha }\). It is easy to see that \(g(t):={_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y(t)=\Gamma (\alpha +1)+\frac{\Gamma (2\alpha +1)}{\Gamma (\alpha +1)} t^{\alpha }\), which satisfies Assumption 1 with \(\sigma =\alpha \).
(a) Convergence order of the numerical solution \(y_{n}\)of the scheme (1.6) We use the scheme (1.6) to solve the above problem numerically. Table 1 shows the maximum error \({\textrm{E}}(N)\) and the convergence order \({\textrm{O}}(N)\) of the numerical solution \(y_{n}\) of (1.6) with different \(\gamma \), N and \(\alpha \). The results show clearly that the convergence order \({\textrm{O}}(N)\) is \(\min \{2\gamma \alpha , 3+\alpha \}\), which agrees precisely with the theoretical order given in Theorem 5.1.
(b) Numerical comparisons of the scheme (1.6) with the schemes given in [47, 51]
For comparison, we also solve the above problem by the schemes given in [47, 51]. In theory, these two schemes in solving the above problem has the convergence orders \(\min \{ 2\gamma \alpha ,1+\alpha \}\) (see Theorem 1.5 of [47]) and \(\min \{ 2\gamma \alpha ,3\}\) (see Lemma 3.1 of [51]), respectively. Taking different \(\gamma \), N and \(\alpha \), in Tables 2 3 and 4, we give the maximum error \({\textrm{E}}(N)\) and the convergence order \({\textrm{O}}(N)\) of the numerical solution \(y_{n}\) of the scheme (1.6) and the schemes in [47, 51]. It can be seen from these tables that
- \(\bullet \):
-
the convergence order \({\textrm{O}}(N)\) is \(\min \{ 2\gamma \alpha ,3+\alpha \}\) for our scheme (1.6), while it is only \(\min \{ 2\gamma \alpha ,1+\alpha \}\) for the scheme in [47] and \(\min \{ 2\gamma \alpha ,3\}\) for the scheme in [51];
- \(\bullet \):
-
when \(\gamma =\frac{1+\alpha }{2\alpha }\)—the optimal mesh parameter of the scheme in [47], our scheme (1.6) has roughly the same convergence order as the schemes in [47, 51];
- \(\bullet \):
-
when \(\gamma =\frac{3}{2\alpha }\)—the optimal mesh parameter of the scheme in [51], the convergence order of our scheme (1.6) is almost the same as that of the scheme in [51], but higher than that of the scheme in [47];
- \(\bullet \):
-
when \(\gamma = \frac{3+\alpha }{2\alpha }\)—the optimal mesh parameter of our scheme (1.6), our scheme (1.6) can achieve the convergence order \(3+\alpha \), while the convergence orders of the schemes in [47, 51] are only \(1+\alpha \) and 3, respectively.
Example 7.2
In this example, we use the scheme (6.3) to solve the following initial value problem of multi-term nonlinear fractional ordinary differential equation:
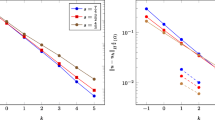
We choose suitable F(t) such that the problem has the solution \(y(t)=\phi _{0}+t^{\alpha }+t^{2\alpha }\). This solution satisfies Assumption 2 with \(\sigma _{y}=\alpha \) and \(\sigma _{f}=\alpha -\beta \). For computation, we take \(\alpha =0.9\), \(\beta =0.4\), \(\phi _{0}=1\). The numerical results in Table 5 show that the scheme (6.3) works well for solving the above problem, and its convergence order is close to \(\min \{\gamma (2\alpha -\beta ), 3+\alpha -\beta \}=\min \{1.4\gamma , 3.5\}\), which is consistent with the theoretical order given in Theorem 6.2. In Fig. 1, we plot the pointwise errors \(|y(t_{n})-y_{n}|\) for the case of \(N=2^{8}\).
Example 7.3
In order to test the effectiveness of the scheme (6.21), we consider the following initial value problem of multi-order nonlinear fractional ordinary differential system:
We take suitable \(F_{1}(t)\) and \(F_{2}(t)\) such that the solution (y, z) of the above problem is given by
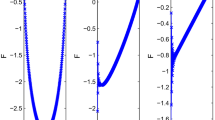
It is clear that \(g_{y}:={_{~0}^{C}}{{\mathcal {D}}}_{t}^{\alpha }y\) and \(g_{z}:={_{~0}^{C}}{{\mathcal {D}}}_{t}^{\beta }z\) satisfy Assumption 1 with \(\sigma =\alpha \) and \(\sigma =\beta \), respectively. Table 6 shows the maximum error \({\textrm{E}}(N)\) and the convergence order \({\textrm{O}}(N)\) of the numerical solution \((y_{n},z_{n})\) of the scheme (6.21) when solving the multi-order problem (7.4), where \(\alpha =0.5\), \(\beta =0.8\) and \(\phi _{y,0}=\phi _{z,0}=1\). The corresponding numerical results for the case of \(\alpha =0.4\), \(\beta =0.7\) and \(\phi _{y,0}=1.5\) and \(\phi _{z,0}=3\) are given in Table 7. It can be seen from these two tables that the convergence order \({\textrm{O}}(N)\) is about \(\min \{2\gamma \alpha ,2\gamma \beta ,3+\alpha ,3+\beta \}\). This coincides with the theoretical order given in Theorem 6.6. In Figs. 2 and 3, we present the pointwise errors \(|y(t_{n})-y_{n}|\) and \(|z(t_{n})-z_{n}|\) for the case of \(N=2^{8}\). The above numerical results demonstrate that the scheme (6.21) is effective for solving the multi-order nonlinear fractional ordinary differential system with non-smooth data.
8 Conclusion
We proposed a fractional Adams–Simpson-type method for nonlinear fractional ordinary differential equations with fractional order \(\alpha \in (0,1)\). We proved the convergence and the nonlinear stability of the method by developing a modified fractional Grönwall inequality and using a perturbation technique. In constructing our method, we used a nonuniform mesh, so that with a proper mesh parameter, the proposed method can achieve the optimal convergence order \(3+\alpha \) even if the given data is not smooth. We further discussed how to extend the proposed method to multi-term nonlinear fractional ordinary differential equations and multi-order nonlinear fractional ordinary differential systems.
We provided numerical results to confirm the theoretical analysis results and demonstrate the effectiveness of the proposed method for non-smooth data when solving a single-term or multi-term nonlinear fractional ordinary differential equation and a multi-order nonlinear fractional ordinary differential system. We also compared our method with the existing methods through some numerical results. It was observed that our method is more effective.
References
Alikhanov, A.A.: A new difference scheme for the time fractional diffusion equation. J. Comput. Phys. 280, 424–438 (2015)
Amblard, F., Maggs, A.C., Yurke, B., Pargellis, A.N., Leibler, S.: Subdiffusion and anomalous local viscoelasticity in actin networks. Phys. Rev. Lett. 77, 4470–4473 (1996)
Bagley, R.L., Calico, R.A.: Fractional order state equations for the control of viscoelastically damped structures. J. Guidance Control Dyn. 14, 304–311 (1991)
Benson, D.A., Wheatcraft, S.W., Meerschaert, M.M.: Application of a fractional advection-dispersion equation. Water Resour. Res. 36, 1403–1412 (2000)
Benson, D.A., Wheatcraft, S.W., Meerschaert, M.M.: The fractional-order governing equation of lévy motion. Water Resour. Res. 36, 1413–1423 (2000)
Bouchaud, J.P., Georges, A.: Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications. Phys. Rep. 195, 127–293 (1990)
Brunner, H., van der Houwen, P.J.: The Numerical Solution of Volterra Equations. North Holland, Amsterdam (1986)
Cao, Y., Herdman, T., Xu, Y.: A hybrid collocation method for Volterra integral equations with weakly singular kernels. SIAM J. Numer. Anal. 41, 364–381 (2003)
Cao, J.X., Li, C.P., Chen, Y.Q.: High-order approximation to Caputo derivatives and Caputo-type advection–diffusion equations (II). Fract. Calc. Appl. Anal. 18, 735–761 (2015)
Cao, J., Xu, C.: A high order schema for the numerical solution of the fractional ordinary differential equations. J. Comput. Phys. 238, 154–168 (2013)
Cao, W., Zeng, F., Zhang, Z., Karniadakis, G.E.: Implicit-explicit difference schemes for nonlinear fractional differential equations with nonsmooth solutions. SIAM J. Sci. Comput. 38, A3070–A3093 (2016)
Chen, H., Stynes, M.: Error analysis of a second-order method on fitted meshes for a time-fractional diffusion problem. J. Sci. Comput. 79, 624–647 (2019)
Daftardar-Gejji, V., Sukale, Y., Bhalekar, S.: A new predictor–corrector method for fractional differential equations. Appl. Math. Comput. 244, 158–182 (2014)
Deng, W.H.: Short memory principle and a predictor–corrector approach for fractional differential equations. J. Comput. Appl. Math. 206, 1768–1777 (2007)
Deng, W.H.: Numerical algorithm for the time fractional Fokker-Planck equation. J. Comput. Phys. 227, 1510–1522 (2007)
Dentz, M., Cortis, A., Scher, H., Berkowitz, B.: Time behavior of solute transport in heterogeneous media: transition from anomalous to normal transport. Adv. Water Resour. 27, 155–173 (2004)
Diethelm, K.: Multi-term fractional differential equations, multi-order fractional differential systems and their numerical solution. J. Eur. Syst. Autom. 42, 665–676 (2008)
Diethelm, K.: The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type. Springer, Berlin (2010)
Diethelm, K., Ford, N.J.: Analysis of fractional differential equations. J. Math. Anal. Appl. 265, 229–248 (2002)
Diethelm, K., Ford, N.J.: Numerical solution of the Bagley–Torvik equation. BIT Numer. Math. 42, 490–507 (2002)
Diethelm, K., Ford, N.J.: Multi-order fractional differential equations and their numerical solution. Appl. Math. Comput. 154, 621–640 (2004)
Diethelm, K., Ford, J.M., Ford, N.J., Weilbeer, M.: Pitfalls in fast numerical solvers for fractional differential equations. J. Comput. Appl. Math. 186, 482–503 (2006)
Diethelm, K., Ford, N.J., Freed, A.D.: A predictor–corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 29, 3–22 (2002)
Diethelm, K., Ford, N.J., Freed, A.D.: Detailed error analysis for a fractional Adams method. Numer. Algorithms 36, 31–52 (2004)
Du, R., Yan, Y., Liang, Z.: A high-order scheme to approximate the Caputo fractional derivative and its application to solve the fractional diffusion wave equation. J. Comput. Phys. 376, 1312–1330 (2019)
Ford, N.J., Morgado, M.L., Rebelo, M.: Nonpolynomial collocation approximation of solutions to fractional differential equations. Fract. Calc. Appl. Anal. 16, 874–891 (2013)
Galeone, L., Garrappa, R.: Fractional Adams–Moulton methods. Math. Comput. Simulation 79, 1358–1367 (2008)
Gao, G.-H., Sun, Z.-Z., Zhang, H.-W.: A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. J. Comput. Phys. 259, 33–50 (2014)
Garrappa, R.: On linear stability of predictor–corrector algorithms for fractional differential equations. Int. J. Comput. Math. 87, 2281–2290 (2010)
Garrappa, R.: Trapezoidal methods for fractional differential equations: theoretical and computational aspects. Math. Comput. Simulation 110, 96–112 (2015)
Hatano, Y., Hatano, N.: Dispersive transport of ions in column experiments: an explanation of long-tailed profiles. Water Resour. Res. 34, 1027–1033 (1998)
Huang, J., Tang, Y., Vázquez, L.: Convergence analysis of a block-by-block method for fractional differential equations. Numer. Math. Theor. Methods Appl. 5, 229–241 (2012)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier Science B.V., Amsterdam (2006)
Klages, R., Radons, G., Sokolov, I.M.: Anomalous Transport: Foundations and Applications. Wiley-VCH, Weinheim (2008)
Koeller, R.C.: Application of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. 51, 299–307 (1984)
Kumar, P., Agrawal, O.P.: An approximate method for numerical solution of fractional differential equations. Signal Process. 86, 2602–2610 (2006)
Langlands, T.A.M., Henry, B.I.: The accuracy and stability of an implicit solution method for the fractional diffusion equation. J. Comput. Phys. 205, 719–736 (2005)
Li, H.F., Cao, J.X., Li, C.: High-order approximations to Caputo derivatives and Caputo-type advection–diffusion equations (III). J. Comput. Appl. Math. 299, 159–175 (2016)
Li, B., Ma, S.: A high-order exponential integrator for nonlinear parabolic equations with nonsmooth initial data. J. Sci. Comput. 87, 23 (2021)
Li, B., Ma, S.: Exponential convolution quadrature for nonlinear subdiffusion equations with nonsmooth initial data. SIAM J. Numer. Anal. 60, 503–528 (2022)
Li, C., Tao, C.X.: On the fractional Adams method. Comput. Math. Appl. 58, 1573–1588 (2009)
Li, C., Yi, Q., Chen, A.: Finite difference methods with non-uniform meshes for nonlinear fractional differential equations. J. Comput. Phys. 316, 614–631 (2016)
Liao, H.-L., Li, D., Zhang, J.: Sharp error estimate of the nonuniform L1 formula for linear reaction-subdiffusion equations. SIAM J. Numer. Anal. 56, 1112–1133 (2018)
Lin, R., Liu, F.: Fractional high order methods for the nonlinear fractional ordinary differential equation. Nonlinear Anal. 66, 856–869 (2007)
Lin, Y., Xu, C.: Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 225, 1533–1552 (2007)
Liu, Y., Roberts, J., Yan, Y.: A note on finite difference methods for nonlinear fractional differential equations with non-uniform meshes. Int. J. Comput. Math. 95, 1151–1169 (2018)
Liu, Y., Roberts, J., Yan, Y.: Detailed error analysis for a fractional Adams method with graded meshes. Numer. Algorithms 78, 1195–1216 (2018)
Lubich, C.: Fractional linear multistep methods for Abel-Volterra integral equations of the second kind. Math. Comput. 45, 463–469 (1985)
Lubich, C.: Discretized fractional calculus. SIAM J. Math. Anal. 17, 704–719 (1986)
Lv, C., Xu, C.: Error analysis of a high order method for time-fractional diffusion equations. SIAM J. Sci. Comput. 38, A2699–A2724 (2016)
Lyu, P., Vong, S.: A high-order method with a temporal nonuniform mesh for a time-fractional Benjamin–Bona–Mahony equation. J. Sci. Comput. 80, 1607–1628 (2019)
Perdikaris, P., Karniadakis, G.E.: Fractional-order viscoelasticity in one-dimensional blood flow models. Ann. Biomed. Eng. 42, 1012–1023 (2014)
Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)
Richtmyer, R.D., Morton, K.W.: Difference Methods for Initial-Value Problems. Interscience, New York (1967)
Stetter, H.J.: Analysis of Discretization Methods for Ordinary Differential Equations. Springer, Berlin (1973)
Stynes, M., O’Riordan, E., Gracia, J.L.: Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM J. Numer. Anal. 55, 1057–1079 (2017)
Sun, Z.Z., Wu, X.N.: A fully discrete difference scheme for a diffusion-wave system. Appl. Numer. Math. 56, 193–209 (2006)
Wang, W., Chen, X., Ding, D., Lei, S.-L.: Circulant preconditioning technique for barrier options pricing under fractional diffusion models. Int. J. Comput. Math. 92, 2596–2614 (2015)
Yan, Y., Pal, K., Ford, N.J.: Higher order numerical methods for solving fractional differential equations. BIT Numer. Math. 54, 555–584 (2014)
Zeng, F., Li, C., Liu, F., Turner, I.: Numerical algorithms for time-fractional subdiffusion equation with second-order accuracy. SIAM J. Sci. Comput. 37, A55–A78 (2015)
Zhang, Z., Zeng, F., Karniadakis, G.E.: Optimal error estimates of spectral Petrov–Galerkin and collocation methods for initial value problems of fractional differential equations. SIAM J. Numer. Anal. 53, 2074–2096 (2015)
Zhao, L., Deng, W.H.: Jacobian–predictor–corrector approach for fractional ordinary differential equations. Adv. Comput. Math. 40, 137–165 (2014)
Acknowledgements
The authors would like to thank the referees for their valuable comments and suggestions which improved the presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no competing interests.
Additional information
Communicated by Mihaly Kovacs.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported in part by Science and Technology Commission of Shanghai Municipality (STCSM) (No. 22DZ2229014, No. 21JC1402500).
A Appendix
A Appendix
In this appendix, we prove Lemma 4.1.
Proof
It is clear that
This proves
and so (4.5) is proved. By Taylor expansion with integral remainder,
This implies
and
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Wang, YM., Xie, B. A fractional Adams–Simpson-type method for nonlinear fractional ordinary differential equations with non-smooth data. Bit Numer Math 63, 7 (2023). https://doi.org/10.1007/s10543-023-00952-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10543-023-00952-4
Keywords
- Fractional ordinary differential equations
- Fractional derivative
- Adams–Simpson-type method
- Non-smooth data
- High-order accuracy