Finite Element Method for Two-Sided Fractional Differential Equations with Variable Coefficients: Galerkin Approach

Abstract

This paper develops a Galerkin approach for two-sided fractional differential equations with variable coefficients. By the product rule, we transform the problem into an equivalent formulation which additionally introduces the fractional low-order term. We prove the existence and uniqueness of the solutions of the Dirichlet problems of the equations with certain diffusion coefficients. We adopt the Galerkin formulation, and prove its error estimates. Finally, several numerical examples are provided to illustrate the fidelity and accuracy of the proposed theoretical results.

1 Introduction

Fractional order differential equations are generalizations of classical differential equations. Over the past two decades, fractional differential equations have been used in modeling turbulent flow [5, 23], chaotic dynamics of classical conservative systems [32], groundwater contaminant transport [3], and applications in biology [16], physics [12], chemistry [13], and even finance [20]. The main reason for their popularity is that they are equipped with the ability to capture nonlocal phenomena and long-range interactions, and can model phenomena exhibiting anomalous diffusion that cannot be modeled adequately and accurately by canonical second-order diffusion equations.

The classical one-dimensional diffusion equation

$$\begin{aligned} \partial _tu(x,t) - \partial _x[k(x) \partial _xu(x,t)] = f(x,t), \end{aligned}$$

(1.1)

is derived from the mass balance equation

$$\begin{aligned} \partial _tu(x,t) + \partial _x F = f(x,t), \end{aligned}$$

(1.2)

and the Fick’s first law

$$\begin{aligned} F = -k(x)\partial _xu(x,t), \end{aligned}$$

(1.3)

where u is the concentration of the diffusing material at x and time t, F is the flux of the material, and k is the diffusion coefficient.

Recently, researchers found that the classical Fick’s law (1.3) does not describe anomalous diffusion in heterogeneous porous media [2, 3]. Instead, a fractional Fick’s law was proposed in [22]:

$$\begin{aligned} F = -k(x)\left( \theta \ _0\partial _{x}^{1-\beta } u(x,t) + (1-\theta )\ _x\partial _{1}^{1-\beta }u(x,t)\right) , \end{aligned}$$

(1.4)

where $\beta \in (0,1)$, $\theta \in [0, 1]$ is a parameter describing the relative probability of particle traveling ahead or behind the mean velocity, and $\ _0\partial _{x}^{1-\beta }$ and $_x\partial _{1}^{1-\beta }$ are left- and right-sided Riemann–Liouville fractional derivatives with respect to variable x, respectively, which will be defined in Sect. 2. Combining (1.2) with (1.4), we obtain the following fractional diffusion equation (FDE):

$$\begin{aligned} \partial _t u(x,t) - \partial _x \left( k(x)\left( \theta \ _0\partial _{x}^{1-\beta } u(x,t) + (1-\theta )\ _x\partial _{1}^{1-\beta }u(x,t)\right) \right) = f(x,t). \end{aligned}$$

(1.5)

Since in most cases the closed-form of the solution is not available, numerical approaches are preferred to understand the behavior of the solution. Even though the solution can be sought in constant-coefficient case, it is challenging to evaluate the fractional derivative for most functions involved in the explicit solution. Therefore, it is essential to develop efficient numerical methods. Liu et al. [15] and Meerschaert and Tadjeran [17, 18] were the first to develop finite difference method for fractional partial differential equations (1.5) with constant coefficients and other kinds of equations. Subsequently, many high-order finite difference schemes [6, 11, 24] have been developed. One of the main reasons for the popularity of finite difference methods is that the resulting discrete stiffness matrix is equipped with Toeplitz-like structure so that existing fast methods can be applied to the resulting discretized matrix directly, with storage of O(N) and computational operations of O(NlogN) with respect to unknowns, where N is the number of grid points; see [26, 27].

In the context of finite element method, Ervin and Roop [8] are the first to carry out a rigorous analysis to prove the well-posedness of a Galerkin weak formulation to fractional differential equations with a constant diffusion coefficient. In addition, they proved the optimal-order convergence for the corresponding finite element methods [6,7,8] based on the assumption of a suitably smooth solution. Subsequently, many researchers extended their analysis to other methods such as the discontinuous Galerkin method [30] and spectral method [14]. Numerous works have been focused on either one-sided fractional equations $\theta = 0, 1$ in (1.5) or two-sided case but only with constant coefficient, $k(x) \equiv constant$. For the stationary one-sided diffusion equations with variable coefficient which corresponds to $\theta = 1$ in (1.5), Wang and Yang [25] showed that the bilinear form of the Galerkin formulation may lose coercivity. To circumvent the difficulty, they proposed a Petrov–Galerkin formulation and established its well-posedness. Based on the Petrov–Galerkin formulation, they developed discontinuous Petrov–Galerkin method [28] and indirect method [29]. Here, we have a natural question for two-sided fractional differential equations with $\theta \in (0,1)$ and variable coefficients: for what kind of diffusion coefficients can we use the Galerkin approach for the equations? To get an answer for the question, we derive an required condition for the wellposedness of the Dirichlet problem of the equations, discretize the equations and provide its error estimates.

The remainder of this paper is organized as follows. In Sect. 2, we describe basic notations, introduce some important properties of fractional derivatives and integrals, and recall existing known results about fractional differential operators, Sobolev spaces as well as fractional derivative spaces. In Sect. 3, we prove the wellposedness of the Dirichlet problem of the two-sided fractional differential equation with variable coefficient. In Sect. 4, we set up the Galerkin formulation of the equation and present error estimates for the approach. In Sect. 5, we give several numerical examples to validate theoretical results. Some concluding remarks and comments are included in Sect. 6. Throughout this paper, both c and C with or without the subscript denote generic constants which are independent of the step size h, and may vary at different occasions.

2 Preliminary

We restrict the domain into an unit interval (0, 1) for simplicity. The left- and right-sided fractional integrals [19] are defined as

$$\begin{aligned} _0D_x^{-\mu } v(x) = \frac{1}{\Gamma (\mu )}\int _0^x \frac{v(\xi ) }{(x-\xi )^{1-\mu }} d\xi , \quad x> 0, \quad \mu > 0, \end{aligned}$$

(2.1)

and

$$\begin{aligned} _xD_1^{-\mu } v(x) = \frac{1}{\Gamma (\mu )}\int _x^1 \frac{v(\xi ) }{(\xi -x)^{1-\mu }} d\xi , \quad x < 1, \quad \mu > 0, \end{aligned}$$

(2.2)

respectively. It is easily shown that

$$\begin{aligned} _0D_x^{-\mu }x^{\sigma } = \frac{\Gamma (\sigma +1 )}{\Gamma (\sigma +1+\mu )}x^{\sigma +\mu },\quad _xD_1^{-\mu }(1-x)^{\sigma } = \frac{\Gamma (\sigma +1 )}{\Gamma (\sigma +1+\mu )} (1-x)^{\sigma +\mu } \end{aligned}$$

(2.3)

hold for any $x \in (0,1)$, $\mu \in (0,1)$ and $\sigma > -1$. The formulas in (2.3) will be used in Sect. 5.

Let $L^p(0,1)$ with $p \ge 1$ be the space of p-th power Lebesgue integrable functions on the interval (0, 1). The integrals are related by the so-called fractional integration by parts as follows [19, 21].

Lemma 1

The left- and right-sided fractional integral operators are adjoint, i.e., for any $\mu \in (0, 1)$,

$$\begin{aligned} \left( \ _0D_x^{-\mu }v, w\right) = \left( v, \ _xD_1^{-\mu }w\right) , \quad \forall v, w \in L^2(0,1), \end{aligned}$$

(2.4)

where $(\cdot , \cdot )$ denotes the $L^2-$inner product. The fractional integral operators follow the semigroup property i.e., for any $v\in L^{p}(0,1)$ with $p \ge 1$,

$$\begin{aligned}&\ _0D_x^{-\mu } \ _0D_x^{-\nu }v(x) =\ _0D_x^{-(\mu + \nu )}v(x), \quad \forall x \in (0,1), \quad \forall \mu , \nu > 0, \end{aligned}$$

(2.5a)

$$\begin{aligned}&\ _xD_1^{-\mu }\ _xD_1^{-\nu }v(x) =\ _xD_1^{-(\mu + \nu )}v(x), \quad \forall x \in (0,1), \quad \forall \mu , \nu > 0. \end{aligned}$$

(2.5b)

The $\mu \, (n-1< \mu < n)$ order left- and right-sided Riemann-Liouville fractional derivatives of v(x) are defined as

$$\begin{aligned} _0D_x^{\mu }v(x) = D^n \ _0D_x^{-(n - \mu )} v(x), \quad _xD_1^{\mu }v(x) = (-1)^n D^n \ _xD_1^{-(n - \mu )} v(x), \end{aligned}$$

(2.6)

where $D^{n} := d^{n}/dx^n$. If $\mu = n$, then $_0D_x^{\mu }v(x) = D^{n}v(x)$ and $_xD_1^{\mu }v(x) = (-1)^n D^{n}v(x)$.

The $\mu \, (n-1< \mu < n)$ order left- and right-sided Caputo fractional derivatives of v(x) are defined as

$$\begin{aligned} _0^{C}D_x^{\mu }v(x) = \ _0D_x^{-(n - \mu )} D^n v(x), \quad _x^{C}D_1^{\mu }v(x) = (-1)^n\ _xD_1^{-(n - \mu )} D^n v(x). \end{aligned}$$

(2.7)

The Rieman–Liouville and Caputo fractional derivatives are strongly related by the following lemma.

Lemma 2

[19] For $\mu \in (n-1, n)$, we have

$$\begin{aligned} _0D_x^{\mu }v(x)= & {} \ _0^{C}D_x^{\mu }v(x) + \sum _{j=0}^{n-1}\frac{v^{(j)}(0)}{\Gamma (1+j-\mu )}x^{j-\mu }, \end{aligned}$$

(2.8)

$$\begin{aligned} _xD_1^{\mu }v(x)= & {} \ _x^{C}D_1^{\mu }v(x) + \sum _{j=0}^{n-1}\frac{(-1)^{j}v^{(j)}(1)}{\Gamma (1+j-\mu )}(1-x)^{j-\mu }. \end{aligned}$$

(2.9)

Remark 1

From this lemma, we can immediately see that if $v^{(j)}(0) = 0$ and $v^{(j)}(1) = 0$, $j = 0,1, \ldots , n-1$, then

$$\begin{aligned} _0D_x^{\mu }v(x)\,= & {} \, _0^{C}D_x^{\mu }v(x), \qquad _xD_1^{\mu }v(x)\ =\ _x^{C}D_1^{\mu }v(x). \end{aligned}$$

(2.10)

Under the homogeneous Dirichlet boundary conditions, we do not need to distinguish the fractional derivative of Caputo form from that of Riemann–Liouville form for $\mu \in (0, 1)$.

Let $C_0^{\infty }(0,1)$ be the space of infinitely differentiable functions on (0, 1) that are compactly supported within (0, 1). We use the standard notations in Sobolev spaces [1]. Let

$$\begin{aligned} W^{m}_p(0,1) := \left\{ v\in L^p(0,1): D^k v \in L^p(0,1), \quad 0 \le k \le m \right\} \end{aligned}$$

and

$$\begin{aligned} \Vert v\Vert _{W_p^m(0,1)}:=\left\{ \begin{array}{ll} \left( \sum \limits _{n=0}^m\Vert D^n v\Vert ^p_{L^p(0,1)} \right) ^{1/p}, &{} \quad 1\le p<\infty ,\\ &{} \\ \text{ ess } \max \limits _{0\le n\le m}\Vert D^nv\Vert _{L^{\infty }(0,1)},&{} \quad p = \infty . \end{array} \right. \end{aligned}$$

(2.11)

For $\mu \in (0, 1)$ and $p \in [1, \infty )$, let $W_p^{\mu }(0,1)$ be the fractional Sobelov space [1] with the semi-norm

$$\begin{aligned} |v|_{W_{p}^{\mu }(0, 1)} = \bigg (\int _{0}^1\int _{0}^1\frac{|v(x)-v(y)|^p}{|x-y|^{1+\mu p}}\, dxdy\bigg )^{1/p}, \end{aligned}$$

and let

$$\begin{aligned} \Vert v\Vert _{W^{m+\mu }_p(0,1)} = \bigg (\Vert v\Vert ^p_{W^{m}_p(0,1)} + |D^mv|^p_{W^{\mu }_p(0,1)} \bigg )^{1/p}. \end{aligned}$$

In particular, we let $H^{\mu }(0,1):=W_{2}^{\mu }(0,1)$, and $H_0^{\mu }(0,1)$ be the completion of $C_0^{\infty }(0,1)$ with respect to the norm $\Vert \cdot \Vert _{H^{\mu }(0,1)}$. Let $H^{-\mu }(0, 1)$ be the dual space of $H_0^{\mu }(0,1)$ with the dual pair, $\left\langle \cdot , \ \cdot \right\rangle : H^{-\mu }(0, 1) \times H_0^{\mu }(0,1) \rightarrow {\mathbb {R}}$.

Lemma 3

[19] Let $0< \mu < 1$. Then for any $v\in L^p(0,1)$

$$\begin{aligned} \ _0D_x^{\mu }\ _0D_x^{-\mu }v = v, \quad \ _xD_1^{\mu }\ _xD_1^{-\mu }v = v. \end{aligned}$$

(2.12)

For any $v\in W_1^1(0,1)$ with $v(0)=0$ and $v(1)=0,$ the following holds

$$\begin{aligned} \ _0D_x^{-\mu }\ _0D_x^{\mu }v=v,\quad \ _xD_1^{-\mu }\ _xD_1^{\mu }v = v. \end{aligned}$$

(2.13)

The above lemma indicates that fractional derivatives and fractional integrals are inverse to each other under homogeneous Dirichlet boundary conditions for a class of suitably smooth functions.

Next, we introduce fractional derivative spaces which are essential to characterize the solution spaces. We define the (semi) norms as

$$\begin{aligned} |v|_{J_{L}^{\mu }(0,1)}:= & {} \Vert \ _0D_x^{\mu } v \Vert _{L^2(0,1)}, \quad \Vert v\Vert _{J_{L}^{\mu }(0,1)} \, = \, \left( \Vert v \Vert ^2_{L^2(0,1)} + |v|^2_{J_{L}^{\mu }(0,1)} \right) ^{1/2}, \\ |v|_{J_{R}^{\mu }(0,1)}:= & {} \Vert \ _xD_1^{\mu } v \Vert _{L^2(0,1)}, \quad \Vert v\Vert _{J_{R}^{\mu }(0,1)}\, = \, \left( \Vert v \Vert ^2_{L^2(0,1)} + |v|^2_{J_{R}^{\mu }(0,1)} \right) ^{1/2}. \end{aligned}$$

We define $J_{L,0}^{\mu }(0,1)$ and $J_{R,0}^{\mu }(0,1)$ as the closures of $C_0^{\infty }(\Omega )$ under the norms $\Vert \cdot \Vert _{J_{L}^{\mu }(0,1)}$ and $\Vert \cdot \Vert _{J_{R}^{\mu }(0,1)}$, respectively.

We will use the following lemmas when we develop our Galerkin formulation of fractional differential equations and prove the error estimate.

Lemma 4

[8] The spaces $J_{L,0}^{\mu }(0,1),$$J_{R,0}^{\mu }(0,1)$ and $H_0^{\mu }(0,1)$ are equal and have the equivalent semi-norms and norms.

Lemma 5

[8] Let $\mu > 0$ with $\mu \in (n-1, n)$. Then for $u(x) \,$ a real valued function

$$\begin{aligned} \left( _0D_x^{\mu } u, \, _xD_1^{\mu } u \right) = - \cos (\mu \pi ) \Vert _0D_x^{\mu } u \Vert ^2 = - \cos (\mu \pi ) \Vert _xD_1^{\mu } u \Vert ^2 \end{aligned}$$

(2.14)

The next lemma is the fractional version of Poincaré–Friedrichs inequality.

Lemma 6

[8] For any $u \in H_0^{\mu }(0, 1)$, we have

$$\begin{aligned} \Vert u\Vert _{L^2(0,1)} \le C |u|_{H^{\mu }(0,1)}, \end{aligned}$$

(2.15)

where $C = 1/\Gamma (\mu + 1)$, and for $0< s < \mu ,$$s\ne n-1/2, n\in \mathbf{N}$

$$\begin{aligned} |u|_{H^s(0,1)}\le C |u|_{H^{\mu }(0,1)}. \end{aligned}$$

(2.16)

3 Variational Formulation and Regularity

For $\theta \in (0,1)$, we consider the Dirichlet boundary value problem of a steady state two-sided variable-coefficient fractional differential equation

$$\begin{aligned}&- D(k(x) D_{\theta }^{-\beta } Du(x)) = f(x), \quad x \in (0,1), \end{aligned}$$

(3.1a)

$$\begin{aligned}&u(0)=0, \quad u(1)=0, \end{aligned}$$

(3.1b)

where $D_{\theta }^{-\beta } = \theta \, _0D_x^{-\beta } + (1-\theta )\, _xD_1^{-\beta }$. We assume that $k \in W^1_{\infty }(0, 1)$, and k(x) is bounded:

$$\begin{aligned} 0 < k_{min} \le k(x) \le k_{max}, \quad x \in (0,1). \end{aligned}$$

(3.2)

By using the product rule and dividing by k(x), (3.1) can be transformed into the following equivalent form

$$\begin{aligned}&- D(D_{\theta }^{-\beta }Du) + KD_{\theta }^{-\beta }Du = g, \quad x\in (0,1), \end{aligned}$$

(3.3a)

$$\begin{aligned}&u(0) = u(1) = 0, \end{aligned}$$

(3.3b)

where $K = - k^{\prime }/k \in L^{\infty }(0,1), g=f/k$. We denote $\alpha = 2 - \beta \in (1,2)$, which represents the order of the equation. Here, our approach introduces an extra low-order term $KD_{\theta }^{-\beta }Du$.

We first consider the fractional differential equations without any lower order term, i.e., $K(x) \equiv 0$:

$$\begin{aligned}&- D(D_{\theta }^{-\beta }Du) = g(x),\quad x\in (0,1), \end{aligned}$$

(3.4a)

$$\begin{aligned}&u(0) = u(1) = 0. \end{aligned}$$

(3.4b)

We multiply (3.4a) by $v \in H_0^{\alpha /2}(0,1)$, take integral by parts and use (2.4). Then, we obtain the variational problem: find $u \in H_0^{\alpha /2}(0,1)$ such that

$$\begin{aligned} A_{\theta }(u, v) = (g, v), \quad \text{ for } \text{ any } \ v \in H_0^{\alpha /2}(0,1), \end{aligned}$$

(3.5)

where the bilinear form $A_{\theta }: H_0^{\alpha /2}(0,1)\times H_0^{\alpha /2}(0,1) \rightarrow \mathbb {R}$ is

$$\begin{aligned} A_{\theta }(u,v) = \theta \left( \ _0D_{x}^{\alpha /2}u,\ _xD_{1}^{\alpha /2}v\right) + (1 - \theta )\left( \ _xD_{1}^{\alpha /2}u,\ _0D_{x}^{\alpha /2}v\right) , \quad \text{ for } \text{ any } \ u, \, v \in H_0^{\alpha /2}(0,1). \end{aligned}$$

(3.6)

By using Fourier transform and Parseval’s theorem, Ervin and Roop showed that the bilinear form $A_{\theta }(\cdot , \cdot )$ is coercive and continuous on the space $H_0^{\alpha /2}(0,1)$ [8]. More precisely, there are two positive constants $A_{\min }$ and $A_{\max }$ such that

$$\begin{aligned} A_{\theta }(w, w)\ge & {} A_{\min }\Vert w \Vert ^2_{H^{\alpha /2}(0,1)}, \quad \text{ for } \text{ any } \ w \in H_0^{\alpha /2}(0,1), \end{aligned}$$

(3.7a)

$$\begin{aligned} A_{\theta }(v, w)\le & {} A_{\max }\Vert v \Vert _{H^{\alpha /2}(0,1)}\Vert w \Vert _{H^{\alpha /2}(0,1)}, \quad \text{ for } \text{ any } \ v, \, w \in H_0^{\alpha /2}(0,1), \end{aligned}$$

(3.7b)

where $A_{\min } = -\cos (\alpha \pi /2) =\cos (\beta \pi /2)$ is positive.

We now return to the general case (: $K \not \equiv 0$) and define the bilinear form

$$\begin{aligned} a(v, w) := A_{\theta }(v, w) + \left( K D_{\theta }^{-\beta }Dv, w\right) \quad \text{ for } \text{ any } \ v, w \in H_0^{\alpha /2}(0,1). \end{aligned}$$

(3.8)

Then the variational formulation for problem (3.3a) is given by: find $u \in H_0^{\alpha /2}(0,1)$ such that

$$\begin{aligned} a(u,v) = (g,v) \quad \text{ for } \text{ any } \ v \in H_0^{\alpha /2}(0,1). \end{aligned}$$

(3.9)

By Lemma 6, we have

$$\begin{aligned} \left| (K D_{\theta }^{-\beta }Dv, w)\right| \le C\Vert K \Vert _{L^{\infty }(0,1)} |v|_{H^{1-\beta }(0,1)} \Vert w \Vert _{L^2(0,1)} \le C \Vert K \Vert _{L^{\infty }(0,1)} | v |_{H^{\alpha /2}(0,1)} | w |_{H^{\alpha /2}(0,1)} \end{aligned}$$

(3.10)

for any v, $w \in H_0^{\alpha /2}(0, 1)$. Thus, the continuity of bilinear form $a(\cdot , \cdot )$ is obtained as follows:

Theorem 1

Let $K \in L^{\infty }(0,1)$. Then, for any v, $w \in H_0^{\alpha /2}(0, 1)$ there exists a constant $C_1$ such that

$$\begin{aligned} |a(v, w)| \le C_1 \Vert v\Vert _{H^{\alpha /2}(0,1)} \Vert w\Vert _{H^{\alpha /2}(0,1)}. \end{aligned}$$

(3.11)

The coercivity of the bilinear form is obtained in the following theorem for the $\alpha \in (1, 2)$.

Theorem 2

Let $0< \beta < 1$, and let $K \in L^{\infty } (0, 1)$ satisfy

$$\begin{aligned} \Vert K \Vert _{\infty } < \cos (\beta \pi /2) \Gamma (\beta /2 + 1) \Gamma (\alpha /2 + 1). \end{aligned}$$

(3.12)

Then, there exists a positive constant $C(\beta , K)$ such that for any $v \in H_0^{\alpha /2}(0, 1)$

$$\begin{aligned} a(v, v) \ge C(\beta , K) \Vert v \Vert _{H^{\alpha /2}(0, 1)}. \end{aligned}$$

(3.13)

Proof

By using Lemmas 5 and 6 in the previous section we have

$$\begin{aligned} \left( K D_{\theta }^{1-\beta } v, v\right)\ge & {} - \, \theta \Vert K \Vert _{\infty } \int _0^1 | v(x) _0D_x^{1-\beta } v(x)|\, dx \nonumber \\&-\, (1 - \theta ) \Vert K \Vert _{\infty } \int _0^1 | v(x) _xD_1^{1-\beta } v(x)|\, dx \nonumber \\\ge & {} - \, \theta \Vert K \Vert _{\infty } \Vert v \Vert \Vert _0D_x^{1-\beta } v\Vert \, - \, (1 - \theta ) \Vert K \Vert _{\infty } \Vert v \Vert \Vert _xD_1^{1-\beta } v \Vert \nonumber \\\ge & {} - \, \Vert K \Vert _{\infty } \Vert v \Vert \Vert _0D_x^{1-\beta } v(x)\Vert \nonumber \\\ge & {} -\, \frac{\Vert K \Vert _{\infty } }{\Gamma (\beta /2 + 1)\Gamma (\alpha /2 + 1)} \Vert v \Vert _{H^{\alpha /2}}^2, \quad \forall v \in H^{\alpha /2}(0, 1). \end{aligned}$$

(3.14)

Therefore the bilinear form is bounded below as follows.

$$\begin{aligned} a(v, v) \ge \left( \cos (\beta \pi /2) - \frac{\Vert K \Vert _{\infty } }{\Gamma (\beta /2 + 1)\Gamma (\alpha /2 + 1)} \right) \Vert v \Vert _{H^{\alpha /2}}^2. \end{aligned}$$

(3.15)

(3.12) implies that

$$\begin{aligned} C(\beta , K) = \cos (\beta \pi /2) - \frac{\Vert K \Vert _{\infty }}{\Gamma (\beta /2 + 1) \Gamma (\alpha /2 + 1)} > 0. \end{aligned}$$

$\square$

Remark 2

Since $\Vert Dk \Vert _{\infty } = \Vert K k \Vert _{\infty } \le \Vert K \Vert _{\infty } \Vert k \Vert _{\infty }$, (3.12) means

$$\begin{aligned} \Vert Dk\Vert _{\infty } \le \cos (\beta \pi /2)\Gamma (\beta /2 + 1)\Gamma (\alpha /2 + 1) \Vert k\Vert _{\infty }. \end{aligned}$$

(3.16)

Therefore the assumption in Theorem 2 means that the first order derivative of the diffusion coefficient is bounded by the $L^{\infty }$-norm of the coefficient multiplied by a constant. As $\beta$ goes to one, then $\cos (\beta \pi /2)$ converges to zero, and hence the coercivity is obtained for a constant coefficient k. In [25] the authors introduced an example of diffusion coefficient which does not satisfy (3.12), and generates a bilinear form that is not coercive.

Since the bilinear form is continuous and coercive on $H^{\alpha /2}(0, 1)$, by the Lax–Milgram theorem [4] we obtain the existence and uniqueness of the solution as follows.

Theorem 3

Let $k \in W_{\infty }^1 (0, 1)$ satisfy the inequality (3.12), and $g \in H^{-\alpha /2}(0, 1)$. Then, there exists a unique solution $u \in H^{\alpha /2}(0, 1)\,$ of the variational form (3.9) and

$$\begin{aligned} \Vert u \Vert _{H^{\alpha /2}(0, 1)} \le C \Vert g \Vert _{H^{-\alpha /2}(0, 1)}. \end{aligned}$$

(3.17)

We now turn to the adjoint problem. The strong formulation for the adjoint problem is stated as follows:

$$\begin{aligned}&- D(D_{1-\theta }^{-\beta }Du^{*}) - DD_{1-\theta }^{-\beta } (K u^{*} ) = g^{*}, \quad x\in (0,1), \end{aligned}$$

(3.18a)

$$\begin{aligned}&u^{*}(0) = u^{*}(1) = 0. \end{aligned}$$

(3.18b)

The variational formulation for the adjoint problem (3.18) is given by: find $u^{*} \in H_0^{\alpha /2}(0,1)$ such that

$$\begin{aligned} a^*(v, u^{*}) = (g^*,v), \quad \text{ for } \text{ any } \ v \in H_0^{\alpha /2}(0,1), \end{aligned}$$

(3.19)

where

$$\begin{aligned} a^*(v, w) = A_{1-\theta }(v, w) - \left( v, D_{1-\theta }^{1-\beta }(K w)\right) \quad \text{ for } \text{ any } \ v, w \in H_0^{\alpha /2}(0,1). \end{aligned}$$

To prove the coercivity of $a^*(\cdot , \cdot )$, we use the following lemma which is proved in [9]. We prove it by computing the coefficient.

Lemma 7

[9] For $0< \mu< s < 1$ with $s > 1/2$, p and q such that the given norms are finite, we have

$$\begin{aligned} \Vert p q \Vert _{H^{\mu }} \le C(\mu , s) \Vert p \Vert _{H^{1}(0, 1)} \, \Vert q \Vert _{H^{s}(0, 1)}, \end{aligned}$$

where

$$\begin{aligned} C(\mu , s) = \frac{2}{\min \{ \Gamma (s - \mu + 1),\, \Gamma (2 -\mu )\} }. \end{aligned}$$

Proof

By the definition of fractional semi-norm, we have

$$\begin{aligned} |p q|_{H^{\mu }(0, 1)}^2= & {} \int _0^1 \int _0^1 \frac{\left( p(x)q(x) - p(y)q(y)\right) ^2}{|x - y|^{1+2\mu }} \, dx dy \nonumber \\\le & {} \, 2 \int _0^1 \int _0^1 \frac{p(x)^2 \left( q(x) -q(y)\right) ^2}{|x - y|^{1+2\mu }} \, dx dy +\ 2 \int _0^1 \int _0^1 \frac{\left( p(x) - p(y)\right) ^2 q(y)^2}{|x - y|^{1+2\mu }} \, dx dy \nonumber \\\le & {} \, 2\, \Vert p \Vert _{\infty }^2 \, |q|_{H^{\mu }(0, 1)}^2+ 2\, \Vert q \Vert _{\infty }^2 \, |p|_{H^{\mu }(0, 1)}^2 \nonumber \\\le & {} \frac{2}{\Gamma (s - \mu + 1)^2} \, \Vert p \Vert _{H^{1}(0,1)}^2 \, |q|_{H^{s}(0, 1)}^2 + \frac{2}{\Gamma (2 - \mu )^2} \, \Vert p \Vert _{H^{1}(0, 1)}^2 \, \Vert q \Vert _{H^{s}(0, 1)}^2, \end{aligned}$$

(3.20)

where the Sobolev imbedding theorem [7] and Lemma 6 are used in the last inequality. By taking the constant $C(\mu , s)$, the result is obtained. $\square$

If $0< \beta < 1$, then for $\mu = 1 - \beta$ and $s= 1 - \beta /2$ this lemma implies

$$\begin{aligned} \Vert DD_{1-\theta }^{-\beta } (K v)\Vert _{L^2(0,1)} \le \frac{2\Vert K\Vert _{H^{1}(0, 1)} }{\min \{\Gamma (\beta + 1), \Gamma (\beta /2 + 1)\}} \Vert v \Vert _{H^{\alpha /2}(0, 1)}. \end{aligned}$$

(3.21)

Therefore, we obtain the coercivity of $a^*(\cdot , \, \cdot )$.

Theorem 4

Let $\beta \in (0, 1)$, and $K \in H^{1}(0, 1)$ satisfy

$$\begin{aligned} \Vert K \Vert _{H^{1}(0, 1)} < \frac{1}{2} \cos (\beta \pi /2) \Gamma (\alpha /2 + 1) \min \{\Gamma (\beta + 1), \Gamma (\beta /2 + 1)\} \end{aligned}$$

(3.22)

Then there exists a constant $C^*(\beta , K)$ such that for any $v \in H^{\alpha /2}_0 (0, 1)$

$$\begin{aligned} a^*(v, v) \ge C^*(\beta , K) \Vert v \Vert _{H^{\alpha /2}(0, 1)}^2. \end{aligned}$$

(3.23)

Proof

By using (3.21) we have

$$\begin{aligned} - \left( v, \, D_{1-\theta }^{1-\beta } (Kv) \right)\ge & {} - \, \Vert v\Vert \Vert D_{1-\theta }^{1-\beta } (Kv) \Vert \\\ge & {} - \, \frac{2\Vert K \Vert _{H^{1}(0, 1)}}{\Gamma (\alpha /2 + 1) \min \{\Gamma (\beta + 1), \Gamma (\beta /2 + 1)\}} \Vert v \Vert _{H^{\alpha /2}(0, 1)}^2. \end{aligned}$$

Then,

$$\begin{aligned} a^*(v, v) = A_{1-\theta } (v, v) - \left( v, D_{1-\theta }^{1-\beta } (Kv)\right) \ge C^*(\beta , K) \Vert v \Vert _{H^{\alpha /2}(0, 1)}^2, \end{aligned}$$

where

$$\begin{aligned} C^*(\beta , K) = \left( \cos (\beta \pi /2) - \frac{2\Vert K \Vert _{H^{1}(0, 1)} }{\Gamma (\alpha /2 + 1)\min \{\Gamma (\beta + 1), \Gamma (\beta /2 + 1)\}} \right) . \end{aligned}$$

Here, $C^*(\beta , K)$ is positive due to (3.22). $\square$

Note that (3.22) implies (3.12). Therefore, to the end of this paper we assume that K satisfies the inequality (3.22). By the Lax–Milgram theorem we also obtain the existence and uniqueness of the solution of the adjoint problem.

Theorem 5

Let $\beta \in (0, 1)$, let $g^* \in H^{-\alpha /2}(0,1)$ and let $K \in H^1(0,1)$ satisfy (3.22). Then, there exists a unique solution $w\in H_0^{\alpha /2}(0, 1)$ of the adjoint problem (3.19) and

$$\begin{aligned} \Vert w \Vert _{H^{\alpha /2}(0,1)} \le C \Vert g^* \Vert _{H^{-\alpha /2}(0,1)}. \end{aligned}$$

(3.24)

Since

$$\begin{aligned} |Dk|_{H^1} = |K k|_{H^1} \le \Vert k DK \Vert + \Vert K Dk \Vert \le \Vert K \Vert _{H^1} \left( \Vert k \Vert + \Vert Dk \Vert \right) \le \sqrt{2} \Vert K \Vert _{H^1} \Vert k \Vert _{H^1}, \end{aligned}$$

(3.22) means that

$$\begin{aligned} |Dk|_{H^1} \le \frac{1}{\sqrt{2}}\cos (\beta \pi /2)\Gamma (\alpha /2 + 1) \min \{\Gamma (\beta + 1), \Gamma (\beta /2 + 1)\} \Vert k \Vert _{H^1}. \end{aligned}$$

Therefore, the wellposedness of the adjoint problem is obtained for the diffusion coefficient whose $H^1$-seminorm of its first derivative is bounded by the $H^1$-norm of the coefficient.

Remark 3

If k(x) is differentiable, (3.1) and (3.3) are equivalent. But when we use Galerkin method, their discretizations can be different. For a certain diffusion coefficient k(x) the standard Galerkin method for (3.1) can generate a bilinear form which is not coercive [25, 31]. In the next section we present Galerkin method for the variational form (3.9) with the coercive bilinear form and prove its error estimates by using the adjoint problem.

4 Finite Element Approximation

We introduce a finite element approximation based on a partition of the interval (0, 1) with h being the largest length of subintervals. Consider the nodes $x_i$, $i = 0, 1, \dots , N$. We then define $V_h$ to be the set of continuous functions which are linear polynomials on each subinterval, $[x_{i-1}, x_i],$$i = 1, 2, \dots , N$. Then $V_h \subset H_0^{\alpha /2}(0,1)$ by the Sobolev embedding theorem [1].

Let $u_h$ be the solution of the finite-dimensional variational problem: find $u_h\in V_h$ such that

$$\begin{aligned} a(u_h, v) = (g, v), \quad \text{ for } \text{ any } \ v \in V_h. \end{aligned}$$

(4.1)

By substracting (4.1) from (3.9) we obtain

$$\begin{aligned} a(u - u_h, v) = 0, \quad \text{ for } \text{ any } \ v \in V_h. \end{aligned}$$

(4.2)

Then, for any $v \in V_h$ we have

$$\begin{aligned} C(\beta , K) \Vert u - u_h \Vert ^2_{H^{\alpha /2}}\le & {} a(u - u_h, u - u_h) = a(u - u_h, u - v)\\\le & {} C_1 \Vert u - u_h \Vert _{H^{\alpha /2}} \Vert u - v \Vert _{H^{\alpha /2}}. \end{aligned}$$

Theorem 6

Let u be the solutions of (3.9). Then there exists a unique solution to (4.1) such that

$$\begin{aligned} \Vert u - u_h \Vert _{H^{\alpha /2}} \le C \inf _{v \in V_h} \Vert u - v \Vert _{H^{\alpha /2}} \le C \Vert u - {\mathcal {I}}_h u \Vert _{H^{\alpha /2}}, \end{aligned}$$

(4.3)

where ${\mathcal {I}}_h u$ is the interpolant of u in $V_h$.

The interpolant ${\mathcal {I}}_h u$ satisfies the next lemma.

Lemma 8

[4] Let the mesh $\mathcal {T}_h$ be quasi-uniform, and $s \le \mu$. If $u \in H^{\mu }(0, 1) \cap H_0^{s}(0, 1)$, then

$$\begin{aligned} \Vert u - {\mathcal {I}}_h u\Vert _{H^{s}(0,1)} \le C_0 h^{\mu -s} \Vert u \Vert _{H^{\mu }(0,1)}. \end{aligned}$$

(4.4)

Therefore, we obtain the following error estimate.

Theorem 7

Let $0< \beta < 1$, and let $K \in H^1(0, 1)$ satisfy (3.22). Let $u \in H^{\alpha /2}_0 (0, 1) \cap H^r(0, 1), \ r \ge \alpha /2$, and $u_h \in V_h$ be solutions of (3.9) and (4.1), respectively. Then there exists a constant C such that

$$\begin{aligned} \Vert u - u_h\Vert _{H^{\alpha /2}(0, 1)} \le C h^{r-\alpha /2} \Vert u \Vert _{H^r(0, 1)}. \end{aligned}$$

(4.5)

To obtain an error estimate in the $L^2$ norm, we apply the duality technique by taking the assumption:

Assumption 1

For the solution w of the adjoint problem with $g^* \in L^2(0, 1)$ we have

$$\begin{aligned} \Vert w \Vert _{H^r(0, 1)} \le C \Vert g^* \Vert _{L^2(0, 1)} \quad \text{ for } \ r > \alpha /2. \end{aligned}$$

(4.6)

Remark 4

Unlike the integer order differential equations, we do not have full regularity for the fractional differential equations. Recently, Hao et al. studied the regularity for the two-sided fractional order differential equations with lower order term in the weighted Sobolev spaces and gave a rigorous analysis. However, the regularity in standard Sobolev spaces well suited for the finite element method is still missing in the literature. To the authors’ best knowledge, the first attempt to discuss the regularity of the equation in two-sided case is from the work by Ervin et al in [10], where they conjectured the regularity of solution in standard Sobolev space by seeking a closed form expression for the kernel of fractional diffusion operator and assuming the data f sufficiently smooth. A solution is numerically shown to be in the standard Sobolev space $H^{\gamma }$ with regularity index $\gamma = \min \{ \sigma , \sigma ^* \} + 1/2 - \epsilon$, where $\epsilon > 0$ is an arbitrary small number, $\sigma$ and $\sigma ^*$ are constants depending on the order $\alpha$ and parameter $\theta$, see [10]. In particular, the regularity index is $\alpha /2 + 1/2 - \epsilon$ for the symmetrical case $\theta = 1/2$ and $\alpha - 1/2 + \epsilon$ for the one-sided asymmetrical case $\theta = 1$ or 0. We will illustrate the regularity in our numerical examples; see Example 2 in Sect. 5.

Theorem 8

Let $0< \beta < 1$, let $g^* \in L^2(0, 1)$ and let $K \in H^1(0, 1)$ satisfy (3.22). Let $u \in H^{\alpha /2}_0 (0, 1) \cap H^r(0, 1), \ r > \alpha /2$, and $u_h \in V_h$ be solutions of (3.9) and (4.1), respectively. Then there exists a constant C such that

$$\begin{aligned} \Vert u - u_h\Vert _{L^{2}(0, 1)} \le Ch^{2r -\alpha } \Vert u\Vert _{H^r(0, 1)}. \end{aligned}$$

(4.7)

Proof

For $g^* = u - u_h,$ let w be the solution of the adjoint problem.

$$\begin{aligned} a^*(v, w) = (u - u_h, v), \quad \text{ for } \text{ any } \ v \in H_0^{\alpha /2}(0, 1). \end{aligned}$$

(4.8)

By letting $v = u - u_h$ and using (4.2) and (3.11) we have

$$\begin{aligned} (u - u_h, u - u_h)= & {} a(u - u_h, w) = a(u - u_h, w - z_h) \\\le & {} \ C_1 \Vert u - u_h\Vert _{H^{\alpha /2}(0,1)}\Vert w - z_h\Vert _{H^{\alpha /2}(0,1)}, \quad \forall z_h\in V_h. \end{aligned}$$

By using (4.4) and (4.5), we have

$$\begin{aligned} \Vert u - u_h\Vert ^2\le & {} C_1 \Vert u - u_h\Vert _{H^{\alpha /2}(0,1)} \inf _{z_h \in V_h} \Vert w - z_h\Vert _{H^{\alpha /2}(0,1)}\\\le & {} C_1 \Vert u - u_h\Vert _{H^{\alpha /2}(0,1)} \Vert w - {\mathcal {I}}_h w\Vert _{H^{\alpha /2}(0,1)} \\\le & {} C h^{2r - \alpha } \Vert u \Vert _{H^{r}(0, 1)} \Vert w \Vert _{H^{r}(0,1)} \le C h^{2r - \alpha } \Vert u \Vert _{H^{r}(0, 1)} \Vert u - u_h\Vert , \end{aligned}$$

where the assumption (4.6) is used. Dividing by $\Vert u - u_h\Vert$, we obtain the result. $\square$

Note that if $r < \alpha$, then the convergence rate $2r - \alpha < r$. Therefore in that case the convergence rate is not optimal.

5 Numerical Experiments

We present numerical experiments to verify our error estimates. The computations were performed on uniform meshes of mesh sizes $h=1/2^n, n = 5, 6, \dots , 10$. We first briefly discuss an implementation of the Galerkin method by computing the stiffness matrix.

Let $u_h(x) = \sum _{i=1}^{N-1} u_i \phi _i(x)$,

$$\begin{aligned} S_D = (d_{i,j}), \quad d_{ij} = \left( \ _0D_x^{-\beta }D\phi _j,\ D\phi _i \right) , \quad \text{ and } \quad S_C = (e_{ij}), \quad e_{ij} = \left( \ _0D_x^{-\beta }D\phi _j,\ \phi _i\right) \end{aligned}$$

with $\ i,j = 1, 2, \dots , N-1$, where $\{\phi _i\}_{i=1}^{N-1}$ is a basis for $V_h$ consisting of the piecewise linear functions. Let

$$\begin{aligned} w_{i}^{(\gamma )} = [-(i - 3)^{3 -\gamma } +4(i-2)^{3 -\gamma } -6(i-1)^{3 -\gamma } + 4i^{3-\gamma } - (i+1)^{3-\gamma }]/\Gamma (4-\gamma ), \end{aligned}$$

where $j^{3 -\gamma } = 0$ for $j < 0$. Then $S_D$ and $S_C$ are lower Hessenberg matrices with Toeplitz structure. More precisely,

$$\begin{aligned} S_D={h^{1-\alpha }} \left( \begin{array}{llllll} w_1^{(\alpha )} &{}\quad w_0^{(\alpha )}&{} \quad &{} \quad &{}\quad &{} \\ w_2^{(\alpha )} &{}\quad w_1^{(\alpha )}&{} \quad w_0^{(\alpha )} &{}\quad &{} \quad &{} \\ w_3^{(\alpha )} &{}\quad w_2^{(\alpha )} &{} \quad w_1^{(\alpha )} &{}\quad \ddots &{}\quad &{} \\ \vdots &{}\quad \vdots &{}\quad \vdots &{} \quad \ddots &{}\quad \ddots &{}\quad \\ w_{N-2}^{(\alpha )} &{} \quad w_{N-3}^{(\alpha )} &{}\quad w_{N-4}^{(\alpha )} &{}\quad \dots &{}\quad w_{1}^{(\alpha )} &{} \quad w_{0}^{(\alpha )} \\ w_{N-1}^{(\alpha )} &{} \quad w_{N-2}^{(\alpha )} &{}\quad w_{N-3}^{(\alpha )}&{}\quad \dots &{}\quad w_{2}^{(\alpha )} &{}\quad w_{1}^{(\alpha )} \\ \end{array} \right) , \end{aligned}$$

(5.1)

$$\begin{aligned} S_C = {h^{2-\alpha }} \left( \begin{array}{llllll} w_1^{(\alpha -1)} &{}\quad w_0^{(\alpha -1)}&{}\quad &{}\quad &{}\quad &{} \\ w_2^{(\alpha -1)} &{}\quad w_1^{(\alpha -1)}&{}\quad w_0^{(\alpha -1)} &{}\quad &{}\quad &{} \\ w_3^{(\alpha -1)} &{}\quad w_2^{(\alpha -1)} &{}\quad w_1^{(\alpha -1)} &{}\quad \ddots &{}\quad &{} \\ \vdots &{} \quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \ddots &{} \\ w_{N-2}^{(\alpha -1)} &{} \quad w_{N-3}^{(\alpha -1)} &{}\quad w_{N-4}^{(\alpha -1)} &{}\quad \dots &{}\quad w_{1}^{(\alpha -1)} &{}\quad w_{0}^{(\alpha -1)} \\ w_{N-1}^{(\alpha -1)} &{}\quad w_{N-2}^{(\alpha -1)} &{}\quad w_{N-3}^{(\alpha -1)}&{}\quad \dots &{} \quad w_{2}^{(\alpha -1)} &{}\quad w_{1}^{(\alpha -1)}\\ \end{array} \right) . \end{aligned}$$

(5.2)

5.1 Example 1

To test the approach presented in the previous section, we first consider the problem (3.1) with the exact solution $u(x) = x^3(1-x)^3$, and the diffusion coefficient, $k(x) = (x + 4)/2$. The coefficient matrix of the derived linear system, $AU = b$, is

$$\begin{aligned} A = \theta S_D + (1 -\theta ) S_D^{T} + {\bar{K}} [\theta S_C - (1-\theta ) S_C^{T}], \end{aligned}$$

where $U = (u_i),$${\bar{K}} = diag(K(x_1), K(x_2), \dots , K(x_{N-1}))$, $b = (b_i)$, $b_i = (g, \phi _i)$, and T means the transpose. Let

$$\begin{aligned} F_h(x) = - k(x)D_{\theta }^{-\beta }Du_h(x) \end{aligned}$$

be an approximate flux. For numerical implementation, we approximate the flux as follows:

$$\begin{aligned} \mathbf{F}_h (\mathbf{x}) = - k(\mathbf{x}) \left( \theta S_C - (1 - \theta ) S_C^T \right) \mathbf{u}_h(\mathbf{x}), \end{aligned}$$

where $\mathbf{x} = (x_1, x_2, \dots , x_{N-1})$.

Table 1 $\Vert u-u_h\Vert _{\infty }$ for the problem (3.9) with the exact solution $u(x) = x^3(1-x)^3, k(x) = x/2 + 2$ and $h = 1/2^n$

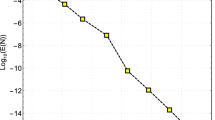
Table 1 shows that the proposed numerical scheme (4.1) has $O(h^2)$ convergence in the $L^{\infty }$ norm because $u \in H^2(0,1)$. From Table 2, we see that the convergence rate of the flux is O(h) in the same norm.

Table 2 $\Vert F-F_h\Vert _{\infty }$ for the problem (3.9) with the exact solution $u(x) = x^3(1-x)^3,$$k(x) = x/2 + 2$ and $h = 1/2^n$

5.2 Example 2

Let the diffusion coefficient be $k(x) = (x + 4)/2$, and the exact solution [10]

$$\begin{aligned} u(x) = x^{\sigma }(1-x)^{(\alpha -\sigma )}. \end{aligned}$$

The corresponding right hand side is

$$\begin{aligned} f(x) = -\frac{\sin (\alpha \pi )\Gamma (\alpha )}{\sin (\sigma \pi ) + \sin [(\alpha - \sigma )\pi ]}(\alpha x+3\alpha /2+ \sigma /2), \end{aligned}$$

(5.3)

and the flux F(x) is

$$\begin{aligned} F(x) = -k(x)DD_{\theta }^{-\beta } u(x) = -\frac{\sin (\alpha \pi ) \Gamma (\alpha )}{\sin (\sigma \pi )+\sin [(\alpha -\sigma )\pi ]} (\alpha x-\alpha +\sigma )(x/2+2). \end{aligned}$$

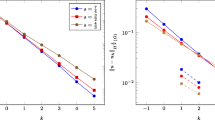
Tables 3 and 4 show that the Galerkin method (4.1) has $O(h^{\min \{\sigma ,\alpha -\sigma \} + 1/2})$ convergence in $L^2$ norm and $O(h^{\min \{\sigma ,\alpha -\sigma \} + 1/2 - \alpha /2})$ convergence in $H^{\alpha /2}$ norm, respectively. Table 5 shows the small convergence rate for the flux in $L^2$ norm because the numerical flux has oscillation around the left boundary point for the one-sided case $\theta = 1$ (see Fig. 1).

Table 3 $\Vert u-u_h\Vert _{L^2}$ for the problem (3.9) with the right hand side (5.3), $k(x) = x/2 + 2$ and $h=1/2^n$

Table 4 $\Vert u-u_h\Vert _{H_{\alpha /2}}$ for the problem (3.9) with the right hand side (5.3), $k(x)=x/2+2$ and $h=1/2^n$

Table 5 $\Vert F-F_h\Vert _{L^2}$ for the problem (3.9) with the right hand side (5.3), $k(x)=x/2+2$ and $h=1/2^n$

Fig. 1

The numerical flux for $\alpha =1.1$ and $h=2^{-8}$. Case 1: $k(x)=1,$$f(x)=1.$

5.3 Two-Dimensional Case

Consider the following two-dimensional problem

$$\begin{aligned}&-\partial _x\bigg (k(x,y)\big [\partial _{\theta }^{-\beta }\partial _xu(x,y)\big ]\bigg ) -\partial _y\bigg (k(x,y)\big [\partial _{\chi }^{-\gamma }\partial _yu(x,y)\big ]\bigg )=f(x,y), \quad (x,y) \in \Omega , \nonumber \\ \end{aligned}$$

(5.4)

$$\begin{aligned}&u(x,y)=0,\quad (x,y) \in \partial {\Omega }, \end{aligned}$$

(5.5)

where $\Omega = (0,1)\times (0,1), \gamma \in (0,1)$ and $\chi \in [0,1], \partial _{\chi }^{-\gamma }=\chi \ _0\partial _y^{-\gamma }+(1-\chi )\ _y\partial _1^{-\gamma }$ is defined similarly as x direction. By the product rule, the problem (5.4)–(5.5) can be reformulated as

$$\begin{aligned}&-\partial _x\big [\partial _{\theta }^{-\beta }\partial _xu(x,y)\big ] -\partial _y[\partial _{\chi }^{-\gamma }\partial _yu(x,y)\big ] -K_1(x,y)\big [\partial _{\theta }^{-\beta }\partial _xu(x,y)\big ]\nonumber \\&\quad -K_2(x,y)\big [\partial _{\chi }^{-\gamma }\partial _yu(x,y)\big ] =\tilde{f}(x,y),\quad (x,y) \in \Omega , \end{aligned}$$

(5.6)

$$\begin{aligned}&u(x,y)=0,\quad (x,y) \in \partial {\Omega }, \end{aligned}$$

(5.7)

where $K_1(x,y)=\frac{\partial _xk(x,y)}{k(x,y)},$$K_2(x,y) = \frac{\partial _yk(x,y)}{k(x,y)},$ and $\tilde{f}(x,y)=\frac{f(x,y)}{k(x,y)}.$ In this example, we take $\theta =\chi =1, \beta =\gamma , k(x,y)=\exp (x+y)$ and the exact solution is $x^{3-\beta }(1-x)y^{3-\beta }(1-y).$ Define the bilinear form in two dimensional case as follows:

$$\begin{aligned} \hat{a}(u,v):=\left( \partial _{\theta }^{-\beta }\partial _xu, \, \partial _xu\right) + \left( K_1 \partial _{\theta }^{-\beta }\partial _xu, \, v\right) + \left( \partial _{\theta }^{-\beta }\partial _yu,\, \partial _yu\right) + \left( K_2 \partial _{\theta }^{-\beta }\partial _yu, \, v\right) . \end{aligned}$$

We obtain the Galerkin formulation: find $u_h\in X_h$ such that

$$\begin{aligned} \hat{a}(u_h, v)=(\tilde{f}, v),\quad \forall v\in X_h. \end{aligned}$$

(5.8)

We construct two-dimensional basis functions by using the tensor product of one-dimensional basis functions. More precisely,

$$\begin{aligned} X_h=V_h\otimes V_h=\textit{span}\{\phi _i(x)\phi _j(y): i,j=1,2,\dots ,N-1 \}. \end{aligned}$$

Table 6 shows that the scheme (5.8) can achieve $O(h^2)$ convergence. The analysis provided in this paper can be extended to two-dimensional case.

Table 6 $\Vert u-u_h\Vert _{\infty }$ for the problem (5.8) with $\theta =\chi =1,$$\beta =\gamma ,$$k(x,y)=\exp (x+y)$ and the exact solution is $u(x,y) = x^{3-\beta }(1-x)y^{3-\beta }(1-y).$ ($h=1/2^n$)

5.4 Numerical Flux for $f(x) = 1$

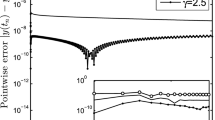
Flux is one of the important variables in many problems including transport in porous media. We compute the approximate flux of the problem (3.1) with $f(x) = 1$, and two different diffusion coefficients: $\ k_1(x) = 1$. Since the solution is symmetrical with respect to $\theta = 0.5$, we consider the case for $\theta \in [0.5,1]$. As shown in Fig. 1, for $\alpha = 1.1$ the approximate flux has oscillations around the left boundary point. However, for $\alpha = 1.9$, no oscillations are observed in Fig. 2. For $\alpha = 1.1$, the numerical flux is negative in most points, however, for $\alpha = 1.9$, $F_h$ is almost symmetrical around $x = 0.5$. In addition, it seems that the numerical flux variation is smaller for $\theta =0.5$, comparing with the results obtained for $\theta =1$, and 0.7.

Fig. 2

The numerical flux for $\alpha =1.9$ and $h=2^{-8}$. Case 1: $k(x)=1,$$f(x)=1.$

6 Concluding Remarks

In this paper, we have investigated the Galerkin approach to discretize two-sided fractional differential equations with variable-coefficients. We reformulated the problem into the equivalent one by introducing an extra low-order fractional term, and proved the wellpossedness of the Dirichlet problem of the equations by deriving a required condition for the diffusion coefficient. Based on the new reformulation, we have introduced the Galerkin approach and proved its error estimates under a reasonable regularity assumption for the adjoint problem

It is of immense interest to study two-sided fractional equations, especially with variable coefficients. There are some remarks we need to point out here. First, an obvious advantage of Galerkin approach developed in this paper over Petrov–Galerkin formulation proposed in [25, 28, 29] is that it can be straightforwardly extended to a class of two-dimensional variable coefficient problems. Second, we claim that high order methods are not expected to obtain high order accuracy due to the limited regularity of the problem, which has been demonstrated by numerical examples. Note that the singularity only occurs at end points. Although adaptive methods are natural to enhance the convergence rate, it will also make the computational cost grow up quickly. Because the nice Toeplitz-like structure of resulting matrix will be destroyed if the nonuniform mesh is taken. Other alternatives such as enriched finite element methods, singularity reconstruction techniques will be better choices. We will address this issue in our future work.