Parametric finite elements with bijective mappings

Abstract

The discretization of the computational domain plays a central role in the finite element method. In the standard discretization the domain is triangulated with a mesh and its boundary is approximated by a polygon. The boundary approximation induces a geometry-related error which influences the accuracy of the solution. To control this geometry-related error, iso-parametric finite elements and iso-geometric analysis allow for high order approximation of smooth boundary features. We present an alternative approach which combines parametric finite elements with smooth bijective mappings leaving the choice of approximation spaces free. Our approach allows to represent arbitrarily complex geometries on coarse meshes with curved edges, regardless of the domain boundary complexity. The main idea is to use a bijective mapping for automatically warping the volume of a simple parameterization domain to the complex computational domain, thus creating a curved mesh of the latter. Numerical examples provide evidence that our method has lower approximation error for domains with complex shapes than the standard finite element method, because we are able to solve the problem directly on the exact domain without having to approximate it.

1 Introduction

Simulating physical phenomena often requires to deal with complex geometric objects, generated, for instance, by computer aided design (CAD) software or captured from real life objects or organisms (e.g., 3D scans, MRI, etc.). When focusing on the finite element method (FEM), such highly complex geometries need to be represented in a sufficiently accurate way. This is the case because the accuracy of the geometric representation influences the approximation error of the discrete solution of a partial differential equation. In this paper we present a novel discretization combining FEM with bijective mappings. This combination allows solving the model problem on the exact geometry with the freedom of choosing the discretization independently.

The influence of the accuracy of the geometric representation on the approximation error has been studied for curved boundaries for iso-parametric discretizations [11, 38, 39] and for contact problems [24]. More recent research focuses on numerical studies for elliptic and Maxwell problems [43], and for different approximation spaces [4, 5]. In contrast, our approach always reproduces the exact geometry, hence has zero geometric error. Moreover, it can be applied to the numerical simulation of different physical phenomena.

During a simulation the approximation space might not be descriptive enough to represent the solution. This problem is usually solved by means of adaptive refinement strategies, such as h-refinement [6, 8] and p-refinement [33]. When using such strategies, a higher resolution at the boundary should be accompanied by a better approximation of the original surface [13]. However, due to the traditional one-way connection between geometric information and simulation environment, adaptive refinement is rarely accompanied by decrease of the geometric error, that is a better approximation of the underlying geometry. In other words, the mesh is generated within a modelling software and used in simulation environment without considering the original surface, preventing a better surface approximation.

Iso-geometric analysis (IGA) [20] allows to overcome this limitation by working directly with the geometric description provided by CAD software, such as non-uniform rational B-splines (NURBS). However, IGA is subject to several challenges such as the treatment of non-watertight surfaces, local refinement and topological flexibility [29]. Moreover, IGA approximations, similarly to many mesh-free methods, lead to complications in the imposition of essential boundary conditions, which can be either imposed in a weak sense [3], or least-square satisfied in the strong sense [20].

Additionally, when dealing with three-dimensional shapes, CAD models usually describe only the boundary. Creating a NURBS volume parameterization is a complex task, for which many different approaches exits. For instance, some of them require particular shapes [1], need special geometric information [31], or do not reproduce the surface exactly [28].

Fig. 1

Transient non-linear elasticity simulation of a gear for a warped quadrilateral mesh with compressible-neo-Hookean material. The elastic gear is subject to vertical body forces (gravity) and has a fixed tooth on the top boundary. The colour represents the von Mises stress for the solution at the different time-steps t (color figure online)

An alternative to IGA is the NURBS-enhanced finite element method (NEFEM) [40] that allows exploiting CAD geometries for the exact description of the boundary. However, this method requires creating a parameterization mesh, and a special handling of the boundary, which according to [40] is still an open problem.

Another challenge regards geometric multigrid methods, which are based on a hierarchy of nested spaces for achieving optimal convergence [10, 18]. Such requirement can be satisfied by generating the hierarchy by refining a coarse mesh representation of the shape. However, such refinement usually does not improve improve the shape accuracy. An alternative approach [12] is to employ a parameterization such as transfinite interpolation [34, 35] and to build nested hierarchies in the parameterization domain. However, transfinite interpolation requires a surface parametrization, a specific parametrization domain, and it is not guaranteed to be bijective for general polytopes.

Here, we present a novel discretization which enables exploiting exact geometric descriptions (e.g., splines or surface meshes) together with strategies employed in standard finite element simulations (Sect. 2). This discretization has the advantage of decoupling the geometry and the approximation space, thus allowing for sub/iso/super-parametric elements. Although the presentation is based on the Poisson problem, our discretization can be naturally employed to solve more complex problems, such as transient non-linear elasticity shown in Fig. 1.

The problem of dealing with exact geometries has been deeply studied for CAD geometries by the IGA community. Unfortunately, a similar study for surface meshes is missing. For this reason, we focus on the exact representation provided by surface meshes, and present the construction of a bijective volume parameterization from arbitrarily shaped domains to arbitrarily shaped meshes (Sect. 3). Finally, we empirically illustrate that our new discretization can be used to remove geometric error while being comparable to the classical finite element method in terms of conditioning of the stiffness matrix and convergence of the solution (Sect. 4).

2 Parametric finite elements with bijective mappings

In this section we introduce the notation and derive the weak formulation for the Poisson problem including the change of metric needed by our method. Let us consider the standard Poisson problem

$$\begin{aligned} -\varDelta u = f, \qquad u|_{\partial \varOmega }=g, \end{aligned}$$

(1)

where $\varOmega \in {\mathbb {R}}^d$ is the computational domain, $\partial \varOmega$ is the boundary of $\varOmega$, and g describes the boundary values. In contrast to the classical construction where $\varOmega$ is defined by means of a mesh, here

$$\begin{aligned} \varOmega =b(\varOmega _0)\subseteq \varTheta \end{aligned}$$

is given as the image of a sufficiently smooth bijective mapping

$$\begin{aligned} b:\varTheta _0\rightarrow \varTheta , \end{aligned}$$

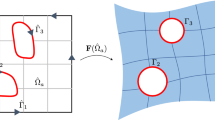
where $\varOmega _0\subseteq \varTheta _0$ is the source domain, $\varTheta _0\subset {\mathbb {R}}^d$ is the parameterization domain, and $\varTheta \subset {\mathbb {R}}^d$ is the parameterization image. Note that $\varOmega$ and $\varTheta$ are different mathematical objects: $\varOmega$ is a domain, whereas $\varTheta$ is a polytope. Figure 2 shows an overview of our construction and the solution of the Poisson problem (1).

Fig. 2

Overview of parametric finite elements with bijective mappings, with colour-coded solution of the Poisson problem (1) on a warped domain $\varOmega$, with zero boundary conditions and constant right-hand side (color figure online)

Let $u\in {V}= H^1_0(\varOmega )$ be the Sobolev space of weakly differentiable functions vanishing on the boundary, $f \in L^2(\varOmega )$, and $g\in H^{1/2}(\partial \varOmega )$. Using integration by parts, we rewrite (1) in its weak form, which is: find $u \in {V}$ such that

$$\begin{aligned} \int _{\varOmega }\nabla u\cdot \nabla v=\int _{\varOmega } f v \qquad \forall v \in {V}. \end{aligned}$$

Fig. 3

The standard linear and quadratic shape functions $N_i$ on the element of the source mesh and the corresponding warped element

Using b, we express the previous integral with respect to the source domain $\varOmega _0$. Considering that $u({\varvec{x}}{})=u(b({\varvec{x}}{}_0))$ and $v({\varvec{x}}{})=v(b({\varvec{x}}{}_0))$ where ${\varvec{x}}{}\in \varOmega$ and ${\varvec{x}}{}_0 = b^{-1}({\varvec{x}})\in \varOmega _0$, and applying change of variables in the integrals, we rewrite the weak form: find $u\in {V}$ such that

$$\begin{aligned} \int _{\varOmega _0} J_b^{-T}\nabla u \cdot J_b^{-T} \nabla v ~ \det {(J_b)}=\int _{\varOmega _0} f v ~ \det {(J_b)}\qquad \forall v \in {V}, \end{aligned}$$

(2)

where $J_b$ is the Jacobian matrix of the mapping b.

In order to solve this problem, we represent the computational domain $\varOmega$ by means of a warped mesh ${\mathscr {T}}=b({\mathscr {T}}_0)$, where ${\mathscr {T}}_0=\{ E_0\subseteq \varOmega _0 | \bigcup \bar{E}_0 = \bar{\varOmega }_0\}$ is a conforming mesh (i.e., the intersection of two different elements is either empty, a common node, edge, or side), which describes the source domain $\varOmega _0$. By $\bar{\varOmega }$ we denote the closure of $\varOmega$. Note that, as described in (2), the bijective mapping warps the entire volume, creating warped elements $E=b(E_0)$. Let the finite element space associated to ${\mathscr {T}}$ be $V_h{}=V_h{}({\mathscr {T}}{})$, where h stands for the discretization parameter, and let $\{N_1, \ldots , N_m\}$ be a basis of $V_h{}$, where m is the number of basis functions. Figure 3 depicts an example of such basis functions for a warped element. We approximate the function u by means of $u_h\in V_h{}$, by expressing $u_h$ in terms of its basis, obtaining $u_h=\sum _{i=1}^m u_i N_i$, where $u_i$ are real coefficients. By choosing the test space as $V_h{}$, we discretize (2) as

$$\begin{aligned} \sum _{i=0}^{m} u_i \int _{\varOmega } J_b^{-T}\nabla N_i \cdot J_b^{-T} \nabla N_j ~ \det {(J_b)}= \sum _{i=0}^{m} f_i \int _{\varOmega } N_i N_j ~ \det {(J_b)}\qquad \forall j=1,\ldots , m, \end{aligned}$$

which can be represented in the classical matrix form

$$\begin{aligned} {\varvec{L{}}} {\varvec{u}} = {\varvec{M{}}} {\varvec{f}}, \end{aligned}$$

(3)

with ${\varvec{u}}=[u_1,\ldots ,u_m]^T$ and ${\varvec{f}}=[f_1,\ldots ,f_m]^T$

To assemble the stiffness matrix ${\varvec{L{}}}$ and the mass matrix ${\varvec{M{}}}$ we perform numerical quadrature. Because of the non-linearity of $J_b$ we need to choose a quadrature scheme of possibly higher order (Sect. 3.3) even when the basis functions of the approximation space $V_h$ are low order polynomials.

Fig. 4

Overview of the geometric transformations from the reference element ${\hat{E}}$ to the source element $E_0\in {\mathscr {T}}_0$ and to the warped element $E\in {\mathscr {T}}$

As usual, we introduce the reference element ${\hat{E}}$ and the transformation $G:{\hat{E}}\rightarrow E_0$ from the reference element to the corresponding element $E_0$ in the source domain. We perform the quadrature in ${\hat{E}}$, using quadrature points ${\hat{{\varvec{x}}{}}}_k \in {\hat{E}}, {\varvec{x}}_k =G({\hat{{\varvec{x}}}}_k)$ with the respective quadrature weights $\alpha _k \in {\mathbb {R}}$, $k=1,\ldots , K$. Figure 4 shows all the geometric transformations from the reference element ${\hat{E}}$ to the warped element E. We denote by ${\hat{N}}_i$ the basis functions on the reference element and by $J_G$ the Jacobian of G. This allows assembling the local matrices for the element E

$$\begin{aligned} \begin{aligned} L{}^E_{i,j} =&\sum _{k=1}^{K} \beta _k~ J^{-T}({\varvec{x}}_k) ~ \nabla {\hat{N}}_i(\hat{{\varvec{x}}{}}_k) \cdot J^{-T}({\varvec{x}}_k) \nabla {\hat{N}}_j(\hat{{\varvec{x}}{}}_k),\\ M{}^E_{i,j} =&\sum _{k=1}^{K} \beta _k~ {\hat{N}}_i(\hat{{\varvec{x}}{}}_k) ~ {\hat{N}}_j(\hat{{\varvec{x}}{}}_k), \end{aligned} \end{aligned}$$

(4)

where $J({\varvec{x}}_k)=J_b({{\varvec{x}}{}}_k) J_G(\hat{{\varvec{x}}{}}_k)$ and $\beta _k=\alpha _k\det {(J({\varvec{x}}_k))}{|{\hat{E}}|}$, with ${|{\hat{E}}|}$ the volume of ${\hat{E}}$. These local contributions are then gathered to compute the matrices ${\varvec{L}}$ and ${\varvec{M}}$.

Note that the weak formulation and the assembly procedures are very similar to classical finite elements. In fact, the only difference is the usage of the geometric terms depending on the bijective mapping b, such as $J_b$ which contributes to $J = J_b \, J_G$. As in standard FEM, the choice of the basis of $V_h{}$ is independent from the geometric description, leading to super/sub/iso-parametric approximations. In our method the geometric description is given by the mapping b, which is usually non-linear, so that our discretization falls into the category of super-parametric elements.

If we assume that $b({\mathscr {T}}{}_0)$ describes the exact geometry, then the geometric error is zero. However, the error in the solution is also connected to the choice of the approximation space and the shape of the elements. This error is influenced by the Jacobian $J_b$ of the bijective mapping. We estimate it by means of the condition number

$$\begin{aligned} \kappa = \sup _{{\varvec{x}}_0 \in \varOmega _0} \Vert J_b({\varvec{x}}_0) \Vert \, \Vert J_b^{-1}(b({\varvec{x}}_0)) \Vert \end{aligned}$$

(5)

as in standard parametric finite elements estimates [7, 9].

3 Shape and volume parameterization

The quality of a numerical solution of a partial differential equation is influenced by the accuracy of the geometric description and by the choice of the approximation space. In other words, a parameterization which describes the geometry exactly does not introduce any error related to the shape. The choice of this parameterization depends on the input geometry and includes every smooth bijective mapping, such as bijective spline mappings [15] (see Fig. 5), composite mean value mappings [37], or harmonic mappings [36].

Fig. 5

Example of parametric finite elements using a B-spline as the parameterization b. The colour describes the solution of the Poisson problem (1) (color figure online)

Since for CAD geometries the problem has been widely studied by the IGA community, we focus our study on volume parameterization between arbitrary surface meshes. The first challenge is the construction of a simpler surface $\varTheta _0$, a coarse source domain $\varOmega _0$, and a paramaterization image $\varTheta$, such that $\varOmega = b(\varOmega _0)$ (Sect. 3.1). The other challenges are the construction of the volume parameterization b (Sect. 3.2), an accurate quadrature procedure (Sect. 3.3), and the efficient evaluation of the forms within a simulation work-flow (Sect. 3.4).

3.1 Constructing the parameterization domain

In order to solve the model problem with the exact input geometry, the shape of $\varTheta$ must coincide with $\varOmega$, which describes the exact shape. As carried out in detail in Sect. 2, our approach still requires a parameterization domain $\varTheta _0$ and a source domain $\varOmega _0$. Hence, we first need to construct $\varTheta _0$ with the same mesh connectivity as $\varTheta$ while ensuring that $\varTheta _0$ describes a simpler shape. Note that in order to reproduce $\varOmega$ by means of b the shapes of $\varOmega _0$ and $\varTheta _0$ must also coincide, even if two meshes have a different number of faces and vertices.

Fig. 6

Given an input surface $\varTheta$ we simplify it to obtain $\varTheta _0$, which coincides with $\varOmega _0$. We mesh $\varOmega _0$ obtaining ${\mathscr {T}}_0$ and solve the problem with respect to ${\mathscr {T}}$, which has the same boundary as $\varTheta$

Fig. 7

Three-dimensional example of the work-flow of our approach, from the input surface to the solution of the problem in to the warped mesh ${\mathscr {T}}$

The approximation space for the finite element solution for the model problem can now be chosen independently from the shape, since $\varOmega _0$ and $\varTheta _0$ are arbitrary (e.g., the octagon in Fig. 6 or the tetrahedron in Fig. 7). This allows meshing $\varOmega _0$ with arbitrary mesh size to obtain ${\mathscr {T}}_0$. Hence, by applying b to ${\mathscr {T}}_0$, we control the resolution of ${\mathscr {T}}= b({\mathscr {T}}_0)$ independently from the shape of $\varTheta$ without influencing the shape accuracy.

As illustrated in Fig. 6, in the 2D case, $\varOmega _0$ is constructed by removing vertices from $\varTheta$. In order to obtain $\varTheta _0$ we reintroduce the removed vertices on the edges of $\varOmega _0$, without modifying the shape described by $\varOmega _0$. Finally, we mesh $\varOmega _0$ to obtain ${\mathscr {T}}_0$ and solve the problem in ${\mathscr {T}}= b({\mathscr {T}}_0)$.

The 3D case requires to coarsen $\varTheta$ in order to obtain $\varOmega _0$ while constructing a surface parameterization to build $\varTheta _0$ [14, 25, 27]. In our implementation we use the multi-resolution adaptive parameterization of surfaces (MAPS) algorithm [27], which produces a geometrically non-conforming parameterization (i.e., $\varTheta _0$ is not nested inside $\varOmega _0$). To overcome this limitation, we extend the MAPS algorithm by snapping the vertices of $\varTheta _0$ to the edges of $\varOmega _0$, and by applying few element splits to $\varTheta _0$ and $\varTheta$ when that is not feasible. We remark that the only operation performed on $\varTheta$ is splitting, which does not change its shape.

Summing up, we start with a high resolution mesh representing the exact geometry $\varTheta$. Then, from $\varTheta$ we compute a coarse surface $\varOmega _0$ which we mesh to obtain ${\mathscr {T}}_0$. Finally, we use the parameterization obtained with MAPS to construct a surface $\varTheta _0$ with the same connectivity as $\varTheta$ and the same shape as $\varOmega _0$. An example of a result of this procedure is shown in Fig. 7.

Fig. 8

Overview a composite barycentric mapping for $\tau =[0,0.5,1]$

3.2 Composite mean value mappings

To the best of our knowledge only the composite mean value mappings [37] allow creating smooth-bijective mappings between polytopes, such as polygons or polygonal meshes. Convenient properties of such mappings are that they can be evaluated pointwise, are provided in closed form, and are $C^\infty$ in the interior of the domain. These mappings are based on the mean value mapping

$$\begin{aligned} {\tilde{b}}({\varvec{x}}{})=\sum _{j=1}^n\lambda _j({\varvec{x}}{}){\varvec{q}}_j, \end{aligned}$$

where ${\varvec{q}}_j$ are the vertices of $\varTheta$ and the functions $\lambda _j:\varTheta _0\rightarrow {\mathbb {R}}$, $j=1,\dots ,n$ are a set of mean value coordinates [16, 22] with respect to $\varTheta _0$. That is,

$$\begin{aligned} \lambda _j=\frac{w_j}{\sum _{k=1}^n w_k}\qquad \text {with}\qquad w_j=\frac{\tan (\alpha _{j-1}/2)+\tan (\alpha _{j}/2)}{r_j}, \end{aligned}$$

where $\alpha _j$ is the angle between the edges $[{\varvec{x}},{\varvec{q}}^0_{j+1}]$ and $[{\varvec{x}},{\varvec{q}}^0_{j}]$ and $r_j=\Vert {\varvec{x}}-{\varvec{q}}^0_{j}\Vert$, with ${\varvec{q}}^0_{j}$ the vertices of $\varTheta _0$.

Unfortunately, the mapping ${\tilde{b}}$ is not guaranteed to be bijective for all pair of polytopes [21]. To overcome this limitation we follow [37] and “split” the mapping from source to target polytope into a finite number of steps, where each step perturbs the vertices only slightly. To this end, suppose that ${\varvec{\zeta }}_i:[0,1]\rightarrow {\mathbb {R}}^2$, $i=1,\dots ,n$ are a set of continuous vertex paths between each vertex ${\varvec{q}}^0_i={\varvec{\zeta }}_i(0)$ and its corresponding vertex ${\varvec{q}}_i={\varvec{\zeta }}_i(0)$.

Let $\tau _s=(t_0,t_1,\dots ,t_s)$ with $t_k=k/s$ for $k=0,\dots ,s$ be a uniform partitioning of [0, 1] and ${\tilde{b}}_k$ be the barycentric mapping from $\varTheta _{t_k}$ to $\varTheta _{t_{k+1}}$, based on the barycentric coordinates $\lambda ^{t_k}_i:\varTheta _{t_k} \rightarrow {\mathbb {R}}$. Then we define the composite barycentric mapping from $\varTheta _0$ to $\varTheta$ as

$$\begin{aligned} b= {\tilde{b}}_{s-1} \circ {\tilde{b}}_{s-2} \circ \dots \circ {\tilde{b}}_0, \end{aligned}$$

which is bijective for sufficiently large s according to [37]. Figure 8 shows an example of how a composite barycentric mapping is constructed for $s=2$.

3.3 Quadrature

As previously mentioned, the non-linearity of the bijective mapping b may introduce high error when low order numerical quadrature is employed. We implement an adaptive Simpson scheme [32] for accurately computing the stiffness matrix and right-hand side vector. For each element E, we compute the element mass matrix $M^E$ by means of a Gaussian quadrature formula. We subdivide E, and we use the same quadrature formula on each sub-element to re-compute $M^E$ more accurately. We compute the difference of these two results and continue to subdivide until a given numerical tolerance is reached.

Fig. 9

Quadrature error and error in the solution $u_h \in {V}({\mathscr {T}})$ for different levels of quadrature refinements. The level of refinement is higher (white) where the distortion of b is large (in proximity of the boundary), while no refinement is necessary in the interior (dark red color) (color figure online)

Figure 9 shows the convergence behaviour of the adaptive quadrature strategy with respect to the number of maximum refinements for reaching a quadrature tolerance of $10^{-8}$. The same figure shows how this error propagates to the solution for a low resolution mesh. It is interesting to note that the scheme automatically adapts to b, creating more levels where the mapping is less linear.

3.4 Pre-computation of the composite mean value mapping

The evaluation of composite mean value mapping described in Sect. 3.2 is computationally intensive. For this reason we need to avoid computing the mapping and its Jacobian multiple times. Similar to the classical assembly procedure of the system matrices, we start by deciding the order of quadrature. The order of quadrature depends on the problem we want to solve, the choice of the approximation space, and, especially for our approach, the bijective mapping b.

Fig. 10

Running times for computing the composite mean value mapping and its Jacobian. The computational time depends on three parameters: the number of intermediate steps s, the vertices n of $\varTheta$, and the evaluation points. For each of the three experiments we vary only one of the parameters, whose base values are $s = 10$, $n = 62$, and 1800 evaluation points

Instead of directly assembling the system matrices in (3), we divide the assembly procedure into two stages. The first stage consists of generating and storing all the quadrature data associated with the geometry necessary for the assembly, such as the global quadrature points $b(G({\hat{{\varvec{x}}}}))$ and the Jacobian matrices $J_b({\hat{{\varvec{x}}}})$.

The second stage consists of the standard assembly procedure of the element matrices (4), now using the precomputed quadrature quantities. This strategy allows assembling the matrices like for standard finite elements without the need of evaluating b and $J_b$ for each new operator.

For the standard finite element assembly procedure storing the quadrature data is usually not necessary, making our two stage approach less memory-efficient. However, the caching allows both a parallel evaluation of b and the possibility of reusing the quadrature data for different operators (e.g., Laplacian and mass matrix) and multiple time-steps (e.g., in case of transient simulations in non-linear elasticity). For instance, in Fig. 1 the quantities related to b are computed only at the first time-step and reused in the following ones.

Despite the pre-computation, the evaluation of b remains expensive. Fortunately, mean value coordinates are straightforward to parallelize on shared memory processors. In fact, every point-wise evaluation of b and $J_b$ can be computed in a completely independent way. Figure 10 shows the parallel-running times using OpenCL [23] with respect to different input sizes, computed on a laptop computer with Intel Core i7 2.3GHz processor and 16GB RAM, we refer to [41] for a comprehensive explanation of how to compute the gradient of mean value coordinates.

Fig. 11

Top left visualization of $e(u_h)$ against the mesh size h, where the straight dashed lines show the quadratic, cubic, and quartic trends. Top right $L^2$-convergence rates for the different discretizations. Bottom solution of the Poisson problem, where u is the Franke function, for different number of nodes m. We use $s=10$ uniform steps in b. The experiment has the mesh set-up shown in Fig. 13

4 Numerical experiments

We restrict our study to super-parametric discretizations (i.e., discretizations where the geometric mapping is more descriptive than the basis functions) based on composite mean value mappings (Sect. 3.2) with linear, quadratic, and cubic Lagrangian elements (${\mathbb {P}}_1$, ${\mathbb {P}}_2$, and ${\mathbb {P}}_3$). For our experiments the analytical solution is unknown, hence we estimate it by computing a reference solution $u \in V({\mathscr {T}}_f)$ on a very fine mesh ${\mathscr {T}}_f$. To evaluate the quality of our discretization and the standard discretization, we compute different solutions $u_h \in V_h({\mathscr {T}})$ for several mesh sizes h.

4.1 Convergence

The solution is expected to converge quadratically in $L^2(\varOmega )$ to the exact one with respect to the mesh size h for classical FEM with linear elements for $H^2$-regular problems. Hence, we study the convergence related to our approach by measuring the approximation error as

$$\begin{aligned} e(u_h) = {\Vert P(u_h) - u \Vert }_{L^2({\mathscr {T}}_f)}, \end{aligned}$$

where $P :V_h({\mathscr {T}}) \rightarrow V({\mathscr {T}}_f)$ is the $L^2$-projection operator [26, 42] (the assembly of P is performed in the parameterization domain). Similar to standard FEM, our method shows a quadratic, cubic, and quartic convergence behaviour for the Poisson problem, as illustrated in the plot in Fig. 11. Despite the fact that the computation is always performed on the exact geometry, the approximation error is not zero because of the piecewise polynomial approximation of the solution, which is visible for a mesh with small m and decreases for larger m.

Fig. 12

Mesh refinement without shape recovery. Even at fine resolution (last image) we do not recover the original shape (blue polygon) (color figure online)

Fig. 13

Source meshes ${\mathscr {T}}_0$ with boundary $\varTheta _0$ (first row), warped meshes ${\mathscr {T}}$ used by our method (second row) with $s=10$ uniform steps, and convergence plots against different numbers of degrees of freedom m (last row)

4.2 Comparison

We compare our method with the standard finite element discretization for a simple 2D problem (Fig. 13), an extreme 2D problem (Fig. 14), and for a realistic 3D shape (Fig. 15). Since for the standard finite element discretization, the boundary of ${\mathscr {T}}$ differs from $\varOmega$, we measure

$$\begin{aligned} r(u_h) = \left| \frac{ {\Vert u_h \Vert }_{L^2({\mathscr {T}})} }{ {\Vert u \Vert }_{L^2({\mathscr {T}}_f)} } -1 \right| \end{aligned}$$

to estimate the approximation error [30], where ${\Vert u \Vert }_{L^2({\mathscr {T}}_f)}$ is computed on a dense mesh with ${\mathbb {P}}_1$ elements.

Fig. 14

Source meshes ${\mathscr {T}}_0$ with boundary $\varTheta _0$ (first row), warped meshes ${\mathscr {T}}$ used by our method (second row) with $s=50$ uniform steps, and convergence plots against different numbers of degrees of freedom m (last row)

Fig. 15

Convergence plots against different numbers of degrees of freedom m for a 3D experiment. We use $s=10$ uniform steps in the composite mapping integrated with a standard Gaussian quadrature formula

In classical finite element simulations the original shape is usually not recovered when performing mesh refinement as shown in Fig. 12. For this reason, $r(u_h)$ does not converge to zero for the standard solution, while our approach converges (top plots in Figs. 13, 14,  15).

In order to better understand this behaviour, we measure the actual geometric deviation with

$$\begin{aligned} s({\mathscr {T}}) = \left| \frac{ {\Vert 1 \Vert }_{L^2({\mathscr {T}})} }{ {\Vert 1 \Vert }_{L^2(\varOmega )} } -1 \right| \end{aligned}$$

which corresponds to the volume of the mesh (note that ${\Vert 1 \Vert }_{L^2({\mathscr {T}})}$ is equivalent to the square root of the sum of the entries of the mass-matrix). We compute the volume by means of numerical quadrature, which might introduce errors (Sect. 3.3), since our discretization consists of warped elements. For the standard discretization, when refining the mesh without recovering the shape, the volume trivially stays constant. Hence, in order to have a fair comparison, we increase the shape accuracy while refining the mesh to ensure that the shape of the domain also converges to the exact one. The behaviour of $s({\mathscr {T}})$ shows that our discretization has almost zero geometrical error independently of h, while the standard discretization has higher geometrical error (middle plots in Figs. 13, 14, 15).

In order to investigate how the approximation error is influenced by the geometrical error, we measure $r(u_h)$ for our method and classical finite elements with shape recovery. Our discretization always has a smaller approximation error compared to the standard discretization (right plots in Figs. 13, 14, 15). This is due to the fact that our approach allows solving the problem in the exact geometry, even at low resolutions.

4.3 Conditioning

For solution methods such as iterative solvers, the condition number $\kappa$ of the stiffness matrix plays an important role for the convergence rate [2]. In order to understand how our discretization affects the condition number, we compute $\kappa$ for the discrete Laplace operator ${\varvec{L{}}}$ with respect to different mesh sizes h for both our discretization and the standard one. Because of the influence of the bijective mapping b, as shown in (5), our discretization has a slightly larger condition number. Figure 16 shows that $\kappa ({\varvec{L{}}})$ behaves similarly for both discretizations which suggests that iterative solvers perform nearly as well for our discretization as for the standard one.

5 Conclusions

The idea of combining the finite element method with bijective mappings allows representing complex geometries on coarse meshes and enables specifying interpolation conditions as in the classical finite element method. For instance, our method can be used with Lagrange elements, splines, NURBS, or mixed FEM independently from the complexity of the input geometry. We introduce this novel discretization focusing on the particular case of composite mean value mappings which automatically creates a volume parameterization given only the boundary description.

Fig. 16

Condition number of the discrete Laplace operator $\kappa ({\varvec{L}})$ against the mesh size h for the examples in Fig. 13 (left) and Fig. 14 (right)

Fig. 17

Polynomial boundary descriptions (mesh) compared to the exact boundary (blue polygon) (color figure online)

Fig. 18

Handling the interface (grey stars) between the Neumann boundary (blue solid lines) and the the Dirichlet boundary (orange dashed lines) from $\varTheta$ to ${\mathscr {T}}_0$ (color figure online)

An alternative is the use of iso-parametric finite elements, where the geometric mapping is of the same order as the basis functions. Therefore, the domain mesh is composed by piecewise polynomial elements, allowing a higher order description of the boundary shape. This approach describes smooth shapes well, but produces a sub-optimal approximation of non-smooth surfaces, which is the main focus of our discretization. Figure 17 shows how high-order polynomials fail in describing the boundary of a simple gear. Moreover, such approximations do not have any simple construction strategies that guarantee bijectivity (i.e., avoids negative volumes).

Through numerical experiments we show that our discretization has a lower approximation error compared to standard approaches, due to the higher geometric accuracy, without significant changes on the conditioning of the discrete operators. The method becomes computationally more expensive when employing the composite mean value mapping, however much of the related data can be precomputed and reused for different operators, as explained in Sect. 3.4. Moreover from the assembly point of view, our method only requires to change to quadrature procedure (4) by including the terms containing b.

Although we focus our study on the case of discrete geometry and composite mean value mappings, our construction might be suitable for any other choice of bijective mapping b, and it would be interesting to further investigate this flexibility. For instance, within the composite mapping, we can employ other types of smooth barycentric coordinates for which we can compute the Jacobian, such as maximum entropy coordinates [17, 19].

The integration of our approach with efficient and modern solution techniques, such as multigrid methods, is possible. In fact, the flexibility provided by arbitrarily choosing the mesh for describing $\varOmega _0$, allows to naturally generate nested geometric multigrid hierarchies with exact geometry. Moreover, the construction of the interpolation and restriction operators is trivially performed using standard mesh refinement of the source mesh ${\mathscr {T}}_0$, since the mapping b is the same for all levels.

Our discretization with composite mean value mapping enables treating boundary conditions with arbitrary precision even for the non-homogeneous case. For instance, let us consider the example problem in Fig. 18, where Dirichlet boundary conditions are specified on $\partial \varOmega _D\subseteq \partial \varOmega$ (orange dashed lines) and Neumann conditions on $\partial \varOmega _N=\partial \varOmega {\setminus }\partial \varOmega _D$ (blue solid lines). Let the interface (grey stars) between $\partial \varOmega _D$ and $\partial \varOmega _N$ be $\Gamma$ and its corresponding interface in $\varTheta _0$ be $\Gamma _0$ (i.e., $\Gamma =b(\Gamma _0)$). When generating the mesh ${\mathscr {T}}_0$ we preserve $\Gamma _0$ which is then mapped to its image $\Gamma$ in ${\mathscr {T}}$. Since $\Gamma$ is preserved, the boundary conditions which are specified on $\partial \varOmega _D$ and $\partial \varOmega _N$ can be equivalently handled on $\varOmega _0$.

In our presentation we always define the mapping b as a global parameterization from $\varTheta _0$ to $\varTheta$, though, in order to have a faster computation of the quadrature data, strategies for localizing the mapping can be applied. For instance, the mapping can be used to exclusively compute the quadrature data associated with the elements near the boundary, while for the elements in the interior the mapping can be applied to the nodal positions only, generating a piecewise polynomial approximation, similarly to [40].