1 Introduction

Soil–structure interaction (SSI) (Wolf 1986, 1988; Carbonari et al. 2011; Xiong et al. 2016; Zhao et al. 2017; Abel et al. 2018; Huang et al. 2017, 2020) significantly affects seismic responses of infrastructures, such as high-rise buildings, nuclear power plants, large-span bridges, underground structures and so on. In order to perform seismic analysis considering SSI, the suitable numerical model and method should be developed.

Substructure model (Wolf 1994) has been widely adopted in seismic SSI analysis of aboveground structures. The model divides the whole SSI system into two substructures, i.e., a structure with rigid foundation and a massless rigid foundation–soil system. The former is modeled by finite element method so as to perform seismic analysis and design of the structure. Only the seismic SSI effects of the latter, including complex stiffness and earthquake input, require to be considered in the substructure model.

To consider the complex stiffness in time domain, the massless rigid foundation–soil system is usually modelled as a lumped parameter model (LPM) (Wolf 1986, 1994; Barros and Luco 1990; Jean et al. 1990; Lesgidis et al. 2015; Carbonari et al. 2018; González et al. 2019) that consists of springs, dashpots and mass elements. The LPMs can be divided into two main categories, namely the approximate models and the relatively accurate models. The latter is more complex due to the introduction of many auxiliary degrees of freedom. For relatively high structure on soft soil site, the rocking motions of structural foundation may cause significant influence on seismic response of structure. In such cases, the LPM systems have been developed to consider the coupling of horizontal and rocking motions of foundation (Wolf 1994; Wolf and Paronesso 1991; Wolf and Paronesso 1992; Du and Zhao 2010).

To consider the earthquake input, the so-called effective foundation input motion, that is the foundation response of the massless rigid foundation–soil system under earthquake action, should be first obtained and then transformed into an equivalent loading acting on the structural foundation (Wolf 1994). For the shallow surface foundation, the effective foundation input motion is equal to the free field motion (site response) on the ground surface (Wolf 1994).

The response spectrum method (RSM) (Sutharshana and Mcguire 1988; Berrah and Kausel 1992; Singh et al. 2000; Chopra 2011) has been widely incorporated into the codes for seismic analysis and design of aboveground structures in many countries (BSL 2000; Eurocode 8 2003; ICC 2003; GB 2010) due to its simplicity and efficiency. Recently, the method has also been developed for seismic SSI analysis of underground structure (Zhao et al. 2019). The LPM including dashpot elements will make the SSI model into a non-classically damped system. Based on the complex mode superposition RSM (Maldonad and Singh 1991; Der Kiureghian and Neuenhofer 1992; Yu and Zhou 2008; Wang and Der Kiureghian 2015; Liu et al. 2016; Chen et al. 2017), the non-classically damped system has been analyzed (Tongaonkar and Jangid 2003; AIJ 2004; Yu and Zhou 2007; Butt and Ishihara 2012; Raheem et al. 2014; Bhavikatti and Cholekar 2017). However, in the existing works, (1) the coupling between horizontal and rocking motions of structural foundation is lacking, (2) only the simple approximate LPM is used, (3) no over-damped case arise in complex mode superposition analysis, and (4) no design response spectrum is applied.

In this paper, the seismic SSI of structure with shallow foundation is solved by applying RSM to the substructure model, in which the coupled motions of horizontal and rocking of structural foundation are considered. An accurate rational-approximation-based LPM is used to consider the soil complex stiffness in time domain. The over-damped cases arise in complex mode superposition. The design response spectrum is applied to estimate the maximum seismic response of structure.

The resting parts of this paper are organized as follows. The structure with shallow foundation under earthquake is introduced in Sect. 2. The seismic SSI substructure model with LPMs is constructed in Sect. 3. The complex mode superposition RSM is summarized simply in Sect. 4. The numerical examples are given in Sect. 5 to indicate the effectiveness of RSM to analyze the seismic SSI of structure with shallow foundation. Conclusions follow in Sect. 6.

2 Structure with shallow foundation under earthquake

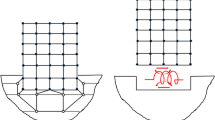
Figure 1a shows the structure with shallow foundation setting on soil subjected to a horizontal earthquake motion. The seismic motion is given at the surface of soil site without the structure and foundation, and its displacement time history is denoted by \(u_{g}\).

Fig. 1
figure 1

Structure with shallow foundation under horizontal earthquake excitation: a physical problem; and seismic analysis model neglecting SSI for b absolute motion and c relative motion

Full size image

The SSI is usually neglected to simplify the analysis. This model neglecting SSI is named as Model 1 in this paper. The Model 1 is the simple total fixity assumption. In this case, the displacement \(u_{g}\) is enforced on the structure foundation, and the soil is not considered. As shown in Fig. 1b, the dynamic finite element equation of structure with respect to absolute motion can be written as

$$ \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{M}}}_{R} } \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\overline{M}_{B} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {{\ddot{\mathbf{u}}}_{R} } \\ {\ddot{u}_{B} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{C}}}_{RR} } \hfill & {{\overline{\mathbf{C}}}_{RB} } \hfill \\ {{\overline{\mathbf{C}}}_{BR} } \hfill & {\overline{C}_{BB} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {{\dot{\mathbf{u}}}_{R} } \\ {\dot{u}_{B} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{K}}}_{RR} } \hfill & {{\overline{\mathbf{K}}}_{RB} } \hfill \\ {{\overline{\mathbf{K}}}_{BR} } \hfill & {\overline{K}_{BB} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {{\mathbf{u}}_{R} } \\ {u_{B} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} {\mathbf{0}} \\ {f_{B} } \\ \end{array} } \right\} $$
(1)

where \({\mathbf{u}}\), \({\dot{\mathbf{u}}}\) and \({\ddot{\mathbf{u}}}\) (or their scalar values) are the absolute horizontal displacement, velocity and acceleration, respectively; the subscripts R and B denote the degrees of freedom of superstructure and foundation, respectively; and \({\mathbf{M}}\), \({\mathbf{C}}\) and \({\mathbf{K}}\) are the lumped mass, damping and stiffness matrices, respectively, with the bar over matrices denoting the degrees of freedom of structure including superstructure and foundation; the three matrices are all symmetric; the displacement boundary condition gives \(u_{B} = u_{g}\); and fB denotes the reaction force of soil to foundation.

The dynamic equation can be written as the following equation with respect to the motion relative to foundation (Chopra 2011), as shown in Fig. 1c.

$$ {\overline{\mathbf{M}}}_{R} {\ddot{\tilde{\mathbf{u}}}}_{R} + {\overline{\mathbf{C}}}_{RR} {\dot{\tilde{\mathbf{u}}}}_{R} + {\overline{\mathbf{K}}}_{RR} {\tilde{\mathbf{u}}}_{R} = - {\overline{\mathbf{M}}}_{R} {\mathbf{I}}\ddot{u}_{g} $$
(2)

where \({\tilde{\mathbf{u}}}_{R} = {\mathbf{u}}_{R} - {\mathbf{I}}u_{g}\) denotes the relative motion; and I denotes the unit column vector here and all in this paper. The damping loading caused by seismic excitation is neglected on the right side of Eq. (2).

3 Seismic SSI model with LPMs

Two seismic SSI models are constructed in this section. One considers only the horizontal motion of foundation, and the other considers the coupling of the horizontal and rocking motions of foundation. In the two models, the rational-approximation-based LPMs are applied to consider the soil complex stiffness in time domain more accurate relatively. Such SSI models are used in this paper to investigate the effectiveness of different SSI models.

3.1 Only horizontal motion of foundation

The seismic SSI model considering only the horizontal motion of foundation is shown in Fig. 2. It is named as Model 2 in this paper. The Model 2 accounts for foundation motion in the horizontal direction only. The physical problem is first divided and decomposed into three parts as shown in Fig. 2a. The corresponding structural model, LPM and seismic load are then presented as shown in Fig. 2b. The seismic SSI model is finally constructed with respect to the absolute and relative motions as shown in Fig. 2c.

Fig. 2
figure 2

Seismic SSI model considering only horizontal motion of foundation: a physical problem, b structural model, LPM and seismic load; and c seismic SSI model

Full size image

3.1.1 Structural model

After the finite element discretization, the dynamic equation of the structure including superstructure and rigid foundation can be written as the same form as Eq. (1) with respect to the absolute motion. Here, \(f_{B}\) is the action force of the massless rigid foundation–soil system to the structure.

The total absolute response in the massless rigid foundation–soil system can be decomposed into the effective foundation input motion and its relative motion on the massless rigid foundation as (Wolf 1994)

$$ u_{B} = u_{B}^{S} + u_{B}^{F} $$
(3)

where \(u_{B}^{F}\) and \(u_{B}^{S}\) are the effective foundation input motion and its relative motion, respectively. For the shallow surface foundation, the effective foundation input motion is equal to the horizontal ground motion of soil site, i.e., \(u_{B}^{F} = u_{g}\) (Wolf 1994).

3.1.2 Rational-approximation-based LPM

The complex stiffness of the massless rigid foundation–soil system can be simulated by the LPM in time domain (Wolf 1994). An accurate and stable rational-approximation-based LPM has been developed by the authors (Du and Zhao 2010) as shown in Fig. 2b.

The complex stiffness relationship between the horizontal action force fB and horizontal relative motion \(u_{B}^{S}\) on the massless rigid foundation is first presented in frequency domain as

$$ f_{B}^{{}} (\omega ) = - S_{h} (\omega )u_{B}^{S} (\omega ) $$
(4)

where \(S_{h} (\omega )\) is the horizontal stiffness of the foundation; and \(\omega\) is the circular frequency with respect to time.

The horizontal stiffness is then simulated as an accurate and stable rational function of N order. The stiffness relationship Eq. (4) with the resulting rational function to replace the stiffness function is finally transformed into time domain as a LPM. The dynamic equation of LPM can be written as

$$ \left[ {\begin{array}{*{20}l} 0 \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {{\mathbf{M}}_{A} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\ddot{u}_{B}^{S} } \hfill \\ {{\ddot{\mathbf{u}}}_{A}^{S} } \hfill \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {C_{BB} } \hfill & {{\mathbf{C}}_{BA} } \hfill \\ {{\mathbf{C}}_{AB} } \hfill & {{\mathbf{C}}_{AA} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\dot{u}_{B}^{S} } \hfill \\ {{\dot{\mathbf{u}}}_{A}^{S} } \hfill \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {K_{B} } \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {u_{B}^{S} } \hfill \\ {{\mathbf{u}}_{A}^{S} } \hfill \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} { - f_{B} } \hfill \\ {\mathbf{0}} \hfill \\ \end{array} } \right\} $$
(5)

with the motion vector of the auxiliary degrees of freedom due to the relative motion

$$ {\mathbf{u}}_{A}^{S} = \left\{ {\begin{array}{*{20}l} {u_{1}^{S} } & {u_{2}^{S} } & \ldots & {u_{N}^{S} } \\ \end{array} } \right\}^{{\rm T}} $$

and the spring, dashpot and mass matrices

$$ \begin{aligned} & K_{B} = K_{0} ,\,C_{BB} = C_{0} + C_{1} ,\,{\mathbf{C}}_{BA} = {\mathbf{C}}_{AB}^{{\text{T}}} = \left\{ {\begin{array}{*{20}l} { - C_{1} } &\quad {0} &\quad {0} &\quad \ldots & {0} \\ \end{array} } \right\}, \\ &\quad {\mathbf{C}}_{AA} = \left[ {\begin{array}{*{20}l} {C_{1} + C_{2} } \hfill &\quad { - C_{2} } \hfill &\quad {0} \hfill &\quad \ldots \hfill &\quad 0 \hfill &\quad 0 \hfill \\ { - C_{2} } \hfill &\quad {C_{2} + C_{3} } \hfill &\quad { - C_{3} } \hfill &\quad \ldots \hfill &\quad 0 \hfill &\quad 0 \hfill \\ 0 \hfill &\quad { - C_{3} } \hfill &\quad {C_{3} { + }C_{4} } \hfill &\quad \ldots \hfill &\quad 0 \hfill &\quad 0 \hfill \\ \vdots \hfill &\quad \vdots \hfill &\quad \vdots \hfill &\quad \ddots \hfill &\quad \vdots \hfill &\quad \vdots \hfill \\ 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad \ldots \hfill &\quad {C_{N - 1} + C_{N} } \hfill &\quad { - C_{N} } \hfill \\ 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad \ldots \hfill & { - C_{N} } \hfill &\quad {C_{N} } \hfill \\ \end{array} } \right]\,{\text{and}} \\ &\quad {\mathbf{M}}_{A} = \left[ {\begin{array}{*{20}l} {M_{1} } \hfill &\quad {0} \hfill &\quad 0 \hfill &\quad \ldots \hfill &\quad 0 \hfill &\quad 0 \hfill \\ 0 \hfill &\quad {M_{2} } \hfill &\quad 0 \hfill &\quad \ldots \hfill &\quad 0 \hfill &\quad 0 \hfill \\ 0 \hfill &\quad 0 \hfill &\quad {M_{3} } \hfill &\quad \ldots \hfill &\quad 0 \hfill &\quad 0 \hfill \\ \vdots \hfill &\quad \vdots \hfill &\quad \vdots \hfill &\quad \ddots \hfill &\quad \vdots \hfill &\quad \vdots \hfill \\ 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad \ldots \hfill &\quad {M_{{N - {1}}} } \hfill &\quad 0 \hfill \\ 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad \ldots \hfill &\quad 0 \hfill &\quad {M_{N} } \hfill \\ \end{array} } \right] \\ \end{aligned} $$

where \(K_{0}\), \(C_{n}\) (n = 0, …, N) and \(M_{n}\) (n = 1, …, N) are the spring, dashpot and mass element parameters; and the superscript T denotes the matrix or vector transposition.

3.1.3 Seismic load

To input earthquake on the substructure model, the effective foundation input motion \(u_{B}^{F} = u_{g}\) is transformed into an equivalent load \(f_{B}^{F}\) acting at the structural foundation (Wolf 1994). The seismic load is equal to that applied on the LPM of Eq. (5) to cause the effective foundation input motion. It can be written as

$$ \left[ {\begin{array}{*{20}l} 0 \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {{\mathbf{M}}_{A} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\ddot{u}_{B}^{F} } \hfill \\ {{\ddot{\mathbf{u}}}_{A}^{F} } \hfill \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {C_{BB} } \hfill & {{\mathbf{C}}_{BA} } \hfill \\ {{\mathbf{C}}_{AB} } \hfill & {{\mathbf{C}}_{AA} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\dot{u}_{B}^{F} } \hfill \\ {{\dot{\mathbf{u}}}_{A}^{F} } \hfill \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {K_{B} } \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {u_{B}^{F} } \hfill \\ {{\mathbf{u}}_{A}^{F} } \hfill \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} {f_{B}^{F} } \hfill \\ {\mathbf{0}} \hfill \\ \end{array} } \right\} $$
(6)

where \({\mathbf{u}}_{A}^{F}\) is the motion vector of the auxiliary degrees of freedom due to the effective foundation input motion.

3.1.4 Seismic SSI model

Adding Eqs. (6) to (5), then substituting Eq. (3) into the result, and finally assembling the result with Eq. (1), the dynamic equation of the seismic SSI model with respect to the absolute motion could be obtained as

$$ {\mathbf{M}\ddot{\mathbf{u}}} + {\mathbf{C}\dot{\mathbf{u}}} + {\mathbf{Ku}} = {\mathbf{F}} $$
(7)

with

$$ \begin{aligned} & {\mathbf{u}} = \left\{ {\begin{array}{*{20}l} {{\mathbf{u}}_{R}^{{\rm T}} } & {u_{B} } & {{\mathbf{u}}_{A}^{{\rm T}} } \\ \end{array} } \right\}^{{\text{T}}} ,\,{\mathbf{u}}_{A} = {\mathbf{u}}_{A}^{S} + {\mathbf{u}}_{A}^{F} ,\,{\mathbf{F}} = \left\{ {\begin{array}{*{20}l} {\mathbf{0}} & {f_{B}^{F} } & {\mathbf{0}} \\ \end{array} } \right\}^{{\text{T}}} , \\ & {\mathbf{M}} = \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{M}}}_{R} } \hfill &\quad {\mathbf{0}} \hfill &\quad {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill &\quad {\overline{M}_{B} } \hfill &\quad {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill &\quad {\mathbf{0}} \hfill &\quad {{\mathbf{M}}_{A} } \hfill \\ \end{array} } \right],\,{\mathbf{K}} = \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{K}}}_{RR} } \hfill &\quad {{\overline{\mathbf{K}}}_{RB} } \hfill &\quad {\mathbf{0}} \hfill \\ {{\overline{\mathbf{K}}}_{BR} } \hfill & {\overline{K}_{BB} + K_{B} } \hfill &\quad {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill &\quad {\mathbf{0}} \hfill &\quad {\mathbf{0}} \hfill \\ \end{array} } \right]\,{\text{and}} \\ & {\mathbf{C}} = \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{C}}}_{RR} } \hfill &\quad {{\overline{\mathbf{C}}}_{RB} } \hfill &\quad {\mathbf{0}} \hfill \\ {{\overline{\mathbf{C}}}_{BR} } \hfill & {\overline{C}_{BB} + C_{BB} } \hfill &\quad {{\mathbf{C}}_{BA} } \hfill \\ {\mathbf{0}} \hfill & {{\mathbf{C}}_{AB} } \hfill &\quad {{\mathbf{C}}_{AA} } \hfill \\ \end{array} } \right]. \\ \end{aligned} $$

Transforming Eq. (7) into relative motion and neglecting the damping loading caused by seismic excitation on the right side of equation, after some manipulations, the finite element equation could be obtained as

$$ {\mathbf{M}\ddot{\tilde{\mathbf{u}}}} + {\mathbf{C}\dot{\tilde{\mathbf{u}}}} + {\mathbf{K}\tilde{\mathbf{u}}} = - {\hat{\mathbf{M}}\mathbf{I}}\ddot{u}_{g} $$
(8)

with the relative motion and the mass matrix of inertia force

$$ {\tilde{\mathbf{u}}} = \left\{ {\begin{array}{*{20}l} {{\tilde{\mathbf{u}}}_{R}^{{\rm T}} } &\quad {u_{B}^{S} } &\quad {{\mathbf{u}}_{A}^{{S{\rm T}}} } \\ \end{array} } \right\}^{{\text{T}}} ,\,{\tilde{\mathbf{u}}}_{R} = {\mathbf{u}}_{R} - {\mathbf{I}}u_{g} \,{\text{and}}\,{\hat{\mathbf{M}}} = \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{M}}}_{R} } \hfill &\quad {\mathbf{0}} \hfill & \quad {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill &\quad {\overline{M}_{B} } \hfill &\quad {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ \end{array} } \right]. $$

3.2 Coupled horizontal and rocking motions of foundation

The seismic SSI model considering the coupled horizontal and rocking motions of structural foundation is shown in Fig. 3. It is named as Model 3 in this paper. The Model 3 incorporates the foundation rotation motion in a coupled manner compared with Model 2. The model is first decomposed into three parts as shown in Fig. 3a. The corresponding structural model, LPM and seismic load are then presented as shown in Fig. 3b. The seismic SSI model is finally constructed with respect to the absolute and relative motions as shown in Fig. 3c.

Fig. 3
figure 3

Seismic SSI model considering the coupled horizontal and rocking motions of foundation: a physical problem, b structural model, LPM and seismic load; and c seismic SSI model

Full size image

3.2.1 Structural model

The dynamic equation of the whole structure including the superstructure and the rigid foundation can be obtained by finite element discretization. The dynamic equation for the horizontal degrees of freedom of structure can be written similarly to the Eq. (1) as

$$ \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{M}}}_{R} } \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\overline{M}_{B} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {{\ddot{\mathbf{u}}}_{R} } \hfill \\ {\ddot{u}_{B} } \hfill \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{C}}}_{RR} } \hfill & {{\overline{\mathbf{C}}}_{RB} } \hfill \\ {{\overline{\mathbf{C}}}_{BR} } \hfill & {\overline{C}_{BB} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {{\dot{\mathbf{u}}}_{R} - {\mathbf{h}}\dot{\theta }_{B} } \hfill \\ {\dot{u}_{B} } \hfill \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{K}}}_{RR} } \hfill & {{\overline{\mathbf{K}}}_{RB} } \hfill \\ {{\overline{\mathbf{K}}}_{BR} } \hfill & {\overline{K}_{BB} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {{\mathbf{u}}_{R} - {\mathbf{h}}\theta_{B} } \hfill \\ {u_{B} } \hfill \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} {\mathbf{0}} \hfill \\ {f_{B} } \hfill \\ \end{array} } \right\} $$
(9a)

and the dynamic equation for the structural rotation satisfies the equilibrium equation as

$$ {\mathbf{h}}^{{\rm T}} {\overline{\mathbf{M}}}_{R} {\ddot{\mathbf{u}}}_{R} + \overline{J}_{B} \ddot{\theta }_{B} = Q_{B} $$
(9b)

where \({\mathbf{u}}_{R}\) and \(u_{B}\) denote the total absolute horizontal displacements of superstructure and rigid foundation, respectively; \(\theta_{B}\) denotes the rotational angle (rocking displacement) of rigid foundation; \(\overline{J}_{B} = {\mathbf{h}}^{{\rm T}} {\overline{\mathbf{M}}}_{R} {\mathbf{h}}\) is the moment of inertia of structure; \(f_{B}\) and \(Q_{B}\) denote the action force and bending moment of the massless rigid foundation–soil system to the structure; and h is a column vector of the heights of structural degrees of freedom relative to foundation.

Pre-multiplying \({\mathbf{h}}^{{\rm T}}\) to the first equation of Eq. (9a) obtains

$$ {\mathbf{h}}^{{\rm T}} {\overline{\mathbf{M}}}_{R} {\ddot{\mathbf{u}}}_{R} + {\mathbf{h}}^{{\rm T}} {\overline{\mathbf{C}}}_{RR} {\dot{\mathbf{u}}}_{R} + {\mathbf{h}}^{{\rm T}} {\overline{\mathbf{C}}}_{RB} \dot{u}_{B} - {\mathbf{h}}^{{\rm T}} {\overline{\mathbf{C}}}_{RR} {\mathbf{h}}\dot{\theta }_{B} + {\mathbf{h}}^{{\rm T}} {\overline{\mathbf{K}}}_{RR} {\mathbf{u}}_{R} + {\mathbf{h}}^{{\rm T}} {\overline{\mathbf{K}}}_{RB} u_{B} - {\mathbf{h}}^{{\rm T}} {\overline{\mathbf{K}}}_{RR} {\mathbf{h}}\theta_{B} = {0}. $$
(10)

Combining Eqs. (10) and (9b) to eliminate the term \({\mathbf{h}}^{{\rm T}} {\overline{\mathbf{M}}}_{R} {\ddot{\mathbf{u}}}_{R}\), and then assembling the result with Eq. (9a), after several manipulations, the structural dynamic equation with respect to absolute motion can be obtained as

$$ \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{M}}}_{R} } \hfill &\quad {\mathbf{0}} \hfill &\quad { 0} \hfill \\ {\mathbf{0}} \hfill &\quad {\overline{M}_{B} \, } \hfill &\quad 0 \hfill \\ 0 \hfill &\quad 0 \hfill &\quad {\overline{J}_{B} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {{\ddot{\mathbf{u}}}_{R} } \hfill \\ \begin{gathered} \ddot{u}_{B} \hfill \\ \ddot{\theta }_{B} \hfill \\ \end{gathered} \hfill \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{C}}}_{RR} } \hfill &\quad {{\overline{\mathbf{C}}}_{RB} } \hfill &\quad { - {\overline{\mathbf{C}}}_{RR} {\mathbf{h}}} \hfill \\ {{\overline{\mathbf{C}}}_{BR} } \hfill & {\overline{C}_{BB} } \hfill &\quad { - {\overline{\mathbf{C}}}_{BR} {\mathbf{h}}} \hfill \\ { - {\mathbf{h}}^{{\rm T}} {\overline{\mathbf{C}}}_{RR} } \hfill &\quad { - {\mathbf{h}}^{{\rm T}} {\overline{\mathbf{C}}}_{RB} } \hfill &\quad {{\mathbf{h}}^{{\rm T}} {\overline{\mathbf{C}}}_{RR} {\mathbf{h}}} \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {{\dot{\mathbf{u}}}_{R} } \hfill \\ {\dot{u}_{B} } \hfill \\ {\dot{\theta }_{B} } \hfill \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{K}}}_{RR} } \hfill & {{\overline{\mathbf{K}}}_{RB} } \hfill &\quad { - {\overline{\mathbf{K}}}_{RR} {\mathbf{h}}} \hfill \\ {{\overline{\mathbf{K}}}_{BR} } \hfill & {\overline{K}_{BB} } \hfill &\quad { - {\overline{\mathbf{K}}}_{BR} {\mathbf{h}}} \hfill \\ { - {\mathbf{h}}^{{\rm T}} {\overline{\mathbf{K}}}_{RR} } \hfill &\quad { - {\mathbf{h}}^{{\rm T}} {\overline{\mathbf{K}}}_{RB} } \hfill &\quad {{\mathbf{h}}^{{\rm T}} {\overline{\mathbf{K}}}_{RR} {\mathbf{h}}} \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {{\mathbf{u}}_{R} } \hfill \\ {u_{B} } \hfill \\ {\theta_{B} } \hfill \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} {\mathbf{0}} \hfill \\ {f_{B} } \hfill \\ {Q_{B} } \hfill \\ \end{array} } \right\}. $$
(11)

For the surface massless rigid foundation–soil system under horizontal earthquake, the effective foundation input motion is the same whether or not the foundation rotation is considered. Therefore, only the total absolute horizontal motion on the foundation is decomposed as same as Eq. (3), even though the rocking motion of foundation is considered here.

3.2.2 Rational-approximation-based LPM system

The complex stiffness of the massless rigid foundation–soil system arising from the coupled horizontal and rocking motions of the foundation can be simulated in time domain by a LPM system consisting three LPMs similar to Eq. (5), as shown in Fig. 3b.

The complex stiffness relationship between force (bending moment) and relative displacement (rotational angle) on the massless rigid foundation is first presented in frequency domain as

$$ \left\{ {\begin{array}{*{20}l} {f_{B} (\omega )} \hfill \\ {Q_{B} (\omega )} \hfill \\ \end{array} } \right\} = - \left[ {\begin{array}{*{20}l} {S_{h} (\omega )} \hfill & {S_{c} (\omega )} \hfill \\ {S_{c} (\omega )} \hfill & {S_{r} (\omega )} \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {u_{B}^{S} (\omega )} \hfill \\ {\theta_{B} (\omega )} \hfill \\ \end{array} } \right\} = - \left[ {\begin{array}{*{20}l} {S_{h}^{m} (\omega ) + S_{c}^{m} (\omega )} \hfill & {rS_{c}^{m} (\omega )} \hfill \\ {rS_{c}^{m} (\omega )} \hfill & {S_{r}^{m} (\omega ) + r^{2} S_{c}^{m} (\omega )} \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {u_{B}^{S} (\omega )} \hfill \\ {\theta_{B} (\omega )} \hfill \\ \end{array} } \right\} $$
(12)

where \(S_{h} (\omega )\), \(S_{r} (\omega )\) and \(S_{c} (\omega )\) are the horizontal, rocking and coupling stiffness functions of foundation, respectively (Wolf 1991; Wolf and Paronesso 1992; Du and Zhao 2010); \(S_{h}^{m} (\omega )\), \(S_{r}^{m} (\omega )\) and \(S_{c}^{m} (\omega )\) are the corresponding stiffness functions of foundation which will be modelled by the three LPMs; and r denotes the half of the foundation width.

Equation (12) can be rewritten based on the modelled stiffness functions as

$$ f_{B} (\omega ) = f_{{B_{1} }} (\omega ) + f_{{B_{2} }} (\omega ) = - S_{h}^{m} u_{B}^{S} (\omega ) - S_{c}^{m} (u_{B}^{S} (\omega ) + r\theta_{B} (\omega )) $$
(13a)
$$ Q_{B} (\omega ) = rf_{{B_{2} }} (\omega ) + Q_{{B_{3} }} (\omega ) = - rS_{c}^{m} (\omega )(u_{B}^{S} (\omega ) + r\theta_{B} (\omega )) - S_{r}^{m} (\omega )\theta_{B} (\omega ) $$
(13b)

where the subscripts 1, 2 and 3 denote the action forces (bending moment) corresponding to the horizontal, coupling and rocking LPMs, respectively.

Three modelled stiffness functions are then simulated as three accurate and stable rational functions of N order. The three stiffness relationships with the three resulting rational functions to replace the corresponding stiffness functions are finally transformed into time domain as three LPMs similar to Eq. (5). The dynamic equations of the horizontal, coupling and rocking LPMs shown in Fig. 3b can be written respectively as

$$ \left[ {\begin{array}{*{20}l} 0 \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {{\mathbf{M}}_{{A_{1} }} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\ddot{u}_{B}^{S} } \hfill \\ {{\ddot{\mathbf{u}}}_{{A_{1} }}^{S} } \hfill \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {C_{{B_{1} B_{1} }} } \hfill & {{\mathbf{C}}_{{B_{1} A_{1} }} } \hfill \\ {{\mathbf{C}}_{{A_{1} B_{1} }} } \hfill & {{\mathbf{C}}_{{A_{1} A_{1} }} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\dot{u}_{B}^{S} } \hfill \\ {{\dot{\mathbf{u}}}_{{A_{1} }}^{S} } \hfill \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {K_{{B_{1} }} } \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {u_{B}^{S} } \hfill \\ {{\mathbf{u}}_{{A_{1} }}^{S} } \hfill \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} { - f_{{B_{1} }} } \hfill \\ {\mathbf{0}} \hfill \\ \end{array} } \right\} $$
(14a)
$$ \left[ {\begin{array}{*{20}l} 0 \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {{\mathbf{M}}_{{A_{2} }} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\ddot{u}_{B}^{S} + r\ddot{\theta }_{B} } \hfill \\ {{\ddot{\mathbf{u}}}_{{A_{2} }}^{S} } \hfill \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {C_{{B_{2} B_{2} }} } \hfill & {{\mathbf{C}}_{{B_{2} A_{2} }} } \hfill \\ {{\mathbf{C}}_{{A_{2} B_{2} }} } \hfill & {{\mathbf{C}}_{{A_{2} A_{2} }} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\dot{u}_{B}^{S} + r\dot{\theta }_{B} } \hfill \\ {{\dot{\mathbf{u}}}_{{A_{2} }}^{S} } \hfill \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {K_{{B_{2} }} } \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {u_{B}^{S} + r\theta_{B} } \hfill \\ {{\mathbf{u}}_{{A_{2} }}^{S} } \hfill \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} { - f_{{B_{2} }} } \hfill \\ {\mathbf{0}} \hfill \\ \end{array} } \right\} $$
(14b)
$$ \left[ {\begin{array}{*{20}l} 0 \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {{\mathbf{M}}_{{A_{3} }} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\ddot{\theta }_{B} } \\ {{\ddot{\mathbf{u}}}_{{A_{3} }} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {C_{{B_{3} B_{3} }} } & {{\mathbf{C}}_{{B_{3} A_{3} }} } \\ {{\mathbf{C}}_{{A_{3} B_{3} }} } & {{\mathbf{C}}_{{A_{3} A_{3} }} } \\ \end{array} } \right]\left\{ \begin{gathered} \dot{\theta }_{B} \hfill \\ {\dot{\mathbf{u}}}_{{A_{3} }} \hfill \\ \end{gathered} \right\} + \left[ {\begin{array}{*{20}l} {K_{{B_{3} }} } \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ \end{array} } \right]\left\{ \begin{gathered} \theta_{B} \hfill \\ {\mathbf{u}}_{{A_{3} }} \hfill \\ \end{gathered} \right\} = \left\{ {\begin{array}{*{20}l} { - Q_{{B_{3} }} } \hfill \\ {\mathbf{0}} \hfill \\ \end{array} } \right\}. $$
(14c)

3.2.3 Seismic load

As done in Sect. 3.1.3, the seismic loads, namely the applied force and bending moment are obtained by imposing the effective foundation input motion \(u_{B}^{F} = u_{g}\) on the LPM system of Eq. (14). They can be written as

$$ f_{B}^{F} = f_{{B_{1} }}^{F} + f_{{B_{2} }}^{F} $$
(15a)
$$ Q_{B}^{F} = rf_{{B_{2} }}^{F} $$
(15b)

with

$$ \left[ {\begin{array}{*{20}l} 0 \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {{\mathbf{M}}_{{A_{1} }} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\ddot{u}_{B}^{F} } \hfill \\ {{\ddot{\mathbf{u}}}_{{A_{1} }}^{F} } \hfill \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {C_{{B_{1} B_{1} }} } \hfill & {{\mathbf{C}}_{{B_{1} A_{1} }} } \hfill \\ {{\mathbf{C}}_{{A_{1} B_{1} }} } \hfill & {{\mathbf{C}}_{{A_{1} A_{1} }} } \hfill \\ \end{array} } \right]\left\{ \begin{gathered} \dot{u}_{B}^{F} \hfill \\ {\dot{\mathbf{u}}}_{{A_{1} }}^{F} \hfill \\ \end{gathered} \right\} + \left[ {\begin{array}{*{20}l} {K_{{B_{1} }} } \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ \end{array} } \right]\left\{ \begin{gathered} u_{B}^{F} \hfill \\ {\mathbf{u}}_{{A_{1} }}^{F} \hfill \\ \end{gathered} \right\} = \left\{ {\begin{array}{*{20}l} {f_{{B_{1} }}^{F} } \hfill \\ {\mathbf{0}} \hfill \\ \end{array} } \right\} $$
(15c)
$$ \left[ {\begin{array}{*{20}l} 0 \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {{\mathbf{M}}_{{A_{2} }} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\ddot{u}_{B}^{F} } \\ {{\ddot{\mathbf{u}}}_{{A_{2} }}^{F} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {C_{{B_{2} B_{2} }} } \hfill & {{\mathbf{C}}_{{B_{2} A_{2} }} } \hfill \\ {{\mathbf{C}}_{{A_{2} B_{2} }} } \hfill & {{\mathbf{C}}_{{A_{2} A_{2} }} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\dot{u}_{B}^{F} } \hfill \\ {{\dot{\mathbf{u}}}_{{A_{2} }}^{F} } \hfill \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {K_{{B_{2} }} } \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {u_{B}^{F} } \hfill \\ {{\mathbf{u}}_{{A_{2} }}^{F} } \hfill \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} {f_{{B_{2} }}^{F} } \hfill \\ {\mathbf{0}} \hfill \\ \end{array} } \right\}. $$
(15d)

3.2.4 Seismic SSI model

Assembling Eqs. (11), (3), (13), (14) and (15) obtains the dynamic equation of the seismic SSI model with respect to the absolute motion as

$$ {\mathbf{M}\ddot{\mathbf{u}}} + {\mathbf{C}\dot{\mathbf{u}}} + {\mathbf{K}}{\mathbf{u}} = {\mathbf{F}} $$
(16)

with

$$ \begin{aligned} & {\mathbf{u}} = \left\{ {\begin{array}{*{20}l} {{\mathbf{u}}_{R}^{{\rm T}} } & {u_{B} } & {\theta_{B} } & {{\mathbf{u}}_{{A_{1} }}^{{\rm T}} } & {{\mathbf{u}}_{{A_{2} }}^{{\rm T}} } & {{\mathbf{u}}_{{A_{3} }}^{{\rm T}} } \\ \end{array} } \right\}^{{\rm T}} ,\,{\mathbf{u}}_{{A_{1} }} = {\mathbf{u}}_{{A_{1} }}^{S} + {\mathbf{u}}_{{A_{1} }}^{F} ,\,{\mathbf{u}}_{{A_{2} }} = {\mathbf{u}}_{{A_{2} }}^{S} + {\mathbf{u}}_{{A_{2} }}^{F} ,\,{\mathbf{F}} = \left\{ {\begin{array}{*{20}l} {\mathbf{0}} & {f_{B}^{F} } & {Q_{B}^{F} } & {\mathbf{0}} & {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right\}^{{\rm T}} , \\ & {\mathbf{M}} = \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{M}}}_{R} } \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\overline{M}_{B} } \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\overline{J}_{B} } \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {{\mathbf{M}}_{{A_{1} }} } \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {{\mathbf{M}}_{{A_{2} }} } \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {{\mathbf{M}}_{{A_{3} }} } \hfill \\ \end{array} } \right], \\ & {\mathbf{C}} = \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{C}}}_{RR} } \hfill & {{\overline{\mathbf{C}}}_{RB} } \hfill & { - {\overline{\mathbf{C}}}_{RR} {\mathbf{h}}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {{\overline{\mathbf{C}}}_{BR} } \hfill & {\overline{C}_{BB} + C_{{B_{1} B_{1} }} + C_{{B_{2} B_{2} }} } \hfill & { - {\overline{\mathbf{C}}}_{BR} {\mathbf{h}} + rC_{{B_{2} B_{2} }} } \hfill & {{\mathbf{C}}_{{B_{1} A_{1} }} } \hfill & {{\mathbf{C}}_{{B_{2} A_{2} }} } \hfill & {\mathbf{0}} \hfill \\ { - {\mathbf{h}}^{{\rm T}} {\overline{\mathbf{C}}}_{RR} } \hfill & { - {\mathbf{h}}^{{\rm T}} {\overline{\mathbf{C}}}_{RB} + rC_{{B_{2} B_{2} }} } \hfill & {{\mathbf{h}}^{{\rm T}} {\overline{\mathbf{C}}}_{RR} {\mathbf{h}} + r^{2} {\mathbf{C}}_{{B_{2} B_{2} }} + {\mathbf{C}}_{{B_{3} B_{3} }} } \hfill & {\mathbf{0}} \hfill & {r{\mathbf{C}}_{{B_{2} A_{2} }} } \hfill & {{\mathbf{C}}_{{B_{3} A_{3} }} } \hfill \\ {\mathbf{0}} \hfill & {{\mathbf{C}}_{{A_{1} B_{1} }} } \hfill & {\mathbf{0}} \hfill & {{\mathbf{C}}_{{A_{1} A_{1} }} } \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {{\mathbf{C}}_{{A_{2} B_{2} }} } \hfill & {r{\mathbf{C}}_{{A_{2} B_{2} }} } \hfill & {\mathbf{0}} \hfill & {{\mathbf{C}}_{{A_{2} A_{2} }} } \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {{\mathbf{C}}_{{A_{3} B_{3} }} } \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {{\mathbf{C}}_{{A_{3} A_{3} }} } \hfill \\ \end{array} } \right], \\ & \quad {\text{and}}\,{\mathbf{K}} = \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{K}}}_{RR} } \hfill & {{\overline{\mathbf{K}}}_{RB} } \hfill & { - {\overline{\mathbf{K}}}_{RR} {\mathbf{h}}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {{\overline{\mathbf{K}}}_{BR} } \hfill & {\overline{K}_{BB} + K_{{B_{1} }} + K_{{B_{2} }} } \hfill & { - {\overline{\mathbf{K}}}_{BR} {\mathbf{h}} + rK_{{B_{2} }} } \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ { - {\mathbf{h}}^{{\rm T}} {\overline{\mathbf{K}}}_{RR} } \hfill & { - {\mathbf{h}}^{{\rm T}} {\overline{\mathbf{K}}}_{RB} + rK_{{B_{2} }} } \hfill & {{\mathbf{h}}^{{\rm T}} {\overline{\mathbf{K}}}_{RR} {\mathbf{h}} + r^{2} K_{{B_{2} }} + K_{{B_{3} }} } \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ \end{array} } \right]. \\ \end{aligned} $$

Transforming Eq. (16) into relative motion and neglecting the damping loading caused by seismic excitation on the right side of equation, after some manipulations, obtain the finite element equation as

$$ {\mathbf{M}\ddot{\tilde{\mathbf{u}}}} + {\mathbf{C}\dot{\tilde{\mathbf{u}}}} + {\mathbf{K}\tilde{\mathbf{u}}} = - {\hat{\mathbf{M}}\mathbf{I}}\ddot{u}_{g} $$
(17)

with the relative motion and the mass matrix of inertia force

$$ {\tilde{\mathbf{u}}} = \left\{ {\begin{array}{*{20}l} {{\tilde{\mathbf{u}}}_{R}^{{\rm T}} } & {u_{B}^{S} } & {\theta_{B}^{S} } & {{\mathbf{u}}_{{A_{1} }}^{{S{\rm T}}} } & {{\mathbf{u}}_{{A_{2} }}^{{S{\rm T}}} } & {{\mathbf{u}}_{{A_{3} }}^{{S{\rm T}}} } \\ \end{array} } \right\}^{{\rm T}} ,\,{\tilde{\mathbf{u}}}_{R} {\rm = }{\mathbf{u}}_{R} - {\mathbf{I}}u_{g} \,{\text{and}}\,{\hat{\mathbf{M}}} = \left[ {\begin{array}{*{20}l} {{\overline{\mathbf{M}}}_{R} } \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\overline{M}_{B} } \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & 0 \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill & {\mathbf{0}} \hfill \\ \end{array} } \right] $$

4 RSM for seismic SSI model

The seismic SSI model of Eqs. (8) or (17) is solved using the complex mode superposition RSM under earthquake design response spectra in this section. The complex mode analysis is first performed to consider the under- and over-damped cases (Inman and Andry 1980; Song et al. 2008; Yu and Zhou 2006). The RSM is then used with earthquake design response spectra input.

4.1 Complex mode analysis

Equations (8) or (17) is a non-classically damped system due to the consideration of SSI using the rational-approximation-based LPMs. It can be decoupled by the complex mode analysis. The details on the complex mode analysis can be seen in the references (Foss 1958; Yu and Zhou 2008). It is summarized in brief as follows.

Equations (8) or (17) can be converted into a first order matrix equation as

$$ {\mathbf{R\dot{X}}} + {\mathbf{SX}} = - {\mathbf{E}}\ddot{u}_{g} $$
(18)

with

$$ {\mathbf{R}} = \left[ {\begin{array}{*{20}l} {\mathbf{0}} \hfill & {\mathbf{M}} \hfill \\ {\mathbf{M}} \hfill & {\mathbf{C}} \hfill \\ \end{array} } \right],\,{\mathbf{S}} = \left[ {\begin{array}{*{20}l} { - {\mathbf{M}}} \hfill & {\mathbf{0}} \hfill \\ {\mathbf{0}} \hfill & {\mathbf{K}} \hfill \\ \end{array} } \right],\,{\mathbf{X}} = \left\{ {\begin{array}{*{20}l} {{\dot{\tilde{\mathbf{u}}}}} \hfill \\ {{\tilde{\mathbf{u}}}} \hfill \\ \end{array} } \right\}\,{\text{and}}\,{\mathbf{E}} = \left\{ {\begin{array}{*{20}l} {\mathbf{0}} \hfill \\ {{\hat{\mathbf{M}}\mathbf{I}}} \hfill \\ \end{array} } \right\}. $$

The generalized eigenvalue problem corresponding to Eq. (18) can be written as

$$ \left( {\lambda {\mathbf{R}} + {\mathbf{S}}} \right){{\varvec{\Phi}}} = {\mathbf{0}} $$
(19)

where \(\lambda\) and \({{\varvec{\Phi}}} = \left\{ {\begin{array}{*{20}l} {\lambda {{\varvec{\upphi}}}^{{\rm T}} } & {{{\varvec{\upphi}}}^{{\rm T}} } \\ \end{array} } \right\}^{{\rm T}}\) are the generalized eigenvalue and eigenvector of Eq. (19), respectively. It can be easily proved that \(\lambda\) and \({{\varvec{\upphi}}}\) is the complex eigenvalue and mode of Eqs. (8) or (17).

Using the above complex eigenvalues and modes, Eqs. (8) or (17) can be decoupled into the following N single-degree-of-freedom equations if the equation dimension is N.

$$ \ddot{q}_{j} + 2\zeta_{j} \omega_{j} \dot{q}_{j} + \omega_{j}^{2} q_{j} = - \ddot{u}_{g} \,{\text{for}}\,j = 1,2, \ldots ,N $$
(20)

where \(q_{j}\) is the displacement response of the single-degree-of-freedom system; and \(\omega_{j}\) and \(\zeta_{j}\) are the natural frequency and damping ratio of the system, respectively.

By the superposition of the solutions of the N single-degree-of-freedom systems, the displacement response of Eqs. (8) or (17) can be written as

$$ {\tilde{\mathbf{u}}} = \sum\limits_{j = 1}^{N} {({\mathbf{A}}_{j} q_{j} } + {\mathbf{B}}_{j} \dot{q}_{j} ) $$
(21)

where Aj and Bj are the real column vectors which are obtained from the function of modes.

4.1.1 Under-damped cases

For an under-damped equation in Eq. (20), the corresponding two eigenvalues are a pair of conjugate complex numbers. They can be written as

$$ \lambda_{j} = - \zeta_{j} \omega_{j} + i\omega_{j} \sqrt {1 - \zeta_{j}^{2} } \,{\text{and}}\,\hat{\lambda }_{j} = - \zeta_{j} \omega_{j} - i\omega_{j} \sqrt {1 - \zeta_{j}^{2} } $$
(22)

where i denotes the imaginary unit. The natural frequency and damping ratio of this under-damping equation can be obtained from Eq. (22) as

$$ \omega_{j} = \left| {\lambda_{j} } \right|\,{\text{and}}\,\zeta_{j} = - \frac{{{\text{Re}} (\lambda_{j} )}}{{\left| {\lambda_{j} } \right|}} $$
(23)

where | | and Re() denote the modulus and real part of a complex number, respectively.

The two modes corresponding to the pair conjugate complex eigenvalues are also complex conjugate, and can be expressed as \({{\varvec{\upphi}}}_{j}\) and \({\hat{\mathbf{\phi }}}_{j}\). Using this pair of conjugate complex eigenvalues and modes and the coefficient matrices of Eqs. (8) or (17), the two vectors in Eq. (21) can be written as

$$ {\text{A}}_{j} = \omega_{j} \zeta_{j} {\mathbf{B}}_{j} - \omega_{j} \sqrt {1 - \zeta_{j}^{2} } {{\varvec{\upchi}}}_{j} \,{\text{and}}\,{\mathbf{B}}_{j} = D_{j} {{\varvec{\upphi}}}_{j} + \hat{D}_{j} {\hat{\mathbf{\phi }}}_{j} $$
(24)

where

$$ {{\varvec{\upchi}}}_{j} = - i(D_{j} {{\varvec{\upphi}}}_{j} - \hat{D}_{j} {\hat{\mathbf{\phi }}}_{j} ),\,D_{j} = \frac{{ - {{\varvec{\upphi}}}_{j}^{{\rm T}} {\hat{\mathbf{M}}\mathbf{I}}}}{{2\lambda_{j} {{\varvec{\upphi}}}_{j}^{{\rm T}} {\mathbf{M}}{{\varvec{\upphi}}}_{j} + {{\varvec{\upphi}}}_{j}^{{\rm T}} {\mathbf{C}}{{\varvec{\upphi}}}_{j} }}\,{\text{and}}\,\hat{D}_{j} = \frac{{ - {\hat{\mathbf{\phi }}}_{j}^{{\rm T}} {\hat{\mathbf{M}}\mathbf{I}}}}{{2\hat{\lambda }_{j} {\hat{\mathbf{\phi }}}_{j}^{{\rm T}} {\mathbf{M}}{\hat{\mathbf{\phi }}}_{j} + {\hat{\mathbf{\phi }}}_{j}^{{\rm T}} {\mathbf{C}}{\hat{\mathbf{\phi }}}_{j} }}. $$

4.1.2 Over-damped cases

For an over-damped equation in Eq. (20), the corresponding two eigenvalues are two different real numbers. They can be written as

$$ \lambda_{j} = - \zeta_{j} \omega_{j} + \omega_{j} \sqrt {\zeta_{j}^{2} - 1} \,{\text{and}}\,\hat{\lambda }_{j} = - \zeta_{j} \omega_{j} - \omega_{j} \sqrt {\zeta_{j}^{2} - 1} $$
(25)

The natural frequency and damping ratio of this over-damped equation can be obtained from Eq. (25) as

$$ \omega_{j} = \sqrt {\lambda_{j} \hat{\lambda }_{j} } \,{\text{and}}\,\zeta_{j} = \frac{{\lambda_{j} + \hat{\lambda }_{j} }}{{2\sqrt {\lambda_{j} \hat{\lambda }_{j} } }}. $$
(26)

The two modes corresponding to the two real eigenvalues are also real, and can be expressed as \({{\varvec{\upphi}}}_{j}\) and \({\hat{\mathbf{\phi }}}_{j}\). Using the two pairs of real eigenvalues and modes and the coefficient matrices of Eqs. (8) or (17), the two vectors in Eq. (21) can be written as

$$ {\text{A}}_{j} = \omega_{j} \zeta_{j} {\mathbf{B}}_{j} - \omega_{j} \sqrt {\zeta_{j}^{2} - 1} {{\varvec{\upchi}}}_{j} \,{\text{and}}\,{\mathbf{B}}_{j} = D_{j} {{\varvec{\upphi}}}_{j} + \hat{D}_{j} {\hat{\mathbf{\phi }}}_{j} $$
(27)

where

$$ {{\varvec{\upchi}}}_{j} = D_{j} {{\varvec{\upphi}}}_{j} - \hat{D}_{j} {\hat{\mathbf{\phi }}}_{j} ,\,D_{j} = \frac{{ - {{\varvec{\upphi}}}_{j}^{{\rm T}} {\hat{\mathbf{M}}\mathbf{I}}}}{{2\lambda_{j} {{\varvec{\upphi}}}_{j}^{{\rm T}} {\mathbf{M}}{{\varvec{\upphi}}}_{j} + {{\varvec{\upphi}}}_{j}^{{\rm T}} {\mathbf{C}}{{\varvec{\upphi}}}_{j} }}\,{\text{and}}\,\hat{D}_{j} = \frac{{ - {\hat{\mathbf{\phi }}}_{j}^{{\rm T}} {\hat{\mathbf{M}}\mathbf{I}}}}{{2\hat{\lambda }_{j} {\hat{\mathbf{\phi }}}_{j}^{{\rm T}} {\mathbf{M}}{\hat{\mathbf{\phi }}}_{j} + {\hat{\mathbf{\phi }}}_{j}^{{\rm T}} {\mathbf{C}}{\hat{\mathbf{\phi }}}_{j} }}. $$

4.2 Complex mode superposition RSM

The complex complete quadratic combination (Yu and Zhou 2008; Chen et al. 2017) is adopted to combine the maximum responses of the N single-degree-of-freedom systems of Eq. (20) to obtain the maximum response of the seismic SSI system of Eqs. (8) or (17) as

$$ |\tilde{u}|_{\max } = \sqrt {\sum\limits_{j = 1}^{N} {\sum\limits_{l = 1}^{N} {\left( {\rho_{jl}^{dd} A_{j} A_{l} S_{j}^{d} S_{l}^{d} + 2\rho_{jl}^{vd} B_{j} A_{l} S_{j}^{v} S_{l}^{d} + \rho_{jl}^{vv} B_{j} B_{l} S_{j}^{v} S_{l}^{v} } \right)} } } $$
(28)

where the scalar \(\tilde{u}\), \(A\) and \(B\) denote an element of \({\tilde{\mathbf{u}}}\), \({\mathbf{A}}\) and \({\mathbf{B}}\) respectively at the same degree of freedom; | |max denote the peak value of time history; \(S_{j}^{d} = \left| {q_{j} } \right|_{\max }\) and \(S_{j}^{v} = \left| {\dot{q}_{j} } \right|_{\max }\) are the relative displacement and relative velocity response spectra of the jth equation in Eq. (20), respectively; and \(\rho_{jl}^{dd}\), \(\rho_{jl}^{vd}\) and \(\rho_{jl}^{vv}\) denote the displacement–displacement, displacement–velocity, velocity–displacement, and velocity–velocity cross-correlation functions between jth and lth equations in Eq. (20), respectively, and can be written as

$$ \begin{aligned} \rho_{jl}^{dd} & = \frac{{8\sqrt {\zeta_{j} \zeta_{l} } (g\zeta_{j} + \zeta_{l} )g^{3/2} }}{{{(1} - g^{2} {)}^{2} { + 4}\zeta_{j} \zeta_{l} g(1 + g^{2} ) + 4(\zeta_{j}^{2} + \zeta_{l}^{2} )g^{2} }} \\ \rho_{jl}^{vd} & = \frac{{{4}\sqrt {\zeta_{j} \zeta_{l} } {(1} - g^{2} {)}g^{{{1/}2}} }}{{{(1} - g^{2} {)}^{2} { + 4}\zeta_{j} \zeta_{l} g(1 + g^{2} ) + 4(\zeta_{j}^{2} + \zeta_{l}^{2} )g^{2} }} \\ \rho_{jl}^{vv} & = \frac{{8\sqrt {\zeta_{j} \zeta_{l} } (\zeta_{j} + g\zeta_{l} )g^{3/2} }}{{{(1} - g^{2} {)}^{2} { + 4}\zeta_{j} \zeta_{l} g(1 + g^{2} ) + 4(\zeta_{j}^{2} + \zeta_{l}^{2} )g^{2} }} \\ \end{aligned} $$

where \(g = \omega_{j} /\omega_{l}\).

The relative displacement and relative velocity response spectra with different damping ratios is required to solve Eq. (28). When using single seismic signal, the response spectra can be obtained by solving Eq. (20). When using the design response spectra, if the pseudo-acceleration response spectrum is given, the relative displacement and relative velocity response spectra can be obtained by using pseudo-spectrum transform relationship (Chopra 2011). On the other hand, the absolute acceleration design response spectrum is provided in the Chinese Code for Seismic Design of Buildings (GB 2010). It is shown in Fig. 4 with the damping ratio \(\zeta\), the characteristic period Tg, the peak ground acceleration \(a_{\max }\), and the attenuation index of descending segment and the adjustment factor of damping, respectively, as

$$ \gamma { = 1}{\text{.0 + }}\frac{{{0}{\text{.05}} - \zeta }}{{{0}{\text{.3 + 6}}\zeta }}\,{\text{and}}\,\eta { = 1}{\text{.0}} + \frac{0.05 - \zeta }{{0.08 - 1.6\zeta }} $$
(29)

From the given absolute acceleration design response spectrum \(S^{a}\), the relative displacement and relative velocity design response spectra \(S^{d}\) and \(S^{v}\) can be obtained approximately by using the so-called quasi spectrum transform relationship as.

$$ S^{d} \approx S^{a} {/}\omega^{2} $$
(30-1)
$$ S^{v} \approx S^{a} {/}\omega $$
(30-2)

where \(\omega\) denotes the natural frequency of single-degree-of-freedom system.

Fig. 4
figure 4

Absolute acceleration design response spectrum in Chinese Code for Seismic Design of Buildings (GB 2010)

Full size image

The above method to obtain the quasi relative displacement and velocity response spectra from the absolute acceleration design one is applicable to the under-damped cases of Eq. (20). Besides, the influence of over-damped modes on computational accuracy of RSM is evaluated in Sect. 5.3. Results indicate that the over-damped mode has less influence on accuracy of RSM even if it is arise from fundamental frequency and can therefore be neglected.

5 Numerical examples

The seismic responses of a 3-story and a 6-story shear structures on two types of sites are calculated using the SSI model and RSM in this section. The problem is introduced in the first. The effects of the SSI on the seismic response of structure are then discussed using time history analysis method, including the foundation rocking effect and the different LPM effect. The RSM is finally used and its effectiveness is verified by comparing with time history analysis.

5.1 Problem statement

Figure 5 shows the 3-story and the 6-story shear structures with circular rigid foundation setting on the surface of homogeneous half-space elastic soil subjected to horizontal seismic excitation. The radius and mass of foundation are 7 m and 2.513 × 105 kg, respectively. The mass moment of inertia of the rotational rigid structure for 3-story and 6-story structures are 4.916 × 106 kg/m2 and 6.858 × 106 kg/m2, respectively. With axial deformations in structural elements neglected, the mass of structures is lumped at the floor level, where mt denotes the mass at the tth floor, while kt denotes the condensed (lateral) stiffness term at the tth floor. The mass and stiffness coefficients are given as: m1 = m2 = m3 = m4 = m5 = 1.036 × 105 kg, m6 = 8.679 × 104 kg; and k1 = k2 = 9.460 × 104 kN/m, k3 = 9.260 × 104 kN/m, k4 = k5 = 8.295 × 104 kN/m, k6 = 3.336 × 104 kN/m. The story heights are 3.658 m.

Fig. 5
figure 5

Structures with shallow foundation subjected to horizontal seismic excitation

Full size image

The damping matrix of structure complies Rayleigh rule, i.e., \({\overline{\mathbf{C}}}_{RR} = \alpha {\overline{\mathbf{M}}}_{R} + \beta {\overline{\mathbf{K}}}_{RR}\), where α and β are 1.0700 and 0.0013 respectively for 3-story structure basing on the modal damping ratio of 5%, and 0.6048 and 0.0023 for 6-story structure.

Two typical sites with homogeneous soil, namely Site 1 and Site 2, are selected to study the influence of different site conditions on structural response and calculation accuracy of RSM. The soil density of 1560 kg/m3, shear wave velocity of 117 m/s, and Poisson ratio of 1/3 are chosen for Site 1; and the soil density of 1670 kg/m3, shear wave velocity of 253 m/s, and Poisson ratio of 1/3 for Site 2 are considered. The two sites belong to Class IV and II respectively according to the Chinese seismic code (GB 2010).

It is assumed that the structure is located in the region of a seismic intensity of Degree 7. The corresponding peak ground acceleration (PGA) is 0.12 g and 0.10 g for Site 1 and Site 2 respectively (i.e. probability of exceedance of 10% in 50 years) according to the Chinese seismic code (GB 2010), as shown in Table 1. Therefore, two different ground design response spectra as shown in Fig. 6 are used for the two sites. For each design spectrum, of which seven artificial ground motions are generated to be compatible with it. The response spectra of the seven artificial ground motions are also given in Fig. 6.

Table 1 Adjustment coefficient of peak ground acceleration of site
Full size table
Fig. 6
figure 6

Seismic acceleration response spectra with 5% damping ratio for a Site 1 and b Site 2

Full size image

5.2 SSI effects on seismic response of structure

The seismic responses of the 3-story and 6-story shear structures on the two sites are calculated using time history analysis method. To study the effects of SSI on the seismic responses of structures, the Models 1, 2 and 3 mentioned above are all used for each case. In Models 2 and 3, the parameters of the rational-approximation-based LPMs are obtained according to the method in (Du and Zhao 2010) and are listed in Tables 2 and 3, respectively. To study the effects by using different LPMs on the structural responses, the simple LPM consisting parallel spring and dashpot elements is used in Model 3, too. The parameters of the simple LPM are same as K0 and C0 of the rational-approximation-based LPM. Signal 1 as shown in Fig. 6 is used for the time history analysis, and its acceleration time history is shown in Fig. 7. The numbers of degrees of freedom of models are presented Table 4.

Table 2 Parameters of rational-approximation-based LPM for Model 2
Full size table
Table 3 Parameters of rational-approximation-based LPMs for Model 3
Full size table
Fig. 7
figure 7

Seismic acceleration time history of Signal 1 for a Site 1 and b Site 2

Full size image
Table 4 Numbers of degrees of freedom of models
Full size table

Peak values of story drifts of the 3-story and 6-story structures are shown in Figs. 8 and 9, respectively. The differences between the results using Model 1, Model 2 and Model 3 with simple LPM and those using Model 3 with accurate rational-approximation-based LPM are calculated, and the maximum values among all floors are shown in figures. Some conclusions can be drawn for the 3-story structure from Fig. 8 as follows. For the soft soil Site 1, the SSI and rocking effects on structural responses are 7.73% and 13.29%, respectively, and the effect of different LPMs is only 0.62%. For the relatively hard soil Site 2, the effects of above factors are all less than 2%. Moreover, the Model 2 considers the SSI in the horizontal direction only, and the soil radiation damping may make the structural response is less than that of Model 1. The Model 3 considers the SSI in the horizontal direction but also rotational direction, and the latter may make the structural response is more than that of Model 1. Therefore, the Model 1 may give results closer to the Model 3 than the Model 2, as shown in Fig. 8. It can be seen for the 6-story structure from Fig. 9 that the effects of above factors are from 14.16 to 16.43% for the soft soil Site 1, and from 10.06 to 11.12% for the relatively hard soil Site 2. By comparing Figs. 8 and 9, it can be seen that the rocking SSI should be considered and the accurate LPM should be used in seismic analysis of relatively high structure on soft soil site.

Fig. 8
figure 8

Peak values of story drifts (PSD) of 3-story structure on a Site 1 and b Site 2 using four calculation models under Signal 1

Full size image
Fig. 9
figure 9

Peak values of story drifts (PSD) of 6-story structure on a Site 1 and b Site 2 using four calculation models under Signal 1

Full size image

5.3 SSI analysis using RSM under response spectra of earthquake motions

The seismic responses of the 6-story shear structure on the two sites are calculated using RSM. The Model 3 with the accurate rational-approximation-based LPM is used to consider the coupled horizontal and rocking SSI. The result is compared with that obtained by time history analysis to evaluate the accuracy of RSM. The fourteen artificial ground motions for two sites as shown in Fig. 6 are chosen for the RSM and time history analysis.

Before using RSM to solve the SSI model, the natural frequencies and damping ratios of all single-degree-of-freedom systems of Eq. (20) are calculated by complex mode analysis in Eq. (19). When solving the generalized eigenvalue problem in Eq. (19), eight zero natural frequencies appear, due to the zero stiffness with respect to the eight auxiliary degrees of freedom in lumped parameter model. Their modes correspond to rigid body motion. Therefore, only the rest fifteen non-zero natural frequencies and corresponding damping ratios are shown in Table 5, and the corresponding fifteen effective modes are used. It can be seen from the table that the over-damped cases arise at the fundamental frequency and some large damping ratios also arise at different natural frequencies even if they belong to the under-damped cases.

Table 5 Natural frequencies and damping ratios of 6-story structure on Sites 1 and 2 using Model 3 with accurate LPMs
Full size table

Contribution of each mode especially the over-damped mode at fundamental frequency to accuracy of RSM is studied because RSM usually uses only several main modes instead of all ones for high efficiency. The contribution ratio of each mode is quantified by defining the following relative error.

$$ \overline{R} = \frac{{\left| {\left| {\overline{u}(t)} \right|_{{{\rm max}}} - \left| {u(t)} \right|_{{{\rm max}}} } \right|}}{{\left| {u(t)} \right|_{{{\rm max}}} }} $$
(31)

where \(\left| {u(t)} \right|_{\max }\) and \(\left| {\overline{u}(t)} \right|_{\max }\) are the peak values of story drifts obtained by RSM using fifteen modes and neglecting the jth mode, respectively.

The contribution ratio of mode is calculated according to Eq. (31) and shown in Fig. 10. Dotted line in Fig. 10 denotes the level of a contribution ratio of only 1%, and the jth mode can be neglected in the subsequent analysis if the result of the Eq. (31) is below this line. Some conclusions can be drawn from Fig. 10 as follows. The over-damped mode arising at the fundamental frequency has the contribution ratio of far less than 1% of the calculation accuracy of RSM, and it can be neglected in subsequent analysis. The 2nd mode corresponding to damping ratio of about 5% has the greatest contribution ratio, and it must be included in RSM. The 3rd and 4th modes corresponding to damping ratio of near 5% have relatively great contribution, and they should be considered for high accuracy in RSM. The other modes corresponding to damping ratio from 4 to 95% have the contribution ratios of less than 1%, and they can be neglected in subsequent RSM analysis.

Fig. 10
figure 10

Contribution ratio of jth mode on accuracy of RSM for 6-story structure on a Site 1 and b Site 2 using Model 3 with accurate LPMs under artificial ground motions

Full size image

The structural response is calculated using RSM and time history analysis respectively under each artificial ground motions. To improve efficiency, only the 2nd–4th order modes of structure are used in RSM. The results are also compared with that obtained using the RSM with all fifteen effective modes. The corresponding natural frequencies and damping ratios for the fifteen modes are shown in Table 5. To quantify the accuracy of RSM, an error of RSM relative to time history analysis is defined as

$$ R = \frac{{\left| {\left| {u(t)} \right|_{{{\rm max}}} - \left| {u_{0} (t)} \right|_{{{\rm max}}} } \right|}}{{\left| {u_{0} (t)} \right|_{{{\rm max}}} }} $$
(32)

where \(\left| {u(t)} \right|_{\max }\) and \(\left| {u_{0} (t)} \right|_{\max }\) are the peak values of story drifts obtained by RSM and time history analysis, respectively.

The results are shown in Fig. 11. The error of RSM relative to time history analysis according to Eq. (32) is given for each floor in the figure, and the error of RSM using fifteen modes at the location where maximum seismic response among six floors using time analysis method is listed in red box. It can be seen that the error of RSM using fifteen modes in the red box varies from 1.45 to 4.83% for the seven ground motions of soft soil Site 1, and from 1.33 to 16.65% for the seven ground motions of relatively hard soil Site 2. The mean values of the seven ground motions are 3.55% and 7.21% for the two sites. This indicates that RSM for the SSI model is accurate enough and can be used in seismic analysis. Besides, the error of RSM result from fifteen modes and only the 2nd–4th order modes are very close. It indicates that only several main modes can be used in RSM.

Fig. 11
figure 11

Peak values of story drifts (PSD) of 6-story structure on a Site 1 and b Site 2 using Model 3 with accurate LPMs under artificial ground motions

Full size image

5.4 SSI analysis using RSM under design response spectra

The example and model same as Sect. 5.3 are analyzed using RSM under design response spectra shown in Fig. 6 instead of response spectra of artificial ground motions.

The 2nd–4th order modes are used in RSM for higher efficiency. The studies in Sect. 5.3 indicate that the three modes result in very close computational results with fifteen modes. The relative displacement and relative velocity design response spectra of the 2nd–4th order modes with different damping ratios are required in RSM. They are obtained from the given absolute acceleration design response spectrum with a 5% damping ratio shown in Fig. 6 by the approximately quasi spectrum transform relationship presented in the Sect. 4.2. In order to verify the process, the so-called quasi relative displacement and velocity response spectra are compared with the mean response spectra of seven artificial ground motions obtained by solved Eq. (20), as shown in Fig. 12. In this figure, the blue circle locates at the natural frequencies shown in Table 5, which are used in calculation. It can be seen from the figure that the obtained quasi relative displacement and velocity response spectra are very close to the corresponding mean response spectra of seven artificial ground motions.

Fig. 12
figure 12

Quasi spectra and mean spectra of seven ground motions for different damping ratios on a Site 1 and b Site 2

Full size image

Peak values of story drifts of the 6-story structure obtained using RSM under the design response spectra and mean spectra of seven artificial ground motions are shown in Fig. 13. In addition, the mean value of peak value responses of structure obtained by time history analysis under seven artificial ground motions shown in Fig. 6 are also shown in Fig. 13 for comparison. The numbers at the side of the striped columns denote the errors in Eq. (32) between RSM and time history analysis method, and the error at the location where maximum seismic response among six floors using time analysis method is listed in red box. The following conclusions can be drawn from the Fig. 13. The errors in the red boxes under design response spectra are close to those under mean response spectra of artificial ground motions, indicating that the method of obtaining quasi relative displacement and relative velocity response spectra is feasible. The errors in the red boxes for the Site 1 and Site 2 are less than 3% and 12% respectively, indicating that RSM is accurate enough and can be used in the seismic analysis.

Fig. 13
figure 13

Peak values of story drifts (PSD) of 6-story structure on a Site 1 and b Site 2 using Model 3 with accurate LPMs under design response spectra

Full size image

6 Conclusion

Seismic SSI of structure with shallow foundation was studied using RSM. Several conclusions are drawn by analyzing the 3-story and 6-story shear structures on two different types of sites under design response spectra. (1) The coupling of the rocking motion of structural foundation with its horizontal motion should be considered for relatively high structures on soft soil site. (2) The accurate LPM such as that based on rational approximation of foundation impedance function should be used in the SSI substructure model to consider the soil complex stiffness more accurate. (3) RSM is effective and applicable to seismic SSI analysis of structure with shallow foundation, where the over-damped mode can be neglected and the design response spectra can be used.

It should be noted that the above conclusions are obtained based on only the present models and examples in this paper. A complex stiffness of foundation and its time-domain model considering the hysteretic damping of site soil and deep foundation will be studied in the later work.