1 Introduction

The seismic performance of underground structures is generally regarded to be much better than aboveground structures. However, as one of the most characteristic cases of seismic damage to underground structures during the past earthquakes, severe damage to Daikai subway station during the Hyogoken-Nanbu earthquake in 1995 revealed the importance of seismic analysis and design of underground structures. Research on analysis and design of underground structures has developed rapidly in recent years (Amorosi and Boldini 2009; Hatzigeorgiou and Beskos 2010; Cilingir and Madabhushi 2011; Abuhajar et al. 2015; Tsinidis et al. 2016a, b, c; Yu et al. 2016, 2017; Huang et al. 2017; Tsinidis 2017; Zhao et al. 2017; Li et al. 2018). The existing methods for the seismic design of cross section of underground structures mainly include the seismic coefficient method, the free-field deformation method, the flexible coefficient method, the response deformation method, the response acceleration method and the Pushover analysis method (Hashash et al. 2001; GB 2014; Pitilakis and Tsinidis 2014).

Response spectrum method (RSM) has been widely applied in engineering practice to estimate the seismic response of aboveground structures such as buildings and bridges and so on since 1950s for its simplicity and efficiency (Sutharshana and Mcguire 1988; Singh et al. 2000; Chopra 2001, 2010; Berrah and Kausel 2010). RSM has also been incorporated into the codes for seismic design of aboveground structures in many countries (BSL 2000; Eurocode 8 2003; ICC 2003; GB 2010; CJJ 2012). In the last three decades, RSM has been further developed for more complicated aboveground systems with non-proportional damping and multi-point excitation (Maldonad and Singh 1991; Der Kiureghian and Neuenhofer 1992; Yu and Zhou 2008; Wang and Der Kiureghian 2015; Liu et al. 2016; Chen et al. 2017).

However, the RSM for underground structures in details is currently not available in the literatures. The main difficulties of applying RSM directly to the seismic analysis of underground structures include the following two aspects. On one hand, the underground design response spectra should be given in advance for the seismic analysis of underground structures using RSM. Unfortunately, many existing seismic codes and specifications provide only design response spectra on the ground surface, such as (Eurocode 8 2003; ICC 2003; GB 2010; CJJ 2012), expect for the Building Standard Law of Japan (BSL 2000). On the other hand, dynamic soil–structure interaction (SSI) (Luco and Contesse 1973; Wolf 1985, 1988; Lou et al. 2011) needs to be effectively considered in the seismic analysis of underground structures. Artificial boundary conditions (Zienkiewicz et al. 1988; Du and Zhao 2010a, b; Zhao et al. 2011, 2018a, b) and spatially varying seismic excitations are usually introduced into the SSI analysis models to reduce the geometrical scale of the model and improve computational efficiency. However, it will lead to a non-proportional damped SSI system subjected to multi-point excitations, which is very complicated and difficult for underground structure to solve using the RSM.

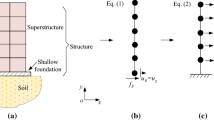
For RSM considering SSI, it can be generally divided into three main types, as shown in Fig. 1. Figure 1a presents the schematic of a typical aboveground structure considering SSI. Generally, the aboveground structure can be divided into two parts, namely the superstructure and the foundation. The soil below the foundation can be simplified as a multi-layer soil lying on a half-space bedrock. The left part of Fig. 1a shows one-dimensional (1D) site responses, where \(\ddot{u}_{bx}\), \(\ddot{u}_{by}\), \(\ddot{u}_{gx}\), and \(\ddot{u}_{gy}\) denote the horizontal and vertical earthquake motions at the soil–bedrock interface and on the ground surface, respectively.

Fig. 1
figure 1

Three main SSI analysis models for RSM: a SSI problem, b Model 1, c Model 2, and d Model 3

Full size image

Figure 1b shows the first type of the SSI analysis model of ground structure with shallow foundation that can be solved using RSM. The model divides the whole SSI system into two substructures, i.e., the superstructure and the foundation–soil–bedrock system. The former is modeled by finite element method and the latter is simplified as a lumped parameter model (Wolf 1994) that can be regarded as a generalized artificial boundary condition. Since the interface between two substructures consists of only one node due to the assumption of rigid foundation, it further simplifies the model subjected to a single-point excitation. Traditional RSM was adopted by researchers (Butt and Ishihara 2012; Raheem et al. 2014; Bhavikatti and Cholekar 2017) to calculate the above SSI analysis model with the lumped parameter model as horizontal, vertical and rotational linear springs. Other researchers (Asthana and Datta 1990; Gupta and Trifunac 1991; Tongaonkar and Jangid 2003; AIJ 2004; Yu and Zhou 2007) introduced dashpots into the lumped parameter model to simulate SSI and developed RSM for a non-proportional damping system.

Figure 1c shows the second type of SSI analysis model of ground structure with deep foundation such as pile foundation. This model divided the whole SSI system into the structure and soil–bedrock substructures. The former is modeled by finite element method and the latter as lumped parameter model that consists of either linear springs (Thakkar et al. 2002; Ates and Constantinou 2011; Chen 2014) or spring-dashpots (Kishida and Takewaki 2010; Kojima et al. 2014). The ground response spectrum is commonly used as the earthquake input by neglecting the space variations of earthquake ground motions, which simplifies the problem into a uniform excitation problem. RSM is subsequently adopted to estimate the seismic response of the structure.

Figure 1d shows the third type of model in which both the structure and a part of soil are modeled by the finite element method (Vidya et al. 2015; Singh and Mala 2017; Suman and Tengali 2017). In this model, the soil domain is truncated at the locations sufficiently far from the structure and no artificial boundary condition is applied at the truncation boundary of the soil domain. The response spectrum at the soil–bedrock interface is assumed to be given and enforced on the bedrock. The traditional RSM is then applied to solve the SSI model.

However, to the authors’ best knowledge, the detailed RSM for the seismic analysis and design of underground structure including SSI remains unavailable in literature. To develop RSM for underground structures, two important issues should be addressed as illustrated in Fig. 2. First, for an engineering site without site-specific seismic hazard analysis, only the ground design response spectrum is available in the seismic design codes, such as in the Chinese codes (GB 2010, 2014). A practical method should be developed first to appropriately estimate the underground design response spectrum at the soil–bedrock interface from the given ground design response spectrum, as shown in Fig. 2a. Second, the reasonable SSI analysis model for the underground structure should be established so that the traditional RSM can be applied directly to the model, as shown in Fig. 2b.

Fig. 2
figure 2

Schematic of RSM for seismic analysis of underground structure including SSI

Full size image

In this paper, the RSM is developed for the seismic analysis of underground structure including SSI. The resting parts of this paper are organized as follows. The underground design response spectrum at the soil–bedrock interface is derived from the given one on the ground surface in Sect. 2. The SSI analysis model consisting of the underground structure and its adjacent soil is established in Sect. 3. The RSM is used to solve the SSI analysis model under the underground design response spectrum in Sect. 4. The numerical examples are given to demonstrate the effectiveness of the RSM in Sect. 5. Conclusions follow in Sect. 6.

2 Underground design response spectrum

Underground design response spectrum at the soil–bedrock interface can be obtained by two ways. The first way is to perform the site-specific seismic hazard analysis to obtain the response spectrum at bedrock outcrop, and then derive the response spectrum at the soil–bedrock interface through 1D site response analysis. When no site-specific seismic hazard analysis is performed, the response spectrum at the soil–bedrock interface can be determined only according to the seismic design code such as the Chinese Code for Seismic Design of Urban Rail Transit Structures (GB 2014). However, only the design response spectrum at the ground surface is available in the seismic design code, and therefore the underground design response spectrum at the soil–bedrock interface requires back-calculation. In this section, two different methods are presented to back-calculate the underground design response spectrum at the soil–bedrock interface from a given design response spectrum at the ground surface, as shown in Fig. 3.

Fig. 3
figure 3

Design response spectrum at soil–bedrock interface obtained from that on ground surface: a Method 1 and b Method 2

Full size image

2.1 Method 1

Method 1 is developed based on the approximate relationship between the power spectral density function and the response spectrum proposed by Gasparini and Vanmarcke (1976). The basic steps of this method are illustrated in Fig. 3a and summarized as follows. First, the power spectral density function on the ground surface, \(G_{g}\), is derived from a given ground acceleration response spectrum, \(S_{g}^{{}}\). Second, the power spectral density function at the soil–bedrock interface, \(G_{b}\), is back-calculated by the 1D site transfer function. Third, the underground design acceleration response spectrum at the soil–bedrock interface, \(S_{b}^{{}}\), is obtained based on the approximate relationship between the power spectral density function and the response spectrum.

Details of the procedure are illustrated as follows. According to the random vibration theory, the acceleration response spectrum can be obtained from the power spectral density function of the stationary excitation (Gasparini and Vanmarcke 1976). The relation between the ground response spectrum and its corresponding power spectral density function can be written as

$$S_{g}^{{}} (\zeta ,\omega ) = r(\omega )\sigma (\zeta ,\omega )$$
(1)

with

$$r(\omega ) = \sqrt {2\ln ( 2ft_{1} )} + \frac{0.5772}{{\sqrt {2\ln (2ft_{1} )} }}$$
(2)
$$\sigma (\zeta ,\omega ) = \sqrt {\int_{0}^{\infty } {G_{g} (\bar{\omega })\frac{{\omega^{4} + 4\omega^{2} \zeta^{2} \bar{\omega }^{2} }}{{(\bar{\omega }^{2} - \omega^{2} ) + 4\omega^{2} \zeta^{2} \bar{\omega }^{2} }}} d\bar{\omega }}$$
(3)

where \(\omega\) and \(\zeta\) are the natural circular frequency and damping ratio of a single-degree-of-freedom system, respectively; \(S_{g}^{{}} (\zeta ,\omega )\) is the ground acceleration response spectrum; \(r(\omega )\) and \(\sigma (\zeta ,\omega )\) are the peak factor and standard deviation of the response spectrum, respectively; f is the expected frequency and \(f \approx \frac{\omega }{2\pi }\); t1 is the duration of the ground acceleration time history; \(\bar{\omega }\) is the circular frequency; and \(G_{g} (\bar{\omega })\) is the power spectral density function of the stationary ground earthquake excitation.

Using Eqs. (1)–(3) and iteration approach, the power spectral density function of the earthquake excitation is first obtained from the given design response spectrum on the ground surface. An initial power spectral density function \(G_{g}^{ ( 1 )} (\bar{\omega })\) is given according to Kaul (1978), and the corresponding response spectrum \(S_{g}^{ ( 1 )} (\zeta ,\omega )\) is calculated from Eqs. (1) to (3). The following iteration is performed

$$G_{g}^{{ (l{ + 1)}}} (\bar{\omega }) = G_{g}^{ (l )} (\bar{\omega })\frac{{S_{g}^{2} (\zeta ,\omega )}}{{S_{g}^{ (l ) 2} (\zeta ,\omega )}}\quad {\text{for}}\quad l = 1,2, \ldots$$
(4)

In each iteration step, the response spectrum \(S_{g}^{ (l )} (\zeta ,\omega )\) is calculated from the power spectral density function \(G_{g}^{ (l )} (\bar{\omega })\) by using Eqs. (1)–(3). The iteration is terminated until the maximum relative error calculated using Eq. (5) less than a given tolerance such as 1%.

$$E\text{(}\omega \text{) = }\frac{{\left| {S_{g}^{(l)} (\zeta ,\omega ) - S_{g}^{{}} (\zeta ,\omega )} \right|}}{{S_{g}^{{}} (\zeta ,\omega )}}$$
(5)

where | | denotes the absolute of a real value.

The power spectral density function is subsequently transferred from the ground surface to the soil–bedrock interface through the transfer function obtained from 1D site response analysis. The power spectral density function at the soil–bedrock interface, \(G_{b} (\bar{\omega })\), can be written as (Afra and Pecker 2002).

$$G_{b} (\bar{\omega }) = \left| {H_{bg} (\bar{\omega })} \right|^{2} G_{g} (\bar{\omega })$$
(6)

where | | denotes the modulus of a complex number; \(H_{bg} (\bar{\omega })\) is the 1D site transfer function from the ground surface to the soil–bedrock interface, which is written as (Liu et al. 2017).

$$H_{bg} (\bar{\omega }) = \frac{ 2}{{\text{sum(}{\mathbf{E}}_{N} )}}$$
(7)
$${\mathbf{E}}_{N} = \left( {\mathop \prod \limits_{n = 1}^{N} {\mathbf{T}}_{n} } \right){\mathbf{I}}$$
(8)
$${\mathbf{T}}_{n} = \frac{1}{2}\left[ \begin{aligned} \left( {1 + \frac{{\rho_{n} c_{n} }}{{\rho_{{n{ + 1}}} c_{n + 1} }}} \right)e^{{\frac{{i\bar{\omega }h_{n} }}{{c_{n} }}}} \, \left( {1 - \frac{{\rho_{n} c_{n} }}{{\rho_{{n{ + 1}}} c_{n + 1} }}} \right)e^{{ - \frac{{i\bar{\omega }h_{n} }}{{c_{n} }}}} \hfill \\ \left( {1 - \frac{{\rho_{n} c_{n} }}{{\rho_{{n{ + 1}}} c_{n + 1} }}} \right)e^{{\frac{{i\bar{\omega }h_{n} }}{{c_{n} }}}} \, \left( {1 + \frac{{\rho_{n} c_{n} }}{{\rho_{{n{ + 1}}} c_{n + 1} }}} \right)e^{{ - \frac{{i\bar{\omega }h_{n} }}{{c_{n} }}}} \hfill \\ \end{aligned} \right]$$
(9)
$$c_{n} = \sqrt {\frac{{G_{n} (1 + i2\hat{\zeta }_{n} )}}{{\rho_{n} }}}$$
(10)

where sum() denotes the sum of all elements of a vector; N denotes the total number of soil layers; I is the unit vector; \(\prod\) denotes the continued multiplication; i is the imaginary unit; and \(\rho_{n}\), \(G_{n}\), \(\hat{\zeta }_{n}\), cn and hn are the density, shear modulus, hysteretic damping ratio, complex wave velocity and height of the n-th soil layer, respectively.

Based on the relation between the response spectrum and the power spectral density function as listed from Eqs. (1) to (3), the underground response spectrum at the soil–bedrock interface can be finally obtained from the power spectral density function at the soil–bedrock interface trough numerical quadrature.

2.2 Method 2

Method 2 is established based on the random vibration theory and the synthesis of ground motions (Gasparini and Vanmarcke 1976). The basic steps of this method are illustrated in Fig. 3b and summarized as follows. First, an ensemble of artificial ground earthquake motions, \(\ddot{u}_{g}\), which are compatible with the given ground acceleration response spectrum, \(S_{g}^{{}}\), is generated. Second, the corresponding motions at the soil–bedrock interface, \(\ddot{u}_{b}\), are subsequently obtained using the 1D site transfer function between the soil–bedrock interface and the ground surface. Third, the design acceleration response spectrum at the soil–bedrock interface, \(S_{b}^{{}}\), is established as the average response spectrum of the ensemble of motions at the soil–bedrock interface.

Details of the procedure are illustrated as follows. An ensemble of artificial ground earthquake motions are first generated based on the given ground design response spectrum using the method developed by Gasparini and Vanmarcke (1976). Each artificial ground earthquake motion is then transferred from the ground surface to the soil–bedrock interface by the following relation

$$A_{b} (\bar{\omega }) = H_{bg} (\bar{\omega })A_{g} (\bar{\omega })$$
(11)

where \(A_{b} (\bar{\omega })\) and \(A_{g} (\bar{\omega })\) are the Fourier spectra of the artificial earthquake motions at the soil–bedrock interface and on the ground surface, respectively; and \(H_{bg} (\bar{\omega })\) is the same 1D site transfer function as shown in Eq. (7). The average response spectrum of the artificial earthquake motions at the soil–bedrock interface is finally obtained as the underground design response spectrum at the soil–bedrock interface.

Statistically, with the generation of sufficient number of the artificial ground earthquake motions, the accurate underground design response spectrum at the soil–bedrock interface can be basically obtained using Method 2. However, it is much more computationally costly compared to Method 1. The two methods will be compared in this Sect 5.3 by the numerical cases.

3 SSI analysis model

Figure 4 presents a schematic of SSI analysis model for the underground structure for RSM. Both the underground structure and the finite soil domain are modeled by the finite element method. Moreover, it is assumed full bond at the interface between the soil and the underground structure without slippage at low intensity of ground shaking. The contact between soil and structure is adopted by tied approach. In the SSI analysis model, roller boundary conditions are applied to the truncation side boundaries of the soil domain in order to consider the effect of the truncated infinite soil domain. The 1D free field motion at the soil–bedrock interface is enforced at the bottom boundary of the model to consider the uniform input of earthquake excitation. That means all the nodes at the bottom boundary of the SSI analysis model are excited using the same input motions, i.e., the earthquake excitation does not vary along the soil–bedrock interface. The dynamic equation of the finite element model of SSI system as shown in Fig. 4 can be written as

$${\mathbf{M}}{\mathbf{\ddot{u}}}\text{(}t\text{)} + {\mathbf{C}}{\dot{\mathbf{u}}}\text{(}t\text{)} + {\mathbf{K}}{\mathbf{u}}\text{(}t\text{)} = - {\mathbf{MI}}\ddot{u}_{bx} \text{(}t\text{)}$$
(12)

where M and K are, respectively, the mass and stiffness matrices of the SSI system including the structure and its adjacent soil; C is the modal damping matrix; I is the unit vector; t is the time; \({\mathbf{u}}\text{(}t\text{)}\) is the displacement vector relative to the bedrock motion; the dot over the variable denotes the derivative to time; and \(\ddot{u}_{bx} \text{(}t\text{)}\) is the acceleration time history of the bedrock motion that is the 1D free field response at the soil–bedrock interface.

Fig. 4
figure 4

SSI analysis model of underground structure for RSM

Full size image

The above SSI analysis model including the underground structure and the finite part of soil can consider the SSI effect more accurate than the substructure model. The reason is that the roller boundary condition at the two side boundaries can effectively simulate the seismic free field response of 1D site, and the seismic response at the side boundaries are dominated by the free field response when the side boundaries are sufficiently far from the structure. Based on the numerical studies presented later in Sect. 5.4, it was found that the roller boundary condition at the side boundaries can effectively simulate the seismic response of SSI with high accuracy. Besides, the roller boundary condition also has the advantage of avoiding introducing non-proportional damping and multi-point excitation to the SSI system. Therefore, the traditional RSM can be directly applied to this SSI system to estimate the seismic response of underground structures.

4 RSM for SSI analysis model under underground design response spectrum

For a site with multiple soil layers and a given ground design response spectrum, the detailed procedures of the RSM for the seismic analysis of underground structures are summarized as follows. First, for a given site with multiple soil layers, determine the ground design response spectrum according to the seismic design codes, such as the Chinese Seismic Design Code of Urban Rail Transit Structures (GB 2014). Second, adopt either Method 1 or Method 2 as illustrated in Sect. 2 to obtain the underground design response spectrum at the soil–bedrock interface. Third, build a finite element model of the underground structure considering SSI as discussed in Sect. 3 in commercial finite element software such as ABAQUS (2012). Fourth, use the traditional RSM to solve the above finite element model with the underground design response spectrum at soil–bedrock interface. The RSM is briefly introduced in this section for completeness.

For the SSI analysis model mentioned in Sect. 3, the generalized eigenvalue problem of the mass and stiffness matrices of Eq. (12) can be written as

$$({\mathbf{K}} - \omega^{2} {\mathbf{M}}){\mathbf{X}} = {\mathbf{0}}$$
(13)

The natural frequencies \(\omega_{j}\) and modal shape vectors Xj of the first J order for j = 1, 2, … J can be obtained by solving Eq. (13).

The displacement vector can be written as the following modal superposition form

$${\mathbf{u}}(t) = \sum\limits_{j = 1}^{J} {{\mathbf{X}}_{j} \gamma_{j} \delta_{j} (t)}$$
(14)

where \(\delta_{j} (t)\) is the displacement of a single-degree-of-freedom system; and \(\gamma_{j}\) is the modal participation coefficient as

$$\gamma_{j} = \frac{{{\mathbf{X}}_{j}^{T} {\mathbf{MI}}}}{{{\mathbf{X}}_{j}^{T} {\mathbf{MX}}_{j} }}$$
(15)

where the superscript T denotes the transposition of a vector; and I is the unit vector.

Substituting Eq. (14) into Eq. (12) and using the orthogonality of the modal shapes, obtain the dynamic equations of the single-degree-of-freedom systems of the j modal shapes. The equation of the j-th order modal shape can be written as

$$\ddot{\delta }_{j} \text{(}t\text{)} + \text{2}\zeta_{j} \omega_{j} \dot{\delta }_{j} \text{(}t\text{)} + \omega_{j}^{\text{2}} \delta_{j} \text{(}t\text{)} = - \ddot{u}_{bx} \text{(}t\text{)}$$
(16)

where \(\zeta_{j}\) is the modal damping ratio that satisfies the following relation

$$2\zeta_{j} \omega_{j} = \frac{{{\mathbf{X}}_{j}^{T} {\mathbf{CX}}_{j} }}{{{\mathbf{X}}_{j}^{T} {\mathbf{MX}}_{j} }}$$
(17)

The RSM calculates the maximum response of Eq. (16) by using the response spectrum of the earthquake motion at the soil–bedrock interface. The complete quadratic combination (CQC) (Wilson et al. 1981) is adopted to combine these maximum responses of the modal shapes to obtain the maximum response of the SSI system as

$$\left| {{\mathbf{u}}(t)} \right|_{{\text{max}}} = \sqrt {\sum\nolimits_{l = 1}^{J} {\sum\nolimits_{j = 1}^{J} {\beta_{lj} \gamma_{l} \tilde{S}_{b} (\omega_{l} ,\zeta_{l} )\gamma_{j} \tilde{S}_{b} (\omega_{j} ,\zeta_{j} ){\mathbf{X}}_{l} * {\mathbf{X}}_{j} } } }$$
(18)

where | | and max denote the absolute and maximum of each element of a vector; \(\tilde{S}_{b} (\omega_{j} ,\zeta_{j} ) = \left| {\delta_{j} (t)} \right|_{{\text{max}}}\) is the underground displacement response spectrum at the soil–bedrock interface; * denotes the multiplies arrays Xi and Xj element by element; and \(\beta_{lj}\) is the cross-correlation function between the l-th and j-th modal shapes, which can be written as

$$\beta_{lj} = \frac{{8(\omega_{l} \zeta_{l} + \omega_{j} \zeta_{j} )(\omega_{l} \omega_{j} )^{3/2} (\zeta_{l} \zeta_{j} )^{1/2} }}{{ 2(\omega_{l} \zeta_{l} + \omega_{j} \zeta_{j} )^{2} (\omega_{l}^{2} + \omega_{j}^{2} ) + (\omega_{l}^{2} - \omega_{j}^{2} )^{2} }}$$
(19)

The maximum response of the SSI system can also be expressed by the acceleration response spectrum \(S_{b} (\omega_{j} ,\zeta_{j} )\) by using the relation between the acceleration and displacement response spectrums.

It should be noted that the modal analysis and CQC can be also performed in the commercial finite element software such as ABAQUS. Numerical examples will be represented later in Sects. 5.5 and 5.6 to further demonstrate the procedures and accuracy of the RSM for underground structures considering SSI.

5 Validation of RSM for seismic analysis of underground structure

To demonstrate the effectiveness of the RSM for the underground structures considering SSI, the numerical results from three case studies, namely a one-storey two-span subway station, a two-storey three-span subway station, and a bored tunnel are presented in this section. Besides, the RSM is applied to calculate the dynamic response of a three-dimensional (3D) model of the one-storey two-span station to further demonstrate the feasibility of the RSM to more complicated case study. The accuracy of results from the RSM for the underground structure is also discussed herein.

5.1 Problem statement

Three typical cross sections of underground structures with detailed geometries are shown in Fig. 5. The burial depth and material properties for the structures are listed in Table 1. Two typical sites with multiple soil layers on half-space bedrock, namely Site 1 and Site 2, were selected in this study. The site conditions including the geometry and material constants of each soil layer and bedrock are listed in Tables 2 and 3. The bedrock is assumed as linearly elastic material. The soil parameters for equivalent linearization (curves of dynamic shear modulus ratio and dynamic equivalent hysteretic damping ratio with shear strain) are obtained from reference (Schnabel et al. 1972) and Site Safety Assessment Report, respectively, for Site 1 and Site 2. They are shown in Fig. 6 according to soil class numbers that are listed in Tables 2 and 3 for each soil layer. Therefore, a total of six two-dimensional (2D) SSI analysis models were built in ABAQUS as shown in Fig. 7 to validate the RSM for underground structure. The widths of model for one-storey two-span station, two-storey three-span station and tunnel are 85 m, 110 m and 50 m, respectively. The finite element mesh size of soils and structures are 1 × 1 m and 0.2 × 0.2 m, respectively, which satisfies the accuracy requirement for the dynamic analysis. The roller boundary conditions as discussed in the previous section were applied at the two side boundaries of the models.

Fig. 5
figure 5

Three kinds of underground structures: a one-storey two-span subway station, b two-storey three-span subway station, and c bored tunnel. The unit of length is m

Full size image
Table 1 Burial depth and material properties for three structures
Full size table
Table 2 Geometry and material constants of Site 1
Full size table
Table 3 Geometry and material constants of Site 2
Full size table
Fig. 6
figure 6

Curves of dynamic shear modulus ratio and dynamic equivalent hysteretic damping ratio with shear strain, where number denotes soil class

Full size image
Fig. 7
figure 7

Finite element models of SSI systems: a 1-storey 2-span station with site 1, b 2-storey 3-span station with site 1, c tunnel with site 1, d 1-storey 2-span station with site 2, e 2-storey 3-span station with site 2, and f tunnel with site 2

Full size image

According to the Chinese Code for Seismic Design of Urban Rail Transit Structures (GB 2014), it is assumed that the underground structure is located in the region of a seismic intensity of Degree 7. Two sites as shown in Tables 2 and 3 are class II and III respectively according the seismic design code (GB 2014). Besides, the corresponding peak ground acceleration (PGA) is 0.1 g and 0.125 g for Site 1 and Site 2, respectively (i.e. probability of exceedance of 10% in 50 years). Therefore, two different ground design response spectra as shown in Fig. 8 are used for the two sites. The standard damping ratio of 5% is chosen. Fourteen artificial ground motion time histories were generated to be compatible with the ground design response spectrum, of which thier response spectra are shown in Fig. 8.

Fig. 8
figure 8

Seismic acceleration response spectra on ground surface for a site 1, and b site 2

Full size image

5.2 Damping model

Given the low seismic intensity of the design earthquake and the relatively good site conditions, the underground structure and the surrounding soil can be assumed as linear elastic material with damping during the design earthquake according to the requirement of the seismic design code (GB 2014).

It should be noted that the determination of the underground design response spectrum requires the hysteretic damping \(\hat{\zeta }_{n}\) in Eq. (10), while the RSM requires the modal damping \(\zeta_{j}\) of SSI system in Eq. (16). In this study, the modal damping of the SSI system is assumed to be the same as the modal damping of the site, due to the small dimension of structure relative to site.

The hysteretic damping and modal damping of the two sites are determined by comparing the results of the site response analysis using the hysteretic damping and modal damping with that based on the equivalent linearization. Figure 9 shows the acceleration time histories used in the site response analysis, where Fig. 9a shows the Record 1 in Figs. 8a, 9b shows the Record 1 in Figs. 8b, 9c, d are the corresponding records at the soil–bedrock interface obtained by Method 2 of Sect. 2, respectively, for Sites1 and 2. Figure 10 shows the peak relative horizontal displacements with respect to the bedrock varying as depth. The hysteretic damping ratio in each soil layer and the modal damping ratio for each modal shape of whole soil system are all 5%. It can be seen from Fig. 10 that the 1D site responses using both the hysteretic and modal damping are close to that based on the equivalent linearization. Actually, it has been demonstrated in the reference (Hu 2006) that the difference of results between using the hysteretic and modal damping is small when the damping is small.

Fig. 9
figure 9

Acceleration time histories of record 1 a on ground surface for site 1, b on ground surface for site 2, c at soil–bedrock interface for site 1, and d at soil–bedrock interface for site 2

Full size image
Fig. 10
figure 10

The peak values of horizontal displacements relative to that at soil–bedrock interface varying as depth. The results are obtained by three different soil models, i.e., equivalent linearization, hysteretic damping and modal damping

Full size image

5.3 Underground design response spectrum

The underground design response spectra obtained from the two methods in Sect. 2 are compared here by the numerical cases. The hysteretic damping ratio in 1D site transfer function as shown in Eq. (7) is 5% for each soil layer, and the rationality is illustrated in previous section. The underground design response spectra at the soil–bedrock interface obtained using the two methods are compared in Figs. 11 and 12, respectively, for Site 1 and Site 2. Figure 11a shows the transfer function for Site 1 using Eq. (7). The response spectrum at the soil–bedrock interface obtained using the Method 2 from the seven artificial records compatible with the ground design response spectra are shown in Fig. 11b. Figure 11c compares the response spectrum calculated using Method 1 and the average response spectrum at the soil–bedrock interface shown in Fig. 11b, which shows favorable agreement. Similar results can be found in Fig. 12 for Site 2.

Fig. 11
figure 11

Seismic acceleration response spectrums at soil–bedrock interface of Site 1: a amplitude of 1D site transfer function, b response spectrums of artificial earthquake motions, and c design response spectrums

Full size image
Fig. 12
figure 12

Seismic acceleration response spectrums at soil–bedrock interface of site 2: a amplitude of 1D site transfer function, b response spectrums of artificial earthquake motions, and c design response spectrums

Full size image

5.4 Accuracy of SSI analysis model

Before the validation of the RSM for the seismic response analysis of underground structures, the accuracy of the truncation SSI analysis model as discussed in Sect. 3 is verified first. A reference SSI analysis model with sufficiently large geometries were used and obtained by extending the truncation model. The width of reference model is 8000 m, which is sufficiently large to ensure no wave reflected from the two side boundaries to affect the structural response in the finite analysis time. The same finite element mesh size, boundary condition, earthquake motion and damping are used in the reference model as those for the truncation model. The roller boundary conditions were also applied to the side boundaries of reference model. The same free field motion is inputted at the bottom boundary of the reference model.

The artificial records at the soil–bedrock interface obtained from Record 1 as shown in Fig. 9 are used as the input for both models. As mentioned in Sect. 5.2, the modal damping ratio of 5% is used for each modal shape of the SSI analysis model. In order to study the accuracy of only the SSI analysis model and avoid introducing the error of RSM, the time history analysis should be performed for both the SSI analysis model and reference models. However, because the modal damping cannot be provided in the time history analysis of ABAQUS, the modal superposition method (Clough and Penzien 1993) is adopted in this study, which can give the same accurate solution as the time history analysis if a sufficient number of modes are selected.

The top of the central column of one-storey two-span station, the top of the left column of first floor of two-storey three-span station, and the vault of the bored tunnel, as shown in Fig. 5, are selected as the representative nodes and the seismic response of those nodes were extracted from the numerical analyses for comparison purposes. Besides, a relative error of peak displacements of a representative node on the structure obtained from the SSI analysis model and the reference models, as defined in Eq. (20), is used to quantify the solution accuracy.

$$R_{\hbox{max} } = \frac{{\left| {\left| {r(t)} \right|_{{\text{max}}} - \left| {r_{0} (t)} \right|_{{\text{max}}} } \right|}}{{\left| {r_{0} (t)} \right|_{{\text{max}}} }}$$
(20)

where r(t) and r0(t) are the peak displacements of a representative node on the structure obtained from the SSI analysis model and the reference models, respectively; | | and max denote the absolute and maximum values, respectively.

Figure 13 presents the horizontal displacement time histories of the representative nodes on the structures relative to bedrock motions obtained from the aforementioned two models. It can be seen from Fig. 13 that all the horizontal displacement time histories of the representative nodes relative to bedrock motions obtained from the SSI analysis model and the reference model agree very well. The relative errors of peak displacement for three structures with Site 1 are smaller than 2%. Even for more complicated Sites 2, the error of peak displacements for three structures are also smaller than 3%, indicating that the SSI analysis models as shown in Fig. 4 and concretely in Fig. 7 are accurate enough and can be used in the numerical analyses. Besides, it can also be seen from the figure that the seismic responses of same underground structures in two sites are obvious different because of the different site conditions.

Fig. 13
figure 13

Horizontal displacement time histories of structures relative to bedrock motions under record 1 at a the top of central column of 1-storey 2-span station with site 1, b the top of left column on first floor of 2-storey 3-span station with site 1, c the crown of tunnel with site 1, d the top of central column of 1-storey 2-span station with site 2, e the top of left column on first floor of 2-storey 3-span station with site 2, and f the crown of tunnel with site 2

Full size image

5.5 Accuracy of RSM for 2D SSI analysis

The RSM is evaluated in this subsection by calculating the dynamic responses of three different underground structures in two different sites as shown in Fig. 7. For conciseness, only the dynamic responses of the representative nodes of each model are plotted.

The response spectra of seven artificial records at the soil–bedrock interface as shown in Figs. 11b and 12b obtained using the Method 2 of Sect. 2 from the ones on the ground surface are used as the inputs for the SSI analysis models to validate the accuracy of RSM itself. Moreover, the underground design response spectra at the soil–bedrock surface obtained using the Methods 1 and 2 of Sect. 2 as shown in Figs. 11c and 12c are used to evaluate the effectiveness of RSM under underground design response spectra and to compare the differences of deriving underground design response spectra using the two methods.

In the numerical analyses using RSM, the first 20 modal shapes are extracted from the modal analyses and the CQC is adopted to estimate the maximum response of the underground structures. The number of modal shapes can ensure to obtain the sufficiently accurate results. The modal damping ratio of 5% is used for each modal shape of the SSI system. The rationality of the damping model is presented previously in Sect. 5.2. To consider the modal damping, as stated in Sect. 5.4, the numerical results of the case studies obtained using the modal superposition method (Clough and Penzien 1993) instead of the time history method is used as reference to validate the proposed RSM.

Seismic responses of the three types of structures in Sites 1 and 2 (Fig. 7) under the artificial earthquake motions (Figs. 11b and 12b) are shown in Figs. 14, 15, 16. The seismic responses include the displacements at the top of the central column of one-storey two-span station, and the top of the left column of first floor of two-storey three-span station and the vault of tunnel relative to bedrock motions, and the shear and normal stresses at the bottom of these columns and vault. In Figs. 14, 15, 16, the numbers above the striped columns denote the error in Eq. (20) between the RSM and modal superposition method. It can be seen from the three figures that the average errors of the displacements of the one-storey two-span station, the two-storey three-span station and the tunnel relative to bedrock motions are all less than 6%. The average errors of the shear and normal stresses of the three structures are all less than 10%. Moreover, on the right side of the figures, the average responses of underground structures obtained from the modal superposition method, and the responses obtained directly from the RSM with the underground design response spectrum generated through Methods 1 and 2 are compared. It can be seen from these figures that the differences of the displacement and stresses for Method 1 relative to modal superposition method are less than 15%. The differences of the displacement and stresses for Method 2 relative to modal superposition method are less than 10%.

Fig. 14
figure 14

Peak displacement solutions of three structures relative to bedrock motions in two sites under artificial earthquake motions and design spectra

Full size image
Fig. 15
figure 15

Shear stress solutions of three structures in two sites under artificial earthquake motions and design spectra

Full size image
Fig. 16
figure 16

Normal stress solutions of three structures in two sites under artificial earthquake motions and design spectra

Full size image

5.6 Accuracy of RSM for 3D SSI analysis

The 3D SSI analysis of the one-storey two-span subway station with Site 1 is performed using the RSM. The finite element model is shown in Fig. 17. The longitudinal width of the central column of the station is 1 m and the column spacing is 2.5 m. The number of nodes and elements are 552,041 and 450,323, respectively. The finite element mesh size satisfies the accuracy requirement for the dynamic analysis. The computational results of the modal superposition method are taken as the reference solution.

Fig. 17
figure 17

Finite element model of 3D SSI system of 1-storey 2-span station in Site 1

Full size image

Seismic responses under the artificial earthquake motions and underground design response spectra are shown in Fig. 18. It can be seen that the average errors of the displacement relative to bedrock motions and stresses under artificial earthquake motions are less than 2%. The differences of the displacement and stresses under design response spectrum for Method 1 relative to modal superposition method are less than 1%. The differences of the displacement and stresses for Method 2 relative to modal superposition method are less than 2%.

Fig. 18
figure 18

Seismic responses of 3D 1-storey 2-span station in site 1 under artificial earthquake motions and design spectra

Full size image

For the 3D SSI analysis, the computational time of the RSM is about 18 min when the 6 CPUs of computer is used.

Generally, the proposed RSM in this paper can be used for both 2D or 3D seismic analyses of underground structures. The SSI analysis model consisting of the underground structure and its adjacent soil, as shown in Fig. 4, is simulated by finite element method. Therefore, the method in this paper is applicable to the complex geometries of structure and soil presents in the finite element model. Besides, this method requires that the truncated soil area outside the SSI analysis model satisfies approximately the horizontal layered assumption, and the earthquake motion does not spatially vary along the soil–bedrock interface.

6 Conclusions

The RSM is developed for the seismic analysis of the underground structures considering SSI in this paper. The underground design response spectrum at the soil–bedrock surface and seismic SSI analysis model of underground structure for RSM are studied. The seismic responses of a one-storey two-span subway station, a two-storey three-span subway station, and a tunnel are analyzed to study the effectiveness of the RSM. The preliminary studies show the RSM is an effective method for seismic analysis and design of underground structure including SSI. The RSM has the similar computation accuracy for the underground structures as for the structures on the ground. Engineers are familiar with the theory of the RSM. The RSM can be easily implemented in the commercial finite element software such as ABAQUS, and has the high computation efficiency due to only one time calculation using the design response spectrum. More numerical examples should be given in the future to indicate the effectiveness of the proposed RSM. More importantly, it is necessary to consider the nonlinearity of soil under strong earthquakes in the future.