Convex model-based calculation of robust seismic fragility curves of isolated continuous girder bridge

Abstract

The convex model approach is applied to derive the robust seismic fragility curves of a five-span isolated continuous girder bridge with lead rubber bearings (LRB) in China. The uncertainty of structure parameters (the yield force and the post-yield stiffness of LRB, the yield strength of steel bars, etc.) are considered in the convex model, and the uncertainty of earthquake ground motions is also taken into account by selecting 40 earthquake excitations of peak ground acceleration magnitudes ranging from 0.125 to 1.126 g. A 3-D finite element model is employed using the software package OpenSees by considering the nonlinearity in the bridge piers and the isolation bearings. Section ductility of piers and shearing strain isolation bearings are treated as damage indices. The cloud method and convex model approach are used to construct the seismic fragility curves of the bridge components (LRB and bridge piers) and the bridge system, respectively. The numerical results indicate that seismic fragility of the bridge system and bridge components will be underestimated without considering the uncertainty of structural parameters. Therefore, the failure probability P _f,max had better be served as the seismic fragility, especially, the fragility of the bridge system is largely dictated by the fragility of LRB. Finally, the probabilistic seismic performance evaluation of the bridge is carried out according to the structural seismic risk estimate method.

1 Introduction

Since pacific earthquake engineering research (PEER) put forward the theoretical framework of the next generation performance-based earthquake engineering (PBEE), structure seismic fragility analysis have gained more concern as an important component of the PBEE (FEMA 2006; Padgett et al. 2008). Seismic fragility analysis evaluates the probability of a certain damage state when structures are subjected to different earthquake magnitudes. The analysis methods of seismic fragility commonly include empirical, statistical and numerical analysis (Shinozuka et al. 2000a, b; Karim and Yamazaki 2001a, b; Hwang et al. 2001; Moschonas et al. 2009; Billah and Alam 2015). Although, the seismic isolation technique has been widely used in bridge engineering, the destruction data of isolated bridges subjected to earthquakes is still rare. Thus, the numerical analysis method is the only effective way to derive the seismic fragility of isolated bridges. Currently, probability model is usually employed in the seismic fragility analysis of the bridge structures, the characteristics of the model is that probability density function of random variables must be defined in advance. Nevertheless, the probability density functions of mechanical parameters (e.g. yield force and post-yield stiffness) of lead rubber bearings (LRB) are unknown and rarely reported in present papers. Therefore, how to accurately take into account uncertainties of lead rubber bearings will be a significant factor of seismic fragility analysis of isolated bridges.

The probabilistic seismic demand model (PSDM), which represents the statistical relationship between intensity measure (IM) and engineering demand parameters (EDPs), is commonly considered as the base of seismic fragility analysis. Traditional probabilistic seismic demand analysis (PSDA) was proposed by Shome (1999) for the first time, then Cornell and Krawinkler (2000) improved the theoretical system of this method in order to enhance its practicability. Generally, there are two kinds of calculation methods for seismic demand: one is parametric analysis method which assumes that earthquake demand parameters obey definite probability distribution (such as normal distribution or exponential normal distribution). Moreover, probability distribution functions of EDPs can be confirmed by estimating a little amount of model parameters (e.g. mean value adn variance value), and then the probabilistic seismic demand model could be established. Karim and Yamazaki (2007) employed the simplified fragility analysis method to derive the fragility curves of piers of isolated bridges, and the result showed that LRBs could effectively reduce the possible damage of bridge piers. Zhang and Huo (2009) studied the optimal design of isolated bearings of isolated bridges using seismic fragility method. The second method is called non-parametric analysis that the empirical probability of probabilistic seismic demand models can be directly calculated under different earthquake ground motion intensity measures. However, distribution types of EDPs may be not assumed in this method.

Probabilistic model method needs a great amount of sample data that is very hard to receive in practical engineering, while non-probabilistic convex model approach can be established with less information. Although probability distribution functions remain unknown, the boundaries of uncertainty parameters can be determined according to the available information and be described with the convex set (such as interval set or ellipsoid set), so that the non-probabilistic set-theory can be introduced into engineering to solve all kinds of uncertain problems (Qiu and Wang 2010). The description method on the uncertain set first appeared in the 1960s. Elishakoff (1995) compared stochastic model and non-stochastic model with convex model to illustrate the defections of probabilistic method, which need enough accurate data and the significant result errors induced by input errors. Moreover, he also put forward the non-probabilistic convex model for the unknown probabilistic distribution of design parameters. Pantelides and Tzan (1996) illustrated that the responses obtained by the convex model were relatively larger than the results calculated by the normal way, so they developed a reduction factor to adjust the results obtained by the convex model. Fan et al. (2014) considered uncertainties of isolated structure parameters with the convex model and proposed a new calculation method for collision fragility curves of base isolated building subjected to near-fault earthquake excitation, and uncertainties of structures and earthquake ground motion were simultaneously taken into account.

For the seismic response analysis of structures, two methods may be employed by considering structural uncertainty factors: probabilistic model based on the mathematical statistics and non-probabilistic convex model based on the convex theory. The design mechanical parameters (e.g. yield force, post-yield stiffness) of the isolated bridge are very sensitive to isolation effect on the structure. Though the probabilistic distribution functions of LRBs are rarely mentioned in the recent research, national standard for rubber bearings provides the bound values of these parameters (such as allowable deviation of shearing property of bearings type S–A is within ±10%, and that of shearing property of bearings type S–B is within ±20%) (GB/T 20688.1-2007 2007). In order to better describe the uncertainties of structure parameters, the convex model is introduced into seismic fragility analysis of isolated bridge in this paper. The objective of the work is to access the vulnerability and seismic performance of a isolated continuous girder bridge with Lead rubber bearings (LRB) when subjected to a total of 40 earthquake excitations of peak ground acceleration (PGA) magnitudes ranging from 0.125 to 1.126 g. The cloud method and convex model approach are used to evaluate the seismic fragility, respectively, which is based on the results obtained from the nonlinear time-history analysis using software package OpenSees (McKenna and Fenves 2001). A 3-D finite element model with the nonlinear beam-column element for bridge piers and and zero length bilinear link element for LRBs is built. The response functions in variable space of bridge components can be obtained by the response surface method, and the maximum and minimum values of response surfaces can be calculated by the optimization function in MATLAB. Thus, robust fragility curves of bridge components and the bridge system bridge piers and LRBs can be constructed. Finally, the probabilistic seismic performance evaluation of the bridge is carried out according to the structural seismic risk estimate method.

2 Convex model approach

Here is the definition of convex set: Let $S \in E^{N}$, if random points P and Q belong to S ($P \in S,Q \in S$), and the point αP + (1 − α)Q also belongs to S, in which 0 ≤ α ≤ 1, then we call S a convex set. According to this definition, we can know that the convex set has the following characteristic: if two points belong to one convex set, the line segment between two points must belong to the convex set, this property which can be applied to the fitting of response surface. There are several convex models which can be selected by considering features of uncertain variables. And the simpler model is the maximum bound convex model (MB), which has been widely used for the simple form and few information. The MB model is defined as follow: absolute value of each component of uncertain variables is under a limit, which can be expressed as

$$\Omega_{MB} = \left\{ {\alpha (t) \in R^{r} :\left| {\alpha_{j} (t) \le \overline{\alpha }_{j},\quad j = 1, \ldots ,r} \right.} \right\}$$

(1)

where $\bar{\alpha }_{j}$ are constant.

Let $X = [X_{1} ,X_{2}, \ldots ,X_{n} ]$ is the convex vector that represents uncertainties of structure material, and the uncertain variable I is described as uncertainty of earthquake ground motions. So, the structural seismic response can be expressed as $S(X,I)$, where $x_{i} \in X_{i}$, x _i can be written as

$$x_{i} = (1 + \gamma_{i} \delta_{i} )x_{i}^{c}$$

(2)

where $x_{i}^{c} = (x_{i}^{l} + x_{i}^{u} )/2$ is the mean value of x _i , γ _i is the deviation rate of x _i , $x_{i}^{l} ,x_{i}^{u}$ are the upper and lower bounds of x _i , respectively, and standardized variable $\delta_{i} \in [ - 1,1]$. In consideration of the related restriction or mutual independence among uncertain parameters, which would be grouped according to the correlation. Three parameters are selected as uncertain variables, namely yield force of LRBs δ ₁, the post-yield stiffness of LRBs δ ₂, the yield strength of steel bars δ ₃. Therefore, the standard variable can be expressed as ${\varvec{\updelta}}{\text{ = [\{ }}\delta_{1} ,\delta_{2} \} ,\delta_{3} ]$. If we define δ _i with multi-unit super-sphere set, standard variables can be defined as

$${\varvec{\updelta}} \in E = \{ {\varvec{\updelta}}:\delta_{i} \delta_{i}^{T} \le 1, \quad i = 1 ,2, \ldots ,m \}$$

(3)

where δ ₁ and δ ₂ are combined as one group by considering of the correction. E is a multi-unit super-sphere set containing two groups of uncertain parameters. Since E represents a convex set, the uncertain parameters model expressed as Eq. (3) is defined as the convex model.

N earthquake ground motions are selected by latin hypercube sampling (LHS), and the ith of them is chosen as seismic input to conduct nonlinear time history analysis in order to obtain the maximum responses of LRBs and bridge piers, which can be assumed as $S({\varvec{\updelta}},I = i)$. Since ${\varvec{\updelta}}$ belongs to the convex domain described by Eq. (4), $S({\varvec{\updelta}},I = i)$ also have boundaries as shown below

$$\begin{aligned} S_{\hbox{max} } (I = i){ = }\mathop {\sup }\limits_{\delta \in E} \{ S({\varvec{\updelta}},I = i)\} , \hfill \\ S_{\hbox{min} } (I = i) = \mathop {\inf }\limits_{\delta \in E} \{ S({\varvec{\updelta}},I = i)\} . \hfill \\ \end{aligned}$$

(4)

The boundaries can be obtained by solving constrained optimization problems.

$$\begin{aligned} & find \, \delta \\ & S_{\hbox{min} } (I = i) = \hbox{min} (S({\varvec{\updelta}},I = i)) \\ & S_{\hbox{max} } (I = i) = \hbox{max} (S({\varvec{\updelta}},I = i)) \\ & s.t. \quad \delta_{i} \cdot \delta_{i}^{T} \le 1, \quad i = 1 ,2, \ldots ,m \\ \end{aligned}$$

(5)

where $S({\varvec{\updelta}},I = i)$ is not an explicit expression. Obviously, this implicit function needs to be transformed into explicit expression just to gain its extreme value. Quadratic polynomial response surface method is applied in this paper to acquire the explicit expression $\overline{S} ({\varvec{\updelta}},I = i)$, Subsequently, the maximum value $S_{\hbox{max} } (I = i)$ and the minimum value $S_{\hbox{min} } (I = i)$ of this expression can be solved.

3 Methodology of fragility analysis and seismic performance evaluation

3.1 Cloud method

Probabilistic seismic demand model (PSDM) is used to derive analytical fragility functions. PSDM is to establish a statistical relationship between engineering demand parameters (EDP) and the ground motion Intensity Measure (IM). The PSDA method utilizes regression analysis to obtain the mean and standard deviation for each limit state by assuming the logarithmic correlation between the median EDP and the selected IM.

$$\ln (EDP) = \ln a + b\ln (IM)$$

(6)

where the parameters a and b are regression coefficients obtained from the nonlinear time-history response analysis. The standard deviation can be estimated as

$$\xi_{EDP/IM} = \sqrt {\frac{{\sum\nolimits_{i = 1}^{n} {[\ln (EDP_{i} ) - (\ln a + b\ln IM_{i} )]^{2} } }}{n - 2}}$$

(7)

seismic fragility functions of the bridge structure describe the conditional probability of reaching a certain limit state (LS) under different seismic IM. The failure probability of the certain LS can be expressed as (Alam et al. 2012)

$$P_{f} = P(DI \ge LS/IM) = \Phi \left( {\frac{{\ln (aIM^{b} ) - \ln (LS)}}{{\xi_{EDP/IM} }}} \right)$$

(8)

where $\xi_{EDP/IM}$ is the standard deviation of the logarithmic distribution that computed from Eq. (7), and $\Phi ( \cdot )$ is the standard normal distribution function.

Different definitions exist among the engineering field in different countries for the definition of the structural damage state in the seismic fragility analysis. The common damage indices for bridge structures are shown in Table 1. Based on the results of numerous studies, the ductility of a pier section μ _κ is selected as the pier damage index and the shear strain γ is selected as the damage index (DI) for isolation bearings under different limit states (LS).

Table 1 Damage indices of piers and isolation bearings under different limit states

3.2 Convex model method

The detailed calculation method consists of the following steps:

• 1. Choose uncertain parameters of isolated bridge. The standard random variable δ is sampled by the LHS method and is satisfied with the necessary condition $\delta_{1}^{2} + \delta_{2}^{2} \le 1$. Sampling results should be transformed into structure parameters and then nonlinear time history analysis would be carried out. Moreover, the number of standard variables must guarantee the enough accuracy of response surface.

• 2. Conduct the nonlinear time history analysis of the structure using OpenSees. The structural seismic responses, i.e. shearing strain of LRBs and curvature of piers, can be obtained under different peak ground accelerations (PGAs).

• 3. Fit the seismic fragility response surface of the isolated continuous bridge. The quadratic polynomial is selected to fit the response surface of seismic fragility based on to least square method. The selected samples are treated as the training set with quadratic polynomial response surface method to calculate the limit state function. Furthermore, reasonable selection of experimental points and iterative calculation can ensure that polynomial functions are converged to real limit state function as far as possible.

  The fitting function $\overline{S} ({\varvec{\updelta}},I = i)$ of output variables can be written as follows

  $$\overline{S} ({\varvec{\updelta}},I = i) = a + \sum\limits_{i = 1}^{n} {b_{i} \delta_{i} } + \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {c_{ij} } \delta_{i} } \delta_{j}$$

  (9)

  where n is the number of random variables, a is the constant term, b _i (i = 1,…,n) are linear coefficients, c _ij (i = 1,…,n; j = 1,…,n) are quadratic coefficients and δ _i , δ _j are uncertain variables.

  Regression coefficients in response surface functions can be obtained by the least square estimation, and the number of undetermined coefficients is (n + 1)(n + 2)/2. And the real responses of structure can be approximated by response surface functions in subsequent analysis after response surface functions of the structure are obtained.

• 4. Substitute Eq. (9) into Eq. (5) to replace $S({\varvec{\updelta}},I = i)$. Using function ‘fmincon’ in MATLAB to solve constrained optimization problems with constraint conditions $\delta_{1}^{2} + \delta_{2}^{2} \le 1$ and $\left| {\delta_{3}^{{}} } \right| \le 1$, $S_{\hbox{max} } (I = i)$ and $S_{\hbox{min} } (I = i)$ can be calculated by iteration. The function command ‘fmincon’ can be adopted.

  $$[x,\;{\text{fval}},\;{\text{exitflag}}] = {\text{fmincon}}(`{\text{bearings}}',\;[0,\;0,\;0.5],\;[],\;[],\;[],\;[],\;{\text{l}},\;u,\;`{\text{constrains}}');$$

  where, x returns regression coefficients, fval returns minimum values of the function, exitflag returns states of output values, [0, 0, 0.5] is the initial iteration value. Number 1 and u represent the lower and upper limit of parameters, respectively. The 'constrains' is defined as the nonlinear constraint function which must meet $\delta_{1}^{2} + \delta_{2}^{2} \le 1$.

• 5. Acquire the values of S _max and S _minwhen the structure is subjected to the ith earthquake excitation at a given PGA from step 1) to 4). Due to the random of earthquake excitation, S _max and S _min are two uncertain variables. Thus, the corresponding maximum and minimum seismic responses of the structure at different PGAs can be obtained.

• 6. Combined with damage indices as described before, seismic fragility curves of different damage states of LRBs and piers can be derived by Eq. 10. Thus, the maximum and minimum failure probability can be solved according to Eq. 11.

  $$P_{f} = \frac{{n\{ S \ge LS\left| {IM} \right|\} }}{N}$$

  (10)

  where n is the number of earthquake ground motions which satisfies failure conditions, and N is the total number of earthquake ground motion records.

  $$\begin{aligned} & P_{f,\hbox{min} } (im) = P(S_{\hbox{min} } \ge LS\left| {IM} \right.),P_{f,\hbox{max} } (im) = P(S_{\hbox{max} } \ge LS\left| {IM} \right.) \\ & P_{f,\hbox{min} } (im) \le P_{f} (im) \le P_{f,\hbox{max} } (im) \\ \end{aligned}$$

  (11)

  where P _f,min and P _f,max are the lower and upper bound of P _f , respectively.

• 7. Fit the failure probability P _f based on the lognormal distribution function by the command ‘nlinfit’ in MATLAB. Finally, the robust seismic fragility curves of LRBs and bridge piers can be obtained.

3.3 Seismic fragility of the bridge system

For bridge structures, the fragility of system is more convincing than the fragility of components (Choi et al. 2004; Nielson and DesRoches 2007; Zhang and Huo 2009). However, the fragility curve of bridge system can be constructed according to the fragility curves of bridge components (bridge piers and isolation bearings). There are two methods to deal with the complicated calculation problem. One method is using the joint probabilistic seismic demand model and capacity model of the bridge components (Nielson and DesRoches 2007), and the other method is employing the first order reliability theory to obtain the upper and lower bounds on the system fragility function. Nevertheless, the latter has been widely utilized to derive the fragility curve of the bridge system in the current study.

The common system may be divided into series, parallel and hybrid system. Because the damage states of bridge components reflect the degree of the function loss in the system, it is suitable that the bridge system is considered as a series system. For the series system, the first order bound of system can be defined as Eq. (12) using the first order reliability theory.

$$\hbox{max} [P(E_{i} )] \le P_{fs} \le \hbox{min} \left[\sum\limits_{i = 1}^{n} {P(E_{i} )} ,1\right]$$

(12)

where $P(E_{i} )$ and P _fs is the failure probability of bridge components and system, respectively. The lower bound of system fragility indicates the un-conservative estimate of the failure probability of the system, whereas the upper bound gives the conservative estimate of the failure probability of the system.

When the failure events of components are independent each other in the statistical sense, the upper bound can be expressed as follows

$$P_{fs} \le 1{ - }\prod\limits_{i = 1}^{n} {[1 - P(E_{i} )]}$$

(13)

3.4 Probabilistic seismic performance evaluation of the bridge

The next-generation performance-based seismic design evaluation method, which is based on the full probability theory, had been proposed by PEER. The propose of probabilistic seismic demand analysis of structures is to predict the annual average exceeding frequency (λ _EDP ) of engineering demand parameters (EDP). In this paper, the curvature of bridge piers and shear displacement of LRBs are assigned as the EDP.

$$\lambda (EDP > edp) = \int {P(\left. {EDP > edp} \right|IM = im)} \left| {\frac{d\lambda (im)}{d(im)}} \right|dim$$

(14)

where IM is the intensity measure of earthquake ground motion(e.g. PGA. Sa(T1)). $P(\left. {EDP > edp} \right|IM = im)$ is the conditional probability of reaching a certain limit state (LS) under different IM, which is also known as the seismic fragility analysis of structures, λ(im) is the annual average exceeding frequency related to IM.

According to the energy law (Sewll et al. 1996), λ(im) can be expressed as

$$\lambda (im) = k_{0} im^{ - k}$$

(15)

where k ₀ and k can be calculated by fitting method according to PGA under the two seismic fortification criterion and characteristic of the bridge site. $P(\left. {EDP > edp} \right|IM = im)$ is generally assumed as the lognormal distribution, which can be expressed as follows

$$P(\left. {EDP > edp} \right|IM = im) = 1 - \Phi \left( {\frac{{\ln (im) - \ln (\eta_{edp} )}}{{\beta_{edp} }}} \right)$$

(16)

Where η _edp and β _edp can be obtained by the least square nonlinear fitting of the seismic fragility curves under the different PGA.

The annual average exceeding frequency (λ _EDP ) can be rewritten by substituting Eqs. (16) and (15) into Eq. (14)

$$\lambda (EDP > edp) = k_{0} \eta_{edp}^{ - k} \exp \left( {\frac{1}{2}k^{2} \beta_{edp} } \right)$$

(17)

The probability of earthquake occurrence is assumed as the Poisson distribution model, seismic hazard exceeding probability (EDP > edp) of the bridge in 50 years can be expressed as

$$P_{50} (EDP > edp) = 1 - e^{ - \lambda (EDP > edp) \times 50}$$

(18)

4 Seismic fragility analysis of isolated continuous girder bridge

4.1 Structural properties and analytical modeling of the bridge

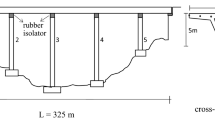
The bridge was built in Tibet located in the southwest of China in 2003, which is a reinforced concrete isolated continuous bridge with five equal spans and an overall length of 100 meters. The geometric detail of the seismic isolated continuous girder bridge is presented in Fig. 1, respectively. The seismic isolation bearing is used to connect the girder and the tops of the bridge piers. The expansion joints in this bridge are set on the proscenia of both sides and the girder is supported by a gravity U-shaped abutment with an expansion base at each end of the bridge. The material parameters used in the bridge are shown in Table 2. The seismic fortification intensity of this site is 9; the site classification type is II, and the characteristic period of site is 0.4 s. The corresponding fortification peak acceleration of earthquake ground motion is 0.40 g in the horizontal direction of the bridge.

Fig. 1

Geometric details of the seismic isolated continuous girder bridge. a Longitudinal view of the bridge. b Double column bridge pier. c Single column bridge pier. d Arrangement chart of LRBs on the top of bridge piers

Table 2 Geometries and material properties of the bridge

Using the finite element analysis software OpenSees, the box section girder is modeled with an elastic beam-column element, while a nonlinear beam-column element is adopted in the finite element modeling of bridge piers. A constitutive model of concrete is selected, which represents experimental results for the confined concrete and non-confined concrete in a circular cross-section subjected to the axial force (Fig. 2). The elastic-linear hardening (bilinear) model is used for the rebar (Fig. 3). Both models are represented with uniaxial materials in OpenSees.

Fig. 2

Constitutive model of concrete

Fig. 3

Constitutive model of rebar

In Fig. 3, f _y is the yield strength of the rebar. E _s is the elastic modulus, E ₀ is the secondary hardening stiffness, and E ₀  = 0.01E _s . The mechanical properties of compression rebar are considered to be the same as those of tensile rebar in this case.

The non-linear material properties of bridge (Fig. 4) piers are considered and the cross section of the bridge pier is divided into some elements to form the concrete and rebar fiber based on the element types described above and the constitutive model of the materials (Fig. 5).

Fig. 4

Cross section of bridge pier

Fig. 5

Fiber cross section of pier

The force–displacement relationship of the LRB500 type isolation bearing is shown in Fig. 6. The area enclosed by the hysteresis curve indicates its energy dissipating capacity. Thus, the larger this area is, the greater the equivalent damping of bearing and the stronger the energy-dissipating capacity are. The isolation bearing is usually simulated with a bi-linear model in numerical calculation, and its mechanical properties are described using the pre-yield stiffness K ₁, post-yield stiffness K ₂ and yield shear force Q The values of these variables are shown in Table 3.

Fig. 6

Hysteresis curve and bilinear model of LRB. a Experiment hysteresis curve of LRB. b Theoretical bilinear model of LRB

Table 3 Design parameters of LRB500

The Isolation bearing is simulated by combining a zero-length element with a uniaxial material model in OpenSees. K ₂ = 0.1K ₁ when defining the parameters of the material models. A rigid bar is used to connect the isolation bearings, girder and bridge piers, and is simulated with an elastic beam-column element with a stiffness set to infinity.

The 3-D finite element model of the bridge by OpenSees is shown in Fig. 7. Modal analysis is conducted using the Ritz vector method on the model to obtain the dynamic characteristics of structures.

Fig. 7

3-D Finite element model of the seismic isolated continuous girder bridge in OpeeSess

In order to verify the reliability and effectiveness of the finite element model by software package OpenSees (Fig. 7), another finite element model is also built by software package SAP2000. The modal analysis is carried out using SAP2000, and the first four order periods and mode shapes are shown in Fig. 8.

Fig. 8

The first four order mode shapes of the finite element model (SAP2000). a The first mode shape (T₁ = 1.700 s). b The second mode shape (T₂ = 0.610 s). c The third mode shape (T₃ = 0.172 s). d The fourth mode shape (T₄ = 0.152 s)

The modal analysis results using SAP2000 and OpenSees are compared in Table 4, respectively. The maximum relative deviation is 2.35% for the third order period, and the first four order mode shapes are same. It is indicated that the modal analysis of the isolated continuous girder bridge is reliable using OpenSees.

Table 4 Comparison of the first four order mode shapes of the bridge

4.2 Selection of earthquake ground motions

It is important to properly select the input of the earthquake ground motion to conduct structural seismic fragility analysis, because the seismic response of structures is subsequently dependent on the uncertainty characteristics of earthquake ground motions. Characteristics of earthquake ground motions considering site type, intensity and frequency contents have a great effect on nonlinear time history response of structural members. Some indices of earthquake ground motion, e.g., peak ground acceleration(PGA), peak ground velocity(PGV), peak ground displacement(PGD), spectral acceleration(Sa), spectral velocity(Sv), spectral displacement(Sd) and time duration of strong motion(Td) can be taken into account. The index PGA is a widely used to describe the severity of the earthquake ground motion (Mackie and Stojadinovi¢ 2004; Padgeet and DesRoches 2008).

The Chinese Code”Guideline for Seismic Design of Highway Bridges (JTG/T B02-01-2008 2008)” involves a demand: calculation results of the linear time history analysis should be not less than 80% that of response spectrum method under the earthquake action E1. In order to decrease the dispersion of structural response caused by different inputs of earthquake ground motion records in the time history analysis, geometry mean response spectra of the selected earthquake ground motion records should be closer to the target response spectrum(Code response spectrum). The statistical analysis of numerous ground motion records indicates that it is difficult to match well each other along the whole frequencies range of the target response spectrum. Because the first mode shape of seismic isolated bridge largely makes contribution to the structural seismic response, the selected earthquake ground motion records may be limited at a nearby range around the fundamental period of the bridge (e.g. [T₁ − ΔT₁,T₁ + ΔT₂]).

When considering the uncertainty of earthquake ground motion, the earthquake ground motion records can be obtained from the latest earthquake database disseminated by the Pacific Earthquake Engineering Research Center (PEER) in the United States according to the following steps. (1) Establish a target response spectrum, as shown in Fig. 8, according to some important information, such as the site type of this region, the seismic fortification intensity, the characteristic period, etc. (2) Select earthquake ground motion records and make their geometry mean response spectra closer to the target spectrum in the specified period range of time (e.g., [0.1 s, T _g ] and [T ₁ − ΔT ₁, T ₁ + ΔT ₂]), as shown in Fig. 9. A suite of 40 selected earthquake ground motion records from the PEER database are presented in Table 5. The PGA values ranging from 0.125 to 1.126 g have been considered in the current study.

Fig. 9

Earthquake ground motion records. a Target response spectrum, b Response acceleration spectra

Table 5 Characteristics of the earthquake ground motion records

4.3 Response surface fitting of LRBs and bridge piers

According to the current studies, the yield force of LRBs δ ₁, the post-yield stiffness of LRBs δ ₂ and the yield strength of steel barsδ ₃ are selected as uncertain variables by the sensitivity analysis of structures (Fan et al. 2014). Moreover, x ₁ and x ₂ are described with unit circle model while x ₃ is described with interval model since it is not correlated with the other two variables. Detailed uncertainties are illustrated in Table 6 and 16 sample points are shown in Table 7.

Table 6 Bound values of uncertain variables

Table 7 Calculation values of sample points of uncertain variables

Based on above mentioned sample points, 16 response sample points are treated as training set to conduct the regression analysis. For instance, when the El Centro ground motion (Imperial Valley-06, 1979, PGA = 0.4 g) is selected, the regression coefficients are listed in Table 8.

Table 8 Regression coefficients under El Centro ground motion (PGA = 0.4 g)

Quadratic polynomial response surface function of LRBs can be expressed as Eq. (19)

$$\begin{aligned} \bar{S}(\delta \left| {IM = 0.4\,\text{g}} \right.) & = 0. 10 9 3 7 6 { } - 0.00 3 2 2\delta_{1} - 0.00 5 2\delta_{2} - 0.00 7 7 5\delta_{3} \\ & \quad - 0.00 4 1 2\delta_{1}^{2} - 0.00 3 2 2\delta_{1} \delta_{2} - 0.00 7 5 1\delta_{1} \delta_{3} \\ & \quad { + }0.00 1 3 4 5\delta_{2}^{2} + \, 0.00 9 1 3\delta_{2} \delta_{3} + \, 0.00 2 7 6 1\delta_{3}^{2} \\ \end{aligned}$$

(19)

Similarly, quadratic polynomial response surface function of piers can be written as Eq. (20)

$$\begin{aligned} \bar{S}(\delta \left| {IM = 0.4 \text{g}} \right.) & = 0.00 1 7 2 6 { + 9}. 3 4\times 1 0^{ - 5} \delta_{1} { + }0.000 1 3 5\delta_{2} { + }0.000 1 8 3\delta_{3} \, \\ & \quad + 2. 7 8\times 1 0^{ - 5} \delta_{1}^{2} { + 7}. 8\times 1 0^{ - 5} \delta_{1} \delta_{2} { + }0.000 1 6 7\delta_{1} \delta_{3} \\ & \quad - 4. 8 {\text{E}} \times 1 0^{ - 5} \delta_{2}^{2} \, - 0.000 2 5\delta_{2} \delta_{3} \, - 8. 1\times 1 0^{ - 5} \delta_{3}^{2} \\ \end{aligned}$$

(20)

Using maximum relative deviation Q to assess and analyze the obtained response surface (Duan and Zhao 2009). And Q is the maximum ratio of sample fitting value to calculation value, Q can be defined as Eq. (21)

$$Q = \hbox{max} \left\{ {\frac{{Y_{i} - M_{i} }}{{Y_{i} }}} \right\}, \quad i = 1, \ldots ,n$$

(21)

where Y _i represents observation values of response variables (i.e., calculation values), M _i represents the fitting values of response variables.

The comparisons of absolute and relative deviation of displacement of lead rubber bearings and curvature of bridge piers are presented in Table 9.

Table 9 Comparisons of absolute and relative deviation of bridge components

The maximum relative deviations are almost less than 5% in Table 8. Extreme values can be found by conducting optimization search in the whole random variable space after acquiring response surface function $\bar{S}$. It should be noticed that origin function values need to be negative using function ‘fmincon’ in MATLAB to solve maximum values, while the calculation results needs to be absolute due to function ‘fmincon’ means seeking for the minimum value of functions. For example, the optimization results of isolated continuous girder bridge subjected to El Centro earthquake exciation (Record number: 184-FN, PGA = 0.4 g) are shown in Table 10.

Table 10 Real response values and optimization values of LRBs and bridge piers

From Table 10 it can be observed that the maximum value and minimum value of response surface function contain the real response values. The response surface function value is more inclusive and safer by the optimization search.

4.4 Fragility curves of bridge piers and LRBs

As described above, each earthquake ground motion records with different PGA can be used to calculate S _max and S _min . In other words, N values of S _max and S _min will be obtained under each different PGA. Then, fragility curves of bridge components can be derived according to the frequency method. Equation (11) is used to solve the upper bound P _f,max and lower bound P _f,min of fragility curves of LRBs and bridge piers subjected to earthquake excitations (PGA = 0.2 g, 0.4 g, 0.8 g, 1.0 g). The fragility curves of P _f,max and P _f,min of LRBs and bridge piers are illustrated in Figs. 10, 11, 12, 13, respectively.

Fig. 10

P _f,max fragility curves of LRBs

Fig. 11

P _f,min fragility curves of LRBs

Fig. 12

P _f,max fragility curves of bridge piers

Fig. 13

P _f,min fragility curves of bridge piers

Figure 14 shows the comparison diagrams of seismic fragility curves of the LRB under four limit states, P _f,max and P _f,min represent the upper bound and lower bound failure probability, and P _f (δ = 0) denotes the failure probability without considering uncertainties of structure parameters, respectively. It can be observed that P _f (δ = 0) is located between P _f,max and P _f,min under the same given PGA, and uncertainty of the LRB will make a great effect on the fragility curves of the LRB.

Fig. 14

P _f,max , P _f,min and P _f (δ = 0) fragility curves of LRB. a Slight. b. Moderate. c Extensive. d Collapse

Figure 15 shows the comparison diagrams of fragility curves of the bridge pier under four limit states. The P _f,min fragility curves are very close to P _f (δ = 0) curves, whereas the P _f,max fragility curves are much greater than P _f (δ = 0) curves. It is indicated that the lower bound of uncertain variables are not sensitive to the fragility curves of bridge piers.

Fig. 15

P _f,max , P _f,min and P _f (δ = 0) fragility curves of bridge pier. a Slight. b Moderate. c Extensive. d Collapse

Figure 14, 15 show that P _f,max seismic fragility curves are totally greater than P _f,min , and the failure probability of LRB are greater than that of bridge piers, especially when PGAs range from 0.1 g to 0.4 g. Taking slight damage state of LRB as an example, as illustrated in Fig. 14, the P _f,max fragility curve of LRB gets close to 0.8 (PGA = 0.4 g), while it starts from PGA = 0.6 g in P _f,min fragility curve, and the fragility curve P _f (δ = 0) without considering uncertainties of structure parameters locates between P _f,max and P _f,min . Therefore, failure probability P _f would be underestimated when uncertainties of structure parameters are ignored. In view of safety, P _f,max fragility curves of LRB and bridge piers had better be advised to employ in designing new bridges and prioritization of retrofitting strategies of existing bridges.

Though the probabilistic distribution functions of LRBs are rarely mentioned in the recent research, national standard for rubber bearings provides the bound values of these parameters (such as allowable deviation of shear property of bearings type S-B is within ±20% (GB/T 20688.1-2007 2007). Therefore, the uncertainty of LRB design parameters can be properly taken account into using the convex model approach, whereas that is not considered in cloud method. Figures 16 and 17 present the fragility of the lead rubber bearing(LRB) used in the bridge system under four limit states. Figure 16 displays that the failure probability P _f,max using convex model is greater than that using cloud method for the given limit state. However, the failure probability P _f,min using convex model is less than that using cloud method for the given limit state in Fig. 17. It is indicated that the fragility curves of LRB using cloud method is distributed between P _f,min and P _f,max . Consequently, if the the uncertainty of LRB design parameters is not properly considered, the seismic fragility of LRB will be underestimated. The median value of PGA, which corresponds to failure probability P _f  = 50%, is determined for the LRB at each damage level. That comparison is presented in Table 11. From this table it can be observed that the maximum percent difference of median values of PGA is −25.00% between the cloud method and convex model-P _f,max at the collapse level, while the minimum percent difference is 9.84% between the could method and convex model-P _f,min at the extensive level.

Fig. 16

P _f,max fragility curves of LRB

Fig. 17

P _f,min fragility curves of LRB

Table 11 Median value of PGA for LRB with respect to P _f  = 50%

In view of structural safety in designing new bridges and prioritization of retrofitting strategies of old bridges, the failure probability P _f,max had better be served as the seismic fragility curves, which are referred as robust seismic fragility curves. In addition, similar trends can also be observed in the seismic fragility curves for the bridge pier in Figs. 18 and 19.

Fig. 18

P _f,max fragility curves of bridge pier

Fig. 19

P _f,min fragility curves of bridge pier

The numerical results as depicted in Figs. 16, 17, 18 and 19 illustrate the relative likelihood of reaching/exceeding certain limit state at a given PGA input for bridge components (isolation bearing and bridge pier), which indicates that the damage of LRB is prior to that of the bridge pier. Because of the energy dissipation of isolation bearings, the earthquake action of bridge piers is greatly decreased and seismic safety of bridge piers are assured.

4.5 Seismic fragility curve of bridge system

The seismic fragility curve of a bridge system can be subsequently obtained by the seismic fragility curves of bridge components (bridge piers and isolation bearings). This can be carried out by the Monte Carlo simulation, but this method is extremely time-consuming. Therefore, the first order reliability theory (Eq. 12) is adopted to construct the seismic fragility curve of bridge system. In view of the structural seismic safety, the upper bound of the fragility curve of the bridge system is assigned.

The fragility curves of the LRB and bridge pier are obtained using the convex model approach (according to the upper bound P _f,max ), and then the fragility curves of the bridge system can be constructed using the first order reliability theory. Figure 20a–d present the robust seismic fragility curves of the bridge system, LRB and bridge pier under four limit states, respectively. It can be observed that the robust seismic fragility curve of the bridge system is closer to the robust seismic fragility curve of LRB at each limit state, whereas it is much greater than fragility curve of the bridge pier. The results indicate that the seismic fragility of the bridge system is largely dictated by the fragility of LRB.

Fig. 20

Fragility curves of LRB, bridge pier and bridge system. a Slight. b Moderate. c Extensive. d Collapse

4.6 Probabilistic seismic performance evaluation of the bridge system

The seismic fragility curves of the bridge system have been derived under four limit states using cloud method and convex model approach, respectively. Exceeding probability curves of bridge system in 50 years can be calculated to conduct the probabilistic seismic performance evaluation of the bridge using structural seismic risk estimate method.

According to Chinese Code: Guidelines for seismic design of highway bridge (JTG/T B02-01-2008 2008), the two seismic fortification criterion (Table 12) and two stages design are adopted for the seismic design of the isolated continuous girder. Through the calculation of the bridge, $k_{0} = 2.14563$, $k = 0.0000254$.

Table 12 Seismic fortification criterion of highway bridge

Under the earthquake action E1 and E2, the exceeding probability curves of the isolation bearing and bridge pier in 50 years are calculated using the cloud method and convex model, respectively (Figs. 21, 22). it can be observed that the exceeding probability of LRB is 4.49% (convex model) and 2.05% (cloud method), while that of the bridge pier is 1.21% (convex model) and 0.86% (cloud method) when the bridge is subjected to the earthquake action E1. Under the earthquake action E2, the exceeding probability of LRB is 1.56% (convex model) and 0.67% (cloud method), while that of bridge pier is 0.39% (convex model) and 0.04% (cloud method). It is indicated that exceeding probability of bridge components using the convex model are greater than that using the cloud method. If the uncertainty of LRB design parameters can not be properly considered, the exceeding probability of isolation bearing will be underestimated. Therefore, It is suggested that calculation results based on the convex model are served as the important reference to the probabilistic seismic evaluation of bridge components in view of the structural seismic safety.

Fig. 21

Exceeding probability of LRB

Fig. 22

Exceeding probability of bridge pier

Under the earthquake action E1 and E2, the exceeding probabilities of the bridge components and bridge system in 50 years are presented in Table 13 using the convex model approach, respectively.

Table 13 Exceeding probabilities of the bridge components and bridge system

From Table 12 it can be observed that seismic performance of the isolated continuous girder bridge fully meets the demand of two seismic fortification criterion (JTG/T B02-01-2008 2008). The exceeding probability of the bridge system is 5.65% when the bridge is subjected to the earthquake action E1. It is shown that the bridge system possess more seismic safety capacity. However, The exceeding probability of the bridge system is 1.94% under the earthquake action E2, and that is closer to 2.47%. Thus, seismic safety capacity of the bridge system is less. In addition, the exceeding probability of LRB is greater than that of the bridge pier under the same seismic fortification criterion. It is indicated that the damage of LRB is prior to that of bridge piers. The earthquake action of the bridge pier is greatly decreased through the energy dissipation of LRB. Finally, the bridge piers is preserved.

5 Conclusion

The seismic fragility curves of a five-span isolated continuous girder bridge with lead rubber bearings are derived using convex model approach and cloud method, respectively. The uncertainty of structure parameters is taken into account. The fragility curves of the bridge components and the bridge system can be potentially used to evaluate the probabilistic seismic performance of the bridge, retrofitting prioritization and post-earthquake rehabilitation decision making. The concluding remarks are summarized as follows:

• There are only a few studies on the probability distribution function of mechanical parameters of rubber bearings. However, national standard for rubber bearings (GB/T 20688.1-2007 2007) provides the bound values of design parameters. Convex model approach can be successfully introduced into the seismic fragility analysis of isolated bridges, and it is feasible and reliable for no need to assume the probability distribution of rubber bearing parameters.

• The numerical results indicate that the failure probabilities P _f of the bridge components and the bridge system using cloud method are distributed between P _f,min and P _f,max . If the the uncertainty of structural parameters is not properly considered, the seismic fragility of the bridge components and the bridge system will be underestimated. In view of structural safety in designing new bridges and prioritization of retrofitting strategies of old bridges, the failure probability P _f,max obtained from the convex model approach had better be served as the seismic fragility curves.

• Through the comparisons of the relative likelihood of reaching/exceeding certain limit state at a given PGA input for the bridge components, the damage of LRB is prior to that of the bridge pier. Because of the energy dissipation of isolation bearings, the earthquake action of bridge piers is greatly decreased and seismic safety of bridge piers are assured.

• The convex model-based robust seismic fragility curves of the bridge can be potentially used to the probabilistic seismic performance. The calculation results show that seismic performance of the isolated continuous girder bridge fully meets the demand of two seismic fortification criterion in 50 years. (Chinese Code: JTG/T B02-01-2008).

In summary, convex model approach can provide a new way to derive robust fragility curves of isolated bridges when double uncertainties of structural parameters and earthquake ground motions are taken into account. Future study should include the effect of abutments and the foundation on the seismic fragility analysis.