Keywords

1 Introduction

Bridges are critical elements in the road infrastructure network, which are expected to be functionally active during seismic events. The seismic risk of these structures is expressed in probabilistic terms by employing fragility functions [1]. Fragility functions describe the probability of reaching or exceeding a certain damage state level for the given intensity of ground motion. The theory of fragility provides a useful account of how a particular system behaves across a wide range of ground motions. In recent years, there has been an increasing amount of literature on the fragility assessment of geometrically curved bridges. Primarily, the focus has been made on different factors which might affect the seismic performance of curved steel bridges. Vulnerability estimation of curved bridges using the Hazard U.S. platform may underestimate the seismic vulnerability due to the impact of horizontal curvature, which can be avoided by using the modification factor [2]. Probabilistic seismic hazard assessment has lately gained popularity due to the widespread use of these bridges in California [3, 4]. These studies have evaluated the effect of different structural and geometrical parameters on the seismic fragility of curved bridges, among which curvature is one of the significant influencing factors. Abbasi et al., [4] evaluated the sensitivity of the component and system fragility functions for different limit states due to the change in structural layout in horizontal and vertical planes. Another study ranked the span length, span width, and stiffness of supporting piers causing substantial variation in the seismic fragility of curved bridges [3].

Previously, evaluating system fragility without considering component correlations, leading to a conservative fragility estimate [5]. To reduce such errors, it's important to consider the dynamic correlations among components. Additionally, it is already widely acknowledged that for the straight bridge systems, the fragility is defined in the principle loading directions, i.e., longitudinal and transverse [1]. The seismic response of geometrically curved bridges is more complex due to the irregular distribution of mechanical characteristics such as damping, stiffness, and strength, making them highly sensitive to the impact of seismic-incidence orientation. However, there has been little discussion about developing the system fragility of geometrically irregular bridges with a specific focus on the effect of seismic loading direction.

This paper describes the development of bridge-system fragility functions for a geometrically curved bridge structure using a multi-component and multi-directional loading approach. Initially, a finite element model for a geometrically curved bridge is developed. Next, the global-system fragility is evaluated in multiple loading directions based on components fragility, while considering the correlation dependency between various components. Finally, the variation in the fragility profile is evaluated in terms of median peak ground acceleration (PGA) values for varying input loading directions.

2 Analytical Fragility Development

Fragility functions use reliability theory to assess the seismic risk of civil infrastructure by determining the probability that seismic demand (D) will exceed structural capacity (C) given ground motion intensity [1]. This can be mathematically described by an equation.

$$Fragility=P[D\ge C|IM]$$
(1)

Seismic demand and structural capacity can be modeled by PSDM and limit states, respectively. Seismic demand can be estimated using the power law in Eq. (2).

$${S}_{d}^{ }=a{(IM)}^{b}$$
(2)

where a and b are regression coefficients, which can be estimated from non-linear time history analysis. Assuming the demand distribution around the median of a PSDM follows the log-normal distribution, then the PSDM can be modified as in Eq. (3).

$$P\left[D\ge d|IM\right]=1-\Phi \left(\frac{\mathrm{ln}\left(di\right)-\mathrm{ln}(Sd)}{\beta d}\right)$$
(3)

where \(\Phi (*)\) is the standard normal cumulative distribution function, di is the realization of component demand in each simulation, Sd represents the median seismic demand, and \(\beta d\) is the demand dispersion conditioned upon the IM. Following the lognormal distribution assumption for the capacity limit states the fragility functions of the components can be expressed as in Eq. (4) [5].

$$P\left[D\ge C|IM\right]=\Phi \left[\frac{\mathrm{ln}(Sd/Sc)}{\sqrt{{\beta }_{d}^{2}+{\beta }_{c}^{2}}}\right]$$
(4)

where Sc and \({\beta }_{c}\) are the median and dispersion of the component’s capacity limit state.

While component fragility is useful in identifying the most vulnerable components and retrofit decision-making, system fragility is more significant for transportation network risk assessments. System-wide fragility is developed using reliability principles, assuming the bridge system as a series system with failure of one component leading to failure of the system, defined by bounds and expressed by Eq. (5).

$${\mathrm{max}}_{i=1}^{m}\left[P\left({F}_{i}\right)\right]\le P\left({F}_{sys}\right)\le 1-{\varPi }_{i=1}^{m}\left[1-P\left({F}_{i}\right)\right]$$
(5)

where P[Fi] and P[Fsys] are the failure probability of component i and system, respectively. Equation (6) suggests that the lower-bound yields un-conservative estimates of the system fragility while the upper bound is more conservative. For a real-world system, the actual fragility will lie between these two extremes. To calculate the exact fragility curve, another alternative is the joint probabilistic seismic demand model (JPSDM) method combined with Monte Carlo simulation, which considers the correlation dependency between different components [1]. Using MCS, N random demand samples are generated and compared with the capacity limit states. For the given IM the failure probability of the system is calculated using Eq. (6).

$$P\left[{F}_{sys}|IM\right]=\frac{{\sum }_{i=1}^{N}{I}_{Fi}}{N}$$
(6)

where the failure is tracked by using the indicator function IF, defined in Eq. (7).

$$ I_F = \left\{ {\begin{array}{*{20}c} {1 \,\,\, {\rm if}\left( {x_1 ,x_2 ...x_n } \right) \in F_{1,2,...,n} } \\ {0 \,\,\, {\rm if}\left( {x_1 ,x_2 ...x_n } \right) \notin F_{1,2,...,n} } \\ \end{array} } \right. $$
(7)

where (x1, x2, …. xn) represents the random demand sample and (F1,2,.… n) is the failure domain defined by n components capacity limit states. The current study looks for both methods and the comparison is made in terms of median PGA values.

3 Bridge Description and Numerical Modeling

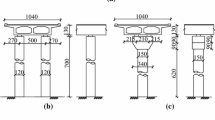
To develop fragility functions and their sensitivity to the input loading direction, an existing horizontally curved highway bridge structure in Japan was considered. The bridge has a 327.9 m span, is 16.95 m to 13 m wide, and is a composite system of steel and reinforced concrete. It has 6 unequal spans and is supported by five steel and one reinforced concrete (RC) pier. The characteristic strengths of the concrete used in the superstructure and sub-structure are 30 and 24 N/mm2, respectively. Throughout the structure, SM 490Y, 400, and SS 400 steel framing sections are employed, which are super heavy steel plates used for welded structures in bridge construction.

Fig. 1.
figure 1

Numerical modeling of the target bridge structure

Full size image

The 3-dimensional modeling was carried out using the non-linear analysis program Engineer Studio, as shown in Fig. 1. The superstructure and bent-top beams were modeled as a linear beam element and the supporting steel piers were represented using fiber elements. Two types of fibers were used for the composite sections: the confined concrete and the confining steel sections. The plastic hinge element was employed for the RC pier and represented by Takeda nonlinear model. The LRB’s mechanical response was represented by using the bi-linear shear spring model, which was characterized by the initial stiffness until the yielding and the reduced secondary stiffness in the strain-hardening region. The shear modulus of the bearings was specified according to the hardness as per the Japan Road Association design specifications [6]. Since the direction of the bridge is continuously changing in the horizontal plane, the bearings were represented by multi-shear springs (MSS) elements [7]. To account for the soil-structure interaction, equivalent linear translational and rotational springs were defined at the soil-foundation interfaces. The stiffness values were calculated based on the foundation type and soil characteristics.

4 Input Ground Motions

For the non-linear time history analysis, a suit of 20 ground motions was retrieved from the JMA, K-Net, and KiK-Net strong ground motion database. The selected records consist of level-1 and level-2 types of waveforms. Figure 2 shows the acceleration response spectra of the recorded ground motions. The different percentiles of the acceleration response spectra are also accompanied by the same figure, which illustrates the general intensity variation for the selected ground motions. The selected waveforms were applied in the horizontal plane with an incrementation of 30° to look for the variation in system fragility as a function of the input loading direction.

Fig. 2.
figure 2

Acceleration response spectra of the selected waveforms

Full size image

5 Limit States Definition

The definition of component limit states is crucial in fragility estimation and has a direct impact on disaster-management decisions. In seismic events, the bridge bearings and piers are the most critical components and often reach the non-linear range. The damage behavior of a component is measured using appropriate Engineering Demand Parameters (EDPs). In the current study the shear strain, ductility, and distortion strain were used as the EDPs for the LRB, concrete pier, and steel piers, respectively. The damage states are defined based on HAZUS criteria and the limit states for the bearings were based on experiments and the secondary effects of unseating and pounding [8]. The details of various damage states are summarized in Table 1. The damageability of the concrete pier was characterized by the displacement ductility factor, which is the ratio of maximum displacement to yield displacement [9]. The limit states for the bearings were defined based on experimental observations and consideration of secondary effects, with complete damage defined at a shear strain of 250% to avoid undesirable pounding at the abutments [9]. The damage states for steel piers are based on the design documentation, which combinedly takes into consideration the effect of axial and bending deformation.

Table 1. Components limit states definition
Full size table

6 Probabilistic Seismic Demand Models (PSDMs)

The PSDMs were derived for all examined excitation directions following the NLTHA results for all components according to Eq. (2). Table 2 presents the median estimates of the PSDMs and the demand dispersion for the selected EDPs in logarithmically transformed states. Results show that the dispersion estimates are not significantly direction-dependent for curved bridges.

Table 2. PSDMs for different components in different loading directions
Full size table

The variation in median estimates of PSDMs considering the loading direction can be reflected more directly using the polar diagrams in Fig. 3. The radial coordinates represent the component's response in their respective EDPs (ln (γ), ln (μd), and ln (ϵ)). Different components undergo different levels of dependence on the load incidence direction. For example, in Fig. 3a, the maximum shear strain for the PGA = 0.1g and 0.5g shows high fluctuation. For the bearings, the maximum shear strain appears at θ = 150°. Contrary, concrete piers show high sensitivity to the load incidence direction, for which the maximum curvature ductility ratio is attained at θ = 90° (\({e}^{1.89}=6.62\) from Fig. 2b). Steel piers yield lower EDP results even at higher demand values, still the effect of load-incidence angle is noticeable from Fig. 3c, where the maximum and minimum distortion strain appears at θ = 120° and θ = 0°, respectively.

Fig. 3.
figure 3

Variation in median estimates for components PSDMs in different loading directions

Full size image

7 Results and Discussion

7.1 Fragility Functions for the Bridge’s Components

Fragility curves for each limit state, developed from the component’s PSDMs, are shown in Fig. 4 (a, b & c). A closer inspection of the results showed that among the bridge components, rubber bearings were the most vulnerable followed by the concrete pier for the given limit state, which was consistent with the seismic isolation requirement of the structure to reduce the force demand associated with the inertial mass. For bearing, concrete pier, and steel pier, the median failure probability of yielding was attained at 0.13 g, 0.39 g, and 1.06 g, respectively. Among the components, the failure probability of the steel piers was also much lower, which can be attributed to the sophisticated design requirement of the structures located in high-intensity seismic zones. These findings confirmed those of earlier studies [1].

7.2 System Fragility Using Reliability Bounds and JPSDM

While the fragilities of individual components can provide useful information on the vulnerability, an assessment of the fragility of the whole bridge system is more convincing for seismic risk assessment of the road network and decision-making. The bounds-based fragility curves for the 0° loading case are presented in Fig. 4d. Result shows that the fragility of the bridge system was higher than the components’ fragility and largely dictated by the bearings’ response. These findings support the importance of considering multi-component system fragility calculation. The relative difference in bounds corresponding to the median demand were 18.18%, 18.75%, 18.18%, and 10.34% for the slight, moderate, extensive, and collapse states, respectively. Unlike the reliability bounds method, the JPSDM considers the exact correlation among the components, representing a more realistic approach. For system fragility, shown in Fig. 5a, the JPSDM was developed by considering the correlation dependency between components. To evaluate the difference between the JPSDM and reliability bounds results for system fragility, the median PGA values corresponding to different limit states are compared in Fig. 5b. Since the JPSDM considers the exact correlation among the components, the JPSDM results lie within these extreme bounds and represent a more realistic approach. The JPSDM results closely match the lower bounds due to a strong correlation between the bridge components.

Fig. 4.
figure 4

Fragility curves for components and bridge system in 0° loading direction

Full size image
Fig. 5.
figure 5

System fragility for 0° loading case

Full size image

7.3 Effect of Seismic Excitation Direction on System Fragility Functions

Fragility functions are sensitive to the input loading directions and should not be decided based on principle loading directions only. As shown in Fig. 6, the 150° direction-loading results in higher fragility demand than the two orthogonal loading directions (0° and 90°) for all the limit states. The relative difference in median PGA values corresponding to the two extreme loading directions was 45.45%, 31.25%, 40.91%, and 36.67% for the slight, moderate, extensive, and collapse states, respectively. A closer inspection of the results showed that the curves are following a similar trend across the different damage states, except the 30° and 60° loading cases. In the slight damage state, the 60° loading curve was slightly higher than the 30° loading curve. With successive increases in the intensity of the damage state, the fragility curves converged at moderate damage levels and drifted at higher damage levels. This shift was due to the relative contribution of the bearing’s fragility in the selected damage states. In the slight damage state, the bearings were found to be more fragile in the 60° loading direction, which then fell in line with the 30° loading case at the moderate damage state, and finally showed less fragility in the high damage modes. Overall, these results indicate that for geometrically curved structures, a multi-direction fragility approach will result in more accurate fragility estimation.

Fig. 6.
figure 6

Variation in system fragility for different input loading directions

Full size image

8 Conclusions

This study evaluated the fragility of a curved bridge under seismic events by developing fragility functions at component and system levels. The errors in system fragility estimation using the reliability bounds method can be minimized if the exact correlation between the components is taken into consideration. Results showed that the high fragility demand was observed in non-orthogonal directions. The relative change in the component’s vulnerability ultimately leads to system-fragility change. Therefore, a higher fragility demand was observed for the system when subjected to 150° loading direction. These findings may help understand the importance of considering components’ interaction and the impact of the load incidence angle in the system fragility estimation. Further research is needed to examine the effect of uncertainties on system fragility. This will help increase the robustness of the system-fragility development which is readily applicable for system performance evaluation and loss estimation.