Asymptotically optimal kinematic design of robots using motion planning

Abstract

In highly constrained settings, e.g., a tentacle-like medical robot maneuvering through narrow cavities in the body for minimally invasive surgery, it may be difficult or impossible for a robot with a generic kinematic design to reach all desirable targets while avoiding obstacles. We introduce a design optimization method to compute kinematic design parameters that enable a single robot to reach as many desirable goal regions as possible while avoiding obstacles in an environment. Our method appropriately integrates sampling-based motion planning in configuration space into stochastic optimization in design space so that, over time, our evaluation of a design’s ability to reach goals increases in accuracy and our selected designs approach global optimality. We prove the asymptotic optimality of our method and demonstrate performance in simulation for (1) a serial manipulator and (2) a concentric tube robot, a tentacle-like medical robot that can bend around anatomical obstacles to safely reach clinically-relevant goal regions.

1 Introduction

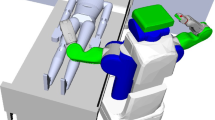
In a cluttered environment, the ability of a robotic manipulator to reach desired targets while avoiding obstacles depends significantly on the robot’s kinematic design. A robot’s kinematic design can be seen as a set of kinematic parameters that define a robot’s shape and are fixed throughout the robot’s use, e.g., the length of each link of a serial manipulator or the lengths and curvatures of tubes in a concentric tube robot (Dupont et al. 2010; Gilbert et al. 2013). In highly constrained settings, e.g., a tentacle-like robot maneuvering through narrow cavities in the body for minimally invasive surgery, it may be difficult or impossible for a robot with a generic kinematic design to reach all desirable targets while avoiding obstacles (see Fig. 1).

Fig. 1

Optimizing the kinematic design of a robotic manipulator can enable it to reach more goal regions in a cluttered environment. In this example, the objective is to optimize the design of a concentric tube robot, a surgical manipulator composed of nested, precurved tubes (cyan, yellow, magenta) whose lengths and curvatures can be customized (top). The objective is to move from a bronchial tube (white arrow) to reach goal regions (green spheres) in the lung while avoiding anatomical obstacles, e.g., blood vessels (red, blue) and bronchial tubes (off-white). A generic design may fail to reach some goal regions in a cluttered environment (right column), while an optimized design (left column) has the potential to reach more goal regions (Color figure online)

Fortunately, advances in methods that enable the rapid fabrication of customized robot designs is introducing the potential to create robots that are kinematically optimized on a task-specific basis. Advances in 3D printing enable the rapid creation of robots with links of customizable lengths. Customized medical robots, like concentric tube robots, can be created in minutes by shape-setting or 3D printing (Gilbert and Webster 2016; Morimoto and Okamura 2016). Our objective is to computationally optimize the kinematic design parameters of a robotic manipulator on a task-specific basis: given the shapes of obstacles in the environment as well as goal regions the robot should be capable of reaching, we aim to compute a single robot design that can reach as many of the goal regions as possible while avoiding obstacles.

In this paper, we focus on optimizing the kinematic design of a general class of robots whose shapes can be modeled as a continuous mapping from a compact set. This model can be applied to standard serial manipulators, where the length of each link is a kinematic design parameter, as well as concentric tube robots, tentacle-like robots for minimally invasive surgery that can curve around anatomical obstacles to reach surgical sites in constrained spaces (Dupont et al. 2010; Gilbert et al. 2013). Concentric tube robots are composed of nested, pre-curved tubes, where each tube is typically shaped with a straight section followed by a pre-curved constant-curvature section. Each of the robot’s component tubes can be independently rotated or extended, enabling the entire device to change shape as the nested tubes elastically interact. This robot’s kinematic design parameters include the pre-curvatures and lengths of each constituent tube. These parameters have a significant impact on the surgical targets reachable by the device in constrained spaces, so proper selection of kinematic design parameters for a patient’s anatomy is critical to the success of a medical procedure.

Optimizing a robot’s kinematic design on a task-specific basis is challenging. We desire to compute high quality designs reasonably quickly (i.e., minutes, not days), particularly for medical applications in which the physician customizes the robot design based on a patient-specific anatomy identified in medical images. However, the kinematic design space of a robot may be large, and for any candidate design we must evaluate whether that design can move from an initial configuration to reach a volume of goal points in the target set while avoiding obstacles. This implies we need to compute motion plans to multiple goal regions for successively selected designs, but current state-of-the-art motion planners based on sampling-based methods cannot determine with certainty in finite time whether a goal region can be reached by a particular design.

Our novel contributions are as follows. First, we introduce a unified framework for optimizing the kinematic design parameters of a wide class of robots on a task-specific basis by appropriately integrating sampling-based motion planning into iterations of a stochastic optimization method for design selection. We implement the integration so that, over time, our reachability evaluations increase in accuracy and our design selections improve toward global optimality. Second, we analyze our algorithm and prove asymptotic optimality, i.e., almost sure convergence to a globally optimal design, under a mild continuity assumption on the robot’s shape and the design objective, which guarantees that our method avoids getting trapped in local optima. Third, we demonstrate the broad applicability and effectiveness of our design optimization method via evaluations for two distinct robots: (1) a 4-link serial manipulator, and (2) a concentric tube medical robot.

2 Related work

Our approach to optimizing the kinematic design of robots integrates prior work in robot design optimization, stochastic search, and robot motion planning. Prior work has investigated combinatorial approaches to design optimization over a finite and discrete set of robot features. Examples include optimizing over discrete components of modular robots (Jing et al. 2016; Rus and Tolley 2015), monopedal jumping robots (Plecnik et al. 2017), snake-like and multi-modal robots (Mulgaonkar et al. 2016; Wright et al. 2012), and kinematic chains such as proteins (Denarie et al. 2016). In this paper, we focus on robots with continuous design parameters.

There has been extensive work on optimizing the kinematic design of serial manipulators. Approaches have optimized various metrics and have used genetic algorithms (Chocron 2008; Katragadda 1997; Leger 1999; Salle et al. 2004), interval analysis (Merlet 2005), geometric methods (Vijaykumar et al. 1986), and grid-based methods (Park et al. 2003). These methods typically lack theoretical performance guarantees or achieve computational tractability by imposing significant assumptions on the robot’s workspace and by using simplified kinematic models, which limit the effectiveness and applicability of the optimization procedure.

Kinematic design optimization for concentric tube robots is particularly challenging due to their complex kinematics, which is computationally expensive to evaluate due to the complex elastic and torsional interactions of their constituent tubes. Morimoto et al. present a complementary approach to automatic design optimization by providing a human with an intuitive interface to manually design the tubes (Morimoto et al. 2016). Bergeles et al. computationally optimize the robot’s design to reach a set of points without colliding with anatomical obstacles (Bergeles et al. 2015). For computational efficiency, they reduce the motion planning problem to finding goal configurations that can reach the targets and do not offer a global optimality guarantee. Burgner et al. combine a grid-based evaluation of the robot’s kinematics in configuration space with a nonlinear optimization method over the design space to maximize the reachable region of points subject to anatomical constraints (Burgner et al. 2013). Burgner et al. extended this work to characterize the workspace of concentric tube robots (Burgner-Kahrs 2015; Burgner-Kahrs et al. 2014). Ha et al. present a method for generating designs to maximize device stability (Ha et al. 2014).

By focusing only on computing designs and goal configurations, the works above cannot guarantee that a collision-free path from start to goal exists for the computed design. Torres et al. integrated a motion planner into concentric tube robot design using an RRT to sample in the design space and another RRT in the configuration space to ensure the computed design is able to avoid obstacles en route to specific points (Torres et al. 2012), but offers slow performance. Baykal et al. investigated computing minimal sets of concentric tube robot designs to reach multiple targets (Baykal et al. 2015), although no analysis was provided regarding a guarantee on optimality.

Recent work includes approaches that simultaneously optimize the design and motion of the robot with respect to a given objective. Ha et al. introduce a design optimization procedure that leverages the Implicit Function Theorem to computationally optimize the morphological design of manipulators and quadruped robots (Ha et al. 2017). Taylor et al. present a nonlinear optimization based approach to simultaneous design and motion optimization of dynamic planar manipulators (Taylor and Rodriguez 2017). However, these methods only apply to specific design objectives, do not provide global optimality guarantees, and are prone to getting stuck in locally optimal solutions. We present a unified approach to asymptotically optimal kinematic design optimization that is applicable to a wide class of robots and objectives.

In this paper, we present a refined and extended version of our methods and analysis originally introduced in Baykal and Alterovitz (2017). Our prior work in Baykal and Alterovitz (2017) focused on design optimization for piecewise cylindrical robots to maximize end-effector reachability to specified goal regions. We relax the previously imposed assumption on the robot’s shape and generalize our prior method and analysis to a much larger class of robots whose shapes can be modeled as a continuous mapping from a compact set. We also provide additional experimental results demonstrating the scalability of our algorithm with respect to varying dimensionality of the design space.

3 Problem definition

A robot’s design $\mathbf {d}$ is an n-dimensional vector of kinematic parameters that correspond to physical properties of the robot’s shape that are fixed for the duration of a given task. This vector includes kinematic parameters such as the length of each link of a serial manipulator or the lengths and curvatures of tubes in a concentric tube robot. The design space${\mathcal {D}}\subset {\mathbb {R}}^{n}$ of a robot is the n-dimensional open set corresponding to the space of all possible kinematic designs of the robot. We assume that the robot operates in a workspace ${\mathcal {W}} \subseteq {\mathbb {R}}^l$ containing a compact set of obstacles ${\mathcal {O}} \subset {\mathcal {W}}$, where $l\in \{2,3\}$.

Our overarching goal is to design the robot so it can safely, i.e., without colliding with the obstacles, reach as many points in a specified goal region ${\mathcal {G}}\subset {\mathcal {W}}$ as possible. That is, the optimization problem is to generate an optimal design $\mathbf {d}^* \in {\mathcal {D}}$ such that the robot under design $\mathbf {d}^*$ maximizes the reachable volume of points in ${\mathcal {G}}$. Formulating the design optimization problem in this continuous, volume-based manner formally captures the objective of maximizing reachability, however, it also renders the problem computationally intractable to exactly solve algorithmically. This challenge stems from the fact that the volume-based objective requires the evaluation of reachability to an uncountable set of points in ${\mathcal {G}}$ in order to measure volume. Evaluating this objective is both algorithmically challenging in theory and computationally intractable in practice.

Motivated by these practical and theoretical concerns, we consider a discretized version of the problem where the objective of maximizing the reachable volume is replaced by its discretized analogue of maximizing the number of discrete goal regions that can be reached. This discretization alleviates the challenges associated with the volume-based objective without significantly altering the core problem that we address in this paper. That is, the robot should be designed so it can reach (while avoiding obstacles) a set of m user-specified goal regions, where each goal region ${\mathcal {G}}_i \subset {\mathcal {W}}$, $i \in \{1,\dots ,m\}$ is defined as a volume of workspace positions. We define ${\mathcal {G}}= \{{\mathcal {G}}_i : i = 1,\dots ,m\}$ as the union of the goal regions.

Let the open set ${\mathcal {Q}} \subset {\mathbb {R}}^d$ denote the d-dimensional configuration space of the robot. Since the shape of a robot at any configuration is a function of its design $\mathbf {d}$, the set of configurations for which the robot’s shape does not intersect an obstacle is dependent on $\mathbf {d}$. Thus, we denote the set of collision-free configurations for a robot of design $\mathbf {d}$ as ${\mathcal {Q}}_{\mathbf {d}}^\text {free} \subset {\mathcal {Q}}$. We model the shape of a robot with design $\mathbf {d}\in {\mathcal {D}}$ at configuration $\mathbf {q}\in {\mathcal {Q}}$ by the mapping $\mathrm {Shape}: {\mathcal {D}}\times {\mathcal {Q}}\times {\mathcal {K}}_\mathrm {robot}\rightarrow {\mathcal {W}}$, where ${\mathcal {K}}_\mathrm {robot}$ is a compact set used for parameterization (e.g., a parameterization of points in the volume of a manipulator or along the central axis of a thin tubular robot). Namely, $\mathrm {Shape}(\mathbf {d}, \mathbf {q}, \cdot )$ defines the workspace points that the robot occupies under design $\mathbf {d}$ at configuration $\mathbf {q}$. We assume $\text {Shape}$ is computed using an accurate kinematic model. We let $\mathbf {k}_\text {base}, \mathbf {k}_\text {end} \in {\mathcal {K}}_\mathrm {robot}$ denote elements of ${\mathcal {K}}_\mathrm {robot}$ such that $\mathrm {Shape}(\cdot , \cdot , \mathbf {k}_\text {base})$ and $\mathrm {Shape}(\cdot , \cdot , \mathbf {k}_\text {end})$ correspond to the robot’s base and end-effector points, respectively.

We define $\mathbf {q}_0 \in {\mathcal {Q}}$ as the robot’s start configuration. The robot’s motion is a path in the configuration space ${\mathcal {Q}}$ defined by the continuous function $\sigma :[0,1] \rightarrow {\mathcal {Q}}$, where $\sigma (0)=\mathbf {q}_0$. A path $\sigma$ executed under robot design $\mathbf {d}$ is collision-free if it lies entirely in the collision-free configuration space, that is, if $\sigma (\tau ) \in {\mathcal {Q}}_\text {free}^{\mathbf {d}}$ for all $\tau \in [0,1]$.

We define our design optimization objective with respect to a user-defined reachability function$f: {\mathcal {D}}\times {\mathcal {Q}}\times {\mathcal {K}}_\mathrm {reach}\rightarrow {\mathcal {W}}$ for a non-empty, compact set ${\mathcal {K}}_\mathrm {reach}\subseteq {\mathcal {K}}_\mathrm {robot}$. The function f can be thought of as a mapping from a robot design $\mathbf {d}\in {\mathcal {D}}$ at configuration $\mathbf {q}\in {\mathcal {Q}}$ to an objective-specific point in the workspace. In particular, in this paper we consider the objective of reaching as many goal regions in ${\mathcal {G}}$ as possible with the robot’s end-effector, where we define ${\mathcal {K}}_\mathrm {reach}= \mathbf {k}_\text {end}$ and f as the mapping from a design-configuration pair $(\mathbf {d}, \mathbf {q})$ to the robot’s end effector position, $\mathrm {Shape}(\mathbf {d}, \mathbf {q}, \mathbf {k}_\text {end})$.¹ We compute f via the kinematics evaluation for $\mathrm {Shape}$ for some ${\mathcal {K}}_\mathrm {reach}$ corresponding to the points on the robot that we desire to reach the goal.

More generally, given a user-specified f and a non-empty compact set ${\mathcal {K}}_\mathrm {reach}$, the reachability of any goal region ${\mathcal {G}}_i \in {\mathcal {G}}, i \in [m]$ under design $\mathbf {d}\in {\mathcal {D}}$ at configuration $\mathbf {q}$ can be defined entirely in terms of f and ${\mathcal {K}}_\mathrm {reach}$, as formalized below.

Definition 1

(Reachable design-configuration pair) A design-configuration pair $(\mathbf {d}, \mathbf {q}) \in {\mathcal {D}}\times {\mathcal {Q}}_\mathbf {d}^\text {free}$ is said to be reachable if there exists a collision-free path $\sigma :[0,1] \rightarrow {\mathcal {Q}}_\mathbf {d}^\text {free}$ from the initial configuration $\mathbf {q}_0$ to $\mathbf {q}$ under design $\mathbf {d}$.

Definition 2

(Reachable goal region under a design-configuration pair) A goal region ${\mathcal {G}}_i \in {\mathcal {G}}, \, i \in [m]$ is said to be reachable by the design-configuration pair $(\mathbf {d},\mathbf {q})$ with respect to the reachability function f and a non-empty compact set ${\mathcal {K}}_\mathrm {reach}\subseteq {\mathcal {K}}_\mathrm {robot}$ if:

• 1. the pair $(\mathbf {d},\mathbf {q})$ is reachable and,

• 2. there exists $\mathbf {k}\in {\mathcal {K}}_\mathrm {reach}$ such that $f(\mathbf {d}, \mathbf {q}, \mathbf {k}) \in {\mathcal {G}}_i$.

Definition 3

(Reachability under a design) A goal region ${\mathcal {G}}_i \in {\mathcal {G}}, \, i \in [m]$ is said to be reachable by a robot of design $\mathbf {d}\in {\mathcal {D}}$ if there exists a configuration $\mathbf {q}\in {\mathcal {Q}}$ such that ${\mathcal {G}}_i$ is reachable by the design-configuration pair $(\mathbf {d}, \mathbf {q})$.

Our over-arching goal is to compute an optimal robot design $\mathbf {d}^* \in {\mathcal {D}}$ that enables the robot to reach as many goal regions in ${\mathcal {G}}$ as possible in a safe manner, i.e., via collision-free paths that avoid the workspace obstacles ${\mathcal {O}}$. The quality of a design $\mathbf {d}\in {\mathcal {D}}$ is defined with respect to the extent of the design’s reachability to the goal regions in ${\mathcal {G}}$ (Definition 3). That is, the objective function value of $\mathbf {d}$ is expressed as the percentage of goal regions in ${\mathcal {G}}$ that are reachable with design $\mathbf {d}$ relative to the total number of goal regions in ${\mathcal {G}}$.

Formally, the reachability of design $\mathbf {d}$ is given by the mapping $R(\mathbf {d}): {\mathcal {D}}\rightarrow [0,1]$:

$$\begin{aligned} R(\mathbf {d}) = \frac{|\text {GoalRegionsReachable}(\mathbf {d})|}{|{\mathcal {G}}|}, \end{aligned}$$

(1)

where $\text {GoalRegionsReachable}(\mathbf {d}): {\mathcal {D}}\rightarrow 2^{|{\mathcal {G}}|}$ denotes the set of goal regions that the robot of design $\mathbf {d}$ can reach with respect to the reachability function f and compact set ${\mathcal {K}}_\mathrm {reach}$, by following a collision-free path. $R(\mathbf {d})$ expresses the reachable goal percentage of the robot under design $\mathbf {d}$, which we seek to maximize. We formalize the kinematic design optimization problem as follows:

Given an environment ${\mathcal {W}}\subseteq {\mathbb {R}}^l$ (where $l=2$ or 3), a set of obstacles ${\mathcal {O}}\subset {\mathcal {W}}$, a set of user-specified goal regions ${\mathcal {G}}$, an objective-specific non-empty compact set ${\mathcal {K}}_\mathrm {reach}\subseteq {\mathcal {K}}_\mathrm {robot}$, and a reachability function $f:{\mathcal {D}}\times {\mathcal {Q}}\times {\mathcal {K}}_\mathrm {reach}\rightarrow {\mathcal {W}}$, generate a design $\mathbf {d}^*$ that maximizes the reachable goal percentage, i.e.,

$$\begin{aligned} \mathbf {d}^* \in {{\mathrm{\arg \!\max }}}_{\mathbf {d}\in {\mathcal {D}}} R(\mathbf {d}). \end{aligned}$$

(2)

4 Methods

In this section, we present our algorithm for optimizing the kinematic design parameters of a robot whose shape can be modeled as a continuous mapping from a compact set, to maximize the robot’s reachable goal percentage while avoiding obstacles in a task-specific environment.

4.1 Method overview and the key challenge

Our design optimization approach combines a stochastic search in the robot’s design space ${\mathcal {D}}$ with a sampling-based motion planner in the robot’s configuration space ${\mathcal {Q}}$ to efficiently generate designs with high reachability. To select candidate designs for evaluation, we use Adaptive Simulated Annealing (ASA) (Ingber 1989), a global optimization algorithm. For each selected design, we use the Rapidly-exploring Random Tree (RRT) (LaValle 2006) algorithm to estimate the design’s reachable workspace and evaluate its reachable goal percentage. We provide an overview of our approach in Algorithms 1 and 2 and formally prove the method’s asymptotic optimality in Sect. 5.

To ensure that we converge toward a globally optimal design, a key challenge we must address is that state-of-the-art, practical motion planners cannot guarantee completeness (LaValle 2006), i.e., they cannot always in finite time answer the question of whether a collision-free motion plan exists from the start configuration to a goal region. This limitation of current state-of-the-art motion planners introduces a significant challenge for design optimization; to use a standard optimization algorithm to optimize the design $\mathbf {d}$ in Eq. 2, a motion planner must evaluate the reachable goal percentage accurately and in finite time in each iteration of the optimization algorithm. Commonly used sampling-based motion planners only offer probabilistic completeness (and in some cases also asymptotic optimality in terms of path quality), meaning the probability that they will produce a collision-free path (if one exists) to a goal region approaches 1 as more time is spent (LaValle 2006). Terminating a sampling-based motion planner after finite time may result in an incorrect computation of the reachable goal percentage. The lack of full completeness makes it impossible to simply plug a standard sampling-based motion planner into a standard optimization algorithm and expect convergence toward a globally optimal design. We address this challenge by appropriately integrating sampling-based motion planning into stochastic optimization in design space so that, over time, our reachable goal percentage evaluations increase in accuracy and our selected designs approach global optimality.

4.2 Evaluating a design’s reachable goal percentage

Evaluating the objective function value $R(\mathbf {d})$ in equation (1) for an arbitrary design $\mathbf {d}\in {\mathcal {D}}$ requires computing $\text {GoalRegionsReachable}(\mathbf {d})$, the set of goal regions that design $\mathbf {d}$ can reach by executing collision-free paths. Thus, evaluating the reachability of a design is fundamentally a motion planning problem, which is known to be PSPACE-hard (Reif 1979). This renders the use of exact evaluation methods computationally intractable and motivates the use of a sampling-based motion planning algorithm, such as the Rapidly-exploring Random Tree (RRT) (LaValle 2006), to generate approximations of a design’s reachability (albeit an approximation that can improve over time, as will be discussed in Sect. 4.4).

For a given design $\mathbf {d}\in {\mathcal {D}}$ and a start configuration $\mathbf {q}_0$, the RRT algorithm incrementally constructs a tree of configurations that can be reached by collision-free paths from the root of the tree, $\mathbf {q}_0$. For a given design, we run the RRT algorithm for $i \in {\mathbb {N}}_+$ iterations and iterate over the configurations in the constructed tree to compute the set of goal regions that can be feasibly reached by the robot with design $\mathbf {d}$ (Line 2, Algorithm 1). From this we can approximate the design’s reachable goal percentage in a computationally tractable manner (Line 3, Algorithm 1). Because RRT provides probabilistic completeness, as we increase the iterations i of RRT, the probability of our approximation ${\hat{R}}_i(\mathbf {d})$ being equal to the true $R(\mathbf {d})$ approaches 1. For any finite i, our approximations of the reachable goal percentage at each iteration is ensured to be a lower bound of the ground-truth reachability, i.e., ${\hat{R}}_i(\mathbf {d}) \le R(\mathbf {d})$.

A key challenge is appropriately setting the number of iterations i the RRT will run for. In Sect. 4.4, we introduce an approach to setting i in Algorithm 1 that ensures asymptotic optimality of the design optimization.

4.3 Selecting designs

We use the ASA algorithm (Ingber 1989; Locatelli 2002) for optimizing the kinematic design to maximize the reachable goal percentage. We use ASA because it is a global optimization method that escapes local optima, it is efficient in practice for problems in high dimensional spaces, and it has favorable algorithmic properties which we exploit. Specifically, we are able to use sampling-based motion planning in each iteration of ASA in a manner that ensures asymptotic optimality of the design, as discussed in Sect. 4.4. Our ASA-based algorithm is shown as Algorithm 2 and operates similar to a hill climbing algorithm in that it is centered on a design $\mathbf {d}_\text {current}$ that it incrementally attempts to improve. However, unlike a hill climbing algorithm, the algorithm may in some iterations select an inferior design, which enables escaping local minima. Next designs are determined by sampling a new design ($\texttt {SampleDesign}$; Line 1, Algorithm 1) and deciding whether to accept that new design ($\texttt {Accept}$; Line 6, Algorithm 2), with both procedures being highly dependent on a temperature parameter $T \in {\mathbb {R}}_{\ge 0}$. $\texttt {Accept}$ returns true if the sampled design $\mathbf {d}'$ is higher quality than $\mathbf {d}_\text {current}$ (i.e., ${\hat{R}}' > {\hat{R}}_\text {current}$) or with some probability (dependent on T) if $\mathbf {d}'$ is inferior. In particular, for a sampled state $\mathbf {d}'$ the probability of accepting the state $\mathbf {d}'$ from the current state $\mathbf {d}_\text {current}$, denoted by ${{\mathrm{{\mathbb {P}}}}}_\texttt {Accept}$, is defined to be

$$\begin{aligned} {{\mathrm{{\mathbb {P}}}}}_{\texttt {Accept}} = {\left\{ \begin{array}{ll} 1 &{} \text {if } {\hat{R}}' > {\hat{R}}_\text {current}, \\ \exp \left( - \frac{{\hat{R}}_\text {current} - {\hat{R}}'}{T} \right) &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

The temperature variable T is initially set to a sufficiently high value,²$T_\mathrm {init} \in {\mathbb {R}}_+$, to ensure convergence to the globally optimal solution and is decreased after each iteration based on a cooling schedule (Algorithm 2, Line 18),

$$\begin{aligned} \mathtt {UpdateTemperature}(T_\text {init}, k) = T_\text {init} \exp (-c \, k^\frac{1}{n}), \end{aligned}$$

where c is an appropriate constant (Ingber 1989; Ingber et al. 2012) and n is the number of design parameters (see Sec. 4.2.7 of Ingber et al. (2012) for full details).

When T is high, ASA is more likely to sample states that are far away from $\mathbf {d}_\text {current}$ and also more likely to probabilistically accept inferior designs, which leads to exploratory behavior initially. As T is cooled down over time, ASA samples states in smaller neighborhoods around $\mathbf {d}_\text {current}$ and is increasingly less likely to accept inferior designs, which leads to eventual convergence to a high quality design. We cache the best found design (Algorithm 2, Line 10) so the best found design is returned when the algorithm terminates.

Full details of the Adaptive Simulated Annealing algorithm can be found in the publicly available codebase of Ingber (1993); Ingber et al. (2012).

4.4 Integrating motion planning into stochastic optimization

A key requirement to converging toward a globally optimal design is an accurate evaluation of any candidate design’s reachable goal percentage. This implies we need to compute motion plans to multiple goal regions for each design considered in the optimization, but current state-of-the-art motion planners based on sampling-based methods cannot specify with certainty in finite time whether a goal can be reached by a particular design.

To address this challenge, we use a simple-to-implement idea: we incrementally increase the number of RRT iterations by $i_\Delta$ after each sampled design (Line 13, Algorithm 2). This approach ensures that our approximations become increasingly accurate over time. This approach is sufficient for establishing the asymptotic optimality of our algorithm (see Sect. 5). This approach also has a secondary benefit: it enables us to more quickly (but more coarsely) evaluate many designs in the initial iterations and subsequently evaluate candidate designs with higher accuracy (albeit at a slower rate) in later iterations.

5 Analysis

We prove under mild assumptions that the design computed by our algorithm almost surely converges (Durrett 2010) to a globally optimal design. The outline of our proof is as follows. First, we establish that the set of optimal designs with respect to the reachability problem (2) is non-empty and open, and thus has strictly positive measure. Then, we show that by property of the ASA algorithm, optimal designs will be sampled and evaluated infinitely often. We conclude by proving that, eventually, an optimal design will be sampled and evaluated accurately by the RRT algorithm.

5.1 Preliminaries

We remind the reader that the inverse images of open and closed sets under continuous functions are themselves open and closed respectively where the inverse image of $A \subseteq B$ under $f : C \rightarrow B$ (denoted $f^{-1}[A]$) is the set $\{ c \in C \mid f(c) \in A \}$. In the following proofs, we will also frequently refer to the topological projection (or simply projection) from a Cartesian product of topological spaces $X \times Y$ to X. The projection of a set $Z \subseteq X \times Y$ to X is the set $\{x \in X \mid \exists y \in Y : (x,y) \in Z\}$. Two useful properties of projections enable the proofs below. First, the projection of an open set is itself open. Second, if Y is compact, then the projection $X \times Y \rightarrow X$ of a closed set is itself closed. This latter property is referred to as the Tube Lemma (Munkres 2000).

Assumption 1

(Goal Regions as Open Sets) Each goal region ${\mathcal {G}}_i \subset {\mathcal {W}}$, $i \in [\hbox {m}]$, is defined as an open set.

Assumption 2

(Continuity of the Shape Function) $\text {Shape}: {\mathcal {D}} \times {\mathcal {Q}} \times {\mathcal {K}}_\mathrm {robot}\rightarrow {\mathcal {W}}$ is continuous.

Assumption 3

(Continuity off) $\text {f} : {\mathcal {D}} \times {\mathcal {Q}} \times {\mathcal {K}}_\mathrm {reach}\rightarrow {\mathcal {W}}$ is continuous.

Assumption 1 rules out pathological problem instances where only a single optimal design lying on the boundary of the design space exists. Assumption 2 guarantees that robots of similar designs have similar shapes at similar configurations. Finally, Assumption 3 is a technical assumption that ensures the pertinent design optimization objective is sufficiently well-behaved.

Let ${\mathcal {R}}\subseteq {\mathcal {D}}\times {\mathcal {Q}}$ denote the set of reachable design-configuration pairs. The following lemma is an extension of the analysis introduced in Baykal and Alterovitz (2017), and establishes that the set of reachable design-configuration pairs, ${\mathcal {R}}$, is open.

Lemma 1

The set of reachable design-configuration pairs ${\mathcal {R}}\subseteq {\mathcal {D}}\times {\mathcal {Q}}$ is open.

Proof

Our proof of this lemma is based on the result in Kuntz et al. (2018). Consider a reachable design-configuration pair $(\mathbf {d},\mathbf {q}) \in {\mathcal {D}}\times {\mathcal {Q}}_\mathbf {d}^\text {free}$ for which we wish to construct a reachable neighborhood. By definition of reachable, there must exist some collision-free path $\sigma \in [0,1] \rightarrow {\mathcal {Q}}_\mathbf {d}^\text {free}$ with $\sigma (1) = \mathbf {q}$, i.e.,

$$\begin{aligned} \forall {s \in [0,1], \mathbf {k}\in {\mathcal {K}}_\mathrm {robot}} \,\, \mathrm {Shape}(\mathbf {d}, \sigma (s), \mathbf {k}) \in {\overline{{\mathcal {O}}}}, \end{aligned}$$

where ${\overline{{\mathcal {O}}}}$ denotes the set complement of ${\mathcal {O}}$. Let $\sigma _{\mathbf {q}'}(s) = \sigma (s) + s \cdot (\mathbf {q}' - \mathbf {q})$. $\sigma _{q'}$ is continuous by continuity of $\sigma$ and $\sigma _{\mathbf {q}'}(1) = \mathbf {q}'$ by construction, so $\sigma _{\mathbf {q}'}$ is a path to $\mathbf {q}'$. We thus have only to show that $\sigma _{\mathbf {q}'}$ is collision-free under each design $\mathbf {d}'$ for all $(\mathbf {d}',\mathbf {q}')$ in a neighborhood of $(\mathbf {d},\mathbf {q})$.

Observe that the mapping $L :{\mathcal {D}}\times {\mathcal {Q}}\times {\mathcal {K}}_\text {robot} \times [0,1] \rightarrow {\mathcal {W}}$ given by:

$$\begin{aligned} \mathbf {d}', \mathbf {q}', \mathbf {k}, s \mapsto \mathrm {Shape}(\mathbf {d}', \sigma _{\mathbf {q}'}(s), \mathbf {k}) \end{aligned}$$

is continuous by continuity of $\sigma _{q'}$ and $\mathrm {Shape}$. We then have that $B = L^{-1}[{\mathcal {O}}] \subseteq {\mathcal {D}}\times {\mathcal {Q}}\times {\mathcal {K}}_\mathrm {robot}\times [0,1]$ is closed by closedness of ${\mathcal {O}}$. Let C be the projection of B to ${\mathcal {D}}\times {\mathcal {Q}}$. C is thus the set of all $(\mathbf {d}', \mathbf {q}')$ for which $\sigma _{\mathbf {q}'}(s)$ is in collision under design $\mathbf {d}'$ for some $s \in [0,1]$, and is closed by compactness of ${\mathcal {K}}_\mathrm {robot}\times [0,1]$ and the Tube Lemma.

Now observe that $(\mathbf {d}, \mathbf {q}) \in {\overline{C}}$ because $\sigma _{q} = \sigma$, and $\sigma$ is collision-free for design $\mathbf {d}$ by definition. But ${\overline{C}}$ is open, so it covers some neighborhood N of $(\mathbf {d},\mathbf {q})$. N is thus a neighborhood of $(\mathbf {d},\mathbf {q})$ in which $\sigma _{\mathbf {q}'}$ is collision-free under design $\mathbf {d}'$ for all $(\mathbf {d}',\mathbf {q}') \in N$. $\square$

Now, let ${\mathcal {R}}_{g} \subseteq {\mathcal {D}}\times {\mathcal {Q}}_\mathbf {d}^\text {free}$ denote the set of design-configuration pairs under which the goal region $g \in {\mathcal {G}}$ is reachable. The following lemma establishes that ${\mathcal {R}}_{{\mathcal {G}}_i}$ is open for all of the m goal regions ${\mathcal {G}}_i \in {\mathcal {G}}, \, i \in [m]$.

Lemma 2

For any goal region ${\mathcal {G}}_i \in {\mathcal {G}}, \, i \in [m]$, the set of design-configuration pairs under which goal region ${\mathcal {G}}_i$ is reachable, denoted by ${\mathcal {R}}_{{\mathcal {G}}_i}$, is open.

Proof

For any arbitrary goal region ${\mathcal {G}}_i \in {\mathcal {G}}$, consider the set $A = {\overline{{\mathcal {G}}}}_i = {\mathcal {W}}{\setminus } {\mathcal {G}}_i$. Note that A is closed since ${\mathcal {W}}$ is compact and ${\mathcal {G}}_i$ is open. The remainder of the proof proceeds in a manner similar to Lemma 1.

Let $B = f^{-1}[A] \subseteq {\mathcal {D}}\times {\mathcal {Q}}\times {\mathcal {K}}_\mathrm {reach}$ and note that B is closed since A is closed and f is continuous. Now let $C \subseteq {\mathcal {D}}\times {\mathcal {Q}}$ be the projection of B to ${\mathcal {D}}\times {\mathcal {Q}}$, i.e., C is the set of design-configuration pairs that cannot reach the goal region ${\mathcal {G}}_i$ for any $\mathbf {k}\in {\mathcal {K}}_\mathrm {reach}$:

$$\begin{aligned} \forall {(\mathbf {d}, \mathbf {q}) \in C} \, \not \exists {\mathbf {k}\in {\mathcal {K}}_\mathrm {reach}} : f(\mathbf {d}, \mathbf {q}, \mathbf {k}) \in {\mathcal {G}}_i. \end{aligned}$$

Since ${\mathcal {K}}_\mathrm {reach}$ is compact, it follows by the Tube Lemma that the set C is closed. Therefore, its complement, ${\overline{C}}$, is open. Now, note that the set of reachable design-configuration pairs from which goal ${\mathcal {G}}_i$ is reachable is defined as ${\mathcal {R}}_{{\mathcal {G}}_i} = {\overline{C}} \cap {\mathcal {R}}$, where ${\mathcal {R}}$ is the set of all reachable design-configuration pairs as before. By Lemma 1, ${\mathcal {R}}$ is open, thus ${\mathcal {R}}_{{\mathcal {G}}_i}$, the intersection of two open sets, is also open. $\square$

Let $R^* = \max _{\mathbf {d}\in {\mathcal {D}}} R(\mathbf {d})$ denote the optimal objective value with respect to the non-empty compact set ${\mathcal {K}}_\mathrm {reach}$ and the reachability function f, and let ${\mathcal {D}}^* = \{\mathbf {d}\in {\mathcal {D}} \mid R(\mathbf {d}) = R^*\}$ be the optimal set of designs with respect to the optimization problem defined by (2) in Sect. 3. The following lemmas establish that designs from the optimal design set will be sampled infinitely often.

Lemma 3

The set of optimal designs, ${\mathcal {D}}^* \subseteq {\mathcal {D}}$, is open.

Proof

For all $i \in [m]$, let ${\mathcal {R}}_{{\mathcal {G}}_i}$ denote the set of design-configuration pairs under which goal region ${\mathcal {G}}_i$ is reachable, and note that by Lemma 2, ${\mathcal {R}}_{{\mathcal {G}}_i}$ is open. Now, let ${\mathcal {D}}_{i}$ denote the projection of ${\mathcal {R}}_{{\mathcal {G}}_i}$ to the set of designs ${\mathcal {D}}$. Projection is an open mapping, so each ${\mathcal {D}}_i$ is open. Let $m^*$ be the number of goal regions reachable by an optimal design. Observe that the union of all $m^*$-wise intersections of $\{ {\mathcal {D}}_1, \ldots , {\mathcal {D}}_m \}$ is the set of optimal designs. This is a finite union of finite intersections of open sets, and is thus open itself. $\square$

Corollary 1

(Frequency of Sampling Optimal Designs) Algorithm 2 will sample designs from the optimal design set ${\mathcal {D}}^*$ infinitely often.

Proof

It is known that designs that are an element of any subset of ${\mathcal {D}}$ with non-zero measure will be sampled infinitely often by the ASA algorithm (Ingber 1989; Locatelli 2002). By Lemma 3 we have that ${\mathcal {D}}^*$ is open and non-empty. Lebesgue measure is strictly positive on non-empty open sets, thus the set of optimal designs ${\mathcal {D}}^* \subseteq {\mathcal {D}}$ has non-zero measure and the result follows. $\square$

5.2 Asymptotic optimality

Let ${\mathcal {Y}}_k$ be a random variable that denotes the maximum reachable goal percentage attained over all the designs sampled in optimization iterations $1, \ldots , k$.

Theorem 1

(Asymptotic Optimality) Let Assumptions 1–3 hold. Then, the solution generated by Algorithm 2 almost surely converges to a globally optimal design $\mathbf {d}^* \in {\mathcal {D}}^*$, i.e.,

$$\begin{aligned} {{\mathrm{{\mathbb {P}}}}}{\left( \lim _{k \rightarrow \infty } {\mathcal {Y}}_k = R^*\right) } = 1. \end{aligned}$$

Proof

Application of Corollary 1 implies that the optimal set of designs ${\mathcal {D}}^* \subset {\mathcal {D}}$ will be sampled infinitely often. Let $j \in {\mathbb {N}}_+$ denote the $j^\text {th}$ occurrence of sampling any arbitrary optimal design $\mathbf {d}^* \in {\mathcal {D}}^*$ and let $I_j$ denote the number of iterations that the RRT algorithm is executed for. Note that by the procedure used to increase the number of RRT iterations by $i_\Delta \in {\mathbb {N}}_+$ (Algorithm 2) after each sampled design, we have that $I_j + 1 \le I_{j+1}$ for all j and that $1 \le I_1$.

For each occurrence of sampling an optimal design $\mathbf {d}^* \in {\mathcal {D}}$, a random approximation of the reachable goal percentage is generated by running the RRT algorithm for $I_j$ iterations. Let ${\hat{{\mathcal {G}}}}_j(\mathbf {d}^*)$ and ${\hat{R}}_j(\mathbf {d}^*) = \frac{|{\hat{{\mathcal {G}}}}_j(\mathbf {d}^*)|}{|{\mathcal {G}}|}$ denote the approximation of $\text {GoalRegionsReachable}(\mathbf {d}^*)$ and $R(\mathbf {d}^*)$ for the $j^\text {th}$ sampled optimal design respectively. For any arbitrary $\epsilon \in {\mathbb {R}}_+$, let $A_j$ denote the event $|{\hat{R}}_j(\mathbf {d}^*) - R^*| \ge \epsilon$ for each j. Note that event $A_j$ is equivalent to the event that the RRT algorithm fails to find a collision-free path to at least one goal region $g \in {\mathcal {G}}^* {\setminus } {\hat{{\mathcal {G}}}}_j(\mathbf {d}^*)$ within $I_j$ iterations. Thus, we have

$$\begin{aligned} {{\mathrm{{\mathbb {P}}}}}{(A_j)}&= {{\mathrm{{\mathbb {P}}}}}{(\exists g \in {\mathcal {G}}^* {\setminus } {\hat{{\mathcal {G}}}}_j(\mathbf {d}^*) )} \\&\le \sum _{g \in {\mathcal {G}}^*} {{\mathrm{{\mathbb {P}}}}}{(g \in {\mathcal {G}}^* {\setminus } {\hat{{\mathcal {G}}}}_j(\mathbf {d}^*))} \\&\le \sum _{g \in {\mathcal {G}}^*} a e^{-b I_j} \\&= |{\mathcal {G}}^*| a e^{-bI_j}, \end{aligned}$$

for some constants a, b, where the first inequality is by the union bound and the second by RRT’s exponential decay of the probability of failure to find a path after $I_j$ iterations (LaValle and Kuffner 2001; Karaman and Frazzoli 2011).

Consider the sum of the probabilities of $A_j$ over all j:

$$\begin{aligned} \sum _{j=1}^\infty {{\mathrm{{\mathbb {P}}}}}{(A_j)}&\le \sum _{j=1}^\infty |{\mathcal {G}}^*| a e^{-bI_j} \\&\le \sum _{j=1}^\infty |{\mathcal {G}}^*| a e^{-bj} \\&= \frac{|{\mathcal {G}}^*|a}{e^b - 1} < \infty . \end{aligned}$$

By the Borel-Cantelli Lemma we have that

$$\begin{aligned} {{\mathrm{{\mathbb {P}}}}}{\left( \limsup _{j \rightarrow \infty } A_j \right) } = 0, \end{aligned}$$

that is, the probability that $A_j$ occurs infinitely often is 0. This implies that

$$\begin{aligned} {{\mathrm{{\mathbb {P}}}}}{\left( \liminf _{j \rightarrow \infty } |{\hat{R}}_j(\mathbf {d}^*) - R^*| < \epsilon \right) } = 1, \end{aligned}$$

which is precisely the definition of ${\hat{R}}_j(\mathbf {d}^*) \overset{a.s.}{\rightarrow } R^*$.

Thus, with probability 1, at least one optimal design $\mathbf {d}^* \in {\mathcal {D}}^*$ will be sampled and evaluated accurately as the number of optimization iterations of Algorithm 2 approaches infinity. Since the best solution found thus far is cached in Algorithm 2, it follows that ${\mathcal {Y}}_k \overset{a.s.}{\rightarrow } R^*$. $\square$

Corollary 2

The design optimization procedure is asymptotically optimal with respect to the objective of reaching as many goal regions as possible with the robot’s end-effector, i.e., Algorithm 2 is asymptotically optimal for the choice of reachability function $f:{\mathcal {D}}\times {\mathcal {Q}}\times {\mathcal {K}}_\mathrm {reach}\rightarrow {\mathcal {W}}$ with ${\mathcal {K}}_\mathrm {reach}= \mathbf {k}_\text {end}$, defined as the mapping

$$\begin{aligned} f(\mathbf {d}, \mathbf {q}, \mathbf {k}) \mapsto \mathrm {Shape}(\mathbf {d}, \mathbf {q}, \mathbf {k}). \end{aligned}$$

Proof

Observing that ${\mathcal {K}}_\mathrm {reach}= \mathbf {k}_\text {end}$ is compact and f is continuous (since $\mathrm {Shape}$ is continuous), and applying Theorem 1 yields the result. $\square$

6 Results

We apply our design optimization algorithm to two distinct robots: (1) a serial manipulator and (2) a concentric tube robot, a tentacle-like robot designed for minimally invasive medical procedures. In particular, we consider the design objective of maximizing the reachability of the robot’s end effector to the specified goal regions, i.e., we define ${\mathcal {K}}_\mathrm {reach}= \mathbf {k}_\text {end}$ and $f: {\mathcal {D}}\times {\mathcal {Q}}\times {\mathcal {K}}_\mathrm {reach}\rightarrow {\mathcal {W}}$ as the mapping

$$\begin{aligned} f(\mathbf {d}, \mathbf {q}, \mathbf {k}) \mapsto \mathrm {Shape}(\mathbf {d}, \mathbf {q}, \mathbf {k}), \end{aligned}$$

for all $\mathbf {d}\in {\mathcal {D}}, \mathbf {q}\in {\mathcal {Q}}, \mathbf {k}\in {\mathcal {K}}_\mathrm {reach}$.

We assess the performance of our method (ASA+MP) in computing designs with high reachable goal percentage and compare its computational efficiency and results with the following variants of our method and other state-of-the-art design optimization algorithms.

Fig. 2

First row: example configurations of robot designs (where the links are colored green, cyan, magenta, and orange) computed by our algorithm for three randomly generated 2D environments containing obstacles (red) and a grid of goal regions colored green for grid cells reachable using the optimal design and blue for unreachable cells. Second row: in contrast to optimal designs, generic (i.e., randomly generated) robot designs operating in the same three scenarios are unable to reach the goal regions (Color figure online)

• NM+G: The Nelder–Mead optimization algorithm is used instead of ASA for sampling designs. For evaluation of the reachable goal percentage, a grid-based approach is used instead of motion planning; the configuration space is discretized into a grid and the robot configuration at each grid point is evaluated to determine if it is collision-free and reaches a goal region (Burgner et al. 2013).

• NM+MP: Nelder–Mead is used for optimizing the design. In contrast to prior work using Nelder–Mead (Burgner et al. 2013), we use motion planning using the same number of initial and additional RRT iterations as our algorithm to approximate the reachable goal percentage of candidate designs.

• ASA+G: In this simplified form of our approach, we use ASA to sample designs, but we use the grid approach (as described in NM+G) to evaluate reachable goal percentage for a candidate design.

• RRT of RRTs: An RRT-based algorithm is run both in the design space (Torres et al. 2012) and in the configuration space for estimating reachable goal percentage.

We emphasize that the grid-based algorithms (ASA+G and NM+G) only consider final configurations when evaluating reachable goal percentage during design optimization. This implies that grid-based evaluations generate upper bounds on the ground-truth reachable goal percentage, since the actual motion of the device from its start configuration to a goal region is not considered, and no motion may be feasible due to obstacles. In our results graphs, we do not display this upper bound; instead, we run a post-processing step (that is not counted towards method computation time) and estimate the reachable goal percentage of each returned design by running the RRT algorithm for 300,000 iterations.

We implemented all design optimization algorithms in C++. The experiments were conducted on a PC with two 2.40 GHz Intel Xeon E5620 processors (8 cores total) and 12 GB RAM.

6.1 Design optimization of a serial manipulator in 2D

We consider the design optimization of a serial manipulator with 4 revolute joints and 4 straight links operating in a 2D environment. The configuration space of the robot is defined by the angles of the four links, i.e., ${\mathcal {Q}}\subset ({\mathcal {S}}^1)^4$. We define a robot’s design space as the length of each of the four links, thus, ${\mathcal {D}}\subset {\mathbb {R}}^4$. We evaluated each design optimization method on 40 randomized problem instances. For each instance, we randomly generated between 4 and 8 rectangular or right triangular obstacles with sides of random length and a set of 100 goal regions arranged in a regular grid and placed randomly in the workspace. The robot’s start configuration $\mathbf {q}_0$ was fixed for all instances and the robot’s base position was randomly placed so that the robot was collision-free. Figure 2 depicts three examples of the problem instances.

Figure 3 shows the reachable goal percentage (averaged over the 40 problem instances) achieved by each design optimization algorithm as a function of computation time. The robot design generated by our algorithm is capable of reaching a significantly higher percentage of the goal regions compared to the designs found by the other algorithms.

Figure 4 depicts the performance of each design optimization algorithm for a single scenario, specifically Example Instance 3 in Fig. 2. Each line is an average over 10 runs of the corresponding algorithm. We note the methods that use grid-based evaluation of the objective function are not guaranteed to improve over time since ignoring motion planning implies they are optimizing a potentially incorrect approximation of the objective function. Our method improves the design in an asymptotically optimal manner.

Our results indicate that our approach for blending ASA for searching the design space and motion planning for design evaluation helps in attaining computational efficiency and escapes local optima via asymptotic optimality.

We also demonstrate the scalability of our method in simulation by optimizing the design parameters of an $n=2,\ldots , 6$-link serial manipulator respectively over an allotted computation time of 4 hours per trial. For each problem instance we randomly generated between 6 to 10 obstacles.

Fig. 3

The performance over time of the design optimization methods for a 4-link serial manipulator. The plot shows the reachable goal percentage of the best design found thus far with respect to computation time, averaged over 40 randomized problem instances

Fig. 4

Plot of the reachable goal percentage over computation time for each design optimization method run 10 times for the problem instance in Fig. 2 (right column)

Figure 5 depicts the performance of our algorithm with respect to different values for the dimensionality of the design space. The results confirm the intuition that when the number of links is small, e.g., $n=2$, the robot’s shape is not sufficiently flexible to maneuver around the obstacles in the environment to reach goal regions. On the other hand, when the number of links is relatively large, e.g., $n=6$, the robot’s initial configuration may be in collision, e.g., with other links, the boundary of the workspace, or obstacles, which makes it more difficult for the robot to follow collision-free paths from the initial configuration, causing an increase in the computation time needed for design optimization.

Fig. 5

The reachable goal percentage over computation time for optimizing the design of n-link manipulators, for various values of n. The results are averaged across 10 different problem instances

6.2 Design optimization of a concentric tube robot

We next apply our design optimization algorithm to a concentric tube robot (Dupont et al. 2010; Gilbert et al. 2013), a medical robot composed of nested nitinol tubes that can be rotated and translated independently to change the shape of the entire robot and achieve tentacle-like motion. Unlike traditional medical instruments that are constrained to straight-line paths, these robots are capable of curving around anatomical obstacles, e.g., blood vessels, to reach clinical targets in a safe, minimally-invasive manner.

We consider in simulation a concentric tube robot with 3 tubes. In configuration space, each tube adds two degrees of freedom (since each tube can be independently inserted and rotated), resulting in a 6 dimensional configuration space, i.e., ${\mathcal {Q}} \subset ({\mathcal {S}}^1)^3 \times {\mathbb {R}}^3$. The curvilinear shapes that the robot can achieve are highly dependent on the physical specifications of the robot’s tubes, i.e., its design. In this study, each tube of the concentric tube robot is described by (1) the length of its straight section, (2) the length of its pre-curved section, and (3) the curvature of its pre-curved section. Thus, for our 3-tube robot the design space is 9 dimensional, i.e., ${\mathcal {D}}\subset {\mathbb {R}}^{9}$. To evaluate the robot’s shape given its configuration, we use an accurate mechanics-based kinematic model to account for the elastic and torsional interactions between the tubes (Rucker 2011).

Figure 6 illustrates a potential medical application of these devices for biopsy of suspicious nodules in the lung for early-stage lung cancer diagnosis. The concentric tube robot is deployed near the base of the primary bronchus of the right human lung using a rigid bronchoscope with the objective of reaching a clinical target for biopsy. We discretized the interior volume of the right human lung into 4156 equally-sized cubic voxels each with volume $\approx 0.7 \hbox { cm}^3$. For each trial, a subset of 8 contiguous voxels (i.e., goal regions) was randomly chosen to represent subregions of a clinical target that should be biopsied.

Fig. 6

A concentric tube robot (composed of cyan, yellow, and magenta tubes) has the potential to reach clinical goal regions (green and blue voxels) within the lung for early-stage lung cancer diagnosis. The figure shows the robot with an appropriate design reaching a point (green sphere) in one of the goal regions (shown as blue) (Color figure online)

Fig. 7

The reachable goal percentage over computation time for the concentric tube robot scenario. The results are averaged across 40 different problem instances, each with randomly selected goal regions in the right lung

The results averaged over 40 trials are shown in Fig. 7. The results for this scenario follow a similar trend as the results obtained from the 4-link serial manipulator scenario. In particular, the figure illustrates our algorithm’s effectiveness in finding a design with high reachable goal percentage and its tendency to efficiently improve the solution over the allotted computation time without being trapped in local optima.

7 Conclusion

We presented a design optimization algorithm applicable to a wide class of robots whose shapes can be modeled via a continuous mapping from a compact set and design objectives that satisfy a mild continuity condition. The algorithm integrates a sampling-based motion planner in the configuration space with stochastic search in the design space to efficiently compute designs that maximize reachability to user-specified goal regions in the workspace. We proved the asymptotic optimality of our algorithm and demonstrated its computational efficiency in simulated scenarios involving serial manipulators and concentric tube robots for medical procedures.

In future work, we plan to consider a mixture of continuous and discrete design parameters and generalize our definition of goal regions to consider goal configurations and end effector poses. We also plan to physically implement the designs computed by our method and conduct experiments in testbeds based on clinically-relevant scenarios, such as lung biopsies and neurosurgery. Since the shape-set or 3D-printed robots may not precisely match our method’s output, we plan to consider design uncertainty in design optimization.