Safe Motion Planning for Imprecise Robotic Manipulators by Minimizing Probability of Collision

Abstract

Robotic manipulators designed for home assistance and new surgical procedures often have significant uncertainty in their actuation due to compliance requirements, cost constraints, and size limits. We introduce a new integrated motion planning and control algorithm for robotic manipulators that makes safety a priority by explicitly considering the probability of unwanted collisions. We first present a fast method for estimating the probability of collision of a motion plan for a robotic manipulator under the assumptions of Gaussian motion and sensing uncertainty. Our approach quickly computes distances to obstacles in the workspace and appropriately transforms this information into the configuration space using a Newton method to estimate the most relevant collision points in configuration space. We then present a sampling-based motion planner based on executing multiple independent rapidly exploring random trees that returns a plan that, under reasonable assumptions, asymptotically converges to a plan that minimizes the estimated collision probability. We demonstrate the speed and safety of our plans in simulation for (1) a 3-D manipulator with 6 DOF, and (2) a concentric tube robot, a tentacle-like robot designed for surgical applications.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

As robotic manipulators enter emerging domains such as home assistance and enable new minimally-invasive surgeries, their designs are increasingly diverging from the designs of traditional manufacturing robots. Home assistance robotic manipulators must feature compliant joints for safety and must be lower cost to spur adoption, which results in decreased precision of sensors and actuators. Medical robots, such as tentacle-like and snake-like robots (e.g., [7, 9, 23, 32]), are becoming smaller and also are gaining larger numbers of degrees of freedom. These features are necessary to enable new, less invasive surgical procedures that require maneuvering around sensitive or impenetrable anatomical obstacles. These trends in robotic manipulator design and applications have an inevitable consequence: uncertainty in robot motion and state estimation. For robotic manipulators to operate with some level of autonomy in people’s homes and inside people’s bodies, uncertainty should explicitly be considered when planning motions to ensure both safety and task success.

In this paper, we introduce a new integrated motion planning and control algorithm for manipulators with uncertainty in actuation and sensing. Our objective is to compute plans and corresponding closed-loop controllers that a priori minimize the probability that any link of the robot will collide with an obstacle. To accomplish this objective, our algorithm incorporates two primary contributions. First, we introduce a fast and accurate method for assessing the quality of a manipulator motion plan by efficiently estimating the a priori probability of collision using fast numerical computations that do not require sampling in configuration space. Second, we introduce a sampling-based motion planner that, under reasonable assumptions, guarantees that the probability of finding a plan that minimizes the estimated probability of collision approaches 100 % as computation time is allowed to increase. We note that current planners such as RRT* [12] cannot guarantee asymptotic optimality for our problem since the optimal substructure property does not hold, i.e., the optimal plan from a particular state is not independent of the robot’s prior history. Our approach is applicable to robotic manipulators for which uncertainty in actuation and sensing can be modeled using Gaussian distributions, a Kalman filter is used for state estimation, and an optimal linear controller (i.e., LQG control) is used to follow the plan. To the best of our knowledge, this is the first approach for computing a plan that minimizes the a priori probability of collision for general robotic manipulators.

For robots with motion and sensing uncertainty, collision detection during motion planning must be done in a probabilistic sense by considering the possibility of collision with respect to all possible states of the robot. Extensive prior work has investigated integrated motion planning and control under uncertainty for robots that can be approximated as points in the workspace (e.g., [4, 20, 26, 27]), but robotic manipulators raise new challenges. Whereas for point robots analytically estimating probability of collisions is facilitated by the fact that the robot’s configuration space and workspace share parameters, for manipulators the configuration space and workspace are disjoint. Furthermore, manipulators (especially tentacle-like and snake-like medical robots) can have large numbers of degrees of freedom.

In our first contribution, we introduce a method to efficiently estimate the a priori probability of collision for a given plan for a robotic manipulator. Given the robot’s uncertainty represented as a distribution in configuration space, efficiently estimating the probability of collision is challenging because the shapes of the obstacles are defined in the workspace and cannot be directly computed in configuration space in closed form [6]. The key insight of our method is that an appropriate minimization of distance from the robot to an obstacle in C-space corresponds to a minimum distance in the workspace. Hence, we propose a fast method using Newton’s method to estimate the closest point in configuration space that will cause a collision, and use this information to estimate the probability of collision. We extend this formulation to multiple obstacles and then propagate these estimates over time (in a manner that considers dependencies across time steps) to estimate the a priori probability of collision for a plan.

In our second contribution, we present an asymptotically optimal motion planner that minimizes the estimated a priori probability of collision for a manipulator. Our motion planner is based on a simple idea: it generates a large number of plans, computes an optimal linear controller for each plan, then estimates the probability of collision for each plan using our approach above, and selects the best plan. By evaluating cost over entire plans, we properly handle the fact that the probability of collision from a configuration onwards depends on prior history. We show that, under reasonable assumptions, the computed plan will converge to a minimum estimated collision probability plan as computation time is allowed to increase.

We evaluate our method using simulated scenarios involving a 6-DOF manipulator and a tentacle-like robot designed for medical applications such as skull base surgery. Our results show that we can quickly estimate the a priori probability of collision of motion plans across highly distinct robotic manipulators and select plans that safely and robustly guide the robot’s end effector to desired goals.

2 Related Work

Since uncertainty is inherent in many robotics applications, approaches for managing uncertainty have been investigated for a variety of settings. Our focus in this paper is on robots with uncertainty in their motion and state estimation; we do not consider uncertainty in sensing of obstacle locations (e.g., [11]) or grasping (e.g., [19]). Extensive prior work has investigated motion planning under uncertainty for mobile robots that can be approximated as points or spheres in the workspace, e.g., [2, 4, 8, 17, 18, 20, 21, 26, 28]. For point or spherical robots, computing an estimate of the probability of collision with obstacles can be done in the workspace since the geometry of the C-obstacles is low dimensional and can be directly computed. It is not trivial to directly extend these methods to robotic manipulators, which are typically articulated and are composed of more complex shapes. Our approach avoids complexity in the configuration space by computing distance only in the workspace, as has been done in other contexts [3]. Another approach to estimate the probability of collision is using Monte Carlo simulation in the space of uncertain parameters, but the computation time needed to run a sufficient number of simulations to achieve a desired accuracy can be prohibitive in some applications.

Our approach computes a plan and controller simultaneously to minimize probability of collision. Approaches that blend planning and control by defining a global control policy over the entire environment have been developed using Markov decision processes (MDPs) [2] and partially-observable MDPs (POMDPs) [14]. These approaches are difficult to scale, and computational costs may prohibit their application to robots with higher dimensional configuration spaces. Another class of approaches rely on sampling-based methods to compute a path and then compute an LQG feedback controller to follow that path [1, 4, 21, 26]. Other approaches compute a locally-optimal trajectory and an associated control policy [20, 27, 30]. Recent work has begun to investigate computing plans for manipulators that are robust to uncertainty using local optimization [15], but place restrictions on robot geometry and do not accurately estimate probability of collision.

For some applications, uncertainty in robot motion and sensing necessitates that the robot perform maneuvers purely to gain information. The general POMDP formulation enables such information gathering. However, this typically comes at the cost of additional computational complexity [14] or the ability to only compute locally optimal rather than globally optimal plans [27]. Although in this paper we address a broad class of problems, the use of sampling-based motion planning in our approach does place restrictions, e.g., the optimal plan must be goal-oriented (i.e., optimality is not guaranteed for problems that require returning to previously explored regions of the state space for information gathering). Because of these restrictions, our method does not address the general POMDP problem.

Sampling-based methods such as RRT* provide asymptotic optimality [12], but they are not suitable for finding the optimal plan for the cost metric of minimizing probability of collision because the required optimal substructure property does not hold. We show that our motion planner, under reasonable assumptions, is asymptotically optimal for goal-oriented problems when minimizing probability of collision.

3 Problem Definition and Overview

We consider an articulated robotic manipulator with l links operating in an environment with obstacles. Let $\mathcal {C}$ be the configuration space of the robot. Let $\mathbf {q} \in \mathcal {C}$ denote a configuration of the robot, which consists of the parameters over which the robot has control (e.g., joint angles). We assume we are given a description of the geometry $X(\mathbf {q})$ of the robot in the workspace for any given configuration $\mathbf {q} \in \mathcal {C}$ and a description of the geometry of the obstacles $\mathcal {O}$ in the workspace. The continuous time $\tau$ is discretized into periods with equal time duration $\varDelta$, and we define $\mathbf {q}(\tau )$ as the configuration at time $\tau$. For simplicity, we define $\mathbf {q}_t = \mathbf {q}(t\varDelta )$ for time step $t \in \mathbb {N}$. Let $\mathbf {u} \in \mathcal {U}$ denote the robot’s control inputs, which are provided at discrete time steps. At time step t, the dynamics of the robot evolves as

$$\begin{aligned} \mathbf {q}_{t+1} = f(\mathbf {q}_t, \mathbf {u}_t, \mathbf {m}_t), \;\;\; \mathbf {m}_t \sim \mathcal {N}(\mathbf {0}, M) \end{aligned}$$

(1)

where $\mathbf {m}_t$ is the process noise with variance M. We assume noisy and partial observation $\mathbf {z_t}$ can be obtained by the sensing model

$$\begin{aligned} \mathbf {z_t} = h(\mathbf {q}_t, \mathbf {n}_t), \;\;\; \mathbf {n}_t \sim \mathcal {N}(\mathbf {0}, N), \end{aligned}$$

(2)

where $\mathbf {n}_t$ is the sensing noise with variance N.

Our objective is to enable the robotic manipulator to move from a start configuration $\mathbf {q}_0$ to a goal $\mathcal {G} \subseteq \mathcal {C}$ in a manner that minimizes the probability of collision with obstacles. We define a motion plan $\pi$ as a sequence of nominal configurations and corresponding control inputs, $\pi = \{\mathbf {q}_0, \mathbf {u}_0, \mathbf {q}_1, \mathbf {u}_1, \ldots , \mathbf {q}_T, \mathbf {u}_T\}$, where $\mathbf {q}_T \in \mathcal {G}$ and $\mathbf {u}_T = \mathbf {0}$. When executing a plan, we assume the robot uses an optimal linear controller (a linear quadratic Gaussian (LQG) feedback controller) in combination with a Kalman Filter for state estimation to guide the robot along the nominal plan.

In Sect. 4, we introduce a method to efficiently estimate the a priori probability of collision for a given plan. In Sect. 5 we introduce an asymptotically optimal motion planner that computes a plan that reaches a goal and asymptotically minimizes the a priori probability of collision.

4 Estimating Probability of Collision

In this section, we present our approach to estimating the probability of collision for a robotic manipulator moving along a planned trajectory. The approach works for complex workspace geometry and configuration spaces of arbitrary dimension and shape (including high-DOF manipulators).

We begin by considering the probability of collision when the robot is at a particular configuration with a given uncertainty distribution. We assume we have access to a collision-checker (e.g., [25]) that can compute the (signed) distance $d(\mathbf {q})$ in the workspace between the geometry of the robot $X(\mathbf {q})$ configured at $\mathbf {q}$ and the geometry of the obstacles $\mathcal {O}$ (the distance is negative if the robot collides with an obstacle, in which case the penetration depth is returned). The goal is to approximate the probability that the robot is in collision, i.e., $p(X(\mathbf {q}) \cap \mathcal {O} \not = \emptyset )$, given a Gaussian distribution of the configuration $\mathbf {q} \in \mathcal {C}$ of the robot;

$$\begin{aligned} \mathbf {q} \sim \mathcal {N}(\hat{\mathbf {q}}, \varSigma ), \end{aligned}$$

(3)

with mean $\hat{\mathbf {q}}$ and variance $\varSigma$.

4.1 Approach

Our approach is as follows. Let us assume that the geometry of the configuration space obstacles is (locally) convex in the neighborhood of $\hat{\mathbf {q}}$ (we will alleviate this assumption below). Then, we can approximate the free part of the configuration space by a single linear inequality constraint $(\mathbf {a}^T\mathbf {q} < b)$ that is tangent to the configuration space obstacles at the point on the C-space obstacles “closest” to $\hat{\mathbf {q}}$. Given a linear inequality constraint, there is a closed-form expression for the probability that the constraint is violated if $\mathbf {q}$ has a Gaussian distribution [26], which serves as a (conservative) approximation of the probability that the robot is in collision. The challenge is to find a “closest” point on the boundary of the C-space obstacles, since we only have access to the geometry of the obstacles in the workspace. In our approach, we make use of one key relation between workspace geometry and configuration space geometry that holds in general: configuration $\mathbf {q} \in \mathcal {C}$ lies on the boundary of a configuration space obstacle if and only if the workspace distance $d(\mathbf {q})$ between the robot $X(\mathbf {q})$ configured at $\mathbf {q}$ and the workspace obstacles $\mathcal {O}$ is zero (i.e., the robot touches an obstacle).

In order to define “closest”, we use the distance metric $\sqrt{(\mathbf {q} - \hat{\mathbf {q}})^T \varSigma ^{-1} (\mathbf {q} - \hat{\mathbf {q}})}$. This ensures that the constraint includes as much probability mass as possible. Hence, decomposing $\varSigma = L L^T$ and defining a transformed configuration space $\mathcal {C}' = L^{-1}\mathcal {C}$ allows us to use the standard Euclidean distance metric $\sqrt{(\mathbf {q}' - \hat{\mathbf {q}}')^T (\mathbf {q}' - \hat{\mathbf {q}}')}$, where $\hat{\mathbf {q}}' = L^{-1} \hat{\mathbf {q}}$ is the mean of the distribution in the transformed configuration space $\mathcal {C}'$. Also, let us define a workspace distance function that takes in configurations $\mathbf {q}' \in \mathcal {C}'$ from the transformed configuration space:

$$\begin{aligned} d'(\mathbf {q}') = d(L\mathbf {q}'). \end{aligned}$$

(4)

We are looking for a transformed configuration $\mathbf {q}'$ for which $d'(\mathbf {q}') = 0$ (i.e., a configuration $\mathbf {q}'$ on the boundary of the transformed C-space obstacles) that is closest to the transformed mean $\hat{\mathbf {q}}'$. For this, we use a variant of Newton’s root finding method with $\hat{\mathbf {q}}'$ as the initial “guess.” Newton’s method (with line search) finds a root close to the given initial “guess,” but does not guarantee to find the actual closest root. (We note that computing the true minimum distance point requires solving an optimization problem subject to a constraint that the solution is on the surface of a C-obstacle, which cannot be efficiently computed). Newton’s method iteratively performs the following update:

$$\begin{aligned} \mathbf {q}'_{i+1} = \mathbf {q}'_i - d'(\mathbf {q}'_i)\frac{\partial {d'}}{\partial {\mathbf {q}'}}[\mathbf {q}'_i] / \left( \frac{\partial {d'}}{\partial {\mathbf {q}'}}[\mathbf {q}'_i]^T\frac{\partial {d'}}{\partial {\mathbf {q}'}}[\mathbf {q}'_i]\right) , \end{aligned}$$

(5)

with $\mathbf {q}'_0 = \hat{\mathbf {q}}'$. Here, $\frac{\partial {d'}}{\partial {\mathbf {q}'}}[\mathbf {q}'_i]$ is the gradient vector of $d'$ at configuration $\mathbf {q}'_i$. The gradient points in the direction of steepest ascent of $d'$ and has a magnitude equal to the slope of $d'$ in that direction. Hence, if the function $d'$ would be linear along the gradient, the above equation gives a configuration $\mathbf {q}'_{i+1}$ for which $d'$ is zero. Since this is in general not the case, the equation is iterated, which lets it approach a root $\mathbf {q}'_\star$ of $d'$ with a second-order convergence rate [16]. In our implementation, we use line search in Newton’s method to ensure that the (absolute value) of the distance strictly decreases with each iteration, i.e., $|d'(\mathbf {q}'_{i+1})| < |d'(\mathbf {q}'_i)|$. The gradient vector $\frac{\partial {d'}}{\partial {\mathbf {q}'}}[\mathbf {q}'_i]$ can be computed using numerical differentiation (recall that $d'(\mathbf {q}')$ can be evaluated for any $\mathbf {q}' \in \mathcal {C}'$ using Eq. (4) and the collision checker).

Fig. 1

Example of our method for estimating the closest collision point. The 2-D manipulator at configuration $\hat{\mathbf {q}}$ with 2 obstacles in the workspace (a). The configuration space of the manipulator defined by ($\theta _1, \theta _2$) zoomed in to the area around $\hat{\mathbf {q}}$ (b). The uncertainty ellipse is shown with greater uncertainty in $\theta _2$ than in $\theta _1$. We transform the C-space such that the ellipse is circular, enabling us to compute distances using a collision checker (c). Using Newton’s method, we compute the closest point ($\mathbf {q}'_\star$) and corresponding constraint tangent for each link that collides with an obstacle. We illustrate in the workspace the $\mathbf {q}'_\star$ that collides with the orange obstacle (d). Using the tangents in c, we truncate the uncertainty distribution and propagate to next time steps, enabling us to estimate probability of collision along a trajectory

Figure 1 shows an example workspace and configuration space of a 2-D manipulator with mean $\hat{\mathbf {q}}'$ and the approximately closest point $\mathbf {q}'_\star$ on the boundary of the C-obstacles as found by Newton’s method. As can be seen, the $\mathbf {q}'_\star$ is indeed close to the mean, but is not the exact closest point. To construct the linear constraint tangent to the transformed C-obstacles at $\mathbf {q}'_\star$, we need the vector $\mathbf {n}'$ normal to the surface of the transformed C-obstacle at $\mathbf {q}'_\star$. For this, we use $\mathbf {n}' = \mathrm {sign}(d'(\mathbf {q}'_{\star -1}))(\mathbf {q}'_\star - \mathbf {q}'_{\star -1})$, where $\mathbf {q}'_{\star -1}$ is the before-last iterate of Newton’s method. Given $\mathbf {n}'$, the linear constraint $(\mathbf {a}^T\mathbf {q} < b)$ in the original configuration space $\mathcal {C}$ is given by:

$$\begin{aligned} \mathbf {a}^T = \mathbf {n}'^T L^{-1}, \; \; \;\; b = \mathbf {n}'^T \mathbf {q}'_\star . \end{aligned}$$

(6)

This equation, as well as the ones above, suggest that we need to decompose $\varSigma$ into $L L^T$ and compute the inverse of L, which are potentially costly operations and require $\varSigma$ to be non-singular. However, this is not necessary. It can be shown that the configurations $\mathbf {q}_i = L\mathbf {q}'_i$ in the untransformed configuration space evolve in Newton’s method as:

$$\begin{aligned} \mathbf {q}_{i+1} = \mathbf {q}_i - d(\mathbf {q}_i) \varSigma \frac{\partial {d}}{\partial {\mathbf {q}}}[\mathbf {q}_i] / \left( \frac{\partial {d}}{\partial {\mathbf {q}}}[\mathbf {q}_i]^T \varSigma \frac{\partial {d}}{\partial {\mathbf {q}}}[\mathbf {q}_i]\right) , \end{aligned}$$

(7)

with $\mathbf {q}_0 = \hat{\mathbf {q}}$. The constraint $(\mathbf {a}^T\mathbf {q} < b)$ upon convergence is then given by:

$$\begin{aligned} \mathbf {a} = -|d(\mathbf {q}_{\star - 1})| \frac{\partial {d}}{\partial {\mathbf {q}}}[\mathbf {q}_{\star -1}], \; \; \;\; b = \mathbf {a}^T \mathbf {q}_\star , \end{aligned}$$

(8)

where the distance and gradient are available from the last step of Newton’s method. From Eq. (7) we can see that in each iteration our method needs O(n) distance queries and $O(n^2)$ operations, where n is the dimension of the configuration space.

4.2 Multiple Constraints

Above we made the assumption that the geometry of the configuration space obstacles is (locally) convex. This is in general not an accurate assumption, in particular if the geometry of the workspace and of the robot is highly non-convex (as is the case with a manipulator). Therefore, we take the following approach to create multiple constraints: we assume that the geometry of the workspace obstacles $\mathcal {O}$ is decomposed into n convex sets $\mathcal {O}_1, \ldots , \mathcal {O}_n$ such that $\bigcup _i \mathcal {O}_i = \mathcal {O}$ and, similarly, that the workspace geometry $X(\mathbf {q})$ of the robot for a configuration $\mathbf {q}$ is decomposed into m convex sets $X_1(\mathbf {q}), \ldots , X_m(\mathbf {q})$ such that $\bigcup _i X_i(\mathbf {q}) = X(\mathbf {q})$. For a manipulator robot for instance, one can imagine that each link of the manipulator forms a convex set.

We then apply the above approach for each pair of workspace obstacle $\mathcal {O}_i$ and robot subset $X_j(\mathbf {q})$, giving a set of nm approximately locally-closest configurations on the geometry of the C-space obstacles and their associated constraints. To avoid having unuseful constraints, we take the following pruning approach: we consider the locally-closest configurations in order of increasing distance from the mean $\hat{\mathbf {q}}$, and remove the configuration from the list if it does not obey one of the constraints associated with configurations that came before it in the list. The intersection of the remaining constraints form an approximate local convexification of the free configuration space around the distribution of the configuration of the robot. We note that this approach relies on an implicit assumption that for a convex (piece of the) robot and a convex obstacle, the corresponding C-space obstacle is (locally) convex. This is not the case in general, but it is reasonable to assume that the surfaces of such C-obstacles are “well-behaved” and that the constraint as found by Newton’s method gives a reasonable local approximation. This is the case for the example in Fig. 1.

Given the set of constraints $\{\mathbf {a}_i^T \mathbf {q} < b_i\}$ thus computed, we can approximate the probability that any of the constraints is violated given the Gaussian distribution of $\mathbf {q}$ (see [18, 30]). In addition, we can truncate the Gaussian distribution to approximate the conditional distribution that the robot is collision free. This conditional distribution can then be propagated along a given motion plan for the robot (e.g., using LQG-MP [26]). Since arriving at a particular time step along a plan is conditioned on the previous time steps being collision free, we account for dependencies between successive time steps by repeating the above procedure for each time step along the plan to approximate the probability that the entire path of the robot is collision free (see, e.g., [18]).

5 Computing Motion Plans that Minimize Collision Probability

We next present a motion planner that guarantees that, as computation time is allowed to increase, the computed plan will approach a plan that minimizes probability of collision estimated using the method in Sect. 4. Guaranteeing asymptotic optimality for motion planning under uncertainty is challenging because it is necessary to not only explore the configuration space but also to consider the a priori uncertainty distribution at each configuration. The uncertainty distribution at a configuration is history dependent, i.e., it depends on the trajectory used to reach the configuration. This breaks the optimal substructure assumption required by prior asymptotically optimal motion planners such as RRT* [12] since the cost of any subpath is dependent on what succeeds and precedes it.

5.1 Multiple Independent RRTs (MIRRT)

Our motion planning method, Multiple Independent RRTs (MIRRT), builds upon the rapidly-exploring random tree (RRT) [6], a well-established sampling-based motion planner for finding feasible plans in configuration space. Our method begins by building an RRT and terminating as soon as a plan is found. For the computed plan, we compute the corresponding LQG controller and estimate the probability of collision of the plan as described in Sect. 4. We then launch a completely new RRT to compute another plan. We continue executing independent RRTs until a maximum time threshold is reached or the user stops the planner. (We note that this planning approach is trivially parallelizable.) As the plans are generated, we save the plan with minimum estimated probability of collision.

A single RRT for general cost functions will not converge to an optimal plan [12]. We show in Sect. 5.2 that, with some reasonable assumptions, MIRRT is asymptotically optimal for minimizing the probability of collision estimated using Sect. 4.

5.2 Analysis of Asymptotic Optimality

We analyze MIRRT for holonomic robotic manipulators for goal-oriented problems, i.e., we require the optimal plan $\pi ^*$ to have the property that state $\mathbf {q}^*_t$ along the plan $\pi ^*$ is closer (based on the Euclidean distance in configuration space) to the state $\mathbf {q}^*_{t-1}$ than to any state $\mathbf {q}^*_{t'}$ where $t' < t - 1$. For any goal-oriented problem, the manipulator will never return to a previous configuration to gain information. We show that for a goal-oriented problem in which a plan is represented by control inputs over a finite number of time steps, the plan returned by MIRRT asymptotically approaches the optimal plan $\pi ^*$ with probability 1.

For purposes of motion planning, we define cost function $c(\pi , \mathbf {q}_0)$ as the estimated probability of collision when plan $\pi$ is executed starting at configuration $\mathbf {q}_0$. Given $\mathbf {q}_0$ and two feasible plans $\pi _1$ and $\pi _2$, we define the distance between $\pi _1$ and $\pi _2$ as $\Vert \pi _1 - \pi _2\Vert = \max _{\zeta \in [0,1] } \Vert \mathbf {q}(\zeta T_1\varDelta , \pi _1) - \mathbf {q}(\zeta T_2\varDelta , \pi _2)\Vert$, where $T_i$ is the number of time steps of $\pi _i$ and $\mathbf {q}(\tau , \pi )$ represents the configuration at time $\tau$ while executing the plan $\pi$. For our cost function, similar plans have similar cost. The cost function $c(\pi , \mathbf {q}_0)$ is Lipschitz continuous, i.e., there exists some constant K such that starting from $\mathbf {q}_0$, for any two feasible plans $\pi _1$ and $\pi _2$, $\Vert c(\pi _1, \mathbf {q}_0) - c(\pi _2, \mathbf {q}_0)\Vert \le K \Vert \pi _1 - \pi _2\Vert$.

To expand an RRT in the direction of a sampled configuration $\mathbf {q}_\mathrm {sample}$, the algorithm uses the function $\text{ Steer }: (\mathbf {q}, \mathbf {q}_\mathrm {sample}) \mapsto \mathbf {q}_\mathrm {new}$, which is defined as in [12]. Steer returns a configuration $\mathbf {q}_\mathrm {new}$ that moves linearly from $\mathbf {q}$ toward $\mathbf {q}_\mathrm {sample}$ up to a predefined distance $\eta \in \mathbb {R}^+$. For the optimal plan $\pi ^*$, we define $d^*= \max _{0\le i \le T-1} \Vert \mathbf {q}^*_i - \mathbf {q}^*_{i+1}\Vert$. We assume $\eta$ is sufficiently large that $\exists \beta \in \mathbb {R}^+$, $d^* +\beta = \eta$.

Because we consider uncertainty, we leverage the assumption that an optimal plan $\pi ^*$ is $\alpha$-collision free, i.e., the nominal plan avoids obstacles by a clearance distance of at least $\alpha$ for some $\alpha \in \mathbb {R}^+$. This assumption is reasonable since moving adjacent to an obstacle would almost surely cause collision.

Motivated by [13], we build “balls” along the optimal plan $\pi ^*$. Given any $\varepsilon \in (0, \min (\frac{\beta }{2}, \alpha ))$, for any $\mathbf {q}^*_t$, we define $(\varepsilon , t)$-ball $B_{\mathbf {q}^*_t}$ as all $\mathbf {q}$ such that $\Vert \mathbf {q}^*_t - \mathbf {q}\Vert \le \varepsilon$. Because of the choice of $\varepsilon$, at time step t, if the robot is at a state $\mathbf {q}$ within $B_{\mathbf {q}^*_t}$, and a sample $\mathbf {q}_\mathrm {sample}$ ends up within $B_{\mathbf {q}^*_{t+1}}$, the function $\text{ Steer }(\mathbf {q}, \mathbf {q}_\mathrm {sample})$ can connect $\mathbf {q}$ and $\mathbf {q}_\mathrm {sample}$ by a straight line in $\mathcal {C}$. The straight line is also collision free. For any feasible plan $\pi$ that has the same number of time steps as $\pi ^*$, we call $\pi$ an $\varepsilon$-close path if and only if for any time step t along $\pi$, $\mathbf {q}_t \in B_{\mathbf {q}^*_t}$.

Theorem 1

(MIRRT is asymptotically optimal) Let $\pi _i$ denote the best plan found after i RRTs have returned solutions. Given the assumptions above and assuming the problem is goal-oriented and admits a feasible solution, as the number of independent RRT plans generated in MIRRT increases, the best plan almost surely approaches the optimal plan $\pi ^*$, i.e., $P(\lim _{i \rightarrow \infty } \Vert c(\pi _i, \mathbf {q}_0) - c(\pi ^*, \mathbf {q}_0)\Vert =0) = 1$.

Proof

For any $\varepsilon$ (without loss of generality, we assume $\varepsilon \in (0, \min (\alpha , \frac{\beta }{2} ))$), we build $(\varepsilon ,t)$-balls along $\pi ^*$. Consider a sequence of events that can generate an $\varepsilon$-close path. In one RRT, we start from the initial state $\mathbf {q}_0$ (we assume $\mathbf {q}_0 = \mathbf {q}^*_0$). The first sample $\mathbf {q}_1$ ends in $B_{\mathbf {q}^*_1}$ with nonzero probability. The steering function connects $\mathbf {q}^*_0$ and $\mathbf {q}_1$. The second sample $\mathbf {q}_t$ ends in $B_{\mathbf {q}^*_2}$ with nonzero probability. Based on the goal-oriented assumption, $\mathbf {q}_t$ is closer to $\mathbf {q}_1$ and hence the steering function connects $\mathbf {q}_1$ and $\mathbf {q}_2$. We repeat until the last sample $\mathbf {q}_T$ ends in $B_{\mathbf {q}^*_T}$ with nonzero probability and the steering function connects $\mathbf {q}_{T-1}$ and $\mathbf {q}_T$. Thus, the probability of generating an $\varepsilon$-close path by one execution of RRT is nonzero, which we express as $P_{\varepsilon } \in \mathbb {R}^+$. Hence we have $P(\Vert \pi _i - \pi ^*\Vert > \varepsilon ) = (1 - P_{\varepsilon })^i = {\bar{P}_{\varepsilon }} ^i$. Thus, $\sum _i P(\Vert \pi _i - \pi ^*\Vert > \varepsilon ) = \sum _i {\bar{P}_{\varepsilon }}^i \le \frac{1}{1 - \bar{P}_{\varepsilon }}$ is finite. Based on a Borel-Cantelli argument [10], we have $P(\lim _{i \rightarrow \infty } \Vert \pi _i - \pi ^*\Vert = 0) = 1$. Since the cost function of estimating probability of collisions is Lipschitz continuous, $P(\lim _{i \rightarrow \infty } \Vert c(\pi _i, \mathbf {q}_0) - c(\pi ^*, \mathbf {q}_0)\Vert = 0) = 1$.    $\square$

We have shown that when the above assumptions hold and the number of feasible plans approaches infinity, the plan returned by MIRRT will almost surely approach a solution that minimizes the estimated probability of collision c.

6 Experiments

We evaluated our methods on two simulated scenarios: (1) a 6-DOF manipulator in a 3-D environment with narrow passages, and (2) a concentric tube robot that has applications to surgical procedures. In both scenarios, the robots have substantial actuation uncertainty and limited sensing feedback. We evaluated our C++ implementation on a 3.33 GHz Intel i7 PC.

For both scenarios, we first evaluated our method for estimating probability of collision by comparing the estimated collision probability with the ground truth probability. We computed ground truth by running at least 5,000 Monte Carlo simulations of the given motion plan and reporting the percentage of collision free simulations. Each simulation was executed in a closed-loop fashion using the given linear feedback controller and a Kalman filter, and with artificially generated motion and sensing noise. We also demonstrated the ability of MIRRT to compute plans that approach optimality as computation time is allowed to increase.

6.1 6-DOF Manipulator Scenario

We first applied our method to a holonomic 6-DOF articulated robotic manipulator in a 3-D environment as shown in Fig. 2a. The robotic manipulator must move from its initial configuration to a configuration in which its end-effector is inside the pre-defined goal region (red ball) while avoiding the cyan obstacles. To reach the goal, the manipulator must pass through one of two narrow passages; the left narrow passage is wider than the upper narrow passage. Although our geometric representation resembles an industrial manipulator, we model the robot as a low-cost, compliant manipulator with uncertainty in actuation and with an encoder only at the base joint, resulting in limited state feedback.

Fig. 2

The 6-DOF manipulator with an encoder only at its base joint must move from its initial configuration shown in a to a goal configuration in which its end-effector reaches the red ball while avoiding the cyan obstacles. An example feasible plan (b), where the trajectory of the robot over time is shown by its yellow, magenta, and blue links. Our method estimates the probability of collision of this plan at 39.39 % and ground truth is 40.68 %. We compare our probability of collision estimation method and Monte Carlo simulation for the example plan (d). For Monte Carlo simulation to achieve similar accuracy to our method, 700 simulations are needed, which requires over 26 s rather than 234 ms for our method. The optimal plan computed by MIRRT run for 20 s passes through the upper passage (c). The estimated probability of collision is 4.19 % while the ground truth is 3.12 %. The performance of the MIRRT converges as the computation time is allowed to increase (e)

We define the configuration of the robot as $\mathbf {q} = ( \theta _1, \theta _2, \theta _3, \theta _4, \theta _5, \theta _6 )$, the manipulator’s joint angles. The control inputs are the angular velocities of the joints, $\mathbf {w} = (w_1, w_2, w_3, w_4, w_5, w_6)$, each corrupted by a process noise $\mathbf {m} = (\tilde{w}_1, \tilde{w}_2, \tilde{w}_3, \tilde{w}_4, \tilde{w}_5, \tilde{w}_6) \sim \mathcal {N}(\mathbf {0}, M)$ where $M = \sigma ^2_1 I$ with $\sigma _1 = 0.03$ rad/s. We define the robot’s discrete dynamics model as

$$\begin{aligned} \mathbf {q}_{t+1} = \mathbf {q}_{t} + \varDelta (\mathbf {w} + \mathbf {m}) \end{aligned}$$

(9)

where $\varDelta$ is the time step size. We assume the robot has an encoder only at its base joint and hence define the sensing model as

$$\begin{aligned} h(\mathbf {q}, \mathbf {n}) = \theta _1 + \mathbf {n} \end{aligned}$$

(10)

where the observation is corrupted by noise $\mathbf {n} \sim \mathcal {N}(0, \sigma ^2_2)$ with $\sigma _2 = 0.03$ rad/s. This is indeed a formally unobservable sensing model.

We first evaluate the ability of our method to accurately estimate the probability of collision for a particular plan. For the example feasible plan shown in Fig. 2b that was computed by an RRT, we compare our method to the alternative of using Monte Carlo simulations for estimating probability of collision. Our method required 234 ms of computation time. Figure 2d shows the deviation in the probability estimates computed using Monte Carlo simulations with varying number of samples (averaged over 100 trials). As expected, the variance decreases as the number of Monte Carlo simulations increases. It takes over 700 Monte Carlo simulations, each simulation requiring an average of 38 ms, to arrive within the accuracy bounds of our method, which corresponds to over 26 s of computation time just to estimate the collision probability. Hence, our method is over 100 times faster than Monte Carlo simulation.

To assess the accuracy of our method across a broader range of plans, we also randomly generated 100 feasible plans using independent RRTs. The average absolute error between the ground truth probability of collision (computed using 10,000 Monte Carlo simulations) and the estimation by our method is 9.78 %. The average computational time of our method for each plan is 158 ms.

We also evaluate our MIRRT approach for computing motion plans with low probability of collision. We executed MIRRT for varying computation times up to 20 s, which allows for computation of $\sim$100 plans. In Fig. 2e, we show the estimated probability of collision of the best plan computed by our method as well as the ground truth probability of collision for that plan. Each bar is the average of 20 executions. As computation time is allowed to increase, the MIRRT approach returns a plan that is almost guaranteed to avoid collisions, and its performance is verified by the ground truth value. In the optimal plan (shown in Fig. 2c) the robot pulls back and then passes through the upper narrow passage rather than through the left passage, even though the left passage would allow a path that is both shorter and has greater clearance from obstacles. The reason for selecting a path through the upper narrow passage is because the robot has low uncertainty for $\theta _1$ due to its ability to sense that joint’s orientation, and that decreases the chances of collision when moving through the upper passageway because the robot’s kinematics for the remaining joints will restrict uncertainty primarily along the z axis.

6.2 Concentric Tube Robot Scenario

We also apply our method to a concentric tube robot, a tentacle-like robot composed of nested, pre-curved elastic tubes. These devices have the potential to enable physicians to perform new minimally-invasive surgical procedures that require maneuvering through narrow passages or around anatomical obstacles. Potential clinical applications include surgeries of the pituitary gland or nearby structures in the skull base [5] as well surgeries that require maneuvering inside the heart [29].

Each tube of a concentric tube robot is pre-curved and can be inserted and axially rotated independently of the other tubes. A device having n tubes thus has 2n degrees of freedom. Due to the elastic interaction of the tubes, the kinematics of concentric tube robots is complex and must be computed numerically [22, 31]. Computing the kinematic model of the concentric tube robot requires over 50 times more computation time than for the 6-DOF manipulator.

Fig. 3

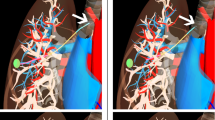
The 3-tube concentric tube robot must reach the yellow goal sphere while avoiding the orange obstacles and remaining inside the cyan cylinder (a). We compare our method with Monte Carlo simulation for the example plan (b). The average computation time per Monte Carlo simulation is 98 ms (which is higher than for the 6-DOF manipulator due to the complex kinematics). For Monte Carlo simulation to achieve a similar accuracy to our method, over 450 simulations are needed, which requires over 44 s rather than 2.4 s total for our method. We also illustrate a clinically-motivated scenario in which a concentric tube robot enters the body via the nasal cavity and reaches a rightward facing pose at the pituitary gland (green) for skull base surgery (c)

We consider a 3-tube robot for which the state $\mathbf {q} = (\theta _1, \theta _2, \theta _3, \beta _1, \beta _2, \beta _3)$ consists of an axial angle $\theta _i$ and insertion distance $\beta _i$ for each tube. We define the control input as $\mathbf {u} = (w_1, w_2, w_3, v_1, v_2, v_3)$, where $w_i$ and $v_i$ represent the axial rotation angular velocity and insertion speed, respectively, for the i’th tube. We assume the control input is corrupted by a process noise $\mathbf {m} = (\tilde{w}_1, \tilde{w}_2, \tilde{w}_3, \tilde{v}_1, \tilde{v}_2, \tilde{v}_3,) \sim \mathcal {N}(\mathbf {0}, M)$. This results in the dynamics model

$$\begin{aligned} \mathbf {q}_{t+1} = \mathbf {q}_t + \varDelta (\mathbf {u} + \mathbf {m}), \end{aligned}$$

(11)

where $\varDelta$ is the time step size. We set M = $\begin{bmatrix} \sigma ^2_1 I&0 \\ 0&\sigma ^2_2 I\end{bmatrix}$ with $\sigma _1$ = 0.02 rad/s and $\sigma _2$ = 0.001 m/s. We assume the concentric tube robot’s tip position can be tracked in 3-D using an electromagnetic tracker (e.g., the NDI Aurora Electromagnetic Tracking System as in [5]). This gives the stochastic measurement model

$$\begin{aligned} h[\mathbf {q}_t, \mathbf {n}] = \begin{bmatrix}x_t&y_t&z_t\end{bmatrix}^T + \mathbf {n}, \end{aligned}$$

(12)

where $\mathbf {n} \sim \mathcal {N}(\mathbf {0}, N)$. We set N = $\sigma ^2_3 I$ with $\sigma _3$ = 0.001 m.

For the concentric tube robot, we evaluate the ability of our method to accurately estimate the probability of collision. As shown in Fig. 3, we consider a tubular environment with spherical obstacles similar to the environments used in prior work [24]. For the example plan shown in Fig. 3a, our method required 2.4 s of computation time. Figure 3b compares the probability of collision estimates computed using Monte Carlo simulation with varying number of samples (averaged over 100 trials). As expected, the variance decreases as the number of Monte Carlo simulations increases. It takes over 450 Monte Carlo simulations to achieve the accuracy of our method, which corresponds to over 44 s of computation time just to estimate the collision probability. Hence, our method is over 10 times faster than Monte Carlo simulation for the concentric tube robot scenario.

To assess the accuracy of our method across a broader range of concentric tube robot plans, we also randomly generated 100 feasible plans using independent RRTs. The average absolute error between the ground truth probability of collision (computed using 10,000 Monte Carlo simulations) and the estimation by our method is 4.36 %. The optimal plan picked by MIRRT using our method has an estimated probability of collision of 9.11 $\times$ $10^{-7}\,\%$ while ground truth is 0 %.

To treat cancers of the pituitary gland, surgeons often must resect the tumor, which requires inserting surgical instruments to reach the skull base. Enabling surgeons to access the pituitary gland (shown in green in Fig. 3c) via the nasal cavity and by drilling through thin sinus bones would be far less invasive than current surgical approaches, but requires controllable, curvilinear instruments for surgical access [5]. For the concentric tube robot, we generated 100 plans for the anatomy in Fig. 3c, avoiding obstacles such as bone and blood vessels and requiring a rightward facing tip pose for the surgical task. MIRRT executed for 100 plans returns a plan with an estimated probability of collision of 0.94 %, while the ground truth is 0 %. In Fig. 3c, we illustrate the optimal plan found by our method.

7 Conclusion

We introduced a new integrated motion planning and control algorithm for robotic manipulators that makes safety a priority by explicitly minimizing the probability of unwanted collisions. Our approach quickly computes distances to obstacles in the workspace and appropriately transforms this information into the configuration space using a Newton method to estimate the most relevant collision points in configuration space. We then presented a sampling-based motion planner that executes multiple independent RRTs and returns a plan that, under reasonable assumptions, asymptotically converges to a plan that minimizes the estimated collision probability. We applied our approach in simulation to a 6-DOF manipulator and a tentacle-like surgical robot. Our results show orders of magnitude speedup over Monte Carlo simulation for equivalent accuracy in estimating collision probability, and the ability of our motion planner to return high quality plans with low probability of collision.

Our method assumes that the manipulator operates under the assumptions of Gaussian motion and sensing uncertainty. Although the class of problems where Gaussian distributions are appropriate is large (as shown by the widespread use of the extended Kalman filter for state estimation), the approximation is not acceptable for some applications. In future work we plan to extend our method to non-Gaussian uncertainty and integrate with local optimization methods in belief space to quickly refine plans. We also will apply the method to meso-scale, flexible surgical robots to improve device safety, effectiveness, and clinical potential.