1 Introduction

Many of today’s theories predict corrections to the theory of Gravitation. The Yukawa Potential has already been studied by a number of researchers as a model that describes deviations from Newton’s inverse square law. Theories like Scalar-Tensor-Vector Gravity Theory (Moffat 2006a) predict a Yukawa-like fifth force. In Iorio (2007), the author finds constraints on the range of the Yukawa interaction \(\lambda \) by comparing corrections to the Newtonian-Einsteinian secular rates of the perihelia of Mercury. Brownstein and Moffat (2006) studied the Yukawa potential as a modification to Newton’s constant \(G\), introducing a distance varying gravitational acceleration corrected by the Yukawa force. In the paper, (De Laurentis et al. 2018), the authors solve the geodesic equation of a particle subjected to a Yukawa corrected gravitational field.

In this contribution, we explore the effect of a Yukawa correction to the gravitational force over large distances (binary star-like orbits). In particular, we are able to study the stability of the closed orbit solutions and compare them to the classical Kepler problem. In particular, we are able to prove using Bertrand’s theorem that closed orbits exists for appropriate values of \(r\). This model is interesting as the simplest correction to gravity over large distance that one can imagine; future astrophysical experiments will ultimately dictate the validity of the model.

This paper specifically builds on work from Haranas et al. (2011, 2016) and Haranas and Ragos (2011) in which the authors calculate various celestial orbital properties under the correction of a Yukawa term. In particular in the contribution, (Haranas et al. 2011), the authors compute the correction to the anomalistic period, in Haranas et al. (2016) the authors calculate the corrected mean motion and in Haranas and Ragos (2011) the authors study the effects of the Yukawa correction on the orbits of satellites. The results from Adelberger et al. (2009) and Borka et al. (2013) were important for confining the range (or coupling) of the Yukawa force for short and large range distances respectively. Borka et al. (2013) is of particular importance as the authors study star-like orbits and show through numerical simulations that precessing orbits are a possible solution for a mass in a Yukawa corrected gravitational potential.

The Yukawa force is particularly valid as a long-range force, as early estimates of its range \(\lambda \) from the papers (Brownstein and Moffat 2006) and (Haranas and Ragos 2011) indicate that \(\lambda \geq 10^{15}\text{ m}\). \(\lambda \) is the Compton wavelength of the particle mediating the interaction, for gravity that is the graviton. The Yukawa potential is used to model the interaction between massive stars; which are separated on average by a distance of \(10^{12}\text{ m}\). Thus, we are interested in studying orbits of size relative to the size of the Solar System; one example we study is the orbit of two stars of mass equal to that of the Sun. The corresponding Newtonian potential is given by:

$$ V_{N} ( r ) =- \frac{GmM}{r}, $$
(1)

where \(r = (r_{x}, r_{y} )\) and \(G = 6.67\times 10^{-11} \frac{N m^{2}}{k g^{2}}\) is Newton’s constant. The form of the potential studied in this report is:

$$ V ( r ) =- \frac{GmM}{r} \bigl( 1+\alpha e^{- \frac{r}{\lambda }} \bigr) = V_{N} ( r ) + V_{\mathit{yk}} (r), $$
(2)

where \(V_{\mathit{yk}} (r)\) is the Yukawa correction to the Newtonian potential, \(\alpha = \frac{k_{N} k_{\mathit{yk}}}{GMm}\) is the coupling constant of the Yukawa force to the Gravitational force following Haranas et al. (2011), and \(\lambda \) is the range of the Yukawa force as previously mentioned. The results from Brownstein and Moffat (2006) and Haranas and Ragos (2011) indicate that \(\alpha = 10^{-8}\) for Solar System orbits. In this contribution, we study the Yukawa correction to the Newtonian gravitational force; we also study the subcases of a purely Yukawa potential and a purely Newtonian potential \(\alpha \rightarrow 0\). The dynamics of the two masses are obtained using the Hamiltonian Formulation of Classical Mechanics; a review found in Jose and Saletan (1998). The two-body problem has been extensively studied in Pollard (1966).

2 Hamiltonian formulation

We can assume the form of the Hamiltonian \(H = T +V\) where \(T\) is the kinetic energy of both masses and \(V\) is the Gravitational potential energy.

$$ H= \frac{p_{1}^{2}}{2 m_{1}} + \frac{p_{2}^{2}}{2 m_{2}} - \frac{k}{ \vert r_{2} - r_{1} \vert ^{2}} \bigl( 1+\alpha e^{- \frac{ \vert r_{2} - r_{1} \vert }{\lambda }} \bigr) ( r_{2} - r_{1} ), $$
(3)

where \(p = mv\) is the momentum of each mass and \(k= m_{1} m_{2}\). Note that \(p_{i} =(p_{ix},p_{iy})\) and \(r_{i}=(r_{ix},r_{iy})\). Changing to the center of mass frame gives

$$ H= \frac{p^{2}}{2\mu } - \frac{k}{r} \bigl( 1+\alpha e^{- \frac{r}{\lambda }} \bigr). $$
(4)

Here we have defined \(\mu = \frac{m_{1} m_{2}}{m_{1} + m_{2}}\) as the reduced mass of the system and \(r= \vert r \vert \). Next, we must switch to polar coordinates; this procedure yields

$$ H= \frac{1}{2\mu } \biggl( p_{r}^{2} + \frac{p_{\theta }^{2}}{r^{2}} \biggr) - \frac{k}{r} \bigl( 1+\alpha e^{- \frac{r}{\lambda }} \bigr). $$
(5)

Following Goldstein (1980) given that the Hamiltonian is cyclic is \(\theta \) (i.e. the Hamiltonian does not depend explicitly on \(\theta \)) we can write Hamilton’s equations for \(\theta \) as:

$$\begin{aligned}& \dot{\theta } = \frac{\partial H}{\partial p_{\theta }} = \frac{p_{\theta }}{\mu r^{2}} \end{aligned}$$
(6)
$$\begin{aligned}& \dot{p_{\theta }} =- \frac{\partial H}{\partial \theta } =0 \end{aligned}$$
(7)

Therefore \(p_{\theta } =l\) is constant. Given that Hamilton’s equations takes this form we can write our Hamiltonian in the following way:

$$ H= \frac{1}{2\mu } \biggl( p_{r}^{2} + \frac{l^{2}}{r^{2}} \biggr) - \frac{k}{r} \bigl( 1+\alpha e^{- \frac{r}{\lambda }} \bigr) $$
(8)

Where \(l\) is the angular momentum of the two body-system and therefore Hamilton’s equations for \(r\) become:

$$\begin{aligned}& \dot{r} = \frac{\partial H}{\partial p_{r}} = \frac{p_{r}}{\mu } \end{aligned}$$
(9)
$$\begin{aligned}& \dot{p_{r}} =- \frac{\partial H}{\partial r} = \frac{l^{2}}{\mu r^{3}} - \frac{k}{r^{2}} \biggl( 1+ \alpha \biggl( 1+ \frac{r}{\lambda } \biggr) e^{- \frac{r}{\lambda }} \biggr). \end{aligned}$$
(10)

It can be shown that \(H ( t ) =H ( t_{0} ) =h\) is constant during the motion of the masses; see (Pollard 1966).

Since \(p_{r}^{2} \geq 0\) we have that, the total energy of the system is bounded by:

$$ h\geq \frac{l^{2}}{2 \mu r^{2}} - \frac{k}{r} \bigl( 1+\alpha e^{- \frac{r}{\lambda }} \bigr). $$
(11)

Here we have defined the reduced potential, which is common to the Kepler problem (with the Yukawa correction)

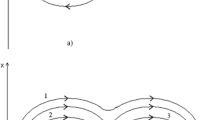
$$ V_{\mathit{red}} ( r ) = \frac{l^{2}}{2 \mu r^{2}} - \frac{k}{r} \bigl( 1+\alpha e^{- \frac{r}{\lambda }} \bigr) $$
(12)

We can graph the function for fixed \(h\) giving us the permissible regions of motion. The graph is shown in Fig. 1. Note that \(\mu > 0\), \(\lambda > 0\) and \(\alpha > 0\).

Fig. 1
figure 1

The reduced potential given fixed initial energy

Full size image

In Fig. 1 we plot, the reduced potential for a given fixed initial energy \(h\) measured in joules (J), i.e. Eq. (11). The dotted line refers to the Kepler problem, the dashed line is a purely Yukawa potential and the solid line refers to the Newtonian plus Yukawa correction. Points lying above the graphs represent possible unbounded motion for a massive body with given initial energy and distance from the central body. For small \(r \) it is clear that bounded motion can exist.

3 The linearization matrix

Following Meiss (2007), to determine the stability of the equilibrium points of the system, we must form a matrix differential equation using the equations of motion of the system (Hamilton’s equations for \(r\)); given by (9)–(10). The linear system has the form:

$$ \frac{d}{dt} \binom{r}{p_{r}} = \left [ \textstyle\begin{array}{c@{\quad }c} \frac{\partial f}{\partial r} & \frac{\partial f}{\partial p_{r}}\\ \frac{\partial g}{\partial r} & \frac{\partial g}{\partial p_{r}} \end{array}\displaystyle \right ] \binom{r}{p_{r}} $$
(13)

Where \(f ( r, p_{r} ) = \frac{p_{r}}{\mu }\) and \(g ( r, p_{r} ) = \frac{l^{2}}{\mu r^{3}} - \frac{k}{r^{2}} ( 1+ \alpha ( 1+ \frac{r}{\lambda } ) e^{- \frac{r}{\lambda }} )\); i.e. the RHS of (9)–(10). Given that \(\lambda = 1015\text{ m}\) for orbits of size comparable to solar system dimensions (Brownstein and Moffat 2006; Haranas and Ragos 2011). Since \(\frac{r}{\lambda }\) is small number we can Taylor expand the exponential and ignore terms of \(( \frac{r^{2}}{\lambda ^{2}} )\). The expansion about the point \(\frac{r}{\lambda } =0\) gives

$$ e^{- \frac{r}{\lambda }} \approx 1- \frac{r}{\lambda } + O \biggl( \frac{r^{2}}{\lambda ^{2}} \biggr). $$
(14)

Thus \(g ( r, p_{r} ) = \frac{l^{2}}{\mu r^{3}} - \frac{k}{r^{2}} ( 1+ \alpha ( 1+ \frac{r}{\lambda } ) ( 1- \frac{r}{\lambda } ) ) \) and so the Jacobian matrix takes the form:

$$ \left ( \textstyle\begin{array}{l} \dot{r}\\ \dot{p_{r}} \end{array}\displaystyle \right ) = \left [ \textstyle\begin{array}{c@{\quad }c} 0 & \frac{1}{\mu }\\ - \frac{3}{\mu r^{4}} + \frac{2k}{r^{3}} (1+\alpha ) & 0 \end{array}\displaystyle \right ] \binom{r}{p_{r}}, $$
(15)

where terms of order \(O ( \frac{r^{2}}{\lambda ^{2}} )\) are ignored. The equilibrium points are points (\(a\), \(b\)) such that \(f (a, b) = 0\) and \(g(a, b) = 0\). Thus, we can choose \(b = pr\) as one coordinate of our equilibrium point. For the value of the equilibrium \(r\) coordinate (i.e. \({r_{\mathit{eq}}} = a\)) using (10) we have that

$$\begin{aligned}& \frac{l^{2}}{\mu r^{3}} - \frac{k}{r^{2}} \biggl( 1+ \alpha \biggl( 1+ \frac{r}{\lambda } \biggr) \biggl( 1- \frac{r}{\lambda } \biggr) \biggr) =0 \end{aligned}$$
(16)
$$\begin{aligned}& \frac{l^{2}}{\mu r^{3}} - \frac{k}{r^{2}} \biggl( 1+ \alpha \biggl( 1- \frac{r^{2}}{\lambda ^{2}} \biggr) \biggr) =0 \end{aligned}$$
(17)

Again ignoring higher order terms the equilibrium points are determined by solving the following equation:

$$ \frac{l^{2}}{\mu } -kr(1+\alpha )=0 $$
(18)

Solving this equation gives us the equilibrium solution:

$$ r_{\mathit{eq}} =a= \frac{l^{2}}{\mu k ( 1+\alpha )} $$
(19)

We can now test for stability by choosing values of \(\mu \), \(\alpha \), \(k\), \(l\) and \(\lambda \) and finding the eigenvalues of the Jacobian matrix (15) after substituting the equilibrium solution found above. Recall that the eigenvalues \(\beta _{1}\), \(\beta _{2}\) are found by solving the following equation:

$$ \det \vert J-\beta I_{2\times2} \vert =0 $$
(20)

Here \(I_{2\times2}\) refers to the \(2\times2\) identity matrix. The characteristic equation (the eigenvalue equation) becomes:

$$ \beta ^{2} - \frac{\mu ^{2} k^{4} ( 1+\alpha )^{4}}{l^{6}} =0. $$
(21)

Following Meiss (2007), we say that the stability is given from the sign of the eigenvalues. For example, if \(\beta _{1} > \beta _{2} > 0\), then the equilibrium is unstable. If \(\beta _{1} < \beta _{2} < 0\) then the equilibrium is stable. Imaginary eigenvalues are also stable if for \(\beta _{1,2} = a \pm ib\) we have that \(a < 0\) (otherwise the equilibrium point is unstable). In the case when \(a = 0\); the equilibrium is called a center (and is stable) (Meiss 2007). Stability refers to how the solution behaves near the equilibrium point; unstable solutions grow to infinity, stable solutions tend to zero and the imaginary cases are the ones which give bound, orbital solutions (specifically the center case, whereas the stable and unstable imaginary cases are bound solutions tending towards or away from zero).

4 Stability & Bertrand’s theorem

We first note that we can study the case for a purely Newtonian Potential by letting \(\alpha \rightarrow 0\). Similarly, we can study the purely Yukawa potential by ignoring the term derived from the Newtonian potential; the characteristic equations become

$$\begin{aligned}& \beta ^{2} - \frac{\mu ^{2} k^{4}}{l^{6}} =0 \end{aligned}$$
(22)
$$\begin{aligned}& \beta ^{2} - \frac{\mu ^{2} k^{4} \alpha ^{4}}{l^{6}} =0 \end{aligned}$$
(23)

These expressions take into account the fact that our new equilibrium points are

$$\begin{aligned}& \alpha _{N} = \frac{l^{2}}{\mu k} \end{aligned}$$
(24)
$$\begin{aligned}& \alpha _{N} = \frac{l^{2}}{\mu k\alpha } \end{aligned}$$
(25)

Where (\(a\), \(pr\)) are the equilibrium points of the systems under study. We now proceed to evaluate (19), (20) and (21) with the equilibrium solutions to determine the stability of the equilibrium points. Evaluating (19) we obtain the following eigenvalues:

$$ \beta =\pm i \frac{ ( 1+\alpha )^{2} k^{2} \mu ^{2}}{l^{3}} $$
(26)

Similarly, for the Newtonian and purely Yukawa cases:

$$\begin{aligned}& \beta _{N} =\pm i \frac{k^{2} \mu ^{2}}{l^{3}} \end{aligned}$$
(27)
$$\begin{aligned}& \beta _{\mathit{yk}} =\pm i \frac{\alpha ^{2} k^{2} \mu ^{2}}{l^{3}} \end{aligned}$$
(28)

Thus, the equilibrium points for the purely Yukawa, Newtonian and the Newton + Yukawa Potential remain center solutions. This would imply that motion is restricted to ellipses about the equilibrium point; and so, we could have orbits near the equilibrium point (further away from the equilibrium point we would have unbounded solutions, which can we seen in Fig. 1). This proves that for small \(r\) we have stable, closed orbits. However, Bertrand’s theorem states that only Newtonian and Harmonic potentials allow closed and bounded solutions. Thus, we confirm that for small \(r \) our equations obey the conditions of the above theorem. We also derive the orbit equation for each case.

For the orbit equation, following Goldstein (1980) the orbit equation for a Keplerian orbit can be written as follow:

$$ \frac{d^{2} u}{d \theta ^{2}} +u=- \frac{\mu }{l^{2}} \frac{d}{du} V \biggl( \frac{1}{u} \biggr), $$
(29)

where \(r= \frac{1}{u}\). We can also derive this using Hamilton’s equations and the fact that:

$$ \frac{dr}{dt} = \frac{dr}{d\theta } \frac{d\theta }{dt} = \frac{dr}{d\theta } \dot{\theta }, $$
(30)

where \(\dot{\theta } \) is given by (6). After subsequent differentiation with respect to \(r\), we obtain the orbital equation. For our modified potential, we have that:

$$ V \biggl( \frac{1}{u} \biggr) =-ku\bigl(1+ \alpha e^{- \frac{1}{\lambda u}} \bigr). $$
(31)

For small \(r \) (i.e. using the approximation (14)) we obtain the following equation:

$$\begin{aligned} \frac{d^{2} u}{d \theta ^{2}} +u&=- \frac{\mu }{l^{2}} \frac{d}{du} \bigl[ -ku-ku \alpha e^{- \frac{1}{\lambda u}} \bigr] \end{aligned}$$
(32)
$$\begin{aligned} &=- \frac{\mu }{l^{2}} \biggl[ -k-k \alpha \biggl( 1+ \frac{1}{\lambda u} \biggr) e^{- \frac{1}{\lambda u}} \biggr] \end{aligned}$$
(33)

Using the approximation in Eq. (14) and ignoring higher order \(O(\lambda ^{2} u^{2})\) terms we obtain the following orbital equation:

$$ \frac{d^{2} u}{d \theta ^{2}} +u=- \frac{k\mu }{l^{2}} (\alpha +1), $$
(34)

which has solution of the form:

$$ u= \frac{1}{r} = \frac{k\mu }{l^{2}} ( \alpha +1 ) \bigl[1+e\cos( \theta - \theta _{0} )\bigr], $$
(35)

where \(e \) is the eccentricity of the orbit. The Newtonian and purely Yukawa cases follow respectively from (34)

$$\begin{aligned}& u= \frac{1}{r} = \frac{k\mu }{l^{2}} \bigl[1+e\cos(\theta - \theta _{0} )\bigr], \end{aligned}$$
(36)
$$\begin{aligned}& u= \frac{1}{r} = \frac{k\mu \alpha }{l^{2}} \bigl[1+e\cos(\theta - \theta _{0} )\bigr]. \end{aligned}$$
(37)

Finally, to satisfy Bertrand’s theorem we must satisfy the condition

$$ \frac{d^{2} V_{\mathit{red}} (r)}{d r^{2}} \left \vert r= r_{0} \right . >0 $$
(38)

where the reduced potential is given by (12). After using the approximation for small \(\frac{r}{\lambda }\) (i.e. (14)) and ignoring terms of order \(O ( \frac{r^{2}}{\lambda ^{2}} )\) this condition becomes

$$ \frac{\mu ^{3} k^{4} ( 1+\alpha )^{4}}{l^{6}} >0, $$
(39)

which is true since \(\mu \), \(\alpha \), \(l\), \(k > 0\). Similarly, it can be shown that this is true for the Newtonian (setting \(\alpha = 0\)) and purely Yukawa cases. This shows that the Yukawa + Newtonian potential satisfies Bertrand’s theorem for small \(\frac{r}{\lambda }\) term. A consequence of Bertrand’s theorem is that the ratio \(\frac{\omega }{\dot{\theta }}\) is a rational number; where \(\omega = \frac{2\pi }{T}\) and \(\dot{\theta }\) is given by (6). In a paper to follow we will show that since for the solar system orbits the theory predicts that \(\lambda \gg r_{\mathit{eq}} = a\); therefore, for any practical purpose \(\frac{\omega }{\dot{\theta }} =1\). This number being rational implies that orbits are bounded indeed. This result is physically reasonable even given our approximations, as mentioned earlier \(\lambda \geq 1015~\text{m}\) for Solar System orbits. Therefore, for bound orbits near the equilibrium point \(r_{\mathit{eq}} = \frac{l^{2}}{\mu k ( 1+\alpha )}\) we expect \(\frac{r}{\lambda }\) to be small. For example, to explore the dynamics of two sun-like stars orbiting at a radius similar to the size of the Solar System; we let \(m_{1} = m_{2} = M_{\mathrm{sun}} = 10^{30}\text{ kg}\). This would imply \(\alpha = 10^{-8}\), \(\lambda =10^{15}\text{ m}\), \(k=Gm_{1} m_{2} =10^{49}\text{ kg}\text{ m}^{3}/\text{s}^{2}\), \(\mu =10^{30}\text{ kg}\) and \(\ell = mvr\approx 10^{45}~\text{kg}\ \text{m}^{2}/\text{s}\). Therefore, \(r_{\mathit{eq}} = 2 \times 10^{11}\text{ m}\approx 1.3\text{ AU}\); this is comparable to the orbit of Mars, and thus \(\frac{r}{\lambda } \ll 1\) and so the approximations we have been using during this contribution are valid.

5 Conclusion

We have demonstrated the dynamics and stability of the two-body problem with the Yukawa correction to the Newtonian potential. To calculate the former, we treated the problem as a modified Kepler problem and derived the equations of motion and the reduced potential of the system; which led us to the discussion of unbounded or bounded motion. To demonstrate the latter, stability, we constructed the Linearization matrix and tested the stability of the equilibrium points of the system for a Yukawa correction. We find that the stability of the equilibrium point is a central solution; which implies stable solutions near the equilibrium point. We repeated the analysis for a purely Yukawa force and find similar results. We also confirm that our modified potential obeys Bertrand’s theorem.