Second-order theory for the two-body problem with varying mass including periastron effect

Abstract

The model of varying mass function, including periastron effect, in terms of Delaunay variables will be expanded. The Hamiltonian of the problem is developed in the extended phase space by introducing a new canonical pair of variable ($q_4, Q_4$). The first “$q_4$” is defined as explicit function of time and the initial mass of the system. The conjugate momenta “$Q_4$” is assigned as the momenta raises from the varying mass. The short-period analytical solution through a second-order canonical transformation using “Hori’s” method developed by “Kamel” is obtained. The variation equations for the orbital elements are obtained too. The results of the effect of the varying mass and the periastron effect in the case $n = 2$ are analyzed.

1 Introduction

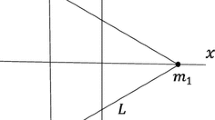
Every star undergoes a continuous time-dependent mass loss from the moment of its formation to its death through complicated chemical and physical processes. Mass loss remains one of the primary uncertainties in the stellar evolution and one of the keys to the binary systems evolution as well. Supernovae are excellent probes for the existence as well as the nature of mass loss process. In the binary systems, in addition to time-dependent mass loss, there exists another mass loss due to the gravitational interaction between the two components of the binary close to periastron. There is an appreciable enhancement of such type of mass loss in the binary systems. It gives rise to secular trends in the orbital elements of the binary system which can be detected by carefully examining its light curve, see [8]. This phenomenon is called the PAE, and it will be more noticeable when the orbits of binary become more eccentric and the distance between the two binary components becomes minimum. Such an effect could possibly explain the relatively high eccentricity found in some tidally strong interacting binary systems. In fact, the PAE could counteract the tidal circularization predicted by Zahn’s theory [28, 29]. For more details, refer to the analyses in the general context of double and triple stars, [4,5,6], and [7]. In 1985, Salamassi [27], the author studied the second-order adiabatic invariants associated with the two-body problem with slowly varying mass. In his paper, using action—angle variables, adiabatic invariants to order one are found.

The PAE has the secular variations in the orbital elements that lead to slight alterations in the light curve in the eccentric eclipsing binaries.

In the framework of celestial mechanics, the problem of the two bodies with VM has roots going back in the history since the middle of the nineteenth century, and it known as Gylden–Mescerskij problem. It has been exhaustively addressed by [2, 11, 13, 14, 22, 23], among others.

A number of binary systems show evidence of enhanced activity of mass loss around periastron passage. Among these, $\upeta$-Car is the extreme and best-documented example of periodic brightening at X-ray, visual and IR wave bands associated with periastron passages. Recently, Van Genderen & Sterken, IBVS, 5782 (2007) suggested that these periastron events may have the same physical cause as the milder “PAE” exhibited by many less renowned eccentric binaries in which small enhancement ($\Delta m \sim {0.01{-}0.03}$) in the visual brightness of the system around periastron passage are observed. They suggested that the fundamental cause of the effects might reside in the enhanced tidal force present during periastron passage.

In the astrophysical events, significant mass loss occurs in two phases: The first is found in red giants before large amplitude pulsation starts. These mass loss rates are slow (${<}10^{-8} \,\,M_{\mathrm{sun}}/\hbox {year}$). This is the dominant form of mass loss in the lowest mass evolved stars—globular cluster stars. It occurs mostly on the RGB, also on the early-AGB. The second is discovered in AGB stars with large amplitude pulsation. Rates can be as high as $10^{-4}\,\, M_{\mathrm{sun}}/\hbox {year}$. These are known as superwinds.

A relatively extensive bibliography on the problem can be found in the published works of [20, 21]. The specific case which results in a slow isotropic mass loss has also been the focus of exhaustive studies carried out by researchers , for instance, [13, 14], to name but a few. The vast majority of these, in search of the stellar application, have taken the so-called Eddington–Jeans law, Jeans (1924; 1925), as a law of the variation of mass

$$\begin{aligned} {\dot{m}} =- \alpha \, m^{n} \end{aligned}$$

(1)

where $\alpha$ and n are real numbers, the first is positive and proximate to zero and the second varying between 1.4 and 4.4, see [8].

Prieto and Docobo [22, 23] intend to present an approximate analytic solution of the two-body problem with slowly decreasing mass which is obtained through the integration of the Hamilton equations using Deprit’s method of perturbations, [10]. The solution, obtained through the Eddington–Jeans law, is put into practice in a specific case and compared with Mestschersky’s exact equation, $n = 2$, and with that which results from numerically integrating the equations.

In the framework of celestial mechanics, this problem has been exhaustively addressed by [2, 11], among others.

Andrade [3] analyzed the dynamics of binary systems with time-dependent mass loss and PAE, i.e., a supposed enhanced mass loss during periastron passage by means of analytical and numerical techniques.

Andrade and Docobo [4] studied the dynamics of binary systems with small parameter perturbation model. The time dependence of the whole set of orbital elements concluded could be calculated over long timescales and even for high eccentricities. In these models, they studied the following time- and distance-dependent mass loss law.

$$\begin{aligned} \dot{\mu }\left( {t; r;P_\theta } \right) =\dot{\mu }\left( {t} \right) -\beta \frac{P_\theta }{r^{2}}, \end{aligned}$$

(2)

where the first term represents time-dependent mass loss, and the second one introduces the PAE, where “r” is the distance between the two components, $P_\theta$ is the total angular momentum and $\beta$ is another small parameter close to zero.

Rahoma et al. [25] published an interesting article concerns with the two-body problem with VM in case of isotropic mass loss from both components of the binary systems. The law of mass variation used gives rise to a perturbed Keplerian problem depending on two small parameters. The problem is treated analytically in the Hamiltonian framework and the equations of motion are integrated using the Lie series developed and applied, separately by [9, 15]. A second-order theory of the two bodies eject mass was also constructed, returning the terms of the rate of change of mass up to second order in the small parameters of the problem. The same author [26] studied the two-body problem with VM in case of isotropic mass loss. In that work, the problem is treated analytically in the Hamiltonian framework and the equations of motion ware integrated using the Lie operator and Lie series.

El-Saftawy and Algethami [12] published a paper treating the problem of VM in the canonical framework taking into consideration the PAE. It was assumed that the PAE is of the same order of VM parameter. In that work, the authors introduced the VM as unspecified new canonical variable with a new unspecified conjugate momentum in the extended phase space. They introduced a second-order solution for the problem of VM using Delva–Hanslmeier canonical method.

In this work, we studied the averaged problem in the case of VM, represented by small parameter $\alpha$, and PAE represented by small parameter $\beta$. The two small parameters $\alpha$ and $\beta$ are assumed of the same order of magnitude. Surfaces for the rate of changes of mean anomaly, argument of periastron and the VM conjugate momenta are represented in three-dimensional graphics in different cases using the values published by [4].

2 The Hamiltonian of the problem

The Hamiltonian for the two-body problem expressed in terms of DV, which derived firstly by Deprit, A., 1983, is:

$$\begin{aligned} \mathcal{H}\left( {q_1 , Q_1 , Q_2 ; t} \right) =-\frac{1}{2}\frac{\mu ^{2}}{Q_1^2 }+\frac{\dot{\mu }}{\mu } Q_{1} \,\textit{e}\, \sin \, \textit{E} \end{aligned}$$

(3)

where the usual DV defined by:

$$\begin{aligned} q_1= & {} \hbox { Mean anomaly}, \quad q_2 =\omega , \quad q_3 =\varOmega ,\\ Q_1= & {} \sqrt{\mu a},, \quad Q_2 = Q_1 \sqrt{1-e^{2}}, \quad Q_3 =Q_2\cos \, \textit{I}, \end{aligned}$$

$q_{i}'s$ are considered as the coordinates, while $Q_{i}'s$ are their corresponding conjugate momenta.

The variation of $\mu$ may be retained from one of the two masses $m_{1}$ or $m_{2}$, and this is the case of one body ejects mass. Otherwise, the case of the two bodies eject masses. We will concern with the first case.

The Hamiltonian $\mathcal{H}$ represented by Eq. (3) is depending implicitly on time through the variable mass $\mu$ and its time derivative $\dot{\mu }$. By modifying Docobo’s law for the rate of change of mass assigned by eq. (2) and use Jeans law described by Eq. (1), we get:

$$\begin{aligned} \dot{\mu }(r,t,\mu )=- \alpha {\varvec{\mu }}^{n}-\beta \frac{Q_2 \mu ^{2}}{Q_1^4 }\left( {\frac{a}{r}} \right) ^{2} \end{aligned}$$

(4)

Substituting from Eq. (4) into Eq. (3) yields:

$$\begin{aligned} \mathcal{H}=-\frac{1}{2}\frac{\mu ^{2}}{Q_1^2 }+\frac{\dot{\mu }}{\mu } Q_1 \textit{e} \, \sin \,\textit{E}-\beta \frac{Q_2 e \mu }{Q_1^3 }\left( {\frac{a}{r}} \right) ^{2}\sin \,\textit{E}\nonumber \\ \end{aligned}$$

(5)

Since the variable mass can be expressed as a Taylor series expansion as:

$$\begin{aligned} \mu= & {} \mu _0 +\frac{d \mu }{d t}\left| {_{t=t_0 } } \right. \frac{\left( {t-t_0 } \right) }{1!}+\frac{d^{2}\mu }{d t^{2}}\left| {_{t=t_0 } } \right. \frac{\left( {t-t_0 } \right) ^{2}}{2!}\nonumber \\&+\cdots , \end{aligned}$$

(6)

From Jeans law of VM, we have:

$$\begin{aligned} \frac{d \mu }{d t}\left| {_{t=t_0 } } \right. = \dot{\mu }_0 = - \alpha \mu ^{n}\left| {_{t=t_0 } } \right. = - \alpha \mu _0^n . \end{aligned}$$

where $\mu _0$ is the mass of the system at time $t_0$.

$$\begin{aligned} \frac{d^{2} \mu }{d t^{2}}\left| {_{t=t_0 } } \right. = \ddot{\mu }_0 = - \alpha n \mu ^{n-1} \dot{\mu }\left| {_{t=t_0 } } \right. = \alpha ^{2}n \mu _0^{2 n-1} . \end{aligned}$$

Substituting the last two equations into Eq. (6), retaining orders up to $\alpha ^{2}$, yields:

$$\begin{aligned} \mu =\mu _0 - \alpha \mu _0^n \left( {t-t_0 } \right) +\frac{1}{2!}\alpha ^{2}\mu _0^{2 n-1} n \left( {t-t_0 } \right) ^{2}. \end{aligned}$$

(7)

With the help of Eq. (7), we can develop the Hamiltonian (5) to be:

$$\begin{aligned} {\mathcal {H}}= & {} - \frac{{\mu _{0}^{2} }}{{2\,Q_{1}^{2} }} + \alpha \,\left[ {\frac{1}{{Q_{1}^{2} }}\,\mu _{0}^{{n + 1}} \,\left( {t - t_{0} } \right) - Q_{1} e \mu _{0}^{{n - 1}} \sin \,E} \right] \nonumber \\&+\,\alpha ^{2} \left[ { - \frac{1}{{2\,Q_{1}^{2} }}} \right. \mu _{0}^{{2\,n}}\left( {n + 1} \right) \left( {t - t_{0} } \right) ^{2} \nonumber \\&+ \left. {Q_{1} e \mu _{0}^{{2\,n - 2}} \,\left( {n - 1} \right) \,\left( {t - t_{0} } \right) ^{2} \sin \,E} \right] \nonumber \\&+\, \beta \left[ {\frac{{Q_{2}^{{}} }}{{Q_{1}^{3} }}\,e\,\mu _{0} } {\left( {\frac{a}{r}} \right) ^{2} \,\sin \,E} \right] \nonumber \\&+\, \beta \,\alpha \,\left[ {\frac{{Q_{2}^{{}} }}{{Q_{1}^{3} }}\,e\,} \right. \mu _{0}^{n} \,\left( {t - t_{0} } \right) \,\left. {\left( {\frac{a}{r}} \right) ^{2} \,\sin \,E} \right] \nonumber \\&+\, \beta \,\alpha ^{2}\left[ { - \frac{{Q_{2}^{{}} }}{{2\,Q_{1}^{3} }}}\cdot {e\,n\,\mu _{0}^{{2n - 1}} \,\left( {t - t_{0} } \right) ^{2} \,\left( {\frac{a}{r}} \right) ^{2} \,\sin \,E} \right] \nonumber \\ \end{aligned}$$

(8)

Since the Hamiltonian represented by Eq. (8) is explicitly time dependence, so we extend the phase space by introducing a new pair of variable ($q_4 ,Q_4 )$. The first is “$q_4 = \mu _0^n \left( {t-t_0 } \right)$” assigned as the variable mass and the second is its conjugate momentum “$Q_4$” which describes the momentum rising due to the variation of the mass.

The new systems of canonical equations of motion will be:

$$\begin{aligned} \dot{q}_i =\frac{{\varvec{\partial }} {\mathcal {K}}}{{\varvec{\partial }} Q_i } \; \hbox {and}\; \dot{Q}_i =-\frac{{\varvec{\partial }} {\mathcal {K}}}{{\varvec{\partial }} q_i } i=1,\ldots ,4 \end{aligned}$$

(9)

With ${\mathcal {K}}$ is the new Hamiltonian in the extended phase space that expressed as:

$$\begin{aligned} {\mathcal {K}}= & {} \mu _{o}^{n} \,Q_{4} + \,{\mathcal {H}}\nonumber \\= & {} - \frac{{\mu _{0}^{2} }}{{2\,Q_{1}^{2} }} + \,\mu _{o}^{n} \,Q_{4} + \alpha \,\left[ {\frac{{\mu _{0}^{{}} }}{{Q_{1}^{2} }}\,q_{4} - Q_{1} e \mu _{0}^{{n - 1}} \sin \,E} \right] \nonumber \\&\alpha ^{2} \left[ { - \frac{1}{{2\,Q_{1}^{2} }} + q_{4}^{2} \left( {n + 1} \right) + \frac{{Q_{1} \,e}}{{\mu _{0}^{{2\,}} }}\left( {n - 1} \right) q_{4}^{2} \sin \,E} \right] \nonumber \\&+\, \beta \left[ {\frac{{Q_{2}^{{}} }}{{Q_{1}^{3} }}\,e\,\mu _{0} \,\left( {\frac{a}{r}} \right) ^{2} \,\sin \,E} \right] \nonumber \\&+\, \beta \,\alpha \,\left[ {\frac{{Q_{2}^{{}} }}{{Q_{1}^{3} }}\,e\,q_{4} } {\left( {\frac{a}{r}} \right) ^{2} \sin \,E} \right] \nonumber \\&-\, \beta \,\alpha ^{2} \,\left[ {\frac{{Q_{2}^{{}} }}{{2\,Q_{1}^{3} }}\,\frac{{e\,n}}{{\mu _{0}^{{}} }}\,q_{4}^{2} \left( {\frac{a}{r}} \right) ^{2} \sin \,E} \right] . \end{aligned}$$

(10)

The Hamiltonian (8) is explicit dependence of time and completely different from the Hamiltonian derived by [12]. The new Hamiltonian, described by Eq. (10), includes higher-order terms such as O($\alpha ^{2})$, O($\alpha \beta )$ and O($\alpha ^{2} \beta )$ and the new pair of variables is defined implicitly.

The first term in equation (10) is the contribution of the two bodies with the constant total mass of the system “$\mu _{o}$” which will be computed at specific time “$t_o$.” The small parameter “$\beta$” is close to zero as well as the small parameter “$\alpha$.”

3 The solution of the averaged problem

If the Hamiltonian function ${\mathcal {K}}\equiv {\mathcal {K}}\left( {u_i , U_i } \right)$, the integrable part of the Hamiltonian, ${\mathcal {K}}_0$, is function of $U _1$. So the variable $u_1$ can be considered as the fast variable.

Hori’s method, [16], developed by [19] is used to eliminate the short-period terms from the Hamiltonian. We denote the transformed Hamiltonian by ${\mathcal {K}}^{*}$, which can be written up to kth orders as follows:

$$\begin{aligned} {\mathcal {K}}_0^*= & {} {\mathcal {K}}_0 \left( { U^{\prime }_1 } \right) \end{aligned}$$

(11a)

$$\begin{aligned} {\mathcal {K}}_k^*= & {} \tilde{{\mathcal {K}}}_k +L_k {\mathcal {K}}_0^*. \end{aligned}$$

(11b)

$$\begin{aligned} {\tilde{\mathcal {K}}}_{k}= & {} {\mathcal {K}}_{k} + \sum \limits _{{j = 1}}^{{k - 1}} {\left[ {\left( {\begin{array}{*{20}c} {k - 1} \\ j \\ \end{array} } \right) G_{j} {\mathcal {K}}_{{k - j}}^{*} + \left( {\begin{array}{*{20}c} {k - 1} \\ {j - 1} \\ \end{array} } \right) L_{j} {\mathcal {K}}_{{k - j}}^{{}} } \right] } \nonumber \\ \end{aligned}$$

(11c)

where $L_j$ is the Lie derivative generated by the j component of the generating function ${\mathcal {S}}$, and $G_j$ can be calculated using:

$$\begin{aligned} G_j =L_j -\sum _{m=0}^{j-2} {\left( {\begin{array}{l} j-1 \\ m \\ \end{array}} \right) L_{m+1} G_{j-m-1} } , \quad 1\le j\le k. \end{aligned}$$

Since $u_1$ is considered as the fast variable in ${\mathcal {K}}$, we choose ${\mathcal {K}}_k^*$ to be the secular part of $\tilde{{\mathcal {K}}}_k$. Then, by averaging over $u^{\prime }_1$, we get:

$$\begin{aligned} {\mathcal {K}}_k^*=\langle \tilde{{\mathcal {K}}}_k \rangle _{\mathop u\nolimits _1^{\prime } } . \end{aligned}$$

(11d)

While the periodic part of $\tilde{{\mathcal {K}}}_k$ can be calculated from:

$$\begin{aligned} \mathcal {P}_k^ =\tilde{{\mathcal {K}}}_k -{\mathcal {K}}_k^*=\left( {{\mathcal {K}}_0; {\mathcal {S}}_k } \right) , \end{aligned}$$

(11e)

and then the generating function, for different order, can be calculated using:

$$\begin{aligned} \mathcal {S}_{k} = \left( {\frac{{\partial \mathcal {K}_{0}}}{{\partial U'_{1}}}} \right) ^{-1}\int {\mathcal {P}_{k}\mathrm{d}u'_{1}}. \end{aligned}$$

(11f)

Noting that the prime over the variable indicates the new variable in the transformed phase space.

Now applying the procedure described by Eq. (11) to our problem noting that the small parameters, $\alpha$ and $\beta$, close to zero, we assume that they have the same order of magnitude.

To drive the variation in the canonical elements due to the variation of mass in this case, we must rewrite the Hamiltonian (10), up to O$\left( {\alpha ^{2}} \right)$, to be in the form:

$$\begin{aligned} {\mathcal {K}}=\sum _{i=0}^2 {\frac{\alpha ^{i}}{i{\textit{!}}}{\mathcal {K}}_i } , \end{aligned}$$

(12)

where

$$\begin{aligned} {\mathcal {K}}_o= & {} -\frac{\mu _0^2 }{2 Q_1^2 }+ \mu _o^n Q_4 , \end{aligned}$$

(12a)

$$\begin{aligned} {\mathcal {K}}_1= & {} \frac{\mu _0}{Q_1^{2}} q_4 -Q_1 e \mu _0^{n-1} \sin \,\textit{E}\nonumber \\&+\,\frac{\beta }{\alpha } \left[ {\frac{Q_2}{Q_1^3 } e \mu _0 \left( {\frac{a}{r}} \right) ^{2} \sin \,\textit{E}} \right] \nonumber \\ \end{aligned}$$

(12b)

$$\begin{aligned} {\mathcal {K}}_2= & {} -\frac{1}{Q_1^2 }q_4^{2} \left( {n+1} \right) +\frac{2 Q_1 e}{\mu _{{0}^{2}} }\left( {n-1} \right) q_4^{2} \sin \, \textit{E}\nonumber \\&+\,\frac{\beta }{\alpha } \left[ {\frac{2 Q_2}{Q_1^{3}} eq_4 } \right. \left. {\left( {\frac{a}{r}} \right) ^{2}\sin \, E} \right] \end{aligned}$$

(12c)

Since “$q_2$” and “$q_3$” are ignorable variables, so Eq. (12) tells us that “$Q_{ 2}$” and “$Q_{ 3}$” are constants of motion while both “$q_2$” and “$q_3$” are linear function of time.

3.1 The averaged Hamiltonian

The Hamiltonian function, ${\mathcal {K}}$, is a function of $q_{ 1} , q_{ 4} , Q_{ 1} , Q_{ 2}$ and $Q_{ 4}$. The integrable part of the Hamiltonian, ${\mathcal {K}}_{ 0}$, is a function of $Q_{ 1}$ and $Q_{ 4}$, so the variables $q_1$ and $q_4$ can be considered as the fast variables.

3.1.1 Zero order

Applying Eq. (11a) to Eq. (12a), the zero-order transformed Hamiltonian can be written as:

$$\begin{aligned} {\mathcal {K}}_0^*={\mathcal {K}}_0 \left( {\_;Q{^\prime }_1, {Q}'_4 } \right) =\frac{-\mu _o^2 }{2Q{^\prime }_1^2 }+ \mu _o^n {Q}'_4 \end{aligned}$$

(13)

3.1.2 First order

The first-order transformed Hamiltonian can be calculated using Eqs. (11b)–(11d), with $k = 1$, and by averaging the Hamiltonian, ${\mathcal {K}}_1$, over the mean anomaly $q_1$. Therefore, the first-order transformed Hamiltonian, ${\mathcal {K}}_1^*$, is

$$\begin{aligned} {\mathcal {K}}_1^*=\frac{1}{2\pi }\int \limits _0^{2\pi } {{\mathcal {K}}_1 \partial q_1 }. \end{aligned}$$

(14)

After calculating the required averages needed in the last equation, we get:

$$\begin{aligned} {\mathcal {K}}_{1}^{*} = \frac{{\mu _{0} }}{{Q_{1}^{{'2}}}}q'_{4}, \end{aligned}$$

(15)

The primes over the variable indicate for the new phase space variables, but for the sake of simplicity of writing, we well drop it in the next subsections.

We need to calculate the generating function for the first order. Using Eq. (11e) the periodic part is calculated, ${\mathcal {K}}_{1P}^*=\tilde{{\mathcal {K}}}_1 -{\mathcal {K}}_1^*$ and then the generating function. Using Eqs. (11f), (12b) and (15), the periodic part can written as:

$$\begin{aligned} {\mathcal {K}}_{1p}^*= & {} -Q_1 e \,\mu _0^{n-1} \sin \, E+\frac{\beta }{\alpha } \left[ {\frac{Q_2}{Q_1^3 } e \, \mu _{0}\left( {\frac{a}{r}} \right) ^{2}\sin \, E} \right] \nonumber \\= & {} \left( {S_1 ; {\mathcal {K}}_o } \right) \end{aligned}$$

(16)

where $\left( {S_1 ; {\mathcal {K}}_o } \right)$ is the Poisson Bracket for the two functions $S_1$ and ${\mathcal {K}}_o$. After calculating the required derivatives and mathematical manipulations, we get:

$$\begin{aligned} S_1 = \sum \limits _{i=0}^1 {B _i^c \left( {\frac{r}{a}} \right) ^{i} \cos \,iE}, \end{aligned}$$

(17)

with, $B_1^C =Q_1^4 e \mu _o^{n-3}$ and $B_0^C = \frac{\beta }{\alpha }\frac{Q_2 }{\mu _0 }$.

3.1.3 Second order

To construct the function $\tilde{{\mathcal {K}}}_2$, Eq. (11c), we need first the calculation of the Poisson bracket $\left( {{\mathcal {K}}_1 +{\mathcal {K}}_1^*;S_1 } \right)$ after that we average the mathematical quantity, ${\mathcal {K}}_2 +\left( {{\mathcal {K}}_1 +{\mathcal {K}}_1^*;S_1 } \right)$, over the mean anomaly $q_1$. After computing the required calculations and with the help of Eqs. (11c), (11d), (12b), (15) and (17), we get:

$$\begin{aligned} {\mathcal {K}}_2^*= {\mathcal {K}}_{2 \alpha }^{*} + \frac{\beta }{\alpha }{\mathcal {K}}_{2 \alpha \beta }^*\ldots \end{aligned}$$

(18)

where the first term, ${\mathcal {K}}_{2 \alpha }^*$, is the contributions of the second order due to VM, the second term, ${\mathcal {K}}_{2 \alpha \beta }^*$, is the second-order coupling effect between the VM and PAE. The contributions, in the second order, for different parts in the Hamiltonian (18) are:

$$\begin{aligned} {\mathcal {K}}_{2 \alpha }^*= & {} -\eta ^{-2,0} \left( {n+1} \right) q_4^2 +\frac{1}{2}\mu _0^{2n-4} \left( {5 \eta ^{2,2}-3 \eta ^{4,0}} \right) \nonumber \\&+\,\mu _0^{n-2} \left( {\eta ^{-2,1}-\eta ^{-1,0}} \right) \left( {1+e} \right) . \end{aligned}$$

(18a)

$$\begin{aligned} {\mathcal {K}}_{2 \alpha \beta }^*= & {} \mu _0^{n-2} \left[ \frac{5 \eta ^{1,2}+8 \eta ^{2,1}-4 \eta ^{3,0}-10 \eta ^{0,3}}{\eta ^{1,1}+\eta ^{2,0}}\right. \nonumber \\&\left. +\,e {\left( {\frac{4 \eta ^{6,5}-3 \eta ^{8,3}}{\left( {1+\eta ^{1,1}} \right) ^{2}}} \right) } \right] \end{aligned}$$

(18b)

where $\eta ^{i,j}=Q_1^i Q_2^j$

Using Eq. (13), (15) and (18), the transformed Hamiltonian can be written as:

$$\begin{aligned} {\mathcal {K}}^*= & {} \frac{-\mu _o^{2}}{2Q{^\prime }_1^2 }+ \mu _o^{n} {Q}'_4 +\alpha \frac{\mu _0}{{Q_{1}^{'2}}} {q}'_4 +\frac{\alpha ^{2}}{2}{\mathcal {K}}_{2 \alpha }^*\nonumber \\&+ \frac{\alpha \beta }{2} {\mathcal {K}}_{2 \alpha \beta }^*. \end{aligned}$$

(19)

According to the new treatment, the averaged Hamiltonian includes terms of the second order for VM ($\alpha ^{2})$, and second-order coupling effects between both ($\alpha \beta )$.

Integrations of the form $\int {\left( {\frac{r}{a}} \right) } ^{i} \cos \, \textit{jE} \ln \left( {\frac{r}{a}} \right) ^{k}dl$ appeared during the averaging processes. The general result of such kind of integration is added as “Appendix” at the end of this paper.

3.2 The variation in the canonical elements

To calculate the variation in the canonical elements with time, we can use Hamilton’s equations of motion, Eq. (9). After deriving the required computations, the variation in the canonical variables can written as:

$$\begin{aligned} \dot{q}_{1}= & {} \mu _{0}^{2} \,\eta ^{{ - 3,0}} - 2\,\alpha q_{4} \mu _{0} \eta ^{{ - 3,0}} + \frac{{\alpha ^{2} }}{2}\,\left[ 2\,\left( {n + 1} \right) \,q_{4}^{2} \eta ^{{ -3,0}}\right. \nonumber \\&+\, \mu _{0}^{{2n - 4}} \left( {5\,\eta ^{{1,2}} - 6\,\eta ^{{3,0}} } \right) + \mu _{0}^{{n - 2}} \frac{1}{e}\nonumber \\&\cdot \left( \eta ^{{ - 2,0}} - \,2\,\eta ^{{ - 3,1}} - \,2\,\eta ^{{ - 4,2}} + \,3\,\eta ^{{ - 5,3}} \right. \nonumber \\&\left. \left. +\, e\,\eta ^{{ - 2,0}} - 2\,e\,\eta ^{{ - 3,1}} \right) \right] + \frac{{\alpha \,\beta }}{2}\left[ {\frac{1}{{\left( {\,\eta ^{{1,0}} + \,\eta ^{{0,2}} } \right) ^{2} }}}\right. \nonumber \\&\cdot \left( 10\,\,\eta ^{{ - 2,4}} + 20\,\,\eta ^{{ - 1,3}} + 3\,\,\eta ^{{0,2}} - 8\,\,\eta ^{{1,1}} - \,\,4\,\eta ^{{2,0}} \right) \nonumber \\&+\, \frac{1}{{e\,\left( {\,1 + \,\eta ^{{1,1}} } \right) ^{3} }}.\left( {24\,\eta ^{{7,3}} + 18} \cdot \eta ^{{8,4}} \right. \nonumber \\&\left. \left. - 45\,\eta ^{{5,5}} - 31\,\eta ^{{6,6}}+ 20\,\eta ^{{3,7}} + 12\,\eta ^{{4,8}} \right) \right] \end{aligned}$$

(20a)

$$\begin{aligned} \dot{q}_2= & {} \frac{\alpha ^{2}}{2}\eta ^{-2,0} \left[ \mu _0^{n-2} \left( {1+e+\frac{e \eta ^{0,1}}{\eta ^{1,0}+\eta ^{0,1}}} \right) \right. \nonumber \\&\left. +\, 5\mu _0^{2n-4} \eta ^{4,1} \right] +\frac{\alpha \beta }{2}\mu _0^{n-2} \left[ {\frac{1}{\left( { \eta ^{1,0}+ \eta ^{0,1}} \right) ^{2}}} \right. \nonumber \\&\cdot \left( {12 \eta ^{2,0}+10 \eta ^{1,1}-25 \eta ^{0,2}-20 \eta ^{-1,3}} \right) \nonumber \\&+\,\frac{1}{e \left( { 1+ \eta ^{1,1}} \right) ^{3}}\left( {9 \eta ^{8,2}+3 \eta ^{9,3}-32 \eta ^{6,4}-} \right. \nonumber \\&\left. -\,18 {\left. {\eta ^{7,5}+24 \eta ^{4,6}+16 \eta ^{5,7}} \right) } \right] \end{aligned}$$

(20b)

$$\begin{aligned} \dot{q}_3= & {} 0. \end{aligned}$$

(20c)

$$\begin{aligned} \dot{q}_4= & {} \mu _o^n . \end{aligned}$$

(20d)

$$\begin{aligned} \dot{Q}_1= & {} 0. \end{aligned}$$

(20e)

$$\begin{aligned} \dot{Q}_2= & {} 0. \end{aligned}$$

(20f)

$$\begin{aligned} \dot{Q}_3= & {} 0. \end{aligned}$$

(20g)

$$\begin{aligned} \dot{Q}_4= & {} -\alpha \mu _0 \eta ^{-2,0}+\alpha ^{2}\left( {n+1} \right) \eta ^{-2,0}q_4 . \end{aligned}$$

(20h)

Equation (20a) tells us that the change in the mean anomaly depends on the coupling effects ($\alpha \,\beta$ term) due to the VM and the PAE too. The coupling terms usually arise from the evaluation of the Poisson brackets in the Lie canonical perturbation theories. That effect depends on both the initial mass of the system “$\mu _0$” and the type of VM represented by the parameter “n.” Equation (20b) indicates that there is no first-order effects, for both the VM and the PAE, to the change of the argument of periapsis. But the effect rises in the second order due to VM and their coupling.

It was obvious from Eqs. (20c) and (20g) that there is no variations in both of argument of ascending node and its conjugate momentum. Finally, Eq. (20h) is new mathematical form to calculate the momentum rises from the VM. From such equation, that momentum depends only on the VM but there is no contribution for the PAE up to the second order.

Fig. 1

a The variation in the mean anomaly for $0 \le e \le 0.9$ & $1 \le a \le 1000$ with $\beta =\alpha =10^-{6}$ and $n = 2$ (Case D: M. Andrade; [4]). b The variation in the argument of periside for $0 \le e \le 0.9$ & $1 \le a \le 1000$ with $\beta =\alpha =10^{6}$ and $n = 2$ (Case D: M. Andrade; 2003). c The variation in the momentum conjugate to the VM for $0 \le e \le 0.9$ & $1 \le a \le 1000$ with $\beta =\alpha = 10^{-6}$ (Case D: M. Andrade; [4])

Fig. 2

a The variation in the mean anomaly for $0 \le e \le 0.9$ & $1 \le a \le 1000$ with $\alpha =10^{6}$ & $\beta =10^{-7}$ and $n = 2$ (Case C: M. Andrade; [4]). b The variation in the argument of periside for $0 \le e \le 0.9$ & $1 \le a \le 1000$ with $\alpha =10^{6}$ & $\beta =10^{7}$ and $n = 2$ (Case C: M. Andrade; 2003). c The variation in the momentum conjugate to the VM for $0 \le e \le 0.9$ & $1 \le a \le 100$ with and $n = 2$ (Case C: M. Andrade; [4])

The rate of changes of mean anomaly, the argument of periapsis and the momentum associated with VM are graphically represented for different closed orbits, $0\le e < 1$ and $1< a < 1000$, in the case ($n = 2$) (Fig. 1a–c, Fig. 2a–c). The small parameters $\alpha$ and $\beta$ are chosen in the two cases as those chosen previously, see Figure legends by [4].

As seen from Eq. (20) and the Figs. 1a–c, 2a–c, the following remarks are obtained:

• The perturbation due to PAE is appeared as a second-order effect. The first order vanishes through the averaging process. The PAE perturbation induces a secular variation in the orbital elements of the system. The evolution of affected orbital elements will depend on the fine adjustment of the small parameters $\alpha$ and $\beta$.

• Since there are no terms factored by $\alpha$ or $\beta$, the first-order secular effects in the argument of periapsis for the VM as well as the PAE vanish. This may be interpreted as the VM, and the PAE still preserve or enhance the nature of slow variation of the argument of periapsis.

• Equations (20e)–(20h) reveal that there is no contribution due to the PAE in all the canonical momenta. These perturbation may appear in higher-order theories. Equation (20h) gives rise to first- and second-order perturbations in $\dot{Q}_4$ due to VM only.

• The variation equations in the mean anomaly and the variation in the argument of periapsis [Eqs. (20a), (20b)] are valid for all types of VM systems which have closed orbits ($0< e < 1$). As is clear from the appearance of terms factored by $\frac{1}{e^{4}}$ which set restrictions on the eccentricity, there is a singularity at $e=0,$ i.e., for circular orbits.

• The variation in mass as well as its conjugate momentum depends on the parameter “n” and its value ranging between 1.4 and 4.4. see [8]. Therefore, a precise determination of a specific value from this range for certain binary system will affect largely the interpretation of the obtained results.

3.3 The element of short-period transformation and it’s inverse

The elements of short-period transformation can be calculated using equations:

$$\begin{aligned} q_i= & {} {q}'_i +{\varvec{\alpha }} \frac{{\varvec{\partial }} S_1 }{{\varvec{\partial }}{Q}'_i }+{\varvec{O}}({\varvec{\alpha ^{2}}}). \end{aligned}$$

(21a)

$$\begin{aligned} Q_i= & {} {Q}'_i +{\varvec{\alpha }} \frac{{\varvec{\partial }} S_1 }{{\varvec{\partial }}{q}'_i }+{\varvec{O}}({\varvec{\alpha ^{2}}}). \end{aligned}$$

(21b)

The inverse transformation equations can be calculated as follows:

$$\begin{aligned} {q}'_i= & {} q_i -{\varvec{\alpha }} \frac{{\varvec{\partial }} S_1 }{{\varvec{\partial }} {Q}'_i }-{\varvec{O}}({\varvec{\alpha ^{2}}}). \end{aligned}$$

(22a)

$$\begin{aligned} {Q}'_i= & {} Q_i +{\varvec{\alpha }} \frac{{\varvec{\partial }} S_1 }{{\varvec{\partial }} {q}'_i }+{\varvec{O}}({\varvec{\alpha ^{2}}}). \end{aligned}$$

(22b)

Where $\frac{{\varvec{\partial }} S_1 }{{\varvec{\partial }} {Q}'_1 }$,$\frac{{\varvec{\partial }} S_1 }{{\varvec{\partial }} {q}'_1 }$,$\frac{{\varvec{\partial }} S_1 }{{\varvec{\partial }} {q}'_4 }$and $\frac{{\varvec{\partial }} S_1 }{{\varvec{\partial }} {Q}'_2 }$ can be calculated using Eq. (17).

4 Discussions and conclusion

We note that in the unperturbed problem, the mean anomaly is a fast changeable parameter but when we consider mass change, we have additional contribution to change the mean anomaly rising from VM, PAE and their coupling terms. That effect depends on both the initial mass of the system “$\mu _{0}$” and the type of VM represented by the parameter “n.” This actually opens a chapter of interpretations for the researchers who have interest in the problem.

The second-order theory changed the picture completely with respect to the rate of changing the argument of periastron, $\dot{q}_2$. Since the first order does not discover the variation in argument of periastron, in the second order it rises as a result of VM, PAE and their coupling. That change depends on the initial mass of the system, the type of VM, the semimajor axis and the eccentricity of the orbit.

Finally, a new mathematical form to calculate the momentum rises from the VM is investigated. From such equation, the first-order effects decrease the momentum of the system and depend only on the initial mass of the system. While in the second-order theory, there is additional term increasing the variation in the momentum, $\dot{Q}_4$, depending on the VM, $q_4$ and the type of the system, n. That momentum does not depend on the PAE up to the second order. We can guess that may be it will start to appear at third order or higher.

For the sake of completeness, we well study, in future work, the case of the two components with varying mass. In such case, the paper by M. [24] will be considered to solve the system of differential equation.

Appendix

Integral of the form $\int {\left( {\frac{r}{a}} \right) } ^{m} \cos \, \textit{jE} ln \left( {\frac{r}{a}} \right) ^{p}\mathrm{d}l$

Let,

$$\begin{aligned} \Psi _{\mathrm{p}, j}^m =\left( {\frac{r}{a}} \right) ^{m} {\cos } \, {\textit{jE}} ln \left( {\frac{r}{a}} \right) ^{p} \mathrm{d}l \end{aligned}$$

(23)

The power series expansion for the function $ln \left( {\frac{r}{a}} \right) ^{m}$, in terms of the eccentric anomaly E, is:

$$\begin{aligned} ln \left( {\frac{r}{a}} \right) =-\sum _{n=1}^\infty {\frac{e^{n}}{n}} \left( {\cos } \,\textit{E} \right) ^{n}. \end{aligned}$$

(24)

From Ahmed, M. K. [1], we have $\left( {\cos \, E} \right) ^{n}=e^{-n}\sum _{k=0}^n {\left( {-1} \right) ^{k+1}} C_k^n \left( {\frac{r}{a}} \right) ^{k}$. Where $C_k^n$ is the binomial defined as $C_k^n =\frac{n !}{k ! \left( {n-k} \right) !}$.

Substituting in Eq. (24) yields:

$$\begin{aligned} \ln \left( {\frac{r}{a}} \right) =\sum _{n=1}^\infty {\sum _{k=0}^n {\frac{\left( {-1} \right) ^{k+2}}{n}} C_k^n \left( {\frac{r}{a}} \right) ^{k}.} \end{aligned}$$

(25)

Then,

$$\begin{aligned} \left( {\frac{r}{a}} \right) ^{m} \ln \left( {\frac{r}{a}} \right) ^{p}\mathrm{d}l=p\sum _{n=1}^\infty {\sum _{k=0}^n {\frac{\left( {-1} \right) ^{k+2}}{n}} C_k^n \left( {\frac{r}{a}} \right) ^{k+m+1}dE.} \end{aligned}$$

But, $\left( {\frac{r}{a}} \right) ^{q}=\sum _{\beta =0}^q {\left( {-1} \right) ^{\beta } C_\beta ^q } e^{\beta } \left( {\cos \, E} \right) ^{\beta }$, then the last equation will be:

$$\begin{aligned}&\left( {\frac{r}{a}} \right) ^{m} \ln \left( {\frac{r}{a}} \right) ^{p}=p\sum _{n=1}^\infty \sum _{k=0}^n \sum _{\beta =0}^{k+m+1} \nonumber \\&\quad \frac{\left( {-1} \right) ^{k+\beta +2}}{n} C_k^n C_\beta ^{k+m+1} e^{\beta } \left( {\cos \, E} \right) ^{\beta }. \end{aligned}$$

(26)

From Ahmed, M. K. [1], we have:

$$\begin{aligned} \left( {\cos \, \theta } \right) ^{k}=2^{1-k}\sum _{\alpha =0}^{\left[ {k/2} \right] } \left( {1-\frac{1}{2} \delta _{\left( {k/2} \right) {^\prime } \alpha } } \right) C_\alpha ^k \cos \left( {k-2 \alpha } \right) \theta \end{aligned}$$

Then, Eq. (26) will be:

$$\begin{aligned} \left( {\frac{r}{a}} \right) ^{m} \ln \left( {\frac{r}{a}} \right) ^{p}\mathrm{d}l= & {} p\sum \limits _{n=1}^\infty {\sum \limits _{k=0}^n \sum \limits _{\beta =0}^{k+m+1} \sum \limits _{\alpha =0}^{\left[ {\beta /2} \right] } \left( {-1} \right) ^{k+\beta +2}} \nonumber \\&\times \frac{2^{1-\beta }}{n} C_k^n C_\beta ^{k+m+1} C_\alpha ^\beta e^{\beta }.\nonumber \\&\cdot \left( {1-\frac{1}{2} \delta _{\left( {\beta /2} \right) {^\prime } \alpha } } \right) \nonumber \\&\times \cos \left( {\beta -2 \alpha } \right) E \,dE \end{aligned}$$

(27)

where $\left[ {S/2} \right]$ is the greatest integer less than or equal to S / 2. The next step is to form the integrand (23) using Eq. (27) such as:

$$\begin{aligned} \Psi _{\mathrm{p}, j}^m= & {} \sum _{\beta =0}^{k+m+1} {\sum _{\alpha =0}^{\left[ {\beta /2} \right] } } \Gamma _{\beta , \alpha }^p \left[ \cos \left( {\beta -2 \alpha +j} \right) E\right. \nonumber \\&\left. +\,\cos \left( {\beta -2 \alpha -j}\right) E \right] dE \end{aligned}$$

where

$$\begin{aligned} \Gamma _{\beta , \alpha }^p= & {} p\sum _{n=1}^\infty {\sum _{k=0}^n } \frac{\left( {-1} \right) ^{k+\beta +2}}{2^{\beta } n}C_k^n C_\beta ^{k+m+1} C_\alpha ^\beta \\&\times \left( {1-\frac{1}{2} \delta _{\left( {\beta /2} \right) {^\prime } \alpha } } \right) e^{\beta } \end{aligned}$$

Finally, the required general form for the integration is:

$$\begin{aligned}&\int {\left( {\frac{r}{a}} \right) } ^{m} \cos \, jE \ln \left( {\frac{r}{a}} \right) ^{p}\mathrm{d}l=\sum _{\beta =0}^{k+m+1} {\sum _{\alpha =0}^{\left[ {\beta /2} \right] } } \Gamma _{\beta , \alpha }^p . \nonumber \\&\quad .\left[ \frac{\sin \left( {\beta -2 \alpha +j} \right) E}{\left( {\beta -2 \alpha +j} \right) }+\,\frac{\sin \left( {\beta -2 \alpha -j} \right) E}{\left( {\beta -2 \alpha -j} \right) } \right] \\ \end{aligned}$$