A review of low-energy transfers

Abstract

Low-energy transfers (LET) for lunar and interplanetary missions has received immense attention of the scientific community during the last few decades as its importance was understood by the success of JAXA’s Hiten, ESA’s SMART-1, NASA’s GRAIL and ARTHEMIS missions, and several proposals, like the BepiColombo, Multi-Moon Orbiter and Europa Orbiter. In this paper the developments in the area of LET and low-thrust trajectories are reviewed. Starting with the basics of the restricted three-body problem and its use in finding invariant manifolds in phase space, the design of LET trajectories and optimisation methods used to find optimal LET and low-thrust transfers is discussed.

1 Introduction

Many space faring nations are planning for interplanetary missions to distant planets, asteroids and comets. The conventional method for the design of an interplanetary trajectory begins with the Hohmann transfer ellipse (Fig. 1), which is further refined using the Lambert conic (Fig. 2) and patched conic methods (Fig. 3). Alternative techniques, like aerobraking (Fig. 4), aerocapture (Fig. 5), gravity assist and ballistic capture trajectories, can be employed for optimising the fuel requirements. In some cases it has been proved that these alternative methods are better than conventional methods as they aid to reduce the total impulse requirement and provide extended launch opportunities. The low-energy transfer (LET) trajectory method is one such new unconventional technique; it was used by the Japanese Hiten Mission in 1991 (Belbruno and Miller 1993; Uesugi 1996), NASA’s ARTEMIS in 2009 (Folta et al. 2011; Sweetser et al. 2011), NASA’s GRAIL in 2011 (Roncoli and Fujii 2010; Chung et al. 2010 and Hatch et al. 2010), shown in Fig. 6, and it is proposed for missions like BepiColombo, Multi-Moon Orbiter (MMO) and Europa Orbiter. The LET trajectories have some advantages over direct transfer trajectories like lower total $\Delta V$, more flexible launch opportunity, longer view opportunity of en route satellites/planets compared to gravity assist (Ross et al. 2003 and Gómez et al. 2004); but they suffer mainly from long flight durations and tracking difficulties as the spacecraft travels longer distances than in the case of direct transfers.

Fig. 1

Hohmann transfer geometry

Fig. 2

Lambert conic method

Fig. 3

Patched conic method

Fig. 4

Aerobraking—MGS (http://spacecraftkits.com/MGSFacts.html)

Fig. 5

Aerocapture (http://www.rpi.edu/dept/chem-eng/WWW/faculty/plawsky/Comsol%20Modules/Aerocapture/Aerocapture.html)

Fig. 6

Trajectory GRAIL spacecraft (www.nasa.gov/pdf/582116main_GRAIL_launch_press_kit.pdf)

Basically the transfer approach to the Moon can be broadly classified into four categories, namely, the direct, phasing loop, weak stability boundary and spiral transfer (Lee 2011). The ‘classical’ direct transfer trajectory to the Moon starts from an Earth Parking Orbit (EPO) with an impulse Trans-lunar Injection ($\Delta V_{\mathit{TLI}}$), usually at perigee, to increase the apogee to 384400 km (mean distance between Earth and the Moon). After reaching near Moon, another impulse (Lunar Orbit Insertion, $\Delta V_{\mathit{LOI}}$) is given, usually at periselenium, so that the spacecraft is captured in an orbit around Moon. The time of flight for direct transfer varies from 2–5 days and the total $\Delta V$ from a 300 km circular EPO varies from 3.5 to 4 km/s. This method was used from 1960s to 1980s including the Luna and Apollo missions, and recently by Lunar Prospector and Lunar Reconnaissance Orbiter. This is the most-proven approach and can provide relatively simple and fast transfer processes and lowest overall risk and cost.

Both the TLI and the LOI burns can be divided into several smaller burns to minimise gravity losses and is known as the phasing loop transfer. This technique was used by Clementine, SELENE, Chandrayaan-1 (Fig. 7) and Chang’E-1. This approach can provide a chance to verify the operating condition, address the status of the orbiter and correct any anomalies before the orbiter arrives at the Moon. In general the time of flight varies from 2–3 weeks and it involves more operational complexities. The initial direct and phasing loop trajectories are designed using the Hohmann transfer or patched conic technique, which are based on an analytical solution of the two-body problem. Later the trajectory is refined using numerical methods taking into consideration other perturbing factors like the third-body perturbation, atmosphere and solar radiation pressure.

Fig. 7

Chandrayaan-1 mission profile (www.isro.gov.in)

Low-energy trajectories are characterised by a low energy with respect to the primaries and are usually associated with ballistic capture (getting captured by the primary without an impulsive manoeuvre). Weak Stability Boundary (WSB) transfer belongs to the category of LET that takes the orbiter to the region of Lagrange points of the Sun–Earth system to arrive at the Moon with low relative velocity, thus reducing $\Delta V_{\mathit{LOI}}$ at Moon. A small manoeuvre in WSB regions can lead to significant change in the trajectory. This approach usually requires a complex mission design requirement and very precise targeting and control of flight parameters (Biesbroek and Janin 2000). These transfers require less fuel, saving up to 150 m/s compared to Hohmann transfer. The time of flight varies from 60–100 days. The Japanese Hiten used the WSB transfer method to reach the Moon (Belbruno 2007).

The spiral approach belongs to the category of low-thrust transfers and requires the longest time of flight of all transfer methods. ESA’s SMART-1 used its low-thrust hall thrusters to expand its EPO to a lunar orbit over a period of 14 months. In the construction of WSB and spiral trajectories the perturbation of the Sun has to be included along with Earth and Moon and thus two-body dynamics is no more applicable. These trajectories are designed using the invariant manifold structures related to periodic orbits in the Restricted Three-Body Problem (R3BP).

The objective of this paper is to show the developments in the area of R3BP transfers and its application to finding LET trajectories. We begin with the developments in the area of R3BP related to capture dynamics, the use of R3BP in finding invariant manifolds in phase space, the use of manifold theory to determine low-energy transfers and methods to find an optimal trajectory. Some of the missions which are planned to use or which have used LET are discussed.

2 Design of low energy transfers

2.1 Restricted Three-Body Problem

The Restricted Three-Body Problem (R3BP) is the problem to describe the motion of an infinitesimally small particle P which is moving under the gravitational influence of two massive bodies $M_{1}$ (more massive primary) and $M_{2}$ (smaller primary). The two massive bodies are moving in a circular orbit about their centre of mass. It is the simplest non-integrable system. Figure 8 shows the R3BP Earth–Moon system. $P_{1}$ is Earth ($E$) and $P_{2}$ is Moon ($M$). Unlike the patched conic approach, simulations in the restricted three-body problem consider the influence of two massive bodies on the spacecraft at all time. Egorov (1958) has presented lunar and circumlunar trajectories in the R3BP and problems like circumnavigation of the Moon with a return to Earth at a flat entry angle, using the Moon’s gravity assist to reach other planets, possibility of the lunar capture etc. He concluded that capture of the projectile launched from Earth by the Moon on the first circuit of the trajectory was not possible. This was based on the analysis in the R3BP. But later it has been established that when Sun’s gravity is considered, ballistic capture is possible.

Fig. 8

Restricted three-body problem (Earth–Moon system)

In the three-body problem, Conley–McGehee tubes, the invariant manifolds of the periodic orbits, play an important role in understanding the transfer mechanism in the solar system (Koon et al. 2006). Hunter (1967) studied the stability conditions and satellite lifetime before escape in the framework of elliptic R3BP. Conley (1968) described the local dynamics near saddle-centre equilibrium points and the construction of a lunar trajectory in the planar circular R3BP. From his work it is known that both the stable and the unstable manifolds of periodic orbits around $L_{1}$ and $L_{2}$ are two-dimensional. He showed that the local invariant hyperbolic manifolds emanate from the Lyapunov orbits. He conjectured that a low-energy transfer between Earth and Moon might exist which leads to capture by the Moon. McGehee (1969), building on the work of Conley, studied homoclinic transfer trajectories that take the spacecraft off a periodic orbit and then return it onto that same orbit at a later time. Heppenheimer (1978a, 1978b) brought out the idea of using these orbits for material transportation from the Moon for space colonisation. Huang and Innanen (1983) numerically explored the stability and capture regions of retrograde Jovian satellites. They also obtained the conditions for temporary capture of retrogate jovicentric satellites in the framework of R3BP and elliptic R3BP. Brunini (1996) investigated stability and capture regions in phase space for direct and retrograde satellites and found possible candidates to be temporary Jovian satellites. Llibre et al. (1985) showed the global extension of invariant hyperbolic manifolds about the smaller primary and showed that they transversally intersect. This means that complicated hyperbolic networks exist about the smaller primary which can be used to design LET. Murison (1989) used a surface of section analysis of a selected region of the C-$x_{0}$ plane to show that the finite capture time areas correspond to motion in chaotic regions while the permanent capture areas are regions where the motion is trapped in quasi-periodic islands surrounding elliptical fixed points. He claims that most, if not all, escape/capture orbits are chaotic and the boundaries of such regions are fractal.

2.2 The weak stability boundary

WSB transfers from Earth to the Moon are constructed using WSB region of Sun–Earth to alter the spacecraft’s velocity as it enters WSB region of Earth–Moon so that it gets ballistically captured by the Moon. WSB transfer introduces more complexities to mission design than direct transfer. In order to design a WSB transfer trajectory, standard astrodynamics tools like the two-body problem cannot be used without modification, as the trajectory does not follow conic sections. When modelled in R3BP, the energy or the Jacobi constant of the trajectory changes due to thrusting. As a result the design of such trajectories is usually performed using optimisation tools. Since the discovery of such chaotic regions in the three-body problem, a lot of research has been done in this area to utilise these regions to design low-energy interplanetary trajectories.

According to Belbruno and Miller (1993), “WSB is transition region in the phase space where the gravitational interactions between Earth, Sun and Moon tend to balance”; also WSB is “a generalisation of Lagrange points and a complicated region surrounding the Moon”; Belbruno (2004) describes WSB as “a region in phase space supporting a special type of chaotic motion for special choices of elliptic initial conditions with respect to $m_{2}$”; Belbruno (2004) defines WSB as “in the circular R3BP, WSB is a boundary set in the phase space between stable and unstable motion relative to hte second primary. Keplerian orbits about the second primary, perturbed by the first primary are stable if after a prescribed number of revolutions they preserve the character of bounded motion. Otherwise they are unstable”; Yagasaki (2004a) describes WSB as “a transition region between the gravitational capture and escape from the Moon in the phase space”.

2.2.1 Analytical definition of capture and WSB is given by Belbruno (2004)

Let us consider the elliptic restricted three-body problem.

Definition

The two-body Kepler energy of $P_{3}$ with respect to $P_{2}$ in $P_{2}$-centred inertial coordinate is given by

$$ E_{2} ( X, \dot{X} ) = \frac{1}{2} \vert \dot{X} \vert ^{2} - \frac{\mu }{r_{23}}, $$

(1)

where $r_{23} = \vert X \vert$, $0\leq \mu < \frac{1}{2}$.

Definition

$P_{3}$ is ballistically captured by $P_{2}$ at time $t = t_{1}$ if

$$ E_{2} \bigl( \varphi ( t_{1} ) \bigr) \leq 0 $$

for a solution $\varphi ( t ) = ( X ( t ), \dot{X} (t) )$ of the elliptic restricted problem relative to $P_{2}$, $r_{23} ( \varphi (t) ) >0$.

In particular, we consider the planar circular restricted problem and determine the set $\overline{J}^{-1} ( C )$ where $\tilde{E}_{2} ( x, \dot{x} ) \leq 0$ and ${x}=( x_{1}, x_{2} )$ are barycentric rotating coordinates. In addition, those points are considered where $\dot{r}_{23} =0$, i.e., local periapsis or apoapsis points. Set

$$ \varSigma = \{ x, \dot{x} \mid \tilde{E}_{2} \leq 0 \},\quad \quad \sigma = \{ x, \dot{x} \mid \dot{r}_{23} =0 \}. $$

Then

$$ W= \overline{J}^{-1} ( C ) \cap \varSigma \cap \sigma $$

(2)

defines a special set where ballistic capture occurs in the restricted problem. $W$ is called the weak stability boundary. The motion of $P_{3}$ near $W$ is sensitive.

Here we are interested to find the trajectories that attain ballistic capture. The trajectory starts close to the primary $P_{1}$ and goes to a point in $W$ near $P_{2}$. This type of trajectory is called a ballistic capture transfer and it has the property that it arrives at a periapsis point near $P_{2}$ with substantially lower Kepler energy $E_{2}$ than the classical Homann transfer trajectories.

Let $\varphi (t)$ be a smooth solution to the elliptic restricted problem for $t_{1}\leq t \leq t_{2}$; $t_{2}$ is finite.

Definition

If $E_{2} ( \varphi ( t_{2} ) ) \leq 0$ then $\varphi (t)$ is called a ballistic capture transfer from $t = t_{1}$ to $t = t_{2}$, relative to $P_{2}$.

Definition

If $E_{2} ( \varphi ( t_{1} ) ) \leq 0$ and $E_{2} ( \varphi ( t_{2} ) ) >0$ then $\varphi (t)$ is called a ballistic ejection transfer from $t = t_{1}$ to $t = t_{2}$, which defines ballistic ejection (or escape) from $P_{2}$.

Definition

Let $\varphi (t)$ be a ballistic capture transfer from $t=t_{1}$ to $t=t_{2}$. If $E_{2} ( \varphi ( t ) ) \leq 0$ for $t_{2}\leq t \leq t_{3}$, $t_{2}< t_{3} < \infty$, and $E_{2} ( \varphi ( t ) ) >0$ for $t = t_{3}$, then $\varphi (t)$ has temporary ballistic capture for $t_{2}\leq t \leq t_{3}$. If $t_{3} = \infty$, then $\varphi (t)$ has permanent ballistic capture for $t_{2}\leq t < \infty$.

Hohmann transfer is referred to as high energy since the hyperbolic excess velocity $V_{\infty }$ ($=V_{{M}}\mbox{--}V_{{F}}$, where $V_{{M}}$ is the magnitude of the velocity of Moon about Earth and $V_{{F}}$ is the magnitude of velocity of $P_{3}$ on the transfer trajectory at lunar periapsis. Also, $E_{2} = (1/2) V_{\infty } ^{2}$) is significantly high, and a ballistic capture transfer is said to be of low energy, since the $V_{\infty }$ is eliminated. This is the fundamental difference between these two types of transfers.

2.2.2 Numerical algorithmic definition of WSB is given by Belbruno (2004)

The numerical algorithmic definition of WSB by Belbruno (2004) is given by considering a radial line $l$ from $P_{2}$ in a $P_{2}$-centred rotating coordinate system $X_{1}$, $X_{2}$. We follow trajectories $\varphi (t)$ of $P_{3}$ starting on $l$, which satisfy the following requirements.

• The initial velocity vector of the trajectory for $P_{3}$ is normal to the line $l$, pointing in the direct (posigrade) or retrograde directions.

• The initial two-body Kepler energy $E_{2}$ of $P_{3}$ with respect to $P_{2}$ is negative or 0.

• The eccentricity $e_{2} \in [0,1]$ of the initial two-body Keplerian motion is fixed along $l$. The initial velocity magnitude $V_{2} = ( \dot{X}_{1}^{2} + \dot{X}_{2}^{2} )^{\frac{1}{2}} = ( {\mu (1+ e_{2} )} / {r_{23}} ) ^{\frac{1}{2}}$, $0<\mu \leq \frac{1}{2}$. It varies along $l$.

Let us assume that $P_{3}$ starts its motion at the periapsis of an osculating ellipse. Hence,

$$ E_{2} = \frac{\mu }{2} \biggl( \frac{e_{2} -1}{r_{23}} \biggr) \leq 0. $$

The motion of $P_{3}$ is stable about $P_{2}$ if

• (i) after leaving $l$ it makes a full cycle about $P_{2}$ without going around $P_{1}$ and returns to a point $b \in l$, where $E_{2}\leq 0$.

The motion of $P_{3}$ is unstable if either

• (ii) it performs a full cycle about $P_{2}$ without going about $P_{1}$ ($\theta _{1} \neq 0$, where $\theta _{1}$ is the polar angle with respect to $P_{1}$) and returns to a point $b \in l$, where $E_{2} > 0$; or

• (iii) $P_{3}$ moves away from $P_{2}$ towards $P_{1}$ and makes a cycle about $P_{1}$ achieving $\theta _{1} =0$, or $P_{3}$ collides with $P_{1}$. It is assumed that for $t > t_{0}$, once $P_{3}$ leaves $l$, where $\theta _{2} = \theta _{2}(t_{0}) \in [0, 2\pi )$, $P_{3}$ needs only cycle about $P_{2}$ until $\theta _{2}(t) = 2\pi$.

It is noted that (i) corresponds to ballistic capture at $b$ with respect to $P_{2}$ and the orbit from $a$ to $b$ is a ballistic capture transfer which is bounded. (ii) corresponds to ballistic escape from $P_{2}$ and (iii) represents a different type of escape, called primary interchange escape.

As the initial conditions vary along $l$ satisfying (i), (ii), (iii), it is numerically found that there is a finite distance $r^{*}$ on $l$ from $P_{2}$ satisfying the following statements:

• If $r_{2}< r^{*}$, the motion is stable.

• If $r_{2}>r^{*}$, the motion is unstable.

$r^{*}$ depends on only two parameters: the polar angle $\theta _{2}$ which $l$ makes with the $x_{1}$-axis and the eccentricity $e_{2}$ of the osculating Keplerian ellipse at the point $a$ at $t=t_{0}$. $r_{2}$ is a well-defined function of $\theta _{2}$, $e_{2}$. Define

$$ W= \bigl\{ r^{*} ( \theta _{2}, e_{2} ) \in \boldsymbol{R}^{\boldsymbol{1}} \mid \theta _{2} \in [ 0,2\pi ], e_{2} \in [0,1] \bigr\} . $$

(3)

$W$ is a two-dimensional stability transition region of position and velocity space, which we call the weak stability boundary. $W$ has two components, one corresponds to retrograde motion about $P_{2}$ and the other to direct motion about $P_{2}$ after propagation from $l$.

The motion of spacecraft is stable/unstable accordingly as it can or cannot perform a full cycle about the smaller primary $P_{2}$ without going around the more massive primary $P_{1}$. In the algorithm stated above, only one orbit around Moon is considered before the spacecraft $P_{3}$ reaches the WSB. García and Gómez (2007) claimed that the geometry of WSB is much more complicated than that defined by Belbruno (2004). Instead of one cycle, García and Gómez (2007) generalised this region by considering the capture of $P_{3}$ by the Moon after it has performed $n$ cycles around it. Hence they defined the $n$th weak stability boundary. They defined the generalised WSB as the union of these sets for $n=1,2,3,\dots$ . They gave a rough estimate of the stable/unstable regions around Moon. They computed the stable and unstable manifolds associated to orbits around the collinear Lagrangian points and established a connection between these manifolds and the stable/unstable regions.

2.2.3 Definition of WSB given by García and Gómez (2007)

In the algorithmic definition given by Belbruno (2004), García and Gómez (2007) pointed out that the requirements on the initial conditions fix the modulus of the velocity and its direction, but not the sense. So, for a fixed position on $l(\theta )$, there are two different initial velocities, fulfilling the four restrictions, which can produce orbits with different stability behaviour. Also, they pointed out that along $l(\theta )$ there are several transitions from stability to instability. The set of stable points resembles a Cantor set. Also some maximum time interval must be fixed for the numerical integration.

García and Gómez (2007) gave the initial conditions along radial segment $l(\theta )$ that must be integrated to determine the stable/unstable regions around $P_{2}$.

Initial conditions with positive velocity (osculating retrograde motions around $P_{2}$):

$$\begin{aligned}& \begin{aligned} &x=-1+\mu + r_{2} \cos \theta , \quad \quad y= r_{2} \sin \theta , \\ & \dot{x} = r_{2} \sin \theta -v\sin\theta , \quad \quad \dot{y} =- r_{2} \cos \theta +v\cos\theta . \end{aligned} \end{aligned}$$

(4)

Initial conditions with negative velocity (osculating direct motions about $P_{2}$):

$$\begin{aligned}& \begin{aligned} &x=-1+\mu + r_{2} \cos \theta ,\quad \quad y= r_{2} \sin \theta ,\\ & \dot{x} = r_{2} \sin \theta +v\sin\theta ,\quad \quad \dot{y} =- r_{2} \cos \theta -v\cos\theta , \end{aligned} \end{aligned}$$

(5)

where $v$ is the modulus of the initial sidereal velocity of $P_{3}$ given by

$$ v^{2} =\mu \biggl( \frac{2}{r_{2}} - \frac{1}{a} \biggr) = \frac{ \mu (1+e)}{r_{2}}. $$

(6)

For fixed value of the eccentricity $e$ and the angle $\theta$, all the possible values of the distance $r^{*}$ along $l$ are searched for which there is a change of the stability property of the orbit. For a finite number of points (up to a certain precision) $r_{1}^{*} = 0, r_{2}^{*},\dots , r_{2n}^{*}$ such that $r_{2} \in [r_{1}^{{*}}, r_{2}^{{*}} ] \cup [{r_{3}}^{{*}} , r_{4} ^{{*}} ] \cup \cdots \cup [ r_{2n-1}^{{*}}, r_{2n}^{{*}} ]$; then motion is stable, and otherwise unstable. The number of points $r_{{i}}^{*}$ and their values depend on $e$, $\theta$ and the precision of the computation. Thus, WSB is defined as

$$\begin{aligned} \overline{W} = &\bigl\{ \bigl[ r_{2k-1}^{*} ( \theta ,e ), r_{2k}^{*} ( \theta ,e ) \bigr],\ k=1,\dots ,n;\theta \in [ 0,2 \pi ], \\ &\phantom{\bigl\{ }\ e\in [0,1) \bigr\} . \end{aligned}$$

(7)

Topputo and Belbruno (2009) found that the variability of mass ratio of the primaries has an important effect in changing the structure of weakly stable sets. Sousa Silva and Terra (2012a, 2012b) demonstrated the selection of suitable stable subsets which can to feasible ballistic capture.

2.3 WSB transfers

Belbruno (1987) discovered this new type of WSB transfer from Earth to the Moon using ballistic lunar capture (i.e., no $\Delta V_{\mathit{LOI}}$), which was demonstrated by Japanese spacecraft Hiten in 1991. When a spacecraft undergoes ballistic capture at Moon, it goes into an unstable orbit around Moon automatically without any $\Delta V$ to slow it down near Moon. The spacecraft remains in this orbit for finite time and then escapes. In this weak capture state it is in the transitional boundary between capture and escape. This orbit can be stabilised by imparting a small impulse $\Delta V$. The mechanism of such capture was studied by Belbruno (2004). He has mapped out the region in the phase space (position-velocity space) where weak capture can occur about the Moon. He called this region WSB. The initial orbit conditions depend on the location of the Sun relative to the Earth and the Moon (Miller 2003). Belbruno (1990) used numerical simulations to demonstrate that the spacecraft undergoes resonance transition via weak capture. They have used the Poincaré surface of section to visualise WSB regions. Belbruno and Marsden (1997) have showed that resonance hopping in comets occur when comets fly by Jupiter in the WSB region. Topputo et al. (2008) illustrated that the resonance transition mechanism is related to weak capture. They numerically demonstrated that the orbits that undergo resonance transition pass through the WSB regions. They incorporate solar perturbation to study ballistic escape. Belbruno et al. (2008) used special normalised resonance Poincaré surfaces to visualise WSB and its role in resonance transitions (Fig. 9). They used a correlation dimension to analyse different kinds of orbits and found that orbits close to resonance exhibit mixed regular-chaotic behaviour.

Fig. 9

Visualisation of ‘classic’ WSB (black bold line) and the extended WSB, B (grey area) on S. (a) $C = C_{2}-0.01$, (b) $C = C(0)$, (c) $C = C(0.1)$, (d) $C = C(0.2)$, (e) $C = C(0.3)$, (f) $C = C(0.4)$, (g) $C = C(0.5)$, (h) $C = 2.9368$, (i) $C = C^{*}+0.01$ (from Belbruno et al. 2008)

2.4 Low-energy trajectory design

The research done in the area of WSB transfers can be classified into three parts; namely, manifold theory, optimisation methods used and mission design.

2.4.1 Design of WSB transfers to the Moon using back-propagation

Belbruno and Miller (1993) have shown the existence of WSB numerically. They compared WSB transfers with Hohmann, biparabolic and bielliptic transfers. They have shown that WSB transfers require 18%, 14% and 37% smaller $\Delta V$ than Hohmann, biparabolic and bielliptic transfers, respectively (Table 1).

Table 1 Comparison between the low-energy, low-thrust (LELT) solutions designed and a set of impulsive reference solutions found in literature (from Mingotti et al. 2009)

They developed the trajectory in the three-dimensional four-body problem consisting of the point mass (spacecraft) $m$, Sun, Earth and Moon. The equations of motion are given by

$$ m_{k} \ddot{x}_{k} = \sum_{ {\scriptstyle i=1\atop\scriptstyle i\neq k} }^{4} G m_{i} m_{k} \vert x_{i} - x_{k} \vert ^{-3} ( \overline{x}_{i} - \overline{x}_{k} ). $$

(8)

Here, $x_{k} =( x_{k1}, x_{k2}, x_{k3} )\in \mathcal{R}^{3}$ is the position in inertial coordinates ($x,y,z$) of the point mass $m$. The initial values $x_{k} ( 0 )$, $\dot{x}_{k} (0)$ for $k = 2,3,4$ for the Sun, Earth and Moon, respectively, are given for an epoch from $t=0$. The coordinates of the solution of Eq. (8) with respect to Earth, called $\overline{x}_{k}$, are defined by the transformation $\overline{x}_{k} = x_{k} - x_{3}$, where $E$ is the origin ($\overline{x}_{3} =0$). This is a non-inertial coordinate system $( \overline{x}, \overline{y}, \overline{z} )$ where the differential equations for $\overline{x}_{k}$, $k=1,2,4$ are

$$\begin{aligned} m_{k} \ddot{\overline{x}}_{k} =& \sum _{ {\scriptstyle i=1\atop\scriptstyle i\neq k} }^{4} G m_{i} m_{k} \vert \overline{x}_{i} - \overline{x}_{k} \vert ^{-3} ( \overline{x}_{i} - \overline{x}_{k} ) \\ &{}- \sum _{ {\scriptstyle i=1\atop\scriptstyle i\neq 3} }^{4} G m_{i} m_{3} \vert \overline{x}_{i} \vert ^{-3} \overline{x}_{i}. \end{aligned}$$

(9)

Their method for calculation of WSB transfer to the Moon consists of the following steps:

• 1. Assume that the position of spacecraft, $m$, with respect to the Moon, $M$, at time $t=t _{F}$ of capture is given at some altitude $h>0$ above the lunar surface. Suppose that the lunar approach direction is given. Let the radial distance of $m$ from $M$ is the stability breakdown distance with respect to $M$, so that $m$ is in the WSB region of Moon. The value of the eccentricity, $e$, is determined from the definition of WSB in (3). Let $\varPhi ( t ) =[ x_{1} ( t ), \dot{x}_{1} (t)]$ be the solution of the equation of motion (9). Increase $e$ to $e+\delta$ and integrate $\varPhi ( t )$ backward in time from the capture state $\varPhi _{C}$ at $t=t _{F}$ to $\hat{\varPhi } = \varPhi _{3} ( T )$ for $T< t _{F}$, which is near the WSB of Earth.

• 2. Let $\varPhi _{E}$ be the initial state of $m$ relative to Earth. Vary the initial velocity $\dot{x} ( t_{0} )$ of $\varPhi _{E}$ so that $m$ leaves Earth and goes to the initial position $\hat{x} \in \mathcal{R}^{3}$ of $\hat{\varPhi }$ at $t=T$ and achieves energy augmentation by lunar gravity assist.

• 3. In general, the initial velocity of the capture trajectory from $\hat{\varPhi }$ to $\varPhi _{C}$ will not be equal to the final velocity of the trajectory arc from $\varPhi _{E}$ to $\hat{\varPhi }$. Let $\Delta V$ be the difference of the two velocities. $\Delta V$ is minimised by varying $t_{0}$, $t _{F}$ and $\delta$.

• 4. The trajectory thus obtained by joining the two trajectory segments is the WSB transfer from $E$ to $M$. A differential correction is used for targeting and the equations of motion are solved using fourth-order Runge–Kutta numerical integration.

• 5. The solution thus obtained is used as an initial guess for a more realistic model.

The WSB theory is used for the trajectory design of Hiten (Belbruno and Miller 1993; Uesugi 1996) and Lunar GAS (Belbruno 1987), the Lunar Observer Mission (Belbruno and Miller 1993), the Blue Moon Mission (Belbruno et al. 1997), SMART-1 (Schoenmaekers et al. 2001), ARTEMIS (Folta et al. 2011) and GRAIL (Chung et al. 2010). Belbruno (2005) gives the concept for the design of a low-energy lunar transportation system for servicing lunar base. The system consists of a Crew Exploration Vehicle and a robotic Tanker Craft. The latter uses WSB transfer to reach Moon and supply necessary fuel to the Crew Vehicle.

Miller and Belbruno (1991) gives the methodology for the design of a WSB trajectory, the so-called Belbruno–Miller (B–M) trajectory, that receives gravity assist from Moon on its way to the Sun–Earth Lagrange point about 1.5 million km from Earth. In that region, the gravitational accelerations of the Earth–Moon system and the Sun tend to balance when combined with the inertial acceleration of spacecraft. A small manoeuvre in this region returns the spacecraft for ballistic capture by the Moon. Krish (1991) has carried out an injection period analysis for a particular B-M trajectory. It is found that the injection period can be increased to 4 and 11 days, respectively, with a maximum allowable $\Delta V$ of 100 m/s and 150 m/s. The results showed that a nominal B-M trajectory can save 150 m/s over the Hohmann transfer.

Yamakawa (1992) and Yamakawa et al. (1992, 1993) have provided a systematic method of construction and a wide variety of examples of ballistic lunar capture trajectories. They classify these trajectories into two categories, namely: (1) an Earth side approach to the Moon through a geocentric orbit with initially small semi-major axis and (2) an anti-Earth side approach through a geocentric orbit of the large semi-major axis. They have identified perilune conditions which take advantage of solar gravity to reduce C3 with respect to the Moon at perilune. They investigated the influence of solar gravity on the geocentric orbit from an angular momentum point of view and showed that the spacecraft location in the second or fourth quadrant in a Sun–Earth fixed frame increases the local perigee distance. They also found that the total flight time of Earth–Moon transfer can be reduced by the use of lunar swing-by, as it reduces the local eccentricity and hence raises the initial perigee of the geocentric orbit. Using the above information they give a systematic method of orbit design which makes use of gravitational capture by the Moon and solar gravity to raise the perigee of the initial EPO.

Capuzzo-Dolcetta and Giancotti (2013) have shown in Fig. 10, the gravity gradient of the Sun in Earth’s surroundings and its effect on orbits around the Earth. When the orbit is oriented within the second or fourth quadrant in a Sun–Earth rotating frame, Sun’s gravity aids the orbit by raising the spacecraft’s energy, especially when it is close to its apogee. This phenomenon is used in the design of outer WSB trajectories (the initial EPO has an apogee beyond the Moon’s orbit). In this case, the spacecraft approaches Moon with a lower relative velocity, compared to Hohmann transfer, possibly resulting in a ballistic capture. Let $\Delta v_{1}$ be the impulse from EPO to begin the transfer and $\Delta v_{2}$ be the impulse to put the spacecraft into a stable orbit around the Moon. Ballistic capture results in a reduction in $\Delta v_{2}$ by up to 44%. The inner resonance or cislunar transfers take advantage of unstable dynamics near the Earth–Moon libration point $L_{1}$ to increase the apogee to the Earth–Moon distance. The inner transfers consist of $\Delta v_{1}<3.1~\mbox{km/s}$ ($\Delta v_{1} ^{{h}}$ is the value of the mean Hohmann transfer), while the outer transfers require $\Delta v_{1}>3.140~\mbox{km/s}$. Figure 11 shows the position of optimal points (in red) falling within the second and fourth quadrants in a Sun–Earth rotating frame. Of all the transfers with $\Delta v_{2}< 1.0~\mbox{km/s}$, 93% have the apogee angle $\alpha$ in the second or fourth quadrant. Figure 12 shows the relation between $\Delta v_{1}$ and $\Delta v_{2}$ for a collection of orbits produced for different simulation modes. Points in the vicinity of [3.1 km/s, 1.093 km/s] represent an average Hohmann transfer. The Pareto fronts are the points highlighted in red colour. Pareto sets are distributed into three different areas, namely, inner transfers, Hohmann transfer and outer transfers (Capuzzo-Dolcetta and Giancotti 2013).

Fig. 10

The angle $\alpha$ and the shape of Sun’s gravity gradient in Earth’s surroundings. (a) When $\alpha$ is in an even quadrant, perigee of initial osculating Kepler orbit (dashed grey line) raises. (b) When $\alpha$ is in an odd quadrant, the length of the semi-major axis is reduced, leading to lower perigee (from Capuzzo-Dolcetta and Giancotti 2013)

Fig. 11

Position of points of the Paerto front (red dots) in whole distribution by date of the orbits. First and third quadrants are shown on a darker background (from Capuzzo-Dolcetta and Giancotti 2013)

Fig. 12

The Pareto front (dots joined by red line) in $\Delta v_{1}\mbox{--}\Delta v_{2}$ plane. The points occupy three distinct areas, highlighted by circles, corresponding to inner, Hohmann and outer transfers, respectively, from left to right (from Capuzzo-Dolcetta and Giancotti 2013)

Dutt et al. (2016) have represented the capture trajectories, obtained by back-propagation of highly elliptical lunar orbits, on the phase space with colour code on time of capture, as shown in Fig. 13. So looking at the phase space diagrams short flight duration trajectories can be differentiated from longer flight duration trajectories. Also the distribution of trajectories with different capture durations in the phase space can be clearly visualised. Similarly, highly eccentric geocentric orbits for which the perigee increases from LEO to Earth–Moon distance are also represented on the phase space with colour code on time of one revolution. Once the geocentric orbit and lunar capture orbits are identified the two are patched using the Fixed Time of Arrival method and optimal patching points are found using a Genetic Algorithm to obtain a WSB transfer trajectory from Earth to the Moon.

Fig. 13

Lunar capture trajectories obtained by back-propagation for 50 days. The initial conditions which lead to a capture trajectory are plotted in the phase space with colour code on time of capture. Left: Direct motion about $m_{2}$, right: retrograde motion about $m_{2}$ (from Dutt et al. 2016)

Graziani et al. (2000) have developed a numerical algorithm using back-propagation to find WSB trajectories to the Moon in four-body problem using real ephemerides. First they found two angles, namely $\alpha$ and $\beta$. $\alpha$ is the angle between Earth to apogee line and the Earth–Sun line. $\alpha$ must lie on the II or IV quadrant with respect to the Earth–Sun direction. $\beta$ is the ecliptic projection of angle between the Earth–Sun and Earth–Moon lines at Moon arrival. There are two allowed regions of $\beta$ split by an angle of amplitude $\pi$, known as the “$\pi$-symmetry”. They also found that most of the transfers tend to remain on the ecliptic plane. They were able to find a number of WSB transfers to the Moon. Working along similar lines, Mora et al. (2003) have studied inner and outer WSB transfers using backward propagation for the LUNARSAT Mission.

Ivashkin (2002, 2004) developed a method to construct transfers between Earth and Moon using the Sun’s gravitational influence. Bollt and Meiss (1995) construct a ballistic capture trajectory using four small manoeuvres which requires less energy when compared to the conventional direct transfer. Schroer and Ott (1997) reduced the time of such transfers from 2.05 years to 0.8 years, by targeting specific three-body orbits near the Earth. The total cost remained approximately the same. Belbruno (2007) has shown the existence of very low-energy orbits around Moon, which can orbit Moon for extended periods and change their inclination using 12 times smaller $\Delta V$ than conventional method.

Circi and Teofilatto (2001) determine the spacecraft-Earth–Moon–Sun configuration that enable WSB transfers and demonstrate the role of the Sun in increasing the spacecraft perigee and allowing lunar capture. It is demonstrated that the Sun provides the spacecraft with minimum energy necessary to reach the Moon. The conditions generating WSB transfer in ‘quasi-ballistic capture’ is estimated by an analytical method. The generalisations of the Tisserand–Laplace definition of the sphere of influence into exterior and interior spheres of influence is accounted for in the study of capture dynamics using analytical and numerical methods. Griesemer et al. (2011) have developed an algorithm for targeting ballistic lunar capture transfer. The algorithm uses a particular member of a family of periodic orbits, documented by Markellos (1974) as family $f16$, as an initial guess for an Earth–Moon transfer.

Parker (2010) investigates annual and monthly variations in low-energy ballistic transfers from Earth to Lunar Halo Orbits. Variations are attributed to Earth’s and Moon’s non-circular and non-coplanar orbits. They have found that some families of transfers exist only in certain months of a year due to their sensitivity to the geometric shifts. Anderson and Parker (2011) have studied lunar landing trajectories at different elevation angles using invariant manifolds both in planar and 3D R3BP. Topputo (2013) has surveyed all the families of two-impulse Earth to the Moon transfers in the framework of the restricted four-body problem. These transfers include Hohmann, Sweetser’s theoretical minimum, and those investigated by Yamakawa, Belbruno, Yagasaki, Pernicka, Mingotti etc. Parker and Anderson (2013) have surveyed two-burn transfers to 100 km polar orbit around Moon. These transfers include 3–6 days direct transfer, transfers including Earth phasing orbits and/or lunar flyby and 3–4 month low-energy transfers.

2.4.2 Design of WSB transfers to the Moon using forward targeting method

Belbruno et al. (1997) discovered a forward search algorithm to generate WSB transfers from Earth to the Moon. Belbruno and Carrico (2000) presented a modified form of that algorithm using the software package STK/Astrogator. Their algorithm is as follows:

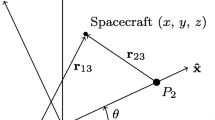
• 1. Consider a point $\mathbf{x}$ with respect to Earth with radial distance $r _{E}$. The spherical coordinates at point $x$ are the radial distance $r _{E}$, the longitude ($\alpha _{E}$), the latitude ($\delta _{E}$), the velocity magnitude ($V _{E}$), the flight path angle ($\gamma _{E}$), and the flight path azimuth, i.e. the angle in local plane from the projection of the positive z-axis to the velocity vector ($\sigma _{E}$). Let $r _{M}$ and $i _{M}$ be the desired radial distance and inclination, respectively, with respect to the Moon. The algorithm varies $V _{E}$ and $\gamma _{E}$ to target $r _{M}$ and $i _{M}$.

• 2. The initial value of $V _{E}$ is chosen so that the spacecraft is in orbit around Earth with an apoapsis of 1.5 million km. The initial value of $\gamma _{E}$ is chosen near zero. These transfers are possible every month. Once the desired month of launch is decided, the day of month for launch is decided such that a specific Sun–Earth–Moon geometry is obtained. Let $\lambda$ be the Sun–Earth–Moon angle, in the Sun–Earth rotating coordinate system. The Earth is in the centre and the Sun–Earth line defines the x-axis. For the second and fourth quadrant transfers, the Sun helps to increase the local periapsis distance. A first guess of the angle between the Sun–Earth line and the trajectory at launch, $\alpha$, is important so that the trajectory will encounter the Moon with proper arrival conditions. The orientation of the line of apsides in the Sun–Earth rotating coordinate system is also an important parameter to be monitored and controlled. The time of launch establishes the Right Ascension of the Ascending Node (RAAN) and the coast time establishes the argument of perigee (AOP).

• 3. Using a second order Newton differential correction targeting algorithm the trajectory usually converges in six iterations.

Ockels and Biesbroek (1999) and Biesbroek et al. (1999) gave a method to find WSB trajectories to the Moon from a geostationary transfer orbit (GTO) for LunarSat Mission. More details are provided in Sect. 2.4. Dutt et al. (2018a) gave a method using forward propagation to find WSB transfer to the Moon. They considered it as an optimisation problem with two loops. The outer loop varies the parameters related to departure from an EPO, while the inner loop varies the small impulse given at WSB of Earth to obtain a capture trajectory at Moon. After attaining a capture orbit at Moon, they wait for the orbit to attain minimum eccentricity for circularisation.

2.4.3 Low-energy transfers to Halo orbits and distant planets

Solar libration points are good locations for space-based observations. There have been several missions to Lagrange points and halo orbits, like International Sun/Earth Explorer 3 (ISEE-3) in 1978, Global Geospace Science (GGS) WIND in 1994, the Solar and Heliospheric Observatory (SOHO) in 1996, the Advanced Composition Explorer (ACE) in 1997 and Genesis in 2001. Earth–Moon libration regions are also interesting locations for space exploration missions for instance, for servicing facilities and launch to outer planets. Farquhar (1968) first proposed the use of halo orbit about the Earth–Moon $L_{2}$ as a communication relay station for an Apollo mission to the far side of the Moon. He used analytical expressions to represent the halo orbits. On the other hand Howell (1984) computed them numerically. Gómez et al. (1992) give a method for construction of trajectory from vicinity of Earth to a halo orbit around the Earth–Sun $L_{1}$ point in the real solar system. They used the simplified models, namely, the R3BP and bicircular problem to understand the geometrical aspects of the problem. They used the hyperbolic character of halo orbits to transfer the spacecraft into a halo orbit using just one manoeuvre. Howell et al. (1994) studied the construction of trajectories from low EPO to halo orbits in the Sun–Earth three-body problem. A number of works have been carried out in this direction; for instance by Starchville and Melton (1997, 1998), Sukhanov and Eismont (2003), Senent et al. (2005), Mingotti et al. (2007), Demeyer and Gurfil (2007), Liu et al. (2007), Cabette and Prado (2008), Canalias and Masdemont (2008), Alessi et al. (2010), and Li and Zheng (2010). Mingotti et al. (2012) demonstrated the construction of transfer trajectory to distant periodic orbits in the Earth–Moon system. They exploited the invariant manifolds of distant periodic orbits for the construction of interior and exterior low-energy transfers.

Strizzi et al. (2001) simulated and analysed Earth to Mars transfers using the Lissajous orbit. They demonstrated that a braking manoeuvre at low altitude Mars periapsis prior to LOI can significantly save fuel. They have used a loose control technique for station keeping. Castillo et al. (2003) have described a numerical method to find WSB transfers to inner planets and outer planets. For inner planets, i.e., Mercury, Venus and Mars trajectory design is discussed for the BepiColombo, Venus Express and Mars Express missions, respectively. They claimed that WSB transfers to inner planets do not decrease the total $\Delta V$ required for the capture but provides greater flexibility when selecting the geometry of the target orbit. They show that for outer planets, when natural moons are available, GA combined with WSB can be used. The combination of both methods provides opportunity to explore the giant planets (e.g. Jupiter and Saturn) and their moons. Kulkarni and Mortari (2005) demonstrated that Earth to distant planet can be reached using hopping between halo orbits and it could save 35% fuel over gravity assist. Nakamiya et al. (2008) described the use of halo/Lyapunov periodic orbits to reduce propellant requirements to reach distant planet. Nakamiya et al. (2010) analysed escape and capture trajectories to and from halo orbits and applied it to the design of Earth–Mars round-trip transportation system. They observed that the $\Delta V$ required for round-trip transfer between low-Earth orbit and low-Mars orbit via spaceports on Earth and Mars Halo orbits is slightly larger than that of direct round-trip transfer. But evaluation in terms of required spacecraft wet mass (propellant) for Earth–Mars transportation system revealed that spacecraft wet mass can be reduced by one-half compared with direct transfer if the propellant for return is left at the spaceports at Earth and Mars halo orbits on the way to low Mars orbit. Such an option to use stored fuel at spaceports is not available during direct round-trip transfers. Topputo and Belbruno (2009) have computed and visualised the WSB regions for the Sun–Jupiter system.

Topputo and Belbruno (2015) gave a new concept for the design of trajectory to Mars with ballistic capture. They targeted a distant point (few million km from Mars) where a manoeuvre is carried out and the trajectory finally leads to a capture orbit at Mars. They claim that 25% $\Delta V_{\mathit{MOI}}$ can be saved with penalty on flight duration which can be 1.5 to 2 years to be compared with conventional direct transfer. The algorithm to compute WSB transfer trajectory to Mars from Topputo and Belbruno (2015) is given below. A point $\mathbf{x} _{ \mathbf{c}}$ is selected near Mars orbit, several million kilometres from Mars as the target point, where a manoeuvre $\Delta V_{ {C}}$ is applied, which leads to a ballistic capture at Mars (Fig. 14). It takes several months to travel from point $x_{ {c}}$ to ballistic capture near Mars with a periapsis distance, $r _{p}$. At the periapsis $r _{p}$ the osculating eccentricity of the spacecraft, $e$, with respect to Mars is less than 1.

Fig. 14

Structure of the ballistic capture transfers to Mars (from Topputo and Belbruno 2015)

The steps involved are as follows:

• 1. For a given periapsis distance $r _{p}$, compute a ballistic capture trajectory to Mars starting from a point $\mathbf{x} _{ \mathbf{c}}$ near Mars orbit. It takes several months to travel from $\mathbf{x} _{\mathbf{c}}$ to ballistic capture near Mars at $r _{p}$. When the spacecraft arrives at $r _{p}$, its osculating eccentricity $e$ with respect to Mars is less than 1. The simulations in this step are carried out in planar elliptic R3BP.

• 2. Design an interplanetary trajectory which starts from the sphere of influence (SOI) of Earth and reaches the point $\mathbf{x} _{\mathbf{c}}$. $\Delta V_{1}$ is applied at SOI of Earth to reach the point $\mathbf{x} _{\mathbf{c}}$ near Mars, and $\Delta V _{C}$ is applied at the point $\mathbf{x} _{\mathbf{c}}$ to match the velocity of the ballistic capture transfer to Mars. An optimisation algorithm is used to minimise $\Delta V _{C}$ by adjusting the location of $\mathbf{x} _{\mathbf{c}}$. The transfer trajectory is viewed as a two-body problem between the spacecraft and the Sun.

• 3. The trajectory thus obtained from SOI of Earth to point $\mathbf{x} _{\mathbf{c}}$ (step 2), together with ballistic capture transfer from $\mathbf{x} _{\mathbf{c}}$ to $r _{p}$ (step 1), where the osculating eccentricity $e<1$, is the desired ballistic capture transfer from Earth to Mars. This is compared with the standard Hohmann transfer starting from SOI of Earth to the periapsis distance $r _{p}$ at Mars with the same eccentricity $e$, where $\Delta V_{2}$ is MOI manoeuvre applied to achieve an orbit around Mars.

Topputo and Belbruno (2015) found that for $r _{p}>22000~\mbox{km}$, $\Delta V _{C}< \Delta V_{2}$ can be achieved. According to them, the reasons for selecting $\mathbf{x} _{\mathbf{c}}$ far away from Mars, are the following:

• 1. If $\mathbf{x} _{\mathbf{c}}$ is sufficiently far from Mars SOI, then the gravitational attraction of Mars on the spacecraft will be negligible. Thus, a more constant arrival velocity from Earth can be obtained.

• 2. Infinitely many possibilities for the location of $\mathbf{x} _{\mathbf{c}}$ gives flexibility of the launch period from Earth.

• 3. Since $\mathbf{x} _{\mathbf{c}}$ is outside the SOI of Mars, $\Delta V _{C}$ can be applied gradually, which is safer from an operational point of view, opposed to a high velocity capture manoeuvre at $r _{p}$ in the case of a Hohmann transfer.

Dutt et al. (2018b) developed a forward propagation algorithm to generate transfer trajectories to Mars with ballistic capture. Their algorithm is a two-step optimisation process. The outer loop varies the control parameters at EPO on the way to Mars to attain different arrival conditions at $\mathbf{x} _{\mathbf{c}}$, while the inner loop varies the three components of the impulse $\Delta V _{C}$ to obtain the capture orbit at Mars. They conclude that the capture orbits at Mars are high-altitude orbits (with semi-major axis of the order of $4\mbox{--}40 \times 10^{8}~\mbox{km}$), which are not a good choice for the majority of science payloads for interplanetary missions. For lower mapping orbits at Mars, a conventional Hohmann transfer trajectory remains the best choice in terms of $\Delta V$ and flight duration, provided the launch is during the launch opportunity.

It remains to be explored whether few gravity assists on the way to Mars or aerobraking at Mars can lead to smaller $\Delta V$ values than those reported by previous work. The resulting trajectory could be a combination of gravity assist and/or aerobraking and ballistic capture. The analysis of the capture corridor at Mars to ensure that the trajectory gets captured at Mars within some tolerance levels for navigational uncertainties will ensure complete mission design. Classification of capture orbits at Mars is also an area to be explored. The above directions hold good for other destination planets as well.

2.5 Invariant manifold theory

Koon et al. (2006) describe the theory of Lagrange point dynamics of the three-body system, the use of stable and unstable manifold tubes to transport to and from the capture region and their application in mission design. The asymptotic orbits are parts of the stable and unstable cylindrical manifolds winding around a Lyapunov orbit and they separate two types of motion namely, transit and non-transit orbits. These tube shaped manifolds facilitate transportation between regions of allowable motion. They describe an algorithm to find a low-energy transfer trajectory with required itinerary. They have suggested the division of the four-body problem into two R3BP for the design of low-energy transfers.

Topputo et al. (2004) have used surface sections to identify the intersections between two manifold tubes from two R3BP. They have assigned a merit function to each intersection and used a systematic search to find optimal starting and arriving trajectories. Once an appropriate first guess is obtained, it is refined using a sequential quadratic programming (SQP) method. This algorithm is used for the design of low-energy interplanetary transfer trajectories.

Villac and Scheeres (2004) have presented a simple corrector algorithm to compute hyperbolic invariant manifolds associated to periodic and quasi-periodic orbits about the libration points $L_{1}$ and $L_{2}$, which are significant for low-energy trajectory design. Gómez and Masdemont (2000) and describe heteroclinc transfer trajectories, to transfer between three-dimensional libration orbits. Parker and Chua (1989); Wiggins (1994) and Gómez et al. (2004) and many more authors describe invariant manifolds which can be used to construct homoclinic and heteroclinic transfer trajectories. Topputo (2016) give a two-step approach for approximating the invariant manifolds in R3BP. This method is helpful for trajectory optimisation problems where a large number of manifold insertion points have to be evaluated.

Gómez et al. (2004) explained geometrically the phenomenon of natural routes among the planets and/or their satellites with the help of invariant manifold structures of the collinear libration points in R3BP. They applied this technique to construct a 3D Petit Grand Tour of the Jovian moon system. This technique has the advantage of more visibility than Voyger-type flybys where the flybys last for only a few seconds. In this technique the spacecraft can be made to orbit about a moon in a temporary capture orbit for a number of revolutions, then it can be made to escape that moon and perform a small manoeuvre to get ballistically captured by a nearby moon for some revolutions. Also the $\Delta V$ in this case is much less than those required for joining two-body motion segments.

Neto and Prado (1998) studied the effect of various parameters like mass ratio, distance between the spacecraft and secondary body at the time of manoeuvre ($r_{{p}}$), the energy C3 of spacecraft at that moment, the direction of velocity at that point and the departure angle ($\alpha$) on the time required for capture. The results show that the time of capture can be reduced without reduction in energy savings by proper selection of initial conditions. Melo et al. (2007) have studied stable and escape-capture trajectories in R3BP (Earth–Moon-Particle) and the four-body (Sun–Earth–Moon-particle) problem. They have mapped out regions in the phase space where these trajectories can be found.

Romagnoli and Circi (2009) studied the geometry and performance of low-energy transfers to the Moon in the framework of three-body and four-body models. They have considered various low-energy transfer orbits by varying the periselenium altitude and eccentricity of the initial osculating orbit of spacecraft. They found that equatorial captures with low pericentre altitude leads to minimum $\Delta V$. Another important observation is that the lunar orbit eccentricity and the presence of Sun does not affect the WSB geometry much, both in the planar and in the 3D case. Castellà and Jorba (2000), Prado (2005), Jorba (2000) used a bicircular problem to study low-energy transfers. Yagasaki (2004a, 2004b) computed optimal low-energy Earth-to-Moon transfers with moderate flight duration by solving a nonlinear boundary value problem in planar circular R3BP. Circi and Teofilatto (2006) presented the design of an economical lunar satellite constellation.

Fantino et al. (2010) considered four combinations of the two collinear libration points namely, $L_{i}^{\mathit{SE}} - L_{j}^{\mathit{EM}}\ (i,j=1,2)$ connections for the determination of low-energy transfers. In the above notation, a subscript denotes the collinear libration point, $L_{1}$ or $L_{2}$ and a superscript denotes the circular R3BP system under consideration, namely, the Sun–Earth (SE) or Earth–Moon (EM) system. They found that $L_{1}^{\mathit{SE}} - L_{2}^{\mathit{EM}}$ and $L_{2}^{\mathit{SE}} - L_{2}^{\mathit{EM}}$ connections can provide low or zero cost transfers. This capability to provide low cost ($\Delta V$ at connection) transfers depends on the energy of libration-point orbits (LPOs) to be connected. The cost is higher for lower energy LPOs. The unstable points of the WSB region effectively confine to the points of invariant manifold trajectories which are characterised by orthogonality between radial and velocity vectors relative to the smaller primary. They also find that the temporary capture is more efficient when the Jacobi constant of the invariant manifold is larger and the size (amplitude) of the progenitor LPO is smaller. Figure 15 gives a global picture regarding temporary capture as a function of energy, over two families of 70 planar Lyapunov orbits each, around $L_{1}$ and $L_{2}$. The two plots give the percentage of trajectories that complete at least five or ten loops around the smaller primary before they escape or the integration ends, respectively.

Fig. 15

Capability of being captured around smaller primary within the unstable invariant manifold of two families of planar Lyapunov orbits around $L_{1}$ (circles) and $L_{2}$ (asterisks), expressed as the percentage of trajectories that perform minimum number of loops (five loops in the left figure and ten loops in the right figure) around smaller primary before the Keplerian energy becomes positive or the integration ends at maximum time limit considered (from Fantino et al. 2010)

Generally, WSB transfers are less expensive than the conventional Hohmann transfer but suffer from long flight durations. In order to reduce the transfer time, it is necessary to hop from one orbit to another using the invariant manifold. There are very many possibilities of switching between orbits to attain the destination. Several researchers have contributed in the use of optimisation methods to find trajectories connecting two or more arcs like Luo et al. (2006, 2007), Yokoyama and Suzuki (2005), Radice and Olmo (2006), Lizia et al. (2005). There are also studies concerning optimisation of transfer trajectories using low-thrust engines and the combination of impulsive and low-thrust engines like Kluever (1997) and Mingotti et al. (2003).

Alessi et al. (2009a) have simulated rescue orbits, trajectories that depart from the surface of Moon and reach a LPO around the $L_{1}$ or $L_{2}$ points of the Earth–Moon system, in the framework of R3BP. They analysed the trajectories that can leave the Moon’s surface that is the accessible regions on the Moon, the velocity and the angle of arrival (angle between the velocity vector and the Moon’s surface normal vector) and the time required for the transfer. They identified regions on the Moon’s surface from which departure is possible and regions where departure is almost orthogonal (departure velocity vector is perpendicular to the Moon’s surface). Longer transfer duration non-direct rescue orbits are available from much larger regions on the Moon than direct rescue orbits. Alessi et al. (2009b), have explored LPO to LEO transfers and found that the minimum cost connection occurs when the LPO around $L_{1}$ increases in size and at maximum distance between Earth and arrival point on the manifold. They refined these trajectories in a realistic model and concluded that the cost of manoeuvres in R3BP does not change much.

2.6 Optimisation for computation of low-energy trajectories

Ockels and Biesbroek (1999), Biesbroek et al. (1999) and Biesbroek and Ancarola (2003) have studied the use of a genetic algorithm to construct WSB trajectories from GTO to the Moon. The parameters chosen to be optimised are the time spent in GTO or the phasing orbit, $\Delta V$ at perigee of GTO, and the magnitude, azimuth and declination of $\Delta V$ at WSB region. The fitness function is negative of the total $\Delta V$. A small population size (10) was sufficient for interplanetary trajectory optimisation problems for example, using multiple swing-by but for WSB higher population size (100) gave better results. GA was able to find WSB transfers to the Moon for each day in a year saving 218–265 m/s $\Delta V$ with respect to the conventional direct transfer.

Moore (2009) utilised invariant manifolds of planar circular R3BP to find an initial guess trajectories from Earth to the Moon which is optimised using the optimal control algorithm DMOC (Discrete Mechanics and Optimal Control) by two different approaches. The first approach is based on patching invariant manifolds of the Sun–Earth and Earth–Moon three-body systems to create a trajectory which is then modified to fit four-body dynamics. The second approach is based on finding out intersections of trajectories that originate at the endpoints on the manifolds near the Earth and Moon. Moore finds that DMOC optimisation trajectories to minimise $\Delta V$ obtained by these two methods generate very different trajectories. Yamakawa (1992) used a modified Newton algorithm with controls on the velocity and the orientation of perigee and perilune, the total time of flight, the Sun phase angle, and the epochs at both ends of intermediate trajectory segments to minimise the total $\Delta V$.

Lantoine et al. (2009) used the multiple shooting technique for the design of missions to inter-moon transfers of the Jovian system. Pre-computed unstable resonant orbits serve as an initial guess for the highly nonlinear optimisation problem along with Tisserand–Poincaré (TP) graph. Assadian and Pourtakdoust (2010) used a non-dominated sorting genetic algorithm with crowding distance sorting (NSGA-II) for multi-objective optimisation of trajectories from EPO around Earth to a circular orbit around Moon in the framework of a 3D restricted four-body problem (R4BP). Apart from $\Delta V_{\mathit{TLI}}$ and $\Delta V_{\mathit{LOI}}$ another mid-course manoeuvre is permitted to patch the Earth escape path to the Moon’s ballistic capture trajectory. The arrival date at Moon, the mid-course manoeuvre time and some of the orbital elements of the ballistic capture orbit around Moon are parameters used to minimise the total $\Delta V$ and the flight time.

Peng et al. (2010) used an improved differential evolution algorithm with self-adaptive parameter control for the design of Earth–Moon low-energy transfer to find the patch point of the unstable and stable manifold of the Lyapunov orbit around Sun–Earth $L_{2}$. They found this optimisation technique to be more effective than three other evolutionary algorithms, namely the genetic algorithm, particle swarm optimisation and standard differential evolution. Peng et al. (2011) used adaptive uniform design differential evolution (AUDE) with self-adaptive parameter control method to find low-energy Earth–Moon transfers. Coffee et al. (2011) describe a two-stage approach to constructing low-energy transfers between arbitrary unstable periodic orbits to reduce fuel requirements. They used an adaptive approach to global optimisation to identify position-space intersections of invariant manifolds. Grover and Andersson (2012) optimised the GTO-to-moon mission by appropriately timed $\Delta V\mbox{s}$ which are obtained by shooting and the Gauss-pseudospectral collocation method for different phases of the mission.

Generally, the optimisation routines employed to find optimal low-energy transfers, employ much time searching in regions where the chance of finding solution is low. If knowledge of invariant manifold theory can be integrated inside the routine, it might enhance the efficiency of the optimisation routines.

2.7 Low thrust trajectories

Low-thrust trajectories (LTTs) use low-thrust propulsion (LTP) systems. LTP systems utilise propellant more efficiently, like electric propellant or a solar sail, and hence they can significantly enhance the payload capability or enable high-$\Delta V$ missions. LTTs are different from ballistic trajectories because the spacecraft is propelled for long periods and sometimes almost continuously by low-thrust engines. So it experiences the gravitational attraction of celestial bodies and other perturbations along with the change in energy due to thrusters. Lo and Parker (2005) showed that the unstable simple periodic orbits can be linked using their invariant manifolds to generate “chains” to build LTT for space exploration. A similar technique was used for the design of the Genesis mission (Howell et al. 1997) and the Lunar Sample Return Mission (Lo and Chung 2002). The incorporation of knowledge of invariant manifolds of unstable orbits within an optimisation tool and a good initial guess are important for reducing the time required for an optimisation routine to search for an optimal LTT. Lo et al. (2004) compared LTT with the invariant manifolds at the same energy level. In order to reduce the time of flight it is important to switch from one manifold to another by application of small manoeuvres. But $\Delta V$ causes a change in energy and hence the Jacobi constant. Anderson and Lo (2004, 2009) analysed the Planar Europa Orbiter (PEO) trajectory and concluded that in order to switch from one manifold to another, an impulsive manoeuvre is required at the point where the manifolds intersect in configuration space but not in phase space. They also found that even with a change in the Jacobi constant, PEO travels along the manifolds. Hence they established that the underlying dynamics of multiple gravity assist is provided by invariant manifold theory. In order to understand the relationship between the optimised low-thrust trajectory and the invariant manifold of an appropriate energy level, Anderson and Lo (2009) plotted a series of intersections where some thrusting occurred but the Jacobi constant did not change dramatically.

Mingotti et al. (2009) formulated a systematic method for the design of low-energy transfers to the Moon using high specific impulse low-thrust engines (e.g. ion engines). They derived the initial guess with no velocity discontinuity at the patching point in the bicircular four-body problem. The search is reduced to the search of a single point on a suitable surface of section. Optimisation is carried out in controlled four-body dynamics using a direct multiple shooting strategy. They found this method to be efficient in finding low-energy transfers that require smaller propellant than standard impulsive low-energy transfers. They provide a comparison table (Table 1), where their solutions LELT#1–3 are provided along with high-thrust solutions for WSB, BP (biparabolic), HO (Hohmann), BE (bielliptic), $L_{1}$ (via $L_{1}$ transit orbits), MIN (minimum theoretical). In the table, $\Delta \upsilon _{\mathit{TLI}}$ is the translunar injection manoeuvre, from a 200 km circular EPO for LELT#1–3, while it is 167 km circular EPO for other reference solutions. In order to compute the propellant mass fraction using the rocket equation, for LELT and high-thrust solutions, the specific impulse is considered to be 3000 s and 300 s, respectively. In the table, $e$ and $h _{p}$ are the eccentricity and periapsis altitude of the final orbit about Moon, respectively, and $\Delta t$ is the flight duration.

Mingotti and Topputo (2011) surveyed the possible routes to the Moon considering both high- and low-thrust propulsion. They have considered three target orbits, namely low lunar orbits, libration-point orbits, and distant periodic orbit. Transfer times for low lunar orbits vary from 14 to 103 days and the best low-energy, low-thrust solution has a 4% of propellant mass fraction (PMF) when the initial burn is not considered. In order to achieve a halo orbit in the Earth–Moon system, starting from a GTO is convenient and the best solution has 7% PMF. They found distant prograde orbits to be appealing, as no insertion manoeuvres are required to achieve the final orbit.

Gurfil and Kasdin (2002) applied a Deterministic Crowding Genetic Algorithm to characterise and design out-of-plane trajectories in the Sun–Earth system. They have addressed the constraints imposed by interplanetary dust (IPD) for space-borne observation missions. They found a low-energy trajectory with a maximum normal displacement of 0.223 AU and maximum reduction of 67% IPD. The second optimal trajectory had a maximum normal displacement of 0.374 AU above the ecliptic and reduction of 97% IPD. Dachwald (2004) demonstrated the use of evolutionary neurocontrollers to find near optimal LTT without an initial guess and without the requirement to embed the knowledge of invariant manifolds in the optimisation code named InTrance (Intelligent Trajectory optimisation using neurocontroller evolution). The performance of InTrance is assessed for interplanetary missions. It was able to reduce the transfer time of a reference trajectory to a near-Earth asteroid by 74%. It was also used for the analysis of the Mars mission using a spacecraft with a nuclear electric propulsion system. Yam et al. (2009) used differential evolution and simulated annealing with an adaptive neighbourhood to find optimal LTT for an Earth–Mars rendez-vous problem. The solution obtained when used as an initial guess for a local optimiser yields high convergence rates.

Xu and Xu (2009) studied the cislunar transfers. They proposed a distant retrograde orbit (DRO) for the design of low-energy transfers to the Moon. Xu et al. (2012) discussed the evolution of invariant manifolds of halo orbits for low-thrust trajectories. They concluded that acceleration or deceleration of low-thrust trajectories near the libration point is inefficient. It is used to increase the velocity and avoid stagnation near the libration point. Secondly, all controlled manifolds are captured, and finally, most of the manifolds preserve their topologies in circular R3BP.

Taheri and Abdelkhalik (2015) used a finite Fourier series for the construction of LTT with thrust acceleration constraints, in RTBP. They used the developed technique to generate Earth to Moon orbit transfers with a number of revolutions around the primaries. These trajectories can be used as an initial guess for high-fidelity solvers.

Xu et al. (2013) explored the dynamics of lunar libration points $\mathit{LL}_{1}$ and $\mathit{LL}_{2}$. They used a Poincaré mapping to show the statistical feature of fuel cost and orbital elements of Moon-captured trajectories for both cislunar and translunar transfers. They found that the asymptotical behaviours of invariant manifolds approaching or travelling from the libration points or halo orbits are destroyed by the solar gravitational perturbation. They found that the energy-minimal cislunar transfer trajectory is acquired by transiting the $\mathit{LL}_{1}$ point, while the energy-minimal translunar transfer trajectory is obtained by transiting the $\mathit{LL}_{2}$ point.

Zhang et al. (2014) formulated low-thrust minimum-fuel, minimum-energy and minimum-time trajectories in the restricted three-body problem. They obtained transfers to halo orbit around the Earth–Moon $L_{1}$ starting from a geostationary transfer orbit. Their technique solves the optimisation problem by introducing energy-to-fuel homotopy, formulating analytical derivatives, implementing a hybrid method for switching point detection, and it avoids splitting up transfers into phases.

Xu et al. (2016) have summarised the developments in the use of libration-point orbits (LPOs) for deep space exploration. They also addressed the application of LPO theory to the fields of lunar transfer, solar sail equilibria and formation flying, and they gave future research directions as regards the proof of existence of halo orbits, orbital design of potential missions motivated by LPOs, etc. Liang et al. (2016) have discussed direct transfer and low-energy transfers to the Moon in the context of R3BP. They used a Poincaré mapping to obtain the feasible cislunar trajectories and to demonstrate the relationship between Jacobi energy, perilune or perigee radius and certain characteristics of cislunar trajectories. They also present the distribution of low-energy transfers, direct cislunar transfers and resonance cyclers. They also demonstrated the applications in geosynchronous orbit deorbiting and lunar relay satellite system.

Qu et al. (2017) have designed an open-loop control law to guide the spacecraft to escape from Earth till it is captured by the Moon. They used a two-dimensional search strategy to find the ON/OFF time of the low-thrust engine during its Earth-escaping and Moon-capture phases. Lin et al. (2017) have proposed a block decomposition algorithm developed in Compute Unified Device Architecture (CUDA) platform for the computation of Lagrangian Coherent Structures (LCSs) of multi-body gravitational regimes. The algorithm utilises a block decomposition strategy to facilitate the computation of finite-time Lyapunov exponent (FTLE) fields of arbitrary size and timespan. Liang et al. (2017) have considered a family of periodic orbits polygonal-like periodic orbits (PLPOs), which are in resonance with respect to the secondary. They constructed PLPOs in the Earth–Moon system using Hori–Lie perturbation method. They used Poincaré surface of section (PSS) to determine the critical states between non-transit and transit and the break of frozen tori. Finally, they propose a cislunar in-orbit infrastructure named “parking apron” system based on the periodicity condition and transition of PLPOs supporting supply and crew transportation. Oshima et al. (2017) used the necessary conditions of optimality based on the Pontryagin principle to search for LTTs to the Moon. They obtained a wide range of Pareto solutions and a Tisserand–Poincaré graph shows that a number of these solutions exploit high-altitude lunar fly-by to reduce fuel consumption.

Pérez-Palau and Epenoy (2017, 2018) used an indirect optimal control approach to determining minimum-fuel LTT starting from a LEO to lunar orbit in the Sun–Earth–Moon bicircular restricted four-body problem. They derived the necessary optimality conditions from Pontryagin’s maximum principle. They have classified the trajectories into various families based on their shape, transfer duration ($\Delta t$) and total fuel consumption ($\Delta m = m_{0}- m(t _{f})$) and obtained a physical interpretation of these families from the dynamical structures of invariant manifolds.

3 Notable missions/plans

The Japanese Hiten mission used both a lunar swing-by and a WSB trajectory to reach the Moon with favourable conditions for capture into a highly elliptic lunar orbit in 6 months (Uesugi 1996).

Kawaguchi et al. (1995) described the use of solar and lunar gravity assist to reduce the propellant required for LUNAR-1 Mission to the Moon and PLANET-B Mission to Mars mission. The LUNAR-A mission (presently cancelled) planned in 1997 to the Moon utilises ballistic capture at Moon. The expected C3 gain is $0.8~\mbox{km}^{2}/\mbox{s}^{2}$ or 5–9% in spacecraft mass assuming a specific impulse of 300–500 s to be compared to Hohmann-type transfer. For the PLANET-B (Nozomi) mission to Mars planned in 1998, they found that triple lunar gravity assist can reduce C3 by $4.5~\mbox{km}^{2}/\mbox{s}^{2}$. Among the three solutions thus obtained they selected one based on the launch window constraints. The expected C3 gain was around $2~\mbox{km}^{2}/\mbox{s}^{2}$.

The Petit Grand Tour of the moons of Jupiter is already discussed in previous section.

Sweetser et al. (1997) discussed a number of trajectory design techniques for Europa Orbiter Mission. The spacecraft shall reach Jupiter by the end of the decade and plan for a follow-up mission to Europa. After it arrives at Jupiter, it will undergo two Ganymede flyby G0 and G1 to reduce its incoming hyperbolic velocity. After reducing arrival $V_{\infty }$, a phase called endgame begins, which requires certain arrival conditions for the final flyby of the tour. The endgame is designed by JPL (Johannesen and D’Amario 1999) to further reduce $\Delta V_{\mathit{POI}}$ using a combination of Europa flybys. Heaton et al. (2002) started investigating the E0 trajectory after G1. They analysed sequences of Jovian satellites flyby to reduce arrival $V_{\infty }$ at Europa. They explored and evaluated an enormous number of possible tours using a graphical method based on Tisserand’s criterion to reduce the arrival $V_{\infty }$ satisfying all the mission constraints. Among all the solutions obtained, the best tour arrival $V_{\infty }$ at Europa was reduced from 3.3 km/s to 2 km/s and the total radiation exposure was reduced by 70%.

Jehn et al. (2004) described the trajectory of BepiColombo mission to Mercury which is a joint exploration mission by ESA and JAXA. Two spacecraft then were proposed for launch in 2015 and were destined to reach Mercury in 2021 utilising several gravity assists and SEP (Solar Electric Propulsion) ion engine thrust arcs. Since the thrust level of SEP is very low for a capture from hyperbolic approach, various options of Mercury Orbit Insertion (MeOI) through gravitational capture were found by varying the capture time and speed of the spacecraft, right before MeOI. The trajectory which provides the best recovery options in the case of a failed orbit insertion is selected for the 2012. The spacecraft on this trajectory arrives with very low excess velocity and from a direction where the gravity of Sun and Mercury have similar effects on the orbit. In the case of failure in orbit insertion on 5 January 2017 (assuming launch on 13 April 2012), the spacecraft would make five revolutions around Mercury before escaping again. It is observed that at the second, fifth and sixth periherm, the altitude, inclination and orientation of the line of apsides for this trajectory are not very far from the nominal values. With small manoeuvres (less than 10 m/s) close to the previous apoherms, new orbit insertion possibilities arise with nearly the same orbital parameters. Campagnola and Lo (2007) find that the manifolds of symmetric quasi-periodic orbits around Mercury play a key role as symmetry properties provide several recovery opportunities to the mission. Jehn et al. (2008) describe the navigation strategy for BepiColombo during the final phase of WSB capture by Mercury.

Ross et al. (2003) found a trajectory for the Multi-Moon Orbiter (MMO) in which the spacecraft would orbit three of Jupiter’s moons, namely Callisto, Ganymede and Europa, using very little fuel. They found a tour trajectory with $\Delta V$ of the order of 22 m/s (vs. 1500 m/s using conventional methods) and will spend about 4 years in the inter-moon phase. Finally, $\Delta V$ of about 450 m/s is required to put the spacecraft into a 100 km orbit about Europa with an inclination of $45 ^{\circ }$. Ross et al. (2004) used the patched three-body approximation method to compare the trade-off between flight time and $\Delta V$ for the MMO. They tried to reduce the flight duration to find another feasible tour trajectory which takes 227 days of flight duration for $\Delta V$ of 211 m/s.

4 Conclusion and scope for future work

The method of low-energy transfers (LETs) has proved revolutionary in reducing the fuel requirements for lunar missions, but it suffers from the major drawback of longer flight durations than conventional direct transfers. The developments in the area of LETs transfers, use of the invariant manifold theory and optimisation techniques to design low-energy and low-thrust trajectories are presented. Some notable missions and planned missions that have been used or have proposed to use the WSB theory for trajectory design are listed. The richness of this area is evident from the work of several researchers in the last decade. Still, this area provides opportunities for further work which can be classified into three parts; namely, manifold theory, optimisation methods and mission design.

New work can be aimed to improve our understanding of the manifold theory behind the existence of such natural routes, improvement in the existing or use of novel optimisation techniques to find an optimal trajectory and the design of an innovative trajectory. For interplanetary transfers, the possibility of combining WSB with alternative methods, like the gravity assist and aerobraking methods to reduce fuel requirement, still remains to be explored. The analysis of the capture corridor at the destination planet to ensure that the trajectory gets captured at the destination planet within some tolerance levels to accomodate for navigational uncertainties will ensure complete mission design. Classification of capture orbits at the destination planet is also an area to be explored. Another promising area is the incorporation of knowledge from invariant manifold theory, for guiding the search for an optimal trajectory, within the search methods to increase their efficiency and reduce the number of failure cases.