Buchdahl–Vaidya–Tikekar model for stellar interior in pure Lovelock gravity

Abstract

In the paper (Khugaev et al. in Phys Rev D94:064065. arXiv: 1603.07118, 2016), we have shown that for perfect fluid spheres the pressure isotropy equation for Buchdahl–Vaidya–Tikekar metric ansatz continues to have the same Gauss form in higher dimensions, and hence higher dimensional solutions could be obtained by redefining the space geometry characterizing Vaidya–Tikekar parameter K. In this paper we extend this analysis to pure Lovelock gravity; i.e. a $(2N+2)$-dimensional solution with a given $K_{2N+2}$ can be taken over to higher n-dimensional pure Lovelock solution with $K_n=(K_{2N+2}-n+2N+2)/(n-2N-1)$ where N is degree of Lovelock action. This ansatz includes the uniform density Schwarzshild and the Finch–Skea models, and it is interesting that the two define the two ends of compactness, the former being the densest and while the latter rarest. All other models with this ansatz lie in between these two limiting distributions.

1 Introduction

A model for a star interior is an important astrophysical question and hence it is pertinent to construct relativistic models as solutions of gravitational equation. For constructing static perfect fluid interiors for compact objects, we have two metric functions to determine while there is only one pressure isotropy equation for determining them. We need therefore to prescribe either a metric ansatz for one of the functions or an equation of state relating pressure and density or a fall off behaviour for density or pressure. In paper [1], we had considered Buchdahl–Vaidya–Tikekar metric (BVT) [2,3,4] ansatz covering a class of physically tenable models and had shown that the pressure isotropy equation bore the same Gauss form in all dimensions $\ge 4$. By exploiting this property we established that a 4-dimensional Einstein solution for a given value of the Vaidya–Tikekar parameter $K_4$, indicating deviation from sphericity of 3-space geometry, could be lifted to a higher n-dimensional solution with K being replaced by $K_n=(K_4 -n +4)/(n-3)$. That is, a static fluid interior solution in the usual 4 dimension could be taken over to a higher dimensional solution.

This is an interesting property of fluid solutions in Einstein gravity and so the natural question that arises is that, is this also carried over to Lovelock theory which is quintessentially higher dimensional? Interestingly the answer is yes, but it singles out pure Lovelock from general Lovelock theory. By pure Lovelock we mean the action and consequently the equation of motion has only one N-th order term with no sum over lower orders. That is, a $(2N+2)$-dimensional solution with a given $K_{2N+2}$ can be taken over to higher n-dimensional solution with $K_n=(K_{2N+2}-n+2N+2)/(n-2N-1)$. It bears out the general feature of pure Lovelock gravity that gravitational dynamics is universal in all critical odd $2N+1$ and even $2N+2$ dimensions [5, 6]. In particular, it turns out that there can occur no bound distribution in the critical odd dimensions while in the critical even dimensions, the solutions have similar behaviour [7].

Lovelock action which is polynomial in Riemann tensor is distinguished from all other modifications of general relativity (GR) by its remarkable property that the equation of motion remains second order. Further pure Lovelock involving only one Nth order term without sum over lower orders is distinguished by two very important properties: (a) gravity is kinematic in the critical odd $n=2N+1$ dimension; i.e. there exists no non-trivial vacuum solution because Lovelock analogue of Riemann [5, 8, 9] is entirely given in terms of corresponding Ricci [10] and (b) existence of bound orbits around a static source [11]. These two properties respectively hold good only in three and four dimensions, and none else. The latter of which is required for existence of planetary orbits around a star and for structure formation in general. It is therefore existence of bound orbits becomes the distinguishing feature for a classical gravitational equation.

The real question is, what is the proper equation for gravity in higher dimensions [6]? As mentioned above, the equation must be second order which singles out besides Einstein’s equation, Lovelock polynomial equation in higher dimensions. Secondly there should be only one coupling constant which could be empirically determined by measuring the strength of gravitational force. In Lovelock equation, there are N dimensionful couplings and there is no way to fix them. However one can prescribe all others in terms of a unique vacuum $\Lambda$ as is done for dimensionally continued black holes [12]. In there, one is not seeking a classical equation in higher dimension but rather quantum corrections to Einstein equation are envisaged in a semi-classical formulation. Einstein equation on the other hand is untenable because it cannot admit bound orbits in higher dimensions. For equation to be second order and yet admitting bound orbits, it is then pure Lovelock. This then uniquely singles out pure Lovelock equation in higher dimensions. Besides all this, pure Lovelock gravity has several very interesting and desirable features as alluded in Refs [23, 24].

One may however still ask that any gravitational theory must include Einstein and hence it should approximate to it in the weak field—asymptotic limit. How is it possible as there is no Einstein term in pure Lovelock equation? It turns out that the static vacuum solution with $\Lambda$ does indeed goes over to Einstein-dS solution in the higher dimensions [16]. It is indeed most remarkable that it includes without the presence of Einstein term its features asymptotically. It perhaps underpins the fact that pure Lovelock gravity indeed captures the elemental character of gravitational field.

Buchdahl ansatz [2, 3] was particularized in Vaidya–Tikekar (VT) [4] ansatz with parameter K characterizing geometry of 3-space, and in the limit it also included the interesting Finch–Skea ansatz (FS) [13]. We also obtain pure Lovelock version of FS solution. In this case the isotropy equation is not in the Gauss but instead in the Bessel form which for a given N is the same in all dimensions. There is universality in behaviour of star interiors corresponding to both BVT as well as FS models relative to a properly defined variable and also the parameter K for the former. Further the compactness hierarchy goes as constant density star defining the limiting upper limit while FS holding the other end. All other BVT models lie between these two limiting distributions. For a given radius of s star in critical $n=2N+2$ dimension, mass is maximum for the Einstein $N=1$ bearing out the fact that pure Lovelock gravity becomes weaker as N increases. This is because potential goes as $1/r^{(n-2N-1)/N}$ [14,15,16].

In this paper, besides establishing the general result of paper [1] of carrying over $2N+2$-dimensional fluid sphere solution to higher dimensions in pure Lovelock gravity, we shall in particular study pure Lovelock VT and FS models and their physical properties. Let us once again reiterate that our main is to demonstrate that the procedure of lifting a four dimensional solution to higher dimension with appropriate Vaidya–Tikekar parameter K is indeed carried forward to pure Lovelock gravity despite its highly non-linear polynomial character.

There is enormous literature on interior of static fluid stars in the usual four dimensions, one can’t do any better than referring to the exact solutions book [17]. Of special mention in this regard should be made of a comprehensive analysis the solution generating schemes and transformations in various coordinates [18,19,20] covering known solutions as well as giving some new ones. It would be interesting in future to see whether these schemes could be extended to pure Lovelock gravity as well. There is also a fairly large body of work on higher dimensional star which was comprehensively reviewed in paper [1]. Instead of repeating that again here we would like to direct the reader to paper [1] for detailed references (also see [7, 21]). It should however be admitted that higher dimensional fluid models are more for exploring and probing the gravitational dynamics rather than their direct physical and astrophysical applications. Of course there always remains a little window open for emergence of a unified field theory involving higher dimensions where it may find some relevance.

The paper is organized as follows: in the next section we recall the pure Lovelock gravitational equation and set it for a perfect fluid distribution. In Sect. 3, we specialize to static spherically symmetric with the Buchdahl ansatz and find solutions for VT and FS ansatzs, which is followed by matching of interior and exterior solution. The physically properties are discussed in Sect. 5 and we conclude with a discussion.

2 Lovelock gravity

There is a natural generalization of Einstein action to Lovelock action which is a homogeneous polynomial in Riemann curvature with Einstein being the linear order and the quadratic is Gauss–Bonnet (GB). It has the remarkable property that on variation it still gives the second order quasi-linear equation which is its distinguishing feature. Note that for pure Lovelock with only one Nth order term in the action without sum over lower orders, it is pure divergence—topological in $n=2N$, and in $n=2N+1$ it has the same behaviour of non-existence of non-trivial vacuum solution relative to Lovelock analogue of Riemann tensor [5, 9] as Einstein has in three dimension; i.e. gravity is kinematic. As for Einstein, pure Lovelock gravity turns dynamic for dimensions $\ge 2N+2$. Clearly Lovelock is therefore a quintessentially higher dimensional gravitational theory for $n\ge 2N+1$.

If we introduce a set of (2N, 2N)-rank tensors [8] product of N Riemann tensors, completely antisymmetric, both in its upper and lower indices,

$$\begin{aligned} ^{(N)}\!I\!\!R^{b_1 b_2 \cdots b_{2N}}_{a_1 a_2 \cdots a_{2N}}= R^{[b_1 b_2}_{\quad \quad [a_1 a_2}\cdots R^{b_{2N-1} b_{2N}]}_{\qquad \qquad a_{2N-1} a_{2N}]}~. \end{aligned}$$

(1)

With all indices lowered, this tensor is also symmetric under the exchange of both groups of indices, $a_i\leftrightarrow b_i$. In terms of these new objects we can now write

$$\begin{aligned} L_N= {}^{(N)}\!I\!\!R \qquad \text {and} \qquad {}^{(N)}\mathbf {G}^\mu _{\ \nu }=N\,\,{}^{(N)}\!I\!\!R^\mu _{\ \nu }- \frac{1}{2} {}^{(N)}\!I\!\!R\,\delta ^\mu _{\ \nu } \end{aligned}$$

(2)

For pure Lovelock of order N we write

$$\begin{aligned} S=\int d^nx\sqrt{-g}{L}_{N}+S_\mathrm{matter}. \end{aligned}$$

(3)

Now the pure Lovelock gravitational equation for $n\ge 2N+1$ has the usual form

$$\begin{aligned} {}^{(N)}\mathbf {G}^\mu _{\ \nu } = T^\mu _\nu ,\quad \mu ,\nu =1\dots n \end{aligned}$$

(4)

We are going to solve this equation for a static spherically symmetric fluid distribution with $T^\mu _\nu = diag(-\rho , p, p, \ldots , p)$ as a model for star interior in hydrostatic equilibrium.

3 Buchdahl ansatz

Let us begin with the general static spherically symmetric metric in n–dimensional space-time,

$$\begin{aligned} ds^2=-f_2(r)^2 dt^2+\frac{1}{1-f_1(r)}dr^{2}+r^{2}d\Omega ^{2}_{n-2}\,. \end{aligned}$$

(5)

Substituting this metric in Nth order pure Lovelock equation Eq. (4), we obtain

$$\begin{aligned} \rho =\frac{1}{2}\frac{(n-2)!}{(n-2N-1)!}\left( \frac{f_1(r)}{r^2}\right) ^N\left( Nr\frac{f'_1(r)}{f_1(r)}+n-2N-1\right) \end{aligned}$$

(6)

$$\begin{aligned} p=\frac{(n-2)!}{(n-2N-1)!}\left( \frac{f_1(r)}{r^2}\right) ^N\left( Nr\frac{1-f_1(r)}{f_1(r)}\frac{f'_2(r)}{f_2(r)}-\frac{1}{2} (n-2N-1)\right) \end{aligned}$$

(7)

and the pressure isotropy equation is given by

$$\begin{aligned} p_\theta -p_r= & {} \frac{N(n-3)!}{(n-2N-1)!}\left( \frac{f_1(r)}{r^2}\right) ^{N-1}\frac{1}{f_2(r)}\Bigg [ (1-f_1(r))f''_2(r)\nonumber \\&-\frac{f'_2(r)}{r}\left\{ (n-2)(1-f_1(r))+\frac{1}{2} rf'_1(r)\left( n-2-\frac{n-3}{f_1(r)}\right) \right\} \nonumber \\&-\frac{n-2N-1}{2}\left( \frac{f'_1(r)}{f_1(r)}-\frac{2}{r}\right) \left( f'_2(r)(1-f_1(r))+\frac{f_1(r)f_2(r)}{r}\right) \Bigg ] = 0\nonumber \\ \end{aligned}$$

(8)

where a prime indicates derivative relative to r. It may be noted that these are general expressions for density, pressure and pressure isotropy for any Lovelock order N which have perhaps not been reported earlier anywhere. These would therefore be useful for all future considerations.

Before we go any further let’s rule out the critical odd $n=2N+1$ dimension case from further discussion. For a bound distribution describing interior of a compact object, the boundary is defined by $p=0$ which requires from Eq. (7), $f'_2(r)=0$ on the boundary. This conflicts with the matching with exterior vacuum solution. There cannot therefore exist bound distribution in the critical odd $n=2N+1$ dimensions [7, 21]. We shall henceforth only consider $n\ge 2N+2$.

Note that we have only one equation (8) to determine the two unknown metric functions $f_1(r)$ and $f_2(r)$ while the other Eqs. (6–7) define the density and the pressure. Hence it is imperative either to have an ansatz specifying one of the metric functions or an equation of state relating density and pressure or a fall off behaviour for density.

We resort to a fairly general ansatz due to Buchdahl [2, 3] prescribing the metric function $f_1(r)$ as

$$\begin{aligned} f_1(r) = \frac{Ar^2}{1+Cr^2} \end{aligned}$$

(9)

with $A> C > 0$. Vaidya and Tikekar (VT) further particularized [4] it by writing $C=K\alpha , A=(1+K)\alpha$, and wrote

$$\begin{aligned} f_1(r)=\frac{(1+K)\alpha r^{2}}{1+K\alpha r^{2}}\, \end{aligned}$$

(10)

where $\alpha = R^{-2}$ (K here is $-K$ in [4]). They had given this parameter an interesting geometric meaning as deviation from sphericity of 3-space geometry. It may also be noted that this parameter is required to be positive for density to be monotonically decreasing outwards from the center of distribution [1]. It is interesting that this is how 3-space geometry is related to density evolution of fluid.

Another interesting ansatz is due to Finch and Skea [13] which is the limiting case of the Buchdahl ansatz when $A=C$, and then

$$\begin{aligned} f_1(r) = \frac{Cr^2}{1+Cr^2}. \end{aligned}$$

(11)

It should be noted that the ansatz (5) is the most general while Buchdahl ansatz (9–11) are special cases. It should be noted that though there are solutions which are lying outside the Buchdahl ansatz but they all seem to suffer from one or the other unphysical feature like density increasing outwards [17]. So Buchdahl ansatz covers all the physically tenable star models satisfying the energy conditions. In the particular cases of Vaidya–Tikekar and Finch–Skea models we have seen that $\rho \ge 0, p\ge 0$ and $dp/d\rho \le 1$ which indicate that the weak and strong energy conditions are satisfied, and also velocity of sound is always less than that of light. Therefore these models are physically tenable.

We would therefore like to employ the ansatz for studying star interiors in pure Lovelock gravity. In particular we would like to obtain solutions for star interior for the two ansatzs: Vaidya–Tikekar (VT) and Finch–Skea (FS).

For the Buchdahl ansatz (9), Eqs. (8–7) take the following form

$$\begin{aligned} \rho (r)= \frac{1}{2}\frac{(n-2)!}{(n-2N-1)!}\left( \frac{A}{1+C r^2}\right) ^N\left( n-1-2N+\frac{2N}{1+C r^2}\right) \end{aligned}$$

(12)

$$\begin{aligned} p(r)= \frac{(n-2)!}{(n-2N-1)!}\left( \frac{N(1-(A-C) r^2)}{A r}\frac{f'_2(r)}{f_2(r)}-\frac{1}{2} (n-2N-1)\right) \left( \frac{A}{1+C r^2}\right) ^N \end{aligned}$$

(13)

that can also be written as:

$$\begin{aligned} p(r)=\rho \left( -1+ \frac{2N}{Cr^2(n-2N-1)+n-1}\left( 1+\frac{(1+Cr^2)(1-(A-C) r^2)}{A r}\frac{f'_2(r)}{f_2(r)}\right) \right) \end{aligned}$$

(14)

and the pressure isotropy equation takes the form

$$\begin{aligned}&(1-(A-C) r^2)(1+C r^2)f''_2(r) +\frac{f'_2(r)}{r}((2N-1)C(A-C) r^4-2NC r^2-1)\nonumber \\&\quad + AC (n-2N-1) r^2 f_2(r)=0. \end{aligned}$$

(15)

As in Ref. [2, 3] we write r to $x=r^2$ to cast the above equation in the form

$$\begin{aligned}&(1-(A-C) x)(1+C x)f''_2(x) + f'_2(x)\left( (A-C)(N-1)C x-C(N-1)-\frac{A}{2}\right) \nonumber \\&\quad +\frac{1}{4} AC(n-2N-1) f_2(x)=0 \end{aligned}$$

(16)

where a prime here as well as henceforth will indicate derivative relative to argument.

Now there arise two cases corresponding to $A\ne C$ (BVT) and $A=C$ (FS).

3.1 Buchdahl–Vaidya–Tikekar model

When $A>C>0$, we do the following change of variable

$$\begin{aligned} z=\frac{A-C}{A}(1+C x) \end{aligned}$$

(17)

then the isotropy equation becomes

$$\begin{aligned} z(1-z)F''(z)+((N-1)z+1/2-N)F'(z)+\frac{1}{4}\frac{A}{A-C}(n-2N-1)F(z)=0. \end{aligned}$$

(18)

This is the Gauss equation [22]

$$\begin{aligned}(1-z)zF''(z)+[c-(a+b+1)z]F'(z)-abF(z)=0\end{aligned}$$

with $c=1/2-N$, $a+b=-N$, $-ab=A (n-2N-1)/(4(A-C))$. The equation in question can be easily solved and the two independent solutions of Eq. (18) around $z=0$ for $n>2N+1$ are the hypergeometric functions, $_2F_1(a,b;c,z)$ and $z^{1-c}\,{}_2F_1(1+a-c,1+b-c;2-c,z)$.

As is the case for N=1 Einstein gravity [1], the Eq. (18) is the same for a given Lovelock order N in all $n>2N+1$ dimensions with the constants A and C are related as follows:

$$\begin{aligned}\frac{A_n}{A_n-C_n}(n-2N-1)=\frac{A_{2N+2}}{A_{2N+2}-C_{2N+2}}\end{aligned}$$

Here a subscript refers to space-time dimension. It means that a $(2N+2)$-dimensional solution could be lifted to a higher n-dimensional solution with $K_{2N+2}$ being replaced by $K_n$ according to the above relation. This is because for a given N, the equation has the same form and hence the same solution with appropriate K parameter.

For the VT case, this relation takes the form

$$\begin{aligned} K_n=\frac{K_{2N+2}+2N+2-n}{n-2N-1} \end{aligned}$$

(19)

This is the pure Lovelock generalization of the Einstein gravity relation for $N=1$ obtained in the paper [1].

The general solution of Eq. (18) around $z=0$ is given by

$$\begin{aligned} F^B(z)=A_1 F^B_1(z)+A_2 F^B_2(z) \end{aligned}$$

(20)

where

$$\begin{aligned}&F^B_1(z)\equiv {_{2}F_{1}}(a,b;1/2-N,z),\nonumber \\&F^B_2(z)\equiv z^{N+1/2}{_{2}F_{1}}(1/2+N+\,a,1/2+N+b;3/2+N,z) \end{aligned}$$

(21)

Here $A_1$ and $A_2$ are arbitrary integration constants and ${_{2}F_{1}}(a,b;c,z)$ is the hypergeometric function with

$$\begin{aligned}&a=-\frac{N}{2}+\frac{1}{2}\sqrt{N^2+\frac{A}{A-C}(n-2N-1)},\\&b=-\frac{N}{2}-\frac{1}{2}\sqrt{N^2+\frac{A}{A-C}(n-2N-1)}. \end{aligned}$$

Note that $z=(A-C)(1+Cr^2)/A$ and when the expression under the radical is whole square, the hypergeometric function becomes a polynomial. We thus have the complete solution for the isotropy equation for the Buchdahl or Vaidya–Tikekar ansatz.

3.2 Finch–Skea model

When $A=C$ we write for $n>2N+1$

$$\begin{aligned} z=(1+C x)(n-2N-1) \end{aligned}$$

(22)

and the isotropy Eq. (16) becomes

$$\begin{aligned} zF''(z)-\left( N-\frac{1}{2}\right) F'(z)+\frac{1}{4} F(z)=0. \end{aligned}$$

(23)

where now z is given in (22) and

$$\begin{aligned} F^{FS}_1(z)\equiv z^{(N+1/2)/2} J_{N+1/2}(\sqrt{z}),\quad F^{FS}_2(z)\equiv z^{(N+1/2)/2} J_{-N-1/2}(\sqrt{z}) \end{aligned}$$

(24)

where J are the Bessel functions. The solution for a given Lovelock order N is the same for any dimension $n>2N+1$.

This is the Bessel equation and it is important to note it remains the same for a given N in all dimensions. That is, for a given Lovelock order N, the solution is universal for the variable z in all dimensions $\ge 2N+2$. The general solution is given by

$$\begin{aligned} F^{FS}(z)=A_1 F^{FS}_1(z)+A_2 F^{FS}_2(z) \end{aligned}$$

(25)

Though in the critical odd $n=2N+1$ dimensions there can be no bound fluid distributions, yet the solution of the isotropy Eq. (15) for BVT and FS ansatz are respectively given as follows:

$$\begin{aligned} F^B_{n=2N+1}(z)= A_1+A_2\,\,{_{2}F_{1}}(1/2+N,1/2;3/2+N,z) \end{aligned}$$

(26)

where z is given in (17) and

$$\begin{aligned} F^{FS}_{2N+1}(z) = A_1+A_2 z^{N+1/2}. \end{aligned}$$

(27)

where now $z=1+C r^2$.

4 Matching with the exterior solution

At the star boundary which is defined by $p=0$, the solution must match with the pure Lovelock vacuum solution in the exterior. This requires that the metric functions $g_{tt}, g_{rr}$ and $g'_{tt}$ must be continuous across the boundary.

In the interior for $n\ge 2N+2$, we have

$$\begin{aligned} ds^2=-f_2(r)^2 dt^2+\frac{1+Cr^2}{1+(C-A)r^2}dr^{2}+ r^{2}d\Omega ^{2}_{n-2}, \end{aligned}$$

(28)

where $f_2(r)$ is $F^B(z_B)$ and $F^{FS}(z_{FS})$ respectively for Buchdahl and FS models and

$$\begin{aligned} z_B=\frac{(A-C)(1+C r^2)}{A},\quad z_{FS}=(1+Cr^2)(n-2N-1). \end{aligned}$$

(29)

Since It has to be matched to the pure Lovelock vacuum exterior metric [16]

$$\begin{aligned} ds^2=-f(r) dt^2+f^{-1}(r)dr^{2}+ r^{2}d\Omega ^{2}_{n-2}, \end{aligned}$$

(30)

where

$$\begin{aligned} f(r)=1-2Mr^{-\frac{n-2N-1}{N}}. \end{aligned}$$

(31)

The continuity of the metric components determines mass

$$\begin{aligned} M=\frac{1}{2}\frac{A r_0^{(n-1)/N}}{1+C r^2_0}, \end{aligned}$$

(32)

where we have $A=(K+1)\alpha ,\, C=K\alpha$ for VT and $A=C$ for FS, and in both cases $g_{tt}$ can be written as $g_{tt}=-(A_1 g_1(r)+A_2g_2(r))^2$. Taking continuity of $g_{tt}$ and $g'_{tt}$ and some further manipulations lead to

$$\begin{aligned} A_1 g_1(r_0)+A_2 g_2(r_0)=\sqrt{1-\frac{Ar_0^2}{1+Cr_0^2}} \end{aligned}$$

(33)

$$\begin{aligned} A_1 g_1'(r)|_{r=r_0}+A_2 g_2'(r)|_{r=r_0}=\frac{r_0 A(n-2N-1)}{2N\sqrt{(1+Cr_0^2)(1+(C-A)r_0^2)}} \end{aligned}$$

(34)

and then $A_1$ and $A_2$ are determined as

$$\begin{aligned} A_1=\left. \frac{\beta \, g_2'(r)-\delta \, g_2(r)}{g_1(r)g_2'(r)-g_2(r)g_1'(r)}\right| _{r=r_0},\qquad A_2=-\left. \frac{\beta \, g_1'(r)-\delta \, g_1(r)}{g_1(r) g_2'(r)-g_2(r)g_1'(r)}\right| _{r=r_0} , \end{aligned}$$

(35)

where

$$\begin{aligned} \beta =\sqrt{\frac{1-(A-C) r^2_0}{1+C r^2_0}} ,\quad \delta =\frac{A r_0(n-2N-1)}{2N\sqrt{(1+C r^2_0)(1+(C-A)r_0^2)}} \end{aligned}$$

(36)

where $r_0$ is the star radius. For $0\le r \le r_{0}$, the pressure from Eq. (14) is determined as

$$\begin{aligned} p(r)=\rho \left( -1+ \frac{2N}{Cr^2(n-2N-1)+n-1}\left( 1+\frac{(1+Cr^2)(1-(A-C) r^2)}{A r}\frac{f_2'(r)}{f_2(r)}\right) \right) \end{aligned}$$

(37)

where $f_2(r)$ is as given in Eqs. (20–21) and (24–25) for Buchdahl and Finch Skea models respectively.

This completes the matching.

5 Physical properties

One of the most important properties for a star model is the compactness. For a given radius how much mass could be packed in. In Ref. [2, 3], Buchdahl has also obtained the compactness limit given by

$$\begin{aligned} r_0>9M/4 \end{aligned}$$

(38)

by requiring density to decrease monotonically from the center. This limit also follows from the constant density distribution [23] for which sound speed becomes infinite. This naturally defines the limiting compactness.

From Eq. (32), it is clear that $M(C= 0)> M(A>C) > M(A=C)$ indicating for a given star radius, mass is maximum for constant density distribution ($C=0$ and minimum for FS ($A=C$ and BVT ($A>C$) lies in between these two limiting distributions. This equation also suggests that volume of star goes as $r_0^{(n-1)/N)}$ for an effective density, $A/2(1+Cr_0^2)$. Now for the critical even dimension $n=2N+2$, we have volume going as $r_0^{2+1/N}$ collapsing to $r_0^2$ for $N\rightarrow \infty$. It seems to indicate that in the large N limit volume effectively becomes area! This clear shows that volume and thereby mass is maximum for $N=1$ and it goes on decreasing with N. This is because unlike Einstein gravity,¹ pure Lovelock gravity becomes weaker with increasing N. This means stars are densest for Einstein gravity and they become rarer as N increases.

On the hand if we look at density as given in Eq. (12), at the center it goes as $A^N$ for Buchdahl and $C^N$ for FS, and $A > C$ always. For a given star radius $r_0$, constant density $\rho _{const}$ will be the maximum, and hence $\rho (r=0)\le \rho _{const}$. Note that constant density cannot be reached for FS because it requires $C=0$.² Since $A\ge C$, hence we shall have $\rho _{FS}(r=0)\le \rho _{B}(r=0)\le \rho (const.)$. This clearly indicates the degree of compactness with constant density giving the upper limit while FS the lower limit, and other physically acceptable models lying in between.

As an aside we also give pressure for constant density star with $K=0$ in VT model, which means $C=0$ for Buchdahl, and it is given by

$$\begin{aligned} p = \frac{n-2N-1}{n-1}\left( -1+\frac{2N}{n-1}\frac{1}{\displaystyle {\frac{\sqrt{1-A r_0^2}}{\sqrt{1-A r^2}}-\frac{n-2N-1}{n-1}}}\right) \end{aligned}$$

(39)

for any Lovelock order N.

5.1 Density and pressure

For $K=0$ we have the constant density solution

$$\begin{aligned}g_{rr}=\frac{1}{1-A r^2,}\end{aligned}$$

with $C=0$ and if we have $T^t_t=-\rho$ where $\rho =constant$

$$\begin{aligned} A=\left( 2\rho \frac{(n-2N-1)!}{(n-1)!}\right) ^{1/N}.\end{aligned}$$

In the plots we have taken the above value for A and have set $\rho =1$, and have set $n=2N+2$, the critical dimension.

Fig. 1

Normalized density plots for both VT and FS in the critical dimensions $2N+2$ for $N=1, n=4$ Einstein (black) and $N=2, n=6$ GB (red). On the left is $K=7$ and $K=14$ on the right (color figure online)

Fig. 2

Normalized pressure plots for VT in the critical dimensions $2N+2$ for $N=1, n=4$ Einstein (black) and $N=2, n=6$ GB (red). On the left is $K=7$ and $K=14$ on the right (color figure online)

Fig. 3

Normalized pressure plots for FS in the critical dimensions $2N+2$ for $N=1, n=4$ Einstein (black) and $N=2, n=6$ GB (red). On the left is $K=7$ and $K=14$ on the right (color figure online)

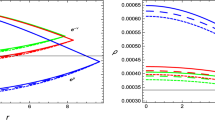
We are going to plot the normalized density and pressure $\rho /\rho (r=0), p/p(r=0)$ for VT and FS models for Einstein and GB gravity. We take $K=7, 14$ and $N=1, 2$ for $n=4, 6$. It turns out that normalized density has the same behaviour for both VT and FS (Fig. 1) while the pressure plots (Figs. 2, 3) differ.

Also note the constants A and C for $n=2N+2$ are given by

$$\begin{aligned} C=K\left( \frac{2}{(2N+1)!})^{1/N}\right) , \quad A=(K+1)\left( \frac{2}{(2N+1)!})^{1/N}\right) . \end{aligned}$$

This may however be noted that though the normalized plots for pressure look quite similar but the actual value differ quite significantly in various cases. In the Table 1 we give some representative values of pressure at $r=0$.

Table 1 The first row in the table indicates N, n, K while the second and the third give central pressure values for FS and B

For VT models, recall the relation $K_n=(K_{2N+2}-n+2N+2)/(n-2N-1)$. Let us consider $N=2$ GB case with $K_6=4$ giving $K_n=4, 3/2, 2/3, 1/4, 0$ for $n=6, 7, 8, 9, 10$, and similarly for $K_6=11$, $K_n=11, 5, \ldots , 0$ for $n=6, 7, \ldots , 17$. The normalized density and pressure (normalization done relative to the central value) for these cases are plotted in Figs. 4 and 5. As dimension increases density goes on increasing until it reaches constant density corresponding to $K=0$ determining the maximum dimension for a given initial $K_{2N+2}$. The pressure however does not show much marked difference between various cases.

Fig. 4

The normalized density, $\rho (r)/\rho (r=0)$, plots show in ascending order for the cases: $K_6=4$ and $n=6, 7, 8$ on the left and $K_6=11$ and $n=6, 7, 8$ on the right respectively

Fig. 5

The normalized pressure, $p(r)/p(r=0)$, plots show in ascending order for the cases: $K_6=4$ and $n=6, 7, 8$ on the left and $K_6=11$ and $n=6, 7, 8$ on the right respectively

5.2 Sound speed

The sound speed in a fluid is defined as

$$\begin{aligned}c^2_s\equiv \frac{dp}{d\rho }=\frac{p'(z)}{\rho '(z)}\end{aligned}$$

From the expression for pressure in Eq. (14), we have $p=\rho (-1+g(r))$ and so we write

$$\begin{aligned}\frac{p'}{\rho '}=-1+g(r)+\frac{\rho }{\rho '}g'(r)\end{aligned}$$

and

$$\begin{aligned} \frac{\rho }{\rho '} = -\frac{(1+Cr^2)((1+Cr^2)(n-2N-1)+2N)}{2CNr((1+Cr^2)(n-2N-1)+2N+2)} \end{aligned}$$

(40)

After some algebra and using the isotropy equation for $f_2''(r)$ we obtain

$$\begin{aligned} S\equiv c^2_s=\frac{1+Cr^2}{Cr(Cr^2(n-2N-1)+n+1)}\frac{f_2'(r)}{f_2(r)} \left( 1+\frac{(1+Cr^2)(1+(C-A)r^2)}{Ar}\frac{f_2'(r)}{f_2(r)}\right) \nonumber \\ \end{aligned}$$

(41)

In this expression we must use for $f_2(r)$ and its derivative the corresponding results obtained after the matching with the exterior solution. The plots for the sound speed, $v=c_s^2$ using the same values of the parameters as for the density and pressure plots and the constants C and A as given in in Eqs. (6) and (7). For FS we have $A=C$.

In Figs. 6 and 7 we plot square of sound speed, $v=c_s^2$ for VT and FS (For FS, we use the same constant C) for $N=1$ in black and $N=2$ in red for $K=7$ on the left and for $K=14$ on the right. Clearly sound speed is much lower for GB as compared to Einstein case. This would be the trend for pure Lovelock as N increases sound speed will go on decreasing. This is because gravitational potential going as $1/r^{(n-2N-1)/N}$ becomes weaker and weaker as N increases. In other words, distribution becomes less compact with increasing N.

Fig. 6

Square of sound speed plots for BVT corresponding to $N=1$ in black and $N=2$ in red for $K=7$ on the left and for $K=14$ on the right (color figure online)

Fig. 7

Square of sound speed plots for FS corresponding to $N=1$ in black and $N=2$ in red for $K=7$ on the left and for $K=14$ on the right (color figure online)

6 Discussion

In the paper [1] we had considered the general Buchdahl ansatz [2, 3] covering a class of physically interesting star models for Einstein gravity and had shown that how a 4-dimensional solution could be taken over to higher dimensions by properly redefining the Vaidya–Tikekar parameter K marking deviation from sphericity of 3-space geometry. It is remarkable that this geometrical property has the physical imprint in the requirement that K has to be non-negative for density to monotonically decrease outwards. This happens because the only equation to be solved is that of the pressure isotropy which remains in the Gauss form in all dimensions.

In this paper we extend this framework from Einstein to pure Lovelock gravity and show that the same features persist. It turns out that for a given N, the equation has the same Gauss form for BVT while for FS it is the Bessel equation in all dimensions $\ge$4. Thus fluid solutions for a star interior have universal character relative to a suitably defined variable and the K parameter for VT models. This universal behavior is true only for pure Lovelock gravity and hence this is yet another of its distinguishing features [6, 24].

One of the most pertinent questions for a star model is its compactness. The constant density distribution is obviously the most compact with star radius, $r_0>9M/4$, the Buchdahl limit [2, 3].³ It turns out that the other end of lower bound is defined by the FS model, and all other models of this ansatz lie between these two limiting distributions. This is reflected clearly in mass and density spectrum as $M_{FS}(A=C)< M_{B}(A>C) < M_{\rho const.}(C=0)$ and $\rho _{FS}(r=0)\le \rho _{B}(r=0)\le \rho (const.)$. Also note that FS model does not admit constant density distribution, this is because the two limiting cases must be exclusive. This is indeed a very important and interesting property which, so far as we know, has not been earlier reported in the literature.

As N increases gravitational potential for pure Lovelock gravity becomes weaker and hence consequently star interior becomes rarer;i.e. for a given radius the most compact distribution would be for $N=1$ Einstein and it goes on becoming less compact with increasing N. What happens is that volume in the critical dimension $n=2N+2$ goes as $r_0^{2+1/N}$ which collapses to two dimensional volume—area in the limit $N\rightarrow \infty$. It indicates that in large N limit space dimension seems to collapse to two! It clearly shows volume and thereby mass for a given star radius is maximum for $N=1$ Einstein gravity, and hence it is most compact.

We have shown that 4-dimensional solution could be taken over to higher dimensions in both Einstein (paper [1]) as well as in pure Lovelock theory. It turns out that higher dimensional solution is always stable for Einstein gravity while for pure Lovelock it requires $n\ge 3N+1$ [23]. The dimension $n=3N+1$ is distinguished for Lovelock potential going 1 / r [24].

As indicated in Introduction, it would be interesting in future to study solution generating schemes [18,19,20] for pure Lovelock gravity.