1 Introduction

Ever since the formulation of Einstein’s field equations researchers have been venturing in the search of exact solutions with certain viable geometrical and physical conditions. Such findings are astrophysically significant because they enable us to find the distribution of matter in the interior of stellar objects in terms of simple algebraic relations. Due to the strong nonlinearity of Einstein’s field equations and the lack of a comprehensive algorithm to generate all solutions, it becomes difficult to obtain new exact solutions. A good number of exact solutions of Einstein’s field equations are known till date but not all of them are physically relevant in the description of relativistic structure of compact stellar objects. There exist a number of comprehensive collections (Delgaty and Lake 1998; Stephani et al. 2003) of static, spherically symmetric solutions which provide useful guide to the literature. Oppenheimer and Volkoff (1939) are the pioneers in this field who analyzed and determined the maximum mass of very compact astrophysical objects. There are several astrophysical objects such as neutron star (bound by gravity) or self-bound strange quark star (bound by the strong interaction) where one needs to reconsider the equation of state (EOS) of matter involving energy densities of the order of \(10^{15}~\mbox{g}\,\mbox{cm}^{-3}\) or higher, exceeding the normal nuclear matter density.

Recent observations show that the estimated mass and radius of several compact objects such as X-ray pulsar Her X-1, X-ray burster 4U 1820-30, millisecond pulsar SAX J 1808.4-3658, X-ray sources 4U 1728-34, PSR 0943+10 and RX J185635-3754 are not compatible with the standard neutron star models (Dey et al. 1998; Li et al. 1999; Weber 2005). In the formalism of such super dense stars, local isotropy is a common assumption. But the theoretical investigations made in the last few decades strongly suggest that at a density of the order of \(10^{15}~\mbox{g}\,\mbox{cm}^{-3}\), nuclear matter may be anisotropic when its interactions are relativistic (Ruderman 1972) and it is also important to include the pressure anisotropy in the fluid approximation to describe the matter distribution inside such astrophysical objects.

No astrophysical object in the real universe may necessarily be entirely composed of perfect fluid (principle stresses equal). The first extensive study on the effect of pressure anisotropy on the structure of such massive objects in the framework of general relativity was made by Bowers and Liang (1974). The importance and physical reasons of inclusion of anisotropic pressure in the solution may be found in the following works (Herrera and Santos 1997; Ivanov 2002). Dev and Gleiser (2002) demonstrated that pressure anisotropy affects the physical properties, stability and structure of stellar matter. The stability of stellar bodies is improved for positive measure of anisotropy when compared to configurations of isotropic stellar objects. It has also been showed in their successive works (Dev and Gleiser 2003; Gleiser and Dev 2004) that the presence of anisotropic pressures enhances the stability of the configuration under radial adiabatic perturbations as compared to isotropic matter.

Electrically neutral/charged anisotropic stellar models of strange quark stars within the framework of linear equation of state (EOS) based on MIT bag model together with a particular choice of metric potentials/mass function have been taken into consideration in the following works (Mak et al. 2002; Mak and Harko 2004; Sharma and Maharaj 2007; Esculpi and Alomá 2010; Komathiraj and Maharaj 2011; Takisa and Maharaj 2013a, 2013b; Maharaj and Takisa 2012; Rahaman et al. 2012; Kalam et al. 2013; Thirukkanesh and Ragel 2013, 2014; Sharma et al. 2006; Deb et al. 2012; Sharma and Ratanpal 2013; Maharaj et al. 2014; Sunzu et al. 2014a, 2014b).

Being inspired by the aforementioned recent works we intend to develop some new analytical relativistic anisotropic stellar models by using Tolman VII type metric function within the framework of linear equation of state based on MIT bag model. Our analysis depends on several mathematical key assumptions. The form of metric potential ensures that the metric function is nonsingular, continuous, and well behaved in the interior of the star. This is one of the desirable features for the model on physical grounds. The solutions obtained in this work are expected to provide simplified but easy to mathematically analyzed stellar models with nonzero super-high surface density which could reasonably model the stellar core of an bare strange quark star by satisfying applicable physical boundary conditions.

The paper is organized as follows. In Sect. 2 we have presented the Einstein’s field equations (EFE’s). Section 3 provides the solution of EFE’s for a particular choice of one of the metric potential together with the linear equation of state. In Sect. 4 we have matched our interior solution to the exterior Schwarzschild spacetime. Some physical properties are discussed in Sects. 5–8 and finally Sect. 9 concludes the work.

2 Einstein field equations

To describe the interior of a static spherically symmetric distribution of matter the line element can be taken in the standard form as (Tolman 1939; Oppenheimer and Volkoff 1939),Footnote 1

$$ ds^{2}=e^{\nu(r)}dt^{2}-e^{\lambda(r)}dr^{2}-r^{2} \bigl(d\theta^{2}+\sin^{2}\theta d\phi^{2}\bigr), $$
(2.1)

where \(\lambda\) and \(\nu\) are the functions of radial coordinate \(r\) only.

Let us further assume that the matter distribution inside the compact star is locally anisotropic in nature whose energy momentum tensor given by the following:

$$ T_{\nu}^{\mu}= \left(\textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \rho & 0 & 0 & 0 \\ 0 & -P_{r} & 0 & 0 \\ 0 & 0 & -P_{t} & 0 \\ 0 & 0 & 0 & -P_{t} \\ \end{array}\displaystyle \right) $$
(2.2)

where \(\rho\) is the matter density, \(P_{r}\) and \(P_{t}\) are respectively the radial and the tangential pressure of the fluid distribution.

Taking \(G=1=c\), Einstein field equations can be written as,

$$\begin{aligned} &{\kappa\rho=\frac{1}{r^{2}} \bigl[r\bigl(1-e^{-\lambda}\bigr) \bigr]^{\prime},} \end{aligned}$$
(2.3)
$$\begin{aligned} &{\kappa P_{r}=-\frac{1}{r^{2}}\bigl(1-e^{-\lambda} \bigr)+\frac{\nu^{\prime}}{r}e^{-\lambda},} \end{aligned}$$
(2.4)
$$\begin{aligned} &{\kappa P_{t}=\frac{e^{-\lambda}}{4} \biggl(2\nu^{\prime\prime}+ \nu^{\prime2}+ \frac{2\nu^{\prime}}{r}-\nu^{\prime}\lambda^{\prime}- \frac{2\lambda^{\prime}}{r} \biggr),} \end{aligned}$$
(2.5)

where \(\kappa=8\pi\) and ′ denotes the derivative with respect to the radial coordinate \(r\).

By defining a quantity, \(m(r)\), which represents the gravitational mass contained in a sphere of radius \(r\), by the following expression,

$$ e^{-\lambda}=1-\frac{2m(r)}{r}, $$
(2.6)

one can integrate Eq. (2.3) which yields,

$$ m(r)=\frac{\kappa}{2}\int_{0}^{r} \rho(\omega)\omega^{2}d\omega. $$
(2.7)

For the regularity at the center, we require \(\lim_{r\rightarrow 0}m(r)=0\). And using Eqs. (2.4) and (2.5), one can arrive at the following equations,

$$\begin{aligned} &{\nu^{\prime}=\frac{(\kappa rP_{r}+2m/r^{2})}{(1-2m/r)},} \end{aligned}$$
(2.8)
$$\begin{aligned} &{\frac{dP_{r}}{dr}=-\frac{(P_{r}+\rho)}{2}\nu^{\prime}+ \frac{2(P_{t}-P_{r})}{r}.} \end{aligned}$$
(2.9)

Finally combining (2.8) and (2.9), one gets the anisotropic generalization of well-known Tolman-Oppenheimer-Volkoff (TOV) equation of hydrostatic equilibrium for stellar configuration (Oppenheimer and Volkoff 1939; Bowers and Liang 1974),

$$ \frac{dP_{r}}{dr}=-\frac{(P_{r}+\rho)}{2}\frac{(\kappa rP_{r}+2m/r^{2})}{(1-2m/r)}+ \frac{2(P_{t}-P_{r})}{r} $$
(2.10)

It is to be noted that the presence of an additional term, \(2(P_{t}-P_{r})/r\), represents additional “force” due to the pressure anisotropy, which is directed outward when \(P_{t}>P_{r}\) and inward when \(P_{t}< P_{r}\). The existence of repulsive force, \(P_{t}>P_{r}\), allows the construction of more compact distribution when using anisotropic fluid than when using isotropic perfect fluid, \(P_{t}=P_{r}\) (León 1987; Gokhroo and Mehra 1994).

From Eqs. (2.4) and (2.5) one gets,

$$\begin{aligned} &{\frac{e^{-\lambda}}{4} \biggl(2\nu^{\prime\prime}+ \nu^{\prime2} +\frac{2\nu^{\prime}}{r}-\nu^{\prime}\lambda^{\prime}- \frac{2\lambda^{\prime}}{r} \biggr)} \\ &{\quad {}+\frac{1}{r^{2}}\bigl(1-e^{-\lambda}\bigr)- \frac{\nu^{\prime}}{r}e^{-\lambda}=\kappa(P_{t}-P_{r}).} \end{aligned}$$
(2.11)

Introducing the transformations

$$ x=r^{2},\qquad Z(x)=e^{-\lambda(r)}, \quad \mbox{and} \quad y(x)=e^{\nu(r)} $$
(2.12)

Eqs. (2.3)–(2.5), and (2.7) take the following form,

$$\begin{aligned} &{\kappa\rho = \frac{1-Z}{x}-2\dot{Z},} \end{aligned}$$
(2.13)
$$\begin{aligned} &{\kappa P_{r} = 2Z\frac{\dot{y}}{y}-\frac{1-Z}{x},} \end{aligned}$$
(2.14)
$$\begin{aligned} &{\kappa P_{t} = Z \biggl[ \biggl(\frac{2\ddot{y}}{y}- \frac{\dot{y}^{2}}{y^{2}} \biggr)x+\frac{2\dot{y}}{y} \biggr] +\dot{Z} \biggl(1+x \frac{\dot{y}}{y} \biggr),} \end{aligned}$$
(2.15)
$$\begin{aligned} &{m(x) = \frac{\kappa}{4}\int_{0}^{x} \sqrt{\omega}\rho(\omega)d\omega,} \end{aligned}$$
(2.16)

where \(\dot{\hphantom{\ }}\) denotes the derivative with respect to \(x\).

Introducing \(\Delta=P_{t}-P_{r}\), the anisotropic factor, which measures the pressure anisotropy within the star and combining Eqs. (2.14) and (2.15) one obtains,

$$ \kappa\Delta=Z \biggl(\frac{2\ddot{y}}{y}-\frac{\dot{y}^{2}}{y^{2}} \biggr)x +\dot{Z} \biggl(1+x\frac{\dot{y}}{y} \biggr) +\frac{1-Z}{x}. $$
(2.17)

Equation (2.17) is first order linear in \(Z\). An algorithm presented by Herrera et al. (2008) shows that all static spherically symmetric anisotropic solutions of Einstein’s field equations may be generated from Eq. (2.11) by two generating functions \(\varPi\) and \(y(x)\).

$$ \frac{dZ}{dx}+P(x)Z=Q(x), $$

with the solution,

$$ Z=e^{-\int{P(x)}\,dx} \biggl[\int \bigl(e^{\int{P(x)}\,dx}Q(x) \bigr)dx +K \biggr], $$

where, \(K\) is a constant of integration and

$$\begin{aligned} &{P(x)=\frac{(\frac{2x\ddot{y}}{y}-x\frac{\dot{y}^{2}}{y^{2}} -\frac{1}{x})}{(1+x\frac{\dot{y}}{y})},} \\ &{Q(x)=\frac{\varPi-\frac{1}{x}}{(1+x\frac{\dot{y}}{y})},} \\ &{\varPi =\kappa\Delta.} \end{aligned}$$

Once the metric potential \(Z\) is obtained, the other physical variables may be expressed in terms of the generating functions \(\varPi\) and \(y\) and the equation of state may be extracted, parametrically, from Eqs. (2.13) and (2.14).

In this work we rather interested in specifying the equation of state first and one of the metric function \(Z\), obtaining the generating function \(y\), and then the other generating function, \(\varPi\), from Eq. (2.17) . To accomplish this we assume that the radial pressure, \(P_{r}\), and the matter density \(\rho\) are related by a linear equation of state of the following form,

$$ P_{r}=\alpha\rho-\beta, $$
(2.18)

where \(\alpha\) and \(\beta\) are constants.

Using Eq. (2.18) together with Eqs. (2.13) and (2.14) we obtain

$$ \frac{\dot{y}}{y}=(1+\alpha)\frac{1-Z}{2xZ}-\alpha \frac{\dot{Z}}{Z}-\frac{\kappa\beta}{2Z}. $$
(2.19)

3 Solution of the Einstein field equations

To solve the system of Eqs. (2.13)–(2.16) let us take Tolman VII potential given by

$$ e^{-\lambda}=1-\frac{x}{R^{2}}+\frac{4}{A^{4}}x^{2}, $$
(3.1)

therefore,

$$ Z=1-ax+bx^{2}, $$
(3.2)

where, \(a=1/R^{2}\) and \(b=4/A^{4}\).

After feeding \(Z\) from Eq. (3.2) into Eq. (2.19) we obtain,

$$ \frac{\dot{y}}{y}=\frac{C_{1}+C_{2} x}{2(1-ax+bx^{2})}, $$
(3.3)

and integrating, we get,

$$\begin{aligned} \ln y =& \frac{1}{\sqrt{4b-a^{2}}} \biggl(C_{1}+ \frac{aC_{2}}{2b} \biggr) \arctan \biggl[\frac{2bx-a}{\sqrt{4b-a^{2}}} \biggr] \\ &{}+\frac{C_{2}}{4b}\ln\bigl(1-ax+bx^{2}\bigr)+C, \end{aligned}$$
(3.4)

where, \(C_{1}=a(1+3\alpha)-\kappa\beta\), \(C_{2}=-b(1+5\alpha)\), and \(C\) is a constant of integration to be determined by using an appropriate physical boundary condition. Therefore Eqs. (2.13)–(2.16), with the help of Eqs. (3.2) and (3.4) become,

$$\begin{aligned} &{\kappa\rho = 3a-5bx,} \end{aligned}$$
(3.5)
$$\begin{aligned} &{\kappa P_{r} = (3a\alpha-\kappa\beta)-5b\alpha x,} \end{aligned}$$
(3.6)
$$\begin{aligned} &{\kappa P_{t} = \kappa P_{r}+\kappa \Delta,} \end{aligned}$$
(3.7)
$$\begin{aligned} &{m(x) = \frac{1}{2}x^{3/2}(a-bx),} \end{aligned}$$
(3.8)

where

$$\begin{aligned} \kappa\Delta =&\frac{x}{4(1-ax+bx^{2})} \bigl[\bigl(2aC_{1}+C_{1}^{2}+4b+4C_{2} \bigr) \\ &{}-(4ab+2aC_{2}-4bC_{1}-2C_{1}C_{2})x \\ &{}+\bigl(4b^{2}+C_{2}^{2}\bigr)x^{2} \bigr]. \end{aligned}$$

4 Physical acceptability conditions

For the well behaved nature of the solution, the following conditions should be satisfied (Abreu et al. 2007):

  1. (i)

    The metric potentials should be free from singularities inside the radius of the star moreover the fluid sphere should satisfy \(e^{\nu(0)}=\) constant, and \(e^{-\lambda(0)}=1\).

  2. (ii)

    The density \(\rho\) and pressures \(P_{r},\,P_{t}\) should be positive inside the fluid configuration.

  3. (iii)

    The radial pressure \(P_{r}\) must be vanishing but the tangential pressure \(P_{t}\) may not necessarily vanish at the boundary \(r=r_{\varSigma}\). However, the radial pressure is equal to the tangential pressure at the center of the fluid sphere, i.e., pressure anisotropy vanishes at the center, \(\Delta(0)=0\) (Bowers and Liang 1974, Ivanov 2002) and \(\Delta(r=r_{\varSigma})=\frac{\kappa}{C}P_{t}(r_{\varSigma})>0\) (Böhmer and Harko 2006).

  4. (iv)

    At the center, \(r=0\), \(dP_{r}/dr=0\) and \(d^{2}P_{r}/dr^{2}<0\) so the radial pressure gradient \(dP_{r}/dr\leq0\) for \(0\leq r \leq r_{\varSigma}\).

  5. (v)

    At the center, \(r=0\), \(d\rho/dr=0\) and \(d^{2}\rho/dr^{2}<0\) so the density gradient \(d\rho/dr\leq0\) for \(0\leq r\leq r_{\varSigma}\).

  6. (vi)

    A physically acceptable fluid sphere must satisfy the causality conditions, the radial and tangential adiabatic speeds of sound should less than the speed of light. In the unit \(c=1\) the causality conditions take the form \(0< v_{sr}^{2}=dP_{r}/d\rho\leq 1\) and \(0< v_{st}^{2}=dP_{t}/d\rho\leq 1\).

  7. (vii)

    The interior solution should satisfy either

    • strong energy condition (SEC) \(\rho-P_{r}- 2P_{t}\geq0,\,\rho-P_{r}\geq0,\,\rho-P_{t}\geq0\) or

    • dominant energy condition (DEC) \(\rho\geq P_{r}\) and \(\rho\geq P_{t}\).

  8. (viii)

    The interior solution should continuously match with the exterior Schwarzschild solution.

Conditions (iv) and (v) imply that pressure and density should be maximum at the center and monotonically decreasing towards the surface.

5 Physical boundary conditions

5.1 Mass to radius ratio

The interior solution should match continuously with an exterior Schwarzschild solution,

$$\begin{aligned} ds^{2} =& \biggl(1-\frac{2M}{r} \biggr)dt^{2}- \biggl(1-\frac{2M}{r} \biggr)^{-1}dr^{2} \\ &{}-r^{2} \bigl(d\theta^{2}+\sin^{2}\theta d \phi^{2} \bigr); \quad r\geq r_{\varSigma}. \end{aligned}$$
(5.1.1)

This requires the continuity of \(e^{\nu}\) and \(e^{\lambda}\) across the boundary \(r=r_{\varSigma}\),

$$ e^{\nu(r_{\varSigma})}=e^{{-\lambda(r_{\varSigma})}}= \biggl(1-\frac{2M}{r_{\varSigma}} \biggr), $$
(5.1.2)

which sets the compactness parameter,

$$ \frac{2M}{r_{\varSigma}}=ar_{\varSigma}-br_{\varSigma}^{2}. $$
(5.1.3)

5.2 Determination of the constant of integration \(C\)

From Eq. (5.1.2), we get,

$$\begin{aligned} C =& \ln \biggl(1-\frac{2M}{r_{\varSigma}} \biggr) -\frac{1}{\sqrt{4b-a^{2}}} \biggl(C_{1}+\frac{aC_{2}}{2b} \biggr) \\ &{}\times \arctan \biggl[\frac{2br_{\varSigma}^{2}-a}{\sqrt{4b-a^{2}}} \biggr] -\frac{C_{2}}{4b}\ln \bigl(1-ar_{\varSigma}^{2}+br_{\varSigma}^{4} \bigr). \end{aligned}$$

6 Some features

6.1 Mass function

The mass function within the radius \(r\) can be obtained by Eq. (3.8) or by,

$$ m(r)=\frac{1}{2}r^{3}\bigl(a-br^{2} \bigr). $$
(6.1)

6.2 Mass radius relation

The ratio of mass to the radius of a compact star can not be arbitrarily large. Buchdahl (1959) showed that for a \((3+1)\)-dimensional fluid sphere \(2M/r_{\varSigma}<8/9\). To see the ratio of mass to the radius for our model we calculate the compactness of the star given by,

$$ u(r)=\frac{2m(r)}{r}= r^{2}\bigl(a-br^{2} \bigr). $$
(6.2)

6.3 Surface redshift

The surface redshift \(z_{s}\) of a star is given by

$$ z_{s}= \biggl(1-\frac{2M}{r_{\varSigma}} \biggr)^{-\frac{1}{2}}-1. $$
(6.1)

7 Construction of physically realistic fluid spheres

7.1 Pressure and density gradients

A straightforward differentiation of the pressure and density equations (3.5)–(3.7) with respect to the auxiliary variable \(x\) one obtains the pressure and density gradients respectively,

$$\begin{aligned} &{\kappa\frac{d\rho}{dx}=-5b< 0,} \end{aligned}$$
(7.1.1)
$$\begin{aligned} &{\kappa\frac{dP_{r}}{dx}=-5b\alpha< 0} \end{aligned}$$
(7.1.2)
$$\begin{aligned} &{\kappa\frac{dP_{t}}{dx}=\kappa\frac{dP_{r}}{dx}+\kappa \frac{d\Delta}{dx},} \end{aligned}$$
(7.1.3)

where

$$\begin{aligned} \frac{d\Delta}{dx} =&\frac{1}{4(1-ax+bx^{2})^{2}} \bigl[\bigl(2aC_{1}+C_{1}^{2}+4b+4C_{2} \bigr) \\ &{}+(8bC_{1}+4C_{1}C_{2}-8ab-4aC_{2})x \\ &{}+\bigl(4a^{2}b+2a^{2}C_{2}-6abC_{1}-2aC_{1}C_{2}-bC_{1}^{2} \\ &{}+8b^{2}-4bC_{2}+3C_{2}^{2} \bigr)x^{2}-\bigl(8ab^{2}+2aC_{2}^{2} \bigr)x^{3} \\ &{}+\bigl(4b^{3}+bC_{2}^{2}\bigr)x^{4} \bigr]. \end{aligned}$$

8 Relativistic adiabatic index and stability

The stability of a relativistic anisotropic sphere is related to the adiabatic index \(\varGamma\) (the ratio of two specific heats) defined by (Chan et al. 1993),

$$ \varGamma=\frac{\rho+P_{r}}{P_{r}}\frac{dP_{r}}{d\rho}. $$
(8.1)

It is well known that the collapsing condition for a Newtonian isotropic sphere is \(\varGamma<4/3\) (Bondi 1964). For an anisotropic general relativistic sphere the collapsing condition becomes

$$ \varGamma< \frac{4}{3}+ \biggl[\frac{4}{3} \frac{(P_{t0}-P_{r0})}{|P_{r0}^{\prime}|r}+\frac{1}{2} \kappa\frac{\rho_{0}P_{r0}}{|P_{r0}^{\prime}|}r \biggr]_{\max}, $$
(8.2)

where, \(P_{r0}\), \(P_{t0}\), and \(\rho_{0}\) are the initial radial, tangential, and energy density in static equilibrium satisfying Eq. (2.10). The first and last term inside the square brackets, the anisotropic and relativistic corrections respectively, being positive quantities, increase the unstable range of \(\varGamma\) (Herrera et al. 1979; Chan et al. 1993).

To study the stability of anisotropic stars under the radial perturbations Herrera (1992) introduced the concept of “cracking”, breaking of self-gravitating spheres, which results from the appearance of total radial forces of different signs in different regions of the sphere once the equilibrium is perturbed. The occurrence of such a “cracking” may be induced by the local anisotropy of the fluid.

By this concept of cracking Abreu et al. (2007) proved that the region of the anisotropic fluid sphere where \(-1\leq v_{st}^{2}-v_{sr}^{2}\leq0\) is potentially stable but the region where \(0< v_{st}^{2}-v_{sr}^{2}\leq 1\) is potentially unstable.

The radial and tangential speeds of sound of the strange star are obtained from Eqs. (3.5)–(3.7),

$$\begin{aligned} v_{sr}^{2} =&\frac{dP_{r}}{d\rho}=\alpha< 1, \end{aligned}$$
(8.3)
$$\begin{aligned} v_{st}^{2} =&\frac{dP_{t}}{d\rho}=\alpha+\frac{d\Delta}{d\rho}. \end{aligned}$$
(8.4)

To remain \(-1\leq v_{st}^{2}-v_{sr}^{2}\leq0\) throughout the fluid distribution we require \(d\Delta/d\rho\leq0\). As we have \(d\rho/dx<0\), we further require that \(d\Delta/dx\geq0\) which will be satisfied as long as \(\Delta\) is an increasing function of \(x\).

9 Physical analysis

As we require \(\kappa\rho_{s}\geq0\) for \(0\leq r\leq r_{\varSigma}\), the radius of the fluid distribution should satisfy \(r_{\varSigma}\leq \sqrt{3a/5b}\). To generate an anisotropic fluid sphere we set, \(a=0.0248~(\mbox{km}^{-2})\) and \(b=0.000178~(\mbox{km}^{-4})\). These values correspond to the surface density \(\kappa\rho_{s}=0.06154840~\mbox{km}^{-2}\) (\(\rho_{s}=3.29\times10^{15}~\mbox{g}\,\mbox{cm}^{-3}\)) and central density \(\kappa\rho_{c}= 0.0744~\mbox{km}^{-2}\) \((\rho_{c}=3.98\times10^{15}~\mbox{g}\,\mbox{cm}^{-3})\). We also set, \(\alpha=1/3\) and \(\beta=\rho_{s}/3\). For these choices the maximum value of compactness parameter is obtained \((2M/r_{\varSigma})_{\max}=0.3209\). The total gravitational mass and other physical quantities are calculated as \(M_{\max}=0.41M_{\odot}\), radius \(r_{\varSigma}=3.8~\mbox{km}\), surface redshift \(z_{s}=0.2135\).

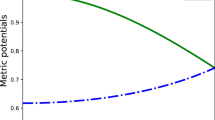
The profiles of \(e^{\nu}\) and \(e^{\lambda}\) are plotted in Fig. 1. The profiles of \(\rho,\,P_{r},\,P_{t}\) are shown in Figs. 2 and 3 respectively which show the positivity of those quantities inside the fluid sphere. The anisotropic factor \(\Delta=P_{t}-P_{r}\) is shown in Fig. 4. The figure indicates that \(\Delta\geq0\) for our model. The strong and dominant energy conditions are presented in Figs. 5 and 6. The profiles of \(v_{st}\) and \(v_{sr}\) are presented in Fig. 7, from which it is clear that the speeds are not superluminal for our model sphere and hence the causality conditions are satisfied. The profile of \(m(r)\) is given in Fig. 8, which shows that the mass function is monotonically increasing function of \(r\) and is positive inside the stellar interior. The stability of the model anisotropic sphere has been investigated by the relativistic adiabatic index \(\varGamma\) and \(-1\leq v_{st}^{2}-v_{sr}^{2}\leq0\) which is presented in Figs. 9 and 10 respectively.

Fig. 1
figure 1

The metric functions \(e^{\nu}\) and \(e^{\lambda}\). The solid (blue) line corresponds to \(e^{\nu}\) and the dash-doted (red) line corresponds to \(e^{\lambda}\) for the anisotropic fluid sphere generated with \(a=0.0248~\mbox{km}^{-2}\), \(b= 0.000178~\mbox{km}^{-4}\), and \(R=3.8~\mbox{km}\)

Full size image
Fig. 2
figure 2

Behavior of energy density \(\rho\) (\(\mbox{MeV}\,\mbox{fm}^{-3}\)) for the same stellar configuration as in Fig. 1

Full size image
Fig. 3
figure 3

Behaviors of pressures in the unit of MeV fm−3 for the stellar configuration as in Fig. 1. The solid (blue) line corresponds to radial pressure, \(P_{r}\), and the dashed (red) line corresponds to the tangential pressure, \(P_{t}\)

Full size image
Fig. 4
figure 4

Behaviour of pressure anisotropy \(\Delta\) in the unit of MeV fm−3 for the stellar configuration as in Fig. 1

Full size image
Fig. 5
figure 5

The strong energy condition for the stellar configuration as in Fig. 1. The solid (blue) line corresponds to \(\rho-P_{r}\), the dash-doted (red) line corresponds to \(\rho-P_{t}\), and the long dashed (black) line corresponds to \(\rho-P_{r}-2P_{t}\)

Full size image
Fig. 6
figure 6

The dominant energy condition for the stellar configuration as in Fig. 1. The solid (blue) line corresponds to \(\rho-P_{r}\) and the dash-doted (red) line corresponds to \(\rho-P_{t}\)

Full size image
Fig. 7
figure 7

The adiabatic speeds of sound for the same stellar configuration as in Fig. 1. The solid (blue) line corresponds to the radial velocity of sound, \(v_{sr}=\sqrt{dP_{r}/d\rho}\), and the dash-doted (red) line corresponds to tangential velocity of sound, \(v_{st}=\sqrt{dP_{t}/d\rho}\)

Full size image
Fig. 8
figure 8

The mass function \(m(r)\) for the same stellar configuration as in Fig. 1

Full size image
Fig. 9
figure 9

The relativistic adiabatic index \(\varGamma\) for the same stellar configuration as in Fig. 1

Full size image
Fig. 10
figure 10

The difference \(v_{st}^{2}-v_{sr}^{2}\) for the same stellar configuration as in Fig. 1

Full size image

10 Concluding remarks

Under the ad hoc assumption on one of the metric potentials \((e^{-\lambda}=1-ax+bx^{2})\) together with the linear equation of state \(P_{r}=(\rho-\rho_{s})/3\) we have solved EFE’s and presented a particular simple class of static spherically symmetric anisotropic strange star models in Tolman VII spacetime.

In the construction of the stellar models we further assumed \(P_{t}>P_{r}\,(\Delta>0)\). The stability is examined by the relativistic adiabatic index, and the adiabatic radial and tangential sound speeds. Even though it is yet unclear to what extent this metric can be applied to describe strange quark stars but the stellar models obtained here with such physical features could play a significant role in the description of internal structure of bare strange quark stars.