1 Introduction

Most of space and astrophysical plasmas environments are observed to have quasi-Maxwellian particle distribution function with non-Maxwellian suprathermal tails (Pierrard et al. 1996; Hellberg and Mace 2002; Shahmansouri 2012). The distribution of superthermal particles is characterized by the spectral index κ, so called kappa-distribution function. The spectral index is a measure of energy spectrum slope of suprathermal particles forming the tail of velocity distribution function. Its smaller value indicates more suprathermal particles in the tail of distribution function, i.e., in the harder side (higher side) of energy spectrum. Kappa distribution approaches the Maxwellian as κ→∞ (Hellberg and Mace 2002). The general form of the kappa distribution was first suggested by Vasyliunas (1968) to model space plasma. Rightly, this was sustained by observations made by The Voyager PLS (Sittler et al. 1983; Barbosa and Kurth 1993) and the Cassini CAPS (Cassini Plasma Spectrometer) (Young et al. 2005). In view of those observations, the electron distribution in Saturn’s magnetosphere is supposed to be the sum of two kappa distribution.

Very recently, CAPS/ELS and MIMI/LEMMS data was analyses (Schippers et al. 2008) from the Cassini spacecraft orbiting Saturn over a range of 5.4 R s (where R s =60300 km is the Saturn’s radius), it was shown that both cool and hot electrons population are κ-distributed, with independent values of κ. Indeed, the hot “suprathermal” component has much lower density than the bulk “thermal” component. These bi-kappa fits have been observed over a wide range of the magnetosphere from 5.4 to 18 R s Saturn radii.

Afterward, these investigations have attracted the attention of many researchers to study the nonlinear wave structures in plasmas with superthermal tails (Moslem and El-Taibany 2005; Choi et al. 2011; Saini et al. 2014, and references therein) and even to investigate the characteristics of solitary structures in different plasma systems.

For example, Baluku and Hellberg (2012) studied the existence domains and characteristic behaviors of the ion acoustic soliton to exist in an unmagnetized plasma with two temperature kappa-distributed electrons. Lately, Shahmansouri and Alinejad (2013a, 2013b) studied the linear and nonlinear excitations of arbitrary amplitude ion acoustic solitary waves in a magnetized plasma comprising two temperature electrons and cold ions. It was observed that a small value of the hot electrons population shift the allowed interval of Mach numbers to a lower value. Both compressive and rarefactive solitary structures have been observed in two temperature electron plasmas. Lastly, Panwar et al. (2014) studied the oblique propagation of ion acoustic cnoidal waves in magnetized plasma consisting of cold ions and two temperature superthermal electrons modeled by kappa-type distributions. They found that the density ratio of hot electrons to ions significantly modifies compressive/refractive wave structures.

Elsewhere, the waves observed in laboratory and space plasmas are certainly not bounded in unbounded planar geometry. Recent theoretical studies indicate that the properties of solitary waves in bounded nonplanar spherical geometry differ from that in unbounded planar geometry (Xue 2003; Annou and Annou 2012b). It is now well known that the transverse perturbation (which always exists in the higher dimensional system) may not only introduce anisotropy into the system but also modify the structure and stability of the solution (Xie et al. 1998). The combined effects of both nonplanar geometry and transverse perturbation on the DAWs have been considered by several authors (Annou and Annou 2011, 2012a).

Up to now, however, there are only a few investigations about the effect of superthermal particles on the characteristics of solitary waves of nonplanar solitary waves in non-Maxwellian plasmas. Therefore, motivated by all previous work, in this paper, we will study the combined effect of bounded spherical geometry and the transverse perturbation in two-temperature electron plasma. The formation of ion acoustic waves generated in the plasma is studied for different parameters. For this purpose, electrons are modeled by bi-kappa distribution. The model is applied to Saturn’s magnetosphere, where electrons are well fitted by such a double-kappa distribution.

The manuscript is arranged in the following fashion. A details description of the kappa distribution is presented in Sect. 2. In Sect. 3 we present the relevant equation governing the dynamics of nonlinear ion acoustic waves. This is followed in Sect. 4 by the use of the reductive perturbation method to derive the spherical Kadomtsev-Petviashvili equation. Afterward, the solitary wave solution is presented in Sect. 5. Results are discussed in Sect. 6. Application to Saturn’s magnetosphere is presented in Sect. 7. The concluding remarks are summarized in the concluding Sect. 7.

2 Basic equations

A three-dimensional isotopic Kappa distribution is given by Baluku and Hellberg (2008, 2012)

$$ f_{\kappa} (v)= \frac{n_{e0}}{\pi v_{\theta}^{2} \kappa^{3/2}} \frac{\varGamma ( \kappa )}{\varGamma ( \kappa-1/2 )} \biggl( 1+ \frac{v^{2}}{\kappa v_{\vartheta}^{2}} \biggr)^{- ( \kappa+1 )}, $$
(1)

where ϑ is the most probable speed (effective thermal speed), related to the usual thermal velocity V t =(k B T/m)1/2 by ϑ=[(2κ−3)/κ]V t , T being the characteristic kinetic temperature, i.e. the temperature of the equivalent Maxwellian with the same average kinetic energy (Hellberg and Mace 2002), n e0 the electron equilibrium density and k B is the Boltzmann constant. Parameter κ is the spectral index, a measure of the slope of the energy spectrum of the suprathermal particles forming the tail of the distribution function. The Gamma function arises from the normalization of f κ (v) such that

$$ \int f_{\kappa} ( v ) d^{3} v= n_{e0}. $$
(2)

Integrating the Kappa distribution over velocity space, the number density for electrons can be obtained as (Panwar et al. 2014)

$$ n_{e} ( \phi ) = n_{e0} \biggl( 1- \frac{e\phi }{ ( \kappa-3/2 ) k_{B} T} \biggr)^{- ( \kappa-1/2 )}. $$
(3)

ϕ is the local electrostatic potential.

3 Ion motion modeling

We consider collisionless, unmagnetized plasma consisting three components, namely fluid ions and two types of electrons with different temperature T c (lower) and T h (higher). We assume that charge neutrality at equilibrium requires that n i0=n ec0+n eh0 where n i0, n ec0 (n eh0) are the unperturbed number density of ions, and cold (hot) temperature electrons, respectively. The nonlinear dynamics of the ion acoustic solitary waves (IASWs) in such a plasma system is described in spherical geometry by the following set of equations:

$$\begin{aligned} &{ \frac{\partial n}{\partial t} + \frac{1}{r} \frac{\partial}{\partial r} \bigl( r^{2} nu \bigr) + \frac{1}{r} \frac{\partial}{\partial\theta} ( nv ) + \frac{nv}{r} \operatorname {cotg}\theta=0,} \end{aligned}$$
(4)
$$\begin{aligned} &{ \frac{\partial u}{\partial t} +u \frac{\partial u}{\partial r} + \frac{v}{r} \frac{\partial u}{\partial\theta} - \frac{v^{2}}{r} = \frac{\partial \varPhi}{\partial\theta},} \end{aligned}$$
(5)
$$\begin{aligned} &{ \frac{\partial u}{\partial t} +u \frac{\partial v}{\partial r} + \frac{v}{r} \frac{\partial v}{\partial\theta} - \frac{uv}{r} = \frac{1}{r} \frac{\partial \varPhi}{\partial\theta},} \end{aligned}$$
(6)
$$\begin{aligned} &{ \frac{1}{r} \frac{\partial}{\partial r} \biggl( r^{2} \frac{\partial \varPhi}{\partial r} \biggr) + \frac{1}{r} \frac{\partial^{2} \varPhi}{ \partial \theta^{2}} + \frac{\operatorname {cotg}\theta}{r^{2}} \frac{\partial \varPhi}{ \partial\theta} = n_{c} + n_{h} -n,} \end{aligned}$$
(7)

where r, θ are the radial and angle coordinates u and v, are the ion fluid velocity in r and θ directions, respectively, n and Φ represent the ion density and the electrostatic potential. The variables t, r, n, u, v and Φ are normalized to the plasma frequency \(\omega_{pi}^{-1} = ( m_{i} /4\pi n_{i0} e^{2} )^{1/2}\) the Debye radius \(\lambda_{D} = \sqrt{T_{c} /4\pi e^{2}}\), the unperturbed number density of ions n i0, the ion fluid velocity C i =(k B T c /m i )1/2 and kT c /e, respectively.

Elsewhere, the densities of κ-distribution cold and hot electrons from Eq. (3) can be read as

$$\begin{aligned} &{ n_{c} = ( 1-\mu ) \biggl( 1- \frac{\varPhi}{\kappa_{c} - \frac{3}{2}} \biggr)^{- ( k_{c} -1/2 )},} \end{aligned}$$
(8)
$$\begin{aligned} &{ n_{h} =\mu \biggl( 1- \frac{\sigma\varPhi}{\kappa_{h} - \frac{3}{2}} \biggr)^{- ( k_{h} -1/2 )},} \end{aligned}$$
(9)

where k c and k h are the spectral index of cold and hot electrons components, respectively.

Here we have denoted, σ=T c /T h as the temperature ratio of cold to hot electrons and μ=n h0/n i0 as the density ratio of hot electrons to ions.

4 Derivation of SKP equation

Since we are dealing with weak nonlinearities, we may linearize our equations using the so-called reductive perturbation method (Washimi and Taniuti 1966), whereby, we expand the variables n, u and ϕ around the unperturbed states in power series of ε (ε is a small parameter measuring the weakness of dispersion) that is,

$$\begin{aligned} &{ n=1+\varepsilon n_{1} + \varepsilon^{2} n_{2} +\cdots} \end{aligned}$$
(10)
$$\begin{aligned} &{ u=1+\varepsilon u_{1} + \varepsilon^{2} u_{2} +\cdots} \end{aligned}$$
(11)
$$\begin{aligned} &{ \phi =\varepsilon \phi _{1} + \varepsilon^{2} \phi _{2} +\cdots} \end{aligned}$$
(12)

We can rewrite Eqs. (4)–(7) taking into account Eqs. (8)–(9) and Eqs. (10)–(12) and the stretched coordinates ξ=ε 1/2(r−V 0 t), η=ε −1/2 θτ=ε 3/2 t to get different powers of ε. Solving for n 1, u 1 and ϕ 1, to the lowest order in ε we acquire the following set of relations:

$$\begin{aligned} &{ n_{1} = \frac{1}{V_{0}^{2}} \phi _{1},} \end{aligned}$$
(13)
$$\begin{aligned} &{ u_{1} =- \frac{1}{V_{0}} \phi _{1}, } \end{aligned}$$
(14)
$$\begin{aligned} &{ V_{0} = \frac{1}{\sqrt{\alpha}}} \end{aligned}$$
(15)

with \(\alpha= ( 1-\mu ) \frac{ ( 2 k_{c} -1 )}{ ( 2 k_{c} -3 )} +\sigma\mu \frac{ ( 2 \kappa_{2} -1 )}{ ( 2 k_{h} -3 )}\), where V 0, is the wave phase speed.

To the next higher order of ε, we obtain the following set of equations:

$$\begin{aligned} &{ \frac{\partial n_{1}}{\partial\tau} - V_{0} \frac{\partial n_{2}}{ \partial\xi} = \frac{\partial u_{2}}{\partial\xi}, } \end{aligned}$$
(16)
$$\begin{aligned} &{ \frac{\partial u_{1}}{\partial\tau} - V_{0} \frac{\partial u_{1}}{ \partial\xi} = \frac{\partial \varPhi_{2}}{\partial\xi}, } \end{aligned}$$
(17)
$$\begin{aligned} &{ \frac{\partial v_{d1}}{\partial\xi} =- \frac{1}{V_{0}} \frac{\partial \phi _{1}}{\partial\eta}, } \end{aligned}$$
(18)
$$\begin{aligned} &{ \frac{\partial^{3} \varPhi_{1}}{\partial \xi^{3}} =\alpha \varPhi_{2} +\beta \varPhi_{1}^{2} - n_{2} } \end{aligned}$$
(19)

with \(= ( 1-\mu ) \frac{ ( 4 k_{c}^{2} -1 )}{2 ( 2 k_{c} -3 )^{2}} + \sigma^{2} \mu \frac{ ( 4 \kappa_{2} -1 )}{2 ( 2 k_{h} -3 )^{2}}\).

Using Eqs. (10)–(18) we finally derived the following equation,

$$ \begin{aligned}[b] & \frac{\partial}{\partial\xi} \biggl[ \frac{\partial \phi _{1}}{ \partial\tau} + A \frac{\partial \phi _{1}}{\partial\xi} + B \frac{\partial^{3} \phi _{1}}{\partial \xi^{3}} + \frac{1}{\tau} \phi _{1} \biggr] \\ &\quad {}+ C \biggl[ \frac{\partial^{2} \phi _{1}}{\partial \eta^{2}} + \frac{1}{\eta} \frac{\partial \phi _{1}}{\partial\eta} \biggr] =0, \end{aligned} $$
(20)

where A=2β/γ, \(B= \frac{V_{0}^{3}}{2}\), \(C= \frac{1}{2 V_{0} \tau^{2}}\) and γ=2(α 3/2+α 2).

Analyze of the SKP equation:

  1. (a)

    Equation (20) is the spherical Kadomtsev-Petviashvili equation describing the nonlinear propagation of the ion acoustic solitary waves in plasma with bi-kappa distributed electrons.

  2. (b)

    In this equation, A is the coefficient of nonlinearity, and B is the coefficient of dispersion. It is worth stressing that the most important nonlinear effect (represented by the coefficient A) is that the higher amplitude parts of a wave travel faster than the lower amplitude parts, leading to a steepening of the wave front. Further, dispersive wave (represented by the coefficient B) boils down to the fact that the waves travel at different speeds, which causes the wave to be stretched over time. Accordingly, soliton arise as a result of the balance between the nonlinear steepening and dispersive stretch of the wave.

  3. (c)

    We note from Eq. (20), that as the value of τ decreases, the effect of spherical geometry (or from the term “\(\frac{1}{\tau} \phi _{1} \)”) becomes stronger in comparison with the typical one-dimensional KdV case.

  4. (d)

    We can notice that the amplitude and wave velocity of the solitary wave described by Eq. (20) are exclusively determined by the parameters of the system and are only depending on the initial conditions. Moreover, the solitary solution of SKP equation indicates that the phase velocity of the solitary wave is angle dependent in the phase. This means that the spherical wave described by the SKP will slightly deform as time goes on.

  5. (e)

    Lastly, we point out, that if the wave propagates without the transverse perturbation, the last term in the left side of Eq. (20) disappears and the SKP equation reduces to the ordinary spherical KdV equation.

5 Solitonic solution

We can find an exact solitary wave solution for the SKP equation (20) by using a suitable variable transformation so the two terms with variable coefficients, can be canceled if we assume, \(\zeta=\xi- \frac{v_{0}}{2} \eta^{2} \tau\), ϕ 1=Φ(ζ,τ) and by imposing the appropriate boundary conditions, namely, Φ→0, dΦ 1/dξ→0, d 2 Φ 1/dξ 2→0 as ξ→±∞.

We adopt the following notation Φ 1≡Φ, then the SKP is reduced to the standard KdV equation,

$$ \frac{\partial \varPhi}{\partial\tau} +A \varPhi \frac{\partial \varPhi}{ \partial\zeta} +B \frac{\partial^{3} \varPhi}{\partial \zeta^{3}} =0 $$
(21)

whose solution is of the form:

$$ \varPhi = \varPhi_{m} \operatorname {sech}^{2} \biggl[ \frac{ ( \zeta- U_{0} \tau )}{ \Delta} \biggr], $$
(22)

U 0 is a constant. As a result we get an exact solitary wave solution of SKP

$$ \varPhi ( \zeta ) = \varPhi_{m} \operatorname {sech}^{2} \biggl[ \frac{ ( \xi- ( U_{0} + \frac{v_{0}}{2} \eta^{2} ) \tau )}{\Delta} \biggr]. $$
(23)

\(\varPhi_{m} = \frac{3 U_{0}}{A}^{2}\) is the maximum amplitude (potential perturbation), and \(\Delta= \sqrt{4B/ U_{0}}\) measures the spatial extension (width) of localized wave.

The maximum amplitude of the wave gives us a very simple criterion for analyzing the range of different parameters, for which a compressive or rarefactive solitary wave can exist. It is worthwhile to mention that the nature of solitary wave can be determined by the sign of parameter “A”. Thus, if A<0 the system can support rarefactive solitary structures (corresponding to negative potential), and if A>0, the system can support compressive solitary structures. In our case, as A can be either positive or negative, our system can support compressive as well as rarefactive structures (corresponding to positive or negative potential well), depending on the plasma parameters.

6 Results and discussion

Now, to investigate the nature and behavior of the solitary waves (represented by Eq. (22)) we have graphically analyzed the potential amplitude and examined how the superthermality and the plasma parameters change the profile of the maximum potential perturbation. The results are displayed in Figs. 1–6 where the effects of different plasma parameters such as spectral index of each of the electron component, temperature ratio of the two electron components, and density ratio of the hot electrons species are varied.

Fig. 1
figure 1

Variation of the solitary wave solution for different values of κ c for κ h =2, μ=0.2 and σ=0.01

Full size image

6.1 Effect of electron spectral indices κ

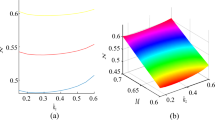
In Fig. 1 we show the effect of varying the cool electron spectral index κ c on the wave behavior for fixed value of κ h =2, density ratio μ=0.2 and temperature ratio σ=0.01. We have illustrated these finding for specific values, namely (κ c =2, κ c =10 and κ c =20). It is clearly seen that as the superthermal concentration of cold electrons increases (κ c  decrease), the spatial extension (width) of the ion-acoustic wave’s increases, while it has no effect on the rarefactive waves (figure not shown here). Conversely, varying the hot electron spectral index κ h have the opposite effect on the rarefactive waves (see Fig. 2).

Fig. 2
figure 2

Variation of the solitary wave solution for different values of κ h for κ c =2, μ=0.2 and σ=0.01

Full size image

6.2 Effect of temperature ratio σ

Figures 3 and 4 depict the effect of temperature ratio (σ=T c /T h ) on compressive and rarefactive solitary waves with fixed plasma parameters, κ c =κ h =2, μ=0.2 (for positive potential) and μ=2 (for negative potential). It is seen that σ changes slightly the amplitude of the structures while it has no real effect on their amplitude. By cons, the amplitude and width of rarefactive waves increase significantly with σ.

Fig. 3
figure 3

Variation of the solitary wave solution for different values of σ for κ c =κ h =2 and μ=0.2

Full size image
Fig. 4
figure 4

Variation of the solitary wave solution for different values of σ for κ c =1, κ h =2 and μ=2

Full size image

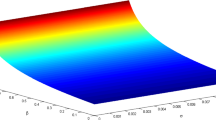
6.3 Effect of electron density μ

Figure 5 shows how the amplitude varies with the density ratio of hot electrons to ions (μ=n h0/n i0) when electron spectral index (κ c =κ h =2) and temperature ratio (σ=0.01) are held constant. The cold electron population leads to reduction of the compressive waves amplitude until change its polarity. Thus, the density ratio of hot electron to ions determines the regime of compressive and rarefactive wave solutions as shown in Fig. 6.

Fig. 5
figure 5

Variation of the solitary wave solution for different values of μ for κ c =κ h =2 and σ=0.01

Full size image
Fig. 6
figure 6

Variation of the solitary wave solution for different values of μ for κ c =κ h =2 and σ=0.01

Full size image

6.4 Electric field

It should be emphasized that we can find the magnitude of the electric field of our ion acoustic waves, by taking the negative gradient of the solution in Eq. (22) which reads as

Fig. 7
figure 7

Spherical soliton for κ c =1, κ h =2, μ=2 and σ=0.01

Full size image
$$ E=- \frac{4\varPhi_{m}}{\Delta} \operatorname {sech}^{2} \biggl( \frac{\zeta- U_{0} \tau}{ \Delta} \biggr) \tanh \biggl( \frac{\zeta- U_{0} \tau}{\Delta} \biggr). $$
(24)

The dependence of the electric field E on κ c and μ is depicted in Figs. 8 and 9. It is seen that the electric field is affected by the population of superthermal electrons, and in fact becomes more localized with higher amplitude with increase κ c (decreased superthermality). Otherwise, as density ratio decrease, the magnitude of the electric field decreases too.

Fig. 8
figure 8

Solitary wave electric field magnitude for different values of κ c for κ h =2, μ=0.2 and σ=0.01

Full size image
Fig. 9
figure 9

Solitary wave electric field magnitude for different values of μ for κ c =κ h =2 and σ=0.01

Full size image

7 Application to Saturn’s magnetosphere

In this section we will give the characteristics of ion waves for parameter values that are typical of the three regions of Saturn’s magnetosphere, viz., the inner magnetosphere, intermediate magnetosphere and the outer magnetosphere as given by Shippers et al. Table 1 list the parameter values, extracted from papers of Schipper et al. and Baluku et al., where they mainly used data values obtained on the Cassini outbound trajectory (Baluku et al. 2011).

Table 1 Parameter values derived from Shippers et al. corresponding to Saturn’s magnetosphere
Full size table

We have illustrated the variation of the nonlinear ion acoustic waves that propagate in the magnetosphere for each region. As it was expected, the solitary waves that occur in Saturn’s magnetosphere are strongly influenced by the occurrence’s region. Indeed, medium effect can be observed on the amplitude and width of IASWs via change in R. It is obvious from Figs. 10, 11 and 12 that as R increase (from inner to outer magnetosphere) the amplitude and width of the solitary waves decrease. Moreover, the electric filed is also plotted in Fig. 13 for three chosen values corresponding to the three region of Saturn’s magnetosphere (inner magnetosphere R=5.4 R S , intermediate R=12 R S and outer magnetosphere R=17.8 R S ). It is shown that the electric field is more localized with much sharper peaks in the inner magnetosphere.

Fig. 10
figure 10

Variation of the solitary wave solution in the inner Saturn’s magnetosphere

Full size image
Fig. 11
figure 11

Variation of the solitary wave solution in the intermediate Saturn’s magnetosphere

Full size image
Fig. 12
figure 12

Variation of the solitary wave solution in the outer Saturn’s magnetosphere

Full size image
Fig. 13
figure 13

Solitary wave electric field magnitude in Saturn’s magnetosphere

Full size image

8 Summary

To conclude, let recall, that this work dealt with the investigation of ions acoustic wave propagation in plasma with bi-kappa distributed electrons components, having different temperatures. Using reductive perturbation theory, we have derived a SKP equation, and its corresponding solitary wave solution. We have analyzed and found that the plasma system under consideration supports ions acoustic waves, whose features, polarity, amplitude, width and electric field, depend on the cool (hot) electron spectral index κ c (κ h ), the temperature ratio of cold to hot electrons (σ=T c /T h ) and the density ratio of hot electrons to ions (μ=n h0/n i0). We also described the wave behavior in each of the three regions of Saturn’s magnetosphere.

The results which have been found from this study can be pinpointed as follows.

  1. (i)

    In the present investigation, the presence of the two temperature electrons leads to the formation of opposite polarity potential solitons. Indeed, both compressive and rarefactive solitons can be supported by the model for some plasma parameters, which is in good agreement with earlier works of Saini et al. (2014), Baluku et al. (2010).

  2. (ii)

    Superthermality of hot and cold electrons (κ h and κ c ) have significant and opposite effects on the solitons profiles. Superthermality of cold electron increases the amplitude of the compressive waves, while it reverses in the rarefactive case.

  3. (iii)

    At higher lever of superthermality, the electric field becomes less localized with lower amplitudes.

  4. (iv)

    It is noticed that the amplitude and width of negative potential solitons are enlarged with increase in σ, but reduced for the case of positive potential solitons, hence, the effects of electron temperatures significantly modify the soliton profiles.

  5. (v)

    Compressive waves are not affected by the Temperature ratio (σ=T c /T h ). Nevertheless, σ increases the height and width of the rarefactive waves.

  6. (vi)

    The polarity of our solitary waves solutions are determined by the density ratio of hot electrons to ions (μ=n h0/n i0).

  7. (vii)

    SKP equation admits spherical soliton as solution as reveals in Fig. 7.

  8. (viii)

    The magnitude of the electric field is proportional to the density ratio μ.

  9. (ix)

    Based on data obtained from Saturn’s magnetosphere (Schippers et al. 2008), we have carried out the IAWs in the inner Saturn’s magnetosphere (R<9 R S ), the intermediate Saturn’s magnetosphere (9≤R≤13 R S ), and the outer Saturn’s magnetosphere (R>13 R S ), as well as the corresponding electric field of each region. It was found that, the solitary structures have greater amplitude (potential perturbation) and width (the spatial extension) in the inner region. This was expected, because this region has the densest plasma in the Saturnian system, and is characterized by low temperature and high equatorial densities. Elsewhere, in the outer region of the magnetosphere which is characterized by low plasma density and is strongly influenced by the solar wind, the amplitude and width of the localized structure are the smaller one. Moreover, the electric field is more localized with much sharper peaks in the inner magnetosphere. Indeed, it was found that as we move away from the center of the magnetosphere, the electric field becomes less localized with reduced amplitude.

It is worthwhile to remind that the above results yield improved understanding of the propagation of non-linear ion acoustic waves in unmagnetized plasma in the case that electrons are κ-distributed. Especially, in Saturn’s magnetosphere where two different temperatures electrons with kappa distribution are often present. As a final point, the results of the present work should also be helpful to explain the basic features of localized electrostatic disturbance observed in laboratory, astrophysical and space plasmas, such as plasma expansion, laser-plasma interaction, the auroral zone and the upper ionosphere, where two temperature electrons population obeying kappa distribution exist. Furthermore, this study is of interest in the context of the investigation of mono-energetic ion beams from intense laser interactions with plasmas. The more about the properties of IAWs in space plasma in which electrons bi-kappa distributed are the major plasma species, viz., pulsar magnetosphere, Earth’s magnetosphere plasma sheet and solar wind are worthy of studying further.