1 Introduction

In 1916, Einstein [1] introduced the general theory of relativity which succeeded in geometrizing gravitation by identifying the metric tensor with gravitational potentials. Since that time, several authors have dealt with space-times in the relativity theory with different forms for the energy momentum tensor which represents the distribution of the matter content. Why time-dependent deceleration parameter is expected? In the past, the expansion of universe was decelerating in nature and in the present time it is accelerating and as a result the deceleration parameter q must show signature flipping which is consistent with CMB anisotropies and type Ia supernovae (SNe Ia) observations [2,3,4].

Some authors studied cosmological models in the theory of relativity and modified theories of relativity with time-dependent deceleration parameter (q). In the case when the relation between the deceleration parameter (q) and the Hubble parameter (H) was considered in a linear form, in the f(R, T) theory of gravity, LRS Bianchi type I model was studied by Tiwari et al. [5], Bianchi type I model in the presence of a dissipative fluid with time-dependent cosmological “constant” \(\Lambda \) in the relativity theory was given by Tiwari et al. [6] and exact solutions of the field equations in the relativity theory for homogeneous and anisotropic Bianchi type I model were studied by Tiwari et al. [7]. Pradhan et al. [8] studied the transit behavior of the universe. They have studied the universe which is modeled by Bianchi type I cosmological models and considered the scale factor as \(a(t)=\sqrt{t^n e^t}\) which yields \( q=-1+\frac{2n}{(k+t)^2}\). In the presence of viscous fluid, Bianchi type I space-times with variable deceleration parameter in the theory of relativity were studied by Chawla [9]. In the Brans–Dicke theory of gravitation, Mishra and Chand [10] studied spatially homogeneous and isotropic Friedmann–Lemaître–Robertson–Walker space-time by considering \(q=\frac{\alpha (1-t)}{1+t}\) and \(q=-\frac{\alpha t}{1+t}\), where \(\alpha \) is a nonnegative constant. Akarsu and Dereli [11] formulated a new law for the deceleration parameter that changes linearly with the time and contains Berman’s law [12, 13] as a special case of it. The new formulation not only gives a generalization for the solutions obtained with constant deceleration parameter, but also indicates a better fit with data (from BAO, CMB and SNIa), particulary concerning the late-time behavior of the universe. Fate and probing kinematics of the universe when q was considered as linear function of t was studied by Akarsu et al. [14]. In the Brans–Dicke gravity theory, Chand et al. [15] dealt with spatially homogeneous and isotropic Friedmann–Robertson–Walker (FRW) space-time with q as a function of t. LRS Bianchi type I model with time-dependent deceleration parameter and \(\Lambda \) term in the general relativity theory was studied by Pradhan and Otarod [16].

In addition to being inhomogeneous, Bianchi type VI0 space-time is a generalization for FRW space-time, has equal parameter and with its family, play an important role in describing the evolution of the universe in early stages [17]. Several investigations for Bianchi type VI0 space-time in different theories of relativity were given by several authors; for example, Priyanka et al. [18] studied Bianchi type VI0 cosmological models filled with dark energy with equation of state parameters being constant and time-dependent. Adhav et al. [19] discussed the anisotropic nature of the dark energy for Bianchi type VI0 cosmological model in the relativity theory. In the f(R) gravity, Bianchi type VI0 space-time in the presence of viscosity was given by Shaikh et al. [20]. Mishra et al. [21] studied five-dimensional Bianchi type VI0 filled with dark energy in the relativity theory. For perfect fluid distribution with pressure and density being equal in the general relativity theory, Sharma et al. [22] studied string inhomogeneous Bianchi type VI0 cosmological model. In the Brans–Dicke theory, Vidyasagar et al. [23] dealt with Bianchi type VI0 bulk viscous string space-time. Bianchi type VI0 model in the presence of flat potential and massless scalar field with constant deceleration parameter was discussed by Bali and Kumari [24]. Exact Bianchi type VI0 cosmological models with matter in the presence of an electromagnetic field were given by Lorenz [25]. Spatially homogeneous and anisotropic Bianchi type VI0 with cosmological constant with anisotropic dark energy was investigated by Sharif and Zubair [26]. Effect of the electromagnetic field in the string Bianchi type VI0 cosmological model was investigated by Amirhashchi [27]. He concluded that for the universe dominated by massive strings, the existence of electromagnetic field is important because it accelerates the rate of expansion of the universe. However, for the universe dominated by Nambu strings, the electromagnetic field does not have effect on the rate of evolution for the universe. Four cosmological models for Bianchi type VI0 space-times in the presence of viscosity were given by Patel and Koppar [28]. Bianchi type VI0 inflationary cosmological model in the relativity theory was studied by Bali and Poonia [29]. Bianchi type \(VI _0\) cosmological models in the presence of viscosity and the fluid satisfying barotropic equation of state with varying cosmological term \(\Lambda \) were investigated by Singh et al. [30]. Bianchi type VI0 anisotropic cosmological models with a bulk viscosity in the presence of time-varying gravitational and cosmological constant were studied by Verma and Ram [31]. Bianchi type VI0 space-times with a perfect fluid as a source for gravitational field were studied by Ram [32].

The magnetic field plays significant role in description of the energy distribution in the universe as it contains highly ionized matter. In intergalactic and galactic spaces, the magnetic field plays an important role at the cosmological scale. Several authors: Singh and Singh [33], Banerjee et al. [34], Tikekar and Patel [35] and Chakraborty [36], argued about the occurrence of magnetic fields on galactic scales.

Melvin [37] has pointed out that existence of magnetic field is realistic as at early stage evolution of the universe matter was highly ionized and field and matter were smoothly coupled. During the cooling (after evolution of the universe), the ions combined to form neutral matter. Hence, the cosmological models in the presence of magnetic field are justified.

In this paper, we consider Bianchi type VI0 cosmological model in the presence of electromagnetic field with variable deceleration parameter in relativity theory. In Sect. 2, we perform the Einstein field equations for the model. Results and discussion are given in Sect. 3. Section 4 deals with conclusions.

2 The metric and field equations

The line element \(({\mathrm{d}}s^2)\) for the Bianchi type VI0 model takes the form:

$$\begin{aligned} {\mathrm{d}}s^{2} &= {\mathrm{d}}t^{2}-[A(t)]^{2}e^{-2nz}{\mathrm{d}}x^{2}\nonumber \\&-\,e^{2nz}[B(t)]^{2}{\mathrm{d}}y^{2}-[C(t)]^{2}{\mathrm{d}}z^{2} \end{aligned}$$
(1)

In relativity theory, Einstein field equations read as:

$$\begin{aligned} G_{ij}=-\chi T_{ij}, \end{aligned}$$
(2)

where \(G_{ij}\) is the Einstein tensor, \(\chi \) is the constant and \(T_{ij}\) is the energy momentum tensor that takes the form:

$$\begin{aligned} T_{ij}=(\rho +p)u_{i}u_{j}-pg_{ij}+E_{ij}, \end{aligned}$$
(3)

where \(E_{ij}\) is the electromagnetic field that satisfies relation [38]:

$$\begin{aligned} E_{ij}={\bar{\mu }}\left[ h_{l}h^{l}\left( u_{i}u_{j}-\frac{1}{2}g_{ij}\right) +h_{i}h_{j}\right] . \end{aligned}$$
(4)

where \({\bar{\mu }}\) is the magnetic permeability, \(\rho \) and p are the energy density and isotropic pressure, respectively, and \(h_{i}\) is the magnetic flux vector which reads as:

$$\begin{aligned} h_{i}=\frac{\sqrt{-g}}{2{\bar{\mu }}}\epsilon _{ijkl}F^{kl}u^{j}, \end{aligned}$$
(5)

where \(\epsilon _{ijkl}\) is the Levi-Civita tensor density and \(F_{ij}\) represents the electromagnetic field tensor. In the co-moving coordinates (\(u^{0}=1, u^1=u^2=u^3=0\)) and for the current flow along z-axis, \(F_{12}\) is the only nonvanishing component of \(F_{ij}\). Maxwell’s equations

$$\begin{aligned} F_{ij;k}+F_{jk;i}+F_{ki;j}=0,\quad \left[ \frac{1}{{\bar{\mu }}}F^{ij}\right] _{;j}=0, \end{aligned}$$
(6)

are satisfied with \(F_{12}\) as a constant (say K).

Equation (5) becomes:

$$\begin{aligned} h_3=\frac{CK}{{\bar{\mu }}AB} , \quad h_lh^l= h_3h^3=g^{33}h_3^2= \frac{K^2}{{\bar{\mu }}^2A^2B^2}. \end{aligned}$$
(7)

From (4) and (7), the components of the energy momentum tensor (3) reduce to:

$$\begin{aligned} T_1^1 &= T_2^2=- \left[ p+\frac{K^2}{2 {\bar{\mu }} A^2B^2}\right] ,\quad T_3^3=- \left[ p-\frac{K^2}{2 {\bar{\mu }} A^2B^2}\right] ,\nonumber \\ T_0^0 &= \rho +\frac{K^2}{2 {\bar{\mu }}A^2B^2}. \end{aligned}$$
(8)

For line element (1) the field Eq. (2) reads as:

$$\begin{aligned} \frac{{\ddot{C}}}{C}+\frac{{\ddot{B}}}{B} +\frac{{\dot{B}}{\dot{C}}}{BC}-\frac{n^{2}}{C^{2}} &= -\chi \left[ p+\frac{K^{2}}{2 {\bar{\mu }} A^{2}B^{2}}\right] ,\end{aligned}$$
(9)
$$\begin{aligned} \frac{{\ddot{C}}}{C}+\frac{{\ddot{A}}}{A} +\frac{{\dot{A}}{\dot{C}}}{AC}-\frac{n^{2}}{C^{2}} &= -\chi \left[ p+\frac{K^{2}}{2 {\bar{\mu }} A^{2}B^{2}}\right] , \end{aligned}$$
(10)
$$\begin{aligned} \frac{{\ddot{B}}}{B}+\frac{{\ddot{A}}}{A} +\frac{{\dot{A}}{\dot{B}}}{AB}+\frac{n^2}{C^{2}} &= -\chi \left[ p-\frac{K^{2}}{2 {\bar{\mu }} A^{2}B^{2}}\right] , \end{aligned}$$
(11)
$$\begin{aligned} n\left[ \frac{{\dot{B}}}{B}-\frac{{\dot{A}}}{A}\right] &= 0, \end{aligned}$$
(12)
$$\begin{aligned} \frac{{\dot{A}}{\dot{C}}}{AC}+\frac{{\dot{A}}{\dot{B}}}{AB} +\frac{{\dot{B}}{\dot{C}}}{BC}-\frac{n^{2}}{C^{2}} &= \chi \left[ \rho +\frac{K^{2}}{2 {\bar{\mu }} A^{2}B^{2}}\right] , \end{aligned}$$
(13)

where dot means ordinary differentiation with respect to t.

3 Results and discussion

From (12), we get:

$$\begin{aligned} A(t)=c_1B(t), \end{aligned}$$
(14)

where \(c_1\) is a constant. Now, let us consider the deceleration parameter of the model as linear function on the time t in the form [11]:

$$\begin{aligned} q=-1+m-kt, \end{aligned}$$
(15)

where m and k are nonzero positive constants. From the definition of the deceleration parameter, we have

$$\begin{aligned} q= \frac{-R\,{\ddot{R}}}{{\dot{R}}^2}=-1+m-kt, \end{aligned}$$
(16)

where R is the scale average factor given by \(R(t)=\root 3 \of {ABC}\). Equation (16) has a solution in the form [11]:

$$\begin{aligned} R(t)= c_2 e^{\frac{2}{m}\tanh ^{-1}\left( \frac{k}{m}t-1\right) }=c_2 \left( \frac{\frac{k}{m}t}{2-\frac{k}{m}t}\right) ^{\frac{1}{m}}, \end{aligned}$$
(17)

where \(c_2\) is a constant. From the definition of the deceleration parameter with definitions of the scale factor R(t), the coefficients of the metric tensor A(t), B(t) and C(t) can be read as:

$$\begin{aligned} A(t)=c_1B(t)=c_1\left( \frac{\frac{k}{m}t}{2-\frac{k}{m}t}\right) ^{\frac{1}{m}},\quad C(t)= c_3 \left( \frac{\frac{k}{m}t}{2-\frac{k}{m}t}\right) ^{\frac{1}{m}}, \end{aligned}$$
(18)

where \(c_3\) is a constant and \(c_1 c_3=c_2^3\). From (9)–(13), the magnetic permeability \({\bar{\mu }}\), the pressure p and the density \(\rho \) read as:

$$\begin{aligned} {\bar{\mu }} &= \frac{\chi K^2c_3^2}{2 n^2 c_1^2}\left( \frac{k t}{2m-kt}\right) ^{\frac{-2}{m}}, \end{aligned}$$
(19)
$$\begin{aligned} p &= -\frac{4(3-2m+2kt)}{\chi t^2 (-2m+kt)^2}, \end{aligned}$$
(20)

and

$$\begin{aligned} \rho =\frac{2}{\chi }\left[ \frac{6}{t^2 (-2m+kt)^2}-\frac{n^2}{c_3^2\left( \frac{kt}{2m-kt}\right) ^{\frac{2}{m}}}\right] . \end{aligned}$$
(21)

The line element (1) reads as:

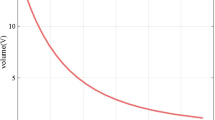
$$\begin{aligned} {\mathrm{d}}s^{2}={\mathrm{d}}t^{2}-\left( \frac{\frac{k}{m}t}{2-\frac{k}{m}t}\right) ^{\frac{2}{m}} \left[ e^{-2nz}c_1^2\,{\mathrm{d}}x^{2}+e^{2nz}{\mathrm{d}}y^{2}+c_3^2{\mathrm{d}}z^{2}\right] . \end{aligned}$$
(22)

For model (22), the volume element \(V = \sqrt{-g}= ABC = c_1 c_3\left( \frac{\frac{k}{m}t}{2-\frac{k}{m}t}\right) ^{\frac{3}{m}}\), the average scale factor \(R=V^\frac{1}{3}= (c_1c_3)^{\frac{1}{3}}\left( \frac{\frac{k}{m}t}{2-\frac{k}{m}t}\right) ^{\frac{1}{m}}\), the expansion scalar \(\Theta = \frac{6}{2m t-kt^2}\), the mean Hubble parameter \(H=\frac{{\dot{R}}}{R}= \frac{2}{2m t-kt^2}\) and the shear \(\sigma = 0\). The behavior of some physical and kinematic quantities can be given below, and in all figures in the paper, we take \(n=1\), \(m=2\) , \(k=0.113\), \(c_1=1=c_2=c_3\) and \(\chi =8\pi \).

Figure 1 shows the behavior of the scale factor R with time t, at the beginning of evolution (\(t=0\)) \(R=0\) and R beginning divergence at \(t=34\); that is, the universe starts with big bang at \(t = 0\) and ends at \(t= 34\). Figure 2 shows deceleration parameter positive to negative during the evolution, which is appropriate as it is believed that universe underwent from deceleration to acceleration after the inflation. The pressure of the universe during the stage of evolution \(0<t<4.42478\) has negative value which means that we have equation of state with \(p = w(t) \rho \), \(w(t)<0\). This type of energy call non-phantom energy matter as (\(w>-1\)) (Fig. 3). The magnetic permeability tends to infinity at \(t=0\) and decreases toward zero as \(t\rightarrow 34\) (Fig. 4). It is important to note that as the current flow K increases, the magnetic permeability decreases faster toward zero and hence accelerates the rate of expansion of the universe.

Fig. 1
figure 1

Scale factor R versus time t, \(0\le t\le \,35\)

Full size image
Fig. 2
figure 2

Deceleration parameter q versus time t, \(0\le t\le 35\)

Full size image
Fig. 3
figure 3

Behaviors of \(w(t)=\frac{p}{\rho }\) versus t, \(0\le t\le 35\)

Full size image
Fig. 4
figure 4

Magnetic permeability (\({\bar{\mu }}\)) versus t, \(0\le t\le 35\) for different values of K. Dotted line (\(K = 1\)), dashed line (\(K = 2\)) and thick line (\(K = 3\))

Full size image

The reality conditions ([39, 40]) \((\rho +p>0,\,\, \rho +3p\ge 0)\) and the dominant energy conditions (\(\rho -p\ge 0,\,\,\rho +p>0\)) are not satisfied for the universe (Fig. 5); to make these conditions satisfactory, we deal with the absolute values of \((\rho +p)\), \((\rho +3p)\) and \((\rho -p)\) (Fig. 6).

Fig. 5
figure 5

\((\rho +p)\) (dotted line), \((\rho +3p)\) (dashed line) and \((\rho -p)\) (thick line) versus t, \(0\le t\le 35\)

Full size image
Fig. 6
figure 6

Absolute values of \((\rho +p)\) (dotted line), \((\rho +3p)\) (dashed line) and \((\rho -p)\) (thick line) versus t, \(0\le t\le 35\)

Full size image

Hegazy [41], in his study of Bianchi type VI space-times in Barber’s second creation theory ([42, 43]), obtained the effect of the scalar field \(\phi \) introduced in Barber’s theory on the entropy \({\mathbf {S}} \) of the universe and an expression for the entropy in the cases when solutions of the field equations were possible. In their studies for Bianchi type VI0 in the self-creation theory in the relativity theory and Lyra geometry, Hegazy and Farook [44] showed that the additional term introduced by Lyra has no effect on the entropy of the universe since it is obtained form geometry and not a part of the energy momentum tensor. Hegazy [45] formulated a new class of Bianchi type I in the self-creation theory in the relativity theory and explained the behaviors of the thermodynamic functions (entropy, enthalpy, Gibbs energy and Helmholtz energy) of the universe with the help of the scalar field \(\phi \). As a consequence for these studies, the thermodynamic functions of the universe in the presence of the electromagnetic field in the relativity theory can be given and studied as follows:

If we use \(\rho V\) as a definition for the internal energy \(({\mathbf {U}} )\) of the universe, then:

$$\begin{aligned} {\mathbf {F}} &= U- {\mathbf {T}} \,{\mathbf {S}} = \rho V-{\mathbf {T\,S}} , \quad {\mathbf {H}} = U+pV= (\rho +p) V,\nonumber \\ {\mathbf {G}} &= {\mathbf {H}} -{\mathbf {T}} {\mathbf {S}} , \end{aligned}$$
(23)

where \({\mathbf {T}} \) is the temperature and defined as \({\mathbf {T}} \simeq \frac{H}{2 \pi }\) [46, 47]. From the entropy equation, we have:

$$\begin{aligned} {\mathbf {T}} {\mathrm{d}}{\mathbf {S}} &= {\mathrm{d}}(\rho V)+p{\mathrm{d}}V=V{\mathrm{d}}\rho +(p+\rho ){\mathrm{d}}V\nonumber \\ &= V\left[ {\mathrm{d}}\rho +(p+\rho )\frac{{\mathrm{d}}V}{V}\right] . \end{aligned}$$
(24)

Equation (24) can be rewritten as:

$$\begin{aligned} {\mathbf {T}} \dfrac{{\mathrm{d}}{\mathbf {S}}}{{\mathrm{d}}t} &= V\left[ {\dot{\rho }}+(p+\rho )\dfrac{{\dot{V}}}{V}\right] \Rightarrow \dfrac{{\mathrm{d}}{\mathbf {S}}}{{\mathrm{d}}t}\nonumber \\ &= \dfrac{2\pi V}{H}\left[ {\dot{\rho }}+(p+\rho )\left( \dfrac{{\dot{A}}}{A} +\dfrac{{\dot{B}}}{B}+\dfrac{{\dot{C}}}{C}\right) \right] \nonumber \\ &= \dfrac{2\pi V}{H}[{\dot{\rho }}+(p+\rho )\Theta ] \end{aligned}$$
(25)

From (20) and (21) with definition of the scalar expansion, Eq. (25) reduces to:

$$\begin{aligned} \dfrac{{\mathrm{d}}{\mathbf {S}}}{{\mathrm{d}}t}=-\dfrac{4 n^2 c_1 \pi \left( \dfrac{k t}{2m - k t}\right) ^{\dfrac{1}{m}}}{\chi c_3}. \end{aligned}$$
(26)

For \(m=2,\) integration of (26) yields:

$$\begin{aligned} {\mathbf {S}} = -\frac{4 n^2 c_1 \pi }{k \chi c_3} \left[ -\,\sqrt{kt} \sqrt{4 - k t} + 4\,\,\sin ^{-1}\left[ \frac{\sqrt{kt}}{2}\right] \right] \end{aligned}$$
(27)

Hence, we get:

$$\begin{aligned} {\mathbf {F}} &= \frac{2c_1}{k t(4-k t)^{\frac{5}{2}}\chi c_3}\left[ n^2(-4+k t)^2\left( \sqrt{k t} (-4+ k t)(2+kt)\right. \right. \nonumber \\&\left. \left. \quad +\,8\sqrt{4-kt} \,\,sin^{-1}\left( \frac{\sqrt{k t}}{2}\right) \right) +6 c_3^2 k^{5/2}\sqrt{t}\right] , \end{aligned}$$
(28)
$$\begin{aligned} {\mathbf {H}} &= - \frac{2\,c_1\,\sqrt{\frac{k t}{4- kt}}\left[ n^2 t (-4+k t)^2-4 k (-2+k t)c_3^2\right] }{t(-4+k t)^3\chi c_3} \end{aligned}$$
(29)

and

$$\begin{aligned} {\mathbf {G}} &= \frac{2c_1}{k t(4-k t)^{\frac{5}{2}}\chi c_3}\left[ n^2(-4+k t)^2\left( \sqrt{k t} (-4+ k t)(2+kt)\right. \right. \nonumber \\&\left. \left. \quad +\,8\sqrt{4-kt} \,\,sin^{-1}\left( \frac{\sqrt{k t}}{2}\right) \right) -4 c_3^2 k^{5/2}\sqrt{t} (-2+kt)\right] , \end{aligned}$$
(30)

For the universe, we deal with absolute values of the enthalpy (\({\mathbf {H}} \)) (heat content), Gibbs free energy \({\mathbf {G}} \) (the energy that is not dissipated through heat of the universe) and Helmholtz’s free energy (\({\mathbf {F}} \)) (the part of the internal energy which is used in useful work) to obtain positive values of them. The absolute value of \({\mathbf {H}} \) begins with zero value at \(t=0\) and increases to reach a constant value 4.000587 at the end of the present evolution. The absolutes values of \({\mathbf {F}} \) and \({\mathbf {G}} \) have a small change about zero in the period \(0\le t\simeq 27\) and at the end of evolution \({\mathbf {F}} =5.34724\) and \({\mathbf {G}} =0.927113\) (Fig. 7).

Fig. 7
figure 7

Absolute value of F [Abs F] (dotted line), the Gibbs energy G (dashed line) and Abs[H] (thick line) versus t, \(0\,\le t\le \, 35\)

Full size image

4 Conclusions

In this paper, we have studied the Bianchi type VI0 cosmological model with electromagnetic field and variable deceleration parameter in the general theory of relativity. The deceleration parameter has been considered as a linear function of t; for \(m=2\) and \(k=0.113,\) we have found that magnetic permeability impacts density is fine. But density will not accelerate the universe. Because of the expansion, density may decrease. Effective pressure would have an effect on the expansion of the universe, but not density. The behaviors of scale factor R show that the universe starts with big bang at \(t = 0\) and ends at \(t= 34\), which is close to the lifetime of the universe provided by Caldwell et al. [48] (\(t_{\mathrm{rip}} = 35\)). The deceleration parameter begins with initial value 1 and at the end of the evolution reaches \(-\,2.842\). During the evolution, the universe passes number of stages: The universe exhibited decelerating expansion for \(0\le t< 8.84956\) as \(q> 0\), at \(t=8.84956\) the universe expanded with constant rate as \(q = 0\), for \(8.84956<t<17.6991\) the universe accelerated with power-law expansion as \(-1< q < 0\), at \(t=17.6991\) the universe will reach exponential expansion since \(q=-1\) and the universe will become super-exponential expansion for \(t>17.6991\). At present \((t\simeq 13.7168)\), the deceleration parameter equals \(-\,0.55\) which is the accepted observed value of the deceleration parameter today. The density \(\rho \) and the pressure p are related by the equation of state \(p=w \rho \) with \(w<0\) in the interval \(0<t<4.42478\) which represents non-phantom type of energy. At the beginning of evolution, the volume element V of the universe was zero and increases with time to reach infinity at the end of evolution.