1 Introduction

The three-body problem is one of the most important problems in celestial mechanics. This problem arises in many different contexts in nature. There are many mechanical systems consisting of three bodies. So it has many applications in scientific research, not only in the fields of astrodynamics but in astrophysics as well. The significance of this problem comes from the fact that it describes actual physical situations. This problem is classified into two classes; the first class is the general problem which describes the motion of three celestial bodies under their mutual gravitational attraction. The second class is the restricted problem where the third body has an infinitesimal mass, it is very small in comparison to the masses of the other two bodies, and the latter’s motions are not affected by this mass. The three-body problem is an old problem and logically follows the two-body problem, which was solved by Newton. He considered also the three-body problem in connection with the motion of the Moon under the influence of the Sun and Earth.

As we know, the classical restricted three-body problem is constructed under the effect of mutual gravitation forces between the bodies with neglecting many perturbing forces. Some perturbations can occur from the radiation pressure, the atmospheric drag, the solar wind, the potential from the belt, small perturbations in Coriolis and centrifugal forces, the variable masses, and the lack of sphericity as in oblate and triaxial bodies.

A great number of researchers devoted their efforts to the study of the existence of libration points, their stability, and sometimes the periodic orbits around these points in the restricted three-body problem under the effects of radiation, the lack of sphericity, and small perturbations in Coriolis and centrifugal forces. See Simmons et al. (1985), Kumar and Choudhry (1986), El-Shaboury et al. (1991); Khanna and Bhatnagar (1999), Sharma et al. (2001) Szebehely (1967), Bhatnagar and Hallan (1978), Devi and Singh (1994), Shu and Lu (2005), Abouelmagd (2012, 2013a, 2013b), Abouelmagd and El-Shaboury (2012), Abouelmagd and Sharaf (2013), Abouelmagd et al. (2013, 2014a, 2014b, 2015a, 2015b).

Some significant contributions were made by Douskos and Markellos (2006), Das et al. (2009), Shankaran et al. (2011a, 2011b), Singh (2012), Singh and Umar (2013), aiming to find the locations of out-of-plane equilibrium points or to examine the stability of motion around these points when one or both primaries are radiating or have an oblate spheroid shape, as well as taking account of the influence of small perturbations in Coriolis and centrifugal forces in some cases.

In variable-mass systems, Newton’s second law of motion cannot directly be applied because it is valid for constant mass systems only; see Plastino and Muzio (1992). Instead, a body whose mass m varies with time can be described by rearranging Newton’s second law and adding a term to account for the momentum carried by the mass entering or leaving the system. The general equation of the variable-mass motion is written as

$$ m\frac{d\underline{u}}{dt} = \underline{F}_\mathit{ext} + \underline{u}_\mathit{rel} \frac{dm}{dt} $$
(1)

where \(\underline{F}_{\mathit{ext}}\) is the net external force on the body, \(\underline{u}_{\mathit{rel}} = \underline{v} - \underline{u}\) is the relative velocity of the escaping or incoming mass with respect to the body and \(\underline{u}\) is the velocity of the body in the inertial frame, while \(\underline{v}\) is the velocity of the escaping or incoming mass to the body. In astrodynamics, which deals with the mechanics of rockets, the term \(\underline{u}_{\mathit{rel}}\) is often called the effective exhaust velocity.

Many authors have paid attention to the study of the restricted three-body problem with variable mass (Shrivastava and Ishwar 1983; Singh and Ishwar 1984, 1985; Das et al. 1988; Singh 2003, 2008, 2009, and 2011; and Zhang et al. 2012). All of them considered the special case of non-isotropic loss of mass law [the mass escaping from or incoming to the body has zero momentum]; see for more details Varvoglis and Hadjidemetriou (2012) and Zhang (2012). Furthermore, there are many precise works related to the restricted three-body problem with variable mass; see Jeans (1928), Meshcherskii (1949, 1952), Jha and Shrivastava (2001), Razbitnaya (1961, 1971), Bekov (1987, 1991), Bekov and Mukhametkalieva (1990), Lukyanov (1988, 1990, 2009), Letelier and da Silva (2011).

Lukyanov (2009) found the possible regions of motions for the small body and surfaces of minimum energy that bound them via the Jacobi quasi-integral in the restricted circular three-body problem when the primary bodies have variable masses but the sum of their masses is constant. He also applied his results to close binary star systems with conservative mass transfer. The differential equations of motion of the elliptical restricted problem of three bodies with variable masses were derived with the help of Meshcherskii’s transformation by Jha and Shrivastava (2001). They established that the equations of motion differ from the classical equations by an extra term. Zhang et al. (2012) studied the triangular libration points and their stability in the photo-gravitational restricted three-body problem when the mass of the infinitesimal body varies with time according to Jeans’ law and both primaries are radiating.

In this work, we focus our efforts on finding the equations of motion of the third body in the restricted three-body problem when the mass of the third body changes according to Jeans’ law in the case that the variation of the mass is from more than one point. We also find an appropriate approximation for the locations of the out-of-plane equilibrium points in the special case of a non-isotropic variation of the mass. In addition we will investigate the regions of possible and forbidden motions for the third body.

2 Model description

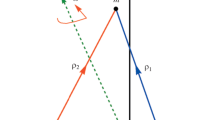
We shall adopt the notation and terminology of Varvoglis and Hadjidemetriou (2012). As a consequence, we impose the requirement that P i is a body of mass m i (i=1,2,3) with the position vectors \(\underline{R}_{i}\) from the origin of the inertial frames XYZ. We also define \(\underline{r}_{1} = \underline{R}_{3} - \underline{R}_{1}\), \(\underline{r}_{2} = \underline{R}_{3} - \underline{R}_{2}\), and \(\underline{r} = \underline{R}_{2} - \underline{R}_{1}\). Now, if we assume the body p 3 has variable mass, i.e., a mass that changes with time [m 3=m 3(t)]. In the framework of the loss of mass being taken non-isotropic, one can apply Newton’s second modified law in Eq. (1) to obtain the equations of motion for the infinitesimal body in the inertial frame in the case that the escaping or incoming mass occurs from n points for the body in the form

$$ m_{3}\underline{\ddot{R}}_{3} = - \frac{\mathit{Gm}_{3}m_{1}}{r_{1}^{3}} \underline{r}_{1} - \frac{\mathit{Gm}_{3}m_{2}}{r_{2}^{3}}\underline{r}_{2} + \dot{m}_{3}\sum_{i = 1}^{n} \underline{u}_{i}. $$
(2)

Equation (2) gives the equation of motion of the third body when its mass changes with time; see Varvoglis and Hadjidemetriou (2012) for further illustrations. In addition, we also impose the requirement that \(\underline{u}_{i} = \underline{v}_{i} - \underline{\dot{R}}_{3}\) where \(\underline{u}_{i} (\underline{v}_{i})\) is the relative velocity (the velocity) of the escaping (incoming) mass with respect to the body from (to) the point i (i=1,2,…,n), while \(\underline{\dot{R}}_{3}\) is the velocity of the body in the inertial frame. Here we would like to refer to the last term in Eq. (2), which will vanish in two cases: when the value of the sum equals zero or \(\underline{v}_{i} = \underline{\dot{R}}_{3}\). Consequently the loss of mass is isotropic in the two cases.

For simplicity, we assume the escaping or incoming mass has zero momentum (\(\underline{v}_{i} = 0\)) for all i and replace \(\underline{R}_{3}\), m 3 by \(\underline{R}\) and m, respectively. Moreover, let us go to the model of the circular restricted three-body problem. Equation (2) will be rewritten in the following form:

$$ m\underline{\ddot{R}} = - \frac{\mathit{Gmm}_{1}}{r_{1}^{3}}\underline{r}_{1} - \frac{\mathit{Gmm}_{2}}{r_{2}^{3}}\underline{r}_{2} - n\dot{m}\underline{\dot{R}}. $$
(3)

Equation (3) describes the motion of the infinitesimal body in terms of a vectorial formula.

3 Equations of motion

Let (XYZ), (xyz) be the inertial and rotating frames, respectively. They have the same origin at the center of mass of the primaries. We also assume that the coordinates of m 1, m 2, and m in the inertial frames are (X 1,Y 1,Z 1), (X 2,Y 2,Z 2), and (X,Y,Z), while in the rotating frame they are (x 1,y 1,z 1), (x 2,y 2,z 2), and (x,y,z), respectively. Consequently the equations of motion for the infinitesimal body that has variable mass are

$$ \ddot{X} + n\frac{\dot{m}}{m}\dot{X} = - \frac{\mathit{Gm}_{1} ( X - X_{1} )}{r_{1}^{3}} - \frac{\mathit{Gm}_{2} ( X - X_{2} )}{r_{2}^{3}}, $$
(4)
$$ \ddot{Y} + n\frac{\dot{m}}{m}\dot{Y} = - \frac{\mathit{Gm}_{1} ( Y - Y_{1} )}{r_{1}^{3}} - \frac{\mathit{Gm}_{2} ( Y - Y_{2} )}{r_{2}^{3}}, $$
(5)
$$ \ddot{Z} + n\frac{\dot{m}}{m}\dot{Z} = - \frac{\mathit{Gm}_{1} ( Z - Z_{1} )}{r_{1}^{3}} - \frac{\mathit{Gm}_{2} ( Z - Z_{2} )}{r_{2}^{3}}. $$
(6)

Here

$$ r_{1}^{2} = ( X - X_{1} )^{2} + ( Y - Y_{1} )^{2} + ( Z - Z_{1} )^{2}, $$
(7a)
$$ r_{2}^{2} = ( X - X_{2} )^{2} + ( Y - Y_{2} )^{2} + ( Z - Z_{2} )^{2}. $$
(7b)

If the rotating frames rotate with the angular velocity ω, the relation between the inertial and rotating coordinates is governed by

$$ X = x\cos\omega t - y\sin\omega t, $$
(8a)
$$ Y = x\sin\omega t + y\cos\omega t, $$
(8b)
$$ Z = z. $$
(8c)

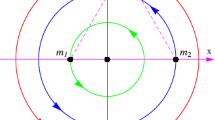
Now we assume that the origin of both coordinates is the center of the masses m 1 and m 2 such that the x-axis passes through their centers with positive direction from m 2 to m 1. Moreover, the units of distance and masses are taken as the distance between the primaries and the sum of their masses, respectively. The unit time is also chosen in such a way that the gravitational constant is unity. It follows that ω=1, m 1=1−μ, m 2=μ≤1/2 as well as that the coordinates of these masses are (μ,0,0) and (μ−1,0,0), respectively, where μ=m 2/(m 1+m 2).

Substituting Eqs. (8a), (8b), (8c) into (4), (5), and (6) using the aforementioned assumptions, the equations of motion in a rotating coordinates system for an infinitesimal body with dimensionless variables are

$$ ( \ddot{x} - 2\dot{y} ) + n\frac{\dot{m}}{m} ( \dot{x} - y ) = V_{x}, $$
(9)
$$ ( \ddot{y} + 2\dot{x} ) + n\frac{\dot{m}}{m} ( \dot{y} + x ) = V_{y}, $$
(10)
$$ \ddot{z} + n\frac{\dot{m}}{m}\dot{z} = V_{z}, $$
(11)

where

$$ V = \frac{1}{2} \bigl( x^{2} + y^{2} \bigr) + \biggl( \frac{ ( 1 - \mu )}{r_{1}} + \frac{\mu}{r_{2}} \biggr), $$
(12)
$$ r_{1}^{2} = ( x - \mu )^{2} + y^{2} + z^{2}, $$
(13a)
$$ r_{2}^{2} = ( x - \mu + 1 )^{2} + y^{2} + z^{2}. $$
(13b)

According to Jeans’ law dm/dt=−αm S, where α is a constant coefficient and 0.4≤s≤4.4. Now, we introduce the space-time transformation (x=γ −q ξ,y=γ −q η, z=γ −q ζ,dt=γ −k dτ) such that γ=m/m 0, m 0 is the mass of the third body at the initial time (t=0). But the applicable values for (s,k,q) are s=1, k=0, and q=1/2 (Shrivastava and Ishwar 1983). Therefore, \(\frac{d\gamma}{dt} = - \alpha \gamma\), \(\frac{\dot{m}}{m} = - \alpha\), x=γ −1/2 ξ, y=γ −1/2 η, z=γ −1/2 ζ, dt=dτ. Hence, the velocity and acceleration components are given as

$$ \dot{x} = \gamma^{ - 1/2} \biggl( \xi ' + \frac{1}{2} \alpha \xi \biggr), $$
(14a)
$$ \dot{y} = \gamma^{ - 1/2} \biggl( \eta ' + \frac{1}{2} \alpha \eta \biggr), $$
(14b)
$$ \dot{z} = \gamma^{ - 1/2} \biggl( \zeta ' + \frac{1}{2} \alpha \zeta \biggr), $$
(14c)
$$ \ddot{x} = \gamma^{ - 1/2} \biggl( \xi '' + \alpha \xi ' + \frac{1}{4}\alpha^{2}\xi \biggr), $$
(15a)
$$ \ddot{y} = \gamma^{ - 1/2} \biggl( \eta '' + \alpha \eta ' + \frac{1}{4}\alpha^{2}\eta \biggr), $$
(15b)
$$ \ddot{z} = \gamma^{ - 1/2} \biggl( \zeta '' + \alpha \zeta ' + \frac{1}{4}\alpha^{2}\zeta \biggr), $$
(15c)

where

$$ ( \cdot ) = \frac{d}{dt},\qquad \bigl( ' \bigr) = \frac{d}{d\tau},\quad \mbox{and}\quad \frac{d}{dt} = \frac{d}{d\tau}. $$

Substituting Eqs. (14a), (14b), (14c) and (15a), (15b), (15c) into (9), (10) and (11) we obtain

$$ \ddot{\xi} - 2\dot{\eta} - \alpha ( n - 1 )\dot{\xi} + \alpha ( n - 1 )\eta = U_{\xi}, $$
(16a)
$$ \ddot{\eta} + 2\dot{\xi} - \alpha ( n - 1 )\dot{\eta} - \alpha ( n - 1 )\xi = U_{\eta}, $$
(16b)
$$ \ddot{\zeta} - \alpha ( n - 1 )\dot{\zeta} = U_{\zeta}, $$
(16c)

where

$$\begin{aligned} U =& \frac{1}{8}\alpha^{2} ( 2n - 1 ) \bigl( \xi^{2} + \eta^{2} + \zeta^{2} \bigr) \\ &{} + \frac{1}{2} \bigl( \xi^{2} + \eta^{2} \bigr) + ( \sqrt{\gamma} )^{3} \biggl( \frac{1 - \mu}{\rho_{1}} + \frac{\mu}{ \rho_{2}} \biggr), \end{aligned}$$
(17)
$$ \rho_{1}^{2} = ( \xi - \sqrt{\gamma} \mu )^{2} + \eta^{2} + \zeta^{2}, $$
(18a)
$$ \rho_{2}^{2} = \bigl( \xi - \sqrt{\gamma} ( \mu - 1 ) \bigr)^{2} + \eta^{2} + \zeta^{2}. $$
(18b)

Equation (16a), (16b), (16c) represent the equations of motion of the restricted three-body problem in the sense that the variation of the mass of the third body is non-isotropic when the variation of the mass is from the whole surface (that is, from more than one point) in the case that the mass that falls to or is ejected from the surface has zero momentum. If we assume that the variation of the mass originates from one point (n=1) these equations can be rewritten in the form

$$ \ddot{\xi} - 2\dot{\eta} = W_{\xi}, $$
(19a)
$$ \ddot{\eta} + 2\dot{\xi} = W_{\eta}, $$
(19b)
$$ \ddot{\zeta} = W_{\zeta}, $$
(19c)

where

$$\begin{aligned} W =& \frac{1}{8}\alpha^{2} \bigl( \xi^{2} + \eta^{2} + \zeta^{2} \bigr) + \frac{1}{2} \bigl( \xi^{2} + \eta^{2} \bigr) \\ &{}+ ( \sqrt{\gamma} )^{3} \biggl( \frac{1 - \mu}{\rho_{1}} + \frac{\mu}{\rho_{2}} \biggr), \end{aligned}$$
(20)
$$\begin{aligned} W_{\xi} =& \frac{1}{4} \bigl( \alpha^{2} + 4 \bigr) \xi - ( \sqrt{\gamma} )^{3} \\ &{}\times \biggl( \frac{ ( 1 - \mu ) ( \xi - \sqrt{\gamma} \mu )}{\rho_{1}^{3}} + \frac{\mu [ \xi - \sqrt{\gamma} ( \mu - 1 ) ]}{\rho_{2}^{3}} \biggr), \end{aligned}$$
(21a)
$$\begin{aligned} W_{\eta} = \biggl[ \frac{1}{4} \bigl( \alpha^{2} + 4 \bigr) - ( \sqrt{\gamma} )^{3} \biggl( \frac{ ( 1 - \mu )}{\rho_{1}^{3}} + \frac{\mu}{\rho_{2}^{3}} \biggr) \biggr]\eta, \end{aligned}$$
(21b)
$$\begin{aligned} W_{\zeta} = \biggl[ \frac{1}{4}\alpha^{2} - ( \sqrt{ \gamma} )^{3} \biggl( \frac{ ( 1 - \mu )}{\rho_{1}^{3}} + \frac{\mu}{ \rho_{2}^{3}} \biggr) \biggr]\zeta. \end{aligned}$$
(21c)

Equation (19a), (19b), (19c) are different from the classical equations by the extra terms \(\frac{1}{4}\alpha^{2}\xi\), \(\frac{1}{4}\alpha^{2}\eta\), and \(\frac{1}{4}\alpha^{2}\zeta\) due to the variation in the mass of the third body.

4 Out of plane equilibrium points locations

In general, the locations of equilibrium points are given by W ξ =W η =W ζ =0, but the solutions of these equations when (η=0,ζ≠0) represent the locations of the out-of-orbital plane (ξ 0,ζ 0). Therefore, Eqs. (21a), (21b), (21c) and (18a), (18b) can be rewritten in the form

$$\begin{aligned} & {\frac{1}{4} \bigl( \alpha^{2} + 4 \bigr)\xi_{0} - ( \sqrt{\gamma} )^{3} } \\ & {\quad {}\times \biggl( \frac{ ( 1 - \mu ) ( \xi_{0} - \sqrt{\gamma} \mu )}{\rho_{1}^{3}} + \frac{\mu [ \xi_{0} - \sqrt{\gamma} ( \mu - 1 ) ]}{\rho_{2}^{3}} \biggr) = 0 } \end{aligned}$$
(22a)

and

$$ \frac{1}{4}\alpha^{2} - ( \sqrt{\gamma} )^{3} \biggl( \frac{ ( 1 - \mu )}{\rho_{1}^{3}} + \frac{\mu}{\rho_{2}^{3}} \biggr) = 0, $$
(22b)

where

$$\begin{aligned} & {\rho_{1}^{2} = ( \xi_{0} - \sqrt{\gamma} \mu )^{2} + \zeta_{0}^{2}, } \end{aligned}$$
(23)
$$\begin{aligned} & {\rho_{2}^{2} = \bigl( \xi_{0} - \sqrt{\gamma} ( \mu - 1 ) \bigr)^{2} + \zeta_{0}^{2}. } \end{aligned}$$
(24)

After elimination of ζ 0 from Eqs. (23) and (24), the value of ξ 0 will be controlled by the following equation:

$$\begin{aligned} 2\xi_{0} + \sqrt{\gamma} ( 1 - 2\mu ) =& \biggl[ \frac{4\gamma^{2}\mu}{4\xi_{0} + \alpha^{2}\sqrt{\gamma} \mu} \biggr]^{2/3} \\ &{} - \biggl[ \frac{4\gamma^{2} ( 1 - \mu )}{4\xi_{0} - \alpha^{2}\sqrt{\gamma} ( 1 - \mu )} \biggr]^{2/3}, \end{aligned}$$
(25)

while the value of ζ 0 which is associated to the value of ξ 0 is given by

$$\begin{aligned} \zeta_{0} = \pm \biggl( \biggl[ \frac{4\gamma^{2}\mu}{4\xi_{0} + \alpha^{2}\sqrt{\gamma} \mu} \biggr]^{2/3} - \bigl( \xi_{0} + \sqrt{\gamma} ( 1 - \mu ) \bigr)^{2} \biggr)^{1/2}, \end{aligned}$$
(26)

or

$$\begin{aligned} \zeta_{0} = \pm \biggl( \biggl[ \frac{4\gamma^{2} ( 1 - \mu )}{4\xi_{0} - \alpha^{2}\sqrt{\gamma} ( 1 - \mu )} \biggr]^{2/3} - ( \xi_{0} - \sqrt{\gamma} \mu )^{2} \biggr)^{1/2}. \end{aligned}$$
(27)

Equations (25)–(27) represent the locations of the out-of-plane equilibrium points when the third body has variable mass. It seems from a first look that Eqs. (25)–(26) can be used to find the locations of the out-of-plane equilibrium points in the classical case if the parameters γ and α are set to one and zero, respectively. But this is not realistic and makes the situation paradoxical, because this consideration will lead us to use Eq. (22b) with γ=1 and α=0. The quantities μ, (1−μ), ρ 1, and ρ 2 are positive, so there are no real values for these quantities such that Eq. (22b) is satisfied in the classical case. Consequently it is unreasonable to use Eqs. (25)–(27) to find the out-of-plane equilibrium points in the classical case, which does not exist in reality.

5 Some analysis for the out-of-plane equilibrium points locations

In general, Eqs. (25), (26), and (27) indicate that there are four out-of-plane equilibrium points. These points can be denoted by L 6,7 and L 8,9 in the plane ξζ where the two points L 6,7(L 8,9) are symmetrical with respect to the ξ-axis, which joins the primaries. They lie on a plane perpendicular to the orbital plane. But the most important point here is that Eq. (25) represents no explicit relation for the ξ 0-coordinates of the out-of-plane equilibrium points. Furthermore, this equation has a singularity when \(\xi_{0} = - \frac{1}{4}\alpha^{2}\sqrt{\gamma} \mu\) and \(\xi_{0} = \frac{1}{4}\alpha^{2}\sqrt{\gamma} (1 - \mu )\). In addition, these singularities will also appear in Eqs. (26), (27), which enable us to calculate the ζ 0-coordinates of the out-of-plane equilibrium points. The aforementioned reasons motivated us to find an appropriate approximation and explicit relations to obtain the coordinates of these points in an easy way. Therefore we will find an appropriate approximation for Eqs. (25), (26), and (27) in the form of a power series in the mass ratio μ. These series will be more powerful for calculating the locations of these points than the relations in Eqs. (25), (26), and (27), because the series can be considered a series of functions of the parameter of the mass ratio μ with constant coefficients which include the parameters α and γ, which characterize the properties of the mass variation. Hence we obtain the locations of these points by an analytical approximation expression and by graphical investigation as in the following subsections, by using a commercial symbolic package for computations and neglecting all terms of powers higher than o[μ]2.

5.1 The locations with the initial approximation from the center of the smaller primary

To examine the motion in the vicinity of the smaller primary, we have to start by the initial approximation \(\xi_{0} = \sqrt{\gamma} ( \mu - 1 )\); the coordinates of out-of-plane equilibrium points are governed by the following parametric equations:

$$\begin{aligned} \xi_{0} =& \biggl[ \biggl( - \frac{1}{2}\sqrt{\gamma} - \sqrt[3]{2} \bigl( \gamma^{3/2}/ \bigl( 4 + \alpha^{2} \bigr) \bigr)^{2/3} \biggr) \\ &{}+ \frac{1}{2}\gamma^{13/3}\mu^{2/3} + \sqrt{\gamma} \mu + \frac{1}{12}\gamma^{13/3} \bigl( 4 + \alpha^{2} \bigr) \mu^{5/3} \biggr] \end{aligned}$$
(28)

and

$$\begin{aligned} \zeta_{0} = \pm \gamma^{13/6} \biggl[ \mu^{1/3} + \frac{1}{12} \bigl( 4 + \alpha^{2} \bigr)\mu^{4/3} \biggr]. \end{aligned}$$
(29)

Or we could write

$$ \zeta_{0} = \pm \sqrt{\gamma} \sqrt{ \bigl( 1 + ( \alpha /2 )^{2} \bigr)^{ - 2/3} - 1}. $$
(30)

It is clear from Eq. (27) with the initial approximation \(\xi_{0} = \sqrt{\gamma} ( \mu - 1 )\), that Eq. (30) does not depend on the critical mass value μ for any power, while it depends on the parameters of variable mass α and γ. On the other hand, (α/2)2>0 for any real value of α, therefore Eq. (30) does not represent real values for ζ 0. Consequently Eqs. (28) and (29) represent the coordinates of the out-of-plane equilibrium points L 6,7 in the case of the initial approximation \(\xi_{0} = \sqrt{\gamma} ( \mu - 1 )\). There is no real existence for the points L 8,9. Indeed we present some graphical investigations for the locations of L 6,7 as follows.

The variations of the coordinates ξ and ζversus mass ratio for the points L 6,7 are presented in Figs. 1, 2, 3. The effects of the parameters α and γ (which characterize the variable mass of the third body) on the coordinates of L 6,7 are shown in Figs. 1–3. It is observed that the points L 6,7 will approach the connecting line between the primaries with decreasing values of γ and may be coincident for some very small values of γ; this means that the third body will be closer to the primaries and the bigger primary may swallow it. In addition, the positions of L 6 and L 7 are symmetric with respect to the connecting line axes.

Fig. 1
figure 1

The coordinates of out-of-plane equilibrium points (L 6,7) versus mass ratio μ when α=0.2 and γ=0.9

Full size image
Fig. 2
figure 2

The coordinates of out-of-plane equilibrium points (L 6,7) versus mass ratio μ when α=0.2 and γ=0.5

Full size image
Fig. 3
figure 3

The coordinates of out-of-plane equilibrium points (L 6,7) versus mass ratio μ when α=0.2 and γ=0.1

Full size image

In Figs. 4, 5, 6 the changes in the locations of the out-of-plane equilibrium points are investigated as regards the parameter effects of the variable mass. We found that these locations will be closer to the more massive body with decreasing value of γ as well as the points L 6 and L 7 becoming nearer to each other with increasing the value of α. But this behavior may change for very small values of the parameter γ in some intervals and the two points may grow farther from each other whatever the increase of α as in Fig. 6.

Fig. 4
figure 4

The locations of out-of-plane equilibrium points (L 6,7) when γ=0.9,α=0.2,α=1.2, and α=2.2

Full size image
Fig. 5
figure 5

The locations of out-of-plane equilibrium points (L 6,7) when γ=0.5, α=0.2, α=1.2, and α=2.2

Full size image
Fig. 6
figure 6

The locations of out-of-plane equilibrium points when γ=0.1, α=0.2, α=1.2, and α=2.2

Full size image

5.2 The locations with the initial approximation from the center of the bigger primary

Here we start by the initial approximation \(\xi_{0} = \sqrt{\gamma} \mu\). Hence the coordinates of out-of-plane equilibrium points will be controlled by the below parametric equations

$$\begin{aligned} \xi_{0} =& \biggl( - \frac{\sqrt{\gamma}}{2} - \sqrt[3]{2}\gamma \alpha^{ - 4/3} + \sqrt[3]{2}\gamma^{13/3} \bigl( 4 + \alpha^{2} \bigr)^{ - 2/3} \biggr) \\ &{}+ \sqrt{\gamma} \biggl( 1 - \frac{8\sqrt[3]{2}}{3}\sqrt{\gamma} \alpha^{ - 10/3} \biggr)\mu \\ &{}- \frac{8}{9}\sqrt[3]{2}\gamma \alpha^{ - 14/3} \bigl( 10 + 3\alpha^{2} \bigr)\mu^{2} \end{aligned}$$
(31)

and

$$ \zeta_{0} = \pm \sqrt{\gamma} \sqrt{ \gamma^{10/3} \bigl( 1 + ( \alpha /2 )^{2} \bigr)^{ - 2/3} - 1}. $$
(32)

Or we could write

$$\begin{aligned} \zeta_{0} = \pm \sqrt{\gamma} \biggl( \frac{2}{\alpha} \biggr)^{2/3} \biggl[ 1 + \frac{4}{3\alpha^{2}}\mu + \frac{4}{9} \biggl( \frac{8 + 3\alpha^{2}}{\alpha^{4}} \biggr)\mu^{2} \biggr]. \end{aligned}$$
(33)

It is supposed that Eqs. (31), (32), and (33) give the locations of the out-of-plane equilibrium points with the initial approximation \(\xi_{0} = \sqrt{\gamma} \mu\) when the third body has a variable mass. But Eq. (32) does not represent any real values for ζ 0 when α are assigned any real values. Therefore, the locations of the out-of-plane equilibrium points L 6,7will be governed by the parametric Eqs. (31) and (33). Finally, we emphasize that there are two out-of-plane equilibrium points L 6,7 with the initial approximation from the centers of the primaries when the mass of the third body is variable.

6 Regions of possible and forbidden motion

Multiplying Eqs. (19a), (19b), and (19c) by \(\dot{\xi}\), \(\dot{\eta}\), and \(\dot{\zeta}\), respectively, and adding as well as integrating with respect to t we obtain a Jacobian quasi-integral or an invariant integral relation in the form

$$ V^{2} - V_{0}^{2} = 2W - 2W_{0} - 2 \int_{t_{0}}^{t}\frac{\partial W}{\partial t}dt. $$
(34)

Here W 0=W(t 0,ξ 0,η 0,ζ 0).

Equation (34) can be rewritten in the form

$$ V^{2} - V_{0}^{2} = 2W - 2W_{0} - 2 \int_{\gamma_{0}}^{\gamma} \frac{\partial W}{\partial \gamma} d\gamma. $$
(35)

But in this case W 0=W 0(γ 0,ξ 0,η 0,ζ 0).

By using the methodology of Lukyanov, the non-integrable part of Eq. (35) satisfies the following inequalities:

$$\begin{aligned} \int_{\gamma_{0}}^{\gamma} \frac{\partial W}{\partial \gamma} d\gamma \ge \left\{ \begin{array}{l@{\quad }l} \frac{\partial W}{\partial \gamma} \bigg\vert _{\gamma_{0}} ( \gamma - \gamma_{0} ) &\mbox{for}\ \frac{\partial W}{\partial \gamma} \ge 0 \\ \frac{\partial W}{\partial \gamma} \bigg\vert _{\gamma} ( \gamma - \gamma_{0} ) & \mbox{for}\ \frac{\partial W}{\partial \gamma} \le 0 \end{array} \right . \end{aligned}$$
(36)

For the motion to be possible, we should have V 2≥0. Using Eq. (35), we get the condition for possible motion in the form

$$ 2W + V_{0}^{2} - 2W_{0} - 2\int _{\gamma_{0}}^{\gamma} \frac{\partial W}{\partial \gamma} d\gamma \ge 0. $$
(37)

Substituting inequality (36) into (37), we obtain

$$\begin{aligned} W \ge - \frac{V_{0}^{2}}{2} + W_{0} + \frac{\partial W}{\partial \gamma} \bigg\vert _{\gamma_{0}} ( \gamma - \gamma_{0} ) \quad \mbox{for}\ \frac{\partial W}{\partial \gamma} \ge 0, \end{aligned}$$
(38a)
$$\begin{aligned} W \ge - \frac{V_{0}^{2}}{2} + W_{0} + \frac{\partial W}{\partial \gamma} \bigg\vert _{\gamma} ( \gamma - \gamma_{0} ) \quad \mbox{for}\ \frac{\partial W}{\partial \gamma} \le 0, \end{aligned}$$
(38b)

where W=W(γ,ξ,η,ζ) and W 0=W 0(γ 0,ξ 0,η 0,ζ 0), consequently inequalities (38a), (38b) could be rewritten

$$\begin{aligned} & {W ( \gamma,\xi,\eta,\zeta ) \ge - \frac{V_{0}^{2}}{2} + W_0 ( \gamma, \xi_{0},\eta_{0},\zeta_{0} ) } \\ & {\quad \mbox{for}\ \frac{\partial W}{\partial \gamma} \ge 0, } \end{aligned}$$
(39a)
$$\begin{aligned} & {W ( \gamma_{0},\xi,\eta,\zeta ) \ge - \frac{V_{0}^{2}}{2} + W_0 ( \gamma_{0},\xi_{0},\eta_{0},\zeta_{0} )} \\ & {\quad \mbox{for}\ \frac{\partial W}{\partial \gamma} \le 0. } \end{aligned}$$
(39b)

It is clear that the conditions of motion (39a) and (39b) can be written in a more compact form as

$$ W ( \gamma ) \ge C ( \gamma ) \quad \mbox{for}\ \frac{\partial W}{\partial \gamma} \ge 0, $$
(40a)
$$ W ( \gamma_{0} ) \ge C ( \gamma_{0} )\quad \mbox{for}\ \frac{\partial W}{\partial \gamma} \le 0, $$
(40b)

where

$$ C ( \gamma ) = - \frac{V_{0}^{2}}{2} + W ( \gamma,\xi_{0}, \eta_{0},\zeta_{0} ). $$
(41)

Equation (41) shows that the energy constant C depends on the parameter γ and the initial conditions; then, in this case, the Jacobi energy constant C can be called the mass ratio energy function. The variation of the energy of the system which determines the regions of possible motions depends on the value of the mass ratio parameter γ. This variation is shown in Fig. 7 when μ=0.3 and α=0.2 with initial position (0.1,0,0.1) and zero initial velocity.

Fig. 7
figure 7

The variation of C with γ when μ=0.3, α=0.2 with initial position (0.1,0,0.1) and zero initial velocity

Full size image

It is clear from Fig. 7 that the value of energy constant C corresponds with the value of parameter γ. This is clear also from Eqs. (18a), (18b), (20), and (41). Furthermore, Eqs. (40a) and (40b) can be combined to simply give the condition for possible motion of

$$ W ( \gamma ) \ge C ( \gamma ). $$
(42)

Comparing the condition (42) with the classical case of a constant mass, we note that the conditions are very close. The only difference is the existence of the variable parameter γ. So, we will get different conditions for different mass ratios m/m 0, which coincides in the limit case γ=1 (equivalently, m=m 0=constant) with the condition of the possible region for a third body with constant mass.

Sometimes it is reasonable to consider the variation in mass in a discrete manner rather than in a continuous scale, especially when the rate of change of mass is small. Following this approach, condition (42) can be thought of as a sequence of conditions for the regions of possible motion associated with the different mass ratio values γ.

Now we are interested in finding the regions of possible and forbidden motion in the ξζ-plane. We draw the surfaces of possible and forbidden regions in the 3-dimensional space ξζγ for values of γ varying from 1 to 0, which is the case of a third body losing its mass up to the limit case m=0. The initial position and velocity are taken (0.1,0,0.1) and zero, respectively, and the mass ratio of the primaries μ=0.3, while α is taken 0.2.

Next, we draw the intersections of the surface of possible motion in Fig. 8 with different values of the mass ratio parameter γ. In Figs. 9–14 the dark regions are the forbidden regions for the motion.

Fig. 8
figure 8

The regions of possible motions (dark) in the 3-dimensional space ξζγ when μ=0.3, α=0.2 with initial position (0.1,0,0.1), and zero initial velocity

Full size image
Fig. 9
figure 9

Section of the region of forbidden motion at γ=0.8

Full size image
Fig. 10
figure 10

Section of the region of forbidden motion at γ=0.6

Full size image
Fig. 11
figure 11

Section of the region of forbidden motion at γ=0.4

Full size image
Fig. 12
figure 12

Section of the region of forbidden motion at γ=0.2

Full size image
Fig. 13
figure 13

Section of the region of forbidden motion at γ=0.01

Full size image
Fig. 14
figure 14

Section of the region of forbidden motion at γ=0.005

Full size image

Figures 9–14 illustrate the sections of the region of forbidden motion at different values of γ for the same numerical values as used in the 3-dimensional Fig. 8. It is clear that the regions of possible motion shrink with the increase of γ, while the region of forbidden motion expands with its increase. This reflects the situation that the more the third body loses its mass, the wider the possible region of motion it has. Since C is increasing with γ, we see also that the regions of possible motion shrink with the increase of the mass ratio energy function C.

7 Conclusion

In the framework of restricted three-body problem, we made an analytical study of the dynamics of the third body in the context of this body having variable mass changes according to Jeans’ law. The equation of motion is derived when the loss of mass is non-isotropic. In addition the appropriate approximation for the locations of the out-of-plane equilibrium points in the special case for a non-isotropic variation of the mass are also found. Some graphical investigations for the parameter effects of the variable mass on the locations of the out-of-plane equilibrium points as well as the regions of possible and forbidden motions for the third body are investigated.

An analytical condition for the regions of possible motion has been derived. It will not give an invariant of motion like the Jacobi integral in the classical case of constant mass, but it will give a sequence of values for the energy C(γ), which is similar to the case of the restricted three-body problem with variable-mass parameter μ described by Lukyanov (2009). In Fig. 7, C is plotted against γ at μ=0.3, α=0.2 with initial position (0.1,0,0.1) and zero initial velocity.

The forbidden and possible regions of motion of the third body with variable mass are investigated graphically in Figs. 8–14. First, a 3D-graph has been plotted in the ξζγ space at μ=0.3 and α=0.2 with initial position (0.1,0,0.1) and zero initial velocity. Then the sections of this surface at different values of the mass parameter γ have been plotted. It is found that the regions of possible motions shrink with the increase of C.