The effect of oblateness in the perturbed restricted three-body problem

Abstract

In this paper the restricted three-body problem is generalized in the sense that the effects of oblateness of the three participating bodies as well as the small perturbations in the Coriolis and centrifugal forces are considered. The existence of equilibrium points, their linear stability and the periodic orbits around these points are studied under these effects. It is found that the positions of the collinear points and y-coordinate of the triangular points are not affected by the small perturbations in the Coriolis force. While x-coordinate of the triangular points is neither affected by the small perturbations in the Coriolis force nor the oblateness of the third body. Furthermore, the critical mass value and the elements of periodic orbits around the equilibrium points such as the semi-major and the semi-minor axes, the angular frequencies and corresponding periods may change by all the parameters of oblateness as well as the small perturbations in the Coriolis and centrifugal forces. This model could be applicable to send satellite or place telescope in stable regions in space.

1 Introduction

In the last decades the restricted three-body problem has been enhanced by a great number of researches. Many of these researches deal with the effects of the perturbed forces like the lack of sphericity, photogravitational force, Coriolis and centrifugal forces, variation of masses, the Pointing-Robertson and Yarkovsky effects, the atmospheric drag and solar wind. The Kirkwood gaps in the ring of the asteroid’s orbits lying between the orbits of Mars and Jupiter are examples of the perturbation produced by Jupiter on an asteroid. This motivates many researchers to study restricted three-body problem under the effects of small perturbations in Coriolis and centrifugal forces when the three participating objects are oblate, etc.

The significance of the restricted problem in describing actual physical situations can be judged by the results obtained when these are compared to observations. The most important, the utility might be prejudged by order of magnitude evaluations regarding the masses and the distances of the participating bodies. A classical example in space dynamics is the sun-earth-moon system.

Some important contributions related to the libration points in the restricted three-body problem with one or both primaries are oblate spheroids when the equatorial plane is coincident with the plane of motion are studied by Subbarao and Sharma [22], Sharma and Subbarao [17] and Markellos et al. [14]. Abouelmagd [3] also studied the effects of oblateness J ₂ and J ₄ for the more massive primary in the planar restricted three-body problem on the locations of the triangular points and their linear stability. He found that these locations are affected by the coefficients of oblateness. Furthermore he investigated that the triangular points are stable for 0<μ<μ _c and unstable when μ _c ≤μ≤1/2, where μ _c is the critical mass parameter which depends on the coefficients of oblateness.

The existence of libration points and their linear stability as well as periodic orbits around these points when the more massive primary is radiating and the smaller is an oblate spheroid were studied by Abouelmagd and Sharaf [5]. Their study also includes the effects of oblateness of $\bar{J}_{2i}$ (i=1,2) with respect to the smaller primary in the restricted three-body problem.

The restricted problem when the three participating bodies are oblate spheroids was also studied by Elipe and Ferrer [9] and El-Shaboury and El-Tantawy [11]. When one or two of the primaries are triaxial bodies this problem was introduced by El-Shaboury et al. [12], Khanna and Bhatnagar [13] and Sharma et al. [18].

Various researchers made studies in the restricted three-body problem under the effects of small perturbations in centrifugal and Coriolis forces as in Szebehely [23], Bhatnagar and Hallan [6], Devi and Singh [8], Shu and Lu [19], AbdulRaheem and Singh [1, 2].

The effect of small perturbations ε, ε′ in Coriolis and centrifugal forces with variable mass in the restricted three-body problem has been studied by Singh [21]. He found that in the nonlinear sense the triangular points are stable for all mass ratios in the range of linear stability except for three mass ratios which depend on ε, ε′ and the constant β due to the variation of mass governed by Jeans’ law.

Mittal et al. [15] have studied periodic orbits generated by Lagrangian solutions of the restricted three-body problem when the bigger body is a source of radiation and the smaller is an oblate spheroid. They used the definition of Karimov and Sokolsky for mobile coordinates to determine these orbits, they also used the predictor method to draw them.

Singh and Begha [20] have studied the existence of periodic orbits around the triangular points in the restricted three-body problem when the bigger primary is a triaxial and the smaller primary is considered as an oblate spheroid in the range of linear stability with the perturbed Coriolis and centrifugal forces. They deduced that long and short periodic orbits exist around these points and their periods, orientation and eccentricities are affected by the non sphericity and the perturbation in Coriolis and centrifugal forces.

The existence of libration points and their linear stability when the three participating bodies are oblate spheroids and the primaries are radiation source as well were studied by Abouelmagd and El-Shaboury [4]. They found that the collinear points are still unstable while the triangular points are stable for 0<μ<μ _c , and unstable for μ _c ≤μ≤1/2, where μ _c ∈(0,1/2). They also deduced that for these points the range of stability will decrease. In addition they studied the periodic orbits around these points in the range 0<μ<μ _c .

From physical point of view, it is unreasonable to consider all objects as being point masses with no physical dimensions. This is conflict with the real cases for the celestial bodies. On the other hand the effect of rotation causes deformation in the shape of the objects at the poles as might be expected. For this reason most objects may be treated to a good approximation as oblate spheroids.

Therefore in this paper we will generalize the restricted three-body, in which the three participating bodies are oblate spheroids as well as the existence of small perturbations in the Coriolis and centrifugal forces. The existence of libration points and their linear stability and the periodic orbits around these points will be studied. This model could be applicable in astrodynamics or astrophysics.

Now we assume that the three participating bodies are oblate spheroids. Therefore we refer to oblateness parameters of the bigger, smaller primaries and infinitesimal body by A ₁, A ₂ and A respectively, We also denote the small perturbations in Coriolis and centrifugal forces by ε _i (i=1,2) where 0<A ₁≪1, 0<A ₂≪1, 0<A≪1 and ε _i ≪1.

2 The equations of motion

It is well known that, there are five exact solutions in three-body problem which the three masses maintain a constant configuration which revolves with constant angular velocity. An important specialization of the three-body problem is the restricted three-body problem in which m is infinitesimal body, m ₁ and m ₂ are the bigger and smaller primaries respectively. They move in circular orbits around their barycenter. The smallness of m means that it does not influence the motion of m ₁ and m ₂. For many purposes it is convenient to describe the motion of m in a coordinate system which is attached to m ₁ and m ₂. In this rotating coordinate system the five Lagrangian solutions show up as five fixed points at which m would be stationary if placed there with zero velocity. Now we suppose that r ₁ and r ₂ are the distance of m from m ₁ and m ₂ respectively, R is the separation distance between the primaries. Furthermore we also suppose that mis moving under their gravitational field in the same plane. In addition we adopt the notation and terminology of Szebehely [24]. As a consequence, the distance between the primaries equals one, the sum of masses of the primaries is also taken as one, the unit time is chosen as to make the unperturbed mean motion and the gravitational constant unity, then it follows that m ₁=1−μ, whose coordinate is (μ,0), m ₂=μ≤1/2 and located at (μ−1,0). Therefore the equations of motion in a synodic coordinate system for infinitesimal body are controlled by (Abouelmagd and El-Shaboury, [4])

$$\begin{aligned} &{\ddot{x} - 2n\dot{y} = U_{x}} \end{aligned}$$

(1.1)

$$\begin{aligned} &{\ddot{y} + 2n\dot{x} = U_{y}} \end{aligned}$$

(1.2)

where

$$\begin{aligned} &{U = \frac{1}{2}n^{2} \bigl[ ( 1 - \mu )r_{1}^{2} + \mu r_{2}^{2} \bigr] } \\ &{\hphantom{U =} {} + ( 1 - \mu )\biggl[\frac{1}{r_{1}} + \frac{(A_{1} + A)}{2r_{1}^{3}}\biggr]} \\ &{\hphantom{U =} {} + \mu \biggl[\frac{1}{r_{2}} + \frac{(A_{2} + A)}{2r_{2}^{3}} \biggr]} \end{aligned}$$

(2)

$$\begin{aligned} &{n^{2} = 1 + \frac{3}{2}(A_{1} + A_{2})} \end{aligned}$$

(3)

$$\begin{aligned} &{r_{1}^{2} = ( x - \mu )^{2} + y^{2}, \qquad r_{2}^{2} = ( x - \mu + 1 )^{2} + y^{2}} \end{aligned}$$

(4)

The equations of motion of the infinitesimal body in a synodic coordinate system are governed by (1.1), (1.2) and (2) when the three participating bodies are oblate spheroids. After that, we denote the Coriolis and centrifugal forces by φ, ψ and the small perturbations in these forces by ε ₁ and ε ₂ respectively, where

$$\begin{aligned} &{\varphi = 1 + \varepsilon _{1},\quad \varepsilon _{1} \ll 1} \end{aligned}$$

(5.1)

$$\begin{aligned} &{\psi = 1 + \varepsilon _{2},\quad \varepsilon _{2} \ll 1} \end{aligned}$$

(5.2)

Therefore (1.1), (1.2) and (2) could be written as

$$\begin{aligned} &{\ddot{x} - 2\varphi n\dot{y} = \varOmega _{x}} \end{aligned}$$

(6.1)

$$\begin{aligned} &{\ddot{y} + 2\varphi n\dot{x} = \varOmega _{y}} \end{aligned}$$

(6.2)

$$\begin{aligned} \varOmega =& \frac{1}{2}n^{2}\psi \bigl[ ( 1 - \mu )r_{1}^{2} + \mu r_{2}^{2} \bigr] \\ &{} + ( 1 - \mu )\biggl[\frac{1}{r_{1}} + \frac{(A_{1} + A)}{2r_{1}^{3}}\biggr] \\ &{} + \mu \biggl[\frac{1}{r_{2}} + \frac{(A_{2} + A)}{2r_{2}^{3}}\biggr] \end{aligned}$$

(7)

where the subscripts on the right hand side denote the partial derivation respect to the x and y respectively.

3 The locations of the libration points

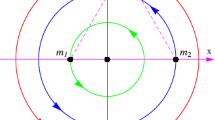
The libration points are singular points of the differential equations of motions in the restricted problem of three bodies. They are also equilibrium points since the gravitational force on a mass placed in such a point are balanced by the centrifugal force. The three libration points are called the collinear points which are found on the line connecting with the primaries. The other two are called the triangular points which are symmetrical with respect to this line and form triangles, see Fig. 1.

Fig. 1

The positions of the equilibrium points L _i (i=1,2,…,5)

From (6.1), (6.2) we can obtain Jacobi integral as

$$ \dot{x}^{2} + \dot{y}^{2} - 2\varOmega + c = 0 $$

(8)

in which c is a constant of integration.

The locations of these points will be determined by solving the following equations

$$ \varOmega _{x} = \varOmega _{\dot{x}} = \varOmega _{y} = \varOmega _{\dot{y}} = 0 $$

(9)

where the first partial derivatives of Ω will be governed by

$$\begin{aligned} &{\varOmega _{x} = (x - \mu )f_{1} ( r_{1} ) + ( x - \mu + 1 )f_{2} ( r_{2} )} \end{aligned}$$

(10.1)

$$\begin{aligned} &{\varOmega _{y} = y \bigl[ f_{1} ( r_{1} ) + f_{2} ( r_{2} ) \bigr]} \end{aligned}$$

(10.2)

$$\begin{aligned} &{f_{1} ( r_{1} ) = ( 1 - \mu )\biggl[\psi n^{2} - \biggl(\frac{1}{r_{1}^{3}} + \frac{3(A_{1} + A)}{2r_{1}^{5}}\biggr)\biggr]} \end{aligned}$$

(11.1)

$$\begin{aligned} &{f_{2} ( r_{2} ) = \mu \biggl[\psi n^{2} - \biggl( \frac{1}{r_{2}^{3}} + \frac{3 ( A_{2} + A )}{2r_{2}^{5}}\bigg)\biggr]} \end{aligned}$$

(11.2)

From (10.1), (10.2), we will have two cases. These cases will be investigated in the following subsection.

3.1 The collinear points

The collinear points L _i (i=1,2,3) are the solutions of (9) and (10.1), (10.2) when y=0, therefore

$$ \nu = ( - 1 )^{i}\frac{r_{2}^{4} ( r_{1}^{5} - pr_{1}^{2} - a )}{r_{1}^{4} ( r_{2}^{5} - pr_{2}^{2} - b )},\quad i = 1,2,3 $$

(12)

where i indicates the value of ν at L _i (i=1,2,3),

$$\begin{aligned} &{\nu = \frac{\mu}{1 - \mu},\qquad p = \frac{1}{q},\qquad q = \psi n^{2}} \end{aligned}$$

(13.1)

$$\begin{aligned} &{a = \frac{3(A_{1} + A)}{2q},\qquad b = \frac{3 ( A_{2} + A )}{2q}} \end{aligned}$$

(13.2)

Lagrange developed a useful method for inverting series expansions. This method could be applicable in the present work. He investigated that if a variable $\mathcal {X}$ can be expressed as a function of $\mathcal {Y}$ as in the below relation (Murray and Dermott [16])

$$ \mathcal {Y} = \mathcal {X} + \vartheta \phi ( \mathcal {Y} ),\quad \vartheta < 1 $$

(14)

therefore $\mathcal {Y}$ can also be expressed as a function of $\mathcal {X}$ as in the following form

$$ \mathcal {Y} = \mathcal {X} + \sum_{k = 1}^{\infty} \frac{\vartheta ^{k}}{k!}\frac{d^{k - 1}}{d\mathcal {X}^{k - 1}}\bigl[\phi ( \mathcal {X} ) \bigr]^{k} $$

(15)

3.1.1 Location of L ₁

The solution of L ₁ lies beyond the smaller mass as in Fig. 1. Therefore r ₁−r ₂=1, hence r ₂=μ−x−1, r ₁=μ−x, this implies that: $\frac{\partial r_{1}}{\partial x} = \frac{\partial r_{2}}{\partial x} = - 1$. If we take r ₂=r, r ₁=1+r and substitute them into (12). After some simple calculations the value of ν will be written as

$$ \nu = a_{4}r^{4} + a_{5}r^{5} + a_{6}r^{6} + a_{7}r^{7} + O \bigl[r^{8}\bigr] $$

(16)

where the values a ₄, a ₅, a ₆ and a ₇ are to be given as in Appendix A.1.

Now, we use Lagrange’s inversion method to invert the above series and express r as function of ν which is written as

$$\begin{aligned} r =& \biggl(\frac{1}{a_{4}}\biggr)^{1/4}\nu ^{1/4} - \frac{1}{4} \biggl( \biggl( \frac{1}{a_{4}} \biggr)^{3/2}a_{5} \biggr)\sqrt{\nu} \\ &{} + \frac{1}{32} \biggl( \frac{1}{a_{4}} \biggr)^{11/4} \bigl( 7a_{5}^{2} - 8a_{4}a_{6} \bigr)\nu ^{3/4} \\ &{} + \frac{ ( - a_{5}^{3} + 2a_{4}a_{5}a_{6} - a_{4}^{2}a_{7} )}{4a_{4}^{4}}\nu + O\bigl[\nu ^{5/4}\bigr] \end{aligned}$$

(17)

Consequently the location of L ₁ will be given by

$$\begin{aligned} x_{1} =& - 1 + \frac{\nu}{1 + \nu} - \biggl( \frac{1}{a_{4}} \biggr)^{1/4}\nu ^{1/4} \\ &{} + \frac{1}{4} \biggl( \biggl( \frac{1}{a_{4}} \biggr)^{3/2}a_{5} \biggr)\sqrt{\nu} \\ &{} - \frac{1}{32} \biggl( \frac{1}{a_{4}} \biggr)^{11/4} \bigl( 7a_{5}^{2} - 8a_{4}a_{6} \bigr)\nu ^{3/4} \\ &{} - \frac{ ( - a_{5}^{3} + 2a_{4}a_{5}a_{6} - a_{4}^{2}a_{7} )}{4a_{4}^{4}}\nu \end{aligned}$$

(18)

3.1.2 Location of L ₂

The solution of L ₂ lies between the two finite bodies as in Fig. 1, here r ₁+r ₂=1, hence r ₂=x−μ+1, r ₁=μ−x, this implies that $\frac{\partial r_{1}}{\partial x} = - \frac{\partial r_{2}}{\partial x} = - 1$. If we take r ₂=ρ, r ₁=1−ρ and substitute them into (12). The value of ν will be given by

$$ \nu = b_{4}\rho ^{4} + b_{5}\rho ^{5} + b_{6}\rho ^{6} + b_{7}\rho ^{7} + O \bigl[\rho ^{8}\bigr] $$

(19)

where the values b ₄, b ₅, b ₆ and b ₇ are governed as in Appendix A.1.

As mentioned before, we use Lagrange’s inversion method to invert the above series and express ρ as function of ν which is written as

$$\begin{aligned} \rho =&\biggl(\frac{1}{b_{4}}\biggr)^{1/4}\nu ^{1/4} - \frac{1}{4} \biggl( \biggl( \frac{1}{b_{4}} \biggr)^{3/2}b_{5} \biggr)\sqrt{\nu} \\ &{} + \frac{1}{32} \biggl( \frac{1}{b_{4}} \biggr)^{11/4} \bigl( 7b_{5}^{2} - 8b_{4}b_{6} \bigr)\nu ^{3/4} \\ &{} + \frac{ ( - b_{5}^{3} + 2b_{4}b_{5}b_{6} - b_{4}^{2}b_{7} )}{4b_{4}^{4}}\nu + O\bigl[\nu ^{5/4}\bigr] \end{aligned}$$

(20)

Therefore the location of L ₂ could be written as

$$\begin{aligned} x_{2} =& - 1 + \frac{\nu}{1 + \nu} + \biggl( \frac{1}{b_{4}} \biggr)^{1/4}\nu ^{1/4} \\ &{} - \frac{1}{4} \biggl( \biggl( \frac{1}{b_{4}} \biggr)^{3/2}b_{5} \biggr)\sqrt{\nu} \\ &{} + \frac{1}{32} \biggl( \frac{1}{b_{4}} \biggr)^{11/4} \bigl( 7b_{5}^{2} - 8b_{4}b_{6} \bigr)\nu ^{3/4} \\ &{} + \frac{ ( - b_{5}^{3} + 2b_{4}b_{5}b_{6} - b_{4}^{2}b_{7} )}{4b_{4}^{4}}\nu \end{aligned}$$

(21)

3.1.3 Location of L ₃

The solution of L ₃ lies beyond the large mass as in Fig. 1, here r ₂−r ₁=1, hence r ₂=1−μ+x, r ₁=x−μ, this implies that $\frac{\partial r_{1}}{\partial x} = \frac{\partial r_{2}}{\partial x} = 1$. If we take r ₁=1+δ, r ₂=2+δ and substitute them into (12). We will obtain

$$ \nu = c_{0} + c_{1}\delta + c_{2}\delta ^{2} + O\bigl[\delta ^{3}\bigr] $$

(22)

where the values c ₀, c ₁, and c ₂ are to be given as in Appendix A.1.

We also use Lagrange’s inversion method to invert the above series and express δ as function of ν as in the following form

$$ \delta = \frac{\nu - c_{0}}{c_{1}} - \frac{c_{2}(\nu - c_{0})^{2}}{c_{1}^{3}} + O\bigl[ ( \nu - c_{0} )^{3}\bigr] $$

(23)

Hence the location of L ₃ will be controlled by

$$ x_{3} = 1 + \frac{\nu}{1 + \nu} + \frac{\nu - c_{0}}{c_{1}} - \frac{c_{2}(\nu - c_{0})^{2}}{c_{1}^{3}} $$

(24)

Equations (18), (21) and (24) represent semi-closed forms for the positions of collinear points. Furthermore, the small perturbation in the Coriolis force has no effect on these positions.

3.2 The triangular points

The solutions of (9) and (10.1), (10.2) when y≠0 will be given the triangular points L ₄ and L ₅. These solutions will establish

$$ f_{1} ( r_{1} ) = 0 = f_{2} ( r_{2} ) $$

(25)

Therefore, we get

$$\begin{aligned} &{\psi n^{2} = \frac{1}{r_{1}^{3}} + \frac{3(A_{1} + A)}{2r_{1}^{5}}} \end{aligned}$$

(26.1)

$$\begin{aligned} &{\psi n^{2} = \frac{1}{r_{2}^{3}} + \frac{3 ( A_{2} + A )}{2r_{2}^{5}}} \end{aligned}$$

(26.2)

To study the effect of oblateness in the perturbed problem on the locations of the triangular points, we will assume that the three participating bodies are not oblate spheroids (A ₁=A ₂=A=0). Hence (26.1), (26.2) will admit $r_{i} = 1/\sqrt[3]{\psi}$. Consequently if the three bodies are oblate, the solution of (26.1), (26.2) will be controlled by

$$ r_{i} = \frac{1}{\sqrt[3]{\psi}} + \varepsilon _{i},\quad \varepsilon _{i} \ll 1\quad (i = 1,2) $$

(27)

where ε _i gives the additive of displacement in r _i as a result for oblateness effects. Substituting (27) into (26.1), (26.2) and restricting ourselves to only linear terms in ε ₁, ε ₂, A ₁, A ₂ and A. The appropriate approximation of ε _i could be written as

$$\begin{aligned} &{\varepsilon _{1} = - \frac{1}{2}(A_{1} + A_{2})\psi ^{ - \frac{1}{3}} + \frac{1}{2}(A_{1} + A) \psi ^{\frac{1}{3}}} \end{aligned}$$

(28.1)

$$\begin{aligned} &{\varepsilon _{2} = - \frac{1}{2}(A_{1} + A_{2})\psi ^{ - \frac{1}{3}} + \frac{1}{2}(A_{2} + A) \psi ^{\frac{1}{3}}} \end{aligned}$$

(28.2)

From (4) the exact solutions of the triangular points could be written as

$$\begin{aligned} &{x = - \frac{1}{2} \bigl[ 1 - 2\mu + r_{1}^{2} - r_{2}^{2} \bigr]} \end{aligned}$$

(29.1)

$$\begin{aligned} &{y = \pm \biggl[ \biggl( \frac{r_{1}^{2} + r_{2}^{2}}{2} \biggr) - \biggl( \frac{r_{1}^{2} - r_{2}^{2}}{2} \biggr)^{2} - \frac{1}{4} \biggr]^{\frac{1}{2}}} \end{aligned}$$

(29.2)

Substituting (28.1), (28.2) and (27) into (29.1), (29.2) with limiting ourselves to previous assumptions we get

$$\begin{aligned} &{x = \mu - \frac{1}{2} - \frac{1}{2}(A_{1} - A_{2})} \end{aligned}$$

(30.1)

$$\begin{aligned} &{y = \pm \frac{\sqrt{3}}{2} \biggl[ 1 - \frac{1}{3}(A_{1} + A_{2} - 2A)} \\ &{\hphantom{y =} {} - \frac{4}{9} ( 1 + A_{1} + A_{2} + A )\varepsilon _{2} \biggr]} \end{aligned}$$

(30.2)

Equations (30.1), (30.2) show that the presence of parameters that represent oblateness of the infinitesimal body, the small perturbations in Coriolis and centrifugal forces have no effect on x-coordinate of the triangular points. While y-coordinate of the triangular points may be affected by all the parameters of the perturbed forces except for the small perturbations in the Coriolis force.

4 The stability of the libration points

The stability of libration points is a well problem studied in the classical literature. Therefore, in this section and the next sections we follow the analysis that is based on Szebehely’s computations [24].

4.1 Characteristic equation

Let x ₀ and y ₀ are the coordinates of one of the five libration points as well as ξ and η are very small displacements from these coordinates where

$$\begin{aligned} &{\xi = x - x_{0}} \end{aligned}$$

(31.1)

$$\begin{aligned} &{\eta = y - y_{0}} \end{aligned}$$

(31.2)

Therefore the linear variational equations could be written as

$$\begin{aligned} &{\ddot{\xi} - 2n\varphi \dot{\eta} = \xi \varOmega _{xx}^{0} + \eta \varOmega _{xy}^{0}} \end{aligned}$$

(32.1)

$$\begin{aligned} &{\ddot{\eta} + 2n\varphi \dot{\xi} = \xi \varOmega _{xy}^{0} + \eta \varOmega _{yy}^{0}} \end{aligned}$$

(32.2)

where the subscripts x and y denoted the second partial derivatives of Ω and superscript 0 indicates that these derivatives are to be evaluated at one of the five equilibrium points (x ₀,y ₀). Furthermore these derivatives will be governed by

$$\begin{aligned} &{\varOmega _{xx} = f_{1} ( r_{1} ) + f_{2} ( r_{2} ) + \frac{1}{r_{1}}\frac{\partial f_{1}}{\partial r_{1}} ( x - \mu )^{2}} \\ &{\hphantom{\varOmega _{xx} =} {} + \frac{1}{r_{2}}\frac{\partial f_{2}}{\partial r_{2}} ( x - \mu + 1 )^{2}} \end{aligned}$$

(33.1)

$$\begin{aligned} &{\varOmega _{xy} = \biggl[ \frac{1}{r_{1}}\frac{\partial f_{1}}{\partial r_{1}} ( x - \mu ) + \frac{1}{r_{2}}\frac{\partial f_{2}}{\partial r_{2}} ( x - \mu + 1 ) \biggr]y} \\ \end{aligned}$$

(33.2)

$$\begin{aligned} &{\varOmega _{yy} = f_{1} ( r_{1} ) + f_{2} ( r_{2} ) + \biggl[ \frac{1}{r_{1}} \frac{\partial f_{1}}{\partial r_{1}} + \frac{1}{r_{2}}\frac{\partial f_{2}}{\partial r_{2}} \biggr]y^{2}} \end{aligned}$$

(33.3)

where

$$\begin{aligned} &{\frac{\partial f_{1}}{\partial r_{1}} = ( 1 - \mu )\biggl[\frac{3}{r_{1}^{4}} + \frac{15 ( A_{1} + A )}{2r_{1}^{6}} \biggr]} \end{aligned}$$

(34.1)

$$\begin{aligned} &{\frac{\partial f_{2}}{\partial r_{2}} = \mu \biggl[\frac{3}{r_{2}^{4}} + \frac{15 ( A_{2} + A )}{2r_{2}^{6}}\biggr]} \end{aligned}$$

(34.2)

The characteristic equation corresponding to (32.1), (32.2) is

$$\begin{aligned} &{\lambda ^{4} + \bigl( 4n^{2}\varphi ^{2} - \varOmega _{xx}^{0} - \varOmega _{yy}^{0} \bigr)\lambda ^{2} + \varOmega _{xx}^{0}\varOmega _{yy}^{0} - \bigl(\varOmega _{xy}^{0} \bigr)^{2}} \\ &{\quad = 0} \end{aligned}$$

(35)

The most fundamental questions about motion near libration points are those about the stability of these points. The next subsections will survey the results obtained in the investigations of the stability.

4.2 Stability of collinear points

In order to investigate the stability of collinear points, we have to study the motion in the vicinity of these points. For this purpose (33.1)–(33.3) could be written at the collinear points as

$$\begin{aligned} &{\varOmega _{xx}^{0} = \psi n^{2} + ( 1 - \mu ) \biggl( \frac{2}{r_{1}^{3}} + \frac{6(A_{1} + A)}{r_{1}^{5}} \biggr)} \\ &{\hphantom{\varOmega _{xx}^{0} =} {} + \mu \biggl( \frac{2}{r_{2}^{3}} + \frac{6 ( A_{2} + A )}{r_{2}^{5}} \biggr)} \end{aligned}$$

(36.1)

$$\begin{aligned} &{\varOmega _{xy}^{0} = 0} \end{aligned}$$

(36.2)

$$\begin{aligned} &{\varOmega _{yy}^{0} = \psi n^{2} - ( 1 - \mu ) \biggl( \frac{1}{r_{1}^{3}} + \frac{3(A_{1} + A)}{2r_{1}^{5}} \biggr)} \\ &{\hphantom{\varOmega _{yy}^{0} =} {} - \mu \biggl( \frac{1}{r_{2}^{3}} + \frac{3 ( A_{2} + A )}{2r_{2}^{5}} \biggr)} \end{aligned}$$

(36.3)

Equations (36.1)–(36.3) show that $\varOmega _{xx}^{0} > 0$, $\varOmega _{xy}^{0} = 0$ and $\varOmega _{yy}^{0} < 0$ at L _i (i=1,2,3), as a result for this $\varOmega _{xx}^{0}\varOmega _{yy}^{0} - (\varOmega _{xy}^{0})^{2} < 0$. Let λ ²=Λ, therefore (35) could be written as

$$ \varLambda ^{2} + \overline{\lambda} _{1c}\varLambda + \overline{\lambda} _{2c} = 0 $$

(37)

where

$$\begin{aligned} &{\overline{\lambda} _{1c} = \bigl( 4n^{2}\varphi ^{2} - \varOmega _{xx}^{0} - \varOmega _{yy}^{0} \bigr)} \end{aligned}$$

(38.1)

$$\begin{aligned} &{\overline{\lambda} _{2c} = \varOmega _{xx}^{0} \varOmega _{yy}^{0}} \end{aligned}$$

(38.2)

where

$$ \varLambda _{1,2} = - \frac{1}{2}\Bigl[\bar{\lambda} _{1c} \mp \sqrt{\overline{\lambda} _{1c}^{2} - 4\overline{\lambda} _{2c}} \,\Bigr] $$

(39)

Equations (38.1), (38.2) and (39) show that the roots of characteristic equation (35) could be written as λ _1,2=±σ, λ _3,4=±iτ where σ and τ are real numbers, where

$$\begin{aligned} &{\sigma ^{2} = \frac{1}{2} \Bigl[ \sqrt{\overline{ \lambda} _{1c}^{2} - 4\overline{\lambda} _{2c}} - \bar{\lambda} _{1c} \Bigr]} \end{aligned}$$

(40.1)

$$\begin{aligned} &{\tau ^{2} = \frac{1}{2} \Bigl[ \sqrt{\overline{ \lambda} _{1c}^{2} - 4\overline{\lambda} _{2c}} + \bar{\lambda} _{1c} \Bigr]} \end{aligned}$$

(40.2)

The general solution of (32.1), (32.2) can be written as

$$ \xi ( t ) = \sum_{i = 1}^{4}\delta _{i}e^{\lambda _{i}t},\qquad \eta ( t ) = \sum _{i = 1}^{4}\rho _{i}e^{\lambda _{i}t} $$

(41)

therefore

$$ \dot{\xi} ( t ) = \sum_{i = 1}^{4}\lambda _{i}\delta _{i}e^{\lambda _{i}t},\qquad \dot{\eta} ( t ) = \sum_{i = 1}^{4}\lambda _{i}\rho _{i}e^{\lambda _{i}t} $$

(42)

Now we establish that the motion around the collinear points is unbounded. However λ _3,4 are pure imaginary, λ _1,2 are real. Therefore the solutions of these points are unstable.

4.2.1 Stability of triangular points

In this case (33.1)–(33.3) could be written as

$$\begin{aligned} &{\varOmega _{xx}^{0} = \frac{3}{4} \biggl[ 1 + \frac{5}{2}(A_{1} + A_{2}) + 2(1 - 2\mu ) (A_{1} - A_{2}) \biggr]} \\ &{\hphantom{\varOmega _{xx}^{0} =} {}+ \frac{5}{4} \biggl[ 1 + \frac{5}{2}(A_{1} + A_{2})} \\ &{\hphantom{\varOmega _{xx}^{0} =} {} + 2(1 - 2\mu ) (A_{1} - A_{2}) \biggr]\varepsilon _{2}} \end{aligned}$$

(43.1)

$$\begin{aligned} &{\varOmega _{xy}^{0} = \mp \frac{3\sqrt{3}}{4} \biggl[ 1 - 2\mu + \frac{19}{6} \biggl( 1 - \frac{26}{19}\mu \biggr)A_{1}} \\ &{\hphantom{\varOmega _{xy}^{0} =} {} + \frac{7}{6} \biggl( 1 - \frac{26}{7}\mu \biggr)A_{2} + \frac{2}{3} ( 1 - 2\mu )A} \\ &{\hphantom{\varOmega _{xy}^{0} =} {} + \frac{11}{9} \biggl[ 1 - 2\mu + \frac{80}{297} ( 1 - 14\mu ) ( A_{1} + A_{2} )} \\ &{\hphantom{\varOmega _{xy}^{0} =} {} + \frac{560}{297} \biggl( 1 + \frac{4}{7}\mu \biggr)A \biggr]\varepsilon _{2} \biggr]} \end{aligned}$$

(43.2)

$$\begin{aligned} &{\varOmega _{yy}^{0} = \frac{9}{4} \biggl[ 1 + \frac{11}{6} ( A_{1} + A_{2} ) + \frac{4}{3}A \biggr]} \\ &{\hphantom{\varOmega _{yy}^{0} =} {} + \frac{7}{4} \biggl[ 1 + \frac{27}{14} ( A_{1} + A_{2} ) + \frac{36}{7}A \biggr]\varepsilon _{2}} \end{aligned}$$

(43.3)

Substituting λ ²=ω into (35) we get

$$ \omega ^{2} + \bar{\lambda} _{1t}\omega + \bar{\lambda} _{2t} = 0 $$

(44)

where

$$\begin{aligned} &{\bar{\lambda} _{1t} = \bigl( 4n^{2}\varphi ^{2} - \varOmega _{xx}^{0} - \varOmega _{yy}^{0} \bigr)} \end{aligned}$$

(45.1)

$$\begin{aligned} &{\bar{\lambda} _{2t} = \varOmega _{xx}^{0} \varOmega _{yy}^{0} - \bigl(\varOmega _{xy}^{0} \bigr)^{2}} \end{aligned}$$

(45.2)

Here superscript 0 indicates to the second partial derivatives are to be evaluated at the triangular points, hence

$$ \omega _{1,2} = - \frac{1}{2}\bigl[\bar{\lambda} _{1t} \mp \sqrt{D} \,\bigr] $$

(46)

where $D = \bar{\lambda} _{1t}^{2} - 4\bar{\lambda} _{2t}$ is the discriminant of the quadratic in (44). Now we can write the discriminant as

$$ D = \alpha \mu ^{2} + \beta \mu + \gamma $$

(47)

where α, β and γ are to be evaluated as in Appendix A.2.

The variations ξ and η will represent stable solutions in the proximity of L ₄ and L ₅, if the four roots of the characteristic equation (35) are purely imaginary numbers. On the other hand, if any of these roots are real or complex, these solutions will increase with time, therefore the solutions are unstable. From (47), it is easily to prove that

$$\begin{aligned} &{D_{\mu = 0} > 0,\quad D_{\mu = 1/2} < 0,\quad \frac{dD}{d\mu} \le 0\quad \forall \mu \in ( 0,1/2 )} \\ \end{aligned}$$

(48)

Equation (48) investigates that D is a decreasing function in the interval (0,1/2). Consequently there is only one value of μ say μ _c in this interval for which D equals zero and D is positive when 0<μ<μ _c in which the solutions are stable.

4.3 Critical mass

Under the previous discussion, from (47) the value of μ when D equals zero is called the critical mass value. This value will be governed by

$$ \mu _{c} = - \frac{1}{2\alpha} \Bigl[\beta + \sqrt{\beta ^{2} - 4\alpha \gamma} \,\Bigr] $$

(49)

Now substituting (48) into (49) and restricting ourselves to the linear terms of A _i , A, ε _i as well as coupling terms in A _i ε _i and Aε _i (i=1,2) the critical mass value could be written as

$$ \mu _{c} = \mu _{00} + p $$

(50)

in which $\mu _{00} = (9 - \sqrt{69} )/18$ is the critical value given by Szebehely [24] when the three participating bodies are considered as points masses as well as negligence the effects of small perturbations of Coriolis and centrifugal forces. While p represents these effects when the three participating bodies are oblate spheroids. Therefore

$$\begin{aligned} p =& \mu _{10} - \mu _{01}A_{1} + \mu _{02}A_{2} - \mu _{03}A \\ &{} - ( \mu _{11}\varepsilon _{1} - \mu _{21}\varepsilon _{2} )A_{1} + ( \mu _{12}\varepsilon _{1} - \mu _{22}\varepsilon _{2} )A_{2} \\ &{} - ( \mu _{13}\varepsilon _{1} - \mu _{23}\varepsilon _{2} )A \end{aligned}$$

(51)

where μ ₀₀, μ ₁₀, μ _i1, μ _i2, μ _i3 as in Appendix A.3.

Equation (51) consists of three main parts, the first part gives the effects of small perturbations ε ₁ and ε ₂ in Coriolis and centrifugal forces respectively. The second part represents oblateness influences of the three participating bodies (A ₁, A ₂ and A). While the third part represents mixed effects for only one of these parameters A ₁, A ₂, A together with ε ₁ and ε ₂, this part will disappear when one of the parameters is ignored.

5 Periodic orbits

5.1 Periodic orbits around collinear points

It is easy to find periodic orbits about the collinear points L _1,2,3. However these points are unstable, i.e. if a body in any of these points is disturbed, it will move away. This is quite reasonable physically, for these points are saddle points of the potential function. Now substituting (41) into (32.1), (32.2) with some simple computations, the relations between the coefficients ρ _i and δ _i will be governed by

$$ \rho _{i} = n_{i}\delta _{i} $$

(52)

where

$$ n_{i} = \pm \sqrt{\frac{\lambda _{i}^{2} - \varOmega _{xx}^{0}}{\varOmega _{yy}^{0} - \lambda _{i}^{2}}} $$

(53)

This relations show that the coefficients δ _i and ρ _i (i=1,2,3,4) are dependent. Therefore the four initial conditions ξ ₀, η ₀, $\dot{\xi} _{0}$ and $\dot{\eta} _{0}$ associated with (32.1), (32.2) will determine the two sets of coefficients. Every set includes eight constants δ _i and ρ _i where the subscript 0 indicates to these quantities are to be evaluated at the initial time (t=t ₀). Substituting (52) into (41) and (42), these equations could be written as

$$\begin{aligned} &{\xi _{0} = \sum_{i = 1}^{4}\delta _{i}e^{\lambda _{i}t},\qquad \eta _{0} = \sum _{i = 1}^{4}n_{i}\delta _{i}e^{\lambda _{i}t}} \end{aligned}$$

(54.1)

$$\begin{aligned} &{\dot{\xi} _{0} = \sum_{i = 1}^{4} \lambda _{i}\delta _{i}e^{\lambda _{i}t},\qquad \dot{\eta} _{0} = \sum_{i = 1}^{4}n_{i} \lambda _{i}\delta _{i}e^{\lambda _{i}t}} \end{aligned}$$

(54.2)

since the determinant (Δ) of system (54.1), (54.2) is not zero:

$$ \Delta = - \sqrt{\frac{\varOmega _{xx}^{0}}{\varOmega _{yy}^{0}}} \bigl(\sigma ^{2} + \tau ^{2}\bigr)^{2} \ne 0 $$

(55)

The coefficients of this system can be written as functions of the initial conditions. If the initial conditions ξ ₀ and η ₀ are chosen properly where δ ₁=δ ₂=0, therefore (41) could be written in the form

$$\begin{aligned} &{\xi = \xi _{0}\cos\tau ( t - t_{0} ) + \frac{\eta _{0}}{m_{3}}\sin\tau ( t - t_{0} )} \end{aligned}$$

(56.1)

$$\begin{aligned} &{\eta = \eta _{0}\cos\tau ( t - t_{0} ) - \xi _{0}m_{3}\sin\tau ( t - t_{0} )} \end{aligned}$$

(56.2)

$$\begin{aligned} &{n_{3} = im_{3}} \end{aligned}$$

(56.3)

From (56.1)–(56.3) we can obtain that

$$ \dot{\xi} _{0} = \frac{\eta _{0}\tau}{m_{3}},\qquad \dot{\eta} _{0} = - \xi _{0}m_{3}\tau $$

(57)

which means that once the components of initial conditions ξ ₀ and η ₀ are chosen, we cannot select the association initial velocities $\dot{\xi} _{0}$ and $\dot{\eta} _{0}$ as wished. After solving (56.1)–(56.3) together to eliminate the time, the periodic orbits could be written in the form

$$ \frac{\xi ^{2}}{(\eta _{0}^{2} + \xi _{0}^{2}m_{3}^{2})/m_{3}^{2}} + \frac{\eta ^{2}}{(\eta _{0}^{2} + \xi _{0}^{2}m_{3}^{2})} = 1 $$

(58)

Equation (58) investigates that the trajectory of the infinitesimal body around the collinear points is an ellipse and its center is at these points. The semi-major (a _c ), the semi-minor b _c axes are parallel to the y-axis and x-axis, respectively. These axes, the eccentricity (e _c ) and the period (T _c ) can, therefore, be written in the form

$$\begin{aligned} &{a_{c}^{2} = \bigl(\eta _{0}^{2} + \xi _{0}^{2}m_{3}^{2}\bigr)} \end{aligned}$$

(59.1)

$$\begin{aligned} &{b_{c}^{2} = \bigl(\eta _{0}^{2} + \xi _{0}^{2}m_{3}^{2}\bigr)\big/m_{3}^{2}} \end{aligned}$$

(59.2)

$$\begin{aligned} &{e_{c}^{2} = \biggl( 1 - \frac{1}{m_{3}^{2}} \biggr)} \end{aligned}$$

(60)

$$\begin{aligned} &{T_{c} = 2\pi /\tau} \end{aligned}$$

(61)

Since $\dot{\eta} _{0} = - \xi _{0}m_{3}\tau$, $\dot{\xi} _{0} = 0$ at ξ ₀≠0 and η ₀=0 the motion along the orbits is retrograde.

5.2 Periodic orbits around triangular points

5.2.1 The mean motion of the periodic orbits

Since the triangular points are linearly stable when 0<μ<μ _c and the characteristic equation has four purely imaginary roots. Therefore we have bounded motion around the triangular points which are composed of two harmonic motions. Consequently this motion will be governed by

$$\begin{aligned} &{\xi = C_{1}\cos s_{1}t + D_{1}\sin s_{1}t + C_{2}\cos s_{2}t} \\ &{\hphantom{\xi =} {} + D_{2}\sin s_{2}t} \end{aligned}$$

(62.1)

$$\begin{aligned} &{\eta = \bar{C}_{1}\cos s_{1}t + \bar{D}_{1}\sin s_{1}t + \bar{C}_{2}\cos s_{2}t} \\ &{\hphantom{\eta =} {} + \bar{D}_{2}\sin s_{2}t} \end{aligned}$$

(62.2)

where s ₁ and s ₂ are the angular frequencies with respect to long and short periodic orbits respectively, the terms with the coefficients C ₁, D ₁, $\bar{C}_{1}$ and $\bar{D}_{1}$ are the long periodic terms while the coefficients C ₂, D ₂, $\bar{C}_{2}$ and $\bar{D}_{2}$ are the short periodic terms. In addition, $s_{1,2}^{2} = - \omega _{1,2}$ hence after substituting (47) into (46) and simplifying it, the angular frequencies s ₁ and s ₂ will be given by

$$\begin{aligned} &{s_{1} = \frac{3\sqrt{3}}{2}\sqrt{\mu} \biggl( 1 - \frac{1}{2} \mu \biggr) 1 - \frac{4}{3}\varepsilon _{1} + \frac{53}{18}\varepsilon _{2}} \\ &{\hphantom{s_{1} =} {} + \frac{1}{6} \biggl( 33 - \frac{52}{3}\varepsilon _{1} + \frac{653}{18}\varepsilon _{2} \biggr) (A_{1} + A_{2})} \\ &{\hphantom{s_{1} =} {} + \frac{1}{3} \biggl( 11 - \frac{4}{3}\varepsilon _{1} + \frac{65}{18} \varepsilon _{2} \biggr)A} \end{aligned}$$

(63.1)

$$\begin{aligned} &{s_{2} = 1 + 8\varepsilon _{1} - 3\varepsilon _{2} - \frac{27}{8} \biggl( 1 - \frac{8}{3}\varepsilon _{1} + \frac{49}{9}\varepsilon _{2} \biggr)\mu ( 1 - \mu )} \\ &{\hphantom{s_{2} =} {} + \frac{3}{4} ( 1 + 8\varepsilon _{1} - 3\varepsilon _{2} ) (A_{1} + A_{2})} \\ &{\hphantom{s_{2} =} {} - \frac{3}{2}\biggl(1 + \frac{5}{3}\varepsilon _{2}\biggr) \bigl[ (A_{1} + A) - \mu ( A_{1} - A_{2} ) \bigr]} \\ &{\hphantom{s_{2} =} {} - \frac{9}{8}\mu ( 1 - \mu ) \biggl( 13 - 104\varepsilon _{1} + \frac{215}{3} \varepsilon _{2} \biggr) (A_{1} + A_{2})} \\ &{\hphantom{s_{2} =} {} + 4\biggl(1 - 8\varepsilon _{1} + \frac{19}{3}\varepsilon _{2} \biggr)A } \end{aligned}$$

(63.2)

Equations (63.1), (63.2) give the frequencies for the orbits of the long and short periodic motion when the influence of oblateness, small perturbations of Coriolis (ε ₁) and centrifugal (ε ₂) forces are considered. But we would like to indicate that these equations are valid in the range 0<μ<μ _c , where μ _c is the critical mass value.

Substituting (62.1), (62.2) into (32.1), (32.2) and equating the coefficients of sine and cosine terms respectively. The relation between the coefficients of the long and short periodic terms will be controlled by

$$\begin{aligned} &{\bar{C}_{i} = \varGamma _{i} \bigl[ 2\varphi ns_{i}D_{i} - \varOmega _{xy}^{0}C_{i} \bigr],\quad i = 1,2} \end{aligned}$$

(64.1)

$$\begin{aligned} &{\bar{D}_{i} = - \varGamma _{i} \bigl[ 2\varphi ns_{i}C_{i} + \varOmega _{xy}^{0}D_{i} \bigr],\quad i = 1,2} \end{aligned}$$

(64.2)

where

$$ \varGamma _{i} = \frac{s_{i}^{2} + \varOmega _{xx}^{0}}{4\varphi ^{2}n^{2}s_{i}^{2} + (\varOmega _{xy}^{0})^{2}} = \frac{1}{s_{i}^{2} + \varOmega _{yy}^{0}},\quad i = 1,2 $$

(65)

and $\varOmega _{xx}^{0}$, $\varOmega _{xy}^{0}$ and $\varOmega _{yy}^{0}$ are given in (43.1)–(43.3).

We can eliminate the short periodic or the long periodic terms from the solution, if the initial conditions are selected properly. Hence we can suppose that ($C_{2} = D_{2} = \bar{C}_{2} = \bar{D}_{2} = 0$) and (ξ ₀, η ₀, $\dot{\xi} _{0}$ and $\dot{\eta} _{0}$) are the initial conditions at (t=0), i.e. we eliminate the short periodic terms. Now substituting these quantities into (62.1), (62.2) and (64.1), (64.2), therefore, we can obtain

$$\begin{aligned} &{C_{1} = \xi _{0}} \end{aligned}$$

(66.1)

$$\begin{aligned} &{\bar{C}_{1} = \eta _{0}} \end{aligned}$$

(66.2)

$$\begin{aligned} &{D_{1} = \frac{\varOmega _{xy}^{0}\xi _{0} + \eta _{0}(s_{1}^{2} + \varOmega _{yy}^{0})}{2\varphi ns_{1}}} \end{aligned}$$

(66.3)

$$\begin{aligned} &{\bar{D}_{1} = - \frac{\xi _{0}(s_{1}^{2} + \varOmega _{xx}^{0}) + \eta _{0}\varOmega _{xy}^{0}}{2\varphi ns_{1}}} \end{aligned}$$

(66.4)

$$\begin{aligned} &{\dot{\xi} _{0} = \frac{\varOmega _{xy}^{0}\xi _{0} + \eta _{0}(s_{1}^{2} + \varOmega _{yy}^{0})}{2\varphi n}} \end{aligned}$$

(67.1)

$$\begin{aligned} &{\dot{\eta} _{0} = - \frac{\xi _{0}(s_{1}^{2} + \varOmega _{xx}^{0}) + \eta _{0}\varOmega _{xy}^{0}}{2\varphi n}} \end{aligned}$$

(67.2)

If the triangular points represent the origin of the coordinates system, and we assume that the infinitesimal body starts its motion at the origin. Consequently from (30.1), (30.2) and (31.1), (31.2) the initial conditions will be controlled by (ξ ₀,η ₀)=(−x ₀,−y ₀) where

$$\begin{aligned} &{\xi _{0} = - \mu + \frac{1}{2} + \frac{1}{2}(A_{1} - A_{2})} \end{aligned}$$

(68.1)

$$\begin{aligned} &{\eta _{0} = \mp \frac{\sqrt{3}}{2} \biggl[ 1 - \frac{1}{3}(A_{1} + A_{2} - 2A)} \\ &{\hphantom{\eta _{0} =} {} - \frac{4}{9} ( 1 + A_{1} + A_{2} + A )\varepsilon _{2} \biggr]} \end{aligned}$$

(68.2)

in which minus (plus) sign refer to the origin is at L ₄ (L ₅).

5.3 Elliptic orbits

After we eliminate the long or the short periodic terms, the path of infinitesimal body will be an ellipse. We can see this just if (62.1), (62.2) is rewritten for the long periodic terms in the form

$$\begin{aligned} &{\xi = C_{1}\cos s_{1}t + D_{1}\sin s_{1}t} \end{aligned}$$

(69.1)

$$\begin{aligned} &{\eta = \bar{C}_{1}\cos s_{1}t + \bar{D}_{1}\sin s_{1}t } \end{aligned}$$

(69.2)

On the other hand if we substitute (66.1)–(66.4) into (69.1), (69.2) and eliminate the time, these equations could be reduced to

$$ \alpha _{1}\xi ^{2} + 2\beta _{1}\xi \eta + \eta ^{2} = \gamma _{1} $$

(70)

This equation represents an ellipse with center at the origin of coordinate system ξ and η, since

$$ \left\vert \begin{array}{c@{\quad}c} \alpha _{1} & \beta _{1} \\ \beta _{1} & 1 \end{array} \right\vert = (2\varphi ns_{1}\varGamma _{1})^{2} > 0 $$

(71)

where

$$\begin{aligned} &{\alpha _{1} = \frac{s_{1}^{2} + \varOmega _{xx}^{0}}{s_{1}^{2} + \varOmega _{yy}^{0}}} \end{aligned}$$

(72.1)

$$\begin{aligned} &{\beta _{1} = \frac{\varOmega _{xy}^{0}}{s_{1}^{2} + \varOmega _{yy}^{0}}} \end{aligned}$$

(72.2)

$$\begin{aligned} &{\gamma _{1} = \alpha _{1}\xi _{0}^{2} + 2\beta _{1}\xi _{0}\eta _{0} + \eta _{0}^{2}} \end{aligned}$$

(72.3)

5.4 The orientation of principal axes of the ellipse

Since (70) include bilinear term ξη, then the principal axes of the ellipse are rotated with an angle θ relative to the coordinate system (ξ,η). This motivates us to introduce a new coordinate ($\bar{\xi},\bar{\eta}$) such that the quadratic term appears only without the bilinear. Hence the old and the new coordinates systems are governed by the following equations

$$\begin{aligned} &{\xi = \bar{\xi} \cos \theta - \bar{\eta} \sin \theta} \end{aligned}$$

(73.1)

$$\begin{aligned} &{\eta = \bar{\xi} \sin \theta + \bar{\eta} \cos \theta} \end{aligned}$$

(73.2)

Substituting (73.1), (73.2) into (70) and equate the coefficient of $\bar{\xi} \bar{\eta}$ by zero. The orientation of principal axes is given as

$$\begin{aligned} \tan 2\theta =& \pm \sqrt{3} \biggl\{ 1 - 2\mu + \frac{8}{3} \biggl( 1 - \frac{19}{8}\mu \biggr)A_{1} \\ &{} - \frac{4}{3} \biggl( 1 + \frac{7}{4}\mu \biggr)A_{2} - \frac{4}{3} ( 1 + \mu )A \\ &{}+\frac{8}{9}\biggl[ \biggl[ 1 - 2\mu + \frac{13}{3} \biggl( 1 - \frac{55}{26}\mu \biggr)A_{1} \\ &{} - \frac{8}{3} \biggl( 1 - \frac{5}{16}\mu \biggr)A_{2} - \frac{11}{3} \biggl( 1 + \frac{5}{11}\mu \biggr)A \biggr]\varepsilon _{2} \bigg\} \end{aligned}$$

(74)

where plus sign refers to the center of ellipse at L ₄ while minus sign at L ₅.

Furthermore the lengths of semi-major (a _t ), semi-minor (b _t ) axes and the eccentricity (e _t ) as well as the period of motion (T _t ) are controlled by

$$\begin{aligned} &{a_{t}^{2} = \frac{2\gamma _{1}}{[ ( 1 + \alpha _{1} ) - ( 1 - \alpha _{1} )\cos 2\theta + 2\beta _{1}\sin 2\theta ]}} \end{aligned}$$

(75.1)

$$\begin{aligned} &{b_{t}^{2} = \frac{2\gamma _{1}}{[ ( 1 + \alpha _{1} ) + ( 1 - \alpha _{1} )\cos 2\theta - 2\beta _{1}\sin 2\theta ]}} \end{aligned}$$

(75.2)

$$\begin{aligned} &{e_{t}^{2} = \frac{2[ ( 1 - \alpha _{1} )\cos 2\theta - 2\beta _{1}\sin 2\theta ]}{[ ( 1 + \alpha _{1} ) + ( 1 - \alpha _{1} )\cos 2\theta - 2\beta _{1}\sin 2\theta ]}} \end{aligned}$$

(76)

$$\begin{aligned} &{T_{t} = \frac{2\pi}{s_{i}},\quad i = 1,2} \end{aligned}$$

(77)

Now we will introduce an algorithm to find the elements of the periodic orbits around the equilibrium points. This algorithm will be formulated in the following steps:

• 1. Determine the parameters μ, A ₁, A ₂, A, ε ₁ and ε ₂ for any given system.

• 2. Evaluate $\varOmega _{xx}^{0}$, $\varOmega _{xy}^{0}$ and $\varOmega _{yy}^{0}$.

• 3. Evaluate τ.

• 4. Evaluate s ₁ and s ₂.

• 5. Evaluate m ₃.

• 6. Evaluate ξ ₀ and η ₀.

• 7. Evaluate α ₁, β ₁ and γ ₁.

• 8. Evaluate sin2θ and cos2θ.

• 9. Use steps 5 and 6 to obtain the lengths of semi-major (a _c ) and semi-minor (b _c ) axes as well as the value of the eccentricity (e _c ).

• 10. Use step 5 to find the period of motion T _c .

• 11. Use steps 7 and 8 to obtain the lengths of semi-major (a _t ) and semi-minor (b _t ) axes as well as the value of the eccentricity (e _t ).

• 12. Use step 4 to find the period of motion T _t .

• 13. Steps 9 and 10 for periodic orbits around the collinear points.

• 14. Steps 11 and 12 for periodic orbits around the triangular points.

6 Conclusions

The restricted three-body problem is generalized in the sense that the three participating bodies are oblate spheroids together with the effect of small perturbations in the Coriolis and centrifugal forces. The existence and the linear stability of libration points are studied, under the parameters effects of the oblateness, the small perturbations in the Coriolis and centrifugal forces. We use Lagrangian method for inverting series expansions to construct a semi-closed form to determine the locations of collinear points.

Under these effects, the collinear points remain unstable and the triangular points are stable for 0<μ<μ _c , and unstable for μ _c ≤μ≤1/2. We find the periodic orbits around the five libration points as well as the frequencies, the semi-major, the semi-minor axes, the eccentricity and period of motion. In addition the directions of principal axes for the orbits around the triangular points and the coefficients of long and short periodic terms are evaluated. Furthermore an algorithm is constructed to calculate the elements of the periodic orbits around these points.

Finally, we would like to indicate that our model can be degraded into many special cases, some of this cases are

• Classical problem: A _i =A=ε _i =0,i=1,2 (Szebehely [24]).

• When the effect in Coriolis force is only considered: A _i =A=0, ε ₁≠0, ε ₂=0, i=1,2 (Szebehely, [23]).

• When the effect in Coriolis and centrifugal forces are considered: A _i =A=0, ε _i ≠0, i=1,2 (Bhatnagar and Hallan [6]).

• When the bigger primary is an oblate spheroid: A ₁≠0, A ₂=A=0, ε _i =0, i=1,2 (Subbarao and Sharma [22]).

• When both primaries are oblate spheroids: A _i ≠0, A=0, ε _i =0, i=1,2 (Bhatnagar and Hallan [7]).

• When the three participating bodies are oblate spheroids: A _i ≠0, A≠0, ε _i =0, i=1,2 (El-Shaboury [10]).

The earlier cases are mentioned as examples but not limited.

Appendix

1.1 A.1 The series coefficients at collinear points

• The series coefficients at L ₁ in (16)

  $$\begin{aligned} &{a_{4} = \frac{ ( 1 - a - p )}{b}, \qquad a_{5} = \frac{ ( 1 + 4a + 2p )}{b}}\\ &{a_{6} = - \frac{(10ab + p - ap + 3bp + p^{2})}{b^{2}}}\\ &{a_{7} = \frac{(20ab - p - 4ap + 4bp - 2p^{2})}{b^{2}}} \end{aligned}$$

• The series coefficients at L ₂ in (19)

  $$\begin{aligned} &{b_{4} = \frac{ ( a + p - 1 )}{b},\qquad b_{5} = \frac{ ( 1 + 4a + 2p )}{b}}\\ &{b_{6} = \frac{(10ab + p - ap + 3bp + p^{2})}{b^{2}}}\\ &{b_{7} = \frac{(20ab - p - 4ap + 4bp - 2p^{2})}{b^{2}}} \end{aligned}$$

• The series coefficients at L ₃ in (22)

  $$\begin{aligned} &{c_{0} = \frac{16 ( a + p - 1 )}{32 - b - 4p}}\\ &{c_{1} = - \mbox{$\dfrac{16 ( 16 + 144a - 3b - 2ab - 12ap + 72p - 4p^{2} )}{ ( 32 - b - 4p )^{2}}$}}\\ &{c_{2} = \frac{8}{ ( 32 - b - 4p )^{3}} \big( 512 + 25088a - 192b}\\ &{\hphantom{c_{2} =} {} - 608ab - 7b^{2} + 7ab^{2} + 8384p - 4160ap }\\ &{\hphantom{c_{2} =} {} + 66bp + 70abp - 40p^{2} + 200ap^{2} + b^{2}p}\\ &{\hphantom{c_{2} =} {} - 832p^{2} + 6bp^{2} + 40p^{3}\big)} \end{aligned}$$

1.2 A.2 The coefficients of the discriminant in (47)

$$\begin{aligned} &{\alpha = 27 \biggl[ 1 + \frac{13}{3} ( A_{1} + A_{2} ) + \frac{4}{3}A }\\ &{\hphantom{\alpha =} {}+ \frac{22}{9} \biggl[ 1 + \frac{49}{11} ( A_{1} + A_{2} ) + \frac{20}{11}A \biggr]\varepsilon _{2} \biggr]}\\ &{\beta = - 27\bigg[ 1 + \frac{1}{9} ( 37A_{1} + 41A_{2} ) + \frac{4}{3}A}\\ &{\hphantom{\beta =} {}+ \frac{2}{9} \bigl[ 11\varepsilon _{2} - ( 16\varepsilon _{1} - 160\varepsilon _{2} )A_{1} + ( 16\varepsilon _{1}}\\ &{\hphantom{\beta =} {} + 134\varepsilon _{2} )A_{2} + 20\varepsilon _{2}A \bigr] \bigg]}\\ &{\gamma = \big[ 1 - 3(A_{1} - A_{2} + 2A) - 10\varepsilon _{1}A_{1} }\\ &{\hphantom{\gamma =} {} + ( 16\varepsilon _{1} - 6\varepsilon _{2} ) ( 1 + 3A_{2} ) - 8 ( 6\varepsilon _{1} - \varepsilon _{2} )A \big]} \end{aligned}$$

1.3 A.3 The coefficients of oblateness parameters for critical mass in (51)

$$\begin{aligned} &{\mu _{00} = \frac{1}{2} \biggl( 1 - \frac{\sqrt{69}}{9} \biggr),}\\ &{\mu _{10} = \frac{4}{27\sqrt{69}} ( 36\varepsilon _{1} - 19 \varepsilon _{2} )}\\ &{\mu _{01} = \frac{1}{9} \biggl( 1 + \frac{13}{\sqrt{69}} \biggr),\qquad \mu _{11} = \frac{16}{9} \biggl( 1 + \frac{325}{23\sqrt{69}} \biggr),}\\ &{\mu _{21} = \frac{61}{81} \biggl( 1 + \frac{20091}{1403\sqrt{69}} \biggr)}\\ &{\mu _{02} = \frac{1}{9} \biggl( 1 - \frac{13}{\sqrt{69}} \biggr),\qquad \mu _{12} = \frac{16}{9} \biggl( 1 - \frac{325}{23\sqrt{69}} \biggr),}\\ &{\mu _{22} = \frac{61}{81} \biggl( 1 - \frac{20091}{1403\sqrt{69}} \biggr)}\\ &{\mu _{03} = \frac{22}{9\sqrt{69}},\qquad \mu _{13} = \frac{8800}{207\sqrt{69}},}\\ &{\mu _{23} = \frac{8296}{621\sqrt{69}}} \end{aligned}$$