1 Introduction

During the last three decades, the investigation of the different nonlinear phenomena (viz. solitary waves, shock waves, and double layers) has been made by numerous authors in electron-positron-ion (e-p-i) plasmas (Shukla et al. 1986, 2004; Tajima and Taniuti 1990; Berezhiani et al. 1994; Popel et al. 1995; Nejoh 1996; Moslem et al. 2007; Tiwari et al. 2007; Tribeche et al. 2009; Tribeche 2010; Sahu 2010; Mottaghizadeh and Eslami 2012; Pakzad and Javidan 2013). The propagation of nonlinear waves in e-p-i plasmas has a considerable importance in understanding the behaviour of the astrophysical environments viz. cluster explosions (Tribeche et al. 2009), active galactic nuclei (Miller and Witta 1987), supernovas (Begelman et al. 1984), and pulsar magnetospheres (Michel 1982). These e-p-i plasmas are usually characterized as a fully ionized gas consisting of electrons and positrons, the masses of which are equal with positive ions. Therefore, study of the nonlinear wave propagation in e-p-i plasmas is a subject of appreciable interest.

Recently, the nonlinear phenomena associated with positron-acoustic (PA) waves in e-p-i plasmas have been studied by several authors (Nejoh 1996; Tribeche et al. 2009; Tribeche 2010; El-Shamy et al. 2012; Rahman et al. 2014a, 2014b, 2014c). PA waves are acoustic type of waves in which, the thermal pressure of electrons and hot positrons provides the necessary restoring force, and the cold positron mass gives the inertia. Nejoh (1996) studied the large amplitude PASWs in an electron-positron plasma with an electron beam. In order to study the small amplitude PA double layers, Tribeche (2010) considered a four component e-p-i plasma consisting of Maxwellian distributed electrons and positrons, inertial cold positrons, and stationary ions. Sahu (2010) investigated the PA shock waves in both planar and nonplanar geometries by considering the same plasma model of Tribeche (2010). However, Tribeche et al. (2009), Tribeche (2010), Sahu (2010) considered Maxwellian electrons and positrons to study the nonlinear propagation of PASWs or PA shock waves or PA double layers in e-p-i plasmas.

Space plasmas are often characterized by a particle distribution function with high energy tail and they may deviate from the Maxwellian (Alam et al. 2013). In a number of heliospheric environments, the plasma contains nonthermally distributed ions (Tasnim et al. 2013; Shuchy et al. 2013) or electrons (Mamun et al. 1996; Shukla and Mamun 2002; Verheest and Pillay 2008). So these energetic nonthermal particles and their distribution have achieved an impressive attention in understanding the nature of nonlinear waves in astrophysical plasmas, especially in the upper Martian ionosphere (Lundin et al. 1989), in the auroral acceleration region (Temerin et al. 1982), in/around the Earth’s bow shock (Matsumoto et al. 1994), etc. Nonthermal distributed electrons and positrons are predicted to exist in the expansion phenomenon of laser induced plasmas (Doumaz and Djebli 2010). Cairns et al. (1995) used nonthermal distribution for electrons to study the ion-acoustic solitary waves (IASWs) and showed that it is possible to obtain both positive and negative solitary waves. Chatterjee et al. (2012) investigated the planar and nonplanar IASWs in e-p-i plasma system consisting of nonthermal distributed electrons and positrons, and singly charged adiabatically hot positive ions. Rahman et al. (2014c) studied the PA shock waves in e-p-i plasmas comprising of nonthermal distributed hot positrons and electrons, inertial cold positrons, and immobile positive ions.

At present, the properties of PASWs have a great importance in understanding the characteristics of the localized electrostatic structures in both space and laboratory plasmas as new sources of cold positrons are now available and well developed (Abdullah et al. 1995; Kurz et al. 1998; Greaves et al. 2002). The nonlinear propagation of PASWs in e-p-i plasmas have been thoroughly studied by several authors (Tribeche et al. 2009; El-Shamy et al. 2012; Rahman et al. 2014a, 2014b). Tribeche et al. (2009) investigated the small amplitude PASWs in a four component e-p-i plasma consisting of Maxwellian distributed electrons and hot positrons, inertial cold positrons, and stationary ions. El-Shamy et al. (2012) considered the same plasma model of Tribeche et al. (2009) and investigated the characteristics of the head-on collision between two PASWs. Moreover, using the well-known reductive perturbation method, Rahman et al. (2014a, 2014b) studied either planar or nonplanar PA Gardner solitons in e-p-i plasmas by considering the same plasma model of Rahman et al. (2014c). However, all of these theoretical works (Tribeche et al. 2009; El-Shamy et al. 2012; Rahman et al. 2014a, 2014b) are either limited to a finite value of A (A is the nonlinear coefficient) or understandable to describe the models in an unmagnetized e-p-i plasma system and the authors of these papers have not considered the effects of magnetic field or obliqueness on those solitary waves (SWs). Thus, to obtain a more generalized work on an e-p-i plasma [containing nonthermal (Cairns distributed) hot positrons and electrons, inertial cold positrons, and immobile positive ions], we have derived and solved the Zakharov-Kuznetsov (ZK) equation, and analyzed the SWs both numerically and analytically in this manuscript.

The manuscript is arranged as follows: The governing equations are given in Sect. 2. The derivation and solution of the ZK equation are provided in Sect. 3. Finally, a brief discussion is presented in Sect. 4.

2 Governing equations

We consider the nonlinear propagation of collisionless PA waves in a magnetized e-p-i plasma consisting of nonthermal (Cairns distributed) hot positrons and electrons, inertial cold positrons, and immobile positive ions. Hence, at equilibrium, n e0=n pc0+n ph0+n i0, where n i0 and n e0 are the number densities of the unperturbed ions and electrons, respectively. n pc0 (n ph0) is the unperturbed number density of cold (hot) positrons. The electrons and the hot positrons follow the nonthermal distribution of Cairns et al. (1995), which is given by the following expressions:

$$\begin{aligned} &{n_e=n_{e0}\bigl(1-\beta\phi+\beta \phi^2\bigr)\exp{\biggl(\frac{e\phi}{T_e}\biggr)},} \\ &{n_{ph}=n_{ph0}\bigl(1+\beta\phi+\beta \phi^2\bigr)\exp{\biggl(-\frac{e\phi}{T_{ph}}\biggr)},} \end{aligned}$$

where β is the nonthermal parameter, n e and n ph are the number densities of the perturbed electrons and hot positrons, T e and T ph are the temperatures of electrons and hot positrons (in the energy units), respectively. The range of the nonthermal parameter β is 0≤β≤4/3 (El-Taibany et al. 2010; El-Labany et al. 2012). When β→0, the above two equations give the Boltzmann distribution of electrons and hot positrons respectively.

The normalized basic equations governing the dynamics of the obliquely propagating PA waves in such a plasma system are given as follows:

$$\begin{aligned} &{\frac{\partial n_{pc}}{\partial t} + \nabla\cdot (n_{pc}\textbf{u}_{pc})=0,} \end{aligned}$$
(1)
$$\begin{aligned} &{\frac{\partial\textbf{u}_{pc}}{\partial t} + (\textbf{u}_{pc} \cdot\nabla) \textbf{u}_{pc} =-\nabla\phi+ \alpha(\textbf{u}_{pc}\times \hat{z}),} \end{aligned}$$
(2)
$$\begin{aligned} &{\nabla^2 \phi=-n_{pc}-\mu_{1}\bigl(1+\beta \sigma\phi+\beta\sigma^{2}\phi^{2}\bigr)\exp {(-\sigma\phi)}} \\ &{\phantom{\nabla^2 \phi=}{}+\mu_{2}\bigl(1-\beta\phi+\beta\phi^{2} \bigr)\exp{(\phi)}-\mu _{3},} \end{aligned}$$
(3)

where n pc is the cold positron number density normalized by its equilibrium value n pc0, u pc is the cold positron fluid speed normalized by C pc =(k B T e /m p )1/2, ϕ is the electrostatic wave potential normalized by k B T e /e, k B is the Boltzmann constant, m p is the positron mass, e is the magnitude of the electron charge, σ=T e /T ph , α=ω c /ω p , μ 1=n ph0/n pc0, μ 2=n e0/n pc0, and μ 3=n i0/n pc0. The time variable t is normalized by \(\omega_{p}^{-1}=(m_{p}/4\pi n_{pc0}e^{2})^{1/2}\), and the space variable x is normalized by the Debye length λ D =(k B T e /4πn pc0 e 2)1/2.

3 Derivation of Zakharov-Kuznetsov equation

To study small but finite amplitude electrostatic PASWs in the e-p-i plasma system under consideration, one can use a scaling of the independent variables through the stretched coordinates (Washimi and Taniuti 1966; Kundu et al. 2013):

$$\begin{aligned} &{{X}={\epsilon}^{1/2}x,} \end{aligned}$$
(4)
$$\begin{aligned} &{{Y}={\epsilon}^{1/2}y,} \end{aligned}$$
(5)
$$\begin{aligned} &{{Z}={\epsilon}^{1/2}(z-V_pt),} \end{aligned}$$
(6)
$$\begin{aligned} &{{\tau}={\epsilon}^{3/2}t,} \end{aligned}$$
(7)

where V p is the phase speed normalized by the positron-acoustic speed (C pc ) and ϵ is a smallness parameter measuring the weakness of the dispersion (0<ϵ<1). It may be noted here that X, Y, and Z are all normalized by the Debye radius λ D , and τ is normalized by the ion plasma period \((\omega_{p}^{-1})\). The perturbed quantities n pc , u pcx , u pcy , u pcz , and ϕ can be expanded along with their equilibrium values as (Washimi and Taniuti 1966; Shukla et al. 1991)

$$\begin{aligned} &{n_{pc}=1+\epsilon n_{pc}^{(1)}+ \epsilon^2n_{pc}^{(2)}+ \cdots,} \end{aligned}$$
(8)
$$\begin{aligned} &{u_{pcx}=\epsilon^{3/2} u_{pcx}^{(1)}+ \epsilon^2u_{pcx}^{(2)}+\cdots,} \end{aligned}$$
(9)
$$\begin{aligned} &{u_{pcy}=\epsilon^{3/2} u_{pcy}^{(1)}+ \epsilon^2u_{pcy}^{(2)}+\cdots,} \end{aligned}$$
(10)
$$\begin{aligned} &{u_{pcz}=\epsilon u_{pcz}^{(1)}+\epsilon^2u_{pcz}^{(2)}+ \cdots,} \end{aligned}$$
(11)
$$\begin{aligned} &{\phi=\epsilon\phi^{(1)}+\epsilon^2\phi^{(2)}+ \cdots.} \end{aligned}$$
(12)

Now, using Eqs. (4)–(7) and substituting Eqs. (8)–(12) into Eqs. (1)–(3), one can obtain the first order continuity equation, the z component of the momentum equation, and Poisson’s equation which, after some simplification, produce

$$\begin{aligned} &{n_{pc}^{(1)}=\frac{\psi}{V_p^2},} \end{aligned}$$
(13)
$$\begin{aligned} &{u_{pcz}^{(1)}=\frac{\psi}{V_p},} \end{aligned}$$
(14)
$$\begin{aligned} &{V_p=\frac{1}{\sqrt{(1-\beta)(\mu_1\sigma+\mu_2)}},} \end{aligned}$$
(15)

where ψ=ϕ (1). Equation (15) indicates the phase speed of the PA waves propagating in the magnetized e-p-i plasma. It is important to note that V p becomes infinity at β→1. To validate V p , we have taken the range of the nonthermal parameter β as 0.1≤β≤0.9 (Jilani et al. 2013). The first order x and y components of the momentum equation can be represented as

$$\begin{aligned} &{u_{pcx}^{(1)}=-\frac{1}{\alpha}\frac{\partial\psi}{\partial{Y}},} \end{aligned}$$
(16)
$$\begin{aligned} &{u_{pcy}^{(1)}=\frac{1}{\alpha}\frac{\partial\psi}{\partial{X}}.} \end{aligned}$$
(17)

Equations (16) and (17) represent the x and y-components of the cold positron electric field drifts respectively. These equations are also satisfied by the second order continuity equation.

Again, using Eqs. (4)–(7) and Eqs. (8)–(12) into Eqs. (1)–(3), and eliminating \(u_{pcx,y}^{(1)}\), the next higher order x and y-components of the momentum equation, and Poisson’s equation can be found as

$$\begin{aligned} &{u_{pcx}^{(2)}=\frac{V_p}{\alpha^2}\frac{{\partial^{2}}{\psi}}{\partial {Z}\partial{X}},} \end{aligned}$$
(18)
$$\begin{aligned} &{u_{pcy}^{(2)}=\frac{V_p}{\alpha^2}\frac{{\partial^{2}}{\psi}}{\partial {Z}\partial{Y}},} \end{aligned}$$
(19)
$$\begin{aligned} &{\frac{\partial^2\psi}{\partial{X}^2} +\frac{\partial^2\psi}{\partial{Y}^2}+\frac{\partial^2\psi}{\partial {Z}^2}=M \psi^2+N\phi^{(2)}-n_{pc}^{(2)}.} \end{aligned}$$
(20)

Where \(M=\frac{1}{2}(\mu_{2}-\mu_{1}\sigma^{2})\) and N=(1−β)(μ 1 σ+μ 2).

Equations (18) and (19) indicate the x and y-components of the cold positron polarization drifts respectively. Following the same procedure as before we can get the next higher order continuity equation, and z-component of the momentum equation. Now employing these new higher order equations along with Eqs. (13)–(20), one can easily eliminate \({n_{pc}^{(2)}}\), \({u_{pcz}^{(2)}}\), and ϕ (2), and can finally obtain

$$\begin{aligned} &{\frac{\partial\psi}{\partial \tau}+AB\psi\frac{\partial \psi}{\partial{Z}}+\frac{1}{2}A \frac{\partial}{ \partial{Z}}} \\ &{\quad{}\times\biggl[\frac{\partial^2}{\partial{Z}^2}+D \biggl(\frac{\partial^2}{\partial {X^2}}+ \frac{\partial^2}{\partial{Y^2}} \biggr) \biggr]\psi=0,} \end{aligned}$$
(21)

where

$$\begin{aligned} &{A=V_{p}^3,} \end{aligned}$$
(22)
$$\begin{aligned} &{B=\frac{1}{2} \biggl[\mu_1\sigma^2- \mu_2-\frac{3}{V_p^4} \biggr],} \end{aligned}$$
(23)
$$\begin{aligned} &{D=1+\frac{1}{\alpha^2}.} \end{aligned}$$
(24)

Equation (21) is the ZK equation describing the nonlinear propagation of the PA waves in a magnetized e-p-i plasma with nonthermal distributed hot positrons and electrons.

We can use linear wave theory to derive the linearized ZK Equation. By linearizing Eq. (21) we have,

$$\begin{aligned} \frac{\partial\psi}{\partial t}+\frac{1}{2}A\frac{\partial}{\partial{Z}} \biggl[ \frac{\partial^2}{\partial{Z}^2}+D \biggl(\frac{\partial^2}{\partial {X^2}}+\frac{\partial^2}{\partial{Y^2}} \biggr) \biggr] \psi=0. \end{aligned}$$
(25)

We assume that the variation of the dispersion equation \((\frac{\omega}{k})\) in the transverse dimensions (the X and Y directions) is much slower than that of the Z direction, then we can neglect the transverse dimensions, i.e., \(\frac{\partial}{\partial{X}}=\frac{\partial}{\partial{Y}}\rightarrow0\). Then from Eq. (25),

$$\begin{aligned} \frac{\partial\psi}{\partial t}+\frac{1}{2}A\frac{\partial^3}{\partial{Z^3}}\psi=0. \end{aligned}$$
(26)

Let us consider, ψ∝exp[−i(ωt+kZ)]. Then from Eq. (26), we have

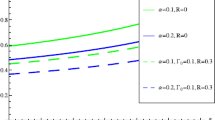
$$\begin{aligned} \begin{aligned} {}&-i\omega\psi+\frac{1}{2}Aik^3\psi=0, \\ &\biggl(\omega-\frac{1}{2}Ak^3\biggr)\psi=0, \\ &\biggl(\omega-\frac{1}{2}Ak^3\biggr)=0,\quad \psi\neq0 \\ &\omega=\frac{1}{2}Ak^3. \end{aligned} \end{aligned}$$
(27)

Where, \(A=V_{p}^{3}\). Equation (27) indicates the linear dispersion relation of PA waves propagating in the plasma system under consideration. The linear dispersion relation graph has been shown in Fig. 1.

Fig. 1
figure 1

Variation of the angular frequency (ω) with wave number (k) for different values of the nonthermal parameter β. Here μ 1=0.25, μ 2=1.5, and σ=2

Full size image

To study the properties of the SWs propagating in a direction making an angle δ with the Z-axis, i.e. with the external magnetic field and lying in the (Z–X) plane, the coordinate axes (X,Z) are rotated through an angle δ, keeping the Y-axis fixed. Thus, we transform our independent variables to

$$\begin{aligned} \begin{aligned} {}&\rho=X \cos\delta-Z \sin\delta,\quad \eta=Y, \\ &\xi=X \sin\delta+Z \cos\delta, \quad\tau=t. \end{aligned} \end{aligned}$$
(28)

The transformation of these independent variables (Washimi and Taniuti 1966; Shukla et al. 1991) helps us to write the ZK equation in the form

$$\begin{aligned} &{\frac{\partial\psi}{\partial t}+\delta_1{\psi} \frac{\partial\psi}{\partial \xi}+\delta_2\frac{\partial^3\psi}{\partial \xi^3}+\delta_3{ \psi}\frac{\partial\psi}{\partial\rho} +\delta_4\frac{\partial^3\psi}{\partial \rho^3}} \\ &{\quad{}+\delta_5\frac{\partial^3\psi}{ \partial\xi^2\partial\rho}+\delta_6 \frac{\partial^3\psi}{ \partial\xi\partial\rho^2}+\delta_7\frac{\partial^3\psi}{ \partial\xi\partial\eta^2}+\delta_8 \frac{\partial^3\psi}{ \partial\rho\partial\eta^2}=0,} \end{aligned}$$
(29)

where

$$\begin{aligned} \begin{aligned} {}&\delta_1=A B\cos\delta, \\ &\delta_2=\frac{1}{2}A\bigl(\cos^3 \delta+D\sin^2\delta\cos \delta\bigr), \\ &\delta_3=-A B\sin\delta, \\ &\delta_4=-\frac{1}{2}A\bigl( \sin^3\delta+D\sin\delta\cos ^2\delta\bigr), \\ &\delta_5=A \biggl[D\biggl(\sin\delta \cos^2\delta-\frac{1}{2}\sin ^3\delta\biggr) - \frac{3}{2}\sin\delta\cos^2\delta \biggr], \\ &\delta_6=-A \biggl[D\biggl(\sin^2\delta \cos\delta-\frac {1}{2}\cos^3\delta\biggr) -\frac{3}{2} \sin^2\delta\cos\delta \biggr], \\ &\delta_7=\frac{1}{2}A D\cos\delta, \\ &\delta_8=-\frac{1}{2}A D\sin\delta. \end{aligned} \end{aligned}$$
(30)

The steady state solution of this ZK equation can be written in the form

$$\begin{aligned} \psi=\psi_0(Z), \end{aligned}$$
(31)

where

$$\begin{aligned} Z=\xi-U_0t, \end{aligned}$$

here U 0 is a constant speed normalized by the positive positron-acoustic speed (C pc ). Using this transformation, the ZK equation can be written in steady state form as

$$\begin{aligned} &-U_0\frac{d\psi_0}{dZ}+\delta_1{\psi_0} \frac{d\psi_0}{dZ} +\delta_2\frac{d^3\psi_0}{dZ^3}=0. \end{aligned}$$
(32)

Now, applying the appropriate boundary conditions, viz. ψ→0, (dψ/dZ)→0, (d 2 ψ/dZ 2)→0 as Z→±∞, the solitary wave solution of this equation is given by

$$\begin{aligned} \psi_0(Z)=\psi_m\mathrm{sech}^2(kZ), \end{aligned}$$
(33)

where ψ m =3U 0/δ 1 is the amplitude and \(k={\sqrt{\frac{U_{0}}{4\delta_{2}}}}\) is the inverse of the width of the SWs. As U 0>0, it is clear from Eqs. (21), (23), and (29) that depending on the sign of B, the SWs will exist with only positive potential (ψ m >0).

We have considered the steady state solution of the ZK Eq. (21) in one dimension in which all δ’s except δ 1 and δ 2 are disappeared. This means that only δ 1 and δ 2 which are functions of δ appear in the solution (Emamuddin et al. 2014). Therefore, we have shown how the width of the SWs vary with δ (displayed in Fig. 5).

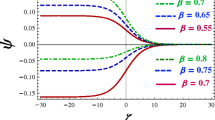
Figure 1 represents the variation of the angular frequency (ω) with wave number (k) for different values of the nonthermal parameter β. Figure 2 represents the variation of the amplitudes of the positive SWs for different values of β, and Fig. 3 also displays the variation of the amplitudes of the positive SWs with the temperature ratio σ for different values of the number density ratio μ 2. Figure 4 indicates the variation of the amplitudes of the positive SWs with the number density ratio μ 1 for different values of β, and Fig. 5 describes the variation of the widths of the SWs with oblique angle δ for different values of the frequency ratio α.

Fig. 2
figure 2

Variation of the amplitudes of the SWs with nonthermal parameter β for μ 1=0.25, μ 2=1.5, δ=18∘, and σ=2

Full size image
Fig. 3
figure 3

Variation of the amplitudes of the SWs with σ for different values of μ 2. The values of other parameters are μ 1=0.25, δ=18∘, and β=0.6

Full size image
Fig. 4
figure 4

Variation of the amplitudes of the SWs with μ 1 for different values of nonthermal parameter β. The values of other parameters are μ 2=1.5, δ=18∘, and σ=2

Full size image
Fig. 5
figure 5

Variation of the widths of the SWs with δ for different values of α. The values of other parameters are μ 1=0.25, μ 2=1.5, β=0.6, and σ=2

Full size image

4 Discussion

We have considered a magnetized e-p-i plasma (containing nonthermal hot positrons and electrons, inertial cold positrons, and immobile positive ions) and investigated the oblique propagation of PASWs. By using the reductive perturbation method, we have derived the ZK equation which is valid for small and finite amplitude limit but not valid for large oblique angle δ that makes the wave amplitude infinitely large. Then we have solved the ZK equation and investigated in brief, the effects of the obliqueness, the magnetic field, the nonthermality effect on electrostatic SWs existing in a magnetized e-p-i plasma. The analysis of our results can be summarized as follows:

  1. 1.

    The angular frequency ω does not change up to the lower value of the wave number k (up to k∼0.375) as depicted in Fig. 1. After that value of k, ω increases significantly with the increase in k. ω is found to increase with increasing nonthermal parameter β. Thus, we can say that the phase speed of PA waves increases with increasing β.

  2. 2.

    The amplitude of the positive potential SWs increases steeply with the increase of β as shown in Fig. 2. Thus the nonthermality has a positive effect on the amplitude, i.e., the amplitude increases with increasing the nonthermality (Fig. 2).

  3. 3.

    Figure 3 indicates that the amplitude of the positive potential SWs decreases almost exponentially with the increase of the temperature ratio of electron and hot positron σ but increases with the increase of the number density ratio of electron and cold positron μ 2.

  4. 4.

    The amplitude of the positive potential SWs decreases with the increase of the number density ratio of hot positron and cold positron μ 1 but increases with the increase of β as depicted in Fig. 4.

  5. 5.

    The effect of variation of the oblique angle δ on the widths of the SWs is that the width of these SWs increases with δ for its lower range (0∘ to 45∘) and decreases for its higher range (45∘ to 90∘). It should be pointed out that for very large value of angle δ (δ∼90∘), the width ⟶0 and the amplitude becomes ∞, thus the assumption of electrostatic wave will no longer be valid and the electromagnetic structure will be dominant. Our present work is only valid for small value of δ but invalid for arbitrary large value of δ. In case of larger values of δ, the wave amplitude becomes large enough to break the validity of the reductive perturbation method (Alinejad 2012). Consequently, it is also marked that with the increase in frequency ratio α (cold positron cyclotron frequency to cold positron plasma frequency ratio), the amplitudes become almost spiky as displayed in Fig. 5.

  6. 6.

    It is found that α increases due to the increase of the external magnetic field causes the width of the SWs to decrease (Fig. 5) supporting some of the published articles of Mamun (1998, 1999), Anowar and Mamun (2008a, 2008b).

To conclude, we have studied and analyzed the basic properties of the obliquely propagating PASWs in a magnetized e-p-i plasma system containing nonthermal hot positrons and electrons, inertial cold positrons, and immobile positive ions. The results of our present investigation can be effective for explaining the various localized structures and the basic features of PASWs in magnetized e-p-i plasmas, and can also be applied to space plasma environments [viz. star formation, auroral acceleration regions (Ergun et al. 1998; Franz et al. 1998), supernovae explosion, cluster explosions, active galactic nuclei, etc.] as well as laboratory plasmas [viz. semiconductor plasmas (Shukla et al. 1986), intense laser fields (Berezhiani et al. 1992)] where nonthermal hot positrons and electrons, inertial cold positrons, and immobile positive ions can be the major plasma components. Finally, it should be mentioned that the time evolution and stability analysis of these solitary structures are problems of great interest but beyond the scope of our present work.