1 Introduction

During the last couple of decades there has been a considerable research activities in understanding issues both in cosmology and in astrophysics in the framework of higher dimensions. Particularly the results obtained in the usual four dimensions are generalized in higher dimensions in addition to new physics. The history of higher dimensions goes back to the work done by Kaluza and Klein in the past (Kaluza 1921; Klein 1926). Kaluza and Klein independently first introduced the concept of extra dimension in addition to the usual four dimensions to unify gravitational interaction with that of electromagnetic interaction. The theory is essentially an extension of Einstein general theory of relativity (henceforth, GTR) in five dimensions which is of much interest in particle physics as well as in cosmology. But the initial approach does not work well. A couple of decades ago the study of higher dimensional theories has been revived once again and it was considerably generalized after realizing that many interesting theories of particle interactions need more than four dimensions for their consistent formulation. On the other hand, GTR was formulated in a space-time with just four dimensions. Thus if some of the theories of particle interactions are consistent in higher dimensions, it is natural to look for the generalization of the theories developed in the usual four dimensions. It became important to generalize the results obtained in four dimensional GTR in the higher dimensional context and probe the effects due to incorporation of one or more than one extra space-time dimensions in the theory. In this direction Chodos and Detweiler (1980) first obtained a higher dimensional cosmological model and thereafter a number of cosmological models in higher dimensions have been discussed in the literature (Shafi and Wetterich 1987; Wetterich 1982; Accetta et al. 1986; Lorentz-Petzold 1988a, 1988b; Paul and Mukherjee 1990) to address different issues not understood in the usual four dimensions. In cosmology it is proposed that a higher dimensional universe might undergo a spontaneous compactification leading to a product space M 4×M d , with M d the compact inner space, describing the present universe satisfactorily. Thereafter the advent of string theory (Green and Schwarz 1984, 1985; Candelas et al. 1985; Witten 1995) particularly a viable description of superstring theory in 10 dimensions led to a spurt in activities in higher dimensions. The work of Randal and Sundrum (1999a, 1999b) led to a paradigm shift in understanding the compactification mechanism. Randall and Sundrum gave an interesting picture of gravity in which the extra dimensions is not compact and it is possible to recover the usual four dimensional Newtonian gravity from a five dimensional anti-de Sitter space-time in the low energy limit. In the context of localized sources in astrophysics, higher dimensional versions of the spherically symmetric Schwarzschild and Reissner-Nördstrom black holes (Chodos and Detweiler 1982; Gibbons and Wiltshire 1986), Kerr Black holes (Mazur 1987; Xu 1988), black holes in compactified space-time (Myers 1986), no-hair theorem (Sokolowski and Carr 1986), Hawking radiation (Myers and Perry 1986), Vaidya solution (Iyer and Vishveshwara 1989) have been generalized. Shen and Tan (1989) also obtained a global regular solution of higher dimensional Schwarzschild space-time. The mass to radius ratio in higher dimensions for a uniform density star is determined which is a generalization of the four dimensions and new results have been reported in the literature (Paul 2001a, 2001b). The consequences of extra dimensions in understanding the structure of neutron stars employing Kaluza-Klein model was investigated by Liddle et al. (1990). The model is constructed making use of a five dimensional energy-momentum tensor described by perfect fluid. The four dimensional version of the theory is found to have a perfect fluid with a scalar source. The effect of the source term is found very large which leads to a substantial lower value in the mass of neutron star associated with a particular central density.

In astrophysics, it is known from recent observational prediction that there exist a number of compact objects whose masses and radii are not compatible with the standard neutron star models. As densities of such compact objects are normally above the nuclear matter density, theoretical studies hints that pressure within such compact objects are likely to be anisotropic, i.e., existence of two different kinds of interior pressures namely, the radial pressure and the tangential pressure (Herrera and Santos 1997). A number of literature (Tikekar and Thomas 1999; Patel and Mehta 1995; Maharaj and Maartens 1989; Gokhroo and Mehra 1994) came up where the solutions of Einstein’s field equations with anisotropic fluid distribution on different space-time geometries are discussed. The role of pressure anisotropy is studied in the context of high-redshift values including the stability of compact objects (see for example Mak and Harko 2003; Dev and Gleiser 2004; Chaisi and Maharaj 2005 and references therein). Bowers and Liang (1974) obtained the corresponding change in the limiting values of the maximum mass of compact stars in the presence of anisotropy. Recently, the maximum mass of an isotropic compact object and that of an anisotropic one in the context of Vaidya-Tikekar model obtained by Sharma et al. (2006) and Karmakar et al. (2007) in four dimension making use of general relativistic solution obtained by Mukherjee et al. (1997). It may be mentioned here that a higher dimensional generalization of the relativistic solution obtained by Mukherjee et al. (1997) has been generalized by one of us (Paul 2004). In the present paper we estimate the maximum mass limit of an anisotropic compact object making use of the above general relativistic solution in higher dimensions. In this case we consider space-time geometry describe by a metric ansatz given by Vaidya and Tikekar (1982). The technique adopted here is different from that usually considered in obtaining relativistic solution from Einstein’s field equation. Usually for a known equation of state (in short, EoS) of matter one obtains solution for the geometry. But in the case of compact objects the equation of state of matter inside a compact object is not yet known except some phenomenological assumptions. In this case making use of a known geometry for compact objects in hydrostatic equilibrium in higher dimensional GTR we explore different physical features of the compact objects. It helps to determine both the mass and radius of compact objects in terms of geometrical parameters as was obtained in Chattopadhyay et al. (2012); Paul and Deb (2014) in four dimensions. We also predict the relevant EoS for a given configuration known from observations. The EoS obtained here satisfies a non linear equation. It may be mentioned here that similar non-linear EoS have been employed by Mafa Takisa and Maharaj (2013) to obtain stellar models for compact objects.

The paper is organized as follows: In Sect. 2 we set up the Einstein field equation for an anisotropic star and presented a class of new solutions in higher dimensions. For physically relevant anisotropic stars, the regularity and matching conditions for the solution at the boundary of the star is ensured to obtain stellar models. In Sect. 3 the role of anisotropy is studied and estimated the probable maximum mass for the class of solutions obtained in Sect. 4. We conclude by summarizing our results in Sect. 5.

2 Field equation in higher dimensions and solutions

The Einstein’s field equation in higher dimensions is given by

$$ {\mathbf{R}}_{AB}-{1\over2} g_{AB}{\mathbf{R}} = 8 \pi G_{D}T_{AB} $$
(1)

where D is the total number of dimensions, G D =GV D−4 is the gravitational constant in D dimensions, G denotes the 4 dimensional gravitational constant and V D−4 is the volume of extra space. R AB is Ricci tensor, R is Ricci scalar, g AB is metric tensor and T AB is the energy momentum tensor in D dimensions. We consider the metric of a higher dimensional spherically symmetric, static space-time given by

$$ ds^{2} = -e^{2\nu(r)}dt^{2}+e^{2\mu(r)}dr^{2}+r^{2}d \varOmega^2_{n} $$
(2)

where ν(r) and μ(r) are the two unknown metric functions, n=D−2 and \(d\varOmega^{2}_{n}=d\theta^{2}_{1}+ \sin^{2}\theta_{1}d\theta ^{2}_{1}+ \sin^{2}\theta_{2}(d\theta^{2}_{3}+\cdots+ \sin^{2}\theta_{n-1}d\theta ^{2}_{n})\) represents the metric on the n-sphere in polar coordinates. The energy-momentum tensor for an anisotropic star in the most general form is given by

$$ T_{AB} = \mathrm{diag}(-\rho,p_{r},p_{t},p_{t},\ldots,p_{t}) $$
(3)

where ρ is the energy-density, p r is the radial pressure, p t is the tangential pressure and Δ=p t −p r is the measure of pressure anisotropy in this model, which depends on metric potential μ(r) and ν(r). Using Eqs. (2) and (3), Einstein’s field equation reduces to the following set of equations:

$$\begin{aligned}& 8\pi G_{D}\rho= \frac{n(n-1) (1-e^{-2\mu} )}{2r^2}+\frac{n\mu 'e^{-2\mu}}{r}, \end{aligned}$$
(4)
$$\begin{aligned}& 8\pi G_{D}p_{r} = \frac{n\nu'e^{-2\mu}}{r}-\frac{n(n-1) (1-e^{-2\mu } )}{2r^2}, \end{aligned}$$
(5)
$$\begin{aligned}& 8\pi G_{D}p_{t}=e^{-2\mu} \biggl(\nu^{\prime\prime}+{ \nu^{\prime }}^{2}-\nu^{\prime }\mu^{\prime}- \frac{(n-1)(\mu^{\prime}-\nu^{\prime})}{r} \biggr) \\& \phantom{8\pi G_{D}p_{t}=} -\frac{(n-1)(n-2) (1-e^{-2\mu} )}{2r^2} \end{aligned}$$
(6)

Using Eqs. (5) and (6), pressure anisotropy condition (Δ=p t −p r ) gives rise to

$$\begin{aligned}& \nu^{\prime\prime}+{\nu^{\prime}}^{2}-\nu^{\prime} \mu^{\prime }-\frac{(n-1)\mu^{\prime}}{r}-\frac{\nu^{\prime}}{r}-\frac{(n-1) (1-e^{2\mu} )}{r^2} \\& \quad =\Delta e^{2\mu} \end{aligned}$$
(7)

To solve the Eqs. (4)–(7), we use the ansatz (Vaidya and Tikekar 1982),

$$ e^{2\mu}=\frac{1+\lambda r^2/R^2}{1-r^2/R^2}, $$
(8)

where λ being the spheroidicity parameter and R is the geometrical parameter. Now from Eq. (7), one obtains a second order differential equation in x, given by

$$\begin{aligned}& \bigl(1+\lambda-\lambda x^2\bigr)\varPsi_{xx} + \lambda x \varPsi_{x} + \lambda(\lambda + 1) (n-1)\varPsi \\& \quad {} - \frac{\Delta R^2(1+\lambda- \lambda x^2)^2}{(1-x^2)} \varPsi= 0 \end{aligned}$$
(9)

where Ψ=e ν(r), with \(x^{2} = 1-\frac{r^{2}}{R^{2}}\).

Now for simplicity we choose the anisotropic parameter Δ (Sharma et al. 2006) as follows,

$$\Delta= \frac{\alpha\lambda^2(1-x^2)}{R^2(1+\lambda-\lambda x^2)^2} $$

The above relation is chosen so that the regularity at the centre of the star is ensured. The method adopted here to obtain solution of the field Eqs. (4)–(7) is similar to that previously obtained by Mukherjee et al. (1997). Using the transformation \(z = \sqrt{\lambda/(\lambda+1)} x\), Eq. (9) can be written as

$$ \bigl(1-z^2\bigr)\varPsi_{zz} + z\varPsi_{z} + \bigl(\beta^2 - 1\bigr)\varPsi = 0 $$
(10)

where \(\beta=\sqrt{(n-1)(\lambda+1)-\lambda\alpha+1}\) is a constant. The general solution of Eq. (10) (Mukherjee et al. 1997) is given by

$$ e^{\nu}=A \biggl[{\frac{\cos[(\beta+1)\zeta+\delta]}{\beta+1}}-{\frac{ \cos[(\beta-1)\zeta+\delta]}{\beta-1}} \biggr] $$
(11)

where ζ=cos−1 z. A and δ are two constants which can be determined from the boundary conditions. For a real β the anisotropy parameter α satisfies a limit determined by the space-time dimensions (D) and spheroidicity parameter λ which is \(\alpha_{\mathit{max}}<(D-3)+\frac{D-2}{\lambda}\). The physical parameters relevant in this model are given below:

$$\begin{aligned}& \rho = {n \over16 \pi G_{D} R^2 (1-z^2)} \biggl[n-1 + {2 \over (\lambda+ 1) (1 - z^2)} \biggr] \end{aligned}$$
(12)
$$\begin{aligned}& p_{r} = - {1 \over8 \pi G_{D} R^2 (1-z^2)} \biggl[ {n(n-1)\over2} + {n z \varPsi_{z}\over (\lambda+ 1) \varPsi} \biggr] \end{aligned}$$
(13)
$$\begin{aligned}& p_{t} = p_{r} + \Delta \end{aligned}$$
(14)
$$\begin{aligned}& \Delta = {\alpha\lambda\over8 \pi G_{D} R^2} \biggl[ {(\lambda+ 1)(1 - z^2) - 1 \over(\lambda+ 1)^2(1 - z^2)^2} \biggr] \end{aligned}$$
(15)

Equations (12)–(15) together with Eqs. (8) and (11) will be employed here to obtain exact solution of the Einstein field equation. The mass of a compact star of radius b (Paul 2004) in higher dimensions is given by

$$ M(b) =\frac{nA_{n}}{16\pi G_{D}} \frac{(1+\lambda)b^{n+1}}{R^2(1+\lambda \frac{b^2}{R^2})}. $$
(16)

We impose the following conditions in our model:

  • At the boundary of the star the interior solution should be matched with the Schwarzschild exterior solution, i.e.,

    $$ e^{2\nu(r=b)} = e^{-2\mu(r=b)} = \biggl(1 - \frac{C}{b^{n-1}} \biggr), $$
    (17)

    where C is a constant related to the mass of the star which is given by \(M=\frac{nA_{n}C}{16\pi G_{D}}\). Here \(A_{n}=\frac{2 \pi ^{(n+1)/2}}{\varGamma(n+1)/2}\). In four dimension (D=4), C=2M and in five dimension (D=5), C=0.84848MG 5 where G 5=GV 1 and V 1 is the volume of extra space in five dimensions.

  • The radial pressure p r should vanish at the boundary of the star which gives,

    $$ \frac{\varPsi_{z}(z_{b})}{\varPsi(z_{b})} = - \frac{(n-1)(1+\lambda)}{2z_{b}} $$
    (18)

    where \(z_{b}^{2} = (\lambda/(\lambda+1))(1 - b^{2}/R^{2})\). From Eq. (11) one obtains

    $$ \frac{\psi{_z}}{\psi} = \frac{(\beta^2-1)}{\sqrt{(1-z^2)}} W $$
    (19)

    where

    $$\begin{aligned}& W=\frac{\sin[(\beta-1)\zeta+\delta]-\sin[(\beta+1)\zeta +\delta]}{(\beta+1)\cos[(\beta-1)\zeta+\delta]-(\beta-1)\cos[(\beta +1)\zeta+\delta]}. \end{aligned}$$

    Using Eqs. (18) and (19) we get

    $$ \tan\delta= \frac{\tau\cot\zeta{_b} - \tan(\beta\zeta{_b})}{1+\tau\cot \zeta{_b} \tan(\beta\zeta{_b})} $$
    (20)

    where \(\tau=\frac{(n-1)(\lambda+1)-2\lambda\alpha}{\beta(1 + \lambda )(n-1)}\) and ζ b =cos−1 z b .

  • As the radial pressure inside the star is positive, the condition p r ≥0 leads to the inequality

    $$ \frac{\varPsi_{z}}{\varPsi} \leq- \frac{(1+\lambda)(n-1)}{2z}. $$
    (21)

  • Using Eqs. (12)–(14), the radial squared speed of sound is obtained which is given by

    $$\begin{aligned}& \frac{dp_{r}}{d\rho} \\& \quad = \frac{z(1-z^2)^2(\varPsi_{z}/\varPsi)^2 -((1-z^2)\varPsi _{z}/\varPsi) - \alpha\lambda z (1 - z^2)}{z(1-z^2)(\lambda+1)(n-1) + 4z} . \end{aligned}$$
    (22)

    The variation of the tangential pressure with density is given by

    $$ \frac{d p_{t}}{d\rho} = \frac{d p_{r}}{d\rho} + {\alpha\lambda\over (1 + \lambda)} \biggl[ {(\lambda+ 1)(1 - z^2) - 2 \over(\lambda+ 1)(1 - z^2) + 4} \biggr]. $$
    (23)

    Now, the parameters are so chosen that the causality conditions are not violated, i.e., \(\frac{dp_{r}}{d\rho}, \frac{dp_{t}}{d\rho} \leq 1\) in the model.

The above constraints are used to obtain physically viable stellar models in the next section.

3 Physical analysis of compact objects

In this section we consider a higher dimensional space-time to determine the maximum mass of compact objects. We explore the effect of increasing the number of space-time dimensions in addition to anisotropy. The methodology adopted here is as follows: For a given mass (M), radius (b), spheroidicity parameter (λ) and space-time dimensions (D), the factor y=b 2/R 2 can be determined from Eq. (16). For a given central or the surface density, the value of the geometrical parameter R can be determined using Eq. (12). Thereafter, the radius of star \(b = R\sqrt{y}\) and mass M can be determined using Eq. (16). It may be mentioned here that for a specific value of anisotropy parameter α, the parameter δ is fixed. However, using Eqs. (22) and (23) one can show that for compact objects with same masses and radii might have different anisotropy for different equation of state (EoS). In Sect. 3.1, it is shown that EoS changes as one varies the anisotropy and space-time dimensions. It is evident from the plot of variations of \(\frac{d p_{r}}{d\rho}\) and \(\frac{dp_{t}}{d\rho}\) with α in Figs. 1 and 2 respectively.

Fig. 1
figure 1

Variations of (\(\frac{dp}{d\rho}\)) at the centre of an anisotropic star with α for λ=53.34, with M=1.435 M ⊙, b=7.07 km (SAX J 1808.4-3658). The solid and dotted lines represent the variation of \((\frac{dp_{r}}{d\rho})_{r=0}\) and \((\frac{dp_{t}}{d\rho})_{r=0}\) with α in four dimensions respectively. The dashed and long dashed lines represent the variation of \((\frac{dp_{r}}{d\rho})_{r=0}\) and \((\frac{dp_{t}}{d\rho})_{r=0}\) in five dimensions respectively

Full size image
Fig. 2
figure 2

Variations of (\(\frac{dp}{d\rho}\)) at the centre of an anisotropic star with α for λ=53.34, M=1.435 M ⊙, b=7.07 km (SAX J 1808.4-3658). The solid and dotted lines represent the variation of \((\frac{dp_{r}}{d\rho})_{r=b}\) and \((\frac{dp_{t}}{d\rho})_{r=b}\) with α in four dimensions respectively. The dashed and long dashed lines represent respectively the variation of \((\frac{dp_{r}}{d\rho})_{r=b}\) and \((\frac {dp_{t}}{d\rho})_{r=b}\) in five dimensions respectively

Full size image

It is also evident that the slope for \(\frac{dp}{d\rho}\) with anisotropy is decreases as the dimension is increased and moreover the value of \(\frac{dp}{d\rho}\) for five dimensions is less than that of four dimensions. Thus the EOS of matter inside the star changes as the number of space-time dimensions are changed for the same set of values of the model parameters. For a given values of α and λ one can determine δ from Eq. (20). In the case of isotropic star (α=0), for a given λ and u iso (isotropic compactness factor), we first calculate y using Eq. (16) thereafter δ is determined from Eq. (20). In the case of anisotropic star we employ same δ to determine y ani for different α. Using Eq. (16) for anisotropic compactness given by

$$u_{\mathit{ani}} = \frac{M(b)}{b} = \frac{nA_{n}}{16\pi}\frac{(1 + \lambda )y_{\mathit{ani}}}{(1 + \lambda y_{\mathit{ani}})} $$

we probe the effect of anisotropy on the compactness of a star for different space-time dimensions. We note that for vanishing anisotropy with D=4, the results are obtained by Karmakar et al. (Sharma et al. 2006; Karmakar et al. 2007).

3.1 Numerical results

In this section we consider two different compact objects of known masses as examples for the above purpose.

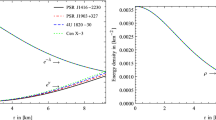
Case I: For the pulsar Her X-1 (Sharma and Mukherjee 2001) which has mass M=0.88 M ⊙ where M ⊙ is the solar mass, radius b=7.7 km, in the framework of the space-time geometry considered here the compactness factor is u iso =0.1686 when λ=2 in four dimensions. Now as mentioned we determine R using Eq. (17) for λ=2 in four and five dimensions which are R=20.2238 km and R=97.2474 km respectively. It is now possible to study the radial variation of energy density (ρ), radial pressure (p r ) and transverse pressure (p t ) using Eqs. (12), (13) and (14) which are plotted in Figs. 3–5 respectively for four (solid line) and five dimensions (dotted line).

Fig. 3
figure 3

Radial variation of energy density \((\widetilde{\rho}=\rho R^{2})\) interior to the star HER X-1 (Mass M=0.88 M ⊙, Radius=7.7 km). Solid line for D=4 and dotted line for D=5 with anisotropy parameter α=0.4 and λ=2

Full size image

In Fig. 3, we plot variation of energy density \((\widetilde {\rho})\) inside the compact objects for a given α and λ with different space-time dimensions. The radial pressure is found to increase with an increase in space-time dimensions (D). In the case of pressures plotted in Figs. 4 and 5, it is evident that both the radial and the tangential pressures decrease with increase of space-time dimensions. The rate of decrease of pressure is more when the dimension is less. The tangential pressure at the surface of the star is more in the case of lower dimension.

Fig. 4
figure 4

Variation of radial pressure (\(\widetilde{p}_{r} = p_{r} R^{2}\)) inside HER X-1 (Mass M=0.88 M ⊙, Radius=7.7 km). Solid line for D=4 and dotted line for D=5 for anisotropy parameter α=0.4 and λ=2

Full size image
Fig. 5
figure 5

Radial variation of tangential pressure (\(\widetilde{p}_{t} = p_{t} R^{2}\)) inside HER X-1 (Mass M=0.88 M ⊙, Radius=7.7 km). Solid line for D=4 and dotted line for D=5 with anisotropy parameter α=0.4 and λ=2

Full size image

In Table 1 we tabulated the calculated values of the compactness factor and mass of compact objects considering HER X-1 an anisotropic star. The observed mass is considered corresponding to isotropic compact object in 4 dimensions. In the case of 5-dimensions mass of compact object is found less than that of 4 dimensional mass. From Table 1 it is evident from columns 3 and 4 that in four dimensions both compactness factor (u) and mass (M) decreases with the increase of anisotropy (α). But in five dimensions both compactness factor (u) and mass (M) are found to increase at first with the increase of anisotropy parameter (α), it attains a maximum value for a certain α then decreases as evident from columns 7 and 8 respectively.

Table 1 Compactness factor and mass calculated for different anisotropy parameter (α) for space-time dimensions D=4 & D=5
Full size table

Case II: For a millisecond pulsar namely, SAX J 1808.4-3658 (Sharma et al. 2002) with mass M=1.435 M ⊙ and radius b=7.07 km, it is found that isotropic compactness u iso =0.2994 corresponds to λ=53.34. In this case also the compact star with the given mass and radius can be modelled as an anisotropic star.

It admits pressure anisotropy in the configuration for a suitable combination of spheroidicity parameter (λ) and anisotropy parameter (α) in four dimensions as evident from Fig. 6. It is observed that the anisotropy parameter α increases with the increase of spheroidicity parameter (λ) for a fixed mass of the star which we call isotropic mass (M=1.435 M ⊙). It is also evident that α increases first with the increase in λ and at a large limiting value of λ the anisotropy parameter α attains a constant value. In this case we obtain α=0.23267 for λ=600. The value of R can be determined using Eq. (17) for λ=53.34 which gives R=43.245 km and R=270.059 km in four and five dimensions respectively. We plot the radial variation of energy density (ρ), radial pressure (p r ) and transverse pressure (p t ) in four and five dimensions in Figs. 7–9 respectively. In Fig. 7, we plot the variation of energy density \((\widetilde{\rho})\) with radial distance and found that energy density is more in five dimensions than that in four dimensions. A star of same radius accommodates more mass in the case of higher dimensions. However radial and transverse pressures are found to have lower values in higher dimensions than that in four dimensions which is evident from Figs. 8 and 9 respectively. In Table 2, the values of y, u and M are given considering an isotropic star (α=0) and also for an anisotropic (α≠0) stellar configuration both in 4 and 5-dimensions. It is evident from columns 3 and 4 that in four dimensions both compactness factor (u) and the corresponding mass of a star (M) first increases with an increase in anisotropy (α), which attains a maximum value and thereafter decreases. But in five dimensions both compactness factor and mass of a compact object are found to decrease with the increase of anisotropy parameter (α) as evident from columns 7 and 8 of Table 2. It is also evident that for the same anisotropy, compactness of a star is found to decrease significantly if the space-time dimensions are increased. We note that there is a limiting value of α above which y=b 2/R 2 becomes zero or negative which is non-physical.

Fig. 6
figure 6

Variation of anisotropy parameter (α) with spheroidicity parameter (λ) for a given mass and radius configuration

Full size image
Fig. 7
figure 7

Radial variation of energy density \((\widetilde{\rho}=\rho R^{2})\) interior to the star SAX J 1808.4-3658 (Mass M=1.435 M ⊙, Radius=7.07 km). Solid line for D=4 and dotted line for D=5 for anisotropy parameter α=0.4 and λ=53.34

Full size image
Fig. 8
figure 8

Variation of radial pressure \((\widetilde{p}_{r} = p_{r} R^{2})\) interior to the star SAX J 1808.4-3658 (Mass M=1.435 M ⊙, Radius=7.07 km). Solid line for D=4 and dotted line for D=5 for anisotropy parameter α=0.4 and λ=53.34

Full size image
Fig. 9
figure 9

Radial variation of tangential pressure \((\widetilde{p}_{t} = p_{t} R^{2})\) interior to the star SAX J 1808.4-3658 (Mass M=1.435 M ⊙, Radius=7.07 km). Solid line for D=4 and dotted line for D=5 for anisotropy parameter α=0.4 and λ=53.34

Full size image
Table 2 Compactness factor and mass for different anisotropy (α) in D=4 & D=5 dimensions with λ=53.34
Full size table

It is noted that for HER X-1, a physically realistic stellar model is obtained with a maximum value of α which are 0.665 and 0.79 for D=4 and D=5 respectively. In the case of SAX J 1808.4-3658, however, a physically realistic stellar model is permissible with a maximum α which are 0.65 and 0.49 for D=4 and D=5 respectively.

4 Maximum mass and surface red-shift

In this section maximum mass of a class of isotropic and anisotropic stars in four (D=4) and in higher (D>4) dimensions will be explored. In determining the maximum mass of a compact object in higher dimensions we follow a technique adopted in Sharma et al. (2006) and Karmakar et al. (2007).

  • The squared speed of sound should satisfy an inequality (\(\frac{d p{_{r}}}{d\rho} \leq1\)) inside the compact object for causality. It decreases away from the centre thus we consider squared speed of sound maximum at the centre which leads to

    $$ \frac{\psi_{z}}{\psi}\bigg|_{zo} \geq\frac{(1+\lambda)}{2\sqrt{\lambda}} \biggl[\sqrt{ \lambda+1} - \sqrt{(4 n +13)\lambda+1 + \frac{4 \alpha \lambda^2}{\lambda+ 1}} \biggr]. $$
    (24)

    Using (18) and (24), one can determine the limiting value of δ which is a function of α for given values of λ and D.

  • Corresponding to the limiting value of δ, a maximum value for y=b 2/R 2 can be determined using Eq. (19).

  • From Eq. (15) the compactness of a compact star in higher dimension can be determined which is given by

    $$ u = \frac{M(b)}{b} =\frac{nA_{n}}{16\pi} \frac{(1+\lambda)}{(\lambda+ \frac{1}{y})}. $$
    (25)

    Thus the maximum value of y corresponds to the maximum compactness of a stellar configuration. The maximum surface red-shift ((Z s ) max ) is given by:

    $$ (Z_s)_{\mathit{max}}= (1-2u_{\mathit{ani}} )^{-1/2} -1. $$
    (26)

Thus, in the above it is noted that once the maximum compactness of a star is known the corresponding maximum mass of the anisotropic star can be determined for a given radius or surface density. In Tables 3, 4 and 5 we have tabulated the maximum mass of stars, surface red-shift for λ=2, 3 and 100 respectively in four and higher dimensions. From Tables 3 and 4, it is evident that both the surface red-shift and maximum mass are found to increase with the increase of anisotropy parameter (α) for a given dimension. However surface red-shift and maximum mass both increases when the space-time dimensions are increased with or without anisotropy. We note that for spheroidicity parameter λ=100, the maximum compactness of an isotropic star is 0.3615 which is same as that obtained in Sharma et al. (2006). We note that the maximum mass of a compact star first increases with the increase of dimensions, attains a maximum value in between D=5 and D=6 (if fractal dimensions exist), thereafter it decreases which is evident in Table 5. In Fig. 14 we plot the variation of maximum mass with dimension. From Table 5, it is evident that maximum compactness factor of a compact object may exceed 0.5 in higher dimensions. In Kaluza-Klein gravity similar limiting value of compactness of a higher dimensional star admitting compactness more than 0.5 without a black hole was reported in the literature (Ponce de Leon 2010). However if one restricts the compactness to a value less then 0.5, then the maximum allowed value of λ found in this case is 10 in isotropic star. In Tables 3, 4 and 5, it is evident that for a given value of λ there exists a upper limit of space-time dimensions for a physically viable model. It is evident that a compact object with spheroidicity parameters λ=2 and 3 can be accommodated consistently in D≤6 and for a large value say, λ=100 it can be accommodated in D≤8.

Table 3 Maximum Mass configurations for a star of radius 10 km. with λ=2
Full size table
Table 4 Maximum Mass configurations for a star of radius 10 km with λ=3
Full size table
Table 5 Maximum Mass configurations for a star of radius 10 km with λ=100
Full size table

4.1 Equation of state (EoS)

Using the above model parameters we plot the radial variation of density and radial pressure vide Eqs. (12) and (13). However, it may be pointed out here that an analytic function of pressure with density in known form cannot be obtained here because of complexity of the equations. We study numerically to obtain a best fitted relation between the energy density (ρ) and radial pressure (p) which are presented in Tables 6 and 7. Theoretically a convenient way of expressing EoS is obtained from energy per unit mass of the fluid which is a function of energy density (u) and entropy (S) respectively. From the first law of thermodynamics,

$$ du=- \, p \, d \biggl(\frac{1}{\rho} \biggr)+T \, dS. $$
(27)
Table 6 Equation of state for different stellar models in 4-dimensions
Full size table
Table 7 Equation of state for different stellar models in 5-dimensions
Full size table

For the description of the fluid flow pressure and temperatures are given by

$$ p=\rho^2\frac{\partial u}{\partial\rho}\bigg|_{S}, \qquad T= \frac{\partial u}{\partial S}\bigg|_{\rho}. $$
(28)

In the case of production of entropy through dissipative processes we restrict to adiabatic flows only. In the isentropic case \(\frac {dS}{dt}=0\), entropy remains constant. Therefore, the energy density becomes a one parameter function. Consequently Eq. (27) is equivalent to

$$ p=p(\rho). $$
(29)

It is evident that the EoS obtained (in Tables 6 and 7) numerically using the Eqs. (12) and (13) is not linear relation of the form p=ωρ where ω is a constant. We found that the models may be fitted with linear, quadratic even with higher order polynomial function in ρ. We determine here two probable EoS in isotropic and anisotropic case both in D=4 and D=5. The EoS obtained here are found to have similar to that recently considered by Maharaj and Mafa Takisa (2012). From Tables 6 and 7 we note that equation of state becomes softer in higher dimensions. Using suitable choice of λ and α in some compact objects it may be possible to fit the equation of state with \(p_{r}=\frac{1}{3}(\rho-4B)\), where B is the Bag constant in MIT Bag model for strange matter. This aspect of the model will be taken up elsewhere.

5 Discussion

In this paper we study compact objects in hydrostatic equilibrium making use of an alternative approach considered by Mukherjee et al. (1997). The interior geometry is described by Vaidya-Tikekar metric both in four and in higher dimensions. The radial variation of pressure (p r ) for HER X-1 and SAX J 1808.4-3658 are shown in Figs. 4 and 8 respectively assuming an anisotropic distribution of fluid. Radial variation of transverse pressure (p t ) for the two stars mentioned here are also shown in Figs. 5 & 9. It is evident from the figures that both p r and p ⊥ decreases from the centre to the surface of the stars both in four and five dimensions. This type of variation is also found for anisotropic stellar models as obtained by Chaisi and Maharaj (2005) and Sharma et al. (2002) for four dimensional space-time geometry. The radial variation of anisotropy in pressure (Δ) in case of HER X-1 are plotted in Figs. 10 and 11 in D=4 and D=5 respectively. The radial variation of anisotropy in pressure (Δ) in case of SAX J 1808.4-3658 are plotted in Figs. 12 and 13 in D=4 and D=5 respectively. The variation in tangential pressure is physically acceptable. Since during the quasi-equilibrium contraction of a massive body, conservation of angular momentum leads to a high value for transverse pressure at the central region of the star. To incorporate the effect of dimensions on the maximum mass of a star, we obtain a class of relativistic solution in spheroidal space-time in Vaidya-Tikekar model with higher dimensions. The solution is then employed to estimate the maximum mass of a star in higher dimensions. The maximum mass of a isotropic star and that in the presence of anisotropy are also discussed in Karmakar et al. (2007) and Sharma et al. (2006) respectively. We recover the maximum mass obtained in four dimensions in isotropic case (2.45 M ⊙) and in presence of anisotropy (2.8 M ⊙) for λ=100. We also note that the maximum mass increases with the increase of space-time dimensions (D) which is maximum in between D=5 and D=6, thereafter it decreases. It is found that M max =3.54 M ⊙ when α=0 and M max =3.9824 M ⊙ when α=0.5 in 5-dimensions as shown in Table 5. It is also noted that in higher dimensions the maximum mass of a anisotropic star is greater than an isotropic star also. From Figs. 10–13, it is evident that at the centre of the star anisotropy (Δ) vanishes both in D=4 and D=5, whereas at the surface it attains a maximum value. Though the nature of radial variation of Δ is same, Δ picks up lower values in higher dimensions. We also note that the surface red-shift has greater value in case of anisotropic star than isotropic one. Also surface red-shift increases with dimensions first, attains a maximum value and then decreases. It picks up a maximum value when mass of the star attains its maximum, i.e., we note a correlation between maximum mass of a star and its surface red-shift.

Fig. 10
figure 10

Radial variation of \(\widetilde{\Delta}=\Delta~R^{2}\) interior to the star HER X-1 with u iso =0.1686, λ=2, α=0.4 and D=4

Full size image
Fig. 11
figure 11

Radial variation of \(\widetilde{\Delta}=\Delta~R^{2}\) interior to the star HER X-1 with u iso =0.1686, λ=2, α=0.4 and D=5

Full size image
Fig. 12
figure 12

Radial variation of \(\widetilde{\Delta}=\Delta~R^{2}\) interior to the star SAX J 1808.4-3658 with u iso =0.2994, λ=53.34, α=0.4 and D=4

Full size image
Fig. 13
figure 13

Radial variation of \(\widetilde{\Delta}=\Delta~R^{2}\) interior to the star SAX J 1808.4-3658 with u iso =0.2994, λ=53.34, α=0.4 and D=5

Full size image
Fig. 14
figure 14

Variation of Maximum mass (M max ) with Dimensions (D) for a compact object with radius b=10 km and λ=100. Solid curve for α=0 and dotted curve for α=0.5

Full size image