Fig. 1
figure 1

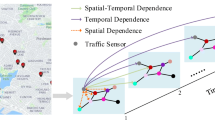
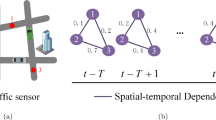
Complex spatial-temporal correlations. The red points distributed in the road network on the map in (a) represent individual sensors, and the connectivity relationship between sensors represents the connectivity relationship between roads. The nodes in (b) represent individual sensors, and the solid line represents the real spatial neighbor relationship. Among them, node No. 1 is the primary node, and the fill colors of the other nodes indicate their spatial correlation with node No. 1. Not only do the nodes that are adjacent to node 1 have a spatial correlation with it, but the nodes that are not directly adjacent to it may also have spatial correlation with it. The dashed line represents the temporal correlation between individual moments due to the nonlinear relationship of traffic flow data

Full size image

1 Introduction

With the continuous expansion of urban transportation networks, increasing traffic flow, and diversifying travel modes, accurately predicting traffic flow has become crucial for optimizing traffic management and planning. As an effective tool for alleviating traffic congestion, intelligent transportation systems (ITSs) are drawing global attention [1]. Traffic flow prediction is an important part of ITSs [2]. Given the sequence of traffic flow and roadway topology networks [3], the purpose of traffic flow prediction is to use historical data to predict future traffic flow [4, 5]. However, the road sensor nodes in road networks are spatially connected and interact with each other; traffic flow data from individual nodes form a long time series with dynamically changing time patterns. Therefore, traffic prediction has always been a challenging task due to its complex spatial-temporal features [6]. In recent years, with the continuous advancement of deep learning technologies, deep learning has been increasingly applied in emerging industrial fields, such as intelligent transportation [7, 8], intelligent manufacturing [9,10,11], and medical diagnosis [12, 13].These applications showcase the robust capabilities and broad prospects of deep learning in industrial domains.

With the continuous development of graph neural networks [14,15,16], determining how to effectively model graph modeling on spatial-temporal data has become a focus of attention. We believe that, as Fig. 1 shows, nodes on a road network mainly exhibit two types of spatial dependencies: one is the propagation of traffic flow due to the physical proximity between nodes; the other is the similarity of changes due to nodes with similar functions, even though they are not directly physically connected, orare even far apart. For the traffic flow on each node as time series data, there is a specific time dependence between the time slices, whether at a similar moment or at a long time interval.

First, an obvious drawback of many previous methods is that is that they fix spatial relationships, such as the DCRNN [17] and ASTGCN [18], usually use static adjacent matrices (either predefined or self-learned) to represent spatial dependencies between nodes. However, there are similarities between nodes from a global perspective, and the spatial dependencies may be dynamically change over time. The fixed adjacencies cannot model the global similarities between nodes that are dynamically change over time. Recently, methods such as STFGCN [19] and DSTAGNN [20] have learned dynamic graphs through a data-driven approach to better reflect the dynamically changing spatial dependencies between nodes. However, these methods also have some drawbacks. They may overemphasize the influence of globally similar nodes on a node and ignore the traffic fluctuations caused by the changes in the traffic of actual adjacent nodes at a single time step. These methods often use a static adjacent matrix or dynamic similarity matrix alone to model the spatial dependency between nodes but do not fully consider the impact of the joint effect of multiple factors on traffic flow prediction. Due to the mutual mapping between sensor nodes, traffic flows are complex and cyclical in the long term but sudden and volatile in the short term [21]. Based on the long-term and global scales, there are similarities between nodes, and the data-driven dynamic adjacency matrix may select the most similar node in the time unit of a day as the neighbor; in the short-term and local scales, for a single time step of a single node, the flow change of adjacent nodes in the real world at the previous time still plays a vital role in its flow fluctuation, which cannot be ignored. Neglecting the influence of any of these factors will lead to incomplete modeling of spatial dependence between nodes. Comprehensive consideration is essential to concurrently address the impact of both actual adjacent nodes and globally similar nodes on traffic flow prediction.

Second, for the data of each node in the road network, due to its nature as time-series data, we need to pay attention to its temporal dependence on both short-term and long-term scales. However, current spatial-temporal prediction studies have certain shortcomings in temporal dependence learning. STGCN [22] uses convolutional neural networks (CNNs) to capture short-term temporal dependencies, while DCRNN [17] uses recurrent neural networks (RNNs), and GraphWaveNet [23] uses diffusion convolution to attempt to capture long-term temporal dependencies. However, these methods often struggle to comprehensively consider short-term and long-term temporal correlations, which may lead to the omission of critical temporal features in temporal dependency capture.

In addition, due to sensor failure, communication errors, storage loss, and other reasons, data collected by sensors inevitably contain missing data [24]. However, complete and correct data are crucial for subsequent data analysis tasks.

In summary, existing methods often only consider the influence of a single factor when modeling spatio-temporal correlations, resulting in incomplete capture of the spatial dependence between nodes and the temporal dependence of node data. Moreover, the existing methods use only simple statistics-based methods to impute missing data in traffic datasets. The prediction accuracy of the traffic flow prediction model is not accurate enough due to the influence of these factors.

Complete traffic flow data are obtained to indirectly improve the model prediction accuracy. Moreover, to comprehensively consider the static local and dynamic global multifactor influences on spatial dependencies and capture multiscale temporal dependencies, we propose a new neural network framework based on graph convolution: the spatial-temporal multifactor fusion graph neural network (STMFGNN). In the data preprocessing stage, we improved the masking mechanism and training process of the generative adversarial imputation network (GAIN) [25] and applied it to traffic data to impute the missing traffic data. In the process of graph convolution, we used the predefined static reachability matrix and the dynamic similarity matrix generated based on the Wasserstein distance [26] to perform graph convolution and then used the dynamic gated fusion module to self-learn to fuse the two results to better capture the spatial dependence of static and dynamic interwoven traffic flow data. Similarly, to overcome the trade-off between the temporal dependence of the short-term scale and the long-term scale in time series prediction, we synergistically employed the multifield gated tanh unit (GTU) and gated recurrent units (GRUs), adjusting the influence weights of the two with a dynamic gate fusion module adaptively, aiming to comprehensively capture the short- and long-term temporal dependencies of traffic flow data. The main contributions of our work are as follows:

  • In the data preprocessing stage, a modified GAIN with an improved masking mechanism and training process is proposed and applied to traffic data. The imputation of commonly missing traffic data indirectly enhances the model performance.

  • A graph convolution method incorporating multiple factors is designed. The dynamic similarity graph is used while the static adjacency graph is retained, and the real prior knowledge and self-learning hidden knowledge are combined through the dynamic gated fusion module to jointly model the complex spatial dependence.

  • A method combining multiscale GTU convolution and GRU is proposed. One-dimensional convolutions with multiple fields capture varying degrees of short-term temporal dependencies, while the GRU captures long-term temporal dependencies. A dynamic gate fusion module is used to autonomously learn integrated multiscale temporal features.

  • Extensive experiments on real-world traffic datasets demonstrate that our method outperforms numerous baseline models, including state-of-the-art methods, and achieves superior performance.

The rest of the paper is organized as follows: Section 2 reviews and summarizes previous works. The traffic flow prediction problem is described in Section 3, and our proposed model is introduced in detail. Section 4 describes our overall experiment, compares it with other models, and analyzes the results. An ablation study, result visualization, and parameter study follow this approach. Finally, we conclude the entire paper in Section 5.

2 Related work

2.1 Data imputation

In data completion, the imputation of time series is a critical component of solving the problem of missing traffic flow data, and there are a variety of methods, including statistical, machine learning, and deep learning methods. Statistics-based imputation methods typically use mean values, with the simplest method using historical averages, which impute missing values based on the average of the same time interval in the past. Many previous studies have shown that machine learning-based methods are very effective for data imputation. For example, a Bayesian network learns probability distributions from observed data and imputes missing data using the best fit method [27]. K-nearest neighbors (KNNs) [28] use the average of the K nearest neighbors to the missing values to repair the data. Other methods include the probabilistic principal component analysis (PPCA) [29] technique, which utilizes the daily periodicity and interval variability of traffic data. With the development of deep learning, many neural network models have also been used to solve the data imputation problem. The missing data imputation method of such models usually starts from the data distribution and fills the missing data by fitting the proper distribution. For example, literature [30] used a bidirectional RNN as a generative model to fill in missing data. A convolutional recursive autoencoder was proposed in the literature [31]. Generative adversarial networks (GANs) [32] are generative models in which two networks are trained against each other to generate new sample datasets that follow the training distribution. The GAIN [25] is a GAN-based method that uses parallel data and a GAN to enhance traffic data and uses a hint matrix based on real observations for unsupervised data generation to fill in missing data.

2.2 Graph convolution

In graph convolution, graph convolutional networks generalize convolutional neural networks from standard grid-like to graph-structured data to efficiently extract local patterns in the data. Graph convolutional networks fall into two main categories: spatial-based and spectral-based [33]. Spectral-based graph convolution mainly utilizes the graph fourier transform (GFT) to achieve convolution. [34] extended convolution to graphs in the spectral domain. ChebNet [35] uses Chebyshev polynomials instead of original polynomials, which avoids eigenvalue decomposition and arithmetic, reduces computational complexity and cost, and takes advantage of the fact that polynomial fitting can optionally use lower order numbers, which transforms computations from global to local. The graph convolution network (GCN) [36] reduces Chebyshev networks to a more straightforward form by invoking a first-order Chebyshev polynomial approximation. Spatial-based graph convolution is applied similarly to convolution in deep learning and centers on updating information by designing different strategies to aggregate neighboring features. Typical works include graph attention networks (GATs) [37], which are the first use of the attention mechanism in the graph domain to learn the weights between two nodes, and graph SAGE [38], which generates node embeddings by sampling a fixed number of neighbors and aggregating their features.

2.3 Traffic prediction

In traffic prediction, researchers have been developing various models and methods to predict traffic flow, congestion, travel time, and other relevant factors to improve traffic management and planning efficiency. After years of research and development, researchers have made many achievements. Classical statistical models such as ARIMA [39] and SVM [40] usually consider only temporal information and require the data to satisfy certain assumptions. However, due to the complexity of the traffic flow data, these methods do not perform well in practical applications. The ConvLSTM [41] model combines CNNs and RNNs to capture spatial and temporal correlations. To better capture the spatial correlation of data, recent works have used graph convolution to learn the spatial correlation of data. DCRNN [17] proposes diffusion graph convolution to describe the information diffusion process in spatial networks and uses an RNN to model the temporal correlation. In [42], GCN and long short-term memory (LSTM) were combined to improve the prediction accuracy. ASTGCN [18] introduces the attention mechanism [43] before spatiotemporal convolution; it uses two attention layers to capture the dynamic spatiotemporal dependencies of neighboring nodes. Graph WaveNet [23] discovers hidden spatial dependencies through learnable node embeddings, which focus spatial dependencies on potential dynamic dependencies of information collocation. Its temporal convolutional layer captures the temporal trend of nodes through dilated causal convolution [44]. Although the transformer algorithm [45] uses a self-attention mechanism to model spatial-temporal correlations, it is prone to the problem of error accumulation. Several studies have focused on designing new graph structures. STFGCN [19] constructs a new spatial-temporal fusion graph through a data-driven approach that can provide correlations that may not be present in predefined spatial graphs and introduces a dilated convolution with a dilatation rate in temporal convolutional layers intending to capture long-range temporal dependencies. DSTAGNN [20] also uses the data-driven construction of a dynamic correlation matrix to generate a new graph structure and a temporal convolutional layer using a multi-scale GTU to capture temporal correlations.

The existing traffic prediction models usually use statistics-based methods to fill in missing data, but these methods need to be more accurate. Moreover, the existing missing data imputation networks cannot be directly applied to traffic datasets. Therefore, in this paper, we will improve the masking mechanism and training process of GAIN in the data preprocessing stage so that it can be applied to traffic datasets and fill in missing data more accurately. Second, the research mentioned above must be more comprehensive for modeling spatial and temporal correlations by considering only single-factor effects. Unlike classical methods that use only a single adjacent matrix, dynamically fusing graph convolution results of static and dynamic adjacency matrices can effectively enhance the model’s ability to fully utilize spatial features. In capturing temporal dependence, a time series prediction method that combines two different methods of working can focus on both short-term and long-term scales and grasp the nonlinear change pattern of time-series data in greater depth.

3 Methodology

In this section, we first present a mathematical formulation of the problem addressed in this paper. We then detail the three critical components of our proposed framework: the data imputation layer, the graph convolution layer, and the time series prediction layer. Collaboratively, these components aim to enhance the model’s performance and improve its prediction accuracy.

3.1 Problem definition

We represent the road network as a graph \(\varvec{G=(V, E, A)}\), where \(\varvec{V}\) denotes the set of sensors within the road network \(\varvec{\left| V \right| = N}\), corresponding to the observations of \(\varvec{N}\) sensors; \(\varvec{E}\) denotes the set of edges connected by sensors; and \(\varvec{A \in \mathbb {R^{N\times N} } }\) denotes the adjacency or similarity matrix representing between nodes. The observed graph signal \(\varvec{X^{(t)} \in \mathbb {R}^{N \times r} }\) represents an arbitrary time step of the traffic state, whose elements are the \(\varvec{r}\) features observed by each sensor, such as flow and speed. We aim to predict only the traffic volume. Given the history of the \(\varvec{S}\) time step data, a model \(\varvec{F}\) can be trained to predict the future \(\varvec{T}\) time step graph signals at a time step on the road network as follows:

$$\begin{aligned} \varvec{X^{(t+1): (t+T)}=F\left[ X^{\left( t-S,t \right) };G \right] } \end{aligned}$$
(1)

3.2 Model architecture

This paper proposes a spatial-temporal multifactor fusion graph neural network model that considers multiple factors when modeling spatial and temporal dependencies and dynamically self-learns parallel data for fusion to capture spatial and temporal dependencies more comprehensively and predict traffic flow more accurately. We illustrate the overall architecture of our proposed STMFGNN model in Fig. 2, which is composed of a data-completion layer, as shown in Fig. 3; stacked spatial-temporal multifactor fusion (STMF) blocks, as shown in Fig. 4; and a prediction layer. The outputs of each STMF block are concatenated and fed into the prediction layer via a residual connection. We provide specific details of the model in the following subsections.

3.2.1 Data imputation layer

Traffic flow data are usually collected by sensors. In practical applications, the data collected by sensors are often subject to damage or loss of content due to equipment changes. Many traffic flow prediction models rely on complete datasets and often require accurate imputation of missing data before statistical analysis. This paper uses the GAIN with an improved masking mechanism and training process to impute the missing data.

Fig. 2
figure 2

Framework of the STMFGNN. The architecture consists of three main components: a data imputation layer, several STMF blocks, and a prediction block

Full size image

Take the traffic data of \(\varvec{N}\) recording points in a day as an example, \(\varvec{\mathcal {X}=\left( \mathcal {x_{1}},\dots ,\mathcal {x}_N\right) \in \mathbb {R}^{d}}\), where \( \varvec{d}\) is the number of recording points in a day (if it is recorded every five minutes, then \( \varvec{d}\) = 288). For any data vector \( \varvec{\mathcal {x_{i}}}\) in \( \varvec{\mathcal {X}}\), there is a corresponding binary mask vector \(\varvec{m_{i}=\left\{ 0,1 \right\} ^d}\) corresponding to it, where if \(\varvec{m_{ij}=1}\), \(\varvec{x_{ij}}\) is observable; if \(\varvec{m_{ij}=0}\), then the data point \(\varvec{x_{ij}}\) is missing. Since the traffic dataset used in this paper is already missing to varying degrees, we mark the location of each naturally missing point in the dataset to form a predefined vector of naturally missing masks \(\varvec{M_{natural}}\). In addition, to train the model, we also need to introduce an artificial missing mask \(\varvec{M_{artificial}}\), \(\varvec{M=M_{natural}+M_{artificial}}\), and train the model through the imputation loss of artificial missing data and the reconstruction loss of the original observable data.

Fig. 3
figure 3

Diagram of the data imputation part of the framework. GAIN with an improved masking mechanism and training process was used. The network consists of a generator and a discriminator

Full size image
Fig. 4
figure 4

An STMF block. This figure shows the details of the STMF block. The STMF block includes a static-dynamic spatial fusion module and a long-short-term temporal fusion module. The spatial fusion module is composed of a static graph convolution module and a dynamic graph convolution module processed by a spatial-temporal attention block working in parallel, followed by a dynamic gated fusion module. The temporal fusion module consists of a multireceptive field GTU responsible for short-range scale feature capture, a GRU responsible for long-range scale feature capture, and a dynamic gated fusion module

Full size image

As shown in Fig. 3, generator G takes the incomplete data vector \(\varvec{x \in \mathbb {R}^d}\), mask vector \(\varvec{m \in \mathbb {R}^d}\), and noise variable vector \(\varvec{z \in \mathbb {R}^d}\) as inputs. The output interpolation vector \(\varvec{\widetilde{x}\in \mathbb {R}^d}\) and hint vector \(\varvec{h=\left\{ 0,0.5,1 \right\} ^d }\) are used as inputs to the discriminator D, which then tries to distinguish which components of the whole vector are observed or estimated, equivalent to predicting the mask vector. The hint vector \(\varvec{h}\) is introduced to provide D with additional information about the missing data, and by defining \(\varvec{h}\) in different ways, it is possible to control the amount of information about the mask vector \(\varvec{m}\) contained in the hint vector \(\varvec{h}\).

The output of generator G is the estimation vector \(\varvec{x_{G}}\), which is defined as follows:

$$\begin{aligned} \varvec{x_{G}=G\left( x,m,\left( 1-m \right) \odot z \right) } \end{aligned}$$
(2)

where \(\varvec{\odot }\) denotes the Hadamard product operation. Note that G generates not only the values of the missing components but also the values of the entire data vector, which includes the values that can be observed. Thus, the imputation vector \(\varvec{\widetilde{x}}\) and the reconstruction vector \(\varvec{\bar{x} }\) are defined as:

$$\begin{aligned} \varvec{\widetilde{x}=m \odot x + \left( 1-m \odot x_{G} \right) } \end{aligned}$$
(3)
$$\begin{aligned} \varvec{\bar{x}=m \odot x_{G} + \left( 1-m \odot x \right) } \end{aligned}$$
(4)

Given a random vector \(\varvec{r=\left\{ 0,1 \right\} ^d }\), the hint vector is generated as follows:

$$\begin{aligned} \varvec{h=m\odot r+0.5\left( 1-r \right) } \end{aligned}$$
(5)

Subsequently, the discriminator D takes the hint vector \(\varvec{h}\) and interpolation vector \(\varvec{\widetilde{x}}\) as inputs, and the output \(\varvec{m_{D}}\) is the prediction of the mask vector \(\varvec{m}\), which is denoted as:

$$\begin{aligned} \varvec{m_{D}=D\left( \widetilde{x},h \right) } \end{aligned}$$
(6)

The cross-entropy between the output of the discriminator \(\varvec{m_{D}}\) and the artificial missing matrix \(\varvec{m_{a}}\) in the generator is used as the loss function of the discriminator, and is calculated as follows:

$$\begin{aligned} \varvec{\mathcal {L}_{D}\left( m_{a},m_{D},r \right) =m_{a}\log {m_{D}}+\left( 1-m_{a}\right) \log {\left( 1-m_{D} \right) } } \end{aligned}$$
(7)

The generator uses the reconstruction loss of the original observable data and the imputation loss of artificial missing data. At the same time, for the iterative optimization of the discriminator, the cross-entropy between the discriminator’s output and the generator’s needs to be calculated. These three parts are added together as the generator’s loss function:

$$\begin{aligned} \varvec{\mathcal {L}_{G_{1}}\left( \bar{x},x \right) =\left\| \bar{x}-x \right\| ^{2} } \end{aligned}$$
(8)
$$\begin{aligned} \varvec{\mathcal {L}_{G_{2}}\left( \bar{x},x,m_{a} \right) =\left\| \bar{x}-x \right\| ^{2}\odot m_{a} } \end{aligned}$$
(9)
$$\begin{aligned} \varvec{\mathcal {L}_{G_{3}}\left( m_{a},m_{D},r \right) =- \left[ \left( 1-m_{a}\right) \log {m_{D}} +m_{a}\log {\left( 1-m_{D} \right) } \right] } \end{aligned}$$
(10)
$$\begin{aligned} \varvec{\mathcal {L}_{G}=\mathcal {L}_{G_{1}}+\alpha \left( \mathcal {L}_{G_{2}} + \mathcal {L}_{G_{3}}\right) } \end{aligned}$$
(11)

where \(\varvec{\alpha }\) is a hyperparameter. The training objectives of D and G are shown below:

$$\begin{aligned}&\nonumber \varvec{\min \frac{1}{N}\sum _{k=1}^{N}\mathcal {L}_{D}\left( m_{a},m_{D},r \right) } \\&\varvec{\min _{G} \frac{1}{N}\sum _{k=1}^{N}\mathcal {L}_{G_{1}}\left( \bar{x},x \right) +\alpha \left( \mathcal {L}_{G_{2}}\left( \bar{x},x,m_{a} \right) +\mathcal {L}_{G_{3}}\left( m_{a},m_{D},r \right) \right) } \end{aligned}$$
(12)

3.2.2 Spatial fusion block

Adjacency matrix generation

Given the graph structure, convolution operations are needed to extract node features, while the adjacency matrix is crucial because it determines how nodes aggregate information about themselves and their neighbors. To fully utilize the topology of the network as well as the information of the data itself, this paper uses ChebNet-based graph convolution combined with a spatial-temporal attention mechanism to learn the network structure and node information. Unlike previous studies that only used static predefined graphs or dynamic graphs in the graph convolution part, the graphs used in graph convolution in this paper are based on two aspects. On the one hand, the predefined static adjacent matrix \(\varvec{A_{SCG}}\) based on the actual sensor connectivity network is used. On the other hand, the dynamic similarity matrix \(\varvec{A_{DSG}}\) is generated by data-driven generation, a binarization of the dynamic correlation matrix \(\varvec{A_{DRG}}\) based on the Wasserstein distance. Through parallel graph convolution from the static localized graph and the dynamic similarity graph, the missing partial spatial dependencies caused by relying only on a single factor are avoided to mine the complex spatial dependencies between nodes more effectively and comprehensively.

There is a specific correlation between the traffic flows of different road nodes, which changes with time, so it is essential to effectively extract the dynamic correlation features between nodes. We regard the traffic data collected at each node as discrete data and split the historical data into a single vector at a specific time step, such as one day; then, the historical traffic data at each node are represented as a sequence of vectors. Then, we transform the data from these nodes into probability distributions and use the Wasserstein distance to calculate the probability distribution similarity between nodes to capture the spatial correlation between nodes. The Wasserstein distance is a method used to measure the difference between two probability distributions. Given two distributions \(\varvec{\varvec{p}}\) and \(\varvec{\varvec{q}}\), the minimum cost required to convert from distribution \(\varvec{\varvec{p}}\) to \(\varvec{\varvec{q}}\) distribution is evaluated. Taking the traffic data of \(\varvec{N}\) recording points on \(\varvec{D}\) days as an example, \(\varvec{X^f \in \mathbb {R}^{D\times d_{t}\times N } }\), where \(\varvec{d_{t}}\) is the number of recording points in a day (if it is recorded every five minutes, then \(\varvec{d_{t}}\) = 288). The sequence of vectors at the \(\varvec{n\left( n \in N \right) }\) node is denoted as \(\varvec{X_{n}^{f}=\left( w_{n_{1}},w_{n_{2}},\dots ,w_{n_{D}} \right) }\), \(\varvec{w_{n_{d}}\in \mathbb {R}^{d_{t}}}\), where \(\varvec{d\in \left[ 1, D \right] }\). Using the cosine distance as the cost function, the conversion cost of the traffic flow vector \(\varvec{w_{n_{1}i}}\) at point \(\varvec{n_{1}}\) on day \(\varvec{i}\) to the traffic flow \(\varvec{w_{n_{2}j}}\) at point \(\varvec{n_{2}}\) on day \(\varvec{j}\) is as follows:

$$\begin{aligned} \varvec{cost\left( w_{n_{1}i},w_{n_{2}j} \right) =1-\frac{w_{n_{1}i}^{\top }\cdot w_{n_{2}j}}{\left\| w_{n_{1}i} \right\| _{2}\times \left\| w_{n_{2}j} \right\| _{2} } } \end{aligned}$$
(13)

where \(\varvec{\top }\) represents the transpose of the matrix, so the dynamic correlation distance can be expressed as:

$$\begin{aligned}&\nonumber \varvec{d_{DRD}\left( n_{1},n_{2} \right) \triangleq DRD\left( X_{n_{1}},X_{n_{2}} \right) =} \\&\nonumber \varvec{_{\gamma \in \prod \left[ P_{n_{1}},P_{n_{2}} \right] }^{\textrm{inf}}\int _{x}\int _{y}\gamma \left( x,y \right) \left( 1-\frac{w_{n_{1}x}^{\top }\cdot w_{n_{2}y}}{\sqrt{w_{n_{1}x}^{\top }w_{n_{1}x}}\times \sqrt{w_{n_{2}y}^{\top }w_{n_{2}y}} } \right) \textrm{d}x \textrm{d}y } \\&\varvec{\mathrm {s.t.}\int \gamma \left( x,y \right) \textrm{d}y=\frac{\left\| w_{n_{1}x} \right\| _{2} }{ {\textstyle \sum _{x=1}^{D}} \left\| w_{n_{1}x} \right\| _{2}},\int \gamma \left( x,y \right) \textrm{d}x=\frac{\left\| w_{n_{2}y} \right\| _{2} }{ {\textstyle \sum _{y=1}^{D}} \left\| w_{n_{2}y} \right\| _{2}} } \end{aligned}$$
(14)

We obtain a matrix \(\varvec{A_{DRD}\in \mathbb {R}^{N\times N} }\) representing the degree of relevance between the recorded points, where \(\varvec{A_{DRD}\left[ i,j \right] \!=\!1\!-\!d_{DRD}\left( i,j \right) \!\in \! \left[ 0,1 \right] }\). Under the premise of maintaining a certain sparsity level \(\varvec{P_{sp}}\)(\(\varvec{P_{sp}}\) as a hyperparameter), for each node of the road network, the \(\varvec{N_{r}=N\times P_{sp}}\) elements with the largest value in row \(\varvec{i}\) are retained (the remaining elements are set to 0). As a result, the dynamic relevance graph \(\varvec{A_{DRG}\in \mathbb {R}^{N\times N}}\) is obtained. The dynamic similarity graph \(\varvec{A_{DSG}\in \mathbb {R}^{N\times N}}\) is obtained as a graph structure by binarizing the \(\varvec{A_{DRG}}\). That is, if the value of these elements is nonzero, these elements are set to 1. This means that the most similar \(\varvec{N_{r}}\) nodes of each given node will be aggregated in the graph convolution. A dynamic similarity matrix \(\varvec{A_{DSG}}\) is availabel for each time step according to the particular time step of the segmented historical data.

Short-term local traffic flow changes are sudden, fluctuating, and transitive. The matrix based on the real road network in the dataset is used as the static predefined adjacency matrix \(\varvec{A_{SCG}\in \mathbb {R}^{N\times N}}\). For the static adjacency matrix , in the actual road network, if two nodes are connected, the value is set to 1; otherwise, it is set to 0. This matrix is represented as follows:

$$\begin{aligned} \varvec{A_{SCG_{ij}}=\left\{ \begin{matrix} 1,if \ v_{i} \ adjecent \ v_{j} \\ 0, otherwise\end{matrix}\right. } \end{aligned}$$
(15)

Graph convolution layer

After obtaining the graph structure based on different factors, a convolution operation is needed to aggregate and update the node features. To fully utilize the topology of the network and the information of the data itself, this paper uses a parallel static-dynamic graph convolution based on ChebNet to learn the network structure and node information. The scaled Laplacian matrices used in the static and dynamic graph convolution parts are defined separately in the graph convolution. The scaled Laplacian matrices used in the static and dynamic graph convolution parts are defined separately in the graph convolution. The scaled Laplacian matrix for the static Chebyshev polynomial is defined as \(\varvec{\tilde{L^{s}}=\frac{2}{\lambda _{max}^{s}}\left( D^{s}-A_{s} \right) -I_{N}}\), where \(\varvec{A^{s}=A_{SCG}}\), \(\varvec{I_{N}}\) is the unit matrix, \(\varvec{D^{s}\in \mathbb {R}^{N\times N} }\) is the degree matrix, and the elements \(\varvec{D_{ii}^{s}= {\textstyle \sum _{j}}A_{ij}^{s}}\) and \(\varvec{\lambda _{max}^{s}}\) are the largest eigenvalues in the Laplace matrix \(\varvec{L_{s}=\left( D^{s}-A^{s} \right) }\). The scaled Laplace matrix of the dynamic Chebyshev polynomial is defined as \(\varvec{L_{d}=\frac{2}{\lambda _{max}^{d} } \left( D^{d}-A^{d} \right) -I_{N} }\), where \(\varvec{A_{d}=A_{DSG}}\), \(\varvec{I_{N}}\) is the unit matrix, \(\varvec{D^{d}\in \mathbb {R}^{N\times N} }\) is the degree matrix, and the elements \(\varvec{D_{ii}^{d}= {\textstyle \sum _{j}}A_{ij}^{d}}\) and \(\varvec{\lambda _{max}^{d}}\) are the the largest eigenvalues in the Laplace matrix \(\varvec{L_{d}=\left( D^{d}-A^{d} \right) }\).

Both the static and dynamic graph convolution parts use \(\varvec{K}\)th-order Chebyshev polynomials to aggregate the graph signals; that is, they perform graph convolution. The difference is that the static part directly processes the graph signals as follows:

$$\begin{aligned} \varvec{g_{\theta }*Gx=g_{\theta }\left( L \right) x= {\textstyle \sum _{k=0}^{K-1}\theta _{k}T_{k}\left( \tilde{L^{s}} \right) x}} \end{aligned}$$
(16)

In the dynamic part, to fully use the dynamics between nodes and the nodes themselves, the graph signal is processed by the widely used spatial-temporal attention module to obtain the attention matrix. The attention matrix adjusts each item of the Chebyshev polynomial and then multiplies it with the original graph signal, which is expressed as follows:

$$\begin{aligned} \varvec{g_{\theta }*Gx=g_{\theta }\left( L \right) x= {\textstyle \sum _{k=0}^{K-1}\theta _{k}\left( T_{k}\left( \tilde{L^{s}} \right) \odot P^{\left( k\right) } \right) x}} \end{aligned}$$
(17)

where \(\varvec{g_{\theta }}\) denotes the approximate convolution kernel, which extracts the information of the \(\varvec{0}\) to \(\varvec{K-1}\)-order surrounding neighbors centered at each node; \(\varvec{*G}\) represents the graph convolution operation; \(\varvec{\theta \in \mathbb {R}^{k} }\) is a learnable vector of polynomial coefficients; \(\varvec{\odot }\) represents the Hadamard product; and \(\varvec{P^{\left( k \right) }\in \mathbb {R}^{N\times N} }\) is the attention matrix. This definition can be extended to graph signals with multichannel inputs, such as inputs \(\varvec{\mathcal {X}^{r}=\left( X_{1},X_{2},\dots ,X_{M} \right) \in \mathbb {R}^{N\times C_{r-1}\times M} }\). Each input feature of each node has \(\varvec{C_{r-1}}\) feature channels, and the convolution kernel parameter is \(\varvec{g_{\theta }\in \mathbb {R}^{K\times C_{r-1}\times C_{r}} }\). Eventually, each node can aggregate \(\varvec{0\sim K-1}\) order neighbor node information to update its node information.

Therefore, the static graph convolution part aggregates information about local neighboring nodes by employing a predefined static adjacent matrix based on the actual sensor connectivity network. The dynamic graph convolution part aggregates information about the most globally similar nodes using a dynamic similarity matrix. The result of static graph convolution is \(\varvec{Z^{s}\in \mathbb {R}^{N\times M\times C_{r}} }\), and the dynamic graph convolution result is \(\varvec{Z^{d}\in \mathbb {R}^{N\times M\times C_{r}} }\). Static and dynamic two-part graph convolutions consider interactions between nodes from local and global perspectives. As a result, they should exert distinct influences on the final prediction. The specific influence should be learned from historical data. To realize this, we introduce a dynamic gating fusion module to rationally assign the respective importance weights and adaptively fuse the static and dynamic convolution results:

$$\begin{aligned} \varvec{Z^{r}=\delta \cdot Z_{s}^{\left( r \right) }+ \left( 1-\delta \right) \cdot Z_{d}^{\left( r \right) } } \end{aligned}$$
(18)

where \(\varvec{\delta \in \left[ 0,1 \right] }\) is the self-learning fusion parameter, which reflects the contribution degree of the static graph convolution and dynamic graph convolution parts to the result. \(\varvec{Z^{\left( r \right) }\in \mathbb {R}^{N\times M\times C_{r}} }\) is the final output of the graph convolution module, which is used as input to the temporal fusion layer of the next module. It is worth noting that as mentioned above, the dynamic graphs are calculated by dividing the data according to a specific time step. Each specific time step has a different dynamic graph, so the fusion parameters are also different at each time step according to this time step.

3.2.3 Temporal fusion layer

Traffic flow data are typical spatial-temporal data. After the extraction and processing of spatial dependencies between road network nodes via graph convolution, the temporal dependencies of data on each node must be further captured. Most traffic prediction models use convolution alone to extract temporal features, which results in the loss of dynamic long-term data features. With the development of deep learning methods, a large number of researchers have found that RNNs can learn time series features better than back propagation (BP) neural networks [46]. As a variant of RNN, GRU [47] is more capable of extracting dynamic long-term features in the time dimension, has fewer parameters and is easier to train than LSTM [48],compensating for the deficiency of convolutional methods. Therefore, to utilize multi-scale temporal features, this paper introduces GRU while using M-GTU, so as to capture the temporal dependencies more comprehensively with two time-series data prediction methods that work in different ways. M-GTU uses gated convolution with three different receptive fields to enhance the model’s ability to perceive different degrees of short-term temporal dependencies. GRU uses a gating mechanism to control the flow of information in the sequence, which can better handle the flow of information between each stage in a long-term sequence and provide more robust long-term time-dependent modeling capabilities. By fusing multiscale temporal features, the patterns of data changes can be better understood, further enhancing the model’s ability to perceive time dependence.

In the GTU section, we use a convolutional kernel \(\varvec{\Gamma \in \mathbb {R}^{1\times S\times C_{r}\times 2C_{r}} }\) to double the number of channels for the input \(\varvec{Z^{\left( r \right) }\in \mathbb {R}^{N\times M\times C_{r}} }\), where \(\varvec{1 \times S}\) represents the kernel size, and the input becomes \(\varvec{Z^{'\left( r \right) }\in \mathbb {R}^{N\times \left( M-\left( S-1 \right) \right) \times 2C_{r}} }\) after the convolution. The GTU of traditional convolution is defined as follows:

$$\begin{aligned} \varvec{\Gamma _{*_{\tau }}Z^{\left( r \right) }=\phi \left( E \right) \odot \sigma \left( F \right) \in \mathbb {R}^{N\times \left( M-\left( S-1 \right) \right) \times 2C_{r} }} \end{aligned}$$
(19)

where, \(\varvec{*_{\tau } }\) is the gated convolution operation, \(\varvec{\phi \left( \cdot \right) }\) and \(\varvec{\sigma \left( \cdot \right) }\) are the tanh function and sigmoid function, respectively, and \(\varvec{E}\) and \(\varvec{F}\) correspond to the pre-\(\varvec{r}\) and post-\(\varvec{r}\) parts of the channel of input \(\varvec{Z^{'}}\), respectively. To enhance the ability of the GTU part to perceive different degrees of time dimensions, gated convolutional modules with different receptive fields are used respectively, and then their outputs are fused and introduced into the residual structure as the output of the M-GTU part, which is defined as follows:

$$\begin{aligned}&\varvec{Z_{mout}^{\left( r \right) }=M-GTU\left( Z^{\left( r \right) } \right) = } \nonumber \\&\varvec{Relu\left( FC\left( Concat\left( \Gamma _{1*_{\tau }}Z^{\left( r \right) } ,\Gamma _{2*_{\tau }}Z^{\left( r \right) },\Gamma _{3*_{\tau }}Z^{\left( r \right) } \right) \right) +Z^{r}\right) } \end{aligned}$$
(20)

where \(\varvec{\Gamma _{1} }\), \(\varvec{\Gamma _{2} }\) and \(\varvec{\Gamma _{3} }\) ls of \(\varvec{1\times S_{1}}\), \(\varvec{1\times S_{2}}\), and \(\varvec{1\times S_{3}}\), respectively. \(\varvec{FC\left( \cdot \right) }\) denotes the fully connected operation to adjust the different sizes of the same feature dimension caused by the operation \(\varvec{Concat\left( \cdot \right) }\) to ensure that it matches the original input size of the M-GTU, and the residual structure is realized by skip connection. Finally, the M-GTU partial output \(\varvec{Z_{mout}^{\left( r \right) }\in \mathbb {R}^{N\times M\times C_{r}} }\) is obtained by the ReLU activation function.

The input of the GRU part is the same as that of the M-GTU part, but since the GRU-Cell is a single-step prediction, the input for each step is . The GRU part is defined as:

$$\begin{aligned} \varvec{z_{t}=\sigma \left( W_{z}\cdot \left[ h_{t-1},x_{t} \right] \right) } \end{aligned}$$
(21)
$$\begin{aligned} \varvec{r_{t}=\sigma \left( W_{r}\cdot \left[ h_{t-1},x_{t} \right] \right) } \end{aligned}$$
(22)
$$\begin{aligned} \varvec{\tilde{h_{t}} =tanh \left( W\cdot \left[ r_{t}*h_{t-1} ,x_{t} \right] \right) } \end{aligned}$$
(23)
$$\begin{aligned} \varvec{h_{t}=\left( 1-z_{t} \right) *h_{t-1}+z_{t}*\tilde{h_{t}} } \end{aligned}$$
(24)
$$\begin{aligned} \varvec{Z_{gout}^{\left( r \right) }=GRU\left( Z^{\left( r \right) } \right) =Stack\left( h_{t_{1}},h_{t_{2}}, \dots ,h_{t_{M}} \right) } \end{aligned}$$
(25)

The input of each moment \(\varvec{t}\) includes the hidden state of the previous moment \(\varvec{h_{t-1}}\) and the input of the current moment \(\varvec{x_{t}}\), and the output of the update gate \(\varvec{z_{t}}\) is used to control the updated degree of the current state. The output of the reset gate \(\varvec{r_{t}}\) is used to control the influence of the past state on the current state to filter unnecessary information; the candidate hidden state \(\varvec{\tilde{h _{t}}}\) is formed by the superposition of the current input and the past state. The hidden state at the current moment \(\varvec{h _{t}}\) is updated by the update gate, the weighted average of the past state, and the weighted average of the candidate’s hidden state. After accumulating predictions for M time steps, the output \(\varvec{Z_{gout}^{\left( r \right) } \in \mathbb {R}^{N \times M\times C_{r}} }\) is obtained as the result of the GRU part.

As a result, the M-GTU mainly captures short-term temporal dependencies, and the output is \(\varvec{Z_{Mout}^{\left( r \right) } \in \mathbb {R}^{N \times M\times C_{r}} }\). In contrast, the GRU part improves the capture of long-term temporal dependencies, and the output is \(\varvec{Z_{gout}^{\left( r \right) } \in \mathbb {R}^{N \times M\times C_{r}} }\) for this part. Similar to the graph convolution static-dynamic parallel module, both the M-GTU and GRU parts also use the dynamic gated fusion module to adaptively fuse the results of these two parts to self-learn the influence of short-term and long-term dependencies from historical data. It is expressed as follows:

$$\begin{aligned} \varvec{Z_{out}^{\left( r \right) }=\lambda \cdot Z_{mout}^{\left( r \right) }+\left( 1-\lambda \right) \cdot Z_{gout}^{\left( r \right) }} \end{aligned}$$
(26)

where \(\varvec{Z_{out}^{\left( r \right) }=\lambda \cdot Z_{mout}^{\left( r \right) }+\left( 1-\lambda \right) \cdot Z_{gout}^{\left( r \right) }}\) is the adaptive learning parameter that also changes dynamically with the specific time step mentioned in the previous section, reflecting the extent to which the short-term versus the long-term influence of the time series prediction component impacts final prediction result, and \(\varvec{Z_{out}^{\left( r \right) } \in \mathbb {R}^{N \times M\times C_{r}} }\) is the final output of the temporal fusion module.

4 Experimentation

In this section, we present experiments conducted on real datasets to verify the effectiveness of the STMFGNN. First, we introduce the datasets used for our experiments. Second, we introduce some baseline methods, conduct comparative experiments with overall and different prediction time targets, and conduct ablation experiments and statistical analysis to showcase the performance of our model compared to the baselines. Finally, we conduct parameter research experiments and time cost experiments, as well as some intermediate component and result visualization experiments.

4.1 Datasets

The experiments were conducted on four actual roadway datasets (PEMS03, PEMS04, PEMS07, and PEMS08) from California. These datasets were collected in real time by the PEMS system every 30 seconds, aggregating the raw data into 5-minute intervals. In addition, the datasets contain spatially adjacent matrices constructed based on actual road networks. Table 1 shows more details about the datasets.

Table 1 Statistics and description of the datasets
Full size table

4.2 Baseline method

We compare our STMFGNN with the following baselines:

  1. 1.

    DCRNN [17]: Diffusion Convolutional Recurrent Neural Network. It captures spatial correlation by modeling traffic flow changes as a one-dimensional convolutional diffusion process.

  2. 2.

    STGCN [22]: Spatio-Temporal Graph Convolutional Network. It integrates graph convolution into 1D convolutional units and incorporates causal convolution to process temporal information.

  3. 3.

    GraphWaveNet [23]: GraphWaveNet combines adaptive graph convolution and extended causal convolution.

  4. 4.

    ASTGCN [18]: Attention Based Spatial-Temporal Graph Convolutional Networks. It introduces an attention mechanism before spatio-temporal convolution.

  5. 5.

    STSGCN [19]: Spatial-Temporal Synchronous Graph Convolutional Networks: A New Framework for Spatial-Temporal Network Data Forecasting. It designs spatio-temporal subgraphs to capture heterogeneity in local spatio-temporal graphs.

  6. 6.

    AGCRN [49]: Adaptive Graph Convolutional Recurrent Network. It proposes an adaptive graph convolutional recurrent network to automatically unify information through node embedding to capture fine-grained spatio-temporal traffic sequence correlations.

  7. 7.

    STFGNN [50]: Spatial-Temporal Fusion Graph Neural Networks for Traffic Flow Forecasting. It proposes the a "temporal graph" and compensates for correlations that may not be reflected in the spatial graph through the spatio-temporal fusion graph.

  8. 8.

    Z-GCNETS [51]: Time Zigzags at Graph Convolutional Networks for Time Series Forecasting. It introduces the concept of time-aware zigzag persistence into learning temporal conditional graph structures and develops a zigzag topology layer (Z-GCNET) for time-aware graph convolutional networks (GCNs).

  9. 9.

    DSTAGNN [20]: Dynamic Spatial-Temporal Aware Graph Neural Network. It uses dynamic spatial-temporal aware graphs to model spatial-temporal interactions in road networks.

4.3 Experiment settings

For a fair comparison with the previous baselines, we divided the data from PEMS03, PEMS04, PEMS07, and PEMS08 into a training set, a validation set, and a test set at the ratio of 6:2:2. We use the historical traffic flow data for the past 1 hour (that is, 12 consecutive time steps) to predict the traffic flow data for the next 1 hour (that is, 12 consecutive time steps). The experiments were conducted in an AMD EPYC 7T83 CPU and an NVIDIA RTX 4090 24 GB GPU environment. We set the following hyperparameters: all experiments stacked 5 layers of STMF blocks. The number of Chebyshev polynomial terms \(\varvec{K}\) is 3. The number of heads of the spatial-temporal multihead attention mechanisms paired with the dynamic graph convolution is 3. The sparsity \(\varvec{P_{sp}}\) of the dynamic graph is 0.01. The convolution kernel of the M-GTU along the time dimension is {\(\varvec{S_{1}}\),\(\varvec{S_{2}}\),\(\varvec{S_{3}}\)}={2, 5, 8}. To train the model, we employed the Huber loss function, and the threshold parameter of the loss function was set to 1. We used the Adam optimizer with a learning rate of 0.0001 for 100 epochs. The settings for the batch size varied from dataset to dataset and were 32, 32, 12 and 64.

4.4 Evaluation indicators

The mean absolute error (MAE), the mean absolute percentage error (MAPE), and the root mean squared error (RMSE) are used to calculate the model’s performance in terms of error [52]. Lower values of MAE and RMSE indicate lower prediction errors of the model, while lower values of MAPE indicate lower relative errors of the model. In addition, some of the baseline method results ( marked with * in Tables 2 and 3 ) were obtained by running the corresponding open-source code. In contrast, the other part was extracted directly from published papers. The above mathematical formulas are as follows:

$$\begin{aligned} \varvec{RMSE\left( y,\hat{y}\right) =\sqrt{\frac{1}{n}\sum _{i=1}^{n}\left( y_{i}-\hat{y_{i}} \right) ^{2} } } \end{aligned}$$
(27)
$$\begin{aligned} \varvec{MAE\left( y,\hat{y}\right) =\frac{1}{n}\sum _{i=1}^{n}\left| y_{i}-\hat{y_{i}} \right| } \end{aligned}$$
(28)
$$\begin{aligned} \varvec{MAPE\left( y,\hat{y}\right) =\frac{100\%}{n}\sum _{i=1}^{n}\frac{\left| y_{i}-\hat{y_{i}} \right| }{y_{i}} } \end{aligned}$$
(29)

4.5 Experimental results and analysis

4.5.1 Overall comparison

Table 2 shows the average results of our STMFGNN and ten baseline methods for 60-minute predictions on the PEMS03, PEMS04, PEMS07, and PEMS08 datasets. The results show that our STMFGNN outperforms the baseline model in terms of all the metrics on all four datasets, achieving the best results.

Table 2 Performance comparison of our STMFGNN and baseline models
Full size table

The relatively poor performance of GraphWaveNet may be due to its inability to superimpose its spatial-temporal layers, resulting in a relatively minor feature receptive range. Moreover, methods such as the DCRNN, STGCN and ASTGCN highly rely on predefined graph structures which is helpful for short-term prediction. However, the dynamic relationship between nodes will be ignored over time, so the effect of long-term prediction is significantly reduced; thus, these methods perform poorly. STSGCN extracts only local spatial dependencies and requires more data to build subgraphs for training; thus, limited by the size of the dataset, it performs generally and may perform better on large-scale graphs. In contrast, the STFGCN and DSTAGNN, which use a dynamic graph structure to model spatial dependencies, significantly improve the prediction performance, indicating that such methods can capture the underlying spatial dependencies over time. However, they discard the predefined graph structure and use only the dynamic graph structure that changes in time units of days, resulting in ignoring the mutual transmission of traffic fluctuations between actual adjacent nodes at a single time point. Furthermore, predefined graphs might contain noise, and the generated dynamic graphs are also constrained by these limitations. Thus, they are not as effective as our STMFGNN. Second, most of the above models still fundamentally rely on variants of 1D convolution for modeling temporal dependence. For time series data, 1D convolution does not fully consider historical data, leading to inaccurate predictions of time series data and affecting overall predictive performance.

Our method comprehensively considers multiple factors, aiming to model spatial and temporal dependencies as thoroughly as possible. In spatial dependency modeling, we utilize both the static adjacency graph as local prior knowledge and the dynamic similarity graph generated based on Wasserstein distance as global hidden knowledge. This design enables our model to comprehensively capture complex spatial dependencies. For temporal dependency, we dynamically fuse short-term temporal features extracted by M-GTU and long-term temporal information captured by GRU, overcoming the trade-off between short-term and long-term temporal dependencies. Therefore, our model avoids the problem of missing spatial-temporal dependency modeling caused by excessive dependence on a single factor. As a result, our model performs better than the baseline methods, especially on the PEMS07 dataset, which has the largest graph size and the longest total time steps.

Table 3 Performance comparison of our STMFGNN and selected baseline models on the PEMS04 and PEMS08 datasets
Full size table
Fig. 5
figure 5

Comparison of the performances of several of the baseline models on the PEMS04 and PEMS08 datasets

Full size image

To demonstrate our model’s performance in both short-term and long-term forecasting tasks, we also selected some of the baseline models and compared their prediction performances with our proposed STMFGNN under the same conditions for different prediction steps. Specifically, Table 3 shows the performance comparison between the STMFGNN and selected baseline models for 15 minutes, 30 minutes, and 60 minutes on the PEMS04 and PEMS08 datasets. The results show that our STMFGNN outperforms the selected baseline models in terms of all the metrics, both for short-term and long-term predictions. This improvement may be attributed to the complex modules in our model, which are tailored to excel in situations where they are most needed for both short-term and long-term predictions. To more visually show the performance of some of the baseline models and our STMFGNN under different prediction steps, Fig. 5 plots the data from Table 3 as a line graph.

In general, as the prediction target time interval becomes longer, the corresponding prediction difficulty increases, leading to larger prediction errors. As shown in Table 3 and Fig. 5, models using predefined graph structures, such as DCRNN, STGCN, and ASTGCN, do not show significant differences in performance compared to improved models using dynamic graphs in short-term predictions. However, as the prediction interval increases, the prediction accuracy of these models decreases significantly. In contrast, DSTAGNN, which uses dynamic graph structures, shows a slower decline in performance. This is mainly because the previously mentioned models only consider the influence of neighboring nodes and fail to capture the time-varying dynamic spatio-temporal correlation. DSTAGNN leverages the generated dynamic graph structure to better model the dynamic spatio-temporal dependencies that are more crucial for long-term predictions. However, DSTAGNN considers only global dynamic spatio-temporal dependencies and overlooks the impact of local neighboring node traffic fluctuations on node traffic changes, resulting in less effective performance compared to our model. The results demonstrate that our STMFGNN outperforms the selected baseline models in all metrics, both in short-term and long-term predictions. This superior performance is due to our model simultaneously modeling both static local and dynamic global spatial dependencies and dynamically integrating GTU, responsible for capturing short-term temporal features, with GRU, responsible for long-term temporal dependency modeling.

4.5.2 Ablation experiments

To further evaluate the effectiveness of the individual components in the STMFGNN, we made the following variants of the STMFGNN:

  1. 1.

    RemDI: removes the data preprocessing layer and uses the original traffic flow data directly as input; that is, there is no complementary processing of missing data;

  2. 2.

    RemSSC: in the graph convolution part, the static graph convolution part that uses static graphs is removed, but the dynamic convolution module is retained;

  3. 3.

    RemGRU: in the time series prediction layer, the M-GTU module is retained, but the GRU module is removed.

Table 4 Ablation experiment of module effectiveness
Full size table

We selected the PEMS08 dataset, which has the smallest graph size, and the PEMS07 dataset, which has the largest graph size, as representative datasets to conduct ablation experiments and compared the results with DSTAGNN, which is the state-of-the-art model in the baseline. Table 4 shows the measurements of each performance metric, and it can be clearly observed that our STMFGNN outperforms the other variants and the baseline, confirming the effectiveness of each individual module in our model.

Table 4 shows the average results of the 60-min prediction performance for comparison, while Figs. 6 and 7 compare the prediction performance at different time settings for the 5-min, 20-min, 40-min, and 60-min settings. These different prediction durations represent short-term predictions (5 and 20 minutes) and long-term predictions (40 and 60 minutes), respectively.

Fig. 6
figure 6

Ablation experiment of the unimputated variant

Full size image
Fig. 7
figure 7

Ablation experiment of other variant

Full size image
Fig. 8
figure 8

Comparison of missing data imputed on the PEMS04 dataset. Figures (a) and (b) show the comparison between the original data and the missing point data after filling on node 10 and node 12 of the PEMS04 dataset, respectively

Full size image
Fig. 9
figure 9

Visualization results of the graphs used for the STMFGNN at nodes 0 to 19 on the PEMS08. Figure (a) shows the predefined static adjacent matrix of the nodes. Figure (b) shows the dynamic correlation matrix. Figure (c) shows the binarization of the dynamic correlation matrix with a specific sparsity setting

Full size image

The results of the ablation study are shown in Figs. 6 and 7, from which it can be seen that each component of the model contributes positively to the performance improvement of the whole model, and the conclusions obtained are as follows:

  • As shown in Fig. 6, for the model without data imputation preprocessing, the effect of the model using the other parts of the critical design also outperforms that of the baseline, indicating the effectiveness of other crucial design aspects. However, as shown in Fig. 7, the variant after data imputation preprocessing consistently outperforms the baseline in various performance metrics, highlighting the vital role of the data imputation module. For the PEMS07 dataset, which is characterized by large-scale and minimal missing data, the impact of data imputation on model performance is not significant since the available data are sufficient to support network training. However, as illustrated in Fig. 6a, for the smaller-scale PEMS08 dataset with existing missing data, the data imputation module significantly enhances model performance.

  • As shown in Fig. 7, removing the static spatial convolution part of the graph convolution layer has a significant impact on the short-range prediction performance. However, due to the combination of short-term and long-term time series prediction methods used in the temporal prediction layer, especially GRU, which is responsible for long-term time series prediction, the long-term prediction performance is better than that of the RemGRU, which illustrates the effectiveness of the GRU component for long-term temporal dependency capture. On the large-scale graph-structured PEMS07 dataset, this effect is even more pronounced. As shown in Fig. 7b, starting from the 20-minute prediction target, the GRU component has already demonstrated a significant enhancement in predictive performance.

  • As shown in Fig. 7, removing the GRU component of the time series prediction layer has a significant impact on the long-term prediction performance. However, due to the effect of the static local spatial convolution module in the graph convolutional layers, the short-term predictive performance is better than that of the non-static spatial convolution variant. Especially for the 5-minute prediction target, the static local spatial convolution has an obvious effect, indicating that it has a good ability to capture traffic fluctuations. This confirms the effectiveness of the static spatial convolution for extracting local static spatial relational dependencies and verifies its effectiveness in improving the performance of short-term traffic prediction.

  • Overall, the results from Table 4 and Figs. 6 and 7 collectively demonstrate that our STMFGNN model outperforms its various variants and baseline models. This confirms the effectiveness of the synergy of the various components in our model.

4.5.3 Visualization of data imputation

The improvement effect of missing data point imputation on the overall model prediction performance has been explained in detail in the previous section on ablation experiments. Since the PEMS04 dataset has a high missing data rate among the four datasets, the nodes with missing data points in this dataset are used as examples to visually compare the effect of imputing to demonstrate the superiority of our method more comprehensively. Each node in the PEMS04 dataset contains 16,992 data points, and Fig. 8 shows the imputation comparison results for node 10, which contains 2,464 missing data points, and node 12, which contains 677 missing data points.

As shown in Fig. 8, our imputation method can accurately learn the distribution trend of the data and reasonably fill in missing data points, whether for continuous or discrete missing points. Specifically, for consecutive missing data points, our method accurately captures the overall trend of the data and performs smooth imputation. For scattered missing data points, our method effectively restores the variability of the data, ensuring that the imputed data aligns with the trend of the surrounding data points. Overall, the data after imputation show a more complete and consistent trend, which is a significant improvement compared to the original data.

4.5.4 Visualization of spatial dependency

To enhance the interpretability of the proposed model and demonstrate its effectiveness in capturing dynamic spatiotemporal dependencies, Fig. 9 shows the visualization results of the STMFGNN’s predefined static adjacent matrix and the dynamic correlation matrix on the first day of recording for 20 nodes from nodes 0 to 19 in the PEMS08 dataset. As seen from Fig. 9, in terms of days, the two nodes adjacent to each other are not necessarily the most correlated, although they are physically closest. In contrast, even when two nodes are not adjacent or are geographically distant, they may be highly relevant to each other due to their similar patterns of change. Our model is able to capture potential spatial correlations in a global scope beyond just the adjacent nodes, indicating that STMFGNN extracts complex information within the road network and can capture time-varying spatial dependencies. This capability allows the model not only to rely on predefined adjacency relationships but also to dynamically adjust the correlations between nodes based on actual observed data, thereby more accurately reflecting the spatio-temporal interactions between nodes in the real traffic network.

The visualized results of these dynamic correlation matrices clearly show how our method surpasses the limitations of traditional static graph structures, revealing deeper associations between nodes. This further demonstrates the effectiveness and superiority of STMFGNN in modeling dynamic spatio-temporal dependencies, providing strong support for understanding and interpreting the model. Additionally, this dynamic modeling capability makes our model more flexible and adaptable in practical applications, allowing it to more accurately tackle complex and variable traffic flow prediction tasks.

4.5.5 Parametric studies

To further investigate the effect of hyperparameter setup on model performance, we conducted a parameter study experiment on the PEMS08 dataset for the control variables that have a significant impact on model performance. This includes the stacked layers of the STMF block, the size of the convolutional kernel along the time dimension in the M-GTU, and the batch size. KS represents the kernel size along the time dimension in the M-GTU module. Tables 5, 6, and 7 show the results of the experiments.

Table 5 Parameter study of STMF block stacking layers
Full size table
Table 6 Parameter study of K-S
Full size table

We observed that the number of STMF blocks significantly affects the performance of our model. There is an optimal range for the number of STMF blocks that balances the benefits of deeper architectures with the risks of overfitting and gradient issues. Typically, a moderate depth outperforms very shallow or excessively deep models. Deeper models performing better than shallow ones because fewer layers lead to model underfitting, but too deep networks may lead to problems such as vanishing gradients, exploding gradients, or model overfitting. As shown in Table 5, the stacking of STMF blocks can significantly improve the model performance. The reason behind this phenomenon is that adding more STMF blocks enables the model to capture more complex spatial-temporal features, enhancing the model’s expressive capability. However, as the number of layers continues to increase, the model performance begins to decline. We attribute this to the issue of vanishing or exploding gradients caused by overly deep network structures, thereby impacting the model’s training effectiveness. Moreover, an excessive number of STMF blocks may introduce too much noise, leading to overfitting of the training data. The experimental results demonstrate that the model achieves optimal performance when stacked with 5 layers of STMF blocks, striking a balance between capturing intricate features and avoiding overfitting.

The kernel size significantly affects temporal feature extraction. In particular, a larger kernel size increases the receptive field, allowing the model to capture longer-term dependencies. However, if the kernel size is too large, it may include irrelevant information and noise, which can degrade performance. Conversely, a smaller kernel size focuses on short-term dependencies and may miss out on important long-term patterns. Table 6 illustrates the impact of different convolution kernel sizes on model performance. It is observed that utilizing a combination of 2, 5, 8 receptive fields significantly enhances the model’s predictive performance. This suggests that when simultaneously utilizing short-term and long-term temporal information, the model can better capture patterns and trends within time series data. Smaller convolution kernels (e.g., 2) are adept at capturing fine-grained short-term variations, while larger kernels (e.g., 8) excel at capturing long-term trends. The combination of varying kernel sizes allows the model to exhibit greater flexibility in processing temporal information, thereby improving prediction accuracy.

Table 7 Parameter study of data batch size
Full size table

Batch size significantly affects the stability and convergence of model training. As shown in Table 7, a batch size of 64 yielded the best performance for the model on the PEMS08 dataset. Smaller batch sizes, such as 32, update the model parameters more frequently, which can introduce high noise levels during the update process, causing the model to get stuck in local minima. Additionally, models trained with small batches may experience unstable convergence due to frequent parameter updates. On the other hand, excessively large batch sizes can lead to each update containing too much information, which may cause the model to overfit the training data and perform poorly on the test set. A batch size of 64 strikes a balance between update frequency and stability, allowing the model to avoid local minima and preventing overfitting. This balanced batch size ensures that the model benefits from stable convergence while maintaining the ability to generalize well to unseen data.

Table 8 \(T_{F}\) values corresponding to each metric
Full size table
Fig. 10
figure 10

Friedman test charts. For each algorithm, the blue dot marks its average rank. The horizontal lines with the dot as the center indicate the critical distance. No overlapping areas of the lines indicate a significant difference

Full size image

These experimental results demonstrate the performance of our model under different hyperparameter settings and help to understand how to optimize model parameters for best performance. By reasonably adjusting the stacked layers of the STMF block, convolution kernel size and data batch size, we can further improve the prediction accuracy and stability of the model.

4.5.6 Statistical analysis

To verify the performance differences between our model and the baseline models listed in Table 2, we conducted the Friedman test and Nemenyi post-hoc test.

The Friedman test assumes that all k compared methods exhibit the same performance across N datasets. The first step is calculating \(T_{x^2}\) and \(T_{F}\) according,

$$\begin{aligned} T_{F}=\frac{\left( N-1 \right) T_{x^{2}}}{N\left( k-1 \right) -T_{x^{2}}} \end{aligned}$$
(30)

where \(T_{x^2}=\frac{12N}{k\left( k+1 \right) }(\sum _{i=1}^{k}r_{i}^{2}-\frac{k(k+1)}{4})\) and \(r_{i}\) represents the average rank value of the i-th model. In addition, \(T_{F}\) obeys the F-distribution with degrees of freedom \(k-1\) and \((k-1)(N-1)\).

The second step tests whether the assumption is true by comparing \(T_{F}\) and its corresponding threshold. If the assumption is denied, there are significant differences in the performance of the models being compared. Then, a post hoc test is required to further distinguish the algorithms. The Nemenyi test is a common post-hoc test.

The Nemenyi calculates the critical distance by Formula 31 to reflect the differences between the average rank values of each method:

$$\begin{aligned} CD=q_{\alpha }\sqrt{\frac{k+1}{6N} } \end{aligned}$$
(31)

where \(q_{\alpha }\) represents the critical value of the Tukey distribution and CD is the critical value for the Nemenyi test. If the difference between the average rank values of two methods exceeds the critical value range, it indicates significant performance differences between the two methods; otherwise, no significant differences are observed.

Table 9 STMFGNN run speed comparison
Full size table
Fig. 11
figure 11

Visualization of the prediction results at node 0 for 15 mins

Full size image

In our experiment, \(N=4\) and \(k=0\). When \(\alpha =0.05\), according to (30), Table 8 displays the corresponding values for the MAE, RMSE, and MAPE, all of which surpass the threshold of 2.2501. In other words, the assumption that all algorithms have the same performance is denied; therefore, we need to use the Nemenyi test to continue verification. With \(CD=6.3113\), as calculated by (31), we generated the Friedman test graph, as shown in Fig. 10.

Overall, we can conclude that, overall, our proposed STMFGNN exhibits significant differences in MAE, RMSE, and MAPE compared to those of the STFGNN, AGCRN, STSGCN, ASTGCN, STGCN, DCRNN, and Graph WaveNet, with no substantial differences observed compared to those of the top-performing methods, DSTAGNN and Z-GCNETS, in recent years. As shown in Fig. 10, our method achieves the best average ranking in comparison with the other methods regardless of which metric is used. In summary, our proposed method is statistically superior.

4.5.7 Time cost study

The time cost of each module in our model is closely related to the size of the dataset. To show the time cost more intuitively, we test the time cost of the proposed model on four datasets under the experimental settings described in Section 4.3, and the results are shown in Table 9.

The data imputation module includes a generative adversarial imputation network, which includes a generator and a discriminator. The time complexity of the generator and discriminator can be expressed as O(1) or O(k), where k is the number of network parameters, and usually does not change significantly with the size of the dataset. The time complexity of training a generative adversarial imputation network is related to the dataset size and is usually expressed as O(TN), where T represents the total time step in the dataset and N represents the number of sensors. Specifically, Table 9 shows that the time cost of the data imputation module on different datasets, and the PEMS07 dataset has the highest time cost of 139 seconds, which correlates with its larger data size.

The time cost of the spatial fusion module mainly stems from the process of precomputing the dynamic graph and graph convolution process. For the precalculated dynamic graphs, the time complexity can be expressed as \(O(DN^{2})\). In this prediction task, sensors collect data every 5 minutes, and the dynamic correlations of nodes change according to the time of day, so the total time steps are divided according to the day as the segmentation step; thus, O(kNd). For graph convolution, the k-order Chebyshev polynomial is used for graph signal aggregation, and the computational time complexity is denoted by O(kNd), where k represents the order of the Chebyshev polynomial, N represents the number of nodes in the graph, and d represents the feature dimension of each node. Table 9 shows that the dynamic graph computation time cost is the highest on PEMS07 dataset, which is 5400 seconds, mainly due to its large number of nodes and long time step.

The time cost of the time series prediction part mainly comes from the GRU. For a sequence length of Q, the total time complexity can be expressed as O(Qd), where Q is the sequence length and d is the dimension of the input features or the dimension of the hidden states. In the traffic flow prediction task, the prediction target is usually the traffic condition for the next hour, which means that Q is 12. Table 9 shows that the time series prediction block has the highest time cost of 500 seconds on the PEMS07 dataset, which is related to the sequence length and feature dimension.

Overall, the time cost of model training increases with the assembly of individual modules and increases with increasing dataset size. However, as seen in the previous ablation experiments, each part is critical to the accuracy of the model’s final prediction of the target. The collaborative work of these modules enables STMFGNN to perform excellently in traffic flow prediction tasks, maintaining high accuracy even with large datasets and missing data.

Fig. 12
figure 12

Visualization of the prediction results at node 0 for 30 mins

Full size image
Fig. 13
figure 13

Visualization of the prediction results at node 0 for 60 mins

Full size image
Fig. 14
figure 14

Visualization of the prediction results at node 1 for 60 mins

Full size image

4.5.8 Visualization of forecast results

We compared the one-week traffic flow predictions on the PEMS08 dataset with the actual values and zoomed in on the data for the first, fourth, and seventh days. Figures 11, 12, and 13 compare the model’s predictions with the actual values on PEMS08 at node 0 for 15 minutes, 30 minutes, and 60 minutes, respectively. In addition, to show that the model performs consistently across nodes, Fig. 14 compares the actual values and the predictions at node 1 for 60 minutes.

We observe that (1) The general trend of the STMFGNN is consistent with the actual values and it can track the change pattern of traffic flow well. This indicates the model’s excellent performance in capturing spatiotemporal dependencies, accurately reflecting real-world traffic flow changes. (2) In instances where the actual values are significantly lower, this discrepancy may be attributed to the presence of missing data points. Our model does not follow these extreme deviations but instead predicts values that conform to the overall distribution. This showcases STMFGNN’s robustness in handling missing data. Through an effective data imputation method, the model maintains high predictive accuracy even with incomplete data. (3) Peak values are further accentuated, illustrating STMFGNN’s ability to perform well under challenging conditions. In the face of sharp changes in traffic flow, the model can still accurately predict the peak flow, which proves its modeling ability under complex spatio-temporal dependencies.

In summary, STMFGNN accurately captures the trends in traffic flow across different nodes and time intervals, exhibiting outstanding performance. These experimental results highlight the model’s significant advantage in capturing spatio-temporal dependencies. Particularly in handling missing data, our imputation strategy enables the model to deliver high-quality predictions despite data incompleteness.

5 Conclusion

This paper proposes a new GNN framework, the STMFGNN, for traffic flow prediction. This model considers the influence of multiple factors when modeling spatial-temporal dependencies and fuses multiple factors by using a dynamic gated fusion mechanism to self-learn dynamic importance. When modeling spatial dependence, we dynamically fuse the static adjacency graph as local prior knowledge and the dynamic similarity graph as global hidden knowledge to model complex spatial dependence as completely as possible. Regarding temporal dependence, the short-term characteristics of different receptive field gated convolutions and the long-term information captured by the GRU are dynamically fused, which overcomes the trade-off problem between short-term and long-term temporal dependence. In addition, we imputed the traffic data presenting incomplete observability using a generative adversarial imputation network with an improved masking mechanism and training process. Experimental results on four real datasets (PEMS03, PEMS04, PEMS07, and PEMS08) show that the STMFGNN achieves state-of-the-art results.

However, the model proposed in this paper has several areas of potential improvement, such as insufficient consideration of the influence of external factors and underutilization of data periodicity. In the future, we will consider the influence of external factors (such as weather) on data fluctuations and model the periodicity of data to further optimize the integrity of traffic flow prediction model modeling and improve the accuracy of prediction. In addition, since STMFGNN is a general spatio-temporal prediction framework for graph-structured data, we can also apply it to other applications, such as traffic speed prediction.