STGHTN: Spatial-temporal gated hybrid transformer network for traffic flow forecasting

Abstract

Accurate traffic forecasting is a critical function of intelligent transportation systems, which remains challenging due to the complex spatial and temporal dependence of traffic data. GNN-based traffic forecasting models typically utilize predefined graphical structures based on prior knowledge and do not adapt well to dynamically changing traffic characteristics, which may limit their performance. The transformer is a compelling architecture with an innate global self-attention mechanism, but cannot capture low-level detail very well. In this paper, we propose a novel Spatial-Temporal Gated Hybrid Transformer Network (STGHTN), which leverages local features from temporal gated convolution, spatial gated graph convolution respectively and global features by transformer to further improve the traffic flow forecasting results. First, in the temporal dimension, we take full advantage of the local properties of temporal gated convolution and the global properties of transformer to effectively fuse short-term and long-term temporal dependence. Second, we mutually integrate two modules to complement each representation by utilizing spatial gated graph convolution to extract local spatial dependence and transformer to extract global spatial dependence. Furthermore, we propose a multi-graph model that constructs a road connection graph, a similarity graph, and an adaptive dynamic graph to exploit the static and dynamic associations between road networks. Experiments on four real datasets confirm the proposed method’s state-of-the-art performance. Our implementation of the STGHTN code via PyTorch is available at https://github.com/JianSoL/STGHTN.

1 Introduction

Traffic forecasting is a core issue in the field of transport planning and management research [1,2,3], aiming to predict traffic based on historical information. Traffic forecasting theories and methods were introduced in the 1930s and they have seen success through years of research and practice. Quick and accurate traffic flow forecasting is an open research field. The advent of big data and technology such as intelligent transportation systems and sensors enables easy access to spatial-temporal data to facilitate traffic volume forecasting, for sensing congestion, control traffic conditions and enable travelers to choose appropriate travel modes and adjust routes [4,5,6].

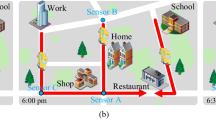
Traffic forecasting has always been a challenge, due to complex temporal and spatial dependence. As shown in Fig. 1, traffic data exhibit temporal, spatial, and spatial-temporal dependence. Temporal dependence refers to the influence of historical moments on future moments, as reflected in the variation of traffic flow over time. Spatial dependence refers to the topology of roads, which directly influence each other at the same time step. This is manifested in the way that traffic flows on upstream roads affect downstream roads, and vice versa. Spatial-temporal dependence refers to the influence between roads at different moments in time. As shown in Fig. 2, temporal dependence usually shows a slight cyclical variation, and spatial dependence between roads shows different correlations depending on the environment.

Fig. 1

Complex spatial and temporal dependence of traffic data

Fig. 2

Temporal and spatial pearson correlation analysis

Earlier traffic prediction methods were mainly based on statistical learning [7,8,9] and machine learning [10,11,12], modeled only on temporal dependence, and could not effectively capture the nonlinear dependence of spatial-temporal data. With the development of deep learning, methods such as DCRNN [13], T-GCN [14] and A3T-GCN [15] tend to capture temporal dependence through Recurrent Neural Networks (RNNs) [16] or variants, such as Long-Short Term Memory (LSTM) [17] and Gated Recurrent unit (GRU) [18]. These methods tend to capture only temporal dependence. GNN-based methods, such as STGCN [19], ASTGCN [20] and STFGNN [21] construct adjacency matrices based on prior knowledge, such as those based on road adjacency relationships and time-series similarity. Although the static spatial dependence between roads is fully considered, the spatial dependence should be dynamic, and road connectivity may change due to congestion. STGNN [22] adopts a learnable position attention mechanism to aggregate information about neighbouring roads, and utilises this aggregated information to generate a dynamic graph structure. This dynamic approach takes into account real-world events without considering the inherent spatial dependencies between roads.

The transformer [23] was first proposed in the NLP domain, and has achieved superior results in machine translation due to its strong ability to model the long-term features of sequences [24]. The transformer for the traffic prediction task is a pioneering work based on its key component, the multi-headed self-attention mechanism (MSA). It is noted that some local features and short-term dependence among input sequences cannot be effectively captured by transformer.

To address the above challenges and limitations, we propose a novel Spatial-Temporal Gated Hybrid Transformer Network (STGHTN) for traffic flow forecasting. In the temporal dimension, Temporal Gated Convolution (TGC) and transformer are hybridized to capture short-term and long-term temporal dependencies respectively. In the spatial dimension, Spatial Gate Graph Convolution (SGGC) and transformer are integrated to obtain local and global spatial dependence. SGGC constructs a multi-graph fusion model that fuses static and dynamic graph features to explore the spatial dependence of local spaces. We summarize our contributions as follows:

• We propose a novel transformer-based network model to effectively capture dynamic complex spatial-temporal features and then solve the prediction problem of spatial-temporal data.

• We design a Temporal Hybrid CNN-Transformer (THCT) to model short-term and long-term temporal dependence by integrating TGC and transformer.

• We propose a Spatial Hybrid GCN-Transformer (SHGT) consisting of SGGC and transformer on multi-graphs to extract local and global spatial dependence. Three different graphs such as road connection graph, similarity graph, and adaptive dynamic graph are constructed to fully exploit the static and dynamic associations between roads.

• We apply the proposed STGHTN to four real-world traffic datasets. STGHTN significantly surpasses SOTA algorithms on all four tasks.

2 Related work

2.1 Spatial-temporal forecasting

Traffic forecasting is an important part of intelligent transportation systems [25]. Early research treated traffic forecasting as a simple time-series problem without considering spatial features. Common traditional machine learning models include the Vector Autoregressive (VAR) model [26], Autoregressive Integrated Moving Average (ARIMA) [27], Support Vector Machine (SVM) [10], and Kalman filtering [9]. It is difficult to model nonlinear spatial-temporal data with these methods. With the development of deep learning, the RNN has been applied to sequence tasks. RNN cannot effectively solve long-term dependencies. And RNN requires iterative propagation, which may lead to cumulative errors.

LSTM and GRU were later proposed to alleviate this problem. LSTM and GRU cannot capture long-term temporal dependence adequately, and their performance may be limited due to an increased sequence length. The emergence of the transformer [23] solves this problem well, allowing better parallel training and capturing the dependence between long sequences. Correlations between multiple domains can be well captured by a self-attention mechanism. To improve the accuracy of the model, the researchers introduced spatial features into the model. Conv-LSTM [28] captures spatial features through a 1-dimensional Convolutional Neural Network (CNN). DMVST-Net [29] captures local features of regions in relation to their neighbors with a local CNN. These methods still capture spatial dependence mainly through CNNs. Although certain results have been achieved, CNNs are not applicable to the non-Euclidean space of roads. Previous network models have handled data with rules on Euclidean space. Graph convolution was created for non-Euclidean space, with great results for several types of tasks based on graph structures. Graph Neural Networks (GNNs) are seeing increased use for modeling spatial-temporal data. DCRNN [13], GCGRU [30] both use GNN to obtain spatial features, and are combined with RNN to obtain temporal features. GraphWaveNet [31] adaptively learns graph structure information without priority knowledge, and efficiently obtains spatial-temporal dependence at the same time.

2.2 Graph convolution networks

GNNs have been widely used in node classification, link prediction, and other graph-structured data tasks. Graph convolution methods include spectral and spatial convolution. Spectral convolution uses a graph Fourier transform for convolution. The original spectral-based approach [32] generalizes CNNs to non-Euclidean spaces. Although this method implements convolution on the graph, it is hard to implement because it is computationally complex and is not localized. ChebNet [33] reduces computational complexity by approximating the convolution kernel with K iterations of Chebyshev polynomials. Spatial convolution is the constant aggregation of information about a node’s neighbors. NN4G [34] is the first spatial-based graph convolution neural network. GraphSAGE [35] extracts information about nodes by sampling and aggregating their neighbors, enabling the application of graph convolution networks to large-scale graphs. GAT [36] introduces an attention mechanism to adjust the weight relationship between neighboring nodes.

2.3 Transformer

The attention model has been widely used in deep learning tasks such as natural language processing[37], speech recognition [38], and computer vision [39] , and has become the basic model for deep learning. The attention model was originally implemented on a model of encoders and decoders and was applied to machine translation [40]. The original transformer is a model of an encoder-decoder implemented using MSA, whose parallelized design improves the training speed. Researchers have introduced attention mechanisms to spatial-temporal data prediction, with respectable performance at many tasks. STGNN [22] uses transformer to capture global temporal dependence and local temporal dependence using GRU and spatial dependence using a GNN layer with a positional attention mechanism. The transformer-enhanced DetectorNet [41] has a multiview temporal attention module to extract temporal dependence at long and short distances, and a dynamic attention module to extract dynamic spatial dependence.

3 Preliminaries

3.1 Problem definition

In this paper, the goal of traffic forecasting is to predict traffic flow data for future periods based on historical traffic flow data. We define the topology of a real traffic road network as a weighted directed graph G = (V,E,A), where $V{}={} \{v_{1},v_{2},v_{3},...,v_{N}\}$ is the set of nodes representing roads, N is the number of road sensor nodes, E denotes the set of edges, and $A\in \mathbb {R}^{N \times N}$ denotes a weighted adjacency matrix, representing the relationship between roads. We express the traffic flow data at time t on the road v_n as ${X^{n}_{t}}$. The purpose of traffic prediction is to learn a mapping function $\mathcal {F}(\cdot )$ that predicts the traffic data $\mathcal {X} = \{X_{1},{\dots } ,X_{T}\} \in \mathbb {R}^{T\times N}$ at the next P time steps based on the traffic data $\mathcal {\hat {X}} = \{X_{T+1},\dots ,Y_{T+P}\} \in \mathbb {R}^{P\times N}$ at the first T time steps. This is defined as follows:

$$ [X_{T+1},\dots,X_{T+P}] =\mathcal{F}([X_{1},{\dots} ,X_{T};G]) $$

(1)

4 Methodology

4.1 Overview

Figure 3 shows the STGHTN framework, which includes an input layer, four stacked Spatial-Temporal Layers (STLs), and a Spatial-Temporal Fusion Layer. The input layer converts the spatial-temporal features to a high-dimensional space by convolution to represent complex spatial-temporal dependence. An STL includes a THCT and a SHGT. THCT extracts short-term and long-term temporal dependence. SHGT is used to extract dynamic spatial dependence on local and global scales. STFL aggregates spatial-temporal features of different granularities to explore spatial dependencies between different time steps and performs downstream prediction tasks using 1×1 convolution.

Fig. 3

STGHTN consists of four stacked spatial-temporal layers and a spatial-temporal fusion layer

4.2 Temporal hybrid CNN-transformer

Although RNN-based models are widely used in time-series analysis, RNN still suffers from time-consuming iterations, unstable gradients, and slow response to dynamic changes. THCT consists of a TGC, a Temporal Multi-Head Self-Attention (TMSA), and a temporal fusion block. TGC adopts a 1D dilated causal convolution [42] and gating mechanism [43] to extract short-term temporal dependence. TMSA adopts a self-attention [23] mechanism to extract long-term temporal dependence. The temporal fusion block is used to integrate short-term and long-term temporal dependence.

4.2.1 Temporal gated convolution

Ordinary CNN-based models cannot effectively model sequence-to-sequence problems. We use dilated causal convolution to capture the temporal trend between time steps of road nodes. As shown in Fig. 4, dilated causal convolution introduces dilation in the standard convolution operation and increases the perceptual field through a deeply stacked network. Given the input time-series $X = \{x_{1},x_{2},...,x_{T}\} \in \mathbb {R}^{T}$ and filters $\mathcal {F} = \{ f_{1},f_{2},..., f_{U}\} \in \mathbb {R}^{U}$, the dilated causal convolution at time step t is calculated as:

$$ X *\mathcal{F}(t) = \sum\limits_{u=1}^{U} \mathcal{F}(u)x_{t-d(u-1)} $$

(2)

where d is the dilation rate, which indicates the distance between convolution kernels.

Fig. 4

Example of dilated causal convolution

The gating mechanism is used in RNNs to control the flow of information. Short-term temporal features are extracted in parallel using the gated convolution on the time-axis, which is more efficient than LSTM for long-term time-series data. Given the input $X^{T} \in \mathbb {R}^{N\times T \times C}$, where C is the number of channels. It takes the form:

$$ TGC(X^{T}) = Sigmoid ({\Phi}_{1}*X^{T}+a )\odot Tanh({\Phi}_{2}*X^{T}+b ) $$

(3)

where Φ₁ and Φ₂ are independent 1D dilated causal convolution operations in the time dimension, a and b are model parameters, ⊙ is the element-wise product, Sigmoid and Tanh are the activation functions.

4.2.2 Temporal multi-head self-attention

We use MSA to model complex temporal dependence. Given the input temporal feature $X^{T} {}\in {}\mathbb {R}^{T\times N \times C}$ and the spatial feature $X^{S} {}\in {}\mathbb {R}^{T\times N \times C}$, we map spatial-temporal features to a high-dimensional space to learn complex temporal dependence. Subspaces ${Q^{T}_{i}} \in \mathbb {R}^{T\times d_{\mathcal {U}}}$, ${K^{T}_{i}}\in \mathbb {R}^{T\times d_{\mathcal {U}}}$, and ${V^{T}_{i}} \in \mathbb {R}^{T\times d_{\mathcal {V}}}$ are generated by linear transformation:

$$ {Q^{T}_{i}} = X^{S}W^{T}_{q_{i}}, {K^{T}_{i}} = X^{T}W^{T}_{k_{i}},{V^{T}_{i}} = X^{T}W^{T}_{v_{i}} $$

(4)

where $W^{T}_{q_{i}}$, $W^{T}_{k_{i}}$, and $W^{T}_{v_{i}}$ are the parameters of the learnable. MSA weights are calculated by the scaled dot product, whcih can be expressed as:

$$ \begin{array}{@{}rcl@{}} &&TMSA(X^{S}, X^{T}, X^{T})= Concat(hea{d^{T}_{1}},hea{d^{T}_{1}},\cdot\cdot\cdot,hea{d^{T}_{n}})W^{T}\\ &&{where}\quad hea{d^{T}_{i}}= Softmax\left (\frac{{Q^{T}_{i}}({K^{T}_{i}})^{T}}{\sqrt{d_{\mathcal{U}}} } \right ){V^{T}_{i}} \end{array} $$

(5)

where n is the number of heads of MSA, W^T is learnable parameters, and Softmax is an activation function.

4.2.3 Temporal fusion block

To consider both short-term and long-term dependence, we fuse the outputs $TMSA(X^{T}) \in \mathbb {R}^{N \times T \times C}$ of TMSA and $TGC(X^{T}) \in \mathbb {R}^{N \times T \times C}$ of TGC, with the following form:

$$ T_{out} = TMSA(X^{S}, X^{T}, X^{T}) \odot Sigmoid(TGC(X^{T}){W^{T}_{1}}) $$

(6)

where ${W^{T}_{1}}$ consists of learnable parameters, and $T_{out} \in \mathbb {R}^{T \times N \times C}$ is a post-fusion temporal feature. We increase the expressiveness of the model using residual connections and linear transformations, and further adjust the dependence between time steps, The specific form is as follows:

$$ \begin{array}{@{}rcl@{}} &&\vec{T}_{out} = LN(T_{out}+X^{T})\\ &&T{tra} = LN(Relu(\vec{T}_{out}{W^{T}_{2}}){W^{T}_{3}}+\vec{T}_{out}) \end{array} $$

(7)

where ${W^{T}_{2}}$ and ${W^{T}_{3}}$ are learnable parameters, LN is layer normalization, and Relu is the activation functions.

4.3 Spatial hybrid GCN-transformer

Most of the existing GNN-based methods for capturing spatial dependence suffer from a lack of extraction of global spatial features. And the predefined graph structure information cannot be adapted to dynamic spatial-temporal data. The SHGT consists of an SGGC, a Spatial Multi-Head Self-Attention (SMHA), and a spatial fusion block. SGGC uses multi-graph graph convolution operations to extract local spatial information. SMHA leverages a self-attention mechanism to excavate connections between distant roads to adjust for global spatial dependence. The spatial fusion block is designed to integrate the dependencies between connected roads and between roads that are far apart.

4.3.1 Multi-graph construction

Graph convolution is an aggregation of information on a graph, whose structure can greatly affect the performance of the model. We usually think that interconnected roads in road networks can have similar properties. However, in the real world, two shopping areas that are far apart may also have similar properties. At the same time, there are hidden potential dependence. This cannot be done by the predefined graph structure, and due to the change of external environment, the predefined graph structure often cannot fully reflect the real road relationship. Therefore, we propose a multi-graph fusion scheme that combines a road connection graph, a similarity graph, and an adaptive dynamic graph, considering both static and dynamic links between roads. The multi-graph formalism is $G {}={}\{G_{1},G_{2},G_{3}\}$, taking the following form:

• Road connection graph G₁ = (V,E^s,A^s) is constructed based on road connection relationships. Its spatial adjacency matrix $A^{s} \in \mathbb {R}^{N\times N}$ is deduced from G. It takes the form:

  $$ A^{s}_{ij}= \begin{cases} 1,&((v_{i},v_{j}) \in V) \And (v_{i},v_{j} \in E^{s}) \\ 0,&otherwise \end{cases}\\ $$

  (8)

• Similarity graph G₂ = (V,E^t,A^t) is constructed based on the Dynamic Time Warping (DTW) algorithm [44], which is widely used in speech recognition. We use Algorithm 1 to calculate the similarity DTW(v_i,v_j) between two roads based on their traffic flow sequences. DTW is more able than Euclidean distance to reflect the similarity of traffic sequences. For example, the change of traffic flow on an upstream road often has a certain lag compared to that on the corresponding downstream road. Euclidean distance cannot effectively measure the similarity between two time-series that have similar shapes but are not synchronized in time. DTW can effectively solve this problem. The temporal similarity matrix $A^{t} \in \mathbb {R}^{N \times N}$ is generated using the following form:

  $$ A^{t}_{ij} = \begin{cases} 1,&exp(-DTW(v_{i},v_{j})) >\rho \\ 0,&otherwise \end{cases}\\ $$

  (9)

  where ρ is a threshold.

• The adaptive dynamic graph G₃ = (V,E^adp,A^adp) is generated based on A^s and A^t. We use learnable parameters $\mathcal {E}^{s}$ and $\mathcal {E}^{t}$, which are respectively the source and target node, to capture the potential and dynamic dependence between two roads. $\mathcal {E}^{s}$ and $\mathcal {E}^{t}$ generate dynamic spatial dependence by matrix multiplication. The adaptive adjacency matrix is as follow:

  $$ A^{adp} = Softmax(ReLU(\mathcal{E}_{s} \mathcal{E}_{t}^{T}))\odot (A^{s}+A^{t}) $$

  (10)

  where ReLU and Softmax are activation functions, used respectively to reduce and normalize the effect of slight perturbations.

Algorithm 1

Temporal similarity calculation.

4.3.2 Spatial gated graph convolution

GCN can efficiently exploit the feature information of nodes. We use this to capture the dependence of the spatial relationships between roads [45], where the representation of nodes is calculated by aggregating information from direct neighbors. Given the input $x \in \mathbb {R}^{N \times C}$, a single-layer GCN expressed as:

$$ \begin{array}{@{}rcl@{}} &&GCN(A,x) = ReLU(D^{-1/2} \hat {A}D^{1/2}xW_{1})\\ &&\hat {A} = A+I_{N}\\ &&D_{ii} = \underset{j}{\sum}\hat{A}_{ij} \end{array} $$

(11)

where D is the degree matrix of $\hat {A}$, and W₁ is a learnable parameter.

As shown in Fig. 5, to increase the expressiveness of GCN representation, we add skip connections and linear transformations to the network. Given input features X^S, we can obtain the static graph convolution to generate static spatial features STA(X^S), and dynamic graph convolution generate dynamic spatial features DY N(X^S). The specific form is as follows:

$$ \begin{array}{@{}rcl@{}} STA(X^{S}) &=& Concat(GCN(A^{s},X^{S}),GCN(A^{t},X^{S}),X^{S})W_{sta}\\ DYN(X^{S}) &=& Concat(GCN(A^{adp},X^{S}),X^{S})W_{dyn} \end{array} $$

(12)

where W_sta and W_dyn are learnable parameters to mitigate GCN over-smoothing. We simultaneously consider static and dynamic graph convolution through a gated fusion mechanism, which obtains a tensor that lies between 0 and 1 by means of a sigmoid activation function. The specific form is as follows:

$$ \begin{array}{@{}rcl@{}} &&z = Sigmoid(STA(X^{S})W_{g1}+DYN(X^{S})W_{g2}+b)\\ &&GFS(X^{S}) = z\odot STA(X^{S})+(1-z)\odot DYN(X^{S}) \end{array} $$

(13)

where W_g1, W_g2, and b are learnable parameters, $GFS(X^{S}) \in \mathbb {R}^{N \times T \times C}$ is a post-fusion feature, and $z \in \mathbb {R}^{N \times T \times C}$ is the gating value.

Fig. 5

Module of spatial gated graph convolution

4.3.3 Spatial multi-head self-attention

In the spatial dimension, we use MSA to capture spatial dependence on a global scale. Given the spatial feature $X^{S} \in \mathbb {R}^{N\times T \times C}$ and the temporal feature $X^{T} \in \mathbb {R}^{N \times T \times C}$, subspaces ${Q^{T}_{i}} \in \mathbb {R}^{N\times d_{\mathcal {K}}}$, ${K^{T}_{i}}\in \mathbb {R}^{N\times d_{\mathcal {K}}}$, and ${V^{T}_{i}} \in \mathbb {R}^{N\times d_{{\mathscr{M}}}}$ are generated by linear transformation. They take the form:

$$ {Q^{S}_{i}} = X^{T}W^{S}_{q_{i}}, {K^{S}_{i}} = X^{S}W^{S}_{k_{i}},{V^{S}_{i}} = X^{S}W^{S}_{v_{i}} $$

(14)

where $W^{S}_{q_{i}}$, $W^{S}_{k_{i}}$, and $W^{S}_{v_{i}}$ are learnable parameters. MSA weights are calculated by the scaled dot product, whcih can be expressed as:

$$ \begin{array}{@{}rcl@{}} &&SMSA(X^{T},X^{S},X^{S})= Concat(hea{d^{S}_{1}},hea{d^{S}_{1}},\cdot\cdot\cdot,hea{d^{S}_{n}})W^{S}\\ &&{where}\quad hea{d^{S}_{i}}= Softmax\left (\frac{{Q^{S}_{i}}({K^{S}_{i}})^{T}}{\sqrt{d_{\mathcal{K}}} } \right ){V^{S}_{i}} \end{array} $$

(15)

where W^S is a learnable parameter.

4.3.4 Spatial fusion block

Since GCN aggregates information about neighbors around a node, it is local in nature, while MSA captures global features and can effectively capture spatial dependence between two roads that are far from each other. We adopt a similar approach to THCT to fuse local and global spatial dependence. Specifically, it takes the form:

$$ S_{out} = SMSA(X^{T},X^{S},X^{S}) \odot Sigmoid(GFS(X^{S}){W^{S}_{1}}) $$

(16)

where ${W^{S}_{1}}$ consists of learnable parameters, and $S_{out} \in \mathbb {R}^{N \times T \times C}$ is the spatial feature after fusion. Further, we adjust the spatial dependence between roads using residual connections and linear transformations. The following form is used:

$$ \begin{array}{@{}rcl@{}} &&\vec{S}_{out} = LN(S_{out}+X^{S})\\ &&S{tra} = LN(Relu(\vec{S}_{out}{W^{S}_{2}}){W^{S}_{3}}+\vec{S}_{out}) \end{array} $$

(17)

where ${W^{S}_{2}}$ and ${W^{S}_{3}}$ are learnable parameters.

4.4 Spatial-temporal fusion layer

After extracting high-level features from the STLs, we aggregate the temporal feature $T_{tra}^{(k)} \in \mathbb {R}^{N \times T \times C}$ and spatial features $S_{tra}^{(k)} \in \mathbb {R}^{N \times T \times C}$ from each STL. To preserve the original features of the data as much as possible, we sum up the features extracted from each layer. The dependence between sequences is further adjusted using linear transformations and residual concatenation to increase the expressiveness of the model. The temporal and spatial features are summed to obtain the fused spatial-temporal feature $FUS(T_{tra}^{(k)}, S_{tra}^{(k)}) \in \mathbb {R}^{N \times T \times C}$. The specific format is as follows:

$$ \begin{array}{@{}rcl@{}} &&X^{T}_{out} = LN({W^{T}_{a}}({W^{T}_{b}}\sum\limits_{k = 0}^{K} T_{tra}^{(k)})+\sum\limits_{k= 0}^{K} T_{tra}^{(k)})\\ &&X^{S}_{out} = LN({W^{S}_{a}}({W^{S}_{b}}\sum\limits_{k = 0}^{K} S_{tra}^{(k)})+\sum\limits_{k = 0}^{K} S_{tra}^{(k)})\\ &&FUS(T_{tra}^{(k)}, S_{tra}^{(k)}) = X^{T}_{out}+X^{S}_{out} \end{array} $$

(18)

where ${W^{T}_{a}}$, ${W^{T}_{b}}$, ${W^{S}_{a}}$, and ${W^{S}_{b}}$ are learnable parameters, and K is the number of layers in the STLs.

Further, we use a two-layer 1 × 1 convolution operations to complete the multi-step prediction, which is more efficient than single-step prediction. The specific format is as follows:

$$ {\mathop{Y}\limits^{\rightarrow}} = {\Theta}_{2} \star ({\Theta}_{1}\star FUS(T_{tra}^{(k)}, S_{tra}^{(k)})) $$

(19)

where Θ₁ and Θ₂ are independent 1 × 1 convolution operations, and $Y \in \mathbb {R}^{N \times T}$ is the multi-step predicted value.

Since the traffic data collection process is error-prone, we use a Huber loss function, which is robust and insensitive to outliers. It is expressed as:

$$ \mathcal{L}(Y, \mathop{Y}\limits^{\rightarrow}) = \begin{cases} &\frac{1}{2}(Y-\mathop{Y}\limits^{\rightarrow})^{2},\lvert Y- \mathop{Y}\limits^{\rightarrow}\rvert \leq \varpi \\ &\varpi \rvert Y - \mathop{Y}\limits^{\rightarrow}\rvert-\frac{1}{2} \varpi^{2},\lvert Y - \mathop{Y}\limits^{\rightarrow}\rvert>\varpi \end{cases} $$

(20)

where Y is real traffic flow, and $\mathop {Y}\limits ^{\rightarrow }$ is predicted traffic flow, and ϖ is a threshold. We summarize the training process of STGHTN in Algorithm 2.

Algorithm 2

Training process of STGHTN.

5 Experiment

5.1 Datasets

We used four large-scale datasets from STSGCN [46]: PEMS03, PEMS04, PEMS07, and PEMS08, which come from four regions of California. Table 1 shows the details of the four datasets. Sensor data was aggregated at 5-minute intervals. We used the first 12 time steps to predict the next 12 time steps. The input data was normalized using the Z-Score as follows:

$$ \hat{X}=\frac{X-{mean}(X_{train})}{{std}(X_{train})} $$

(21)

where mean(X_train) and std(X_train) are the mean and standard deviation, respectively, of the training data.

Table 1 Details of four datasets

5.2 Baseline methods

We compare the STGHTN model with seven state-of-the-art baselines:

• SVR [11]: Linear support vector regression uses SVM to make regression predictions on traffic flow sequences, ignoring spatial dependence.

• LSTM [17]: Long short Term Mempry Network to model time series.

• DCRNN [13]: Diffusion Convolution Recurrent Neural Network, which models spatial dependence using bidirectional random walks and temporal dependence using encoders and decoders.

• STGCN [19]: Spatial-Temporal Graph Convolutional Networks, which use graph convolution and gated causal convolution and do not rely on LSTM or GRU.

• ASTGCN [20]: Attention Based Spatial Temporal Graph Convolutional Networks, where a spatial-temporal attention mechanism captures spatial relationships through graph convolution and temporal relationships through ordinary convolution.

• Graph WaveNet [31]: Graph WaveNet for Deep Spatial-Temporal Graph Modeling uses adaptive adjacency matrices and learns by node embedding. Temporal dependence captures using 1D dilated convolution.

• STSGCN [46]: Spatial-Temporal Synchronous Graph Convolutional Networks capture spatial-temporal relationships and use the same component for both time and space.

• STFGNN [21]: Spatial-Temporal Fusion Graph Neural Networks use a spatial-temporal fusion module that a new graph structure constructs based on a data-driven approach.

5.3 Experiment settings

The datasets were divided into training, testing, and validation sets at a 6:2:2 ratio. Experiments were conducted in a Windows environment. The processor was an Intel Xeon E5-2680 v4 CPU @2.40 GHz with 128 GB RAM. The GPU was a single NVIDIA RTX2080Ti. We used the grid search strategy to determine the optimal hyperparameters. We trained our model using an Adam optimizer. The batch size was 16 and the learning rate was 0.001. There were four spatial-temporal layers and four heads of MSA. The number of channels was 32. The evaluation metrics were Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), and Root Mean Squared Error (RMSE). The specific format is as follows:

$$ \begin{array}{@{}rcl@{}} &&MAE = \frac{1}{N \times T} \sum\limits_{t=1}^{T}\sum\limits_{n=1}^{N} \lvert {Y_{t}^{n}} - \overset{\rightarrow}{{{Y_{t}^{n}}}} \lvert \\ &&RMSE = \sqrt{\frac{1}{N \times T} \sum\limits_{t=1}^{T}\sum\limits_{n=1}^{N} \left ({{Y_{t}^{n}} - \overset{\rightarrow}{{{Y_{t}^{n}}}}} \right )^{2} }\\ &&MAPE = \frac{1}{N \times T} \sum\limits_{t=1}^{T}\sum\limits_{n=1}^{N} \frac{\lvert {Y_{t}^{n}} - \overset{\rightarrow}{{{Y_{t}^{n}}}} \lvert}{{Y_{t}^{n}}} \end{array} $$

(22)

5.4 Experimental results

Table 2 shows the prediction performance of the different models on the four datasets at 15 minutes, 30 minutes, 60 minutes and on average. STGHTN shows the best performance in both short-term and long-term forecasting.

Table 2 Performance comparison of different methods on PEMS03, PEMS04, PEMS07, and PEMS08 datasets

The traditional machine learning method SVR tends to have less-than-ideal prediction performance due to a lack of nonlinear representation capability. Deep learning methods have strong nonlinear representation abilities. Among these, LSTM had poor prediction performance because it only considers temporal correlations and ignores spatial correlations. DCRNN, STGCN, ASTGCN, Graph WaveNet, STSGCN, and STFGNN considered both temporal and spatial correlations to improve prediction performance. The more recent model STFGNN incorporates a spatial graph, temporal graph, and temporal connected graph in a baseline approach that showed greater performance. We propose a model that fuses A^s, A^t, and A^adp, considering both static and dynamic graph feature fusion. The best performance is demonstrated on all datasets.

In the average prediction result, the improvement ratios of the RMSE metrics compared with the baseline optimal model STFGNN on the four datasets are 6.30%, 3.16%, 5.66%, and 7.01%, respectively. The relatively large missing rate in the PEMS04 dataset had a certain impact on the performance of the model. Our proposed model generally has stronger prediction performance because it more comprehensively considers spatial-temporal correlations. Figure 6 shows the predicted results for the 12 time steps in more detail. The results show that the prediction performance of the model decreases as the range of predictions increases. The LSTM model modelling only temporal features has the fastest degradation in prediction performance. Our model shows the best performance overall and also the slowest decline in performance as the prediction horizon increases, as we consider both modelling long-term temporal dependence and short-term temporal dependence.

Fig. 6

The performance of the different models on the four datasets varies with the prediction time step

5.5 Ablation study

5.5.1 Evaluation on multi-graph fusion

To verify the effectiveness of the multi-graph, we designed four combinations of graphs for comparison experiments on PEMS04 and PEMS08, whose results are shown in Table 3. It can be found that the similarity graph method and the adaptive dynamic graph method perform better than the road connection graph method. In the absence of expert domain knowledge, we can achieve relatively effective predictions using only the adaptive adjacency matrix. When we consider the fusion of three adjacency matrices simultaneously, a combination of the predefined prior knowledge and potential information mined from traffic data, the optimal evaluation score is finally achieved. Figures 7 and 8 visualize the three graphs. It can be found that the adjacency matrix A^s constructed based on the road connection relationship is sparse compared to the graph A^t constructed by the DTW method. A^s is only a local spatial connection relationship, and A^t can dig out the spatial dependence relationship at a long distance. The adaptive adjacency matrix A^adp can dynamically adjust the correlations relationship between roads.

Table 3 Combinations of different graphs on PEMS04 and PEMS08

Fig. 7

Heatmap of three kinds of adjacency matrix for 50 nodes on PEMS04

Fig. 8

Heatmap of three kinds of adjacency matrix for 50 nodes on PEMS08

5.5.2 Ablation experiments

To verify the validity of each part of our model, we designed four variant models and conducted ablation experiments with our models on the PEMS04 and PEMS08 datasets. The variant models are as follows:

• Basic: This basic framework does not include TMSA, SMSA, TGC and SGGC.

• +Self-Attention: This model adds TMSA and SMSA to the basic model.

• +TGC: TGC is added to the +Self-Attention model.

• +SGGC: SGGC is added to the +Self-Attention model.

• +T-SGC: This model adds both TGC and SGGC to the +Self-Attention model.

As shown in Fig. 9, the performance after introducing the attention mechanism is clearly due to the basic model, because we use the self-attention mechanism to extract the remote temporal dependence in the temporal dimension and the direct spatial dependence of different roads in the spatial dimension, respectively. TMSA can capture long-term temporal dependence. We add TGC to further capture short-term temporal dependence. SMSA mines dependence from the data to introduce real-world semantic connections. We further use SGGC to model the direct spatial dependence of different roads. It can be found that +T-SGC has a respectable improvement compared to +Self-Attention, while confirming the effectiveness of our model design.

Fig. 9

Ablation study on PEMS04 and PEMS08 datasets

5.6 Effect of hyperparameters

Figures 10 and 11 show the prediction results of our model on PEMS04 and PEMS08 with different hyperparameters. When we adjust one parameter, the others are set optimally by default. Layer denotes the number of STLs. Head indicates the number of heads of MSA. Dimensions indicate the number of channels. It can be found that the appropriate increase of layer, head, and dimensions can improve the performance of the model. However, this will make the model too complex and reduce computational efficiency, while leading to overfitting, which reduces performance.

Fig. 10

Impact of hyperparameter settings on PEMS04

Fig. 11

Impact of hyperparameter settings on PEMS08

5.7 Visualization

Figures 12 and 13 show the absolute errors of the STGHTN model on the 10 minutes, 20 minutes, 30 minutes, 40 minutes, 50 minutes, and 60 minutes prediction tasks on PEMS04 and PEMS08.

Fig. 12

Heatmap shows the absolute errors between true and predicted values for different prediction horizons on PEMS04

Fig. 13

Heatmap shows the absolute errors between true and predicted values for different prediction horizons on PEMS08

We can find that the STGHTN model shows promising forecasting performance for both short-term and long-term forecasts. It can effectively capture the temporal trend of traffic flow. Because real-world traffic conditions are complex and variable, the prediction effectiveness of the model decreases as the prediction range increases. Figure 14 shows the prediction results of our model and the baseline model STFGNN, STSGCN at 500 time steps on the PEMS04 and PEMS08 datasets. We can find that although both exhibit excellent prediction performance, our model more accurately predicts the beginning and end of a traffic peak. Our model convolves separately in the temporal and spatial dimensions and incorporates a self-attention mechanism to respond more quickly to the dynamically changing traffic flow.

Fig. 14

Visualization results of different models on PEMS04 and PEMS08

6 Conclusion

We considered traffic flow forecasting as a spatial-temporal forecasting problem, and proposed STGHTN for traffic flow prediction. We separately performed TGC and SGGC in the temporal and spatial dimensions to extract local temporal and spatial dependence. These dependencies are complementary to the global dependence obtained by transformer. Multiple spatial graph structures were constructed to exploit the static and dynamic associations between roads. Moreover, we employ STFL to explore spatial-temporal dependence across different time periods.

We conducted rich experiments on four real datasets and achieved the optimal performance compared to the state-of-the-art. In future work, we will exploit more effectively fusing mechanisms for transformer, and apply our model to more spatial-temporal sequence tasks, such as rainfall predictions.