Linguistic Pythagorean hesitant fuzzy matrix game and its application in multi-criteria decision making

Abstract

In this study, a new Linguistic Pythagorean Hesitant Fuzzy Set (LPHFS) is introduced by considering the notions of linguistic fuzzy set and Pythagorean hesitant fuzzy set. LPHFS is a suitable path to deal with the hesitant situation in decision making, which is characterized by linguistic membership and non-membership degrees. Multi-Criteria Decision Making (MCDM) process determines multiple competing criteria in decision making. The traditional decision making approaches assume that each player is independent. But in real world competitive situation, the real fact is that each player tries to maximize individual benefit which causes a negative impact on other player. Here we propose a Linguistic Pythagorean Hesitant Fuzzy (LPHF) distance measure based on game theoretical framework to terminate the cross-influence problem. So our intention is to explore the generalized hybrid Euclidean distance measures of LPHFS. Then we analyze the application of LPHFS to MCDM game by using Technique for Order Preference by Similarity to Ideal Solution (TOPSIS). The LPHFS is assumed to explore the uncertainty of Decision Makers (DMs), and the game theory is used to optimize the combination of criteria in interactive conditions. A modified version of TOPSIS and Ambika method are designed in the context of MCDM game with LPHFS. Finally, two real-life problems are considered to illustrate the applicability and feasibility of our proposed method, and then a comparison analysis is drawn among the obtained results with the existing methods to depict the usefulness of it.

1 Introduction

Game theory is the study of conflict and competitive interaction among the DMs. It has been applied in various areas such as politics, business model, social sciences, economics, international relations, computer sciences, etc. Game theory depicts with how DMs make decision when they resist with exact payoffs. Because of this, the idea of game theory is graceful in business world, international relations and politics. Furthermore, several kinds of real-life decision making applications are constituted as a game problem. In a decision making problem, when a DM does not cooperate, the situation lies into the realm of non-cooperation. The DMs are taken here as the players. In real-life problem, players are usually unable to calculate the value of the game due to lack of available information. A two-person zero-sum game is the simplest game including two players, where the payoffs are represented as crisp values. Then player I wins whereas player II loses, although two players consider pure strategies S₁ = {α_i : i = 1,2,…,m} and S₂ = {β_j : j = 1,2,…,n}, respectively.

The equipments of MCDM comprise a set of alternatives, a set of criteria and evaluation values. With the help of MCDM methods, the DMs select appropriate alternatives or obtain their ranking orders according to various criteria. At present, it has been successfully applied in several fields of Operational Research, such as an energy project, an air-condition system selection problem, talent introduction and so on. In real-life decision making process, the DMs cannot give their own ratings for each alternative with respect to each criterion in advance. So there is always occur an uncertain environment. In these situations, the imprecise parameters may be associated with uncertainty of various types such as Fuzzy Sets (FSs) (Zadeh [52]), Intuitionistic Fuzzy Sets (IFSs) (Atanassov [1]), Hesitant Fuzzy Sets (HFSs) (Torra and Narukawa [40]), Dual Hesitant Fuzzy Sets (DHFSs) (Zhu et al. [59]) and Type-2 Fuzzy Sets (T2FSs) (Mendel [24]).

Literature survey reveals that Pythagorean Fuzzy Sets (PFSs) were proposed by Yager ([47, 48]), which are a new rating format. Based on the outcomes of Yager [49], PFSs are differentiated both by a membership degree and a non-membership degree. On the one hand, PFS as a new extension of IFSs, succeed the duality property of IFSs. Contrariwise, PFSs have more potential than IFSs to solve the real-life decision making problems under uncertain environment. It satisfies the condition that the square sum of its membership degree and non-membership degree is equal to or less than 1. For example, the membership degree and the non-membership degree of one alternative in a criterion are 0.8 and 0.6. It is easy to see that $0.8+0.6 \nleq 1$, so this situation cannot be stated by considering the IFSs but (0.8)² + (0.6)² ≤ 1. As a novel evaluation, PFSs have been used in several areas such as service quality of domestic airlines, candidate selection in new development bank and investment problem. In traditional concept of PFSs, there are single valued membership and non-membership degrees. But in MCDM the rating format may be few values rather than a single value. In these circumstances, HFSs are a useful tool. For example, three DMs assess the membership of x into A with anonymity and they assign 0.5, 0.6 and 0.7, respectively. In this situation, the outcome {0.5,0.6,0.7} can be constituted as a set of Hesitant Fuzzy Elements (HFEs) rather than the aggregation of 0.5, 0.6, and 0.7, or an interval between 0.5 and 0.7. So, HFSs employ various opinions of the DMs. These studies can deal with the imprecise information that defined only in quantitative situations. But, in a practical situation, several decision making problems represent the qualitative aspects to present the imprecise information. For example, when rating the “aggregate marks” of a candidate in an examination, DMs prefer to consider the linguistic variables such as “excellent”, “very good”, “good”, “medium”, “bad”, “poor”, etc. To describe it, Xu [45] offered a method for group decision making problem based on linguistic aggregation operators. Zhang [53] analyzed the Linguistic Intuitionistic Fuzzy sets (LIFSs) by combining the concepts of linguistic approach and IFS. Based on the advantages of PFSs, HFSs and LFSs, we introduce the concept of LPHFSs, which is differentiated by linguistic hesitant membership degree and linguistic hesitant non-membership degree.

The rest of the paper is constructed as follows: The literature survey to our related work is presented in Section 2. Section 3 provides some basic backgrounds of LFSs, PFSs and HFSs. In Section 4, we introduce the definition of LPHFSs with some operations and properties. Section 5 explores the LPHFSs based on game theoretical framework. Solution procedure for LPHF-MCDM game with the aid of extended TOPSIS is described in Section 6. In Section 7, two real-life problems are considered to elaborate the feasibility and effectiveness of our proposed method. In Section 8, we sum up the discussion and comparison analysis of our proposed method with the method of Zhang and Xu [55] and Ambika method (Xue et al. [46]). Finally, conclusions are described in Section 9 with suggestions of future study.

2 Literature review

Over the last decades, many researchers have paid great attention to MCDM games under Pythagorean Fuzzy (PF) environment. For instance, Yager [48] proposed Pythagorean membership grades in MCDM. Yager and Abbasove [49] described Pythagorean membership grades, complex numbers and decision making. Garg [12] proposed a new generalized Pythagorean fuzzy information by using Einstein operations. Peng and Yang [28] described some results for PFSs. Ren et al. [29] unfolded Pythagorean fuzzy TODIM approach to MCDM. Song and Kandel [38] analyzed a fuzzy approach to strategic games. Reneke [30] unfolded a game formulation of decision making under condition of uncertainty and risk. Monropy and Fernandez [25] offered the Shapley-Shubik index for multi-criteria simple games. Furthermore, Rodriguez et al. [27] proposed hesitant fuzzy linguistic term sets for decision making. Garg [13] analyzed linguistic PFSs and its applications in Multi Attribute Decision Making (MADM) process. Liao et al. [21] proposed the application of distance and similarity measures for hesitant fuzzy linguistic term sets in MCDM. Xu and Xia [43] studied distance and similarity measures for HFSs. Based on similarity measure, Zhang [54] described a novel approach for Pythagorean fuzzy multiple criteria group decision making. Several methods have been investigated for solving MCDM games by many researchers. Zhang and Xu [55] described an extension of TOPSIS to MCDM with PFSs. Beg and Rashid [3] offered the concept of hesitant fuzzy linguistic-TOPSIS. Roy [31] worked on MCDM and fuzzy set theory in game environment. Singh [37] developed a new method to solve the dual hesitant fuzzy assignment problems with restrictions by using similarity measure. Yang et al. [50] unfolded a note on extension of TOPSIS to MCDM with PFSs. Jana and Roy [17] studied solution of matrix games with generalized trapezoidal fuzzy payoffs. Xue et al. [46] described matrix games based on Ambika method with hesitant fuzzy information and its application in the counter-terrorism issue. Bhaumik et al. [4] analyzed (α,β,γ)-cut set based ranking approach to solving bi-matrix games in neutrosophic environment. Furthermore, Xia et al. [42] presented hesitant fuzzy information aggregation in decision making. Bector et al. [2] formulated matrix games with fuzzy payoffs on duality in linear programming with fuzzy parameters. Roy and Bhaumik [33] unfolded intelligent water management problem with the help of triangular type-2 intuitionistic fuzzy matrix games approach. Campos [8] analyzed fuzzy matrix games with the help of fuzzy linear programming approach. Bhaumik and Roy [6] proposed different aggregation operators in intuitionistic interval-valued hesitant fuzzy matrix games for solving management problems. Nishizaki and Sakawa [26] studied on fuzzy and multi-objective games for conflict resolution. Chen and Larbani [9] presented a problem on fuzzy MADM based on zero-sum game approach. Roy and Mula [32] discussed the solution of matrix game with rough payoffs using genetic algorithm. Sakawa and Nishizaki [36] proposed a maximin solution for fuzzy multiobjective matrix games. Bhaumik et al. [7] described a real-life application into multi-objective linguistic-neutrosophic matrix game. Jana and Roy [18] offered dual hesitant fuzzy matrix games with the help of a new similarity measure. Bhaumik et al. [5] studied Prisoners’ dilemma game theory by using TOPSIS with the help of hesitant interval-valued intuitionistic fuzzy-linguistic term set approach. Jana and Roy [19] worked on soft matrix game by using hesitant fuzzy MCDM approach. Roy and Maiti [34] discussed a reduction method of type-2 fuzzy variables and its applications to Stackelberg game. Moreover, Yang et al. [51] proposed a simple noncooperative games with intuitionistic fuzzy information and its application in ecological management. Liang and Xu [22] discussed the new extension of TOPSIS method for MCDM with hesitant PFSs. Recently, Roy and Jana [35] analyzed the multi-objective linear production planning games in triangular hesitant fuzzy set.

The goal of this study is to develop the MCDM game under LPHF environment and to find the best alternative for the real-life problems simultaneously. Motivated by this concept, we present here a research work in these directions. An extensive comparison of different characteristics between the present study and related works in these directions is shown in Table 1. The following points are considered as the challenges through this work.

• Literature review shows that a few number of researchers have been done on MCDM game under uncertain environments.

• The key drawback of game theory is considered by one dimension situation to make a decision. However, multiple factors are often required to choose by the players in real-life situation.

• Moreover, it often does not envisage the behaviours of the players in decision making process by MCDM method. Actually, the behaviours of the players will influence the rating of alternatives in decision making process. So the best path is to combine MCDM with game theory to successfully develop a decision making model.

• From the above mentioned research works, we formulate an LPHF-MCDM game based on two real-life problems. Two players in this game are considered as DM and Nature (collective risks). The DM guesses that the Nature is an opponent, standing against him, and the DM tries to maximize his desired payoffs, whereas Nature tries to play with opposite actions to minimize them.

As a traditional MCDM method, TOPSIS can give a ranking method, which is measured by the smallest distance from the Positive Ideal Solution (PIS) and the largest distance from the Negative Ideal Solution (NIS). By considering the TOPSIS method (Hwang and Yoon [16]) and the generalized hybrid distance measures, we also discuss the applications of LPHFSs to MCDM game. This paper proposes an idea of LPHFSs and defines their basic operators. To address the challenges, at first, we analyze the normalization method offered by Zhu and Xu [60] and generalized hybrid distance measures for LPHFSs. In the framework of TOPSIS, we introduce an extended TOPSIS method under LPHF environment. We also introduce a modified Ambika method (Xue et al. [46]) for solving LPHF-MCDM game. Compared with the existing works, the LPHFSs can validly depict more general decision making situations. So, this work gives a new direction for the evaluation of MCDM game and also makes our decision by adopting a more complex scenario. This paper provides a five-fold contribution to the ongoing research in LPHF-MCDM games.

• We combine Linguistic Fuzzy Sets (LFSs) and Hesitant FSs into Pythagorean FSs and propose the new Linguistic Pythagorean Hesitant FSs (LPHFSs).

• Considering MCDM game with LPHFSs, we study the generalized hybrid distance measure.

• We propose a LPHF distance measure based on game theoretical framework to terminate the cross-influence problem.

• A modified version of TOPSIS and Ambika method are designed in the context of MCDM game with LPHFS.

• Two real-life examples are discussed, and thereafter comparisons are drawn.

Table 1 Comparisons of different authors’ contributions

3 Preliminaries

In the following, we briefly review the basic concepts of LFSs, PFSs and HFSs over the universal set X and the concept of MCDM game.

Herrera and Martinez [15] introduced the idea of LFSs, which is an extension of fuzzy set in qualitative situation rather than quantitative situation, shown as follows:

Definition 3.1 (Linguistic fuzzy set 15)

Let S = {s₀, s₁, s₂,…,s_τ} be a finite linguistic term set with odd cardinality, where s_i states a probable linguistic term for a linguistic variable. For example, a seven point linguistic scale S = {s₀ = none,s₁ = very low,s₂ = low,s₃ = medium,s₄ = high,s₅ = very high,s₆ = perfect} which satisfies the subsequent conditions as:

• The set is ordered s_i > s_j ⇔ i > j;

• Negation operator: Neg(s_i) = s_j where j = τ − i;

• Max operator: $\max \limits (s_{i}, s_{j})=s_{i} \Leftrightarrow i\geq j;$

• Min operator: $\min \limits (s_{i}, s_{j})=s_{j} \Leftrightarrow i\leq j.$

After that Xu [43] emerged the discrete term set S to a continuous linguistic term set $\bar {S}=\{s_{\alpha }: s_{0}\leq s_{\alpha } \leq s_{\tau },$ α ∈ [0,τ]}, whose elements also satisfy all the conditions mentioned above. If $s_{\alpha } \in \bar {S},$ then we call the key term; otherwise, it is called the virtual term.

The concept of PFSs was initiated by Yager [47] which is an extension of FSs and IFSs. Here we introduce some basic concepts of PFSs and their operations.

Definition 3.2

Pythagorean fuzzy sets (Zhang and Xu [55]) Let X be a reference set. A PFS P on X can be disclosed as:

$$ \begin{array}{@{}rcl@{}} P=\{<x, P(\mu_{p}(x),\nu_{p}(x))>: x \in X\}, \end{array} $$

where the functions $\mu _{p}(x):X\rightarrow [0, 1]$ and $\nu _{p}(x):X\rightarrow [0, 1]$ are the membership degree and non-membership degree of x to P, respectively. For every x ∈ X, it satisfies the condition: 0 ≤ (μ_p(x))² + (ν_p(x))² ≤ 1. The degree of indeterminacy of x to P is $\pi _{p}(x) = \sqrt {1-(\mu _{p}(x))^{2}-(\nu _{p}(x))^{2}}$. To easily understand, Zhang and Xu [53] called P(μ_p(x),ν_p(x)) as a Pythagorean Fuzzy Number (PFN), denoted by η = P(μ_η, ν_η), where $\mu _{\eta }, \nu _{\eta } \in [0, 1], \pi _{\eta } = \sqrt {1-(\mu _{\eta })^{2}-(\nu _{\eta })^{2}}$ and (μ_η)² + (ν_η)² ≤ 1.

Based on the outcomes of Zhang and Xu [55], we consider PFNs to depict our decision. Considering three PFNs $\eta =P(\mu _{\eta }, \nu _{\eta }), \eta _{1}=P(\mu _{\eta _{1}}, \nu _{\eta _{1}})~\text {and}~ \eta _{2}=P(\mu _{\eta _{2}},$ $\nu _{\eta _{2}}),$ then their basic operations are characterized as:

• $\eta _{1}\oplus \eta _{2}=P(\sqrt {\mu ^{2}_{\eta _{1}}+\mu ^{2}_{\eta _{2}}-\mu ^{2}_{\eta _{1}}\mu ^{2}_{\eta _{2}}}, \nu _{\eta _{1}}\nu _{\eta _{2}});$

• $\eta _{1} \otimes \eta _{2}=P(\mu _{\eta _{1}}\mu _{\eta _{2}}, \sqrt {\nu ^{2}_{\eta _{1}}+\nu ^{2}_{\eta _{2}}-\nu ^{2}_{\eta _{1}}\nu ^{2}_{\eta _{2}}});$

• $k \eta =P(\sqrt {1-(1-\mu ^{2}_{\eta })^{k}}, (\nu _{\eta })^{k})$.

HFS is an extremely valuable tools to handle the circumstances where there are some problems to determine the membership function of an element to a set. The idea of HFS was introduced by Torra and Narukawa [40] and later on developed by Torra [39].

Definition 3.3

Hesitant fuzzy set (Torra and Narukawa [40]) Let X be a fixed set, an HFS A on X is in term of a function that when it is applied to an element of X, then it returns an element of a subset of [0,1], which can be stated as follows: A = {< x,h_A(x) >: x ∈ X}, where h_A(x) is a set of various values in [0,1], identifying the probable membership degrees of the element x ∈ X to the set A. For suitability, h_A(x) is considered as an HFE, indicated by h. Assume that h, h₁ and h₂ be three HFEs and then some operations among them are depicted as:

• kh = ∪_γ∈h{1 − (1 − γ)^k},

• $h_{1} \oplus h_{2} = \cup _{\gamma _{1} \in h_{1}, \gamma _{2} \in h_{2}}\{\gamma _{1}+\gamma _{2}-\gamma _{1}\gamma _{2}\},$

• $h_{1} \otimes h_{2} = \cup _{\gamma _{1} \in h_{1}, \gamma _{2} \in h_{2}}\{\gamma _{1}\gamma _{2}\}.$

Definition 3.4 (MCDM game)

The development scenario for game theory is to integrate MCDM to tackle the decision making problems. Game theory plays a significant role in various collective negotiation among various participants. As for example, various negotiations take place when a company (DM) wants to expand their policy but the collective risks are taken together. Then by using game theory, the DM and Nature (collective risks) can arrive at the optimal solution of this issue. The concept of MCDM game is to combine the MCDM with game for developing a decision making model.

4 Linguistic Pythagorean hesitant fuzzy set

Motivated by the ideas of LFSs and HFSs, we extend the definition of PFSs in this Section. Considering the linguistic membership degree and linguistic non-membership degree of PFN with various values, we introduce LFSs and HFSs into PFSs and propose new LPHFSs. Particularly, the LPHFSs return two sets of linguistic hesitant membership degrees and linguistic hesitant non-membership degrees, respectively. So the membership and the non-membership degrees of PFN are Linguistic Hesitant Fuzzy Elements (LHFEs). Here, the definition of LPHFS is developed as follows:

Definition 4.1

(Linguistic Pythagorean hesitant fuzzy set): Let X be a universal set and $\bar {S}=\{s_{\alpha }: s_{0}\leq s_{\alpha } \leq s_{\tau }, \alpha \in [0, \tau ]\}$ be a continuous linguistic term set. Then a LPHFS A on X is represented as:

$$ \begin{array}{@{}rcl@{}} A=\{<x, A(hs_{\theta}(x), gs_{\sigma}(x))>: x \in X\}, \end{array} $$

where $hs_{\theta }(x)=\cup _{s_{\beta _{q}\in hs_{\theta }}}\left \lbrace s_{\beta _{q}}: q=1,\ldots ,\#hs_{\theta }\right \rbrace (\#hs_{\theta }$ is the length of linguistic term in hs_𝜃(x)) and $gs_{\sigma }(x)=\cup _{s_{\gamma _{q}\in gs_{\sigma }}}\left \lbrace s_{\gamma _{q}}: q=1,\ldots ,\#gs_{\sigma }\right \rbrace (\#gs_{\sigma }$ is the length of linguistic term in gs_σ(x)) are the linguistic Pythagorean hesitant membership degrees and linguistic Pythagorean hesitant non-membership degrees of the element x to the set A, respectively, with the conditions:

$$ \begin{array}{@{}rcl@{}} 0 \leq \beta_{q},~\gamma_{q} \leq 1~\text{and}~0 \leq (\beta^{+})^{2}+ (\gamma^{+})^{2} \leq 1, \end{array} $$

(4.1)

where $\beta ^{+} = \max \limits _{s_{\beta _{q} \in hs_{\theta }(x)}}\{\beta _{q}\}$ and $\gamma ^{+} = \max \limits _{s_{\gamma _{q} \in gs_{\sigma }(x)}}\{\gamma _{q}\}~\text {for~all}~x \!\in \! X.$

According to Definition 4.1, the LPHFSs are attached of two elements i.e., the linguistic Pythagorean membership hesitancy function and linguistic Pythagorean non-membership hesitancy function. Actually hs_𝜃(x) and gs_σ(x) are LHFEs. As the statement of DHFSs, LPHFSs also tackle two kinds of hesitancy functions and also provide a better way to assume values for each element in the domain. Comparing with the concepts of PHFSs, DHFSs and LPHFSs, we summarize the utility of these fuzzy sets (see Table 1). From Table 1, PHFSs, DHFSs and LPHFSs can be considered as the extensions of PFSs, HFSs and PHFSs, respectively. The basic difference among PHFSs, DHFSs and LPHFSs is their different constraint conditions, see (4.1). Specifically, the space of the linguistic Pythagorean hesitant membership degree (or the linguistic Pythagorean hesitant non-membership degree) is greater than the space of the PHFSs and DHFSs. To easily understand, the pair A(hs_𝜃(x),gs_σ(x)) is called a LPHFE identified by a = A(hs_𝜃, gs_σ). For example, when the DM figures out that the probable values for the linguistic membership hesitant degree of x to the set A are s_0.5 and s_0.7, for the linguistic hesitant non-membership degrees are s_0.3, s_0.35 and s_0.4, we can express it as a = A({s_0.5, s_0.7},{s_0.3, s_0.35, s_0.4}). In this case, β⁺ = 0.7, γ⁺ = 0.4 and (β⁺)² + (γ⁺)² ≤ 1. Hence, this environment cannot be stated by using the HFSs and DHFSs. Now we define the LPHFE in the following:

Definition 4.2

Considering LPHFE a = A(hs_𝜃, gs_σ), the minimum and maximum of each element are determined as:

$$ \begin{array}{@{}rcl@{}} \beta^{-} = \min_{s_{\beta_{q}\in hs_{\theta}}}\{\beta_{q}\},~\gamma^{-} = \min_{s_{\gamma_{q} \in gs_{\sigma}}}\{\gamma_{q}\} \end{array} $$

(4.2)

$$ \begin{array}{@{}rcl@{}} \beta^{+} = \max_{s_{\beta_{q}\in hs_{\theta}}}\{\beta_{q}\},~\gamma^{+} = \max_{s_{\gamma_{q} \in gs_{\sigma}}}\{\gamma_{q}\} \end{array} $$

(4.3)

where β⁻ and β⁺ are the minimum and maximum of the element hs_𝜃. Likely, γ⁻ and γ⁺ are the minimum and maximum of the element gs_σ.

Definition 4.3 (Operations)

Let us consider that three LPHFEs are as $a=A(hs_{\theta }, gs_{\sigma }),\\ a_{1}=A(hs_{\theta _{1}}, gs_{\sigma _{1}}), a_{2}=A(hs_{\theta _{2}}, gs_{\sigma _{2}}),$ then some operations among them are stated as follows:

• $a_{1} \oplus a_{2} = \cup _{s_{\beta _{1}} \in hs_{\theta _{1}}, s_{\gamma _{1}} \in gs_{\sigma _{1}}, s_{\beta _{2}} \in hs_{\theta _{2}}, s_{\gamma _{2}} \in gs_{\sigma _{2}}}$ $s_{\{\{\sqrt {\beta _{1}+\beta _{2}-\beta _{1}\beta _{2}}\}, \{\gamma _{1}\gamma _{2}\}\}},$

• $a_{1} \otimes a_{2} = \cup _{s_{\beta _{1}} \in hs_{\theta _{1}}, s_{\gamma _{1}} \in gs_{\sigma _{1}}, s_{\beta _{2}} \in hs_{\theta _{2}}, s_{\gamma _{2}} \in gs_{\sigma _{2}}}$ $s_{\{\{\beta _{1}\beta _{2}\},\{\sqrt {\gamma _{1}+\gamma _{2}-\gamma _{1}\gamma _{2}}\}\}},$

• $ka=\cup _{s_{\beta } \in hs_{\theta }, s_{\gamma } \in hs_{\theta }}s_{{\{\{\sqrt {1-(1-\beta )^{k}}\}, \{\gamma ^{k}\}\}}}$ where $k \in \mathbb {R}$ and k ≥ 0.

According to the operations of Definition 4.3, we easily prove the following theorem:

Theorem 4.1 (Zhang and Xu 55)

Let $a_{1}=A(hs_{\theta _{1}},gs_{\sigma _{1}}),$ $a_{2}=A(hs_{\theta _{2}}, gs_{\sigma _{2}})$ be two LPHFEs, then we have

• a₁ ⊕ a₂ = a₂ ⊕ a₁,

• a₁ ⊗ a₂ = a₂ ⊗ a₁,

• k(a₁ ⊕ a₂) = k(a₁) ⊕ k(a₂),

• k(a₁ ⊗ a₂) = k(a₁) ⊗ k(a₂).

Based on the outcomes of Zhang and Xu [55], we also define a score function and accuracy function for the LPHFEs as:

Definition 4.4

Let us consider that a = A(hs_𝜃, gs_σ) be a LPHFE, then the score function of a is S(a) = (1/#hs_𝜃) $\sum \limits _{s_{\beta _{q}} \in hs_{\theta }}(\beta _{q})^{2}-(1/\#gs_{\sigma })\sum \limits _{s_{\gamma _{q}} \in gs_{\sigma }}(\gamma _{q})^{2}$ and the accuracy function of a is $p(a) = (1/\#hs_{\theta })\sum \limits _{s_{\beta _{q}} \in hs_{\theta }}(\beta _{q})^{2}+(1/\#gs_{\sigma })$ $\sum \limits _{s_{\gamma _{q}} \in gs_{\sigma }}(\gamma _{q})^{2},$ where #hs_𝜃 and #gs_σ are the number of elements in hs_𝜃 and gs_σ respectively.

According to the accuracy function of Definition 4.4, we state the following property:

Property 1

Let a = A(hs_𝜃, gs_σ) be a LPHFE, the degree of indeterminacy of a is

$$ \begin{array}{@{}rcl@{}} \pi\!&=&\!{\sqrt{1-p(a)}} \\ \!&=&\! \sqrt{1 - \left( \!(1/\#hs_{\theta})\sum\limits_{s_{\beta_{q}} \in hs_{\theta}}(\beta_{q})^{2} + (1/\#gs_{\sigma})\sum\limits_{s_{\gamma_{q}} \in gs_{\sigma}}(\gamma_{q})^{2}\!\right)} \end{array} $$

(4.4)

Now we analyze the comparison of LPHFEs due to the number of their corresponding element may not be same. For example, assume that two LPHFEs as $a_{1}=A(hs_{\theta _{1}},$$gs_{\sigma _{1}})= A(\{s_{0.2}, s_{0.3}\}, \{s_{0.5}, s_{0.6}\})$ and $a_{2}=A(hs_{\theta _{2}}, gs_{\sigma _{2}})$ = A({s_0.2, s_0.25, s_0.4},{s_0.7, s_0.8}), we obtain $\#hs_{\theta _{1}} \neq \#hs_{\theta _{2}}.$ Zhu and Xu [60] also faced the same situation during the analysis of DHFEs. To solve this situation, Zhu anx Xu [60] analyzed the DHFES by adding some constant values. Its definition is shown as:

Definition 4.5

Considering that a = A(hs_𝜃, gs_σ) be a LPHFE, then we assume $\bar {\beta }=t\beta ^{+}+(1-t)\beta ^{-}$ and $\bar {\gamma }=t\gamma ^{+}+(1-t)\gamma ^{-}$ as added linguistic membership and non-membership hesitant degrees, respectively, where β⁺ and β⁻ are the maximum and minimum elements of hs_𝜃, respectively, γ⁺ and γ⁻ are the maximum and minimum elements of gs_σ and t (0 ≤ t ≤ 1) is a parameter considered by the DM according to his/her risk preference.

For Definition 4.5, it gives a principle to add linguistic hesitant membership degree and linguistic hesitant non-membership degree for the normalization of LPHFE. The various values of t can generate various outcomes for the added linguistic membership and non-membership degrees. Based on Definition 4.4 and the outcomes of Zhu and Xu [60], the bigger values of t correspond with optimistic DM. As discussed earlier and the outcomes of Zhu and Xu [60], we have three particular cases of the preference of the DM.

• When the value of t = 1, the optimistic DM may add the maximum linguistic membership degree β⁺ and maximum non-membership degree γ⁺.

• When the value of t = 0.5, the unbiased DM can include the linguistic membership term 0.5(β⁺ + β⁻) and the non-membership term 0.5(γ⁺ + γ⁻).

• When the value of t = 0, the pessimistic DM may add the linguistic membership term β⁻ and maximum non-membership degree γ⁻.

Given a value of t, we use the result of Definition 4.5 to add the linguistic membership and linguistic non-membership degrees for the LPHFEs. The algorithm of the normalization of LPHFEs is depicted in Algorithm 1. Algorithm 1, depicted the normalization process of LPHFEs in detail. The normalization of LPHFEs has two major steps: (i) find the objects which need to add their elements and (ii) calculate the added value for the corresponding objects. To easily understand, we consider an Example 1 to explain the normalization process of Definition 4.5.

Example 4.1

Assuming that, we have two LPHFEs as $a_{1}=A(hs_{\theta _{1}}, gs_{\sigma _{1}})= A(\{s_{0.3}, s_{0.4}\}, \{s_{0.6}, s_{0.7}, s_{0.75}\})$ and $a_{2}=A(hs_{\theta _{2}}, gs_{\sigma _{2}})=A(\{s_{0.35}, s_{0.4}, s_{0.5}\}, \{s_{0.65}, s_{0.75}\}).$ Here, $\#hs_{\theta _{1}}=2,~\#gs_{\sigma _{1}}=3,~\#hs_{\theta _{2}}=3~\text {and}~\#gs_{\sigma _{2}}=2.$ By comparing the elements of a₁ and a₂, it is clear that $\#hs_{\theta _{1}} \neq \#hs_{\theta _{2}}~\text {and}~\#gs_{\sigma _{1}} \neq \#gs_{\sigma _{2}}.$ So the membership degree of a₁ and non-membership degree of a₂ need to be analyzed.

• If the value of t is 1, then we can add the maximum membership degree or the maximum non-membership degree for the target element. For the LPHFE a₁, the linguistic hesitant membership degree of a₁ can be received as {s_0.3, s_0.4, s_0.4}. In this circumstance, a₁ is analyzed as a₁ = A({s_0.3, s_0.4, s_0.4},{s_0.6, s_0.7, s_0.75}). For the LPHFE a₂, the linguistic hesitant non-membership degree can be obtained as {s_0.65, s_0.75, s_0.75}, i.e., a₂ is modified as A({s_0.35, s_0.4, s_0.5},{s_0.65, s_0.75, s_0.75}).

• If the value of t is 0, then we can include the minimum membership degree or the minimum non-membership degree for the target element. For the LPHFE a₁, the linguistic hesitant membership degree of a₁ can be obtained as {s_0.3, s_0.3, s_0.4}. In this circumstance, a₁ is analyzed as a₁ = A({s_0.3, s_0.3, s_0.4},{s_0.6, s_0.7, s_0.75}). For the LPHFE a₂, the linguistic hesitant non-membership degree can be received as {s_0.65, s_0.65, s_0.75}, i.e., a₂ is modified as A({s_0.35, s_0.4, s_0.5},{s_0.65, s_0.65, s_0.75}).

• If the value of t is 0.5, then we may add the average membership degree or the average non-membership degree for the target element. For the LPHFE a₁, the linguistic hesitant membership degree of a₁ can be obtained as {s_0.3, s_0.35, s_0.4}. In this circumstance, a₁ is analyzed as a₁ = A({s_0.3, s_0.35, s_0.4},{s_0.6, s_0.7, s_0.75}). For the LPHFE a₂, the linguistic hesitant non-membership degree can be received as {s_0.65, s_0.70, s_0.75}, i.e., a₂ is modified as A({s_0.35, s_0.4, s_0.5},{s_0.65, s_0.7, s_0.75}).

However we only consider three cases of t in Example 1 but the other values of t are also useful for the normalization of LPHFEs. Distance measure is an important concept for measuring the uncertain information in LPHFS. The generalized hybrid distance measure is a measure that shows the closeness among LPHFSs. Different distance measures for PHFS are introduced in the literature (Zhang [54], Xu and Xia [43], Liu et al. [23]). The common thread of incompetence of these existing distance measures is their inability to clearly distinguish highly uncertain PHFSs. To handle this situation, we propose a new distance measure for LPHFS to connect with TOPSIS method. Distance and similarity measures are most important in the applications of MCDM. By using our distance measure, we reduce the MCDM game with LPHF payoffs to crisp payoffs. Also, superiority and effectiveness of the prescribed hybrid distance measure are demonstrated via TOPSIS through two real-life problems. Xu [44] calculated the distance measures of intuitionistic fuzzy numbers. According to the outcomes reported by Xu [44], we define the idea of distance measures of the LPHFEs as follows:

Definition 4.6

Let $a_{1}=A(hs_{\theta _{1}}, gs_{\sigma _{1}})$ and $a_{2}=A(hs_{\theta _{2}},$ $gs_{\sigma _{2}})$ be two normalized LPHFEs; furthermore, let $hs_{\theta _{1}}$ $=\cup _{s_{{\beta _{q}^{1}}\in hs_{\theta _{1}}}}\left \lbrace s_{{\beta _{q}^{1}}}: q=1,\ldots ,\#hs_{\theta _{1}}\right \rbrace (\#hs_{\theta _{1}}$ is the length of linguistic term in $hs_{\theta _{1}})$ and $gs_{\sigma _{1}}=\cup _{s_{{\gamma _{q}^{1}}\in gs_{\sigma _{1}}}}\lbrace s_{{\gamma _{q}^{1}}}: q=1,\ldots ,\#gs_{\sigma _{1}}\rbrace (\#gs_{\sigma _{1}}$ is the length of linguistic term in $gs_{\sigma _{1}})$. Similarly, we consider the values of $hs_{\theta _{2}}$ and $gs_{\sigma _{2}}.$ Then we define a LPHF hybrid Euclidean distance between a₁ and a₂ as follows:

$$ \begin{array}{@{}rcl@{}} d_{1}(a_1, a_2)=\sqrt{\begin{array}{l}\frac{1}{2}(\frac{1}{\#hs}{\sum}_{q=1}^{\#hs}|((\beta_{q}^{1})^{2}-(\beta_{q}^{2})^{2})+\max\limits_{q=1,2,\ldots,\#hs}((\beta_{q}^{1})^{2}-(\beta_{q}^{2})^{2})|^{2}+\frac{1}{\#gs}\\ {\sum}_{q=1}^{\#gs}|((\gamma_{q}^{1})^{2}-(\gamma_{q}^{2})^{2})+\max\limits_{q=1,2,\ldots,\#gs}((\gamma_{q}^{1})^{2}-(\gamma_{q}^{2})^{2})|^{2}+|({\pi_{1}})^{2}-({\pi_{2}})^{2}|^{2}) \end{array}}\\ \end{array} $$

(4.5)

where $\#hs= \#hs_{\theta _{1}} = \#hs_{\theta _{2}}$ and $\#gs= \#gs_{\sigma _{1}} = \#gs_{\sigma _{2}}$. π₁ and π₂ are the degrees of indeterminacy of a₁ and a₂, which are determined as:

$$ \pi_{1}= {\sqrt{1-((1/\#hs_{\theta_{1}})\sum\limits_{s_{{\beta_{q}^{1}} \in hs_{\theta_{1}}}}({\beta_{q}^{1}})^{2}+(1/\#gs_{\sigma_{1}})\sum\limits_{s_{{\gamma_{q}^{1}}} \in gs_{\sigma_{1}}}({\gamma_{q}^{1}})^{2})}}, $$

$$ \pi_{2}= {\sqrt{1-((1/\#hs_{\theta_{2}})\sum\limits_{s_{{\beta_{q}^{2}} \in hs_{\theta_{2}}}}({\beta_{q}^{2}})^{2}+(1/\#gs_{\sigma_{2}})\sum\limits_{s_{{\gamma_{q}^{2}}} \in gs_{\sigma_{2}}}({\gamma_{q}^{2}})^{2})}}. $$

Inspired by the generalized concept of Xu [44], we unify the geometric distance measure. Then we generalize the above distance of Definition 4.6 as:

$$ \begin{array}{@{}rcl@{}} d(a_{1},a_{2})=\left( \begin{array}{ll}\frac{1}{2}(\frac{1}{\#hs}{\sum}_{q=1}^{\#hs}|(({\beta_{q}^{1}})^{2}-({\beta_{q}^{2}})^{2})+\max\limits_{q=1,2,\ldots,\#hs}(({\beta_{q}^{1}})^{2}-({\beta_{q}^{2}})^{2})|^{\lambda}+\frac{1}{\#gs}\\ {\sum}_{q=1}^{\#gs}|(({\gamma_{q}^{1}})^{2}-({\gamma_{q}^{2}})^{2})+\max\limits_{q=1,2,\ldots,\#gs}(({\gamma_{q}^{1}})^{2}-({\gamma_{q}^{2}})^{2})|^{\lambda}+|({\pi_{1}})^{2}-({\pi_{2}})^{2}|^{\lambda}) \end{array}\right)^{\frac{1}{\lambda}} \end{array} $$

(4.6)

where λ (> 0) is constant and satisfies the following properties.

• 0 ≤ d(a₁, a₂) ≤ 1.

• d(a₁, a₂) = d(a₂, a₁).

• d(a₁, a₂) = 0 if and only if a₁ = a₂.

• d(a₁, a₂) ≤ d(a₁, a₃) + d(a₃, a₂).

Proof

It is easy to see that distance measure, d(a₁, a₂) satisfies the first two properties (i) and (ii). So we only prove that d(a₁, a₂) satisfies properties (iii) and (iv). (iii) If a₁ = a₂, then we have

$$ \begin{array}{@{}rcl@{}} d(a_{1}, a_{2})=\left( \begin{array}{ll}\frac{1}{2}(\frac{1}{\#hs}{\sum}_{q=1}^{\#hs}|(({\beta_{q}^{1}})^{2}-({\beta_{q}^{1}})^{2})+\max\limits_{q=1,2,\ldots,\#hs}(({\beta_{q}^{1}})^{2}-({\beta_{q}^{1}})^{2})|^{\lambda}+\frac{1}{\#gs}\\ {\sum}_{q=1}^{\#gs}|(({\gamma_{q}^{1}})^{2}-({\gamma_{q}^{1}})^{2})+\max\limits_{q=1,2,\ldots,\#gs}(({\gamma_{q}^{1}})^{2}-({\gamma_{q}^{1}})^{2})|^{\lambda}+|({\pi_{1}})^{2}-({\pi_{2}})^{2}|^{\lambda}) \end{array}\right)^{\frac{1}{\lambda}} = 0 \end{array} $$

where, ${\pi _{1}}^{2}-{\pi _{2}}^{2} = 0$.

Conversely, let d(a₁, a₂) = 0, then we get $\frac {1}{\#hs}{\sum }_{q=1}^{\#hs}|(({\beta _{q}^{1}})^{2}-({\beta _{q}^{2}})^{2})+\max \limits _{q=1,2,\ldots ,\#hs}(({\beta _{q}^{1}})^{2}-({\beta _{q}^{2}})^{2})|^{\lambda } = 0$, $\frac {1}{\#gs} {\sum }_{q=1}^{\#gs}|$ $(({\gamma _{q}^{1}})^{2}-({\gamma _{q}^{2}})^{2})+\max \limits _{q=1,2,\ldots ,\#gs}(({\gamma _{q}^{1}})^{2}-({\gamma _{q}^{2}})^{2})|^{\lambda } = 0$ and |(π₁)² − (π₂)²| = 0, which means for any value $s_{{\beta _{q}^{1}}}$ in $hs_{\theta _{1}},$ there is always a certain value $s_{{\beta _{q}^{2}}}$ in $hs_{\theta _{2}}$ with $s_{{\beta _{q}^{1}}} = s_{{\beta _{q}^{2}}}$ and vice versa.

Consequently, d(a₁, a₂) satisfies the property (iii).

(iv) Here, d(a₁, a₂)

$$ \begin{array}{@{}rcl@{}} &=&\left( \begin{array}{ll}\frac{1}{2}(\frac{1}{\#hs}{\sum}_{q=1}^{\#hs}|(({\beta_{q}^{1}})^{2}-({\beta_{q}^{2}})^{2})+\max\limits_{q=1,2,\ldots,\#hs}(({\beta_{q}^{1}})^{2}-({\beta_{q}^{2}})^{2})|^{\lambda}+\frac{1}{\#gs}\\ {\sum}_{q=1}^{\#gs}|(({\gamma_{q}^{1}})^{2}-({\gamma_{q}^{2}})^{2})+\max\limits_{q=1,2,\ldots,\#gs}(({\gamma_{q}^{1}})^{2}-({\gamma_{q}^{2}})^{2})|^{\lambda}+|({\pi_{1}})^{2}-({\pi_{2}})^{2}|^{\lambda}) \end{array}\right)^{\frac{1}{\lambda}}\\ &=& \left( \begin{array}{ll}\frac{1}{2}(\frac{1}{\#hs}{\sum}_{q=1}^{\#hs}|(({\beta_{q}^{1}})^{2}-({\beta_{q}^{3}})^{2}+({\beta_{q}^{3}})^{2}-({\beta_{q}^{2}})^{2})+ \max\limits_{q=1,2,\ldots,\#hs}(({\beta_{q}^{1}})^{2}-({\beta_{q}^{3}})^{2}+({\beta_{q}^{3}})^{2}-({\beta_{q}^{2}})^{2})|^{\lambda}\\+\frac{1}{\#gs} {\sum}_{q=1}^{\#gs}|(({\gamma_{q}^{1}})^{2}-({\gamma_{q}^{3}})^{2}+({\gamma_{q}^{3}})^{2}-({\gamma_{q}^{2}})^{2})+\max\limits_{q=1,2,\ldots,\#gs}(({\gamma_{q}^{1}})^{2}-({\gamma_{q}^{3}})^{2}+({\gamma_{q}^{3}})^{2}-({\gamma_{q}^{2}})^{2})|^{\lambda}\\+|({\pi_{1}})^{2}-({\pi_{3}})^{2}+({\pi_{3}})^{2}-({\pi_{2}})^{2}|^{\lambda}) \end{array}\right)^{\frac{1}{\lambda}}\\ &\leq& \left( \begin{array}{ll}\frac{1}{2}(\frac{1}{\#hs}{\sum}_{q=1}^{\#hs}|(({\beta_{q}^{1}})^{2}-({\beta_{q}^{3}})^{2})+ \max\limits_{q=1,2,\ldots,\#hs}(({\beta_{q}^{1}})^{2}-({\beta_{q}^{3}})^{2})|^{\lambda}+\frac{1}{\#gs}\\ {\sum}_{q=1}^{\#gs}|(({\gamma_{q}^{1}})^{2}-({\gamma_{q}^{3}})^{2})+\max\limits_{q=1,2,\ldots,\#gs}(({\gamma_{q}^{1}})^{2}-({\gamma_{q}^{3}})^{2})|^{\lambda}+|({\pi_{1}})^{2}-({\pi_{3}})^{2})|^{\lambda}) \end{array}\right)^{\frac{1}{\lambda}} +\\ &&\left( \begin{array}{ll}\frac{1}{2}(\frac{1}{\#hs}{\sum}_{q=1}^{\#hs}|(({\beta_{q}^{3}})^{2}-({\beta_{q}^{2}})^{2})+ \max\limits_{q=1,2,\ldots,\#hs}(({\beta_{q}^{3}})^{2}-({\beta_{q}^{2}})^{2})|^{\lambda}+\frac{1}{\#gs}\\ {\sum}_{q=1}^{\#gs}|(({\gamma_{q}^{3}})^{2}-({\gamma_{q}^{2}})^{2})+\max\limits_{q=1,2,\ldots,\#gs}(({\gamma_{q}^{3}})^{2}-({\gamma_{q}^{2}})^{2})|^{\lambda}+|({\pi_{3}})^{2}-({\pi_{2}})^{2})|^{\lambda}) \end{array}\right)^{\frac{1}{\lambda}}\\ &&\leq d(a_{1}, a_{3}) + d(a_{3}, a_{2}). \end{array} $$

Based on the distance d(a₁, a₂) given in (4.6), we deeply depict the comparison between some special cases of LPHFEs by inspiring the outcomes of Zhang and Xu [58] in Theorems 4.2 and 4.3. □

Theorem 4.2

Let $a_{1}=A(hs_{\theta _{1}}, gs_{\sigma _{1}})$ and a₂ = A({s₁}, {s₀}) be two LPHFEs, then we determine the generalized distance $d(a_{1}^{\prime }, a_{2})$ as:

$$ \begin{array}{@{}rcl@{}} d(a_{1}^{\prime}, a_{2})=\left( \begin{array}{ll}\frac{1}{2}(\frac{1}{\#hs_{\theta_{1}}}\sum\limits_{s_{\beta_{q} \in hs_{\theta_{1}}}}((1-(\beta_{q})^{2})+\max\limits_{q=1,2,\ldots,\#hs_{\theta_{1}}}(1-(\beta_{q})^{2}))^{\lambda}+\frac{1}{\#gs_{\sigma_{1}}} \sum\limits_{s_{\gamma_{q} \in gs_{\sigma_{1}}}}((\gamma_{q})^{2}\\+\max\limits_{q=1,2,\ldots,\#gs_{\sigma_{1}}} (\gamma_{q})^{2})^{\lambda}+(1-(\frac{1}{\#hs_{\theta_{1}}}\sum\limits_{s_{\beta_{q} \in hs_{\theta_{1}}}}(\beta_{q})^{2}+\frac{1}{\#gs_{\sigma_{1}}}\sum\limits_{s_{\gamma_{q}} \in gs_{\sigma_{1}}}(\gamma_{q})^{2}))^{\lambda}) \end{array}\right)^{\frac{1}{\lambda}} \end{array} $$

(4.7)

where $a_{1}^{\prime }$ is the normalization result of a₁ by the comparison of a₁ and a₂.

Proof

By considering the LPHF environment, we apply Definition 4.5 to normalize a₁. a₂ can guide the normalization results of a₁, i.e., $a_{1}^{\prime }$. Here $\#hs = \#hs_{\theta _{1}}^{\prime } = \#hs_{\theta _{2}}$ and $\#gs= \#gs_{\sigma _{1}}^{\prime } = \#gs_{\sigma _{2}}.$ π₁ and π₂ are the degrees of indeterminacy of $a_{1}^{\prime }$ and a₂. They are determined as:

$$ \begin{array}{@{}rcl@{}} (\pi_{1})^{2} = 1-\left( \frac{1}{\#hs_{\theta_{1}}}\sum\limits_{s_{{\beta_{q}^{1}} \in hs_{\theta_{1}}}}({\beta_{q}^{1}})^{2}+\frac{1}{\#gs_{\sigma_{1}}}\sum\limits_{s_{{\gamma_{q}^{1}}} \in gs_{\sigma_{1}}}({\gamma_{q}^{1}})^{2}\right), \end{array} $$

$$ (\pi_{2})^{2} = 1-\left( \frac{1}{\#hs_{\theta_{2}}}\sum\limits_{s_{{\beta_{q}^{2}} \in hs_{\theta_{2}}}}({\beta_{q}^{2}})^{2}+\frac{1}{\#gs_{\sigma_{2}}}\sum\limits_{s_{{\gamma_{q}^{2}}} \in gs_{\sigma_{2}}}({\gamma_{q}^{2}})^{2}\right) = 1-(1+0)=0. $$

According to (4.6) the generalized hybrid distance $d(a_{1}^{\prime },$ a₂) is determined as:

$$ \begin{array}{@{}rcl@{}} d(a_{1}^{\prime}, a_{2})&=&\left( \begin{array}{ll}\frac{1}{2}(\frac{1}{\#hs}{\sum}_{q=1}^{\#hs}|(({\beta_{q}^{1}})^{2}-({\beta_{q}^{2}})^{2})+\max\limits_{q=1,2,\ldots,\#hs}(({\beta_{q}^{1}})^{2}-({\beta_{q}^{2}})^{2})|^{\lambda}+\frac{1}{\#gs}\\ {\sum}_{q=1}^{\#gs}|(({\gamma_{q}^{1}})^{2}-({\gamma_{q}^{2}})^{2})+\max\limits_{q=1,2,\ldots,\#gs}(({\gamma_{q}^{1}})^{2}-({\gamma_{q}^{2}})^{2})|^{\lambda}+|({\pi_{1}})^{2}-({\pi_{2}})^{2}|^{\lambda}) \end{array}\right)^{\frac{1}{\lambda}}\\ &=&\left( \begin{array}{ll}\frac{1}{2}(\frac{1}{\#hs}{\sum}_{q=1}^{\#hs}|(({\beta_{q}^{1}})^{2}-1)+\max\limits_{q=1,2,\ldots,\#hs}(({\beta_{q}^{1}})^{2}-1)|^{\lambda}+\frac{1}{\#gs} {\sum}_{q=1}^{\#gs}|({\gamma_{q}^{1}})^{2}\\+\max\limits_{q=1,2,\ldots,\#gs}({\gamma_{q}^{1}})^{2}|^{\lambda}+|({\pi_{1}})^{2}-0|^{\lambda}) \end{array}\right)^{\frac{1}{\lambda}}\\ &=&\left( \begin{array}{ll}\frac{1}{2}(\frac{1}{\#hs}{\sum}_{q=1}^{\#hs}|(1-({\beta_{q}^{1}})^{2})+\max\limits_{q=1,2,\ldots,\#hs}(1-({\beta_{q}^{1}})^{2})|^{\lambda}+\frac{1}{\#gs} {\sum}_{q=1}^{\#gs}|({\gamma_{q}^{1}})^{2}\\+\max\limits_{q=1,2,\ldots,\#gs}({\gamma_{q}^{1}})^{2}|^{\lambda}+|({\pi_{1}})^{2}-0|^{\lambda}) \end{array}\right)^{\frac{1}{\lambda}}\\ &=&\left( \begin{array}{ll}\frac{1}{2}(\frac{1}{\#hs_{\theta_{1}}}{\sum}_{q=1}^{\#hs_{\theta_{1}}}((1-({\beta_{q}^{1}})^{2})+\max\limits_{q=1,2,\ldots,\#hs_{\theta_{1}}}(1-({\beta_{q}^{1}})^{2}))^{\lambda}+\frac{1}{\#gs_{\sigma_{1}}} {\sum}_{q=1}^{\#gs_{\sigma_{1}}}|({\gamma_{q}^{1}})^{2}\\+\max\limits_{q=1,2,\ldots,\#gs_{\sigma_{1}}}({\gamma_{q}^{1}})^{2})|^{\lambda}+(1-(\frac{1}{\#hs_{\theta_{1}}}\sum\limits_{s_{{\beta_{q}^{1}} \in hs_{\theta_{1}}}}({\beta_{q}^{1}})^{2}+\frac{1}{\#gs_{\sigma_{1}}}\sum\limits_{s_{{\gamma_{q}^{1}}} \in gs_{\sigma_{1}}}({\gamma_{q}^{1}})^{2}))^{\lambda}) \end{array}\right)^{\frac{1}{\lambda}}\\ &=&\left( \begin{array}{ll}\frac{1}{2}(\frac{1}{\#hs_{\theta_{1}}}\sum\limits_{s_{\beta_{q} \in hs_{\theta_{1}}}}((1-(\beta_{q})^{2})+\max\limits_{q=1,2,\ldots,\#hs_{\theta_{1}}}(1-(\beta_{q})^{2}))^{\lambda}+\frac{1}{\#gs_{\sigma_{1}}} \sum\limits_{s_{\gamma_{q} \in gs_{\sigma_{1}}}}((\gamma_{q})^{2}\\+\max\limits_{q=1,2,\ldots,\#gs_{\sigma_{1}}} (\gamma_{q})^{2})^{\lambda}+(1-(\frac{1}{\#hs_{\theta_{1}}}\sum\limits_{s_{\beta_{q} \in hs_{\theta_{1}}}}(\beta_{q})^{2}+\frac{1}{\#gs_{\sigma_{1}}}\sum\limits_{s_{\gamma_{q}} \in gs_{\sigma_{1}}}(\gamma_{q})^{2}))^{\lambda}) \end{array}\right)^{\frac{1}{\lambda}}. \end{array} $$

This evinces the proof of the Theorem. □

Theorem 4.3

Let $a_{1}=A(hs_{\theta _{1}}, gs_{\sigma _{1}})$ and a₂ = A({s₀}, {s₁}) be two LPHFEs, then we calculate the generalized distance $d(a_{1}^{\prime }, a_{2})$ as:

$$ \begin{array}{@{}rcl@{}} d(a_{1}^{\prime}, a_{2})=\left( \begin{array}{ll}\frac{1}{2}(\frac{1}{\#hs_{\theta_{1}}}\sum\limits_{s_{{\beta_{q}^{1}} \in hs_{\theta_{1}}}}((\beta_{q})^{2}+\max\limits_{q=1,2,\ldots,\#hs}(\beta_{q})^{2})^{\lambda}+\frac{1}{\#gs_{\sigma_{1}}}\sum\limits_{s_{{\gamma_{q}^{1}} \in gs_{\sigma_{1}}}}((1-(\gamma_{q})^{2})\\+\max\limits_{q=1,2,\ldots,\#gs_{\sigma_{1}}}(1- (\gamma_{q})^{2}))^{\lambda}+(1-(\frac{1}{\#hs_{\theta_{1}}}\sum\limits_{s_{{\beta_{q}^{1}} \in hs_{\theta_{1}}}}(\beta_{q})^{2}+\frac{1}{\#gs_{\sigma_{1}}}\sum\limits_{s_{{\gamma_{q}^{1}}} \in gs_{\sigma_{1}}}(\gamma_{q})^{2}))^{\lambda}) \end{array}\right)^{\frac{1}{\lambda}} \\ \end{array} $$

(4.8)

where $a_{1}^{\prime }$ is the normalization result of a₁ by the comparison of a₁ and a₂.

Proof

Proof of the Theorem 4.3 is same as Theorem 4.2.

From Theorems 4.2 and 4.3, the generalized hybrid distances of (4.7) and (4.8) mainly based on the linguistic hesitant memberships degrees and the linguistic hesitant non-membership degrees of a₁ and a₂, which do not maintain the order of the evaluation values of the elements. □

5 Linguistic Pythagorean hesitant fuzzy based game theoretical framework

In this section, we analyze the games to define the elements in matrix game, the set of DMs and the set of strategies when they conflict with each other. The framework of this game is developed as follows:

At first we offer some traditional backgrounds of non-cooperative game theory. A two-person matrix game can be expressed with the triplet G = < X,Y,A >, where X,Y are the set of mixed strategies for the DM and Nature, respectively. This means: X = {x_i : i = 1,2,…,m} and Y = {y_j : j = 1,2,…,n}. Furthermore, A is an m × n payoff matrix for DM against Nature, and -A is considered as the payoff matrix for Nature. A matrix game A = [a_ij]_m×n has the maximin value and minimax value which are described gradually, as $v^{-} = \max \limits \limits _{i=1, 2, \ldots , m} \min \limits \limits _{j=1, 2, \ldots , n} a_{ij},~v^{+} = \min \limits \limits _{i=1, 2, \ldots , m} \max \limits \limits _{j=1, 2, \ldots , n} a_{ij}$. Here, v⁻ is the DM’s gain floor, i.e., the minimum payoff DM achieved, and v⁺ is the Nature’s loss celling, i.e., the maximum payoff that Nature can loose. The matrix game has a saddle point if and only if v⁻ = v⁺. If the matrix game has no saddle point, then we choose the mixed strategy to solve the matrix game problems. In practical situation, the elements are described in an imprecise form within a matrix game. At this point, there is some fuzziness regarding the payoffs. In real-life decision making problem, the DMs may face that they partly know the idea to linguistic hesitant membership degree and linguistic hesitant non-membership degree of LPHFSs. For example, when the DM determines the membership and the non-membership of x into A, he/she can assess {0.5,0.6} and {0.2,0.3}, respectively. In this case, there may exist one type of the hesitant situation for PFSs. Since the criteria set is qualitative not quantitative, then the DM cannot make a crisp judgement values on the criteria. In this situation, it is suitable for the DM to use linguistic terms to represent his/her preference according to these criteria. As the preference systems are very complex, it is not possible for the DM to apply only one term to represent his/her view, due to the fact that he/she may be hesitate when calculating the values of alternatives along the criteria. Furthermore, DM may guess that Nature is against him. In light of the context, we choose an MCDM game with LPHF environment under fuzziness of DM who provides no news about the characteristics of the matrix. For example, when the DM assesses criteria as linguistic hesitant fuzzy membership and non-membership degrees, he/she can assign {s_0.2, s_0.3, s_0.4} and {s_0.6, s_0.7, s_0.8}, respectively. In this case, it provides an extra fact about the real-life situation. In the following, a conflicting situation is chosen based on LPHF environment for an MCDM game. An MCDM game can be adopted as a decision matrix whose elements indicate the rating values of all alternatives corresponding to each criterion. Let A = {A₁, A₂,…,A_m} be the set of alternatives and C = {C₁, C₂,…,C_n} be the set of criteria. Assume that W = (w₁, w₂,…,w_n) be the weight vector of all criteria, which satisfies 0 ≤ w_j ≤ 1 and $\sum \limits _{j=1}^{n}w_{j} = 1$. Under the LPHF environment, the rating of the alternative A_i corresponding to the criterion C_j is $A(hs_{\theta _{ij}}, gs_{\sigma _{ij}})~(i = 1, 2,\ldots , m; j = 1, 2,\ldots , n).$ Hence, the LPHF decision matrix A can be written as:

$$ A = \left[ {\begin{array}{ccccc} A(hs_{\theta_{11}}, gs_{\sigma_{11}}) & A(hs_{\theta_{12}}, gs_{\sigma_{12}}) & {\ldots} & A(hs_{\theta_{1n}}, gs_{\sigma_{1n}}) \\ A(hs_{\theta_{21}}, gs_{\sigma_{21}}) & A(hs_{\theta_{22}}, gs_{\sigma_{22}}) & {\ldots} & A(hs_{\theta_{2n}}, gs_{\sigma_{2n}}) \\ {\vdots} & {\vdots} & {\ldots} & {\vdots} \\ A(hs_{\theta_{m1}}, gs_{\sigma_{m1}}) & A(hs_{\theta_{m2}}, gs_{\sigma_{m2}}) & {\ldots} & A(hs_{\theta_{mn}}, gs_{\sigma_{mn}}) \end{array} } \right]. $$

Considering the numbers of the elements of LPHFEs of A may not be in same length, we want to normalize the decision matrix A. By using the value of t, we normalize the rating of all alternatives associates with each criterion C_j by using Definition 3.5, respectively, (j = 1,2,…,n). The normalized decision matrix is denoted as $A^{\prime } = (A(hs_{\theta _{ij}}^{\prime }, gs_{\sigma _{ij}}^{\prime }))_{m \times n}$. For each criterion C_j, we get $hs_{\theta _{1j}}^{\prime } = hs_{\theta _{2j}}^{\prime } = {\ldots } =hs_{\theta _{mj}}^{\prime }$ and $gs_{\sigma _{1j}}^{\prime } = gs_{\sigma _{2j}}^{\prime } = {\ldots } = gs_{\sigma _{mj}}^{\prime }$.

6 Extension of TOPSIS for MCDM game with LPHFEs

Based on the outcomes represented in Hwang and Yoon [16], we calculate two reference solutions when we adopt TOPSIS. The two reference solutions are the PIS and the NIS. Here the PIS maximizes the profit criteria and minimizes loss criteria but with the NIS, the opposite is true. By using the outcomes of Joshi and Kumar [20], we provide a new direction to obtain the PIS and the NIS based on $A^{\prime }$. At this point, the PIS and the NIS are explained as:

${A^{\prime }}^{+} = \{x_{1}^{+}, x_{2}^{+}, \ldots , x_{n}^{+}\}$ and ${A^{\prime }}^{-} = \{x_{1}^{-}, x_{2}^{-}, \ldots , x_{n}^{-}\}.$

For the PIS ${A^{\prime }}^{+}$, it can be calculated by the following formula:

$$ \begin{array}{@{}rcl@{}} {A^{\prime}}^{+} &=& \{x_{1}^{+}, x_{2}^{+}, \ldots, x_{n}^{+}\} \\&=&\{A(\{s_{1}\}, \{s_{0}\}), A(\{s_{1}\}, \{s_{0}\}),\ldots,A(\{s_{1}\}, \{s_{0}\})\}. \end{array} $$

(6.9)

Similarly, the NIS ${A^{\prime }}^{-}$ can be calculated as:

$$ \begin{array}{@{}rcl@{}} {A^{\prime}}^{-} &=& \{x_{1}^{-}, x_{2}^{-}, \ldots, x_{n}^{-}\} \\&=&\{A(\{s_{0}\}, \{s_{1}\}), A(\{s_{0}\}, \{s_{1}\}),\ldots,A(\{s_{0}\}, \{s_{1}\})\}. \end{array} $$

(6.10)

The algorithm for computing the distance between each alternative with PIS and NIS is shown in Algorithm 2.

where $y=\frac {1}{\#hs}{\sum }_{q=1}^{\#hs}|(({\beta _{q}^{1}})^{2}-({\beta _{q}^{2}})^{2})+\max \limits _{q=1,2,\ldots ,\#hs}(({\beta _{q}^{1}})^{2}-({\beta _{q}^{2}})^{2})|^{2}+\frac {1}{\#gs} {\sum }_{q=1}^{\#gs}|(({\gamma _{q}^{1}})^{2}-({\gamma _{q}^{2}})^{2})+\max \limits _{q=1,2,\ldots ,\#gs}(({\gamma _{q}^{1}})^{2}-({\gamma _{q}^{2}})^{2})|^{2}$ and z = |(π₁)² − (π₂)²|²).

Depending on the results of (4.6) and Theorem 4.2, the generalized hybrid distance between the alternative A_i and ${A^{\prime }}^{+}$ can be determined as:

$$ \begin{array}{@{}rcl@{}} &&d(A_{i}, {A^{\prime}}^{+}) \\ &&=\sum\limits_{j=1}^{n}w_{j}d(A(hs_{\theta_{ij}}^{\prime}, gs_{\sigma_{ij}}^{\prime}), A(\{s_{1}\}, \{s_{0}\})) \\ &&=\sum\limits_{j=1}^{n}w_{j}\left( \begin{array}{ll}\frac{1}{2}(\frac{1}{\#hs_{\theta_{ij}}^{\prime}}\sum\limits_{s_{\beta_{q} \in hs_{\theta_{ij}}^{\prime}}}((1-(\beta_{q})^{2})+\max\limits_{q=1,2,\ldots,\#hs_{\theta_{ij}}^{\prime}}(1-(\beta_{q})^{2}))^{\lambda}+\frac{1}{\#gs_{\sigma_{ij}}^{\prime}} \sum\limits_{s_{\gamma_{q} \in gs_{\sigma_{ij}}^{\prime}}}(({\gamma_{q}^{2}})\\+\max\limits_{q=1,2,\ldots,\#gs_{\sigma_{ij}}^{\prime}} ({\gamma_{q}^{2}}))^{\lambda}+(1-(\frac{1}{\#hs_{\theta_{ij}}^{\prime}}\sum\limits_{s_{\beta_{q} \in hs_{\theta_{ij}}^{\prime}}}(\beta_{q})^{2}+\frac{1}{\#gs_{\sigma_{ij}}^{\prime}}\sum\limits_{s_{\gamma_{q}} \in \#gs_{\sigma_{ij}}^{\prime}}(\gamma_{q})^{2}))^{\lambda}) \end{array}\right)^{\frac{1}{\lambda}}. \end{array} $$

(6.11)

Based on the results of (4.6) and Theorem 4.3, the distance between the alternative A_i and ${A^{\prime }}^{-}$ can be calculated as:

$$ \begin{array}{@{}rcl@{}} &&d(A_{i}, {A^{\prime}}^{-}) \\ &&=\sum\limits_{j=1}^{n}w_{j}d(A(hs_{\theta_{ij}}^{\prime}, gs_{\sigma_{ij}}^{\prime}), A(\{s_{0}\}, \{s_{1}\})) \\ &&=\sum\limits_{j=1}^{n}w_{j}\left( \begin{array}{ll}\frac{1}{2}(\frac{1}{\#hs_{\theta_{ij}}^{\prime}}\sum\limits_{s_{\beta_{q} \in hs_{\theta_{ij}}^{\prime}}}((\beta_{q})^{2}+\max\limits_{q=1,2,\ldots,\#hs_{\theta_{ij}}^{\prime}}(\beta_{q})^{2})^{\lambda}+\frac{1}{\#gs_{\sigma_{ij}}^{\prime}}\sum\limits_{s_{\gamma_{q} \in gs_{\sigma_{ij}}^{\prime}}}((1-(\gamma_{q})^{2})\\+\max\limits_{q=1,2,\ldots,\#gs_{\sigma_{ij}}^{\prime}}(1- (\gamma_{q})^{2}))^{\lambda}+(1-(\frac{1}{\#hs_{\theta_{ij}}^{\prime}}\sum\limits_{s_{\beta_{q} \in hs_{\theta_{ij}}^{\prime}}}(\beta_{q})^{2}+\frac{1}{\#gs_{\sigma_{ij}}^{\prime}}\sum\limits_{s_{\gamma_{q}} \in gs_{\sigma_{ij}}^{\prime}}(\gamma_{q})^{2}))^{\lambda}) \end{array}\right)^{\frac{1}{\lambda}} \end{array} $$

(6.12)

It is pointed that first we complete the normalization process of LPHFEs by using Algorithm 1 before the calculation process of (6.11)-(6.12). Next we determine the relative closeness of the alternative A_i corresponding to the PIS and the NIS as:

$$ RC(A_{i}) = \frac{d(A_{i}, {A^{\prime}}^{-})}{d(A_{i}, {A^{\prime}}^{-})+d(A_{i}, {A^{\prime}}^{+})}. $$

(6.13)

The ranking orders of all alternatives can be calculated according to relative closeness coefficient RC(A_i).

6.1 Decision making procedure

Now we develop a decision making procedure of the application of extended TOPSIS in LPHF-MCDM game based on the above-mentioned (see Section 6) results.

• Step 1: In real-life decision making problem, first we determine the set of alternatives A = {A₁, A₂,…,A_m} and the set of criteria C = {C₁, C₂,…,C_n}. Furthermore, the criteria have a weighting vector W = (w₁, w₂,…,w_n), t and λ, where 0 ≤ w_j ≤ 1 and ${\sum }_{j=1}^{n}w_{j}=1$. Finally, we establish LPHF-MCDM game $A = (A(hs_{\theta _{ij}}, gs_{\sigma _{ij}}))_{m \times n}$, where $A(hs_{\theta _{ij}}, gs_{\sigma _{ij}})$ is the rating of the alternative A_i (i = 1,2,…,m) corresponding to the criterion C_j (j = 1,2,…,n).

• Step 2: By using the value of t, we normalize the LPHF-MCDM game based on Definition 4.5, which is indicated as $A^{\prime } = (A(hs_{\theta _{ij}}^{\prime }, gs_{\sigma _{ij}}^{\prime }))_{m \times n}~(i=1, 2,\ldots ,m)~(j=1, 2, \ldots ,n)$.

• Step 3: Depending on (6.9) and (6.10), we determine the PIS ${A^{\prime }}^{+} = \{x_{1}^{+}, x_{2}^{+}, \ldots , x_{n}^{+}\}$ and the NIS ${A^{\prime }}^{-} = \{x_{1}^{-}, x_{2}^{-}, \ldots , x_{n}^{-}\}.$

• Step 4: Based on Definition 4.5, we further normalize the reference solutions ${A^{\prime }}^{+}$ and ${A^{\prime }}^{-}$ according as LPHF-MCDM game $A^{\prime } = (A(hs_{\theta _{ij}}^{\prime }, gs_{\sigma _{ij}}^{\prime }))_{m \times n}.$

• Step 5: For each alternative A_i, we determine the generalized hybrid distance $d(A_{i}, {A^{\prime }}^{+})$ between the alternative A_i and ${A^{\prime }}^{+}$ by using (6.11). Furthermore, the generalized hybrid distance $d(A_{i}, {A^{\prime }}^{-})$ between the alternative A_i and ${A^{\prime }}^{-}$ is computed by using (6.12).

• Step 6: By using the (6.13), we also determine the relative closeness of the alternative A_i corresponding to the respective PIS ${A^{\prime }}^{+}$ and NIS ${A^{\prime }}^{-}$, which is indicated as RC(A_i).

• Step 7: At last we rank all the alternatives according to their score.

7 Real-life problems

In this section, two real-life examples are provided to check the applicability and feasibility of the proposed method for solving an LPHF-MCDM game.

Example 7.1

Assume that a northern American based company wants to expand their policy in several continents to become more popular in the world. The aim is to consider the most effective continent according to the group strategy objective. For this purpose, the company (here as DM) prepare a team to choose the top among five possible alternatives (strategies) after their preliminary analysis and are defined as A₁: Expand to African market; A₂: Expand to the southern American market; A₃: Expand to the Asian market; A₄: Expand to European market and A₅ : Expand to all four continents. To assess these strategies, the company considers the economical condition as the prime factor for the next year. For this purpose, they determine each strategy based on four criteria and they are as follows: C₁: Relaxation in corporate tax; C₂: Risk of production; C₃: Benefit in short term and C₄: Benefit in long term. Moreover, the weight vector of the criteria is given W = (0.15,0.25,0.20,0.40). Since the criteria are qualitative, these are compatible and only feasible for the DM to disclose the ratings by using linguistic terms. Hence, the DM builds a seven point linguistic scale to evaluate the whole problem, which is S = {s₀ = very poor,s₁ = poor,s₂ = slightly poor,s₃ = medium,s₄ = slightly medium,s₅ = good,s₆ = very good}. Based on LPHF environment, DM invites the team to determine these alternatives based on these criteria with LPHFEs. Hence the LPHF-MCDM game A is shown in Table 2.

Table 2 The LPHF-MCDM game A

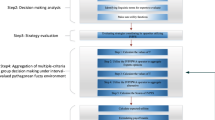
7.1 Decision making analysis based on TOPSIS

Depending on LPHF-MCDM game, we depict the decision making analysis of our proposed method. Assume that t = 0.5 and λ = 2. At first, we normalize the LPHF-MCDM game by using Definition 4.5. So the normalized LPHF-MCDM game $A^{\prime }$ is shown in Table 3.

Table 3 The normalized LPHF-MCDM game $A^{\prime }$

According to the normalized LPHF-MCDM game i.e., Table 3, we obtain the normalization of reference solutions A⁺ and A⁻ which are as:

$$ \begin{array}{@{}rcl@{}} {A^{\prime}}^{+} \!&=&\! \{x_{1}^{+}, x_{2}^{+}, x_{3}^{+}, x_{4}^{+}\}\\ \!&=&\!\left( \begin{array}{ll}A(\{s_{1}, s_{1}, s_{1}, s_{1}\}, \{s_{0}, s_{0}, s_{0}\}), A(\{s_{1}, s_{1}, s_{1}, s_{1}\}, \{s_{0}, s_{0}, s_{0}\}),\\ A(\{s_{1}, s_{1}, s_{1}, s_{1}\}, \{s_{0}, s_{0}, s_{0}\}), A(\{s_{1}, s_{1}, s_{1}, s_{1}\}, \{s_{0}, s_{0}, s_{0}\}) \end{array} \right).\\ {A^{\prime}}^{-} \!&=&\! \{x_{1}^{-}, x_{2}^{-}, x_{3}^{-}, x_{4}^{-}\}\\ \!&=&\!\left( \begin{array}{ll}A(\{s_{0}, s_{0}, s_{0}, s_{0}\}, \{s_{1}, s_{1}, s_{1}\}), A(\{s_{0}, s_{0}, s_{0}, s_{0}\}, \{s_{1}, s_{1}, s_{1}\}),\\ A(\{s_{0}, s_{0}, s_{0}, s_{0}\}, \{s_{1}, s_{1}, s_{1}\}), A(\{s_{0}, s_{0}, s_{0}, s_{0}\}, \{s_{1}, s_{1}, s_{1}\}) \end{array} \right). \end{array} $$

By using (6.11) and (6.12), we calculate the generalized hybrid distances $d(A_{i}, {A^{\prime }}^{+})$ and $d(A_{i}, {A^{\prime }}^{-})$ for the alternatives A_i (i = 1,2,…,5). The outcomes are shown in Table 4.

Table 4 The generalized hybrid distance for each alternative

Based on (6.13), we also determine the relative closeness of each alternative corresponding to the PIS ${A^{\prime }}^{+}$ and the NIS ${A^{\prime }}^{-}$. The outcomes are shown as: RC(A₁) = 0.514,RC(A₂) = 0.504,RC(A₃) = 0.542,RC(A₄) = 0.527 and RC(A₅) = 0.465. So, the ranking order of the five alternatives is A₃ > A₄ > A₁ > A₂ > A₅. In this case, we find A₃ is the best alternative.

7.2 Sensitivity analysis

Here we consider two key parameters t and λ during the decision analysis of our extended TOPSIS. Now we study the effect of changes on the ranking order of alternatives with the help of parameters. The sensitivity analysis is done in two ways by changing each of the parameters. Firstly, taking the fixed values of t, we discuss the score of each alternative with increasing the value of λ. Secondly, taking the fixed value of λ, the score of each alternative is discussed with increasing the value of t. So the impacts of the parameters to select the best alternative are analyzed successively.

• (i) The impact of λ to select the best alternative:

  By using the values of t, we normalize the decision matrix A and determine the relative closeness of the alternatives with the various values of λ. The results are shown in Tables 5 and 6. In Tables 5 and 6, we discuss two cases of t, i.e., t = 0 and t = 1 respectively. Applying the value of t, we can find the relative closeness of each alternative with respect to the PIS and the NIS has a decreasing trend with increasing the value of λ. In most of the cases A₃ is the best alternative.

• (ii) The impact of t to select the best alternative:

  We normalize the decision matrix A with respect to the values of λ and by using the values of t, we calculate the relative closeness of the alternative. The results are shown in Tables 7, 8 and 9, respectively. We discuss three cases of λ, i.e., λ = 1,λ = 2 and λ = 10. Applying the values of λ, we find the relative closeness of each alternative with respect to the PIS and the NIS which have an increasing trend with increasing value of t. In most cases, the ranking order A₃ > A₄ > A₁ > A₂ > A₅ holds.

Table 5 Ranking order of the alternatives for various values of λ with respect to t = 0

Table 6 Ranking order of the alternatives for various values of λ with respect to t = 1

Table 7 Ranking order of the alternatives for various values of t with respect to λ = 1

Table 8 Ranking order of the alternatives for various values of t with respect to λ = 2

Table 9 Ranking order of the alternatives for various values of t with respect to λ = 10

The sensitivity analysis with change trend image that the decision-making results with respect to the parameters t and λ are depicted in Fig. 1.

Fig. 1

Comparison of the closeness coefficient of the alternative with different values of t and λ

The LPHF-MCDM decision matrix (Table 10) is considered as like the matrix game problem within the DM and Nature (the collective risks of entire types performed together).

Table 10 The LPHF-MCDM game B

7.3 Sensitivity analysis

In similar way, the impacts of the parameters t and λ are analyzed to select the best alternative during the decision analysis of our extended TOPSIS for this example.

• (i) The impact of λ to select the best alternative:

  By using the values of t, i.e., t = 0, t = 0.5, t = 0.7 and t = 1, we normalize the decision matrix B and determine the relative closeness of each alternative by using the different values of λ. Applying the value of t, we can find the relative closeness of each alternative with respect to the PIS and the NIS which have a decreasing trend with the increasing value of λ. The results are shown in Tables 11, 12 and 13. In most of the cases, A₃ is the best alternative.

• The impact of t to select the best alternative:

  We normalize the decision matrix A with the various values of λ and by using the values of t, we calculate the relative closeness of the alternatives. The results are shown in Tables 14, 15 and 16, respectively. We discuss three cases of λ, i.e., λ = 1,λ = 2 and λ = 10. Applying the values of λ, we find the relative closeness of each alternative with respect to the PIS and the NIS which have an increasing trend with the increasing value of t. In most cases, the ranking order A₃ > A₄ > A₁ > A₂ holds.

Table 11 Ranking order of each alternative for various values of λ with respect to t = 0

Table 12 Ranking order of each alternative for various values of λ with respect to t = 0.5

Table 13 Ranking order of each alternative for various values of λ with respect to t = 1

Table 14 Ranking order of each alternative for various values of t with respect to λ = 1

Table 15 Ranking order of each alternative for various values of t with respect to λ = 2

Table 16 Ranking order of each alternative for various values of t with respect to λ = 10

The sensitivity analysis with change trend image that the decision-making results with respect to the parameters t and λ are shown in Fig. 2.

Fig. 2

Comparison of the closeness coefficient of the alternative with different values of t and λ

8 Discussion

Here we extend the TOPSIS proposed by Zhang and Xu [55] under LPHF environment, but only focus on the Pythagorean fuzzy environment (Zhang and Xu [55] and Yager [49]). In this situation, the membership degree and non-membership degree of the PFN are single. With respect to our proposed method, the membership degree and the non-membership degree of the LPHFEs are LHFEs. Our method, by extending the TOPSIS to take into account the LPHF information which are well-suited to tackle the ambiguity and impreciseness inherent in MCDM game, does not need to transform PHFEs into HFEs but directly deals with these problems, and thus obtains better final decision results. In particular, when we meet some situations where the information is represented by several possible linguistic values in membership degree and non-membership degree, our method shows its great superiority in handling those MCDM games with LPHF information. In this section, we compare our proposed method with the method of Zhang and Xu [55]. In order to implement the method of Zhang and Xu [55], we consider three classic pretreatments for the elements of LHFEs: (i) the maximum; (ii) the average and (iii) the minimum. For comparison purpose, two primary parameters of our proposed method are considered as: λ = 1 and t = 0.5. Based on Table 2, we calculate individually and compare the obtained results by using the methods of Zhang and Xu [55] and our proposed method.

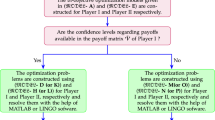
Ambika method: Motivated by Verma and Kumar [41], which overcomes some limitations of matrix games with Atanassov’s intuitionistic fuzzy payoffs, we introduce a modified Ambika method of hesitant fuzzy matrix game which was proposed by Xue et al. [46] to compare with the extended TOPSIS for solving LPHF-MCDM game. HFS is an extension of fuzzy set, which is constituted with only membership function. However, for comparison purpose, we consider the membership and non-membership functions when using the game method in Xue et al. [46]. Since the decision matrix is represented by LPHFEs. Here, first we incorporate the process of modified Ambika method for solving MCDM game with LPHFEs.

• Step 1: At first, we normalize the LPHF-MCDM game by using Definition 8.1 which is stated as follows:

  Definition 8.1

  Let us consider that two LPHFEs as a₁ $=A(hs_{\theta _{1}}, gs_{\sigma _{1}})= A(\{s_{0.2}, s_{0.3}, s_{0.4}\},\{s_{0.5}, s_{0.6}, s_{0.7}\})$ and $a_{2}=A(hs_{\theta _{2}}, gs_{\sigma _{2}})=A(\{s_{0.2}, s_{0.25}, s_{0.4}\},\{s_{0.5},$ s_0.7}), we obtain $\#gs_{\sigma _{1}} \neq \#gs_{\sigma _{2}}.$ To tackle the LPHFEs with various lengths are vital issues in the aggregating process of hesitant fuzzy information. In Definition 3.6, we define the common approaches such as minimum, average or maximum, to the shorter length LPHFEs. However adding the average value to the shorter length is more significant than the minimum or maximum value, original information is still not unchanged. Here $gs_{\sigma _{1}}=\{s_{0.5}, s_{0.6}, s_{0.7}\}$ and $gs_{\sigma _{2}}=\{s_{0.5}, s_{0.7}\}$. If we consider the average value S_0.6 to $gs_{\sigma _{2}}$ then the two LPHFEs have the same length but the method of attaching elements changes the actual information of LPHFEs. Thus the obtained result is inappropriate to some extent. To handle this situation, we introduce a new idea, i.e., the possibility of each linguistic element, to the LPHFEs. We add s_0.7 to $gs_{\sigma _{2}}$, so the possibility of s_0.5 is s₁ and the possibility of s_0.7 is s_0.5. Thus the $gs_{\sigma _{2}}$ can be converted into $\{s_{0.5}^{s_{1}}, s_{0.7}^{s_{0.5}}, s_{0.7}^{s_{0.5}}\}$. Also $gs_{\sigma _{1}}=$ {s_0.5, s_0.6, s_0.7} can be considered as $\{s_{0.5}^{s_{1}}, s_{0.6}^{s_{1}}, s_{0.7}^{s_{1}}\}$. The alteration approach is not only establish a comparison of $a_{1}=A(hs_{\theta _{1}}, gs_{\sigma _{1}})$ and $a_{2}=A(hs_{\theta _{2}},$ $gs_{\sigma _{2}})$, but also abolish any LPHF information loss.

• Step 2: Now we define the Value Index (VI) and Ambiguity Index (AI) of normalized LPHFEs in MCDM game and which are follows: VI and AI: Let us assume that the LPHFEs as $\bar {a}^{\prime }=A(\bar {hs_{\theta }}^{\prime }, \bar {gs_{\sigma }}^{\prime })$, where $\bar {hs_{\theta }}^{\prime }=\cup _{s_{\beta _{q}\in \bar {hs_{\theta }}^{\prime }}}\left \lbrace s_{\beta _{q}}^{s_{p_{q}}} : q=1,\ldots ,\#\bar {hs_{\theta }}^{\prime }\right \rbrace (\#\bar {hs_{\theta }}^{\prime }$ is the length of linguistic term in $\bar {hs_{\theta }}^{\prime })$ and $\bar {gs_{\sigma }}^{\prime }=\cup _{s_{\gamma _{q}\in \bar {gs_{\sigma }}^{\prime }}}\left \lbrace s_{\gamma _{q}}^{s_{r_{q}}}: q=1,\ldots ,\#\bar {gs_{\sigma }}^{\prime }\right \rbrace (\#\bar {gs_{\sigma }}^{\prime }$ is the length of linguistic term in $\bar {gs_{\sigma }}^{\prime })$. Here ${s_{p_{q}}}$ and ${s_{r_{q}}}$ are the corresponding possibility of each linguistic element of $s_{\beta _{q}}$ and $s_{\gamma _{q}}$, respectively. So the VI, $VI(\bar {a}^{\prime })$ is defined as:

  $$ VI(\bar{a}^{\prime}) =\sum\limits_{q=1}^{\#hs}\beta_{q}.\frac{p_{q}}{\sum\limits_{q=1}^{\#hs}p_{q}}-\sum\limits_{q=1}^{\#gs}\gamma_{q}.\frac{r_{q}}{\sum\limits_{q=1}^{\#gs}r_{q}}, $$

  and AI, $AI(\bar {a}^{\prime })$ is defined as:

  $$ \begin{array}{@{}rcl@{}} AI(\bar{a}^{\prime}) &=&\sum\limits_{q=1}^{\#hs}\big|\beta_{q}-\beta_{q}.\frac{p_{q}}{\sum\limits_{q=1}^{\#hs}p_{q}}\big|.\frac{p_{q}}{\sum\limits_{q=1}^{\#hs}p_{q}}\\&&+\sum\limits_{q=1}^{\#gs}\big|\gamma_{q}-\gamma_{q}.\frac{r_{q}}{\sum\limits_{q=1}^{\#gs}r_{q}}\big|.\frac{r_{q}}{\sum\limits_{q=1}^{\#gs}r_{q}}. \end{array} $$

• Step 3: In order to the proposed value and ambiguity indexes, the Ambika method of LPHF-MCDM is developed to find the optimal solutions of Example 1 by solving the linear programming models (Xue et al. [46]).

• Step 4: Finally, based on the VI, score of each alternative is obtained by using the score function $S(A_{i})=y_{j}^{*}({\sum }_{i=1}^{m}\bigoplus VI(A)x_{i}^{*} )$ and based on the AI, the score of each alternative is obtained by using the score function $S(A_{i})=y_{j}^{*}({\sum }_{i=1}^{m}\bigoplus AI(A)x_{i}^{*}).$

Based on linear programming models, we obtain DM’s optimal solutions $(x_{1}^{*}, u_{1}^{*}),$ where $x_{1}^{*}=(1.000, 0.000,$ 0.000,0.000), and $(x_{2}^{*}, u_{2}^{*}),$ where $x_{2}^{*}=(0.000, 0.774,$ 0.008,0.217). The value and ambiguity indexes for player DM’s gain floor are 1.033 and 0.780. Here $u_{1}^{*}>u_{2}^{*},$ then DM’s optimal solution is $x_{2}^{*}=(0.000, 0.774, 0.008,$ 0.217). Similarly, we obtain Nature’s optimal solutions $(y_{1}^{*}, v_{1}^{*}),$ where $y_{1}^{*}=(0.000, 0.000, 0.000, 0.000,$ 1.000), and $(y_{2}^{*}, v_{2}^{*}),$ where $y_{2}^{*}=(0.000, 0.117, 0.576,$ 0.307,0.000). The value and ambiguity indexes for Nature’s loss-ceiling are 0.000 and 0.7802. Here $v_{2}^{*}>v_{1}^{*},$ then Nature’s optimal solution is $y_{2}^{*}=(0.000, 0.117, 0.576,$ 0.307,0.000). However, there are no other optimal solutions. Finally, the score of each alternative based on VI are S(A₁) = 0.000,S(A₂) = 0.139,S(A₃) = 0.631,S(A₄) = 0.338 and S(A₅) = 0.000. Also, the score of each alternative based on AI are S(A₁) = 0.000,S(A₂) = 0.091, S(A₃) = 0.449,S(A₄) = 0.478 and S(A₅) = 0.000. The results are shown in Table 17.

Table 17 The comparison results are obtained by Zhang and Xu [53] and Xue et al. [46] methods

From Table 17, the results obtained by the method of Zhang and Xu [55] with the average and the Ambika method (Xue et al. [46]) with the VI are compatible with our proposed method. It exhibits that our proposed method holds all the linguistic hesitant evaluation information. For maximum and minimum considerations, the results obtained from Zhang and Xu [55] and Ambika method (Xue et al. [46]) are different from those derived by our proposed method. In most of the cases A₃ is the best alternative according to their scores. In this case, the maximum and the minimum pretreatments present the two extremes, which may loss a lot of information.

8.1 Computational complexity analysis with different methods

The complexity of a model is, therefore, sometimes used to mean the difficulty in understanding the model or the difficulty in terms of resources required in generating model behaviour. To analyze the computational complexity of the proposed method and the methods of Zhang and Xu [55] and Ambika method (Xue et al. [46]), we assume that m alternatives and n criteria. Therefore, there is mn evaluation information. For the real-life problem (i.e., Example 1), described in Section 7, four alternatives and four criteria are chosen. Considering that the methods of Zhang and Xu [55] and Ambika method (Xue et al. [46]) are based on MCDM game. Therefore, the comparison is divided into two parts: (i) Zhang and Xu [55] (ii) Ambika method (Xue et al. [46])

8.1.1 Comparative analysis with the existing methods Zhang and Xu [55]

For the method in Zhang and Xu [55], the main idea is to find the Pythagorean fuzzy PIS and Pythagorean fuzzy NIS, and then to incorporate the distance measure to rank the alternatives. But in proposed method, first we determine the normalized LPHF-MCDM game by using Algorithm 1 to obtain the PIS and NIS. After that, we calculate the rank of alternative according to their score based on a new distance measure by applying Algorithm 2. So in the procedures, there is significant difference in the amount of computation due to linguistic preference in the proposed method. Also, the main difference is that our proposed method is scalable to meet a variety of situations by adjusting its own parameters, i.e., it has very good flexibility and extension.

8.1.2 Ambika method (Xue et al. [46])

In Ambika method (Xue et al. [46]), first we determine the VI and AI of normalized LPHFEs in MCDM game and then the Ambika method of LPHF-MCDM is developed to find the optimal solution of Example 1 by using LINGO 17.0.9 software. At last, based on the VI and AI, the score of each alternative is obtained.

Comparing with Zhang and Xu [55] and Ambika method (Xue et al. [46]), our proposed method is very easy to capture and less computational effort for solving purpose. We develop here a simple and effective decision method to solve an MCDM game with LPHFEs. Also two algorithms are emerged to obtain the normalization of LPHFEs and the distance between each alternative with PIS and NIS. All the methods are solved in LINGO 17.0.9 software except extended TOPSIS, which is solved in EXCEL on a computer with 2.10 GH CPU and 8GB RAM. The CPU times for solving Example 1 by considering all the methods are depicted in Table 17. From Table 17, we see that the proposed methods has taken more CPU times but generated efficient solution than the other methods. Also, we see that time for solving two examples by TOPSIS are longest. We accommodate more information by considering LPHF-MCDM game in practical situation. From Algorithm 2, we see that the order of computational complexity is O(mn).

8.2 Pros and cons of the proposed method

The pros and cons of our proposed method are summarized as follows:

• The proposed method is very flexible to deal with several types of situations by adjusting its own parameters.

• The LPHFSs of our proposed method can advantageously discuss more general decision-making situations.

• In addition with TOPSIS, our proposed method avoids the satisfaction level of the alternatives to the ideal solutions for building the decision.

• The existing decision-making methods based on aggregation operators (Du et al. [11], Liu et al. [23]) simply aggregate a series of LPHFSs into a single one. They do not consider the relationships among attributes. But our proposed TOPSIS can efficiently achieve trade-offs among conflicting attributes.

• The proposed TOPSIS method based on LPHF environment uses the distance measure to calculate the proximity between each alternative and ideal solutions. It is a new way to make the decisions under the LPHF environment.

• Ambika method of LPHF-MCDM game fully adopts the effective significance of imprecise information of the LPHF-MCDM games by the optimized method of aggregating the LPHF information.

• In Ambika method, first we obtain the optimal solutions of LPHF-MCDM game then the score of each alternative is determined. But in TOPSIS, the score of each alternative is obtained directly. For this purpose, a comparison can be drawn between TOPSIS and Ambika method to show the changes on ranking order of alternatives.

• The proposed method is applied to solve not only the LPHF-MCDM game, but also develop a primary way of LPHFS theory in decision making process.

• In this paper, the weight of each criterion is given for extended TOPSIS. But in some real-life problems, the weights are unknown. Therefore, it is a questionable to select the proper weight for the decision making problem. This can be treated as one of weak novelty of those methods. However we trust that these could be overcome in coming years.

9 Conclusion and future works

In this study, we have proposed a new idea of LPHFSs by combining the concepts of HFSs, LFSs and PFSs. After that, we have analyzed the normalization procedure and the generalized hybrid distance of LPHFSs. By using these results, we have established the application of LPHFSs to MCDM game based on TOPSIS and Ambika method and develop a ranking approach for the LPHF-MCDM game. Here, LPHFSs are not only employ to disclose the linguistic hesitant fuzzy evaluations of the DM’s, but also remain the advantages of PFSs, LFSs and HFSs, which accommodates more complex decision making conditions. Comparing with the existing research works, LPHFSs as the generalized format which can establish some usual linguistic hesitant fuzzy scenarios. Our proposed method provides a solution in the view of considering linguistic hesitant situations of the DM and generalizes the extension of applications of LPHF-MCDM game.

In the future, one can extend our research work to the interval-valued LPHF environment (Garg [14]), intuitionistic soft set (Cagman and Karatas [10]) and other uncertain environment and further developing its applications.