1 Introduction

The imbalanced distribution problem is a special classification task in machine learning [22, 36, 44] in which the minority classes include a smaller number of samples than the majority classes. Therefore, there is a large number of minority classes, which are ignored and difficult to model effectively. The imbalanced distribution problem exists in numerous areas [7, 12, 29], such as image classification [11], age estimation [24], cancer diagnosis [28], and face recognition [47].

There are three challenges in addressing the imbalanced distribution problem. First of all, the minority classes are an important part of the whole dataset. Thus, we should consider them as seriously as the majority classes. Secondly, traditional classifiers were initially designed for balanced datasets. The lack of ability leads to hyperplane bias in the majority classes. Thirdly, the samples in the minority classes cannot contain rich information. The samples in different classes cannot be correctly recognized.

The existing approaches above have tried to tackle the imbalanced problem in binary and multi-classification. However, many datasets contain dozens or hundreds of imbalanced distribution classes, which are organized in hierarchical trees. Hierarchical tree structures exist in various applications, such as image classification [17, 50], protein classification, and texture classification [35]. The increasing number of classes within a hierarchical structure [48] provides great supplementary information for solving imbalanced distribution problems.

In this paper, we combine hierarchical classification [10, 26, 38] and cost-sensitive learning [25] to address imbalanced distribution datasets. The algorithm takes advantage of the hierarchical information of classes in datasets to design a cost-sensitive model. First, we make use of the hierarchical structure to divide a large-scale classification problem into several small-scale ones. Small-scale classification tasks are much easier to control and compute. Second, the logistic regression algorithm is used to calculate the probabilities of all classes on each level. This model obtains more accurate classification probabilities without assuming the distribution of the datasets. The hierarchical structure provides hierarchical information of different classes. Then, we set a threshold based on information entropy to determine the cost-sensitive factor for balancing the majority and minority classes. The threshold extracts and measures the information of the majority and minority classes to decide the cost-sensitive factor that suits each class. The threshold increases the accuracy of minority classes and reduces inter-level error propagation on each level.

Finally, we design a cost-sensitive model based on hierarchical information entropy [6] and the information [39, 41] of different classes. Two cost-sensitive methods provide different punishments to prevent the classifier from biasing the majority classes. We compare the proposed model with the traditional hierarchical classification approach. In terms of improving the overall accuracy, the accuracies of the minority class are increased significantly.

The contributions of this paper are as follows:

  • We build a quick, cost-sensitive, hierarchical classification model to address imbalanced distribution data problems. It is different from existing cost-sensitive classification models, mainly on hierarchical structure.

  • We construct an adaptive threshold strategy instead of a fixed threshold value. With this strategy, the threshold value is decided by the data rather than given by users.

  • We compare the proposed algorithm with seven state-of-the-art hierarchical algorithms on five imbalanced distribution datasets to demonstrate its great efficiency and effectiveness.

The remainder of this paper is presented as follows. In Section 3, we introduce the proposed cost-sensitive hierarchical classification algorithm. The experiment settings about datasets, compared algorithms and evaluation metrics are given in Section 4. Experimental results and discussion about hierarchical classification on imbalanced distribution datasets are in Section 5. Finally, we present the conclusions and future work of this paper in Section 6.

2 Related work

Resampling [14, 23, 32] and cost-sensitive learning [13] are two traditional solutions to the imbalanced distribution problem.

The resampling method solves this problem by balancing the numbers of samples in the majority and minority classes. The resampling method changes the original data structure, which loses precious data. The resampling methods include undersampling of the majority classes and oversampling of the minority classes. Liu et al. [20] used two undersampling strategies which include the cluster centers to represent the majority class and the nearest neighbors of the cluster centers to address the class imbalanced data. Castellanos et al. [5] proposed an approach based on adapting the well-known synthetic minority oversampling technique algorithm to the string space.

Cost-sensitive learning is a powerful tool for solving the imbalanced distribution problem without altering the original data. Researchers have done much work to address imbalanced distribution problems with cost-sensitive methods [21, 37, 46]. For instance, Sahin et al. [30] proposed a cost-sensitive decision tree algorithm for minimizing the sum of misclassification costs and improving the true-positive proportion of datasets. Similarly, Braytee et al. [2] addressed a cost-sensitive strategy using the imbalanced proportion of classes for feature extraction to punish the majority classes. In addition, Cao et al. [4] designed a novel framework for training a cost-sensitive classifier that is driven by imbalanced evaluation criteria.

Some researchers have focused on cost-sensitive practical applications [33]. For instance, Sheng et al. [34] constructed a decision tree to decrease the total misclassification costs and feature costs of medical diagnostic tests. Zhang et al. [47] proposed two cost-sensitive methods using Bayes decision theory and a k-NN classifier for solving group face-recognition tasks.

3 Cost-sensitive hierarchical classification algorithm

3.1 Basic framework

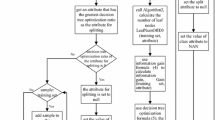
The framework involves cost-sensitive hierarchical classification via multi-scale information entropy for data with an imbalanced distribution. It contains two cost-sensitive weighting processes and an important threshold strategy. The proposed framework is listed in Fig. 1, which contains the following three parts:

  1. (1)

    The first part of Fig. 1 introduces the hierarchical structure used for imbalanced data and hierarchical classification. The hierarchical class structure and number of samples are listed in this tree. For instance, there are three sub-classes of Class Animal, which number 500, 30, and 300, respectively. The number of samples varies greatly from class to class, which results in imbalanced data with a hierarchical structure. For hierarchical classification, the classifier classifies the samples from coarse- to fine-grained. For the new samples, we first divide them into coarse classes and then subdivide them into fine classes.

  2. (2)

    The second part of Fig. 1 presents hierarchical classification with a threshold strategy. The classifier computes the probability on the second level. The algorithm computes the difference between the two maximum probabilities. The algorithm computes information entropy, based on the probability of each class, as the threshold value.

  3. (3)

    The third part of Fig. 1 introduces hierarchical classification with cost-sensitive learning. The algorithm gives different cost-sensitive weights to different classes based on the threshold. The classifier selects the class according to the weighted probability.

Fig. 1
figure 1

The framework of cost -sensitive hierarchical classification via multi-scale information entropy for data with an imbalanced distribution

Full size image

3.2 Hierarchical structure and classification

We decompose a large-scale classification task into multiple controllable small-scale classification tasks. All the classes are grouped into the hierarchical tree structure. The root node is at the top of the hierarchical tree structure. A sibling node means that two or more nodes share the same parent node. Nodes on the second level have sibling and child nodes. Leaf nodes only have sibling nodes. An example of a hierarchical tree structure is shown in Fig. 2. From this figure, we have the following:

  1. (1)

    Root node is Node Object;

  2. (2)

    Node Animal is a sibling node of Node Plant;

  3. (3)

    Node Animal has three leaf nodes.

Fig. 2
figure 2

Hierarchical classification tree structure (h = 3)

Full size image

Let X ∈ \(\mathbb {R}^{m \times n}\) be a data matrix, where m is the number of samples, and n is the number of features. We use xi to represent the i-th sample, xi ∈ \(\mathbb {R}^{m \times n}\) and X= {x1;x2;⋯;xm}. Let Y ∈ \(\mathbb {R}^{m \times 1}\) be a class vector. We use yi to represent the class of xi, where yi ∈ Y and Y= {y1;y2;⋯;ym}.

Logistic regression is a great classification algorithm used in supervised learning and has many advantages. It can directly model the classification possibility without assuming the data distribution in advance, thus avoiding problems caused by an inaccurate hypothesis distribution. It can not only predict the category but can also predict the approximate probability. The computing cost is low and large amounts of data can be processed with few resources. We can obtain parameter w and parameter b after training the training set of the dataset. Parameter w is a matrix and parameter b is a vector. We use a sigmoid function for the probability p. The sigmoid function is denoted as follows:

$$ p = \frac{1}{1+e^{-\mathbf{w}^{T}\mathbf{x}_{i}-\mathrm{b}}}. $$
(1)

In the hierarchical tree structure, logistic regression first computes the probability of every node from the root node to the leaf node. The probability that the i-th sample belongs to j-th class on the h-th level is computed as the following equation:

$$ {p_{h}^{j}} = \frac{1}{1+e^{-(\mathbf{w}_{h}^{i})^{T}\mathbf{x}_{i}-\mathrm{b}_{h}^{i}}}. $$
(2)

We define parameter \(p_{h}^{max}\) as the maximum probability from all \({p_{h}^{j}}\) on the h-th level. Maximum probability means that the node has the shortest distance between itself and the hyperplane that the classifier builds. The classifier selects that node after comparing it with the probability of nodes on the same level. The classifier computes the probability of the child nodes of that node and selects the child node with the maximum probability. In a top-down process, the classifier repeats these two steps until the end is reached. We can understand the process of hierarchical classification better by referring to Fig. 2. The classifier determines the probabilities of Nodes Animal, Furniture and Plant, which are 0.2, 0.6, and 0.2, respectively. The classifier selects the Node Furniture as the best choice. The classifier makes the right choice on this level and computes the probability of nodes that belong to Node Furniture on the next level. The classifier still selects the node with the maximum probability on this level. The leaf label finally selected is the predicted label round after round.

3.3 Hierarchical classification with threshold

Hierarchical classification simply and directly selects the node with the maximum probability as the best choice on one level. However, there is only a slight gap between the maximum probability and others. Direct selection of the classifier leads to errors. The errors are passed to other branches along the tree structure, such that the classifier cannot obtain the correct classification and classification accuracy is reduced. To avoid the classifier directly selecting that node straight, the threshold is used as a judgment condition. We set the threshold for re-measuring the node with maximum probability.

The datasets we build are a collection of information. We extract and measure the information we want from all aspects of the classification. We make decisions about what to do based on mathematical expectations in real life, and information entropy is the mathematical expectation of a random variable. We use information entropy as a quantitative index of the information content of a system so that it can be further used as a criterion for the parameter selection. In the information entropy formula, the negative logarithm of probability indicates the amount of information carried by possible events. The sum of all possible information multiplied by the probability of its occurrence represents the expected value of all information in the whole system.

We define parameter ie as the value of the information entropy factor on each level. Parameter ie can be computed as per the following equation:

$$ ie =\frac{1}{2}*\left( 1-\sum\limits_{j=1}^{k} {p_{h}^{j}}log_{2}{p_{h}^{j}}\right), $$
(3)

where j is the j-th class on this level, and k is the number of classes on this level. We add one to the information entropy value and multiply it by one in two. This step is taken to prevent the information entropy value being > 1. We know that the difference between the two probabilities is < 1. We define parameter \(p_{h}^{max2}\) as the second maximum probabilities on the h-th level, and parameter γ as the difference between \(p_{h}^{max}\) and \(p_{h}^{max2}\). We compare γ with ie and assign a cost weight.

3.4 Hierarchical classification with cost-sensitive learning

After judgment of the threshold, the cost-sensitive method is used. We design a cost-sensitive model to re-measure the importance of the node with maximum probability if γ is greater than the value of the threshold. It combines the prior and posterior probabilities, which avoids the subjective bias of using only the prior probability and the overfitting phenomenon of using the sample information alone. Information entropy is composed of the uncertainty of each node, and the variation in uncertainty between nodes causes them to contribute different proportions to the information entropy. In this way, we set the proportion of information entropy as the posterior probability to determine the greatest importance of each node.

In the hierarchical tree structure, the root node at the top contains the coarse-grained information. By contrast, the leaf node at the bottom has fine-grained information. Different levels of precision result in different information weights, and different levels have different information weights. An imbalanced distribution dataset is built with classes containing more or fewer samples than others. The more similar the numbers of samples in each class, the more fair the classifier is. We consider hierarchical information entropy and the number of samples in each class as two cost-sensitive factors for balancing the gap between the majority classes and minority classes. The value of hierarchical information entropy at the h level can be denoted as ieh and can be computed with the following equation:

$$ ie_{h} =\frac{1}{2}* L_{h}*\left( 1-\sum\limits_{j=1}^{k} {p_{h}^{j}}log_{2}{p_{h}^{j}}\right), $$
(4)

where Lh is the weight of the h-th level in the hierarchical tree structure, h is the height of the hierarchical tree. We set the level of the root node as L0. Since L0 is the root node of the hierarchical tree, the weight of level L0 is set to 0. We set the weight to be the same as the number of levels. For example, the weight of level L1 is set to 1. We can understand the process of calculating hierarchical information entropy on each level more easily by referring to Fig. 3.

Fig. 3
figure 3

The calculation process of hierarchical information entropy on each level

Full size image

The differences between the majority and minority classes include the numbers of samples and the proportions of each child class. The majority classes have more child classes than the minority classes. We define parameter tj as the proportion of child class of the i-th class. Similarly, we count the number of samples of the j-th class as parameter Nj. After comparing the threshold, we propose two cost weights to address the imbalanced distribution of datasets. We multiply \({p_{h}^{j}}\) by tj to solve the imbalanced problem of child classes on the upper level if γ is greater than ie. We offer a cost weight if γ is less than ie. We consider ieh and Nj as a cost weight for balancing the sample gap between the majority and minority classes. We take the square root of Nj as a factor to avoid an extremely imbalanced distribution of sample numbers. We define parameter \(p{c^{j}_{h}}\) as the probability of the j-th class on the h-th level with a cost-sensitive weight. We compute \(p{c^{j}_{h}}\) using the following equation:

$$ p{c^{j}_{h}}={p^{j}_{h}}*\frac{1}{(\sqrt{N^{j}}+ie_{h})}. $$
(5)

In summary, we use information entropy as the threshold in the hierarchical classification system. The cost-sensitive model will be used for measurement work if γ is greater than the threshold. The cost-sensitive model is based on the posterior probability and the proportion of classes. This process re-measures and confirms the advantage of the node with the maximum probability on this level. We use hierarchical information entropy and the number of samples in each class as a cost-sensitive weight. We find the square roots of these numbers to balance and reduce the gap between the majority and minority classes. The cost-sensitive algorithm supports the minority classes for higher costs and reduces the gap between the high and low levels if γ is less than the threshold.

An example of a cost-sensitive hierarchical algorithm with a threshold is shown in Fig. 4. We make \({p_{1}^{2}} = 0.1\), \({p_{1}^{3}} = 0.8\) and \({p_{1}^{4}} = 0.1\). The value of ie is equal to 0.95, so the value of γ is less than the threshold. After reassigning weights, we obtain Class 3 as the best choice. We obtain \({p_{2}^{5}} = 0.1\) and \({p_{2}^{6}} = 0.9\). The value of ie is approximately equal to 0.71 and the value of γ is greater than the threshold. The cost-sensitive hierarchical algorithm assigns different cost weights to different classes based on two conditions. Finally, we obtain the best leaf node as Class 5.

Fig. 4
figure 4

Comparison of hierarchical classification and cost-sensitive hierarchical classification with the threshold

Full size image

The process of cost-sensitive hierarchical classification for imbalanced distribution datasets based on information entropy (CSHC) is set out in Algorithm 1. The threshold strategy of CSHC is introduced in Line 11 of Algorithm 1, and two cost-sensitive weights of CSHC are illustrated in Lines 12, 13, 15, and 16 in Algorithm 1. The computational complexity of the CSHC algorithm is O(cmn), where c is the number of classes, m represents the number of samples, and n is the number of features.

4 Experimental settings

We used 10-fold cross-validation in these experiments. We used a computer with an Intel Core i7-3770 processor, 16 GB of memory, and the Windows 10 operating system.Footnote 1 The five imbalanced distribution datasets in our experiments are introduced in Section 4.1. Seven state-of-the-art algorithms used for comparison with our algorithm are introduced in Section 4.2. In Section 4.3, we introduce the two evaluation metrics used in our experiments.

figure c

4.1 Datasets

A description of five experimental datasets is given in Table 1. The description includes the number of sample, feature, class, and height in these datasets.

Table 1 Data description
Full size table

ILSVRC57 [19]: The dataset is a subset of a public dataset named WordNet. All classes are organized as same as the hierarchical structure in WordNet dataset. The data of ILSVRC57 are built in a three-level tree with 65 categories. There are 57 leaf nodes and 4,096 features. These 57 leaf nodes are basically divided into 5 classes (Bird, Cat, Dog, Boat, and Car). The leaf node with the most samples involves 221 samples, and the leaf node with the least samples includes 155 samples.

CAR196: CAR196 is an image classification dataset which has 196 types of car pictures. There are 206 nodes built in a three-level tree. It contains 15,685 samples into 196 leaf nodes. The leaf node with the most samples contains 67 samples, and the leaf node with the least samples has 18 samples.

SUN [43]: SUN dataset is modified by a scene understanding image classification dataset. There are 343 nodes organized in a four-level height tree. 22,556 samples are divided into 324 leaf nodes. The leaf node with the most samples contains 1,075 samples, and the leaf node with the least samples includes 36 samples.

DD [8]: DD is a protein dataset that contains protein sequences. Protein sequences are represented by 473 features and divided into 27 important classes. It has a three-level hierarchical tree structure that contains 4 non-leaf nodes on the second level and 27 leaf nodes on the third level. The leaf node with the most samples contains 361 samples, and the leaf node with the least samples contains 17 samples.

F194 [42]: F194 is also a protein dataset with a three-level height tree. It includes 7 non-leaf nodes on the second level and 194 leaf nodes on the third level. These 194 leaf nodes stand for 194 protein classes. In these 194 classes, there are 361 samples in the leaf node with the most samples, but only 10 samples in the leaf node with the least samples.

4.2 Compared methods

  1. (1)

    HFSNM: FSNM is a feature selection [3, 40] method based on l2,1-norms minimization [27]. FSNM based on loss function makes the process of feature selection with joint sparsity efficient. The l2,1-norms used is robust in outlier points. We make Transform FSNM into a hierarchical feature selection algorithm named HFSNM that is applied to hierarchical datasets. We use support vector machine to classify the classes after hierarchical feature selection.

  2. (2)

    HmRMR: mRMR [28] algorithm is an approximation of the best maximum dependency feature selection algorithm in theory, which maximizes mutual information between the selected features and the joint distribution of classification variables. HmRMR [15] has feature selection ability for hierarchical datasets. After finishing hierarchical feature selection, we need support vector machine to classify the classes.

  3. (3)

    HRelief: Relief [18] algorithm is a feature selection approach. Relief does subset search work instead of global search and gives different weights to different attributes. We modify Relief to HRelief for suiting hierarchical datasets. After feature selection process, support vector machine identifies the classes.

  4. (4)

    HFISHER: Fisher Score [9] has good discriminating capability for feature selection. Fisher Score finishes the feature selection process using full data, which is totally labeled. We modify FISHER Score feature selection to HFISHER for hierarchical datasets and use support vector machine to identify the labels.

  5. (5)

    LBRM [45]: LBRM algorithm is a hierarchical classification method based on a local Bayes risk minimization approach. The LBRM algorithm balances predicting risks for choose to go to a lower level or to finish the prediction process at nodes on the tree structure. The LBRM algorithm can decide not to go down to the lower level. This step can greatly avoid the inter-level error propagation in the hierarchical structure.

  6. (6)

    HCMP [16]: HCMP is a hierarchical classification algorithm method using the best k-th paths for another round classification at non-leaf nodes in a hierarchical classification. The HCMP algorithm first classifies the best several selection on each tree level with logistic regression method. The HCMP algorithm then uses random forest method to select the best node from these several nodes.

  7. (7)

    FSFHC [49]: FSFHC is a hierarchical classification algorithm based on a recursive regularization feature selection. FSFHC method uses the structural relationship of hierarchical parent-child as its hierarchical regularization strategy. Hilbert-Schmidt Independence Criterion used in this method for measuring the distance of sibling nodes. Support vector machine algorithm is used for identifying classes after hierarchical feature selection.

4.3 Evaluation metrics

Classification accuracy (accuracy)

Accuracy is an important evaluation metric to measure the classification performance of classifiers. We compare the predicted labels of the classifier with the correct labels, and the ratio of the correct number of predicted labels to the total number is accuracy.

Hierarchical measure (F H)

Hierarchical F1 measure (FH) is an important criterion for hierarchical classification. FH measure considers the relationship between all ancestors and descendants of each class. FH includes hierarchical precision (PH), hierarchical recall (RH). PH, RH and FH are defined as follows.

$$ P_{H} =\frac{|\hat{D}_{aug} \cap D_{aug}|}{|\hat{D}_{aug}|}, $$
(6)
$$ R_{H} =\frac{|\hat{D}_{aug} \cap D_{aug}|}{|D_{aug}|}, $$
(7)
$$ F_{H} =\frac{2 \cdot P_{H} \cdot R_{H}}{P_{H} + R_{H}}, $$
(8)

where Daug = D ∪ anc(D), \(\hat {D}_{aug} = \hat {D} \cup {anc}(\hat {D})\), |⋅| is the number of elements, D is the right label, \(\hat {D}\) is the predicted label, and anc(D) is the parent label set of the right label to which the sample belongs.

5 Experimental results and discussion

In this section, we present the experimental results and discussion from three perspectives. In Section 5.1, we compare the running times of eight hierarchical classification methods to verify the efficiency of the CSHC algorithm. In Section 5.2, we compare the local classification accuracy at non-leaf nodes to discuss the impacts of cost sensitivity weights and the threshold strategy on hierarchical classification. In Section 5.3, we report the global hierarchical experimental results of the eight algorithms in terms of the two evaluation metrics to demonstrate the effectiveness of the proposed CSHC algorithm.

Table 2 Running time comparison of six algorithms on five different datasets (s)
Full size table

5.1 Running time comparison

Table 2 reports the performance of the eight hierarchical algorithms on the five datasets. Bold texts in Table 2 are used to emphasize the optimal calculation time of each dataset. LBRM, HCMP, and CSHC are all capable of hierarchical classification. In processing large numbers of samples and features, the hierarchical classification system learned from hierarchical data and quickly completed classification of the ILSVRC57, CAR196, and SUN datasets. The four hierarchical algorithms with feature selection needed a long feature-selection process and took more than 1000 s to classify these three datasets. CSHC achieved the best result on the SUN dataset. HFISHER had the perfect performance on the DD and F194 datasets. The hierarchical classification with feature selection algorithms showed advantages on the two smaller datasets. These two datasets were much smaller than the others in terms of both samples and features. CSHC was a close second place and achieved classification in 11.1 and 77.7 s on these two datasets, respectively. The running time rank of the FSFHC algorithm on the five datasets was stable. HCMP needed two classification methods for data processing. It spent much more than 100 s on each of the five datasets. In terms of average rank, CSHC demonstrated good efficiency in handling large and small datasets.

5.2 Compared with traditional hierarchical classification at non-leaf nodes

In this section, we compare the CSHC algorithm with a traditional hierarchical classifier (THC) on non-leaf nodes of the DD and F194 datasets. Tables 3 and 4 introduce the non-leaf nodes, numbers of child nodes, proportions of each non-leaf node sample in the total samples, and classification accuracy at non-leaf nodes on the DD and F194 datasets.

Table 3 Information of non-leaf nodes and accuracy of two algorithms on DD dataset (%)
Full size table

The DD dataset is built as a three-level tree. There are four child nodes of the root node. Nodes α, β, α/β, and α + β are non-leaf nodes, called Nodes 1 to 4 for short. Nodes 1 and 4 are minority classes that have six and three child nodes, respectively. The proportions of their samples are significantly less than those of the other two nodes. The DD dataset includes 3,625 samples in total, but four of the classes have > 300 samples. Most classes have about 100 samples. There are < 50 samples in three of the classes. We know that CSHC’s classification accuracy of Nodes 1 and 4 is higher than that of THC. The classification accuracy of Node 4 by THC is 72%, while CSHC increases the accuracy to 78%. The accuracy of the other two non-leaf nodes is slightly reduced. In exchange, the accuracy of a minority class and the overall accuracy of this dataset are improved.

Table 4 Information of non-leaf nodes and accuracy of two algorithms on F194 dataset (%)
Full size table

The F194 dataset is built as a three-level tree. There are seven non-leaf nodes on the second level. Nodes α, β, α/β, α + β, Multi-domain, Membrane and cell surface (MCS) and Small-proteins are non-leaf nodes. We call them Nodes 1 to 7 for convenience. We know there is a big difference between the majority and minority classes from Table 4. Nodes 5 to 7 are the minority classes, which occupy a small number of samples and < 10% of the total child nodes. The accuracy of the minority classes is much less than that of the majority. Node 5 has only 0.76% samples in this dataset. We can see more intuitively that the accuracy of the minority classes is significantly higher than that of THC after the cost-sensitive method and threshold strategy are applied. THC works well on several nodes, except for Nodes 5 and 6. The accuracies of Nodes 5 and 6 classified by THC are 1.49% and 26.79%, respectively. CSHC greatly improves the accuracies of Nodes 5 to 7 by 32% and 25% more than THC, respectively.

5.3 Experimental results and discussion on the whole hierarchical tree

In this section, we discuss the experimental results for the whole hierarchical tree. We first discuss the experimental results of two smaller datasets. Figures 5 and 6 show the experimental results in terms of two evaluation metrics on the DD and F194 datasets. HCMP obtained the best results, with classification accuracies of 81.9% and 55.24%. CSHC showed a great performance advantage on the two datasets and is obviously more accurate than the other hierarchical classification with feature selection methods, achieving accuracies of 76.83% and 52.45% on the DD and F194 datasets, respectively. HCMP selects several better nodes on the basis of hierarchical classification and uses the random forest method to perform another classification. However, this causes HCMP to use much more running time than CSHC. The other methods’ accuracies on the two datasets are less than 70% and 50%, respectively. LBRM behaves differently with the two datasets, producing an accuracy of 67.77% on the DD dataset but only 17.92% on the F194 dataset. HFSNM is second only to CSHC on the two datasets, with accuracies of 69.1% and 34.08%, respectively. The accuracy and FH of HFSNM and FSFHC are exactly the same.

Fig. 5
figure 5

Accuracy and FH on the DD dataset

Full size image

The CSHC, HCMP, and LBRM hierarchical classification methods are ahead of the others in terms of the FH metric. CSHC obtained FH of 89.4% and 78.74%, while LBRM obtained FH of 88.65% and 75.52% on the DD and F194 datasets, respectively. CSHC uses the threshold strategy at non-leaf nodes and improves the accuracies of minority classes on the second level. The advantages of this strategy lie in its overall accuracy and hierarchical precision. Improvement in hierarchical precision makes CSHC obtain a better value of the FH metric. LBRM balances risks by considering going down or finishing the prediction process at each node. It is like making decisions at every non-leaf node. This process increases the hierarchical precision. HCMP takes advantage of two classification processes at non-leaf nodes, which reduce errors at non-leaf nodes and improve the FH. LBRM does not have good accuracy on dataset F194, but the FH of LBRM means that it classifies well at non-leaf nodes. HRelief is the worst hierarchical classification algorithm and only obtained FH values of 80.06% and 68.85% on the DD and F194 datasets, respectively.

Fig. 6
figure 6

Accuracy and FH on the F194 dataset

Full size image

Figures 7, 8 and 9 show the experimental results of eight hierarchical classification algorithms on three large datasets. We observe the following:

Fig. 7
figure 7

Accuracy and FH on the ILSVRC57 dataset

Full size image
Fig. 8
figure 8

Accuracy and FH on the CAR196 dataset

Full size image
Fig. 9
figure 9

Accuracy and FH on the SUN dataset

Full size image

The results of the four hierarchical classifiers that use feature selection algorithms, in terms of the two metrics, were averaged and are shown in Fig. 7a and b. The accuracies of HFISHER, FSFHC, and HmRMR were relatively close, at 85.01%, 85.53%, and 84.97%, respectively. The accuracy of CSHC reached 86.61%, which is 1% higher than the second-best classifier, FSFHC. The FH of CSHC was 96.34%. The FH of HFISHER, HFSNM, HmRMR, and HRelief were 95.8%, 95.77%, 95.81%, and 95.79%, respectively. LBRM reduced the gap with the others, with an FH of 95.58%. The FH of HCMP and HFSNM were the same, but the classification accuracy of HFSNM was a little higher. The HCMP result is in sixth place, as its two classification processes do not perform well on this dataset.

The features in the CAR196 dataset were extracted after deep learning. Figure 8 shows that the experimental results of the four hierarchical classifiers with feature selection in terms of the two evaluation metrics were similar, and only a little less than that of CSHC. HCMP obtained a 67.21% classification accuracy, which is at least 1.08% higher than that of the others. The accuracy of LBRM was nearly 10% lower than that of the others. In the same way, the performance of LBRM in terms of the FH evaluation metric was poor. The four hierarchical classifiers with feature selection algorithms use good-quality features to achieve high accuracy and FH values. The accuracy of FSFHC was lower than that of HCMP, but the FH value of FSFHC was better. That shows that FSFHC performs better on the inter-levels. Its accuracy and FH were 68.74% and 83.48%, respectively. Therefore, the experimental results of CSHC are very competitive.

Figure 9a and b reveal very different experimental results. We can see that the accuracy of LBRM was the lowest, but it was in third place in terms of the FH metric. This indicates that LBRM has good performance in improving the precision of non-leaf nodes but not the accuracy of final leaf nodes. The result on the F194 and SUN datasets show that LBRM is good in terms of the FH metric because of its balanced risk strategy at non-leaf nodes. The two evaluation metrics reflect the instability of LBRM and the advantage of CSHC. The experimental results for HCMP and CSHC are ahead of those of the other algorithms on the SUN dataset. The HCMP algorithm had good results because of its two classification processes. The results of FSFHC on this dataset are normal. CSHC identified this image classification dataset best, with accuracy and FH values of 67.01% and 86.06%, respectively. The results of the four other hierarchical classification algorithms are consistent in terms of the two evaluation metrics.

The experimental results for the five imbalanced distribution datasets indicate that CSHC is more competitive than the other algorithms. CSHC can complete classification tasks quickly and maintain high accuracy. CSHC obtained the best accuracy on three large datasets and the second-best on two small datasets.

6 Conclusions and future work

We proposed a cost-sensitive hierarchical classification method based on multi-scale information entropy for addressing imbalanced distribution data. Unlike existing cost-sensitive algorithms, our algorithm uses the hierarchical structure as additional and supplemental information. In addition, we proposed an adaptive threshold method based on hierarchical data that does not require users to specify any parameters. Multi-scale information entropy is used in our hierarchical cost-sensitive learning method to address imbalanced distribution data. We compared our proposed algorithm with seven powerful hierarchical algorithms on five imbalanced distribution datasets. Our algorithm not only improves the accuracy of classification with few samples, but also ensures the overall accuracy of classification. For data with an imbalanced distribution, long-tail distributions create a new challenge because 80% of the samples are distributed in 20% of the majority classes and the minority only contain 20% of the samples. A good point to be considered is that we can get ideas from [1, 31] to build neural network algorithms for big data issues. In future, we will construct a neural network algorithm to address the long-tail distribution problems.