Cost-sensitive hierarchical classification for imbalance classes

Abstract

The hierarchical classification with an imbalance class problem is a challenge for in machine learning, and is caused by data with an uneven distribution. Learning from an imbalanced dataset can lead to performance degradation of the classifier. Cost-sensitive learning is a useful solution for handling the gap probability of majority and minority classes. This paper proposes a cost-sensitive hierarchical classification for imbalance classes (CSHCIC), constructing a cost-sensitive factor to balance the relationship between majority and minority classes. First, we divide a large hierarchical classification task into several small subclassification tasks by class hierarchy. Second, we establish a cost-sensitive factor by more precisely using the number of different samples of subclassifications. Then, we calculate the probability of every node using logistic regression. Lastly, we update the cost-sensitive factor using the flexibility factor and the number of samples. The experimental results show that the cost-sensitive hierarchical classification method achieves excellent performance on handling imbalance class datasets. The running time cost of the proposed method is smaller than most state-of-the-art methods.

1 Introduction

The imbalance class problem [22, 27] is a significant issue in data mining because this problem exists in several domains, such as medical diagnosis [11], text classification, and fraud detection [8]. The problem is that the class boundary learned by traditional machine learning algorithms skews toward the majority classes. The recognized solution to the imbalance class problem is a priori understanding of class imbalanced data [13] or algorithmic level [1, 17, 36]. In terms of data, re-sampling [10, 20, 30] training data is a general way to solve the imbalance class problem because re-sampling training data can balance the class distribution of a dataset. In terms of an algorithm, cost-sensitive learning is a useful method to re-weight training data for the imbalance class problem. Cost-sensitive learning assigns larger weights [38] to the minority classes and punishes the majority classes to fix the imbalance class problem. Compared with re-sampling, the cost-sensitive learning [3, 4] method usually yields better performance [39]. Many studies about cost-sensitive strategies [2] have shown improved performance of support vector machine [28] and other machine learning algorithms [12, 15] in imbalance class learning.

Cost-sensitive learning is an effective tool for solving imbalance class problems. Cost-sensitive learning introduces different penalties for different types of misclassification, and studies under different mechanisms to ensure that the resulting classification allows the overall misclassification minimum cost. Different misclassifications often lead to different misclassification costs [19], and cost-sensitive learning works from different perspectives. For example, in cancer detection [37], a cancer patient misdiagnosed as a healthy person delays treatment or even leads to the death of the patient while the misdiagnosis of a healthy person as a cancer patient will lead to fear and economic loss. In this example, the cost of misclassification is different because of the different results. Cost-sensitive learning can better address the problem of imbalance class in several different types of samples in the training dataset.

In recent years, several studies concerning cost-sensitive learning [24, 31] for imbalance class problems have been presented. Zhou et al. [40] designed a block-structured sparse constraint and deep super-class learning model to address the problem of long-tail distributed image classification. Min et al. [21] proposed an active learning classification algorithm by integrating cost-sensitive and three-way theories. Fan et al. [7] proposed a cost-sensitive learning algorithm to train more discriminative tree classifiers for effectively distinguishing new object classes from large numbers of known object classes. Sun et al. [32] investigated cost-sensitive boosting algorithms for advancing the classification of imbalanced data. These methods have demonstrated the usefulness of cost-sensitive learning for the imbalance class problem. In the era of big data, most real-world datasets have hundreds of classes organized in hierarchical structures such as ImageNet, Wikipedia [42], and biological data [41]. The gradually increasing number of class labels with hierarchy may lead to challenges in addressing the imbalance class problem.

In this paper, we integrate hierarchical classification [18, 33] and cost-sensitive learning into the imbalance class problem. This algorithm considers the hierarchical information of class structure and sets a threshold to penalize the node when the probability of this node is smaller than the threshold. First, we split the large imbalance class task into some small sub-classification tasks by class hierarchy. We reduce the computation time, through this process. Second, we use the number of different samples, the probability of inter-level nodes calculated by logistic regression and the flexibility factor to build a cost-sensitive factor. Lastly, we set a threshold for each class node at every level to stop the node down to the next level if the probability is not great enough, it reduces inter-level error propagation. These three steps increase the ratio of the number of correctly predicted samples to the number of whole test samples and reduce the computation time we need to train the data. We use a cost-sensitive method to reduce the gap between the number of samples of majority and minority classes. Reducing the gap between the number of samples of majority and minority classes prevents the classifier from biasing majority classes. Our method combines cost-sensitive learning and the hierarchical classification method to train datasets with excellent efficiency and effectiveness. Our algorithm spends less running time than most hierarchical classification algorithms on two protein datasets, and our algorithm achieves the best accuracy on two protein datasets. In addition, our algorithm takes the least time to achieve good results on the scene understanding classification dataset.

The remainder of this paper is organized as follows. Section 2 presents the proposed method. In Section 3, we introduce the experimental settings and results. Lastly, the conclusions and future work are given in Section 4.

2 The proposed method

The hierarchical classification framework based on the cost-sensitive consists of two parts: first, the samples are grouped through a bottom-up process based on the hierarchical relationship of the classification tasks; then, cost-sensitive is separately used for each sub-category task. In the process, cost-sensitive optimization is taken into the relationship in the category hierarchy by considering each sub-category task.

2.1 Hierarchical tree structure

In this section, we concentrate on a tree-based hierarchical class structure. Large-scale data include a large amount of information and produce complicated class structures such as hierarchies. In all cases, the hierarchy employs a parent-child relationship among all classes, meaning that a sample belonging to a class also belongs to all its ancestor classes.

A hierarchical tree is defined as a pair (K, ≺), where K = {1, 2, ⋯ } is the set of all classes and “≺” stands for the “is-a” relationship, which is the subclass-of relationship with the following properties:

• (1) Asymmetry: if m ≺ j, then j$\nprec$m for every m, j ∈ K.

• (2) Anti-reflexivity: m$\nprec$m for every m ∈ K.

• (3) Transitivity: if m ≺ j and j ≺ n, then m ≺ n for every m, j, n ∈ K.

Hierarchical classification employs a divide-and-conquer strategy. In a large number of multi-label learning tasks, the labels can be assembled into a hierarchical tree structure from coarse to fine. Hierarchical classification is a top-down process from root node to leaf nodes. A sample to be classified is assigned to one or several subclassification tree nodes, and the process is repeated until the classification cannot be continued or the leaf nodes are reached. In a tree structure, a node with the same parent node is called a sibling node. In addition to the root node, inter-level nodes are assembled in a tree structure of class hierarchy that has its own child nodes and sibling nodes. In a hierarchical tree structure, parameter C_m is the set of child categories of class m, and |C_m| is the number of samples of child categories of class m. Parameter p_m is the parent category of class m. Parameter S_m is the set of sibling categories of class m, and h is the height of the tree structure.

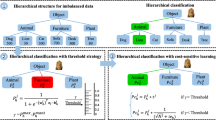
An example of a tree-based hierarchical class structure is shown in Fig. 1. From this figure, we have the following:

• (1) The parent category of class 2 is p₂ = 0;

• (2) The set of child categories of class 3 is C₃ = {7, 8};

• (3) The set of sibling categories of class 1 is S₁ = {2};

• (4) We set |C₇| = 60 and |C₈| = 100; then, we get |C₃| = |C₇| + |C₈| = 160 and |C₄| = |C₉| = 150. Lastly, we get |C₁| = |C₃| + |C₄| = 310. We sum up the number of sub-tasks from the following level. Thus, this method is a bottom-up process.

Fig. 1

Tree structure (h = 4)

2.2 Hierarchical classification

Given data matrix X ∈ $\mathbb {R}^{l \times n}$, l is the number of samples, and n is the number of features. x_i = {x₁, x₂, ⋯ , x_l}, x_i is the i-th sample of X. y_m = { y₁, y₂, ⋯ , y_k}, y_m is the m-th label. ${p_{i}^{m}}$ is the probability that x_i belongs to class m.

The classification process is one of the most significant issues in data mining and machine learning. The logistic regression method is used to train the training set, and logistic regression is a linear classification model based on probability theory. This method has many advantages, e.g., it directly models the classification possibilities without first assuming data distribution, avoiding the problems caused by the inaccurate distribution of assumptions. Rather than predicting only the categories, it is possible to obtain approximate probability predictions, which is useful for many tasks that need to use probabilistic decision making. In addition, the logistic regression function is a convex function that can be derived by any factorial, and has good mathematical properties. Many existing numerical optimization algorithms can be directly used to obtain the optimal solution. We obtain parameters w_m and b_m of each subclassification after training on the training set. In the context of hierarchies, the probability that x_i belongs to class m is calculated as:

$$ {p_{i}^{m}}= \frac{1}{1+e^{-\mathbf{w}_{m}^{T}\mathbf{x}_{i}-\textit{b}_{m}}}, m\in\{1,2,...,k\}. $$

(1)

We use logistic regression to calculate the probability of nodes from the root node to leaf nodes as a top-down process. Then, the node is assigned to the second level for several subclassification tasks. We select the node with the maximum probability on the second level after comparing the probability of each node. The node with the maximum probability is the best choice after comparing it with sibling nodes. We choose its child node with the maximum probability on the next level until the leaf nodes are reached. We then obtain the predicted labels selecting by logistic regression, after selecting from the second level to the last level. Lastly, we compare the predicted labels with the correct labels to obtain the accuracy of the classifier. It is easy to understand the process of the hierarchical classification framework work according to Fig. 2.

Fig. 2

Hierarchical classification process

An example of the hierarchical classification process is shown in Fig. 2. Nodes 1 and 2 on the second level are assigned to the model we obtain after training on the training set by logistic regression. If the probability of node 2 is greater than that of node 1, the classifier selects node 2 as the best choice on this level. Nodes 3 and 4 are the child nodes of node 2. We also select node 3 as the prediction node because the probability of node 3 is greater than that of node 4.

2.3 Cost-sensitive hierarchical classification

In this section, we describe a cost-sensitive hierarchical classification method. Cost-sensitive learning is a method of providing different weights for different categories of samples to allow machine learning models to learn. In a typical learning task, the weights of all samples are generally equal. However, in some specific tasks, different weights can be set for the samples. We consider that each subclassification task is dependent on each other, meaning that the relationship between a node and its sibling nodes is important. We consider the relationship between a node and its sibling nodes into our method, and we make the number of samples of child categories a cost-sensitive factor.

We update the ${p_{i}^{m}}$ using $pcos{t_{i}^{m}}$ when $p_{i max}^{m}\leq \eta$ as follows:

$$ pcos{t_{i}^{m}}= \frac{U^{m}}{1+e^{-\mathbf{w}_{m}^{T}\mathbf{x}_{i}-\textit{b}_{m}}}, $$

(2)

where $p_{imax}^{m}$ is the maximum probability that x_i belongs to class m on this level, and U^m is the cost-sensitive factor of class x_i and is calculated as:

$$ U^{m}=\frac{1}{(\sqrt{|C_{m}|}+\alpha)}, $$

(3)

where C_m represents the set of child samples of class m, parameter |C_m| represents the number of samples of child categories of class m, and α > 0 is the penalty parameter.

If the error is propagated from a high level to a low level, the node with the maximum probability is not the correct choice according to the hierarchical classification method. This condition results in inconsistencies between the correct label and the predicted label, and this is an important factor that causes the low accuracy of the classifier. We set the variable parameter as a threshold that is a condition to avoid inter-level error propagation. The classifier is not certain about the choice of this node when the maximum probability in the child node does not reach the threshold we set. In this case, it is likely to cause error propagation. Other nodes also have the possibility of becoming the correct node when the classifier is not certain about this node. We set the threshold as a tool to immediately stop this subclassification task. A cost-sensitive algorithm is added to the hierarchical classification process after the threshold parameter, and we consider the number of each node’s child nodes into the cost-sensitive factor. It is easy to understand the process of cost-sensitive hierarchical classification with the threshold framework work, as shown in Figs. 3 and 4.

Fig. 3

Cost-senesitive hierarchical classification with threshold process

Fig. 4

Comparison of hierarchical classification and cost-sensitive hierarchical classification with threshold

An example of a cost-sensitive hierarchical classification with the threshold process is shown in Fig. 3. During the hierarchical classification process, the classifier selects the node with the maximum probability as the best node on each level. Hierarchical classification with threshold process considers the threshold as an additional condition into the hierarchical classification process. $p_{imax}^{m}$ is the maximum probability that x_i belongs to class m on this level. We update the ${p_{i}^{m}}$ using $pcos{t_{i}^{m}}$ and select the node with the maximum probability as $pcost_{imax}^{m}$ if $p_{imax}^{m}$ is smaller than or equal to the threshold value η. We also select ${p_{i}^{m}}$ as $p_{imax}^{m}$ if $p_{imax}^{m}$ is greater than the threshold value η. According to the algorithm, the classifier outputs class m until the leaf node.

An example of comparison of hierarchical classification and cost-sensitive hierarchical classification with threshold is shown in Fig. 4. The results show that the hierarchical classification process selects node 3 as $p_{imax}^{m}$ because ${p_{i}^{3}} =$ 0.5. However, if $p_{imax}^{m} = {p_{i}^{3}}$, parameter $p_{imax}^{m}$ is smaller than the threshold value η (η = 0.6). Cost-sensitive hierarchical classification provides different weights for different categories of samples. In this example, our algorithm provides different weights for these three nodes according to number of samples that belongs to each node. We update the ${p_{i}^{m}}$ using $pcos{t_{i}^{m}}$ when $p_{i max}^{m}\leq \eta$, and we select node 1 as $p_{imax}^{m}$ because $pcos{t_{i}^{1}}$ is the greatest number after a cost-sensitive hierarchical classification process on this level.

Parameter D_tree is a tree-based hierarchical structure of the classes. Cost-sensitive hierarchical classification for imbalance classes (CSHCIC) is illustrated in Algorithm 1. The threshold strategy based cost-sensitive hierarchical classification of CSHCIC is provided in line 4 in Algorithm 1, and the cost-sensitive factor of CSHCIC is illustrated in line 7 in Algorithm 1. The computational time cost of CSHCIC algorithm is O(cmn).

3 Experiments

In this section, we introduce our experiments on three imbalance class distribution datasets.¹ Two protein datasets (DD [5] and F194 [34]) and a scene understanding classification dataset (SUN [35]) are described in Section 3.1. We compare the CSHCIC method with some state-of-the-art methods in Section 3.2. We introduce the evaluation metrics of these experiments in Section 3.3. The experimental results and discussion are shown in Section 3.4.

3.1 Datasets

The experiments use two protein datasets and one image dataset to show the performance of our algorithm. All three datasets have the information of class hierarchy and imbalance class distribution. A description of the datasets is given in Table 1.

Table 1 Data description

DD dataset: This dataset has a protein sequence from the bioinformatic filed, and there is a three-level height tree structure in the DD dataset. In this tree structure, the second level contains 4 categories, and the third level contains 27 leaf nodes. DD dataset includes 473 features. There are 27 real classes and 4 important structural classes: α, β, α + β, and α/β [5]. The class with the most samples contains 361 samples, and the class with the least samples contains 17 samples. The sample distribution of the DD dataset in numerical descending order is shown in Fig. 5a.

Fig. 5

Sample distribution of datasets in numerical descending order: a DD; b F194

F194 dataset: The structure of the F194 dataset is similar to the DD dataset that is processed from the latest version of Structural Classification of Proteins [23]. This dataset has a three-level tree structure. In this tree structure, the second level contains 7 categories and the third level contains 194 leaf nodes. These 194 leaf nodes have 8,525 protein sequences which represent 8,525 samples in this dataset. There are also 473 features in the F194 dataset [16]. The class with the most samples includes 361 samples, and the class with the least samples includes 10 samples. The sample distribution of the F194 dataset in numerical descending order is shown in Fig. 5b.

SUN dataset: The SUN dataset has a four-level tree structure with 343 categories and 22,556 samples. There are 324 leaf nodes and 4,096 features in this dataset. The class with the most samples contains 1,075 samples, and the class with the least samples includes 36 samples. The sample distribution of the SUN dataset in numerical descending order is shown in Fig. 6.

Fig. 6

Sample distribution of the SUN dataset in numerical descending order

3.2 Compared methods

In this subsection, we introduce different hierarchical classification methods in detail. We compare our CSHCIC method with other hierarchical classification methods to evaluate its performance.

• (1) HiFISHER: Fisher Score [6] is a common feature correlation criterion with simple calculation and good discriminant effect. Fisher score selects features by fully labeled training data with the best discriminating ability. We use the support vector machine approach after Fisher Score feature selection. HiFISHER is a hierarchical classification method modified by Fisher Score. The computational time cost is O(T(cns+s log m)+V² + nV² + nmV), where T represents the number of iterations needed to converge, c represents the number of classes, n represents the number of samples, s represents the average number of nonzero features among all the training samples, m represents the number of features, and V represents the number of support vectors.

• (2) HiFSNM: Feature selection via joint l_2,1-norms minimization (FSNM) [25] that embeds joint l_2,1-norms minimization on regularization and loss function. The l_2,1-norms based regression loss function is robust in data points that are outliers. It is also efficient to select features across all data points with joint sparsity. We add the support vector machine method after feature selection via joint l_2,1-norms minimization. HiFSNM is a hierarchical classification method transformed by FSNM. The computational time cost of HiFSNM is O(Tcmn+V² + nV² + nmV).

• (3) HimRMR: Minimal-redundancy-maximal-relevance criterion (mRMR) [26] is a useful method that equals the maximal dependency condition for first-order feature selection. The mRMR method avoids the difficult multivariate density estimation in maximizing dependency. HimRMR [9] is a hierarchical classification method based on mRMR feature selection. HimRMR’s computational time cost is O(mn+V² + nV² + nmV).

• (4) HiRelief: Relief [14] algorithm is a feature subset selection for weight search. The Relief algorithm avoids the use of global search and heuristic search methods, assigning different weights to features based only on the correlation of individual features and categories. The support vector machine is joined after the Relief feature selection algorithm. HiRelief is a hierarchical classification method transformed from Relief. The computational time cost of HiRelief is O(Tcn+V² + nV² + nmV).

• (5) HiLBRM [36]: This method uses the structure for effective hierarchical classification that predicts a sample from the root node to the leaf node. The method builds a local bayes risk minimization framework strategy that divides the prediction process into considering to stop or to go down at every node by balancing these two risks. The strategy stops the wrong prediction at an internal node to avoid misclassification. HiLBRM’s computational time cost is O(nm logn).

• (6) HiNBP [29]: A quick inter-class similarity computational approach and spectral clustering are made for a hierarchical visual tree. This method makes a hierarchical visual tree that is built for N-best path class predictions. The method uses the best path algorithm implemented by a joint probability maximization problem to avoid error propagation. The hierarchical class prediction problem is made into the path search problem. The computational time cost of HiNBP is O(cmn).

These six algorithms chosen for comparison include the classic and latest hierarchical classification algorithms. HiFISHER, HiFSNM, HimRMR, and HiRelief are the classic algorithms in the machine learning field. HiLBRM and HiNBP are two recent studies that make good contribution in hierarchical classification.

3.3 Evaluation metrics

Classification accuracy (ACC)

Classification accuracy is a simple evaluation metric for classification and is easily calculated. We obtain the number of predicted labels after hierarchical classification. Classification accuracy equals the ratio of the number of predicted labels to the number of whole test samples.

Hierarchical F₁ measure (F_H)

Hierarchical F₁ measure (F_H) is an important evaluation criterion for the hierarchical classification. All the prediction classes and real classes are considered as important indicators. All the ancestors and descendants of the class are considered. The measure includes hierarchical precision (P_H), hierarchical recall (R_H), and hierarchical F₁ measure (F_H). P_H, R_H, and F_H are defined as:

$$ P_{H} =\frac{|\hat{D}_{aug} \cap D_{aug}|}{|\hat{D}_{aug}|}, $$

(4)

$$ R_{H} =\frac{|\hat{D}_{aug} \cap D_{aug}|}{|D_{aug}|}, $$

(5)

$$ F_{H} =\frac{2 \cdot P_{H} \cdot R_{H}}{P_{H} + R_{H}}, $$

(6)

where D_aug = D ∪ anc(D), $\hat {D}_{aug} = \hat {D} \cup {anc}(\hat {D})$, |⋅| represents the number of elements. D represents the correct class label, $\hat {D}$ represents the predicted class label, and anc(D) represents the parent node set of the correct class label.

3.4 Experimental results and discussion

All experiments are executed on Windows 10 operating system with MATLAB 2016a. The computer has an Intel Core i7-3770 CPU with default frequency of 3.40 GHz and a memory of 12.0 GB. We use 10-fold cross validation for three datasets. We set different parameters for comparison in the experiment to show good performance of our proposed method.

The CSHCIC algorithm has different parameters η and α settings, but the experimental times are similar. We set parameters η = 0.6 and α = 1 to compare with other algorithms. The results demonstrate that the CSHCIC algorithm has good performance on these three datasets in Table 2. The feature selection process leads to the reduction of the time complexity of training when handling the DD dataset. HiFISHER spends less than one second time on this dataset. HiLBRM and HiNBP show good performance with 16.5 and 11.9 seconds, but their running times are still longer than CSHCIC. HiFSNM is nearly 21.6 seconds more than CSHCIC. On the F194 dataset, HiFISHER still shows the best performance, and HimRMR is nearly 20 seconds less than CSHCIC in running time. HiNBP’s running time is 6 seconds more than CSHCIC. CSHCIC algorithm also has a shorter running time than HiFSNM, HiRelief, and HiLBRM algorithm on the F194 dataset. CSHCIC outperforms the other six algorithms on the SUN dataset with 1,098 seconds. HiNBP spends 1,102 seconds handling the SUN dataset, and this result is 3 seconds longer than CSHCIC. The SUN dataset costs HiLBRM 1,322 seconds, which is much less than the other four hierarchical algorithms. Thus, the other algorithms use much more time than CSHCIC to calculate data. HiFISHER, HiFSNM, HimRMR, and HiRelief algorithms are too slow to handle the SUN dataset. On the aspect of efficiency, the time consumed by CSHCIC is much less than that of HiFISHER, HiFSNM, HimRMR, HiRelief, HiLBRM, and HiNBP on this large-scale dataset.

Table 2 Running time comparison of seven algorithms on three different datasets (s)

Different experimental results under different parameters on the DD dataset are shown in Fig. 7a and b. Figure 7a shows that we get the best ACC result with 77.05% when α = 3 and η = 0.55. The results on the F_H evaluation metric are shown in Fig. 7b under different parameters η and α. We can also obtain the best result with 89.45% on the F_H evaluation metric when α = 3 and η = 0.55. The results show that sometimes the performance of parameter η = 0.55 is better than that of η = 0.6. We choose α = 3 and η = 0.55 to achieve the best effectiveness on two evaluation metrics.

Fig. 7

Performance under different parameters on the DD, F194 and SUN dataset: a ACC; bF_H

Figure 7c and d present the ACC and F_H results under different parameters on the F194 dataset. Figure 7c shows we obtain the best ACC result with 52.64% when α = 3. In addition, we can also obtain the best F_H result with 78.81% when α = 3 in Fig. 7d. We have the following observations from the two figures. First, parameter α is more sensitive than η of the proposed algorithm on this dataset. Two lines almost coincide in two figures, and we can know that η = 0.6 is close to η = 0.55 on two evaluation metrics. Second, the parameter η of the proposed method does not greatly affect for the accuracy. Therefore, parameter η does not necessarily lead to high accuracy that provides a good choice of α with a better performance.

The results show that different performance under different parameters on the SUN dataset are shown in Fig. 7e and f. The figures show that the lines of η = 0.55 are higher than those of η = 0.6 in Fig. 7e and f. In addition, the results of η = 0.55 are slightly better than η = 0.6 on the evaluation metric of ACC. Figure 7e shows the best ACC result with 67.08% when α = 2 and η = 0.55. In addition, the best F_H result is obtained with 86.12% when α = 1 or 2 and η = 0.55, as shown in Fig. 7f.

Figure 8a and c show that the ACC and F_H results of seven hierarchical algorithms on the DD dataset. Figure 8a shows that the CSHCIC achieves higher ACC than other algorithms with 76.83%. HiNBP ranks in second place, which is 0.95% less than CSHCIC on the ACC evaluation metric. HiRelief is the last place, as its ACC result is only 52.08%. HiRelief is 24.75% less than CSHCIC. The other four hierarchical classification methods have ACC results below 70%. Figure 8b introduces CSHCIC is 0.44% more than the second place HiNBP on F_H. HiLBRM follows HiNBP with 88.65% in third place. Figure 8a and b show that CSHCIC ranks in first place on ACC and F_H.

Fig. 8

ACC and F_H results of seven hierarchical algorithms on the DD dataset: a ACC; bF_H

Figure 9a and b present the ACC and F_H results of seven hierarchical algorithms on the F194 dataset. Figure 9a shows that the CSHCIC achieves higher ACC than the other six algorithms with 52.57%. HiNBP still ranks in second place with 46.27%. Compared with HiNBP, the result of ACC is increased by 13.6%. HiRelief and HiLBRM do not have good results with 26.06% and 17.92% on the ACC evaluation metric. HiLBRM obtains the lowest ACC result on handing this dataset. Compared with HiLBRM, the results of ACC are increased by 193.4%. CSHCIC is 2.43% more than the second place HiNBP on F_H in Fig. 9b, and HiLBRM follows HiNBP in third place with 75.52%. CSHCIC’s F_H is 3.1% to 14.4% more than the other six algorithms. Thus, the CSHCIC algorithm shows its great performance in handling the F194 dataset.

Fig. 9

ACC and F_H results of seven hierarchical algorithms on the F194 dataset: a ACC; bF_H

The ACC and F_H results of seven hierarchical algorithms on the SUN dataset are shown in Fig. 10a and b. Figure 10a shows that CSHCIC ranks in second place with 67.01% on the ACC evaluation metric. CSHCIC is 5.23% more than HimRMR which is in third place. CSHCIC is 1.62% less than HiNBP which obtains the best ACC result. HiNBP employs the best path search method into the calculation process, and the best path search method travels around the whole visual tree to find the most possible path. HiNBP needs to calculate the edge score of all nodes at the same level, and it trades more complex calculations for better results. Based on effectiveness, the classification accuracy of CSHCIC is much more than that of HimRMR, HiFISHER, HiFSNM, HiRelief, and HiLBRM. CSHCIC outperforms these four hierarchical algorithms on F_H with 86.07%, and CSHCIC is 1.01% more than the third place HiLBRM in Fig. 10b. At the same time, the process of complex calculations have increased their running times of these six hierarchical classification algorithms. The CSHCIC algorithm handles data with the least running time, because of a number of samples and features in this dataset. CSHCIC has shown its good result both on efficiency and effectiveness on the SUN dataset.

Fig. 10

ACC and F_H results of seven hierarchical algorithms on the SUN dataset: a ACC; bF_H

4 Conclusions and future work

In this paper, we have proposed a hierarchical classification method based on cost-sensitive learning. The method uses a cost-sensitive factor to assign larger weights to the minority classes and punish the majority classes. The method sets a flexible threshold to decrease inter-level error propagation. We used logistic regression to calculate the probability of the node. The predicted node is selected through the cost-sensitive factor and flexible threshold by class hierarchy until the leaf node level. We use 10-fold cross validation for all datasets. The cost-sensitive method balances majority and minority classes, and keeps the classifier from skewing toward majority classes. Our method has combined the cost-sensitive method and threshold strategy to increase the accuracy of minority classes. We have also compared our CSHCIC method with different hierarchical classification methods on three datasets. The CSHCIC method uses the smallest computational time cost to train the model of seven hierarchical classification methods, and the CSHCIC method obtains the best accuracy on two datasets. The experimental results prove the efficiency and effectiveness of the proposed algorithm. For other datasets, we need to manually adjust the parameters. In the future, we will continue to work on finding good parameters that are suitable for more datasets.