1 Introduction

Classification and feature selection are important research fields in pattern recognition and machine learning. Classification is a technique modeled by the labeled data and then the label of unlabeled data is identified by this model [1, 2]. Feature selection, as the pre-processing part of the classification technique, can remove redundant features and simplify the construction process of the classifier [3, 4]. Many attribute reduction methods often set the same neighborhood size for all attributes. However, this setting will bring large error due to the fact that there are large differences in the distribution of each attribute data. To handle above issue, a forward greedy fast feature selection algorithm based on neighborhood rough set (NRS_FS_FAST) was proposed [5].

Classification technology based on IF-THEN rules, due to its broad applications, has received increasing interests during the past decades [6, 7]. There are many kinds of classification methods, and decision trees become one of the most well-known classification methods on account of their good learning capability and understanding capability [8,9,10]. In general, they grow in a top-down way and terminate when all data associated with a node belong to the same class. The existing decision trees can be divided into three types: “standard” decision trees [11,12,13,14], fuzzy decision trees [15,16,17,18], and oblique decision trees [19,20,21,22,23,24]. “Standard” decision trees can be used to deal with classification problems. However, they are often not capable of handling uncertainties consistent with human cognitive, such as vagueness and ambiguity. To overcome these deficiencies, fuzzy decision trees have been developed by incorporating the fuzzy uncertainty measure in decision tree construction [16, 25,26,27,28]. For example, Liu et al. introduced the coherence membership functions of fuzzy concepts and studied the AFS fuzzy rule-based decision tree classifier [16]. An inductive learning method “HAC4.5 fuzzy decision tree” was proposed to obtain a fuzzy decision tree with high predictability by using fuzziness intervals matching with hedge algebra [26]. And a new fuzzy decision tree approach based on Hesitant Fuzzy Sets (HFSs) was introduced to classify highly imbalanced datasets [27]. “Standard” decision trees and fuzzy decision trees are called single variable decision trees (or axis-parallel decision trees) as a result of considering only one attribute at each node to partition the training samples. These decision trees cannot effectively handle these classification problems — the classification boundary is not parallel to axis.

To solve the above-mentioned problem, oblique decision trees were proposed by using the linear combination of all feature components as decision functions [20, 22, 23, 29, 30]. Specifically, a novel bottom-up oblique decision tree induction framework (BUTIF), which did not rely on an impurity-measure for dividing nodes, was proposed in [20]. A new decision tree algorithm, called HHCART, was presented in [22]. It utilized a series of Householder matrices to reflect the training data at each node during the tree construction. The authors in [23] described the application of a differential evolution based approach for inducing oblique decision trees in a recursive partitioning strategy. And the work in [29, 30] adopted geometric structure in the data to assess the hyper planes. However, oblique decision trees were lack of explanation and their computational complexities were high [31].

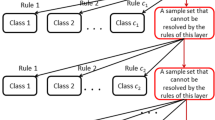
In order to address the above issues, Wang [17] presented a new architecture of a fuzzy decision tree based on fuzzy rules — fuzzy rule based decision tree (FRDT), which involved multiple features at each node endowed with semantic interpretation. However, some unnecessary fuzzy numbers were considered in fuzzy rules extraction; the same fuzzy numbers were used in all layers of the FRDT, while the data samples on each additional node have changed; and the threshold δ is determined by two-step cross-validation method, of which the search purpose is not clear. Motivated by the above discussions, this paper puts forward a new fuzzy oblique decision tree (FODT), and its growth structure is depicted in Fig. 1.

Fig. 1
figure 1

The growth structure of fuzzy oblique decision tree

Full size image

It stores all training samples at root node. In the first layer of the FODT, the fuzzy rules generated by the FRGA are used to construct leaf nodes as pure as possible. The samples that are not processed by these fuzzy rules are then put into an additional node, which is the only non-leaf node in this layer. If the additional node is not empty and the class number of this node samples is more than two, the FODT continues to grow. In the second layer of the FODT, the fuzzy numbers on additional node are recalculated, and the fuzzy rules generated by the FRGA are used again to construct leaf nodes as pure as possible. Similarly, the samples that cannot be handled by the fuzzy rules in the second layer are then put into a new additional node. Repeating the procedure until the termination condition (the additional node is null, or the samples in the additional node have the same label) is met.

The main contributions of this paper are as follows:

  • The NRS_FS_FAST algorithm is introduced to eliminate data redundancy and improve classification efficiency.

  • The fuzzy numbers on additional node in each layer are recalculated to obtain fuzzy partition more precisely.

  • A new fuzzy rule generation algorithm (FRGA) is put forward to simplify the rules.

  • To effectively keep balance between the classification accuracy and tree size, the threshold δ is optimized by the genetic algorithm.

The rest of this paper is organized as follows: the NRS_FS_FAST algorithm and FRGA algorithm are introduced in Section 2. The construction process of the FODT is described in Section 3. In Section 4, several comparative experiments are carried out to verify the effectiveness of the FODT. Section 5 concludes this paper.

2 The extraction of fuzzy rules

Before extracting the fuzzy rules, we first preprocess the raw data, as follows.

2.1 The NRS_FS_FAST algorithm

In recent years, with the development of computer and network technology, a variety of information technologies are widely used in commercial transactions. However, amounts of redundant data might exist in practical applications. Therefore, eliminating these ineffective data and gaining valuable knowledge have become a hot spot.

As we know, attribute reduction is one of the methods for dealing with the problem of data redundancy. Skowron, a famous mathematician in Poland, proposed the method of using discernibility matrix to represent knowledge and then using it to reduce attributes [32], which is simple and easy, but time-consuming. Zhang proposed an efficient heuristic attribute reduction algorithm based on information entropy [33], and Yang proposed an improved heuristic attribute reduction algorithm based on information entropy in rough set [34], which could not only improve the efficiency of attribute reduction, but decrease the number of attribute reduction. To solve inefficiencies, a kind of rough set attribute reduction algorithm was put forward [35] by combining the attribute compatibility model and the attribute importance model. Most of these algorithms set the same neighborhood size for all attributes, which can bring large error if there are large differences in the distribution of each attribute data. In order to reduce these errors, the NRS_FS_FAST algorithm [5] was proposed, which could not only select attributes effectively, but also obtain higher classification accuracy. This paper uses NRS_FS_FAST algorithm to reduce properties, as described in Algorithm 1.

figure e

2.2 Formation of the fuzzy numbers

The training samples are denoted by X = [xij]n × m, where n is the number of samples, and m is the number of attributes. xi = [xi1, xi2, …, xim](i = 1, 2, …, n) represents the i-th sample, fj(j = 1, 2, …, m) denotes the j-th attribute of X, xi, j is the j-th attribute value of the i-th sample xi, C = {1, 2, …, c} is a set of class labels, where c is the number of classes. X contains c equivalence classes Xl(l = 1, 2, …, c).

This paper adopts the combination of triangular functions and trapezoidal functions, and stipulates that the number of fuzzy membership functions defined on each attribute is equal to c. For each attribute, the first and the last function are trapezoidal functions, and the rest are triangular functions. Let fj, k denote the k-th(k = 1, 2, …, c) fuzzy number of the j-th attribute fj. If the class number c = 4, the fuzzy membership functions can be depicted as Fig. 2, which shows that the core of fuzzy membership functions lies in the values of parameters {msj, k}(k = 1, 2, …, c). These values are taken as the mean values of all patterns falling in the k-th equivalence class Xk in this paper. The values of \( \left\{{ms}_{j,k}^{\prime}\right\}\left(k=1,2,\dots, c\right) \) can be obtained by Eq. (1), and the values of {msj, k}(k = 1, 2, …, c) are the same values after sorting \( \left\{{ms}_{j,k}^{\prime}\right\}\left(k=1,2,\dots, c\right) \) in an ascending order.

$$ {ms}_{j,k}^{\prime }=\frac{\sum_{x_i\in {X}_k}{x}_{ij}}{\mid {X}_k\mid }, $$
(1)
Fig. 2
figure 2

The triangular and trapezoidal functions on attribute fj

Full size image

Example 2

Considering a set of weather data (see Table 1). X = [xi, j] = {x1, …, x10} is a set of 10 samples, xi ∈ R3 denotes weather condition of the i-th day, fj(j = 1, 2, 3) means the tj-th attribute. According to Eq. (1), we can get ms1, 1 = (45 + 48 + 26 + 99 + 69 + 74)/6 = 60.1667, ms1, 2 = (42 + 90 + 92 + 73)/4 = 74.25, ms2, 1 = 0.275, ms2, 2 = 0.4167, ms3, 1 = 2.75, and ms3, 2 = 3.667. Because c = 2, so K = 2, namely, it only generates two fuzzy numbers on each attribute. The semantics of all fuzzy numbers are f1, 1: “ Low temperature ”, f1, 2: “ High temperature ”, f2, 1: “ Low humidity ”, f2, 2: “ High humidity ”, f3, 1: “ Small wind ”, and f3, 2: “ High wind ” respectively. The membership functions of fuzzy numbers are shown in Fig. 3.

Table 1 A synthetic weather data
Full size table
Fig. 3
figure 3

The membership functions of fuzzy numbers

Full size image

2.3 Formation of fuzzy rules

Fuzzy IF-THEN rules can be described as follows [36]:

  • R: IF the value of xi1 is small and the value of xi2 is big, THEN xi belongs to class 1.

Taking the fuzzy numbers defined in Section 2.2 into account, the fuzzy IF-THEN rule can be rewritten as follows:

  • R: IF xi is f1, 1 and f2, 2, THEN xi belongs to class 1.

For each fuzzy set A ⊆ F, ∏f ∈ A represents the conjunction of fuzzy numbers in A. For instance, A = {f1, 1, f2, 2} ⊆ F, ∏f ∈ Af = f1, 1f2, 2. Therefore, the fuzzy rule can be further rewritten as:

  • R: IF xi is f1, 1f2, 2, THEN xi belongs to class 1.

2.4 The fuzzy rule generation algorithm (FRGA)

Fuzzy IF-THEN rules play a vital role in constructing the FODT. A classical association between properties A and B can be described as A ⇒ B, which indicates that an element satisfying property A is also able to satisfy property titB. Two indices (Support and Confidence [37]) are often used to measure the validity of such association rule. The support degree is defined as Supp(A ⇒ B)=∣A ∩ B ∣ / ∣ X∣, and the confidence degree is defined as Conf(A ⇒ B)=∣A ∩ B ∣ / ∣ A∣. When applying fuzzy rules to study the classification problem, we can generalize two measures: fuzzy support degree (FSupp) and fuzzy confidence degree (FConf) [38]. Specific formulas are as follows:

$$ FSupp\left(A\Rightarrow l\right)=\frac{\sum_{x\in {X}_l}A(x)}{\mid X\mid }, $$
(2)
$$ FConf\left(A\Rightarrow l\right)=\frac{\sum_{x\in {X}_l}A(x)}{\sum_{x\in X}A(x)}, $$
(3)
$$ A(x)=\frac{\sum_{f\in A}f(x)}{\mid A\mid }, $$
(4)

where A indicates ∏f ∈ Af, A(x) is the average membership degree that x belongs to the fuzzy set ∏f ∈ Af. ∣ · ∣ represents the number of elements over a set. When confirming the fuzzy number with the maximum fuzzy confidence degree, we determine the corresponding attribute of this fuzzy number and then remove the remaining fuzzy numbers concerning this attribute to reduce unnecessary fuzzy numbers. The specific steps of the FRGA are shown in Algorithm 2.

3 The construction of the FODT

3.1 The theory and algorithm of the FODT

The architecture of the FODT is developed by using fuzzy “if-then” rules, shown in Fig. 4.

Fig. 4
figure 4

The overall structure of the FODT

Full size image

Firstly, putting all training data X into the root node of the tree. The fuzzy rules extracted by the FRGA are denoted as R1, l(l = 1, …, c1), where c1 represents the class number of X. Only one rule is extracted for each class, so c1 = c. The subscript “1” of the rule R1, l indicates the first layer of the tree, the subscript “l” indicates the l-th class. Each class is assigned a leaf node, which contains as many samples that belongs to this class as possible. The samples that can not be contained in these leaf nodes are put into an additional node X1, δ, which is the only non-leaf node in first layer.

figure f

Secondly, the FODT continues to grow on additional node X1, δ. The fuzzy numbers of X1, δ are recalculated, and the FRGA based on these new fuzzy numbers is adopted again to extract fuzzy rules for each class contained in X1, δ, denoted by R2, l(l = 1, …, c2) respectively, where c2 represents the class number of X1, δ. And then we put the samples that cannot be determined by the second layer rules R2, l(l = 1, …, c2) into an additional node X2, δ, which is also an only non-leaf node in second layer.

⋱

Finally, the FODT continues to grow on additional node Xh, δ until one of the termination conditions is satisfied:

  1. (i)

    Xh, δ = ∅, which means that all samples have been determined by the rules Rh, l(l = 1, …, ch).

  2. (ii)

    Xh, δ = Xh − 1, δ, which means that the rules in the h-th layer lose its effect.

  3. (iii)

    ch = 1, which means that the samples in the h-th layer have the same class label.

Definition 1

Assuming the antecedent part of the rule Rh, l is Ah, l, where Ah, l(x) denotes the average membership degree of the sample x belonging to the fuzzy concepts contained in Ah, l. The non-leaf node in the h-th layer is defined as \( {X}^{h,\delta }={X}^{h-1,\delta}\left({R}_{h,1},{R}_{h,2},\dots, {R}_{h,{c}_h},\delta \right) \), which satisfies:

  1. (i)

    Xh, δ ⊆ Xh − 1, δ.

  2. (ii)

    ∀x ∈ Xh, δ, ∀l ∈ 1, 2, …, ch, Ah, l(x) < δ.

The FODT algorithm is shown in Algorithm 3. After constructing the FODT, each leaf node corresponds to a fuzzy IF-THEN rule.

3.2 Determination of the optimal threshold δ

The growth process and tree structure of the FODT can be controlled by the threshold δ. If the given threshold δ is small, we will get a larger decision tree, and if δ is large, the decision tree will be small. Obviously, the classification results of the fuzzy decision tree greatly depends on δ. However, it is difficult to directly obtain the optimal threshold δ from the training data. In this paper, we construct an objective function and use genetic algorithm to optimize δ, as follows:

$$ F\left(\delta \right)=\mid X\mid \ast {C}_a-\delta \ast N, $$
(5)

where ∣X∣ is the number of training samples, Ca is the classification accuracy of the training samples, and N is the number of leaf nodes.

figure g

3.3 Rules of the FODT

Let x be a test sample, h represent the h-th layer of the FODT, l indicate the l-th class. Ah, l denotes the antecedent part of the fuzzy rule Rh, l and ch represents the number of class in the h-th layer. The specific rules of the FODT are as follows:

figure h

3.4 Analysis of the time complexity

In this section, we study the time complexity of the FODT. Assuming that the FODT is built on one dataset with n training instances, m attributes, and c class label. The FODT is composed of two main phases: NRS_FS_FAST and FRGA. However, the major computation cost is used over the second phase. For the FRGA phase, the maximum length of fuzzy rules is H, thus the time complexity of FRGA is O(H ∗ c ∗ n). The number of layers of FODT, in the worst situation, is the number of samples, i.e., only one sample of training data is determined on each layer of the tree. Therefore, the time complexity of FODT is O(H ∗ c ∗ n ∗ n) in the worst situation. Moreover, the depth of the tree is on the order of O(logn). Thus, the total time complexity of the FODT is O(H ∗ c ∗ n ∗ logn).

4 Experimental results and analysis

In this section, we evaluate the performance of the FODT in several experiments. To verify the effectiveness of the FODT, we compare our method with some well-known decision tree algorithms, such as “traditional” decision tree algorithms (C4.5 [11], BFT [39], LAD [40], SC [41], and NBT [42]) and recently proposed decision tree algorithms (FRDT [17], HHCART [22], and FMMDT-HB [43]). In addition, we conduct experiments with ten-times ten-folds cross validation on twenty datasets acquired from the UCI Machine Learning repository [44] and one biomedical dataset [45]. The features of these datasets are given in Table 2. In the experiment, the parameter L in the NRS_FS_FAST is set to 2, and the adjustment parameters H and β in the FRGA are set to 5 and 0.02 respectively. Moreover, for all the traditional algorithms, we use their Weka implementation [46], and the values of the parameters for all the traditional algorithms are set to their default values.

Table 2 Description of the experimental datasets
Full size table

4.1 The experiment on iris data

We illustrate the performance of the FODT on Iris data. The iris data can be described by X = [xi, j]150 × 4 with three species: iris-setosa (class 1), iris-versicolor (class 2) and iris-virginica (class 3), and the data contains four attributes: sepal length (f1), sepal width (f2), petal length (f3), and petal width (f4). xi = [xi, 1, xi, 2, xi, 3, xi, 4] (1 ≤ i ≤ 150) represents the i-th sample.

The NRS_FS_FAST algorithm in Table 1 is firstly used to reduce attributes. Iris data is not reduced by the NRS_FS_FAST algorithm, i.e., we get all attributes of iris data after NRS_FS_FAST algorithm.

Next, the fuzzy numbers F = {fj, k| 1 ≤ j ≤ 4, 1 ≤ k ≤ 3} are obtained by the definition of fuzzy numbers in Section 2.2. And the semantics of the fuzzy numbers are as follows: f1, 1: “ The length of sepal is short ”, f1, 2: “ The length of sepal is medium ”, f1, 3: “ The length of sepal is long ”; f2, 1: “ The width of sepal is short ”, f2, 2: “ The width of sepal is medium ”, f2, 3: “ The width of sepal is long ”; f3, 1: “ The length of petal is short ”, f3, 2: “ The length of petal is medium ”, f3, 3: “ The length of petal is long ”; f4, 1: “ The width of petal is short ”, f4, 2: “ The width of petal is medium ”, and f4, 3: “ The width of petal is long ”. The fuzzy membership functions of these fuzzy numbers are shown in Fig. 5. Given parameter δ =0.5, the FODT is shown in Fig. 6. And the corresponding rules are as follows:

  • IF x is f1, 1f2, 1, THEN class 1

  • ELSE IF x is f1, 2f2, 2, THEN class 2

  • ELSE IF x is f1, 3f2, 3, THEN class 3

  • ELSE x belong to class 3.

Fig. 5
figure 5

Membership functions of fuzzy numbers on iris data

Full size image
Fig. 6
figure 6

The structure of the FODT on Iris data with δ = 0.5, H = 5

Full size image

The semantics of the fuzzy rules are “the samples which the petal length is short and the petal width is short belong to class 1; the samples which the petal length is medium and the petal width is medium belong to class 2; and the samples which the petal length is long and the petal width is long belong to class 3”. It can be seen that the rules obtained by the FRGA are easy to understand. Figure 7 shows the C4.5 decision tree. From Figs. 6 and 7, we can see that the tree structure obtained by the FODT is more concise, that is, the rules of the FODT are obviously less than that of the C4.5 tree.

Fig. 7
figure 7

The tree obtained by C4.5 on Iris data

Full size image

Moreover, the three-dimensional classification result of Iris training data by fuzzy rules R1, 1, R1, 2, and R1, 3 is shown in Fig. 8. The red circles indicate the samples determined by the rule R1, 1, the green squares representthe samples determined by the rule R1, 2, and the blue diamonds stand for the samples determined by the rule R1, 3. Besides, arrow 1 indicates that the rule R1, 2 divides the samples that belong to the third class into the second class, andarrow 2 represents that the rule R1, 3 divides the samples that belong to the second class into the third class. The membership degrees of Iris training data belonging to fuzzy rules R1, 1, R1, 2 and R1, 3 are depicted in Fig. 9. It shows that the samples in the first class originally belong to the rule R1, 1 with the largest membership degrees, the samples in the second class originally belong to the rule R1, 2 with the largest membership degrees, and the samples in the third class originally belong to the rule R1, 3 with the largest membership degrees. That is, we can obtain satisfactory results by using the fuzzy rules R1, 1, R1, 2 and R1, 3 to clarify the iris dataset.

Fig. 8
figure 8

The three-dimensional classification result of Iris training data by fuzzy rules R1, 1, R1, 2 and R1, 3

Full size image
Fig. 9
figure 9

The membership degrees of Iris training data belonging to fuzzy rules R1, 1, R1, 2 and R1, 3

Full size image

4.2 Comparison of the FODT with FMMDT-HB

FMMDT-HB [43] was a decision tree learning algorithm proposed by Mirzamome and Kangavar in 2017. In this subsection, we compare the presented algorithm with FMMDT-HB regarding both the classification accuracy and tree size. For better comparison, we use the datasets in [43], and the parameter settings of FMMDT-HB are consistent with [43].

Table 3 shows the number of misclassified instances (MI) and tree sizes (TS) along with the respective standard deviations of the FMMDT-HB and FODT. The results are the average results over ten runs of ten-folds cross validation. It can be observed that for most of the datasets, the FODT presents the less number of MI and TS. Specifically, the FODT, in the number of MI, is less than FMMDT-HB tested for the all datasets except Breast Cancer and Haberman. Besides, the decision trees generated by FODT are much smaller than those generated by FMMDT-HB, and FODT outperforms FMMDT-HB with eight of the nine datasets. We can conclude that the performance of the FODT has been verified. Moreover, Fig. 10 depicts these results. Compared with these results, we can see that the FODT achieves the better performance than the rival algorithm.

Table 3 The number of MI and TS along with the respective standard deviations of FMMDT-HB and FODT, and the best scores are indicated in boldface
Full size table
Fig. 10
figure 10

The number of MI and TS along with the respective standard deviations of FMMDT-HB and FODT

Full size image

4.3 Comparison of the FODT with HHCAT

HHCART [22] was a well-known oblique decision tree proposed in 2016. In this subsection, we compare FODT with HHCART in terms of classification accuracy, tree size, and time complexity. Similarly, the datasets in [22] are applied to carry out thecomparative experiments.

From the work in [22], the time complexities of HHCART(A) and HHCART(D) are O(c ∗ n2 ∗ m3) and O(c ∗ n2 ∗ m2) respectively. The time complexity of FODT is O(H ∗ c ∗ n ∗ logn) obtained from Section 3.4. Obviously, the time complexity of HHCART(A) is higher than that of HHCART(D). Therefore, we only need to compare the time complexity of HHCART(D) and FODT. In general, logn < n, m2 > H = 5, thus, it can be concluded that the time complexity of FODT is the lowest compared with the chosen benchmarks.

Table 4 shows the detailed comparison results in terms of the number of MI and TS along with the respective standard deviations of the HHCART and FODT. It is clear that the accuracy of our method is significantly higher than those of the HHCART(A) and HHCART(D) for all datasets except Breast Cancer. Besides, for each dataset, FODT produces fewer leaf nodes than HHCART(D), especially in datasets “Heart”, “Pima Indian”, “Wine” and “Survival”. It also denotes that the average tree size of the FODT is only 1.1 more than that of HHCAT(D). It is worth mentioning that, although the average number of TS in this paper is more than HHCART(A) and HHCART(D), the performances of classification accuracy and time complexity are better than those of the comparison algorithms. Moreover, the results in Table 4 are also depicted vividly in Fig. 11. These results advocate the superiority of FODT in producing more accurate decision trees.

Table 4 The number of MI and TS along with the respective standard deviations of HHCART(A), HHCART(D) and FODT, and the best scores are indicated in boldface
Full size table
Fig. 11
figure 11

The number of MI and TS along with the respective standard deviations of HHCART(A), HHCART(D) and FODT

Full size image

4.4 Comparison of the FODT with five conventional decision trees and FRDT

4.4.1 Comparison on number of MI and TS

In order to better demonstrate the superiority of the FODT, this paper compares our method with its state-of-the-art competitors: C4.5 [11], BFT [39], LAD [40], SC [41], NBT [42] and FRDT [17].

Table 5 summarizes the results on the number of MI of the FODT and the chosen benchmarks. The average number of MI by ten-times ten-folds cross classifications are listed in Table 5. The notation “∗” here indicates that the NBT algorithm is ineffective for ALLAML dataset. Compared with six state-of-the-art methods, our method obtains the highest accuracy in all datasets than decision trees: SC, BFT, LAD, and SC. It is not as good as the C4.5 onlyin one dataset (Wobc) and FRDT only in two datasets (Wobc and Waveform1). These results indicate that the FODT provides higher classification accuracy compared with the rival algorithms.

Table 5 The number of MI and standard deviation for the FODT and the chosen benchmarks, and the best scores are indicated in boldface
Full size table

The number of TS and standard deviation for the FODT and the chosen benchmarks is showed in Table 6. The notation “∗” here share the same meaning as Table 5. It is clear that the scale of the FODT isnot as good as the traditional decision trees (LAD, BFT, C4.5 and NBT) only in one dataset and SC only in two datasets. Tables 5 and 6 also show that the average number of MI and TS of the FODT is significantly less than the chosen benchmarks. Therefore, we can conclude that the FODT can generate more accurate and simpler decision trees. To better demonstrate the superiority of our approach, we draw a bar graph in Figs. 12 and 13. Obviously, our method has the better performance on both the classification accuracy and the size of tree.

Table 6 The number of TS and standard deviation for the FODT and the chosen benchmarks, and the best scores are indicated in boldface
Full size table
Fig. 12
figure 12

The number of MI for the FODT and the chosen benchmarks

Full size image
Fig. 13
figure 13

The number of TS for the FODT and the chosen benchmarks

Full size image

It is worth noting that the NRS FS FAST is used flexibly. On the one hand, some datasets, due to their data distribution, may be empty after the reduction of attributes. At this moment we do not reduce the attributes. On the other hand, if the datasets are too large (such as waveform1 and waveform2), the efficiency of the NRS FS FAST itself will be low, it is not necessary to reduce the attributes at this time.

4.4.2 Comparison on time complexity

This subsection compares the time complexities of the FODT with its state-of-the-art competitors: C4.5 [11], BFT [39], LAD [40], SC [41], NBT [42] and FRDT [17]. The time complexities of the chosen benchmarks are shown in Table 7.

Table 7 The time complexity of the FODT and its state-of-the-art competitors
Full size table

In order to compare the time complexity of our method with the state-of-the-art competitors more clearly, the datasets in Table 2 are used for complexity ranking. Without loss of generality, logn > c, therefore, the time complexities of BFT, LAD and SC are the same. When MaxL = H, the time complexities of FRDT and FODT are also the same. Thus, we only need to compare our method with BFT, C4.5, and NBT. The time complexity is ranked in ascending order, i.e. higher ranking means lower time complexity. Table 8 shows the time complexity ranking of BFT, C4.5, NBT and FODT. It can be observed that the average ranking of the FODT is better than BFT, C4.5 and NBT. Therefore, the proposed method has obvious advantages in terms of time complexity.

Table 8 The time complexity ranking of BFT, C4.5, NBT and FODT on nine datasets
Full size table

4.4.3 Holm test

To arrive at strong evidence, the statistical test is used to analyze whether the FODT is significantly better than other decision trees. Holm test [47] is applied in this paper, and the test statistic for comparing the j-th classifier and the k-th classifier is expressed as:

$$ Z=\frac{Ran{k}_j- Ran{k}_k}{SE}, $$
(6)
$$ SE=\sqrt{\frac{l\left(l+1\right)}{6\times N}}, $$
(7)
$$ Ran{k}_j=\frac{1}{N}\sum \limits_{i=1}^N{r}_i^j, $$
(8)

where l is the number of classifiers, N is the number of datasets, \( {r}_i^j \) is the rank of the classifier j on the i-th dataset, and Rankj is the average rank of the classifier j on the entire dataset.

Statistic Z follows the standard normal distribution, and the z value is used to determine the corresponding probability p from the table of normal distribution. We denote the ordered p values by p1, p1, …, so that p1 ≤ p2 ≤ … ≤ pl − 1 and then compare pj with a/(1 − j) (a stands for confidence level, usually is set to 0.05). If p1 < a/(l − 1), the corresponding hypothesis (two classifiers have the same performance) should be rejected, and then we compare p2 with a/(l − 2). If the second hypothesis is rejected, the test proceeds with the third one, etc. As long as there is a hypothesis cannot be rejected, all the remaining assumptions shall not be rejected.

According to Table 5 and Eq. (8), the average ranking of all decision trees can be obtained, RankLAD = 5.75, RankBFT = 5.08, RankSC = 4.83, RankC4.5 = 4.67, RankNBT = 3.45, RankFRDT = 2.33, and RankFODT = 1.58. With a = 0.05, l = 7 and N = 12, the standard deviation SE = 0.88. The results of the Holm test are shown in Table 9, which indicate that the Holm procedure rejects the first four hypotheses since the corresponding p values are smaller than the adjusted a′s, and only the last two hypotheses are accepted. This means that the classification accuracy of the FODT is significantly better than that of traditional decision trees NBT, SC, BFT, and LAD. Although the FODT is not significantly higher than the C4.5 and FRDT, the average classification accuracy of the FODT is higher than that of the C4.5 and FRDT.

Table 9 The Holm test
Full size table

5 Conclusion

In this paper, we propose a novel fuzzy oblique decision tree, called FODT, which can achieve high classification accuracy and small tree size. Different from traditional axis-parallel decision trees and oblique decision trees, the FODT takes dynamic mining fuzzy rules as decision functions. In order to eliminate data redundancy and improve classification efficiency, the NRS_FS_FAST algorithm is first introduced to reduce attributes. Then, the FRGA is proposed to generate fuzzy rules, and these rules are used to construct leaf nodes for each class in each layer of the FODT. The growth of the FODT is developed by expanding an additional node, which is the only non-leaf node of each layer of the tree, and the fuzzy numbers of additional node in each layerare recalculated to get more accurate fuzzy partition. Finally, the parameter δ that can control the size of the tree is optimized by genetic algorithm. A series of comparative experiments on twenty UCI machine learning datasets and one biomedical dataset have verified the effectiveness of the proposed method. Therefore, our method is feasible and promising for dealing with the classification problem.