Axiomatic fuzzy set theory-based fuzzy oblique decision tree with dynamic mining fuzzy rules

Abstract

This paper proposes a novel classification technology—fuzzy rule-based oblique decision tree (FRODT). The neighborhood rough sets-based FAST feature selection (NRS_FS_FAST) is first introduced to reduce attributes. In the axiomatic fuzzy set theory framework, the fuzzy rule extraction algorithm is then proposed to dynamically extract fuzzy rules. And these rules are regarded as the decision function during the tree construction. The FRODT is developed by expanding the unique non-leaf node in each layer of the tree, which results in a new tree structure with linguistic interpretation. Moreover, the genetic algorithm is implemented on $\sigma$ to obtain the balanced results between classification accuracy and tree size. A series of comparative experiments are carried out with five classical classification algorithms (C4.5, BFT, LAD, SC and NBT), and recently proposed decision tree HHCART on 20 UCI data sets. Experiment results show that the FRODT exhibits better classification performance on accuracy and tree size than those of the rival algorithms.

1 Introduction

Decision trees have received great attention on account of its significant potential applications, especially in statistics, machine learning and pattern recognition [1,2,3]. They have been widely used in classification problems due to the following three advantages: (1) the classification performance of the decision trees is close to or even outperforming other classification models, (2) the decision trees can handle different types of attributes, such as numeric and categorical, and (3) the results of decision trees are easy to be comprehended [4,5,6].

The decision trees grow in a top-down way, and recursively divide the training samples into segments having similar or the same outputs. Until now, there are three types of decision trees: “standard” decision trees [7,8,9,10], fuzzy decision trees [11,12,13,14,15], and oblique decision trees [16,17,18,19,20,21,22]. “Standard” decision trees are the simplest decision trees. However, they are incapable of addressing uncertainties consistent with human cognitive, such as vagueness and ambiguity. In this case, fuzzy decision trees with fuzzy uncertainty measure came into fashion [11,12,13,14,15]. For example, a novel fuzzy decision tree was introduced for the data mining task [11]. A new type of coherence membership function based on AFS theory was established to describe the fuzzy concepts, and fuzzy rule-based classifier was proposed in [12]. Moreover, based on fuzzy set theory, the new tree construction technology for data classification problem was presented in [14]. The above decision trees [6,7,8,9,10,11,12,13,14,15] take one attribute as decision function during the tree construction. However, if these data are more properly segmented by the hyperplanes, they may lead to complex and inaccurate trees. In this event, oblique decision trees are more suitable.

Many profound results on oblique tree induction algorithms have been obtained [16,17,18,19,20,21,22]. For example, Erick et al. improved the decision function by combining evolutionary algorithm with genetic algorithm to increase the efficiency of tree building [17]. A new bottom-up oblique decision tree structure framework was presented in [19]. Moreover, Wickramarachchi et al proposed an effective heuristic approach to build oblique decision trees [22]. These evolutionary algorithms greatly improve the efficiency of tree building; however, they lack of semantic interpretation. Fortunately, the AFS theory-based classification methods have received extensive attention because of its significant advantage with semantic interpretation for classification results. Motivated by the above discussion, this paper combines AFS theory with decision tree technology to construct the new fuzzy oblique decision tree endowed with readable linguistic interpretation.

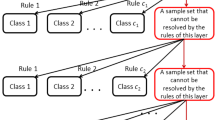
The structure of the FRODT is depicted in Fig. 1. All sample data are contained at the root node of the FRODT. At this node, we adopt the FREA to extract fuzzy rules and the samples that have not been classified by these rules are placed on an additional non-leaf node. At the non-leaf node, we use the FREA again to generate new fuzzy rules. And the samples that have not been classified by these new rules are also placed on an additional non-leaf node. The growth of the FRODT is repeated until the stopping condition has been satisfied.

Fig. 1

The overall structure of the FRODT

The main contributions of the current work are summarized as four aspects:

• The Neighborhood Rough Sets-based FAST Feature Selection (NRS_FS _FAST) algorithm is introduced to reduce data redundancy and improve classification efficiency.

• A new fuzzy rule extraction algorithm (FREA) is proposed to decrease the scale of the tree.

• The AFS theory is adopted to increase semantic interpretation and decrease the human subjectivity in selecting membership functions.

• The genetic algorithm is implemented on $\sigma$ to balance the results between classification accuracy and tree size.

This paper is arranged as follows: the NRS_FS_FAST algorithm is introduced in Sect. 2. In Sect. 3, the basic notions and properties of the AFS theory are provided. Section 4 describes the construction of the FRODT in detail. In Sect. 5, several comparative experiments are conducted to verify the superiority and interpretability of the FRODT. Section 6 concludes this paper.

2 The neighborhood rough sets-based FAST feature selection (NRS_FS_FAST) algorithm

2.1 The neighborhood rough set

The basic notations of the neighborhood rough set are introduced in this section, and the readers can refer to the details in [23, 24].

The data can be denoted as $NDT=\langle U,A,D \rangle$, where U is a non-empty set of samples $\{x_{1}, x_{2}, x_{3},\ldots ,x_{n}\}$, A is a condition attribute set and D is a decision attribute. $NDT=\langle U, A, D \rangle$ is called as a neighborhood decision system.

Definition 1

([24]). Consider a neighborhood decision system $NDT=\langle U,A,D\rangle$, for $\forall x_{i}\in U$ and $B\subseteq A$, the neighborhood $\delta _{B}(x_{i})$ of $x_{i}$ is defined as:

$$\begin{aligned} \delta _{B}(x_{i})=\{x_{j}\mid x_{j}\in U, \varDelta _{B}(x_{i},x_{j})\le \delta \}, 1\le i, j \le n, \end{aligned}$$

(1)

where the metric $\varDelta$ is a metric function.

Definition 2

([24]). Let $NDT=\langle U,A,D\rangle$ be a neighborhood decision system, the decision attribute D partitions the domain U into N equivalence classes with $X_{1}, X_{2},\ldots , X_{N}$. For arbitrary $B\subseteq A$, the lower and upper approximations of the decision attribute D with regard to the condition attribute set B are described as:

$$\begin{aligned}&\underline{N_{B}}D=\bigcup _{k=1}^{N}\underline{N_{B}}X_{k}, \end{aligned}$$

(2)

$$\begin{aligned}&\overline{N_{B}}D=\bigcup _{k=1}^{N}\overline{N_{B}}X_{k}, \end{aligned}$$

(3)

where:

$$\begin{aligned}&\underline{N_{B}}X_{k}=\{x_{i}\mid \delta _{B}(x_{i})\subseteq X_{k},x_{i}\in U, 1 \le i\le n\}, \end{aligned}$$

(4)

$$\begin{aligned}&\overline{N_{B}}X_{k}=\{x_{i}\mid \delta _{B}(x_{i})\cap X_{k}\ne \varnothing ,x_{i}\in U, 1 \le i\le n\}, \end{aligned}$$

(5)

and the lower approximation is usually called decision positive region, denoted by $POS_{B}(D)$.

The decision boundary region of the decision attribute D with regard to the condition attribute set B is defined as:

$$\begin{aligned} BN(D)=\overline{N_{B}}D-\underline{N_{B}}D. \end{aligned}$$

(6)

Figure 2 shows a binary classification problem with two condition attributes $B_{1}$ and $B_{2}$. The decision attribute D partitions the domain U into two equivalence classes $X_{1}$ and $X_{2}$. $X_{1}$ is labeled with “*” and $X_{2}$ is labeled with “+”. Let the metric $\varDelta$ be a circular neighborhood with radius $\delta$ for each condition attribute. Given three samples $x_{1}$, $x_{2}$ and $x_{3}$, on the basis of above definitions, we can get $\delta _{B_{1}}(x_{1})\subseteq X_{1}$, $\delta _{B_{1}}(x_{3})\subseteq X_{2}$, $\delta _{B_{1}}(x_{2})\cap X_{1}\ne \varnothing$ and $\delta _{B_{1}}(x_{2})\cap X_{2}\ne \varnothing$. Therefore, $x_{1}\in \underline{N_{B_{1}}}X_{1}$, $x_{3}\in \underline{N_{B_{1}}}X_{2}$ and $x_{2}\in B_{1}N(D)$. Similarly, we can obtain $\delta _{B_{2}}(x_{1})\subseteq X_{1}$, $\delta _{B_{2}}(x_{3})\subseteq X_{2}$, $\delta _{B_{2}}(x_{2})\cap X_{1}\ne \varnothing$ and $\delta _{B_{2}}(x_{2})\cap X_{2}\ne \varnothing$. Therefore, $x_{1}\in \underline{N_{B_{2}}}X_{1}$, $x_{3}\in \underline{N_{B_{2}}}X_{2}$ and $x_{2}\in B_{2}N(D)$.

Fig. 2

The binary classification example

Definition 3

([24]). The dependence degree of the decision attribute D on the condition attribute set B is defined as:

$$\begin{aligned} \gamma _{B}(D)=|POS_{B}(\textit{D})|/|\textit{U}|. \end{aligned}$$

(7)

Obviously, $0\le \gamma _{B}(D)\le 1$. If $\gamma _{B}(D)=1$, the decision attribute D completely depends on the condition attribute set B.

Definition 4

([24]). Consider a neighborhood decision system $\langle U, A, D \rangle$, for any $B\subseteq A$, $a\in A-B$, the significance of the attribute a to condition attribute set B is given as:

$$\begin{aligned} \mathrm{SIG}(a,B,D)=\gamma _{B\cup a}(D)-\gamma _{B}(D). \end{aligned}$$

(8)

2.2 The NRS_FS_FAST algorithm

As we all know, setting the same neighborhood size for all attributes can affect the results of feature selection, due to the fact that the data distribution of each attribute is often different. To settle this issue, the NRS_FS_FAST algorithm is introduced in this paper, and the pseudo-code is summarized in Algorithm 1.

Definition 5

([25]). Let $NDT=\langle U, A, D \rangle$ be a neighborhood decision system, $SD=\{SD_{1}, SD_{2},\ldots ,SD_{m}\}$ is a set of standard deviation of each attribute, where m is the number of attributes. The relationship matrix of neighborhood relation $N_{i}$ of the attribute i on U is defined as:

$$\begin{aligned} M_{(N_{i})}=(r_{p,q})_{n\times n}, \end{aligned}$$

(9)

where

$$\begin{aligned} r_{p,q}=\left\{ \begin{array}{ll} 1, \quad &\varDelta (x_{p},x_{q})\le \delta _{i} \\ 0, \quad &\mathrm{others} \\ \end{array} \right. , 1\le p\le n,1\le q\le n, \end{aligned}$$

(10)

$\delta _{i}=SD_{i}/L$ denotes the threshold of neighborhood size, and L is a given parameter to control the size of neighborhood.

3 The introduction of the AFS theory

This section mainly recalls the notations of the AFS theory. The detailed introduction can be referred to [26,27,28,29,30,31].

3.1 AFS algebra

In order to explain the AFS algebra, the following example is given.

Example 1

Consider a set of data with 10 samples $X=\{x_{1},\ldots ,x_{10}\}$ and the features of data are described by real numbers (age, appearance, and wealth), Boolean values (gender) and the order relations (hair color), shown in Table 1.

Table 1 The description of samples

In Table 1, the order number i in the “hair color” columns denotes that the hair color of $x\in X$ has ordered according to our perception. Take the order relations of “hair black,” for example, $x_{7}>x_{10}>x_{4}=x_{8}>x_{2}=x_{9}>x_{5}>x_{6}=x_{3}=x_{1}$, where $x_{i}>x_{j}$ means that the hair of $x_{i}$ is more closer to black color than that of $x_{j}$.

Let $M=\{m_{1},m_{2},\ldots , m_{12}\}$ be a set of simple fuzzy concepts on X and each $m\in M$ associates with one single attribute. These fuzzy concepts can be explained as follows: $m_{1}$: “old persons”, $m_{2}$: “tall persons”, $m_{3}$: “heavy persons”, $m_{4}$: “high salary”, $m_{5}$: “more estate”, $m_{6}$: “male”, $m_{7}$: “female”, $m_{8}$: “black hair persons”, $m_{9}$: “white hair persons”, $m_{10}$: “yellow hair persons”, $m_{11}$: “young persons”, and $m_{12}$: “the persons about 40 years old”. For any $A\subseteq M$, $\prod _{m\in A}m$ indicates the conjunction (i.e., the logic operator “and”) of concepts in A. For example, for $A=\{m_{1},m_{6}\}\subseteq M$, $\prod _{m\in A}m$ indicates the new complex fuzzy concept “old males” associated with two attributes “age” and “gender”.

$\sum _{i\in I}(\prod _{m\in A_{i}}m)$ is the formal sum of $\prod _{m\in A_{i}}m \, (A_{i}\subseteq M, i\in I$, and I is a non-empty index set), which denotes the disjunction (i.e., the logic operator “or”) of the complex fuzzy concept $\prod _{m\in A_{i}}m$. For example, $\gamma =m_{1}m_{6}+m_{1}m_{3}+m_{2}$ can be interpreted as “old males” or “heavy old persons” or “tall persons”. By the comparison of the complex fuzzy concepts $m_{3}m_{8}+m_{1}m_{4}+m_{1}m_{6}m_{7}+m_{1}m_{4}m_{8}$ and $m_{3}m_{8}+m_{1}m_{4}+m_{1}m_{6}m_{7}$, we can get that the fuzzy concepts in the left side and right side are equivalent. This is due to the fact that, for any sample x, the degree of x belonging to the fuzzy concept $m_{1}m_{4}m_{8}$ is always less than or equal to that of $m_{1}m_{4}$. Therefore, the term $m_{1}m_{4}m_{8}$ is redundant in the left side.

Take two complex fuzzy concepts with the form $\alpha : m_{1}m_{4}+m_{2}m_{5}m_{6}$ and $\upsilon : m_{5}m_{6}+m_{5}m_{8}$ into consideration, the semantics of “$\alpha$ or $\upsilon$” and “$\alpha$ and $\upsilon$” can be explained as:

• “$\alpha$ or $\upsilon$”: $m_{1}m_{4}+m_{2}m_{5}m_{6} +m_{5}m_{6}+m_{5}m_{8}$ = $m_{1}m_{4}+m_{5}m_{6}+m_{5}m_{8}$;

• “$\alpha$ and $\upsilon$”: $m_{1}m_{4}m_{5}m_{6}+m_{2}m_{5}m_{6}+m_{1}m_{4}m_{5}m_{8}+m_{2}m_{5}m_{6}m_{8}= m_{1}m_{4}m_{5}m_{6}+m_{2}m_{5}m_{6}+m_{1}m_{4}m_{5}m_{8}$.

The $\sum _{i\in I}(\prod _{m\in A_{i}}m)$ forms AFS algebra, and the set $EM^{*}$ is given as:

$$\begin{aligned} EM^{*}=\left\{ \sum _{i\in I}\left( \prod _{m\in A_{i}}m \right) |A_{i}\subseteq M, \ I\ \text {is}\ \text {a}\ \text {non-empty} \ \text {index} \ \text {set}\right\} , \end{aligned}$$

(11)

where the symbols $\varSigma$ and $\varPi$ denote the disjunction and conjunction of fuzzy concepts, respectively.

For any fuzzy concepts m, n, and $h\in M$, the AFS algebra is based on the following assumptions:

• (1) “m and m and n” is equivalent to “m and n”;

• (2) “m and n” is equivalent to “n and m”;

• (3) “ m and n and h” or “n and m” is equivalent to “n and m”.

Definition 6

([27]) Consider a simple fuzzy concept set M, the binary equivalence relation R on $EM^{*}$ can be described as: for any $\sum _{i\in I}(\prod _{m\in P_{i}}m)$, and $\sum _{j\in J}(\prod _{m\in Q_{j}}m)\in EM^{*}$, $(\sum _{i\in I}(\prod _{m\in P_{i}}m)) R (\sum _{j\in J}(\prod _{m\in Q_{j}}m))\Leftrightarrow$

• (1) for arbitrary $P_{i}(i\in I)$, there exists $Q_{h}(h\in J)$ such that $P_{i}\supseteq Q_{h}$;

• (2) for arbitrary $Q_{j}(j\in J)$, there exists $P_{k}(k\in I)$ such that $Q_{j}\supseteq P_{k}$.

The notation $\sum _{i\in I}(\prod _{m\in P_{i}}m)R\sum _{j\in J}(\prod _{m\in Q_{j}}m)$ means that $\sum _{i\in I}(\prod _{m\in P_{i}}m)$ and $\sum _{j\in J}(\prod _{m\in Q_{j}}m)$ are equivalent under equivalence relation R. For example, $\xi =m_{3}m_{8}+m_{1}m_{4}+m_{1}m_{6}m_{7}+m_{1}m_{4}m_{8}$, $\zeta =m_{3}m_{8}+m_{1}m_{4}+m_{1}m_{6}m_{7}\in EM$, by Definition 6, we have $\xi =\zeta$.

Theorem 1

([27]) Consider a simple fuzzy concept setM, the$(EM,\vee ,\wedge )$constitutes a completely distributive latticeif$\sum _{i\in I}(\prod _{m\in P_{i}}m)\in EM$and$\sum _{j\in J}(\prod _{m\in Q_{j}}m)\in EM$satisfythe following conditions:

$$\begin{aligned}&\sum _{i\in I}\left( \prod _{m\in P_{i}}m \right) \vee \sum _{j\in J}\left( \prod _{m\in Q_{j}}m \right) \nonumber \\&\quad = \sum _{k\in I\lfloor \rfloor J}\left( \prod _{m\in W_{k}}m\right) , \end{aligned}$$

(12)

$$\begin{aligned}&\sum _{i\in I}\left( \prod _{m\in P_{i}}m \right) \wedge \sum _{j\in J}\left( \prod _{m\in Q_{j}}m\right) \nonumber \\&\quad =\sum _{i\in I,j\in J}\left( \prod _{m\in P_{i}\cup Q_{j}}m\right) , \end{aligned}$$

(13)

where $I\lfloor \rfloor J$ denotes the disjoint union of I and J. Therefore, $W_{k}=P_{k}$ if $k\in I$, and $W_{k}=Q_{k}$ if $k\in J$.

Definition 7

([30]) Given a simple fuzzy concept m on X, the binary relation $R_{m}$ is described as: for any $u,v \in X, (u,v)\in R_{m}\Leftrightarrow$u belongs to the fuzzy concept m, and the degree of u belonging to m is larger than or equals to that of v; or u belongs to m to some extent while v does not belong to m.

3.2 AFS structure

AFS structure can produce various lattice representations of the fuzzy logic operations and fuzzy membership degrees [27, 30].

Definition 8

([30]) Given a simple fuzzy concept set M, $\tau (u,v)$=$\{\xi |\xi \in M,(u, v)\in R_{\xi }\}\in 2^{M}$, if $\tau$ meets the following conditions:

• (1) for any $(u, v)\in X \times X,\tau (u, v)\subseteq \tau (u, u)$,

• (2) for any $(u, v),(v, w)\in X \times X,\tau (u, v)\cap \tau (v, w)\subseteq \tau (u, w)$,

where $2^{M}$ is the power set of M, and $(M,\tau ,X)$ is considered as AFS structure.

For instance, when $x=x_{4}, y=x_{1},x_{2}\ldots ,x_{10}$, respectively, one has

$$\begin{aligned} \tau (x_{4}, x_{1})&= {} \{m_{1}, m_{4}, m_{5}, m_{6}, m_{8}, m_{10}\},\\ \tau (x_{4}, x_{2})&= \{m_{1}, m_{2}, m_{3},m_{4}, m_{5}, m_{6}, m_{8}\},\\ \tau (x_{4}, x_{3})&= \{m_{1}, m_{2}, m_{3},m_{5}, m_{6}, m_{8}, m_{10}\},\\ \tau (x_{4}, x_{4})&= \{m_{1}, m_{2}, m_{3}, m_{4}, m_{5}, m_{6}, m_{8}, m_{9}, m_{10}, m_{11}, m_{12}\},\\ \tau (x_{4}, x_{5})&= \{m_{1}, m_{2}, m_{3},m_{4}, m_{5}, m_{6}, m_{8}, m_{10}\},\\ \tau (x_{4}, x_{6})&= \{m_{1}, m_{2}, m_{5}, m_{6}, m_{8}, m_{10}\},\\ \tau (x_{4}, x_{7})&= \{m_{1},m_{2}, m_{6}, m_{9}, m_{10}\},\\ \tau (x_{4}, x_{8})&= \{m_{1},m_{2}, m_{3},m_{5},m_{6},m_{8}, m_{9}, m_{10}\},\\ \tau (x_{4}, x_{9})&= \{m_{1},m_{6},m_{8}\},\\ \tau (x_{4}, x_{10})&= \{m_{1}, m_{2}, m_{3},m_{4}, m_{5}, m_{6},m_{9},m_{10}\}. \end{aligned}$$

Definition 9

([30]) Given a simple fuzzy concept set M, for any $A\subseteq M$ and $x\in X,$$A^{\tau }(x)\subseteq X$ is defined as:

$$\begin{aligned} A^{\tau }(x)=\{y\in X|\tau (x,y)\supseteq A\}. \end{aligned}$$

(14)

For instance, if $x=x_{4}$, $A=\{m_{1},m_{2},m_{3}\}\subseteq M$, we have $\tau (x_{4}, x_{2})\supseteq A$, $\tau (x_{4}, x_{3})\supseteq A$, $\tau (x_{4}, x_{4})\supseteq A$, $\tau (x_{4}, x_{5})\supseteq A$, $\tau (x_{4}, x_{8})\supseteq A$, and $\tau (x_{4}, x_{10})\supseteq A$ (refer to Definition 8). Then $A^{\tau }(x_{4})=\{x_{2},x_{3},x_{4},x_{5},x_{8},x_{10}\}$ can be obtained. In summary, $A^{\tau }(x)$ is determined by data distribution and the semantic interpretations of fuzzy sets.

Definition 10

([27]) Given a simple fuzzy concept $\omega$ on X, if $\rho _{\omega }:X\rightarrow R^{+}$ satisfies the following two conditions:

• (1) $\rho _{\omega }(x)=0\Leftrightarrow (x,x)\notin R_{\omega }, \forall x\in X$;

• (2) $\rho _{\omega }(x)\ge \rho _{\omega }(y)\Leftrightarrow (x,y)\in R_{\omega }, \forall x,y\in X$,

$\rho _{\omega }$ is called as the weight function of fuzzy concept $\omega$.

Definition 11

([27]). Consider a simple fuzzy concept set M and weight function $\rho _{m}$ of $m\in M$, for any $x\in {{X}}$, $A_{i}\subseteq M$, the membership degree of x belonging to $\zeta =\sum _{i\in I}(\prod _{m\in A_{i}}m)\in EM$ is given as:

$$\begin{aligned} \mu _{\zeta }(x)=\mathrm{sup}_{i\in I}inf_{m\in A_{i}}\frac{\sum \nolimits _{u\in A_{i}^{\tau }(x)} \rho _{m}(u)N_{u}}{\sum \nolimits _{u\in X}\rho _{m}(u)N_{u}}, \end{aligned}$$

(15)

here $N_{u}$ is the number that how many times u has been observed.

From Eq. (15), we can see that $\mu _{\zeta }(x)$ is determined by $A_{i}^{\tau }(x)$, simple concept set $A_{i}$ and weight function $\rho _{m}(u)$. From Definition 9, $A^{\tau }(x)$ is determined by data distribution and the semantics of fuzzy sets. Thus, if the weight function has been determined, the membership function is only related to the data distribution and the semantics of fuzzy sets.

4 The construction of the FRODT

4.1 The expression of fuzzy rules

Let $X=[x_{ij}]_{n\times m}$ be a sample data set, here m is the feature numbers and n is the sample numbers. The set of class labels of X is $C=\{1,2,\ldots ,c\}$, and the jth feature of X is $f_{j}(j=1,2,\ldots ,m)$. Moreover, $X_{l}(l=1,2,\ldots ,c)$ is the set of samples belonging to the lth class.

For simplicity, the fuzzy concepts “small”, “medium” and “big” are adopted to describe the characteristics of each feature $f_{j}$. We use $f_{j,p}$ to represent the pth fuzzy concept of the jth attribute. The linguistic interpretation of $f_{j,p}(p=1,2,3)$ is that $f_{j}$ is small, medium, and big, respectively.

The main features of data can be well described by the fuzzy IF-THEN rules. In 1997, Zadeh proposed a method of expressing fuzzy rules [32]:

Rule: if $x_{i1}$ is big and $x_{i2}$ is small, then the sample $x_{i}$ falls into the first class.

By the defined fuzzy concepts $f_{j,p}$, we can rewrite the above rule:

Rule: if the sample $x_{i}$ is $f_{1,3}$ and $f_{2,1}$, then it is classified as the first class.

According to the definitions of logical operations “and” and “or” in Example 1, we can redescribe the above rule:

Rule: if the sample $x_{i}$ is $f_{1,3}f_{2,1}$, then it falls into the first class.

4.2 Fuzzy rule extraction

Fuzzy IF-THEN rules are critical for constructing the FRODT. The classical form of fuzzy association rules is $A\Rightarrow B$. It means that an element satisfies the condition A can also satisfy the condition B. The association degrees of association rules were measured by the Support and Confidence indices [33]. Later, Fuzzy Support and Fuzzy Confidence indices were applied in classification problems [34]. Inspired by [34], based on AFS theory, we define the Fuzzy Confidence indice of this paper, as follows:

$$\begin{aligned}&FConf(F \Rightarrow c)=\frac{\sum \nolimits _{x\in X_{c}}{\mu _{F}(x)}}{\sum \nolimits _{x\in X}{\mu _{F}(x)}}, \end{aligned}$$

(16)

$$\begin{aligned}&\mu _{F}(x)=\frac{\sum \nolimits _{f\in A}{\mu _{f}(x)}}{|A|}, \end{aligned}$$

(17)

where the former part of the fuzzy rule corresponds to the complex fuzzy concept F, and the class label corresponds to c. $\mu _{F}(x)$ ($\mu _{f}(x)$) demonstrates the average membership degree (membership degree) of x that is described by the complex fuzzy concept F (simple fuzzy concept f), and |.| represents the cardinality of a set. Moreover, A is the set of all simple fuzzy concepts contained in F, for example, if $F=f_{11}f_{22}$, then $A=\{f_{11},f_{22}\},|A|=2$. The bigger the fuzzy confidence degree is, the more suitable complex fuzzy concept F is for describing the lth class.

The FREA based on Fuzzy Confidence is proposed to extract only one single rule for each class, shown in Algorithm 2.

4.3 The architecture of the FRODT

The architecture of the FRODT is shown in Fig. 3, and the build-up process is as follows.

Fig. 3

The overall structure of the FRODT

Firstly, all sample data X is contained at the root node of the FRODT. At this node, we use the FREA to extract fuzzy rules, expressed as $R_{1,l} (l=1,\ldots ,c_{1})$ with “1” denoting the first layer and “l” indicating the lth category. Since only one rule is extracted for each class, thus $c_{1}=c$. Each class is assigned a leaf node, which contains as many samples that belongs to this class as possible. The samples that cannot be covered by these rules are placed on an non-leaf node $X^{1,\sigma }$. Besides, the threshold $\sigma$ is applied to judge whether the sample can be covered by these rules or not. In order to balance the accuracy of classification and the size of tree, we propose a new algorithm—Rules Covering Samples Algorithm (RCSA), as shown in Algorithm 3.

Secondly, on the non-leaf node $X^{1,\sigma }$, we use the FREA again to extract fuzzy rules, expressed as $R_{2,l} (l=1,\ldots ,c_{2})$. Each class is also assigned a leaf node and the samples that cannot be covered by these rules are placed on the second non-leaf node $X^{2,\sigma }$.

$\ddots$

Finally, on additional non-leaf node $X^{h,\sigma }$, the FRODT continues to grow until it meets one of the three stopping conditions: (1)$X^{h,\sigma }=\varnothing$, (2) $X^{h,\sigma }=X^{h-1,\sigma }$ and (3) $c_{h}=1$. They, respectively, represent that, in the hth layer of the FRODT, the rules cover all samples; the rules lose its effect; and the samples belong to the same class. In the second case, we select the class with the largest number of samples as the final category.

The construction process of FRODT is summarized in Algorithm 4.

4.4 Analysis of the time complexity

In this subsection, we analyze the time complexity of Algorithms 1–4. Assuming that the Algorithms 1–4 are conducted on one data set with n training instances, m attributes, and c class label. In general, the number of training instances is greater than that of attributes, i.e., $n>m$. Algorithm 1 is composed of two main phases: GetNeighborRelation and SelectAttributes. By Definition 5 and Algorithm 1, we can get that the time complexity of GetNeighborRelation is $O(m *n*n)$, and the time complexity of SelectAttributes is $O(m *m*n)$. Since $n>m$, thus the time complexity of Algorithm 1 is $O(m *n*n)$. For Algorithm 2, the maximum length of fuzzy rule is $H=min\{MaxR, c*m\}$, thus the time complexity of Algorithm 2 is $O(H*c)$. For Algorithm 3, it is easy to get that the time complexity of Algorithm 3 is O(1). For Algorithm 4, the number of layers of the FRODT is the number of samples in the worst situation, i.e., only one sample of training data is determined on each layer of the tree. Therefore, the time complexity of Algorithm 4 is $O(H*c*n)$ in the worst situation. However, the depth of the tree is on the order of O(logn). Thus, the total time complexity of the Algorithm 4 is $O(H*c*logn)$.

5 Experimental results and analysis

In this section, we compare the FRODT with HHCAT [19] and five classical classification algorithms such as SC [5], C4.5 [7], BFT [35], LAD [36], and NBT [37] under the Waikato environment for knowledge analysis (WEKA) 3.6 framework [38]. We use ten times tenfold cross-validation to estimate the classification accuracy and tree size of the FRODT. In the experiment, the parameter L in the NRS_FS_FAST is set to 2, the number of simple fuzzy concepts on each attribute is set to 3, and the adjustment factors MaxR and $\beta$ in the FREA are set to 5 and 0.02, respectively. For the sake of simplicity, $N_{u}=1$ and $\rho _{m}(u)=1$ in this paper.

5.1 The experiment on Iris data

Iris data is one of the most commonly used data in the UCI machine learning database. We apply the proposed algorithm to Iris data set, and the detailed process is as follows.

First, the NRS_FS_FAST algorithm is applied to select an attribute subset, which has petal length, petal width, sepal length and sepal width, respectively. That is, the number of attributes is not reduced on iris data.

Second, according to the AFS theory, we can get the fuzzy concepts $f_{i,j}, i=1,2,3,4, j=1,2,3$ of each attribute. For example, the semantics of $f_{2,2}$ is “ the width of sepal is medium ”. Moreover, by Eq. (15), we can get the membership functions of these concepts.

Then, we adopt the FREA to generate fuzzy rules that are used for building the FRODT. Given parameter $\sigma$ =0.6, we can get a tree depicted in Fig. 4a. And the corresponding rules of the FRODT are given as:

• IF the sample x is $F_{1,1}$, THEN it belongs to class 1 $\longrightarrow R_{1,1}$,

• ELSE IF x is $F_{1,2}$, THEN it belongs to class 2 $\longrightarrow R_{1,2}$,

• ELSE IF x is $F_{1,3}$, THEN it belongs to class 3 $\longrightarrow R_{1,3}$,

where $F_{1,1}=f_{3,1}f_{4,1}f_{1,1}f_{2,3}$, $F_{1,2}=f_{3,2}f_{4,2}$, $F_{1,3}=f_{3,3}f_{4,3}f_{1,3}$.

Fig. 4

a The structure of the FRODT, b the tree obtained by C4.5

The linguistic interpretations of the fuzzy rules are that “ the samples that have short petal length, short petal width, short sepal length and long sepal width belong to class 1; the samples that have medium petal length, medium petal width belong to class 2; and the samples that have long petal length, long petal width and long petal length belong to class 3 ”. Moreover, Fig. 4b presents the tree builded by the C4.5 algorithm. It can be observed that the structure of the FRODT is obviously simpler than that of C4.5 tree. Therefore, the tree size in this paper is less than C4.5.

Moreover, the three-dimensional classification result of Iris data by fuzzy rules $R_{1,1}, R_{1,2},$ and $R_{1,3}$ is shown in Fig. 5. The red circles indicate the samples determined by the rule $R_{1,1}$, the green squares represent the samples determined by the rule $R_{1,2}$, and the blue diamonds stand for the samples determined by the rule $R_{1,3}$. Besides, arrow 1 indicates that the rule $R_{1,2}$ classifies the samples that belong to the third class into the second class, and arrow 2 represents that the rule $R_{1,3}$ classifies the samples that belong to the second class into the third class. In addition, the membership degrees of iris training data on fuzzy rules $R_{1,1}, R_{1,2}$ and $R_{1,3}$ are depicted in Fig. 6. It shows that the samples in the first class originally belong to the rule $R_{1,1}$ with the largest membership degrees, the samples in the second class originally belong to the rule $R_{1,2}$ with the largest membership degrees, and the samples in the third class originally belong to the rule $R_{1,3}$ with the largest membership degrees. That is, we can obtain satisfactory results by using fuzzy rules $R_{1,1}, R_{1,2}$ and $R_{1,3}$ to classify the iris data set.

Fig. 5

The three-dimensional classification result of Iris training data by fuzzy rules $R_{1,1}, R_{1,2}$ and $R_{1,3}$

Fig. 6

Membership degrees of Iris training data on fuzzy rules $R_{1,1}, R_{1,2}, R_{1,3}$

5.2 Comparison of the FRODT and HHCART

In order to demonstrate the superiority of the proposed method, we compare FRODT with HHCART of [19] in this section.

Table 2 summarizes the results in terms of classification accuracy and tree size along with the respective standard deviations. It shows that the classification accuracy of the FRODT is higher than HHCART tested for all data sets except Boston Housing and Glass. From the “tree size” column, it demonstrates that the FRODT produces fewer leaf nodes than the chosen benchmarks on Boston Housing, Bupa, Glass, Heart and Survival data sets. Moreover, from the last line of Table 2, we can obtain that the average classification accuracy and tree scale of the FRODT are better than those of the rival algorithms. Moreover, Fig. 7 depicts these results. These results advocate that our strategy has more preferable performance than the comparison algorithms.

Table 2 The classification accuracy (%) and tree size along with the respective standard deviations of the HHCART(A), HHCART(D) and FRODT, and the best scores are indicated in boldface

Fig. 7

The classification accuracy (%) and tree size of the HHCART(A), HHCART(D) and FRODT

5.3 Comparison of the FRODT and five conventional decision trees

In order to better verify the superiority of the FRODT, we also compare FRODT with five conventional decision trees such as SC, C4.5, BFT, LAD, and NBT on 20 UCI data sets, shown in Table 3.

Table 3 Description of data sets in UCI database

The classification accuracies of the FRODT and five state-of-the-art methods on 20 UCI data sets are presented in Table 4. The overall picture conveyed by the results in Table 4 is clearly in favor of the FRODT. The FRODT outperforms the other methods on most data sets. In particular, it is not as good as the traditional decision tree SC only in three data sets and BFT or C4.5 only in four data sets and LAD only in five data sets. Besides, compared with the chosen benchmarks, the FRODT obtains the highest average classification accuracy. Note that the symbol “$\star$” indicates that the NBT is inoperative on AMLALL data set.

Table 5 shows the tree sizes of the FRODT and five chosen benchmarks on 20 UCI data sets. It can be observed that the FRODT is better than BFT, C4.5, LAD, and SC on all data sets. In particular, from the last line of Table 5, we can get that the FRODT has the least average tree size. Therefore, we can conclude that the FRODT can generate more simpler decision trees. Moreover, we plot the results in Tables 4 and 5 as two bar diagrams, as shown in Figs. 8 and 9. It can be seen that the FRODT obtains superior classification performance than the chosen benchmarks on accuracy and tree scale.

Table 4 The classification accuracy (%) and standard deviation of different decision trees

Table 5 The tree size and standard deviation of different decision trees

Fig. 8

The classification accuracy of different decision trees

Fig. 9

The tree size of different decision trees

Remark 1

The unique features of the FRODT are highlighted in the following four aspects. Firstly, the use of AFS theory can reduce the subjectivity of choosing membership functions. Secondly, the dynamic mining fuzzy rules that are used as the decision functions at each non-leaf node can reduce the size of the tree. Thirdly, FRODT overcomes the shortcoming that the oblique decision trees lack semantic interpretation. Finally, the ideal threshold $\sigma$ can be obtained by using the genetic algorithm, and the balance between classification accuracy and tree size can be achieved.

The main advantages of the results over others are as follows: (1) the FRODT performs better in both average classification accuracy and tree size than the chosen benchmarks; (2) different from the “traditional” decision trees where only one feature is considered on each node, the FRODT takes one dynamic mining fuzzy rule which involves multiple features at each node to simplify tree structure; and (3) the FRODT is endowed with readable linguistic interpretation.

5.4 The Holm test

The Holm test [39] is applied to analyze whether FRODT is significantly better than other decision trees, and the test statistic for comparing the jth classifier and the kth classifier is as follows:

$$\begin{aligned} Z= & {} \frac{\mathrm{Rank}_{j}-Rank_{k}}{SE}, \end{aligned}$$

(18)

$$\begin{aligned} Rank_{j}= & {} \frac{1}{N}\sum _{i=1}^{N}r_{i}^{j}, \end{aligned}$$

(19)

here $SE=\sqrt{l(l+1)/(6\times N)}$, l is the number of classifiers, N is the number of data sets, $r_{i}^{j}$ is the ranking of the jth classifier on the ith data set, and $Rank_{j}$ is the average ranking of the jth classifier on the entire data sets.

Statistic Z follows the standard normal distribution. According to Z value, we can get the corresponding probability p. Moreover, the number of classifiers is l, the number of Z needed to calculate is l, and the number of the corresponding probability p is l − 1. We sort $p_{1}\le p_{2}\le \ldots \le p_{l-1}$, and compare $p_{j}$ with $a/(1-j)$. If $p_{1}<a/(l-1)$, the hypothesis (two classifiers have the same performance) should be rejected, and then compare $p_{2}<a/(l-2)$ until the last.

According to Table 4 and Eq. (19), the average accuracy ranking of all decision trees can be obtained, $Rank_{LAD}=4.25$, $Rank_{SC}=4.05$, $Rank_{BFT}=4$, $Rank_{C4.5}=3.40$, $Rank_{NBT}=3.15$, and $Rank_{FRODT}=2.15$. The confidence level a is set to 0.05 and the results of the Holm test are presented in Table 6. It shows that the first three hypotheses are rejected and the last two hypotheses are accepted. This means that the classification accuracy of the FRODT is significantly better than that of traditional decision trees LAD, SC, and BFT. Although the FRODT is not significantly higher than C4.5 and NBT, the average classification accuracy of the FRODT is higher than that of C4.5 and NBT.

Table 6 The Holm test

6 Conclusion

This paper proposes a new architecture of the FRODT based on dynamic mining fuzzy rules. It is different from the traditional tree construction methods that take one single attribute or the combination of several attributes as decision function. In order to eliminate data redundancy and improve classification efficiency, the NRS_FS_FAST algorithm is first introduced. And the AFS theory is adopted to increase semantic interpretation and decrease human subjectivity in selecting membership functions. In the AFS theory framework, the FREA is proposed to dynamically extract fuzzy rules. And in each layer of the tree, the build-up of the FRODT is achieved by developing the only one non-leaf node. Moreover, the genetic algorithm is adopted to optimize the threshold $\sigma$ that can affect the scale of the tree. Finally, a series of comparative experiments have been carried out to show the superiority of our algorithm.

It should be noted that the main disadvantage of the FRODT is that the FREA extracts only one fuzzy rule for each class. When dealing with large data sets, it is difficult to discover more potential knowledge by leveraging one rule extracted for each class. Therefore, how many rules are extracted for each class is a direction of future research.

Moreover, the application of decision trees is often related to the analysis goal and scenario. For example, financial industry can use decision tree to evaluate loan risk, insurance industry can use decision tree to forecast the promotion of insurance products, medical industry can use decision tree to generate assistant diagnostic disposal model and so on. The decision trees are largely used in all area of real life. Several typical applications on this topic were discussed in [40] for business, in [41] for power systems, in [42] for medical diagnosis, in [43] for intrusion detection, and in [44] for energy modeling. Our paper also deals with the data sets from different application domains, such as the data sets including Wdbc, Heart, Haberman, Column, Breast Cancer, Bupa, Pima Indian and Wpbc in medical diagnosis area, and the data sets including Credit and Australian in business area. How to apply the proposed method to other application scenarios is also our future research direction.