Self-adaptive differential evolution algorithm with improved mutation mode

Abstract

The optimization performance of the Differential Evolution algorithm (DE) is easily affected by its control parameters and mutation modes, and their settings depend on the specific optimization problems. Therefore, a Self-adaptive Differential Evolution algorithm with Improved Mutation Mode (IMMSADE) is proposed by improving the mutation mode of DE and introducing a new control parameters adaptation strategy. In IMMSADE, each individual in the population has its own control parameters, and they would be dynamically adjusted according to the population diversity and individual difference. IMMSADE is compared with the basic DE and the other state-of-the-art DE algorithms by using a set of 22 benchmark functions. The experimental results show that the overall performance of the proposed IMMSADE is better than the basic DE and the other compared DE algorithms.

1 Introduction

Differential evolution, proposed by Storn and Price [1], is a competitive global optimization algorithm to solve real-world optimization problems. DE requires few control parameters and is easy to implement. So far, DE has been widely applied in many fields, such as image processing [2], industrial control [3, 4] and function optimization [1, 5, 6].

However, the optimization performance of DE is very sensitive to control parameters (i.e., population size NP, amplification factor F and crossover probability CR) and mutation modes. Generally, their settings should be first determined when using DE to solve optimization problems. However, choosing appropriate settings is often time-consuming. Although many researchers have given different choice rules [5–7], these rules are not general and unsuitable for practical applications.

In order to deal with the above problems, researchers have proposed many improved DE algorithms. Some work mainly focused on the control parameters adaptation strategy. Liu and Lampien [8] introduced a Fuzzy Adaptive Differential Evolution algorithm (FADE), which uses fuzzy logic controllers to adapt the control parameters for mutation and crossover. Brest et al. [9] proposed an adaptive Differential Evolution algorithm (jDE), which assigns control parameters values to each individual and dynamically adjusts them according to two specified thresholds. Guo et al. [10] proposed a Chaos Differential Evolution algorithm (chDE), where chaos theory is used to dynamically adjust control parameters values. Nasimul et al. [11] developed a new Adaptive Differential Evolution algorithm (aDE), wherein the control parameters values are adaptively adjusted by comparing individual fitness of the offspring with average fitness of the parent population. Brest and Maucec [12] proposed a novel adaptive DE algorithm that uses a self-adaptation scheme for the control parameters F and CR, and a dynamic population size reduction scheme. Zhu et al. [13] proposed an adaptive population tuning scheme for DE, which uses the solution-searching status and population distribution to dynamically adjust the population size.

Many researchers have also focused on the mutation mode of DE. Qin et al. [14] proposed a Self-adaptive Differential Evolution algorithm (SaDE), in which the adaptation of multiple mutation modes is implemented and the control parameters values are generated according to two normal distributions. Zhang and Sanderson [15] proposed an Adaptive Differential Evolution algorithm with Optional Archive (JADE), which uses a new mutation mode (DE/current-to-pbest/1) and employs an adaptive strategy for control parameters. Wang et al. [16] introduced a Composite Differential Evolution algorithm (CoDE), which randomly combines three mutation modes with three fixed parameters settings to generate three trail vectors. Thus, the best among them will enter the next generation if it is better than its target vector. Mallipeddi et al. [17] proposed an ensemble of mutation strategies and control parameters of DE algorithm, wherein different mutation strategies are incorporated into a pool and different control parameters settings are incorporated into the other pool. Islam et al. [18] presented an adaptive DE algorithm that uses a novel mutation mode and a modified crossover operation. Elsayed et al. [19] proposed two novel self-adaptive DE algorithms, which incorporate a heuristic mixing of operators and utilize the strengths of multiple mutation and crossover operations. Elsayed et al. [20] proposed a DE with self-adaptive multi-combination strategies, in which the strengths of four mutation strategies, two crossover strategies and two constraint handling techniques are combined. Yi et al. [21] utilized a hybrid mutation operation and self-adaptive control parameters to propose a new DE algorithm, which categorizes the population into two parts. Fan and Yan [22] introduced a Self-adaptive Differential Evolution algorithm with Discrete Mutation Control Parameters (DMPSADE), in which each individual has its own mutation mode and crossover probability, and each variable of the individual has its own amplification factor.

Furthermore, many attempts have also been made to improve the performance of DE by using other methods. Poikolainen et al. [23] proposed a cluster-based population initialization mechanism for DE that consists of three stages, including multiple local search, K-means clustering and composition of the population. Tang et al. [24] introduced an individual-dependent scheme for DE, including individual-dependent control parameters setting and individual-dependent mutation mode. Guo et al. [25] proposed a successful-parent-selecting framework for DE, which can adapt to the selection of parents by storing successful solutions into an archive and select parents from the archive when the stagnation occurs. Wu et al. [26] introduced a multi-population ensemble DE algorithm, in which a multi-population based approach is used to realize an ensemble of three mutation modes.

To further improve DE’s performance and make the selections of control parameters values independent of specific optimization problems, based on encoding for control parameters in jDE, a Self-adaptive Differential Evolution algorithm with Improved Mutation Mode (IMMSADE) is proposed by improving “DE/rand/1” mutation mode of the basic DE. In IMMSADE, each individual has its own control parameters, and they will be dynamically adjusted according to the population diversity and individual difference.

The proposed IMMSADE is different from the rest of the improved DE algorithms in two aspects. First and foremost, most work in previous literature mainly focused on the effect of differential vector of “DE/rand/1” mode on DE’s performance and neglected the effect of the mutated individual. By contrast, both are simultaneously considered in this paper. Second, most of the previous studies did not quantitatively analyze the population diversity or generate parameter settings in a random manner, while in IMMSADE the population diversity and individual difference are computed quantitatively and utilized to guide the generation of control parameters values throughout the evolution process, and thus it is beneficial to maintain the population diversity and improve the global exploration capability. Therefore, we believe the proposed IMMSADE will be an effective approach to global optimization.

In this paper, a total of 22 benchmark functions from the literatures [27, 28] are used to investigate the performance of the proposed IMMSADE. The experimental results show that the overall performance of IMMSADE on the tested problems is better than the basic DE and the other improved DE algorithms (i.e., jDE, chDE, aDE, SaDE, JADE, CoDE and DMPSADE) on the same problems.

The rest of the paper is organized as follows. Section 2 briefly introduces the basic DE. Section 3 presents the proposed IMMSADE. Section 4 reports the experiments and results analysis. Finally, Section 5 summarizes the conclusions.

2 Differential evolution algorithm

Suppose that the objective function of the optimization problem is $\min f(x)$ and the search space is $S\!\subset \!\mathrm {R}^{D}$. The population of the t ^th generation is denoted by using $\textbf {X}^{t}=\{{\textbf {X}}_{1}^{t} ,\;\textbf {X}_{2}^{t},\cdots , \textbf {X}_{NP}^{t}\}$, which contains N P D-dimensional vectors called individuals ${\textbf X}_{i}^{t} =\{x_{i1}^{t} ,\;x_{i2}^{t},\cdots ,x_{iD}^{t}\}\in S$ (i = 1, 2, ⋯ , N P), where D is the dimension of the problem and NP is the population size. The mutation, crossover and selection operations of the basic DE are shown as follows.

• Mutation. For each target individual $\textbf {X}_{i}^{t}$ in the parent population, a mutant vector $\textbf {V}_{i}^{t+1} =\left [v_{i1}^{t+1},v_{i2}^{t+1},\right .$ $\left .\cdots ,v_{iD}^{t+1} \right ]$ is generated according to the following equation, which is called “DE/rand/1” mutation mode.

  $$ \textbf{V}_{i}^{t+1} =\textbf{X}_{r1}^{t} +F\cdot (\textbf{X}_{r2}^{t} -\textbf{X}_{r3}^{t} ) $$

  (1)

  where the indexes r1, r2 and r3 are distinct integers randomly chosen from the set {1,2,⋯ ,N P}∖{i}. The amplification factor F ∈ [0, 2] is a real number that controls the amplification of the difference vector $\textbf {X}_{r2}^{t} -\textbf {X}_{r3}^{t}$.

• Crossover. A trial vector $\textbf {\hspace *{-.22pt}U}_{i}^{t+1} = \left [u_{i1}^{t+1}, u_{i2}^{t+1},\cdots ,\right .$ $\left . u_{iD}^{t+1} \right ]$ is generated using the following equation.

  $$ u_{ij}^{t+1} =\left\{ {\begin{array}{l} v_{ij}^{t+1} \;\;\;rand_{ij} \le CR\;\;or\;\;j=j_{rand} \\ x_{ij}^{t} \;\;\;\;rand_{ij} >CR\;and\;j\ne j_{rand} \;\; \\ \end{array}} \right. $$

  (2)

  where CR is the crossover probability within the range [0, 1]. r a n d _{i j} ∈[0,1] (j = 1,2,⋯,D) is a uniform random number. j _{r a n d} is a randomly chosen integer within [1, D], which ensures that $\textbf {U}_{i}^{t+1}$ gets at least one element from ${\textbf V}_{i}^{t+1}$, and avoids evolutionary stagnation.

  During the evolution process, some components of the trial vector ${\textbf U}_{i}^{t+1}$ may violate the search space S. Thus, the invalid components of $\textbf {U}_{i}^{t+1}$ should be processed as follows.

  $$ u_{ij}^{t+1} =\left\{ {\begin{array}{l} S_{l} +rand_{ij} \cdot (S_{u} -S_{l} )\;\;\;\;u_{ij}^{t+1} \notin [S_{l} ,\;S_{u} ] \\ u_{ij}^{t+1} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;otherwise \\ \end{array}} \right. $$

  (3)

  where r a n d _{i j} is uniform random number within the range [0,1]. S _l and S _u are the lower and upper bounds for the search space S, respectively.

• Selection. A greedy strategy is used to perform the selection operation of DE.

  $$ \textbf{X}_{i}^{t+1} =\left\{ {\begin{array}{l} \textbf{U}_{i}^{t+1} \;\;\;f(\textbf{U}_{i}^{t+1} )<f(\textbf{X}_{i}^{t} )\\ \textbf{X}_{i}^{t} \;\;\;\;\;\;\;\;otherwise\; \\ \end{array}} \right. $$

  (4)

  If and only if, the trial vector $\textbf {U}_{i}^{t+1}$ yields a smaller function value than the target vector $\textbf {X}_{i}^{t}$, $\textbf {X}_{i}^{t+1}$ is set to $\textbf {U}_{i}^{t+1}$, otherwise $\textbf {X}_{i}^{t}$ is retained to enter the next generation.

3 IMMSADE

During the evolution process, each individual $\textbf {X}_{i}^{t}$ represents a solution to the optimization problem, and the final goal of DE is to make $\textbf {X}_{i}^{t}$ infinitely close to the global optimum. The updating of $\textbf {X}_{i}^{t}$ is derived from the mutant vector $\textbf {V}_{i}^{t+1}$, which is composed of two components. One is the individual $\textbf {X}_{r1}^{t}$ to be mutated, and the other is the difference vector $F\cdot (\textbf {X}_{r2}^{t} -\textbf {X}_{r3}^{t})$, called the perturbation. So far, most of the improved DE algorithms were based on the latter, while few algorithms studied the effect of the former on DE’s performance.

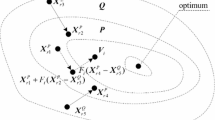
As illustrated in Fig. 1 (two-dimensional example), a large value of $\textbf {X}_{r1}^{t}$ may lead to individual divergence and thus is not beneficial to converge. To address this issue, an improved “DE/rand/1” mode described in (5) is proposed to serve as the basis of IMMSADE.

$$ \textbf{V}_{i}^{t+1} =\lambda \cdot \textbf{X}_{r1}^{t} +F\cdot (\textbf{X}_{r2}^{t} -\textbf{X}_{r3}^{t} ) $$

(5)

where λ is a benchmark factor within the range (0,1]. It is clear that (1) is a special case of (5) by setting λ to 1.

Fig. 1

Improved mutation mode in IMMSADE

To make the selections of control parameters values independent of specific optimization problems, this paper proposes an improved control parameters adaptation strategy. As illustrated in Fig. 2, the control parameters values of DE are applied at the population level while the control parameters values of IMMSADE are applied at the individual level. In IMMSADE, each individual has its own benchmark factor ${\lambda _{i}^{t}}$, amplification factor ${F_{i}^{t}}$ and crossover probability $C{R_{i}^{t}}$, and they will be dynamically adjusted during the evolution process. Compared to the fixed parameters values used in the DE, self-adaptively adjusting parameters values is more beneficial to population evolution.

Fig. 2

Encoding for control parameters in IMMSADE

In view of the above analysis, a new differential evolution algorithm, IMMSADE, is proposed in this paper. The mutation and crossover operations of IMMSADE are shown in (6) and (7), respectively.

$$ \textbf{V}_{i}^{t+1} ={\lambda_{i}^{t}} \cdot \textbf{X}_{r1}^{t}+{F_{i}^{t}} \cdot (\textbf{X}_{r2}^{t} - \textbf{X}_{r3}^{t}) $$

(6)

$$ u_{ij}^{t+1} =\left\{ {\begin{array}{l} v_{ij}^{t+1} \;\;\;rand_{j} \le C{R_{i}^{t}} \;\;or\;\;j=j_{rand}\\ x_{ij}^{t} \;\;\;\;rand_{j} >C{R_{i}^{t}} \;and\;j\ne j_{rand} \;\;\\ \end{array}} \right. $$

(7)

The contradiction between global exploration and local exploitation affects the performance of DE. Chakrabory et al. [29] considered that the local exploitation capability of DE is strong, while the global exploration capability is poor. Thus, it is more likely to get stuck at a local optimum and thereby lead to premature convergence due to the reduced population diversity. Therefore, properly controlling the population diversity can effectively improve global exploration capability.

During the evolution process, the population fitness diversity can be described using the following equation.

$$ \alpha^{t}=\frac{f_{max}^{t} -f_{avg}^{t}} {f_{max}^{t}} $$

(8)

where $f_{max}^{t}$ and $f_{avg}^{t}$ denote the maximum fitness and the average fitness of the t ^th generation, respectively. α ^t is a real number between 0 and 1. A larger value of α ^t indicates that the individual similarity is lower and the population is more diverse. On the contrary, a smaller value of α ^t indicates that the individuals are more similar and the population is less varied.

Additionally, the individual difference in the population can be described using the (9).

$$ {\beta_{i}^{t}} ={f_{i}^{t}} -f_{avg}^{t} $$

(9)

If ${\beta _{i}^{t}} <0$, it indicates that the new offspring $\textbf {X}_{i}^{t}$ of the target individual $\textbf {X}_{i}^{t-1}$ is better. On the contrary, if ${\beta _{i}^{t}} \ge 0$, it indicates that the new offspring is worse.

Based on the above analysis, the rules for adjusting control parameters values are obtained, as shown in Table 1.

Table 1 The rules for adjusting control parameters in the IMMSADE

Important results can be observed from Table 1. First, when the current population presents good diversity whatever the individual’s fitness, retaining the current control parameters values is beneficial to improve the global exploration capability. Second, if the population diversity decreases and the individual fitness is less than the average fitness of the current population, the current control parameters values should be protected so that the individual can continue to evolve in the right direction. Third, when the population diversity decreases and the individual fitness is greater than or equal to the average fitness of the current population, the control parameters values should be adjusted so that the new offspring is generated. These new offspring will be beneficial to improve the current population diversity and help the individual escape from a local optimum, and thus avoid premature convergence. Therefore, the rules for adjusting control parameters values not only maintain the population diversity, but also ensure the convergence performance of the algorithm.

If the individual fitness is much greater than the average fitness of the current population, a smaller $\lambda _{i}^{t+1}$ and $F_{i}^{t+1}$, and a larger $CR_{i}^{t+1}$ are beneficial to promote the generation of new individual and accelerate the convergence speed. If the individual fitness is close to the average fitness of the current population, a larger $\lambda _{i}^{t+1}$ and $F_{i}^{t+1}$, and a smaller $CR_{i}^{t+1}$ are beneficial to maintain the population diversity and enhance the global exploration capability. Thus, $\lambda _{i}^{t+1}$, $F_{i}^{t+1}$ and $CR_{i}^{t+1}$ are calculated as follows.

$$ \lambda_{i}^{t+1} =\left\{ {\begin{array}{l} \lambda_{max} -\!\frac{f_{i}^{t+1} -f_{avg}^{t+1}} {f_{max}^{t+1} -f_{avg}^{t+1}} \cdot (\lambda_{max} \!-\lambda_{min} )\;\;\;\!\!\alpha^{t+1}\!\!<\tau \;and\;\beta_{i}^{t+1} \!\ge 0 \\ {\lambda_{i}^{t}} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;otherwise \\ \end{array}} \right. $$

(10)

$$ F_{i}^{t+1} =\left\{ {\begin{array}{l} F_{max} -\!\frac{f_{i}^{t+1} -f_{avg}^{t+1}} {f_{max}^{t+1} -f_{avg}^{t+1}} \cdot (F_{max} \!-F_{min} )\;\;\;\!\!\!\alpha^{t+1}\!\!<\tau \;and\;\beta_{i}^{t+1} \!\ge 0 \\ {F_{i}^{t}} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;otherwise \\ \end{array}} \right. $$

(11)

$$ CR_{i}^{t+1} =\left\{ {\begin{array}{l} CR_{min} \!+\frac{f_{i}^{t+1} -f_{avg}^{t+1}} {f_{max}^{t+1} -f_{avg}^{t+1}} \!\cdot (CR_{max} \!-CR_{min} )\;\;\;\!\!\alpha^{t+1}\!<\tau \;and\;\beta_{i}^{t+1} \!\ge 0 \\ C{R_{i}^{t}} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;otherwise\\ \end{array}} \right. $$

(12)

where λ _{m i n} and λ _{m a x} are the minimum and maximum values of λ, respectively. F _{m i n} and F _{m a x} are the minimum and maximum values of F, respectively. C R _{m i n} and C R _{m a x} are the minimum and maximum values of CR, respectively. τ ∈ [0, 1] denotes the probability for adjusting population diversity. In this paper, λ _{m i n} =0.7, λ _{m a x} =1.0, F _{m i n} =0.1, F _{m a x} =0.8, C R _{m i n} =0.3, C R _{m a x} =1.0 and τ = 0.7 are set. Note that the updating of $f_{avg}^{t+1}$, $f_{max}^{t+1}$, α ^t+1 and $\beta _{i}^{t+1}$ is real-time, and they will be recalculated when a new offspring is generated.

We have made a decision about the values of λ _{m i n} , λ _{m a x} , F _{m i n} , F _{m a x} , C R _{m i n} and C R _{m a x} , which are based on the suggested values in the literature [9] and the experimental results. Additionally, the value of τ can refer to Section 4.4.

$\lambda _{i}^{t+1} , \quad F_{i}^{t+1}$ and $CR_{i}^{t+1}$ are updated before the mutation operation is performed, and thus these new control parameters values will affect the mutation, crossover and selection operations of the next generation. Moreover, compared with the basic DE, although the space complexity of IMMSADE increases from O(N P∗D) to O(N P∗(D+3)), the time complexity is still O(T∗N P∗D).

IMMSADE tracks the current population diversity and individual difference in real time and uses them to guide the generation of control parameters values, it is helpful to diversify the difference vector, and thus it effectively avoids premature convergence and is beneficial to search a relatively large space so that more promising regions can be found. Therefore, IMMSADE is able to obtain higher convergence precision within a limited number of evolution generations, and utilize the lesser number of evolution generations to reach the specified convergence precision. Furthermore, the proposed IMMSADE is more reliable.

4 Experiments and results analysis

In this section, IMMSADE is applied to minimize a total of 22 benchmark functions from the literatures [27, 28], as shown in Table 2. IMMSADE is compared with the basic DE and 7 other state-of-the-art DE algorithms, i.e., jDE, chDE, aDE, SaDE, JADE, CoDE and DMPSADE.

Table 2 Benchmark functions

Different characteristics for benchmark functions are summarized as follows. f ₁ ∼ f ₇ are unimodal functions. f ₈ has one minimum and is discontinuous. f ₉ is a noisy quadratic function. f ₁₀ ∼ f ₂₂ are multimodal functions.

4.1 Comparison with the basic DE and 7 improved DE

In this experiment, IMMSADE is compared with the basic DE, jDE [9], chDE [10] and aDE [11]. The parameters of DE are set to F = 0.5 and C R = 0.9, as recommended in [9]. The parameters settings for jDE, chDE and aDE are the same as in their original papers. The initial parameters ${\lambda _{i}^{0}}$, ${F_{i}^{0}}$ and $C{R_{i}^{0}}$ of IMMSADE are randomly chosen from [0.7,1.0], [0.1,0.8] and [0.3,1.0], respectively. In all experiments, we set the dimension D = 30 and the population size N P = 100. For each algorithm and each function, 30 independent runs with 3000 maximum number of evolution generations are conducted.

The Mean and the Standard Deviation (STD) of the optimal solutions obtained by each algorithm for each function are summarized in Table 3. The Success Rate (SR) of each algorithm and the Mean Number of Evolution Generations (MNEG) required to reach the specified convergence precision for each function are reported in Table 4, where ”N/A” denotes Not Applicable. The convergence precisions are set as follows: 1.0 for f ₂₀, 10⁻¹ for f ₁₆, f ₂₁ and f ₂₂, 10⁻³ for f ₉, and 10⁻⁸ for all others. MNEG and SR are mainly used to compare the convergence speed and the reliability of each algorithm, respectively. For convenience of illustration, the evolution curves for some functions are plotted in Fig. 3.

Table 3 The mean and standard deviation of the solutions obtained by DE, chDE, jDE, aDE and IMMSADE

Table 4 SR and MNEG obtained by DE, chDE, jDE, aDE and IMMSADE

Fig. 3

Evolution curves of DE, chDE, jDE, aDE and IMMSADE for test functions

Some important observations can be obtained from Fig. 3, Tables 3 and 4:

• 1 In terms of convergence precision and convergence speed, IMMSADE is the best among the five DE algorithms. This can be because IMMSADE can dynamically adjust the population diversity and improve the convergence performance by improving “DE/rand/1” mode and introducing control parameters adaptation strategy. DE performs worst because it converges very slowly and results in the optimal solutions found with lower precisions. jDE, chDE and aDE outperform DE on most functions due to the use of parameters adaptation strategies. It is interesting to note that chDE is slightly better than IMMSADE on f ₁₄ and f ₂₀, and DE is slightly better than IMMSADE on f ₁₇ and f ₁₈.

• 2 In terms of the reliability, it is clear that DE, jDE, chDE and aDE perform worse than IMMSADE. For DE, the use of fixed parameters setting is not suitable for various test functions. For example, better results are obtained on unimodal functions f ₁ and f ₃, while DE fails on multimodal functions f ₁₀, f ₁₃ and f ₁₆. For chDE and jDE, although the parameters adaptation strategy is used to improve DE’s performance, the updating of control parameters values is a random manner and lacks the guidance of the evolution process. For aDE, the differences of the individuals are not considered when generating new control parameters values, thus easily leading to premature convergence. In contrast, the control parameters values in IMMSADE will be automatically adjusted according to the population diversity, and the differences of the individuals are used to guide the generation of new parameters, thus it is beneficial to improve the ability to escape a local minimum and promote the individuals to search towards the right direction. Therefore, IMMSADE performs best.

Additionally, IMMSADE is further compared with SaDE [14], JADE [15], CoDE [16] and DMPSADE [22]. 50 independent runs with 300000 function evaluations are performed and [−100, 100] for f ₁₅ is used in this simulation. Mean and STD for D = 30 and D = 50 are summarized in Tables 5 and 6, respectively. The results of SaDE, JADE, CoDE and DMPSADE are taken from [22]. Moreover, two nonparametric statistical tests with a significance level of 5 %, namely, Friedman test and Kruskal-Wallis test [30], are used to carry out multiple comparisons. Table 7 depicts the ranks computed through these two tests. It can be seen from Tables 5, 6 and 7 that IMMSADE significantly performs better than the other competitive DE algorithms.

Table 5 The mean and standard deviation of the optimal solutions obtained by SaDE, JADE, CoDE, DMPSADE and IMMSADE on 30-dimensional problems

Table 6 The mean and standard deviation of the optimal solutions obtained by SaDE, JADE, CoDE, DMPSADE and IMMSADE on 50-dimensional problems

Table 7 The ranks obtained by Friedman test and Kruskal-Wallis test for SaDE, JADE, CoDE, DMPSADE and IMMSADE

4.2 Multiple comparisons using nonparametric statistical tests

Recently, nonparametric statistical tests have been widely used to compare the performance of a new proposed algorithm with the existing algorithms, and Derrac et al. [30] also gave a set of nonparametric procedures for multiple comparisons. In this section, to further compare IMMSADE with DE, jDE, chDE and aDE, we label IMMSADE as the control algorithm and reuse the results shown in Tables 3 and 4 to apply the Multiple Sign test with a significance level of 5 %. Table 8 summarizes the statistical analysis results.

Table 8 Multiple Sign test results

Reference to [30] (Table A.21) for m = 4 (number of algorithms excluding IMMSADE) and n = 22 (number of test functions) reveals the critical value is 5. Since the number of minus signs in the pairwise comparison between IMMSADE and DE, chDE, jDE and aDE is less than the critical value, it may be concluded that IMMSADE has a significantly better performance than the comparison algorithms.

Moreover, Friedman test and Kruskal-Wallis test in [30] are also used to detect significant differences for multiple algorithms. The ranks obtained are depicted in Table 9. As can be seen in the table, IMMSADE is the best among these five algorithms.

Table 9 The ranks obtained by Friedman test and Kruskal-Wallis test for DE, chDE, jDE, aDE and IMMSADE

4.3 Effectiveness study of the improved mutation mode in IMMSADE

As shown in Section 4.1, IMMSADE improves DE’s performance by improving ”DE/rand/1” mutation mode and introducing control parameters adaptation strategy. However, the effectiveness of the improved mutation mode shown in Eq. (5) is not evaluated. To address this issue, IMMSADE without parameters adaptation is compared with the basic DE and IMMSADE. For DE, F = 0.5 and C R = 0.9 are set. For IMMSADE without parameters adaptation, λ = 0.8, F = 0.5 and C R = 0.9 are set. The parameters settings of IMMSADE are the same as in Section 4.1. The optimization results are shown in Table 10, where the results of the best and second best algorithms are marked in bold and italic, respectively. Moreover, Table 11 gives the ranks computed by using Friedman test and Kruskal-Wallis test.

Table 10 Optimization results of DE and IMMSADE

Table 11 The ranks obtained by Friedman test and Kruskal-Wallis test for DE and IMMSADE

From Table 10, it can be concluded that compared to DE, IMMSADE without parameters adaptation performs remarkably better because the improved mutation mode improves the convergence performance by speeding the optimization search in the promising direction. In addition, as can be seen from Table 11, IMMSADE is the best, IMMSADE without parameters adaptation ranks second, whereas DE is the worst. It indicates that the improved mutation mode is effective.

Compared to IMMSADE without parameters adaptation, IMMSADE performs better in terms of convergence precision and convergence speed. It indicates a beneficial cooperation between the improved mutation mode and the parameters adaptation. The parameters adaptation strategy is able to adapt parameters to appropriate values and thus improves the convergence performance. Interestingly, IMMSADE without parameters adaptation is better than IMMSADE on functions f ₄, f ₇, f ₁₆ and f ₂₂. This might be due to the fact that IMMSADE implements the control parameters adaptation strategy, which may need to frequently adjust the parameters values owing to the reduced population diversity in the later stage of the evolution. However, these parameters values may not be beneficial to the algorithm convergence within a limited number of evolution generations and thereby lead to the final solution with a lower precision. In addition, the parameters adaptation also further improves the success rates on functions f ₉, f ₁₃, f ₂₀ and f ₂₁. This can be because the parameters adaptation could help the algorithm search better solutions as well as maintain higher convergence speed when solving the functions with a number of local minima.

To further confirm the superiority of the improved mutation mode shown in (5), DE/rand/1 shown in (1) and the improved mutation mode are used to generate two trail vectors for each target vector at each generation. Then, we choose the better one to compare with its target vector. It needs to record n _t at generation t, which is the number of the trail vectors generated by the improved mutation mode which are better than DE/rand/1. Thus, the probability p _t of the better trail vectors generated by the improved mutation mode is calculated according to the following equation, and the probability of DE/rand/1 is 1−p _t .

$$ p_{t} =\frac{n_{t}} {NP} $$

(13)

Figure 4 gives the probability distribution for DE/rand/1 and the improved mutation mode in the evolution process. In Fig. 4, X-axis represents the generation count, while Y-axis represents the probabilities of the improved mutation mode and DE/rand/1, which are the average values of 30 independent runs. It can be seen from this figure that the probability of the improved mutation mode is always larger than DE/rand/1. Accordingly, the improved mutation mode can generate better trail vectors and is more beneficial to search the optimal solutions.

Fig. 4

The probability distribution for DE/rand/1 and the improved mutation mode

4.4 Parameter study of IMMSADE

IMMSADE introduces the parameter τ which determines the updating rates of control parameters (${\lambda _{i}^{t}}$, ${F_{i}^{t}}$ and $C{R_{i}^{t}} )$. Therefore, it is interesting to determine the range of τ which is appropriate for different optimization problems. Table 12 reports the experimental results obtained by setting τ to 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 and 1.0, respectively. Moreover, the ranks obtained by Friedman test and Kruskal-Wallis test are summarized in Table 13 and the curves of MNEG for some functions are plotted in Fig. 5.

Fig. 5

Curves of MNEG obtained by IMMSADE for benchmark functions

Table 12 Experimental results of IMMSADE with different τ

Table 13 The ranks obtained by Friedman test and Kruskal-Wallis test for IMMSADE with different τ

As shown in Table 12 and 13, and Fig. 5, IMMSADE performs worse when τ is set to τ ≤ 0.6. A smaller value of τ decreases the updating rates of control parameters and thus is not beneficial to generate new individuals and maintain the population diversity. The reduced population diversity leads to premature convergence and thereby decreases convergence precision and convergence speed. In contrast, IMMSADE performs better by setting τ to τ≥0.7. A larger value of τ is beneficial to adjust the population diversity and thus improves the global exploration capability. Therefore, IMMSADE can work best with parameter τ ∈ [0.7, 1.0].

Based on the above empirical analysis, it can be concluded that the proposed IMMSADE has faster convergence speed, higher convergence precision and stronger robustness, thus meeting the requirements for the real time, accuracy and stability of process optimization. Moreover, IMMSADE has been successfully applied to solve arrival flights scheduling, including single runway optimization and dual-runways optimization. The optimization results indicate that IMMSADE can effectively decrease the total delay time of arrival flights sequence, improve the throughput of runways, and relieve the scheduling pressure of controllers.

5 Conclusions

The performance of DE is very sensitive to its control parameters and mutation modes, and choosing appropriate settings for different problems is very time-consuming. Therefore, the paper proposed an IMMSADE to improve DE’s performance. A set of test functions from the literatures are used to validate the performance of IMMSADE. Furthermore, IMMSADE is compared with the basic DE and the other improved DE algorithms (i.e., jDE, chDE, aDE, SaDE, JADE, CoDE and DMPSADE). The experimental results show that IMMSADE performs better than the basic DE and the other improved DE algorithms on most test functions.

There are 10 low-dimensional functions in [28], and most algorithms can locate the global optimum within the lesser number of evolution generations. Therefore, we mainly focus on the optimization of high-dimensional functions, and the results of low-dimensional functions are not reported in this paper. Moreover, for some hybrid and composition functions shown in [27], the results of IMMSADE are not satisfactory at this point, but the improved experiments incorporating the advantages of the other evolutionary algorithms are being carried out.

For our future work, the proposed IMMSADE will be used to solve additional optimization problems from various fields, such as PID controller [31], image segmentation [32], pattern recognition [33], financial time series prediction [34], waveform inversion [35] and power system planning [36]. In addition, since the objective function is more than one in many real-world applications, we intend to extend the current research to multi-objective optimization (MOO), especially the conditions optimization of multi-runways arrival flights scheduling. Finally, it is also worthwhile to incorporate the advantage of the other evolutionary algorithms (i.e., particle swarm optimization, simulated annealing and bacterial foraging algorithm) to further improve the performance of the proposed algorithm.