Tree-based localized fuzzy twin support vector clustering with square loss function

Abstract

Twin support vector machine (TWSVM) is an efficient supervised learning algorithm, proposed for the classification problems. Motivated by its success, we propose Tree-based localized fuzzy twin support vector clustering (Tree-TWSVC). Tree-TWSVC is a novel clustering algorithm that builds the cluster model as a binary tree, where each node comprises of proposed TWSVM-based classifier, termed as localized fuzzy TWSVM (LF-TWSVM). The proposed clustering algorithm Tree-TWSVC has efficient learning time, achieved due to the tree structure and the formulation that leads to solving a series of systems of linear equations. Tree-TWSVC delivers good clustering accuracy because of the square loss function and it uses nearest neighbour graph based initialization method. The proposed algorithm restricts the cluster hyperplane from extending indefinitely by using cluster prototype, which further improves its accuracy. It can efficiently handle large datasets and outperforms other TWSVM-based clustering methods. In this work, we propose two implementations of Tree-TWSVC: Binary Tree-TWSVC and One-against-all Tree-TWSVC. To prove the efficacy of the proposed method, experiments are performed on a number of benchmark UCI datasets. We have also given the application of Tree-TWSVC as an image segmentation tool.

1 Introduction

Machine learning approaches can be broadly classified as supervised and unsupervised learning, based on the availability of data labels or output. Supervised learning uses labelled training samples, while unsupervised learning is ‘learning without label information’. Maximum margin classifiers like support vector machines (SVM) [1] have been successfully used for supervised classification. An improvement over SVM was proposed by Jayadeva et al. termed as TWSVM [2, 3]. TWSVM is a supervised learning method that classifies data by generating two nonparallel hyperplanes which are proximal to their respective classes and at least unit distance away from the patterns of other class. TWSVM solves a pair of quadratic programming problems (QPPs) and is based on empirical risk minimization principle; it is proved to be almost four times faster than SVM [2]. Many variations of TWSVM have been proposed, which include Least Squares TWSVM (LS-TWSVM) [4], fuzzy version of LS-TWSVM [5] and robust energy-based LS-TWSVM [6]. LS-TWSVM solves a system of linear equations and hence, it is faster than TWSVM. Shao et al. proposed least square twin parametric-margin SVM [7]. Recently, Khemchandani et al. proposed multi-category Laplacian TWSVM [8].

In many practical problems, the cost of obtaining the labels is very high as compared to the cost of generating the data, for example speech recognition, web page classification, video surveillance, etc. In this scenario, unsupervised learning approaches can be exploited, but they are more challenging as the data labels are not available. Clustering is an unsupervised learning task, which aims at partitioning data into a number of clusters [9–11]. Patterns that belong to the same cluster should have an affinity with each other and must be distinct from the patterns in other clusters. Clustering has its application in various domains of data analysis which include medical science, finance, pattern recognition and image analysis [12–14].

Clustering algorithms aim at partitioning the data into a number of clusters [9] based on similar features by using algorithms like K-means clustering [10] and hierarchical clustering [11]. The K-means algorithm [10] is a centroid-based clustering method that represents each cluster by its mean vector. Hierarchical clustering [11] is based on distance connectivity. Clusters can be identified by using statistical distributions, such as multivariate normal distributions used in expectation-maximization algorithm [15]. Al-Harbi et al. proposed adaptive K-means clustering [16]. Plane-based clustering methods have been proposed such as K-plane clustering (KPC) [17] and local k-proximal plane clustering (LkPPC) [18] by Bradley et al. and Yang et al. respectively. For a K-cluster problem, theses algorithms identify K clusters by generating K planes.

Following the success of margin-based classifiers in supervised learning, researchers have been trying to extend them to unsupervised learning. Recently, Xu et al. [19] proposed maximum margin clustering (MMC) which performs clustering in SVM framework and finds a maximum margin separating hyperplane between clusters. Valizadegan et al. proposed a variation of MMC termed as generalized MMC [20]. Large margin supervised learning methods are usually formulated as QPPs, which suggests that they could be computationally more expensive. Since the labels are missing in unsupervised problems, the resulting optimization problem would be hard and non-convex that considers all the combinations over possible discrete class labels. MMC based methods [20] resort to relaxing the non-convex clustering problem as a semidefinite program (SDP) [21]. MMC can not be used for very large datasets because SDP is computationally expensive [22]. Zhang et al. [23] proposed a feasible variation for MMC and implemented MMC as an iterative support vector machine (iterSVM).

Recently, Wang et al. proposed TWSVM for clustering (TWSVC) [24] that uses information from both within the cluster and between clusters. It requires that the plane of one cluster should be a unit distance away from patterns of other clusters on both the sides. TWSVC is an iterative clustering algorithm that solves K QPPs for a K-cluster problem using one-against-all approach (OAA) [25]. Due to the nature of loss function used by TWSVC (as discussed in Appendix A), the labels flip rarely in successive iterations i.e. change their value from 0 to 1 or vice-versa. Hence, the accuracy of TWSVC is limited by the performance of initialization algorithm and the labels seldom change in the iterations. Recently, Khemchandani et al. [26] proposed fuzzy least squares TWSVC (F-LS-TWSVC) that uses fuzzy membership to create clusters, which are further obtained by solving systems of linear equations only.

In this paper, we propose Tree-TWSVC which is motivated by MMC [19] and TWSVC [24]. Tree-TWSVC can overcome the limitations of TWSVC and has the following characteristics:

• Unlike MMC that solves expensive SDP problems, the proposed clustering algorithm Tree-TWSVC formulates convex optimization problems which are solved as a system of linear equations. Also, MMC identifies only two clusters whereas Tree-TWSVC identifies multiple clusters by building a tree with LF-TWSVM classifiers at each level.

• Tree-TWSVC recursively divides the data to form the tree structure and iteratively generates the hyperplanes for the partitioned data, until the convergence criterion is met. Due to its tree structure, Tree-TWSVC is much faster than the classical approaches like OAA (used in TWSVC or F-LS-TWSVC), for handling multi-cluster data. It can handle very large-sized datasets with comparable or better clustering results than other TWSVM-based clustering methods.

• At each node of the cluster tree, LF-TWSVM creates two clusters so that the data points of one cluster are proximal to their cluster plane and prototype, and the data points of another cluster should be a unit distance away from this cluster plane. The cluster prototype prevents the plane from extending indefinitely and keeps the plane aligned locally to its cluster.

• Tree-TWSVC avoids the approximation through Taylor’s series expansion, as required by TWSVC and F-LS-TWSVC due to constraints with mod (or absolute) function and hence Tree-TWSVC gives more accurate results.

• Tree-TWSVC determines a fuzzy membership matrix for data samples which associates a membership value of each data sample to all the given clusters. The initial fuzzy membership matrix is obtained using localized fuzzy nearest neighbour graph (LF-NNG).

• We have used square loss function which is symmetric and allows the output to change (i.e. flip from +1 to -1 or vice-versa) if required, in successive iterations. By using the square loss function, the optimization problem is solved as a system of linear equations; whereas TWSVC solves QPPs to generate the hyperplanes.

The paper is organized as follows: Section 2 gives a brief introduction of MMC, TWSVC and F-LS-TWSVC; and introduces the notations and symbols used in the paper. Section 3 presents the proposed classifier LF-TWSVM and the clustering algorithm Tree-TWSVC, which is followed by experimental results in Section 4. The paper is concluded in Section 5.

2 Background

Supervised learning algorithms have been used to solve clustering problems such as MMC [19], TWSVC [24] and F-LS-TWSVC [26]. These clustering approaches are briefly explained in the following section.

2.1 Maximum margin clustering (MMC)

Motivated by the success of maximum margin methods in supervised learning, Xu et al. proposed maximum margin clustering (MMC) that aims at extending maximum margin methods to unsupervised learning [19]. Since its optimization problem is non-convex, MMC relaxes the optimization problem as semidefinite programs (SDP).

For the training set $(x_{i})_{i=1}^{m}$, where x _i is the input in n-dimension space and y={y ₁,...y _m } are unknown cluster labels. The primal problem for MMC is given as

$$\begin{array}{@{}rcl@{}} \underset{y}{Min}~\underset{w,b,\xi}{Min} && \lVert w {\rVert_{2}^{2}}+2C \xi^{T}e \\ {\text{subject to}} && y_{i}(w^{T}\phi(x_{i})+b) \geq 1-\xi_{i}, \\ && \xi_{i}\geq0, ~~ y_{i} \in \{+1~, -1\} , ~~~i=1,...,m \\ && -l\leq e^{T}y\leq l,\hspace{2.0cm} \end{array} $$

(1)

where ϕ is the mapping induced by the kernel function and ξ is a vector of error variables. $\Arrowvert .{\Arrowvert _{2}^{2}}$ represents L ₂-norm. e is a vector of ones of appropriate dimension and (w,b) are the parameters of the hyperplane that separates the two clusters. The parameter C is a trade-off factor and l≥0 is a user-defined constant that controls class imbalance. Since the constraint $y_{i}\in \{+1,-1\} \Leftrightarrow {y_{i}^{2}}-1=0$ is non-convex, (1) is a non-convex optimization problem. As discussed in [19], MMC relaxes the non-convex optimization problem and solves it as SDP. SDP is convex but computationally very expensive and can handle small data sets only. Zhang et al. proposed an iterative SVM approach to solve the MMC problem (1) based on alternating optimization [23].

2.2 Twin support vector machine for clustering (TWSVC)

TWSVC [24] is a plane-based clustering method which uses TWSVM classifier and follows OAA approach to determine K cluster center planes for a K-cluster problem. Since TWSVC considers all the data points (in OAA manner) for finding the cluster planes, it requires that each plane should be close to its own cluster and away from other clusters’ data points on both the sides. For a K-cluster problem, let there be m data points X=(x ₁,x ₂,...,x _m )^T where $x_{i}\in \mathbb {R}^{n}$, with their corresponding labels in {1,2,...,K}; X is m×n matrix. Let the data for i ^th cluster be represented by X _i and the data points of all clusters other than i ^th cluster are given by $\widehat {X}_{i}$. For the K-cluster problem, TWSVC seeks K cluster center planes, which are given as

$$\begin{array}{@{}rcl@{}} x^{T}w_{i}+b_{i}=0 \text{, }~~~~~~ i=1,2,...,K. \end{array} $$

(2)

The planes are proximal to the data points of their own cluster. TWSVC uses initialization algorithm to get the initial cluster labels for data points and determines the initial cluster planes. The algorithm alternatively finds the labels of data points and cluster center planes until some termination condition is satisfied [24]. The cluster planes are obtained by considering the following problem, with initial cluster plane parameters [${w_{i}^{0}},~{b_{i}^{0}}$], TWSVC:

$$\begin{array}{@{}rcl@{}} \min_{w_{i}^{j+1},b_{i}^{j+1},\xi_{i}^{j+1}} & & \frac{1}{2}\lVert X_{i}w_{i}^{j+1}+eb_{i}^{j+1} {\rVert_{2}^{2}} +ce^{T}\xi_{i}^{j+1} \\ {\text{subject to}} && T(\lvert \widehat X_{i}w_{i}^{j+1}\!+eb_{i}^{j+1} \rvert)\!+\xi_{i}^{j+1} \geq e, \quad \xi_{i}^{j+1} \geq 0, \\ \end{array} $$

(3)

where i=1,2,...K is index for the cluster and j=0,1,2,... is the index of successive problem. T(⋅) denotes the first-order Taylor’s series expansion and parameter c is the weight associated with the error vector. The optimization problem in (3) determines the i ^th cluster center plane, which is required to be as close as possible to the i ^th cluster X _i and far away from the other clusters’ data points $\widehat {X}_{i}$ on both the sides. The problem also minimizes the error vector ξ _i which measures the error due to wrong assignment of cluster labels. By introducing the sub-gradient of $\lvert \widehat X_{i}w_{i}^{j+1}+eb_{i}^{j+1} \rvert$, (3) becomes

$$\begin{array}{@{}rcl@{}} \min_{w_{i}^{j+1},b_{i}^{j+1},\xi_{i}^{j+1}} & & \frac{1}{2}\lVert X_{i}w_{i}^{j+1}+eb_{i}^{j+1} {\rVert_{2}^{2}} +ce^{T}\xi_{i}^{j+1} \\ {\text{subject to}} & & diag(sign(\widehat X_{i}{w^{j}_{i}} \!+ e{b^{j}_{i}} ))(\widehat X_{i}w^{j+1}_{i} \!+ eb^{j+1}_{i}) \!\geq e,\\ && \xi_{i}^{j+1} \geq 0, \end{array} $$

(4)

The solution of the above problem can be obtained by solving its dual problem [27] and is given by

$$\begin{array}{@{}rcl@{}} \max_{\alpha} && e^{T}\alpha-\frac{1}{2} \alpha^{T}G(H^{T}H)^{-1}G^{T}\alpha \\ \text{subject to}&& 0 \leq \alpha \leq ce, \end{array} $$

(5)

where $G = diag(sign(\widehat X_{i}{w^{j}_{i}} + {b^{j}_{i}} e))[\widehat X_{i}~~~ e]$, H=[X _i e], and $\alpha \in \mathbb {R}^{m-m_{i}}$ is the Lagrangian multiplier vector. The problem in (5) is solved iteratively by concave-convex procedure (CCCP) [28], until the change in successive iterations is insignificant. The problem is extended to manifold clustering [24] by using kernel [29]. TWSVC uses an initialization algorithm [24] which is based on the nearest neighbour graph (NNG) and provides more stability to the algorithm.

2.2.1 Fuzzy least squares twin support vector clustering

Working on the lines of TWSVC [24] and least square SVM [30], Khemchandani et al. proposed F-LS-TWSVC [26] which is fuzzy based clustering method and its solution is obtained by solving a series of system of linear equations. Similar to TWSVC, F-LS-TWSVC uses OAA strategy to determine the K-cluster planes. It uses fuzzy nearest neighbour graph (FNNG) for label initialization and generates fuzzy membership matrix S of size m×K. The i ^th column of S gives the membership value of all data points in i ^th cluster. The K clusters are obtained by solving following optimization problem:

$$\begin{array}{@{}rcl@{}} \min_{w_{i},\;b_{i},\;q_{i},X_{i}} &&\; \frac{1}{2} \|((S_{i}X_{i})w_{i}+b_{i}e)\|_{2}^{2} + \frac{\nu}{2}(\|w_{i}\|^{2}_{2} + {b_{i}^{2}}) + \frac{C}{2}\|q_{i}\|_{2}^{2} \\ \text{subject to}&&\lvert((\overline{S_{i}}\overline{X_{i}})w_{i}+b_{i}e)\rvert+q_{i}= e, \end{array} $$

(6)

where i=1,...,K. The diagonal matrices S _i and $\overline {S_{i}}$ indicate the fuzzy membership value of data points belonging to and not belonging to i ^th cluster respectively [26]. This optimization problem can be solved using the concave-convex procedure(CCCP) similar to TWSVC. However, instead of solving QPPs as in TWSVC, the solution of F-LS-TWSVC is obtained by solving a series of system of linear equations.

2.2.2 Approximation used by TWSVC and F-LS-TWSVC

The shortcoming of both TWSVC and F-LS-TWSVC is that their primal formulations involve constraints with mod (|.|) function. To eliminate the mod function, they resort to Taylor’s series expansion which gives an approximation of the original constraint. This condition is avoided in the proposed clustering algorithm by introducing the tree-based approach.

3 Tree-based localized fuzzy twin support vector clustering (Tree-TWSVC)

Taking motivation from MMC [19] and TWSVC [24], we propose Tree-TWSVC, which is an iterative tree-based clustering procedure that employs fuzzy membership matrix to create clusters using LF-TWSVM. The proposed algorithm can efficiently handle large multi-cluster datasets. For a K-cluster problem, it initially generates a fuzzy membership matrix for two clusters by using LF-NNG initialization algorithm (discussed in Section 3.2.4). Based on higher membership values, the data is partitioned into two clusters. Since membership values are based on the proximity of data points, the patterns of one cluster are similar to each other and distinct from the other cluster’s patterns. Hence, Tree-TWSVC considers the inter-cluster and intra-cluster relationships. Each of the two clusters thus obtained can be recursively divided until K clusters are obtained. With each partition, the size of data is reduced which makes the procedure more time-efficient.

The proposed algorithm Tree-TWSVC starts with initial labels (+1,−1), as generated by LF-NNG. By using the initial labels, the data X with m points is divided into two clusters, A and B, of size m ₁ and m ₂ respectively (where m = m ₁ + m ₂) as shown in Fig. 1. The group A can be further partitioned into A ₁ and A ₂, but Tree-TWSVC does not consider data points of B at this stage. This is because, in the first partition of dataset, the data points of A are separated from B, by considering inter-cluster relationship. In the second partition, the algorithm concentrates on the data points of A only and is able to generate more stable results in lesser time. The proposed algorithm is more efficient than plane-based clustering like TWSVC [24] and F-LS-TWSVC [26] that use classical OAA multi-category approach and the same is established by the results of numerical experiments in Section 4.

Fig. 1

Illustration of tree of clusters. Data is partitioned into two clusters at every internal node by iteratively generating cluster hyperplanes using LF-TWSVM

TWSVM [2] is initially proposed for classification problems and uses L ₁ norm error function. When TWSVM-like formulation is used in clustering framework, as done in TWSVC [24], this could lead to premature convergence as the error function does not facilitate flipping of cluster labels, if required. The procedure gets stuck in a poor local optimum and there is little or no change in the initial and final labels. This happens because the loss function is not symmetric and fails to change the labels in successive iterations (Please see Appendix A). To overcome this issue, we propose a new classifier LF-TWSVM, that efficiently handles the problem of premature convergence and is used to build the cluster model of Tree-TWSVC.

3.1 Proposed classifier: localized fuzzy TWSVM (LF-TWSVM)

In this work, we propose a novel classifier, termed as LF-TWSVM which we further use in an unsupervised framework. Unlike TWSVM, LF-TWSVM uses square loss function and a prototype. The prototype prevents the hyperplane from extending indefinitely and keeps it aligned locally to the data points.

3.1.1 LF-TWSVM: Linear version

Let the dataset X consist of m points in n-dimensional space. The data is divided into two clusters and hyperplanes are generated, which are given by

$$\begin{array}{@{}rcl@{}} x^{T}w_{1}+b_{1}=0, \hspace{8mm} x^{T}w_{2}+b_{2}=0. \end{array} $$

(7)

LF-TWSVM employs the fuzzy membership matrix $F \in \mathbb {R}^{m\times 2}$ generated by LF-NNG and based on higher membership value, it partitions the data X into two clusters A (positive cluster) and B (negative cluster), of size m ₁ and m ₂ respectively. The planes for the two clusters A and B are obtained by solving the following problems:

$$\begin{array}{@{}rcl@{}} \min_{w_{1},b_{1},\xi_{2},A,v_{1}} & & \frac{1}{2}\lVert S_{AA}Aw_{1}+e_{1}b_{1} {\rVert_{2}^{2}} + \frac{c_{1}}{2}\lVert \xi_{2}{\rVert_{2}^{2}} \\ &&+ \frac{c_{2}}{2} \lVert S_{AA}A-e_{1}v_{1} {\rVert_{2}^{2}} + \frac{c_{3}}{2}(\lVert w_{1}{\rVert_{2}^{2}}+{b_{1}^{2}})\\ {\text{subject to}} && -(S_{BA}Bw_{1}+e_{2}b_{1})+\xi_{2} = e_{2}, \end{array} $$

(8)

$$\begin{array}{@{}rcl@{}} \min_{w_{2},b_{2},\xi_{1},B,v_{2}} & & \frac{1}{2}\lVert S_{BB}Bw_{2}+e_{2}b_{2} {\rVert_{2}^{2}} + \frac{c_{1}}{2}\lVert \xi_{1}{\rVert_{2}^{2}} \\ &&+ \frac{c_{2}}{2} \lVert S_{BB} B-e_{2}v_{2} {\rVert_{2}^{2}} + \frac{c_{3}}{2}(\lVert w_{1}{\rVert_{2}^{2}}+{b_{2}^{2}})\\ {\text{subject to}} && (S_{AB} Aw_{2}+e_{1}b_{2})+\xi_{1} = e_{1}. \end{array} $$

(9)

The diagonal matrices S _{A A} (size (m ₁×m ₁)) and S _{B A} (size (m ₂×m ₂)) define the membership value of data points of A and B respectively, in positive cluster, taken from matrix F. Similarly, the other two diagonal matrices S _{A B} and S _{B B} are defined for the negative cluster. The primal problems in (8) and (9) are motivated from TWSVM [2] and are modified on the lines of LS-TWSVM [4]. Thus, the inequality constraints are replaced with equality constraints and L ₂-norm of error variables ξ ₁ and ξ ₂ is used; c ₁ is the associated weight and e ₁ ,e ₂ are vectors of one’s of appropriate dimensions. The constraints of LF-TWSVM (8) and (9) do not require mod (|.|) function as required in the constraints of TWSVC (3). TWSVC determines the cluster planes using OAA multi-category approach and considers all the data points while finding the cluster planes. The data points of other clusters may lie on both sides of the cluster plane and hence, the constraints with mod function are required. For Tree-TWSVC, the data is divided into two clusters at each node, therefore one cluster would lie on only one side of another cluster. Hence, the constraints of Tree-TWSVC are written without mod function.

The first term in the objective function of (8) and (9) is the sum of squared distances of the hyperplane to the data points of its own cluster. Thus, minimizing this term tends to keep the hyperplane closer to the data points of one cluster (say cluster A) and the constraints require the hyperplane to be at unit distance from the points of another cluster (say cluster B). The error vectors ξ ₁ and ξ ₂ are used to measure the error if the hyperplane is not a unit distance away from data points of another cluster. The second term of the objective function minimizes the squared sum of error variables ξ ₁ and ξ ₂. The variable v _i (i=1,2) is the prototype [18] of the i ^th cluster and prevents the cluster plane from extending infinitely and controls its localization, proximal to the cluster. The parameter c ₂ is weight associated with the proximal term. LF-TWSVM takes into consideration the principle of structural risk minimization (SRM) [31] by introducing the term $({w_{i}^{T}}w_{i}+{b_{i}^{2}},~~i=1,2$), in the objective function and thus improves the generalization ability. It also takes care of the possible ill-conditioning that might arise during matrix inversion. The parameter c ₃ is chosen to be a very small value.

The error function of (8) and (9) is different from that of TWSVC (4) and has been modified for two major reasons. First, to allow flipping of labels during subsequent iterations, which is otherwise limited due to hinge loss function. This is required to minimize the total error. The second reason for using square loss function is that it leads to solving a system of linear equations instead of a QPP. After substituting the equality constraints in the objective function of (8) and (9), the problems become: LF-TWSVM1:

$$\begin{array}{@{}rcl@{}} \min_{w_{1},b_{1},A,v_{1}} & P_{1}= & \frac{1}{2}\lVert S_{AA} Aw_{1}+e_{1}b_{1} {\rVert_{2}^{2}} + \frac{c_{1}}{2}\lVert S_{BA} Bw_{1}+e_{2}b_{1}+e_{2} {\rVert_{2}^{2}} \\ &&+ \frac{c_{2}}{2}\lVert S_{AA} A-e_{1}v_{1} {\rVert_{2}^{2}} +\frac{c_{3}}{2}((\lVert w_{1}{\rVert_{2}^{2}}+{b_{1}^{2}}),\\ \end{array} $$

(10)

LF-TWSVM2:

$$\begin{array}{@{}rcl@{}} \min_{w_{2},b_{2},B,v_{2}} & P_{2}= & \frac{1}{2}\lVert S_{BB} Bw_{2}\,+\,e_{2}b_{2} {\rVert_{2}^{2}} \,+\, \frac{c_{1}}{2}\lVert -(S_{AB} Aw_{2}+e_{1}b_{2})+e_{1} {\rVert_{2}^{2}} \\ &&+ \frac{c_{2}}{2} \lVert S_{BB} B-e_{2}v_{2} {\rVert_{2}^{2}} + \frac{c_{3}}{2}((\lVert w_{2}{\rVert_{2}^{2}}+{b_{2}^{2}}).\\ \end{array} $$

(11)

To get the solution of (10), set the gradient of P ₁ with respect to w ₁, b ₁ and v ₁ equal to zero. We get

$$\begin{array}{@{}rcl@{}} &&\frac{\partial P_{1}}{\partial w_{1}}=0 \Rightarrow (S_{AA} A)^{T}(S_{AA} Aw_{1}+e_{1}b_{1})+ c_{3} w_{1} \\ &&\hspace{20mm}+ c_{1} (S_{BA} B)^{T}(S_{BA} Bw_{1}\!+e_{2}b_{1}+e_{2}) =0e_{1}, \hspace{10mm} \end{array} $$

(12)

$$\begin{array}{@{}rcl@{}} &&\frac{\partial P_{1}}{\partial b_{1}}=0 \Rightarrow {e_{1}^{T}}(S_{AA} Aw_{1}\,+\,e_{1}b_{1})\,+\,c_{3} b_{1}\,+\,c_{1} {e_{2}^{T}}(S_{BA} Bw_{1}\!\,+\,e_{2}b_{1}\!\!+e_{2}) =0,\hspace{7mm} \end{array} $$

(13)

$$\begin{array}{@{}rcl@{}} &&\frac{\partial P_{1}}{\partial v_{1}}=0 \Rightarrow \!-c_{2} {e_{1}^{T}}(S_{AA} A-e_{1}v_{1}) =0. \end{array} $$

(14)

Let E=[S _{A A} A e ₁], F=[S _{B A} B e ₂] and z ₁=[w ₁ b ₁]^T, by combining (12) and (13) we obtain

$$\begin{array}{@{}rcl@{}} E^{T}Ez_{1}&+& c_{3} z_{1}+ c_{1}F^{T}Fz_{1} + c_{1}F^{T}e_{1}=0e_{1}, \\ &&\Rightarrow z_{1}=-c_{1}(c_{1}F^{T}F+E^{T}E+c_{3} I)^{-1}F^{T}e_{1}. \end{array} $$

(15)

Here, I is an identity matrix of appropriate dimensions. From (14),

$$ v_{1}=({e_{1}^{T}}S_{AA} A)/({e_{1}^{T}}e_{1}). $$

(16)

The second problem i.e. LF-TWSVM2 can be solved in similar manner. From (11), we get

$$\begin{array}{@{}rcl@{}} G^{T}Gz_{2}&+& c_{3} z_{2}+ c_{1}H^{T}Hz_{2} - c_{1}H^{T}e_{2}=0e_{2}, \\ &&\Rightarrow z_{2}=c_{1}(c_{1}H^{T}H+G^{T}G+c_{3} I)^{-1}H^{T}e_{2}, \end{array} $$

(17)

where G=[S _{B B} B e ₂], H=[S _{A B} A e ₁] and z ₂=[w ₂ b ₂]^T. The prototype variable v ₂ is obtained as

$$ v_{2}=({e_{2}^{T}}S_{BB} B)/({e_{2}^{T}}e_{2}). $$

(18)

The augmented vectors z ₁ and z ₂ can be obtained from (15) and (17) respectively and are used to generate the hyperplanes, as given in (7). The prototypes v _i for the two clusters can be calculated by using (16) and (18) respectively. A pattern $x\in \mathbb {R}^{n}$ is assigned to cluster i (i=1,2), depending on which of the two hyperplanes given by (7) it lies closer to, i.e.

$$\begin{array}{@{}rcl@{}} y=\underset{i}{argmin}~~(\lVert {w_{i}^{T}}x+b_{i} {\rVert_{2}^{2}}+ c_{2}\lVert x-v_{i}{\rVert_{2}^{2}}). \end{array} $$

(19)

It finds the distance of point x from the plane x ^T w _i + b _i =0, where i=1,2 and also considers distance from the corresponding prototype. The predicted label for pattern x is given by y.

3.1.2 LF-TWSVM: Kernel version

The results can be extended to non-linear version by considering the kernel-generated surfaces and are given as

$$\begin{array}{@{}rcl@{}} Ker(x^{T},C^{T})u_{1}+b_{1}=0, \end{array} $$

(20)

$$\begin{array}{@{}rcl@{}} Ker(x^{T},C^{T})u_{2}+b_{2}=0,\\ \end{array} $$

(21)

where C ^T=[A B]^T and K e r is an appropriately chosen positive definite kernel. The primal QPP of the non-linear LF-TWSVM corresponding to the first surface of (20) is given as KLF-TWSVM1:

$$\begin{array}{@{}rcl@{}} \min_{u_{1},b_{1},K_{A},V_{1}} & Q_{1}= & \frac{1}{2}\lVert K_{A}u_{1}+e_{1}b_{1} {\rVert_{2}^{2}} + \frac{c_{1}}{2}\lVert K_{B}u_{1}+e_{2}b_{1}+e_{2} {\rVert_{2}^{2}} \\ &&+ \frac{c_{2}}{2}\lVert K_{A}-e_{1}V_{1} {\rVert_{2}^{2}} +\frac{c_{3}}{2}((\lVert u_{1}{\rVert_{2}^{2}}+{b_{1}^{2}}), \end{array} $$

(22)

where K _A = S _{A A} K e r(A,C ^T), K _B = S _{B A} K e r(B,C ^T). The solution for the problem (22) is obtained in similar manner as the linear case. The augmented vector r ₁=[u ₁ b ₁]^T is given as

$$\begin{array}{@{}rcl@{}} r_{1}=-c_{1}(c_{1}{K_{F}^{T}}K_{F}+{K_{E}^{T}}K_{E}+c_{3} I)^{-1}{K_{F}^{T}}e_{1}. \end{array} $$

(23)

Here, K _E =[K _A e ₁] and K _F =[K _B e ₂]. The identity matrix I is of appropriate dimensions and the prototype V ₁ is determined as

$$ V_{1}=({e_{1}^{T}}K_{A})/({e_{1}^{T}}e_{1}). $$

(24)

The second plane can be retrieved in a similar manner from (25). KLF-TWSVM2:

$$\begin{array}{@{}rcl@{}} \min_{u_{2},b_{2},K_{B},V_{2}} & Q_{2}= & \frac{1}{2}\lVert K_{B}u_{2}\,+\,e_{2}b_{2} {\rVert_{2}^{2}} \,+\, \frac{c_{1}}{2}\lVert -(K_{A}w_{2}+e_{1}b_{2})\!+e_{1} {\rVert_{2}^{2}} \\ &&+ \frac{c_{2}}{2} \lVert K_{B}-e_{2}V_{2} {\rVert_{2}^{2}} + \frac{c_{3}}{2}((\lVert u_{2}{\rVert_{2}^{2}}+{b_{2}^{2}}). \end{array} $$

(25)

Here K _A = S _{A B} K e r(A,C ^T), K _B = S _{B B} K e r(B,C ^T). Once we obtain the surfaces (20), a new pattern $x\in \mathbb {R}^{n}$ is assigned to class 1 or class -1 in a manner similar to the linear case.

3.2 Clustering algorithms: Tree-TWSVC

Tree-TWSVC is a multi-category clustering algorithm that creates a binary tree of clusters by partitioning the data at multiple levels until the desired number of clusters are obtained. Tree-TWSVC uses an iterative approach to generate two cluster center planes, using LF-TWSVM at each node of the tree and updates the hyperplane parameters in each iteration by aligning the cluster plane along the data. Thus, it minimizes the empirical risk. Tree-TWSVC also minimizes structural risk due to the regularization term added to its formulation. In this work, we propose two implementations for Tree-TWSVC, namely BTree-TWSVC and OAA-Tree-TWSVC.

3.2.1 Binary tree-based localized fuzzy twin support vector clustering (BTree-TWSVC)

BTree-TWSVC is an unsupervised learning procedure that creates K clusters from m-data points. The algorithm takes two inputs: $X\in \mathbb {R}^{m \times n}$ and K, where X represents m data points in n-dimension feature space and K is the number of clusters.

The Algorithm 1 for BTree-TWSVC generates the final solution in the form of clusters identified by LF-TWSVM, arranged as nodes of the tree. The root node contains the entire data and leaf nodes correspond to the final clusters. Thus, for a K-cluster problem, we obtain a tree with K leaf nodes and (K−1) internal nodes. Generally, most of the clustering algorithms like K-means [10] and KPC [17] initiate with randomly generated labels which leads to unstable results due to their dependency on the initial labels. For Tree-TWSVC, we use an initialization algorithm based on K-nearest neighbour graph [32], termed as localized fuzzy NNG (LF-NNG), discussed in Section 3.2.4.

BTree-TWSVC generates the fuzzy membership matrix $F_{2} \in \mathbb {R}^{m\times 2}$ through LF-NNG and assigns either of the cluster labels (+1, −1) to all data points based on higher membership value towards cluster 1 or -1 respectively. Then, the two cluster center planes are determined and the membership matrix F ₂ is updated. BTree-TWSVC alternatively determines the cluster planes and membership matrix for data points until the convergence criterion is met (Step 5d) and the two clusters A ^new and B ^new are obtained. To decide whether the obtained clusters, A ^new and B ^new, can be further partitioned or not, the proposed algorithm uses K-means clustering [10] to get K clusters and labels Y _k ∈{1,...,K} for all the data points. If clusters A ^new or B ^new are associated with more than one label from Y _k , then they can be further partitioned by recursively calling the same algorithm with new inputs. With the new inputs, size of the data is approximately reduced to half (assuming A ^new and B ^new contain approximately an equal number of data points), due to partitioning. Thus, the input data diminishes in size as we traverse down the cluster tree and creates a tree of height ⌈l o g ₂ K⌉.

3.2.2 One-against-all tree-based localized fuzzy twin support vector clustering (OAA-Tree-TWSVC)

OAA-Tree-TWSVC is another tree-based implementation of Tree-TWSVC and is explained in Algorithm 2.

The algorithm for OAA-Tree-TWSVC generates cluster model by arranging LF-TWSVM generated clusters in the form of a tree. At each internal node, one cluster is separated from rest of the clusters. Hence, this method represents modified one-against-all (OAA) multi-category strategy. The height of the tree is (K−1).

3.2.3 Binary tree (BTree) vs. One-against-all tree (OAA-Tree)

In this work, we have proposed two implementations for Tree-TWSVC as discussed in Section 3.2.1 and 3.2.2. Out of the two approaches, BTree-TWSVC is more robust and achieves better clustering accuracy than OAA-Tree-TWSVC which is experimentally proved in Section 4. One such scenario is presented in Fig. 2 i.e. clustering problem with four clusters (a.). Here, we present the clustering result with TWSVC, OAA-Tree-TWSVC and BTree-TWSVC. For TWSVC, the hyperplanes are obtained using OAA strategy (b.) and this leads to an ambiguous region i.e. the data points lying in this region might be wrongly clustered. With OAA-Tree-TWSVC, one of the clusters obtained with LF-NNG initialization is selected as the positive cluster (green squares) and the remaining are regarded as the negative cluster (red frames, violet triangles and blue dots), as shown in (c.). The localized hyperplanes are generated using LF-TWSVM, but it still leads to some ambiguity. Once the green cluster is identified, we apply the same procedure on remaining data points, as presented in (d-e.).The final OAA-tree obtained is shown in (e.). For BTree-TWSVC, LF-NNG is used to identify two clusters at a time, as demonstrated in (f.), which separates the blue-violet points from red-green points. BTree-TWSVC is able to generate a stable clustering model as depicted in (f-h.) and has got better clustering ability.

Fig. 2

Clustering with TWSVC and Tree-TWSVC for four clusters (a). Dataset with four clusters (b.) Clustering model with TWSVC (c-e.) Clustering with OAA-Tree-TWSVC and resulting OAA-tree (f–h). Clustering with BTree-TWSVC and resulting binary tree

3.2.4 Initialization with localized fuzzy nearest neighbour graph (LF-NNG)

Wang et al. proposed NNG based initialization method for TWSVC [24] and F-LS-TWSVC [26] used fuzzy NNG (FNNG) to generate the membership values. For this work, we propose localized fuzzy nearest neighbour graph (LF-NNG) which generates a membership matrix F. This matrix is used to obtain the initial data labels to be used by Tree-TWSVC. The steps involved in LF-NNG for getting initial labels of K clusters are given in Algorithm 3.

3.2.5 Complexity analysis

The strength of Tree-TWSVC is the tree-based approach which reduces the complexity of the algorithm. The size of data diminishes as it is partitioned to obtain the clusters. This characteristic is of utmost importance for non-linear (kernel) classifiers where the complexity is dependent on the size of data. For a K-cluster problem, the OAA multi-category approach uses entire dataset K-times to determine the cluster planes. Assuming that all clusters have equal size i.e. m/K, where m is the number of data points. If any TWSVM-based classifier is used with OAA (as done in TWSVC), then the algorithm solves K QPPs, each of size ((K−1)/K)∗m. Hence, the complexity of TWSVM-based clustering algorithm is given by

$$\begin{array}{@{}rcl@{}} &T_{OAA}=K*c* \left( \frac{K-1}{K}*m \right)^{3},\\ & \simeq K*c*m^{3}, \hspace{.3cm} \end{array} $$

(31)

where c is a constant that includes the count for maximum number of iterations for finding the final cluster planes. So, the complexity of OAA TWSVM-based clustering is T _{O A A} = O(m ³).

In BTree-TWSVC, the optimization problem is solved as a system of linear equations. For the linear case, LF-TWSVM finds the inverse of two matrices, each of dimension (n+1)×(n+1), where n is the number of features, for each internal node of the binary tree. As we traverse down the tree, size of the data is approximately reduced to half. Thus, the complexity of BTree-TWSVC can be recursively defined as

$$\begin{array}{@{}rcl@{}} T(m)=&c(n+1)^{3}+2*T\left( \frac{m}{2}\right),&\\ T\left( \frac{m}{K}\right)=&1,\hspace{3cm} & \end{array} $$

(32)

where m is the number of data points and c is the complexity constant. We assume that data is divided into two clusters of almost equal size. The base condition $T\left (\frac {m}{K}\right )=1$ represents cost of leaf node that contains data from one cluster only. The time complexity of (32) is given as [34]

$$\begin{array}{@{}rcl@{}} T(m)&=&c(n+1)^{3}+2*c(n+1)^{3}\\&&+...+2^{h-1}*c(n+1)^{3}+2^{h}*1, \end{array} $$

(33)

where h=⌈l o g ₂ K⌉. The height of the tree ‘ h’ depends on the number of clusters K. The above equation can be solved as

$$\begin{array}{@{}rcl@{}} T(m)&=&c(n+1)^{3}(1+2+4+...+2^{h-1})+2^{h}, \\ & =&c(n+1)^{3}(2^{h}-1)+2^{h},\hspace{2.3cm}\\ & =&c(n+1)^{3}(K-1)+K.\hspace{2.5cm}\\ && \leq cK(n+1)^{3}+K.\hspace{3.4cm} \end{array} $$

(34)

Therefore, the complexity of linear BTree-TWSVC implemented as a binary tree (BT) is T _{B T} = O(K n ³) and is independent of the size of data. For large-sized datasets (m≫n), the efficiency of BTree-TWSVC is not much affected, but for TWSVC (implemented using OAA-TWSVM) the learning time increases with size of data.

For kernel version, the complexity of BTree-TWSVC can be recursively defined as

$$\begin{array}{@{}rcl@{}} T(m)=&c(m+1)^{3}+2*T(\frac{m}{2}),&\\ T\left( \frac{m}{K}\right)=&1,\hspace{3cm} & \end{array} $$

(35)

where m is the number of data points and c is the complexity constant. The complexity (35) can be written as [34]

$$\begin{array}{@{}rcl@{}} T(m)=c(m+1)^{3}&+&\frac{1}{4}c(m+1)^{3}+\frac{1}{16}c(m+1)^{3}\\&+&...+\frac{1}{4^{h-1}}c(m+1)^{3}+2^{h},\hspace{5mm} \end{array} $$

(36)

where h=⌈l o g ₂ K⌉. The above equation can be solved as

$$\begin{array}{@{}rcl@{}} T(m)&=&c(m+1)^{3}(1+\frac{1}{4}+\frac{1}{16}+...+\frac{1}{4^{h-1}})+2^{h}, \\ && \leq \frac{4}{3}c(m+1)^{3}+K,\hspace{3.5cm}\\ && \simeq\frac{4}{3}c(m+1)^{3}.\hspace{4.2cm} \end{array} $$

(37)

So, the complexity of kernel BTree-TWSVC is independent of the number of clusters K. BTree-TWSVC is more time-efficient than OAA multi-category clustering for both linear and kernel versions. We can discuss the time complexity of OAA-Tree-TWSVC in a similar way as TWSVC as both of them are based on OAA strategy. But OAA-Tree-TWSVC is more time-efficient than TWSVC because the number of data points get diminished as we traverse down the OAA-tree. To validate the efficiency of the proposed method, we have compared the learning time of OAA-Tree-TWSVC with TWSVC (also based on OAA strategy) in Section 4.

3.3 Discussion

In this section, we have discussed the comparison of proposed clustering algorithm with MMC [23], TWSVC [24] and F-LS-TWSVC [26].

3.3.1 Tree-TWSVC vs. MMC

The proposed clustering algorithm Tree-TWSVC determines multiple clusters by solving a system of linear equations, whereas MMC is a binary clustering method that solves a non-convex optimization problem which is relaxed to solving expensive SDP. Unlike MMC, Tree-TWSVC does not use alternate optimization to determine w and b, whereas they are obtained as vector z _i =[w _i b _i ]^T, (i=1,2), by solving a system of linear (15) and (17). Therefore, Tree-TWSVC is more time-efficient than MMC. Also, Tree-TWSVC uses fuzzy nearest neighbour based initialization method, which improves its clustering accuracy.

3.3.2 Tree-TWSVC vs. TWSVC

TWSVC involves constraints with mod function (|.|) and it uses Taylor’s series expansion to get an approximation of this function. Whereas Tree-TWSVC considers only two clusters at each level of the tree and these clusters would lie on either side of the mean cluster plane, hence it does not require constraints with mod function. Also, Tree-TWSVC formulation involves square loss function which results in solving a series of systems of linear equations whereas TWSVC solves a series of QPPs using the concave-convex procedure. Therefore, Tree-TWSVC is more efficient in terms of computational effort as well as clustering accuracy than TWSVC. Also, TWSVC is based on OAA strategy, but Tree-TWSVC uses tree-based approach. Tree-TWSVC uses a better initialization algorithm (i.e. LF-NNG) and its decision function for test data also takes into account the distance from the cluster prototype. Hence, Tree-TWSVC achieves better results in lesser time than TWSVC.

3.3.3 Tree-TWSVC vs. F-LS-TWSVC

F-LS-TWSVC solves a series of systems of linear equations to get the cluster planes, but similar to TWSVC, it uses Taylor’s series approximation for the constraints and therefore the results may not be accurate. Tree-TWSVC formulates a convex optimization problem which is solved as a series of systems of linear equations. F-LS-TWSVC is based on OAA multi-category strategy and Tree-TWSVC handles OAA using tree-based approach, which is more efficient. Also, Tree-TWSVC has BTree-TWSVC approach which is even faster than OAA-Tree-TWSVC.

4 Experiments and results

In this section, we compare the performance of two variations of Tree-TWSVC i.e. BTree-TWSVC and OAA-Tree-TWSVC, with other clustering methods and investigate their accuracy and computational efficiency. The other clustering methods used for comparison are Fuzzy C-means (FCM) clustering [35], TWSVC [24] and F-LS-TWSVC [26]. We have also implemented a non-fuzzy version of OAA-Tree-TWSVC, which is referred as OAA-T-TWSVC. These two algorithms are compared to study the effect of adding fuzziness to the clustering model. For OAA-T-TWSVC, the initial clusters are generated using NNG [32]. The experiments are performed in MATLAB version 8.0 under Microsoft Windows environment on a machine with 3.40 GHz CPU and 16 GB RAM. The experiments are conducted on benchmark UCI datasets [36]. In all experiments, the focus is on the comparison of proposed method with clustering methods listed above. The parameters c ₁ and c ₂ are selected in the range {0.01 to 1}; c ₃∈{10⁻ⁱ, i=1,...,5} and t o l is selected to be very small value of order 10⁻⁵. The kernel parameter is tuned in the range {0.1 to 1}. The grid search method [37] is applied to tune the parameters. For each dataset, a validation set comprising of 10% randomly selected samples from the dataset is used.

The metric Accuracy [38] is used to measure the performance of clustering methods. For finding the accuracy of clustering algorithm, a similarity matrix $S \in \mathbb {R}^{m\times m}$ is computed with the given data labels y _i , y _j ∈{1:K}, i=1:m, j=1:m, where

$S(i,j)=\left \{ \begin {array}{ll} 1, & if ~y_{i}=y_{j} \\ 0, & otherwise. \end {array} \right .$

Let S _t and S _p be the similarity matrices computed by the true cluster labels and predicted labels respectively. The accuracy of clustering method is defined as the Rand statistic [38] and is given as

$$ Accuracy=\frac{n_{zeros}+n_{ones}-m}{m^{2}-m} \times 100 $$

(38)

where n _{z e r o s} is the number of zeros at corresponding indices in both S _t and S _p , and n _{o n e s} is the number of ones in both S _t and S _p .

4.1 Out-of-sample testing

In an unsupervised framework, generally the clustering model is built using an entire dataset. But, the formulation of proposed Tree-TWSVC allows it to obtain the clustering model with learning data and the accuracy of the model can be examined using out-of-sample (OoS) or unseen test data [39, 40]. The clustering model is built with some part of learning data provided as input to the Tree-TWSVC algorithm and is used to predict the labels of the unseen OoS data. This feature is particularly useful when working with very large datasets where the clustering model can be built with few samples and rest of the samples are assigned labels using OoS approach. Tree-TWSVC also takes advantage of the tree structure and LF-TWSVM formulation and generates the results in much less time. In our simulations with UCI dataset, we have given the results with entire dataset and OoS testing of clustering model. For OoS, 80 % samples are randomly selected from the entire data for learning the model and the remaining 20 % are used to determine the clustering accuracy.

4.2 Experiments on UCI datasets

We have selected 14 UCI multi-category datasets [36] for the experiments- Zoo, Iris, Wine, Seeds, Segment, Glass, Dermatology, Ecoli, Compound, Libra, Optical digits, Pageblocks, Satimage and Pen digits. The number of samples, features and classes are shown along with the datasets in Table 1.

Table 1 Clustering accuracy for UCI datasets (Linear version)

4.2.1 Results for linear case

The simulation results for UCI datasets with linear clustering methods are recorded in Table 1 for K-means, FCM, TWSVC, F-LS-TWSVC, OAA-T-TWSVC, OAA-Tree-TWSVC and BTree-TWSVC. The simulation results demonstrate that both versions of Tree-TWSVC i.e. BTree-TWSVC and OAA-Tree-TWSVC, outperform K-means, FCM, TWSVC and F-LS-TWSVC for clustering accuracy. In Table 1, the entire dataset is used for building the clustering model. For 13 out of 14 UCI datasets, one of the two versions of Tree-TWSVC achieves the highest accuracy. This can be attributed to the fact that a good initialization algorithm can improve the accuracy of the clustering algorithm. It is also observed that binary tree-based algorithm (BTree-TWSVC) generates better result than OAA-Tree-TWSVC. The table demonstrates that OAA-Tree-TWSVC (fuzzy version) achieves better clustering accuracy than OAA-T-TWSVC (non-fuzzy version). Table 2 shows accuracy result with OoS clustering for OAA-T-TWSVC, OAA-Tree-TWSVC and BTree-TWSVC. The clustering algorithms achieve better results when entire data is used for clustering.

Table 2 OoS Clustering accuracy for UCI datasets (Linear version)

4.2.2 Results for non-linear case

The proposed method is extended using non-linear LF-TWSVM classifier and Table 3 compares the performance of Tree-TWSVC (both versions) with that of TWSVC, F-LS-TWSVC, LkPPC, K-means and FCM using RBF kernel, K e r(x,x ^′) = e x p(−σ∥x−x ^′∥²). The table shows the clustering accuracy of these algorithms on UCI datasets. The results illustrate that Tree-TWSVC (both versions) achieve better accuracy for most of the datasets. It is also observed that the clustering results are better for non-linear versions as compared to linear ones. Table 4 shows accuracy result with OoS clustering for non-linear versions of OAA-T-TWSVC, OAA-Tree-TWSVC and BTree-TWSVC.

Table 3 Clustering accuracy for UCI datasets (Non-linear version)

Table 4 OoS Clustering accuracy for UCI datasets (Non-linear version)

4.3 Learning time:

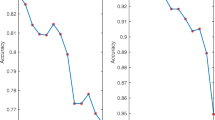
We have compared the learning time (i.e. time for building the clustering model) of OAA-Tree-TWSVC with TWSVC for UCI datasets in Fig. 3. In this figure, Derm, OD, SI, PB and PD represent Dermatology, Optical digits, Satimage, Pageblocks and Pen digits datasets respectively. Although, both of these clustering methods are based on OAA multi-category strategy, but OAA-Tree-TWSVC takes much less time for building the tree-based model than TWSVC. The efficiency of OAA-Tree-TWSVC is significant for datasets with large number of classes i.e. Libra, Compound, Satimage and Pen digits, where OAA-Tree-TWSVC is much faster than TWSVC. For pen digits dataset, OAA-Tree-TWSVC is almost 16 times faster than TWSVC. The learning time of non-linear versions of OAA-Tree-TWSVC and TWSVC are compared in Fig. 4. It is observed that OAA-Tree-TWSVC is very efficient in dealing with large datasets; whereas learning time of TWSVC is highly affected by size and number of classes in the dataset.

Fig. 3

Learning time (Linear)

Fig. 4

Learning time (Non-linear)

4.4 Experiments on large datasets

In order to demonstrate the scalability and effectiveness of Tree-TWSVC, we performed experiments on large UCI datasets i.e. Optical digits, Satimage, Pen digits and Pageblocks. It is observed that the performance of TWSVC deteriorates as the size of data increases; whereas Tree-TWSVC can efficiently handle large datasets. Similarly, FCM fails to give good accuracy for Pen digits and optical digits. From Table 1, there is a significant difference in the clustering accuracy achieved by Tree-TWSVC (both versions) as compared to FCM and TWSVC, for the above mentioned large datasets. Tree-TWSVC scales well on these datasets and is not much affected by the number of classes.

4.5 Application to image segmentation

To evaluate the performance of Tree-TWSVC on large datasets, we present its application on image segmentation which can be considered as a clustering problem. The image is partitioned into non-overlapping regions that share certain homogeneous features. For the experiments, we have taken color images from Berkeley image segmentation dataset (BSD) [41]. These images have dimensions 481×321 or 321×481 i.e. 154,401 pixels in each image. The problem is to partition the image pixels into disjoint sets called the regions. We use a dynamic method to determine the number of regions for each image. The histogram for the image is generated and the prominent peaks are identified. The number of prominent peaks determines the number of regions (L) in the image. The color image is then partitioned using minimum variance color quantization with L levels. For the experiments, we have taken a combination of color and texture features. The image features used for this work are Gabor texture features [42] and RGB color value of the pixel. Gabor features are extracted with 4-orientation (0,45,90,135) and 3-scale (0.5,1.0,2.0) sub-bands and the maximum of the 12 coefficients determine the orientation at a given pixel location.

The segmentation model is built using OoS approach with BTree-TWSVC and 1 % pixels are randomly selected from the image for learning. The rest of the image pixels are used for testing the model. The images are segmented using BTree-TWSVC and the results are compared with linear TWSVC and multiclass semi-supervised kernel spectrum clustering (MSS-KSC) [43] segmentation methods, as shown in Fig. 5. MSS-KSC uses few labelled pixels to build the clustering model with kernel spectrum clustering approach. It is observed that the segmentation results of BTree-TWSVC are visually more accurate than other algorithms. For TWSVC, the image is over-segmented, which results in the formation of multiple smaller regions within one large region. For BSD images, the ground truth segmentations are known and the images segmented by BTree-TWSVC and TWSVC are compared with ground truth. To statistically evaluate the segmentation algorithms, two evaluation criteria are used: F-measure (FM) and error rate (ER). F-measure is determined as

$$ FM=\frac{2\times Precision \times Recall}{Precision+Recall}, $$

(39)

and ER is given by

$$ ER=\frac{FP+FN}{\text{Total pixels}}, $$

(40)

where P r e c i s i o n and R e c a l l are defined as

$$\begin{array}{@{}rcl@{}} Precision =\frac{TP}{TP+FP}, \\ Recall=\frac{TP}{TP+FN}. \end{array} $$

T P, F P, T N, F N are true-positive, false-positive, true-negative and false-negative respectively. These measures are calculated with respect to ground-truth boundaries and results are presented in Fig. 5 and Table 5. BTree-TWSVC achieves better F-measure and error rate values than TWSVC and MSS-KSC.

Fig. 5

Segmentation results on color images from BSD image dataset (a.) Original image (b.) MSS-KSC [43] (c.) TWSVC (d.) BTree-TWSVC

Table 5 Segmentation result for BSD color images

5 Conclusions

In this paper, we propose Tree-based localized fuzzy twin support vector clustering (Tree-TWSVC) which is an iterative algorithm and extends the proposed classifier, localized fuzzy twin support vector machine (LF-TWSVM), in unsupervised framework. LF-TWSVM is a binary classifier that generates the nonparallel hyperplanes by solving a system of linear equations. Tree-TWSVC develops a tree-based clustering model which consists of several LF-TWSVM classifiers. In this work, we propose two implementations of Tree-TWSVC, namely Binary Tree-TWSVC and One-against-all Tree-TWSVC. The proposed clustering algorithm outperforms the other TWSVM-based clustering methods like TWSVC and F-LS-TWSVC, which are based on classical one-against-all multi-category approach and they use Taylor’s series for approximating the constraints of the optimization problem. Experimental results have proved that Tree-TWSVC has superior clustering accuracy and efficient learning time for UCI datasets as compared to FCM, TWSVC and F-LS-TWSVC. The proposed clustering algorithm is extended for image segmentation problems also. The future line of work is to validate the performance of the proposed algorithm with different distance measures for calculating fuzzy memberships.

Appendix A: Loss function of TWSVM

TWSVM uses hinge loss function which is given by

$L_{h}=\left \{ \begin {array}{ll} 0, & y_{i}f_{i} \geq 1 \\ 1-y_{i}f_{i}, & otherwise \end {array} \right .$

For any SVM or TWSVM based clustering method, the clustering error or the hyperplanes change little after initial labeling or during subsequent iterations. This arises due to hinge loss function, as shown in Fig. 6a, where the classifier tries to push y _i f _i to the point beyond y _i f _i =1 (towards right) [23]. Here, solid line shows loss with initial labels and dotted line shows loss after flipping of labels. As observed from the empirical margin distribution of y _i f _i , most of the patterns have margins y _i f _i ≫1. If the label of a pattern is changed, the loss will be very large and the classifier is unwilling to flip the class labels. So, the procedure gets stuck in a local optimum and adheres to the initial label estimates. To prevent the premature convergence of the iterative procedure, the loss function is changed to square loss and is given as L _s =(1−y _i f _i )². This loss function is symmetric around y _i f _i =1, as shown in Fig. 6b and penalizes preliminary wrong predictions. Therefore, it permits flipping of labels if needed and leads to a significant improvement in the clustering performance.

Fig. 6

Flipping of labels. a. Hinge loss function; b. Square loss function