On the local dominance properties in single machine scheduling problems

Abstract

We consider a non-preemptive single machine scheduling problem for a non-negative penalty function f, where an optimal schedule satisfies the left-shifted property, i.e. in any optimal sequence all executions happen without idle time with a starting time $t_0 \ge 0$. For this problem, every job j has a priority weight $w_j$ and a processing time $p_j$, and the goal is to find an order on the given jobs that minimizes $\sum w_j f(Cj)$, where $C_j$ is the completion time of job j. This paper explores local dominance properties, which provide a powerful theoretical tool to better describe the structure of optimal solutions by identifying rules that at least one optimal solution must satisfy. We propose a novel approach, which allows to prove that the number of sequences that respect the local dominance property among three jobs is only two, not three, reducing the search space from n! to $n!/3^{\lceil n/3 \rceil }$ schedules. In addition, we define some non-trivial cases for the problem with a strictly convex penalty function that admits an optimal schedule, where the jobs are ordered in non-increasing weight. Finally, we provide some insights into three future research directions based on our results (i) to reduce the number of steps required by an exact exponential algorithm to solve the problem, (ii) to incorporate the dominance properties as valid inequalities in a mathematical formulation to speed up implicit enumeration methods, and (iii) to show the computational complexity of the problem of minimizing the sum of weighted mean squared deviation of the completion times with respect to a common due date for jobs with arbitrary weights, whose status is still open.

1 Introduction

In this paper, we consider a non-preemptive single-machine scheduling problem, where an optimal schedule satisfies the left-shifted property, i.e. in any optimal sequence all executions happen without idle time with a starting time $t_0 \ge 0$. Formally, we have a set $\mathcal {J}$ of n jobs, where each job j has a processing time $p_j \in \mathbb {N}^+$ and a priority weight $w_j \in \mathbb {Q}^+$ where the objective is to find a schedule of the set $\mathcal {J}$ of jobs defined by a sequence S and a starting time $t_0 \ge 0$ that minimizes $\sum _{j\in \mathcal {J}} w_j f(C_j)$, where f is a given non-negative penalty function and $C_j$ is the completion time of each job $j \in \mathcal {J}$ with a value equal to $t_0 + \sum _{S^i \le S^j} p_i$, where $S^j$ is the order of job $j \in \mathcal {J}$ in the sequence S. Consequently, all executions happen without idle time between times $t_0$ and $t_n=t_0+\sum _{j\in \mathcal {J}} p_j$ in an optimal sequence $S^*$. This problem is denoted by $1 ||\sum _{j\in \mathcal {J}} w_j f(C_j)$ [see Brucker et al. (2023) for notation details], whose complexity status is strongly NP-hard (Höhn & Jacobs, 2015).

We focus on the design of exact algorithms, in particular by using dominance properties, which provide a powerful theoretical tool to better describe the structure of optimal solutions by identifying rules that at least one optimal solution must satisfy. This information can be used to enhance different exhaustive algorithms to find an optimal solution by reducing the search space of n! different schedules and pruning early ineffective partial solutions in several problems with arbitrary (Fomin & Kratsch, 2010), convex, concave, and piecewise linear penalty functions (Bansal et al., 2017; Vásquez, 2015), even when the penalty functions are non-monotone increasing (Díaz-Núñez et al., 2018, 2019; Falq et al., 2021, 2022; Pereira & Vásquez, 2017).

In this setting, we consider an instance $\mathcal {I}$ containing two jobs $i, j \in \mathcal {J}$ and distinguish two kinds of properties:

• We say that jobs $i,j \in \mathcal {J}$ satisfy local precedence at time t, denoted $i\prec _{\ell (t)} j$, if whenever in a sequence S job j starts at time t and is followed immediately by job i then the sequence S is not optimal.

• We say that jobs $i, j \in \mathcal {J}$ satisfy global precedence in the time interval [a, b], denoted by $i\prec _{g[a,b]} j$, if whenever in a sequence S we have $a\le C_j-p_j \le C_i-p_i-p_j \le b$, then S is sub-optimal, no matter if i, j are adjacent or not.

We use the notation $i\prec _g j$ as a shorthand for $i\prec _{g[a,\infty ]} j$. In addition, $i\prec _{\ell [a,b]} j$ means $i\prec _{\ell (t)} j$ for all $t \in [a,b]$.

For convenience, we denote by F(S) the objective value associated with the sequence S with a starting time $t_0$ and define the following function on the domain $t\in [0, \infty )$:

$$\begin{aligned}\nu _{ij}(t)=\left( 1-\frac{w_j}{w_i}\right) f(t+p_i+p_j)+\frac{w_j}{w_i}f(t+p_j).\end{aligned}$$

Let $S_1$ and $S_2$ be sequences of the form $S_1= AijB$ and $S_2= AjiB$, for some sets of jobs A and B. Let t be the sum of processing times of all jobs in A. Thus, we have that $i \prec _{\ell (t)} j$ is equivalent to:

$$\begin{aligned} 0< F(S_2)-F(S_1)=&w_j f(t\!+\!p_j)\!+\!w_i f(t\!+\!p_i\!+\!p_j)\!-\!w_i f(t\!+\!p_i)\!-\!w_j f(t\!+\!p_i\!+\!p_j)\\ =&w_i {\left( \left( 1-\frac{w_j}{w_i}\right) f (t+p_i+p_j) + \frac{w_j}{w_i} f(t+p_j)- f(t+p_i) \right) }\\ =&w_i\left( \nu _{ij}(t)-f(t+p_i)\right) , \end{aligned}$$

and then, the following equivalence holds

$$\begin{aligned}i \prec _{\ell (t)} j\,\equiv \,0<\nu _{ij}(t)-f(t+p_i).\end{aligned}$$

1.1 Our contribution

We explore the local dominance properties in a non-preemptive single-machine scheduling problem, extending some preliminary results presented in Jorquera-Bravo &Vásquez (2022). In particular, we show that the total number of solutions that satisfy the local dominance properties has an upper bound defined by $n!/3^{\lceil n/3 \rceil }$, which is a drastic improvement over the n! different schedules of the search space. This is based on the novel approach, which allows us to prove that the number of sequences that respect the local dominance property among three jobs is only two, not three. In addition, we study the NP-hardness for a convex penalty in a general framework, which allows us to model i) a machine changing its execution speed continuously from a wear and tear effect, resulting in a machine that works less effectively over time, and ii) the just-in-time (JIT) production ideals in which goods are manufactured only when needed and both inventories and delays are penalized. In particular, we prove that for any strictly convex penalty functions, an instance of n jobs with equal Smith ratio (Smith, 1956) admits an optimal schedule where the jobs are ordered in non-increasing weight, where the Smith ratio of job i is defined by $w_i/p_i$. Finally, we provide some insights into three future research directions: (i) to reduce the number of steps $O(n 2^n)$ required by an exact exponential algorithm for the non-preemptive single-machine scheduling problem [see Theorem 3.1 in Fomin and Kratsch (2010)], (ii) to incorporate the dominance properties as valid inequalities, which can be used in a mathematical formulation to speed up implicit enumeration methods such as branch-and-cut algorithm by iteratively strengthening its linear relaxation, and iii) to show the computational complexity of the problem of minimizing the sum of weighted mean squared deviation of the completion times with respect to a common due date for jobs with arbitrary weights, whose status is still open (Vásquez, 2014).

2 Search space and local dominance properties

Given an algorithm that uses some search tree procedure to solve the non-preemptive single-machine scheduling problem, we consider a node of the search tree specified by a partial sequence $S'$ into a backward branching scheme. Let i, j be two jobs not in $S'$, and let t be $t_n-\sum _{k\in {S'}} p_k$. Thus the descendants of this node include the partial right-to-left sequences $\{i\}//S'$ and $\{j\}//S'$, where a//b indicates that the set of jobs b is ordered before the set of jobs a in the sequence. Now except in some degenerate cases (e.g. some set of identical jobs), we have a set of comparable jobs, for which exactly one of $i\prec _{\ell (t)}j$, $j\prec _{\ell (t)}i$ holds for any pair of jobs i and j belonging to the set $\mathcal {J}$. Consequently, this implies that exactly one of the sub-descendants partial right-to-left sequences $\{i\}// \{j\}//S'$ and $\{j\}//\{i\}//S'$ exists in the search tree. By considering the left-shifted property of any optimal schedule, note that here we used the fact that the partial sequence was extended from right to left, and the local precedence property between i and j were done for the same time point, which would not have been the case, if the schedule were constructed from left to right. The effect of this observation is that the number of nodes in the second level of the tree is upper bounded by ${n\atopwithdelims ()2}$. Thus, by multiplying these numbers for all even levels, of the tree is upper bounded by $n!/2^{\lceil n/2\rceil }$,(see for example ${n\atopwithdelims ()2} \cdot {n-2\atopwithdelims ()2} \cdot \dots \cdot {2\atopwithdelims ()2}$ when n is multiple of 2). Note that the upper bound ${n\atopwithdelims ()2}$ also defines the maximum number of job pairs to finish a schedule that satisfies the local precedence property. In addition, an exact exponential algorithm for the non-preemptive single-machine scheduling problem with a number of steps $O(n 2^n)$ can be developed based on this local precedence relation [see Theorem 3.1 in Fomin and Kratsch (2010)].

In this paper, we improve the above upper bound based on a novel approach, which allows to prove that the number of sequences that respects the local dominance property among three jobs is only two, not three. To prove this claim, we introduce the following technical lemma.

Lemma 1

Consider three jobs $i,j,k \in \mathcal {J}$ with $w_i>w_j$ and $i \prec _{\ell (t+p_k)} j$. The following expression holds

$$\begin{aligned} \nu _{jk}(t+p_i)&<\frac{w_k}{w_i}\left( \frac{w_jw_k+w_i^2-2w_iw_k}{w_iw_k}f(t+p_k+p_i+p_j)\right) \\&\quad -\,\frac{w_k}{w_i}\left( \frac{w_j-w_i}{w_i}f(t+p_k+p_j)-f(t+p_k+p_i)\right) . \end{aligned}$$

Proof

By case assumption $i \prec _{\ell (t+p_k)} j$, we have:

$$\begin{aligned} 0&<\nu _{ij}(t+p_k)-f(t+p_k+p_i)=\left( 1-\frac{w_j}{w_i}\right) f(t+p_k+p_i+p_j)\\&\quad +\,\frac{w_j}{w_i}f(t+p_k+p_j)-f(t+p_k+p_i)\\&=\frac{w_j w_i}{w_k(w_i-w_j)} \left( \frac{w_k(w_i-w_j)^2}{w_i^2 w_j}\right) f(t+p_k+p_i+p_j)\\&\quad +\,\frac{w_j w_i}{w_k(w_i-w_j)} \left( \frac{w_k(w_i-w_j)}{w_i^2}f(t+p_k+p_j)\right) \\&\quad -\,\frac{w_j w_i}{w_k(w_i-w_j)}\left( \frac{w_k(w_i-w_j)}{w_j w_i}f(t+p_k+p_i) \right) . \end{aligned}$$

The last equality follows from the assumption $w_i >w_j$. Thus, we have

$$\begin{aligned} 0&<\left( \frac{w_k(w_i-w_j)^2}{w_i^2 w_j}\right) f(t+p_k+p_i+p_j) +\,\frac{w_k(w_i-w_j)}{w_i^2}f(t+p_k+p_j) \nonumber \\&\quad -\,\frac{w_k(w_i-w_j)}{w_jw_i}f(t+p_k+p_i) \end{aligned}$$

(1)

We use the following equality

$$\begin{aligned} \frac{w_k(w_i-w_j)^2}{w_i^2 w_j}&=\left( \frac{w_k^2w_i^2-2w_k^2w_iw_j+w_k^2w_j^2+w_i^2w_jw_k-w_i^2w_jw_k}{w_i^2 w_j w_k}\right) \nonumber \\&=\left( \frac{w_k}{w_j}-\frac{2w_kw_i}{w_i^2}+\frac{w_kw_j}{w_i^2}+\frac{w_i^2}{w_i^2}-\frac{w_j}{w_j}\right) \nonumber \\&=\left( \frac{w_jw_k+w_i^2-2w_iw_k}{w_i^2}-\left( 1-\frac{w_k}{w_j}\right) \right) , \end{aligned}$$

(2)

replacing it in expression (1). Then, we obtain

$$\begin{aligned} 0&<\left( \frac{w_jw_k+w_i^2-2w_iw_k}{w_i^2}\right) f(t+p_k+p_i+p_j) -\,\left( 1-\frac{w_k}{w_j}\right) f(t+p_k+p_i+p_j) \nonumber \\&\quad +\,\frac{w_k(w_i-w_j)}{w_i^2}f(t+p_k+p_j)-\,\frac{w_k(w_i-w_j)}{w_jw_i}f(t+p_k+p_i) \nonumber \\&=\left( \frac{w_jw_k+w_i^2-2w_iw_k}{w_i^2}\right) f(t+p_k+p_i+p_j) -\,\left( 1-\frac{w_k}{w_j}\right) f(t+p_k+p_i+p_j) \nonumber \\&\quad +\,\frac{w_k(w_i-w_j)}{w_i^2}f(t+p_k+p_j)-\frac{w_k}{w_j}f(t+p_k+p_i) +\,\frac{w_k}{w_i}f(t+p_k+p_i) \end{aligned}$$

(3)

We reorder the terms of expression (3) and have

$$\begin{aligned}&\left( 1-\frac{w_k}{w_j}\right) f(t+p_k+p_i+p_j)+\frac{w_k}{w_j}f(t+p_k+p_i)\\&\quad =\nu _{jk}(t+p_i) \\&\quad <\left( \frac{w_jw_k+w_i^2-2w_iw_k}{w_i^2}\right) f(t+p_k+p_i+p_j) \\&\qquad +\,\frac{w_k(w_i-w_j)}{w_i^2}f(t+p_k+p_j)+\frac{w_k}{w_i}f(t+p_k+p_i) \\&\quad =\frac{w_k}{w_i}\left( \frac{w_jw_k+w_i^2-2w_iw_k}{w_iw_k}f(t+p_k+p_i+p_j)\right) \\&\qquad -\,\frac{w_k}{w_i}\left( \frac{w_j-w_i}{w_i}f(t+p_k+p_j)-f(t+p_k+p_i)\right) , \end{aligned}$$

concluding the proof. $\square$

We now prove that the number of sequences that respect the local dominance property among three jobs is only two.

Fig. 1

Exclusion relations among all possible sequences for three jobs i, j and k

Theorem 1

Fix the sequences with three comparable jobs i, j and k in some consecutive order, where $t_0$ and ${t_0}+(p_i+p_j+p_k)$ are the starting time and completion time of them, respectively. The number of sequences that respect the local precedence of jobs is two.

Proof

Without loss of generality, we adopt ${t_0}=0$. We know that the total of sequences induces by three comparable jobs is $3!=6$. We denote $S_1,S_2,S_3,S_4,S_5$ and $S_6$ the sequences ijk,ikj,jki,jik,kij and kji, respectively.

Note that for any jobs x and y are comparable, and therefore one of $x\prec _{\ell (t)}y$, $y\prec _{\ell (t)}x$ holds.

Let $\overleftrightarrow {b}$ and $\overleftrightarrow {e}$ be the exclusion relations between two sequences with the same pair of jobs ordered in inverse form at the beginning and the end, respectively. These two exclusions capture the fact that a single order is possible between two comparable jobs at the same point in time, e.g., $ijk\overleftrightarrow {b}jik$ as jobs i and j are ordered in inverse form at the beginning of the two sequences.

By using the exclusion relations, we have:

$$\begin{aligned}S_1 \overleftrightarrow {e} S_2 \overleftrightarrow {b} S_5 \overleftrightarrow {e} S_6 \overleftrightarrow {b} S_3 \overleftrightarrow {e} S_4 \overleftrightarrow {b} S_1\end{aligned}$$

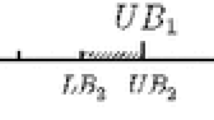
Therefore, the sequences that respect the exclusion relations can be partitioned in two sets, grouping in each set those sequences that do not maintain exclusion relationships among themselves (see Fig. 1):

$$\begin{aligned} \mathcal {A}=\{S_1,S_3,S_5\}\quad \text{ or }\quad \mathcal {B}=\{S_2,S_4,S_6\} \end{aligned}$$

In addition, we distinguish six priority weight orders among the jobs defined as follows:

$$\begin{aligned}o_1:\{w_i>w_j>w_k\} \quad o_2:\{w_k>w_i>w_j\}\\o_3:\{w_k>w_j>w_i\}\quad o_4:\{w_j>w_i>w_k\} \\o_5:\{w_i>w_k>w_j\} \quad o_6:\{w_j>w_k>w_i\}.\end{aligned}$$

Now, we prove by contradiction that only 2 of 3 sequences of each set respect the local precedence among the jobs. First, we consider the set $\mathcal {A}=\{S_1,S_3,S_5\}$ and $w_i>w_j$, which covers the order priority weights $o_1,o_2$ and $o_5$.

Formally, suppose the sequence $S_1,S_3$ and $S_5$ with $w_i>w_j$ respect the local precedence among the jobs. Then, we observe the job pairs with the same local precedence for two particular sequences (in bold font) and have:

• 1. $S_1=i{\textbf {jk}} \wedge S_{{3}}={\textbf {jk}}i$ imply $j \prec _{\ell (t)} k$ for $t=\{p_i,0\}$

• 2. $S_1={\textbf {ij}}k \wedge S_{{5}}=k{\textbf {ij}}$ imply $i \prec _{\ell (t)} j$ for $t=\{p_k,0\}$

• 3. $S_{{3}} =j{\textbf {ki}} \wedge S_{{5}}={\textbf {ki}}j$ imply $k \prec _{\ell (t)} i$ for $t=\{p_j,0\}$

In particular,

$$\begin{aligned} f(p_i+p_j)<&\nu _{jk}(p_i):=\left( 1-\frac{w_k}{w_j}\right) f(p_j+p_i+p_k) +\frac{w_k}{w_j}f(p_i+p_k) \end{aligned}$$

(4)

$$\begin{aligned} f(p_k+p_i)<&\nu _{ij}(p_k):=\left( 1-\frac{w_j}{w_i}\right) f(p_j+p_i+p_k)+\frac{w_j}{w_i}f(p_k+p_j) \end{aligned}$$

(5)

$$\begin{aligned} f(p_j+p_k)<&\nu _{ki}(p_j):=\left( 1-\frac{w_i}{w_k}\right) f(p_j+p_i+p_k)+\frac{w_i}{w_k}f(p_j+p_i) \end{aligned}$$

(6)

We use two of the three above inequalities. Without loss of generality, we consider Expressions (5) and (6). Thus, we have

$$\begin{aligned}&f(p_k+p_j)+f(p_i+p_k) \nonumber \\&\quad <\nu _{ij}(p_k)+\nu _{ki}(p_j) = \left( 1-\frac{w_j}{w_i}\right) f(p_i+p_j+p_k)\nonumber \\&\qquad +\,\left( 1-\frac{w_i}{w_k}\right) f(p_i+p_j+p_k)+\,\frac{w_j}{w_i}f(p_k+p_j) +\frac{w_i}{w_k}f(p_j+p_i) \nonumber \\&\quad = \left( 2-\frac{w_j}{w_i}-\frac{w_i}{w_k}\right) f(p_i+p_j+p_k)+\frac{w_j}{w_i}f(p_k+p_j)\nonumber \\&\qquad +\,\frac{w_i}{w_k}f(p_j+p_i) = \left( \frac{-w_jw_k-w_i^2+2w_iw_k}{w_iw_k}\right) f(p_i+p_j+p_k) \nonumber \\&\qquad +\,\frac{w_j}{w_i}f(p_k+p_j)+\frac{w_i}{w_k}f(p_j+p_i) \end{aligned}$$

(7)

We reorder the Expression (7) and have

$$\begin{aligned}&\left( \frac{w_jw_k+w_i^2-2w_iw_k}{w_iw_k}\right) f(p_k+p_i+p_j)+\,f(p_k+p_j)-\frac{w_j}{w_i}f(p_k+p_j){+}f(p_k{+}p_i)\nonumber \\&\quad <\frac{w_i}{w_k} f(p_j+p_i) . \end{aligned}$$

(8)

Finally, expression (8) is regrouped, obtaining

$$\begin{aligned}&\frac{w_k}{w_i}\left( \left( \frac{w_jw_k+w_i^2-2w_iw_k}{w_iw_k}\right) f(p_k+p_i+p_j)\right) \\&\qquad -\,\frac{w_k}{w_i}\left( \frac{w_j-w_i}{w_i}f(p_k+p_j)-f(p_k+p_i)\right) \\&\quad <f(p_j+p_i), \end{aligned}$$

where the left-term is greater than $\nu _{jk}(p_i)$ by Lemma 1. This implies that $k \prec _{\ell (p_i)} j$, which contradicts the case assumption given by Expression (4).

For the case $w_k>w_i$, which covers the order priority weights $o_2$, $o_3$ and $o_6$, the proof considers Expressions (4) and (6) in a similar way, which contradicts Expression (5). To end the analysis for the set $\mathcal {A}$, we have $w_j>w_k$ covering order priority weights $o_1$, $o_4$ and $o_6$. Here, the proof is also by contradiction. Expressions (4) and (5) contradict Expression (6). Thus, we have that the number of sequences that respect the local precedence of jobs is two.

Symmetrically, we prove the case when the set $\mathcal {B}=\{S_2,S_4,S_6\}$ is considered. Suppose $S_2,S_4$ and $S_6$ with respect to the local precedence among the jobs, then we have:

• 1. $S_2=i{\textbf {kj}} \wedge S_6={\textbf {kj}}i$ imply $k \prec _{\ell (t)} j$ for $t=\{p_i,0\}$.

• 2. $S_2={\textbf {ik}}j \wedge S_4=j{\textbf {ik}}$ imply $i \prec _{\ell (t)} k$ for $t=\{p_j,0\}$.

• 3. $S_4={\textbf {ji}}k \wedge S_6=k{\textbf {ji}}$ imply $j \prec _{\ell (t)} i$ for $t=\{p_k,0\}$.

In particular,

$$\begin{aligned} f(p_i+p_k)&<\nu _{kj}(p_i):=\left( 1-\frac{w_j}{w_k}\right) f(p_j+p_i+p_k)+\frac{w_j}{w_k}f(p_i+p_j) \end{aligned}$$

(9)

$$\begin{aligned} f(p_j+p_i)&<\nu _{ik}(p_j):=\left( 1-\frac{w_k}{w_i}\right) f(p_j+p_i+p_k)+\frac{w_k}{w_i}f(p_j+p_k) \end{aligned}$$

(10)

$$\begin{aligned} f(p_k+p_j)&<\nu _{ji}(p_k):=\left( 1-\frac{w_i}{w_j}\right) f(p_j+p_i+p_k)+\frac{w_i}{w_j}f(p_k+p_i) \end{aligned}$$

(11)

Here, we analyze the different cases. For the case where $w_i>w_k$, we have Expressions (10) and (11) that contradict Expression (9), covering the order priority weights $o_1$, $o_4$ and $o_5$. For the case $w_j>w_i$, we consider Expressions (11) and (9), which contradict Expression (10). This covers the order priority weights $o_3$, $o_4$ and $o_6$. Finally, the order priority weights $o_2$, $o_3$ and $o_5$ are covered by the case $w_k>w_j$. This uses Expressions (9) and (10), with respect to Expression (11). Thus, we also have that the number of sequences that respect the local precedence of jobs is two.

Therefore, only two of three sequences of set respect the local precedence among the jobs. Specifically, the pairs sequences are:

$$\begin{aligned}{} & {} \{S_1,S_3\} \quad \{S_1,S_5\} \quad \{S_3,S_5\} \quad \{S_2,S_4\} \quad \{S_2,S_6\} \\{} & {} \{S_4,S_6\} \quad \{S_1,S_6\} \quad \{S_2,S_3\} \quad \{S_4,S_5\}, \end{aligned}$$

which concludes the proof. $\square$

From Theorem 1, we obtain the following corollaries.

Corollary 1

Consider three jobs i, j, k consecutively executed. The local precedence property is satisfied at most for two pairs of jobs at any time into the interval $[t_0,t_0+p_i+p_j+p_k]$, $t_0\ge 0$.

Note that Corollary 1 is to be easily observed from the pairs sequences that respect the local precedence among the jobs defined by Theorem 1.

Corollary 2

The maximum number of three jobs consecutively executed at the end of a schedule that satisfies the local precedence property has an upper bounded equal to 2 ${n\atopwithdelims ()3}$.

Finally, Corollary 3 shows a new upper bound, which represents a drastic improvement over the n! different schedules of the search space.

Corollary 3

Given an algorithm, which uses some search tree procedure to solve the scheduling problem. The total number of leaves of the tree is upper bounded by $n!/3^{\lceil n/3 \rceil }$

Proof

The proof follows the observation from Theorem 1, which implies that the number of nodes in the third level of the tree is upper bounded by $2{n\atopwithdelims ()3}$ and for a multiplying argument, the total number of leaves of the tree is upper bounded by $n!/3^{\lceil n/3 \rceil }$. $\square$

3 Penalty functions where the problem becomes polynomially solvable

In this section, we study the penalty functions where the problem becomes polynomially solvable. We show that for any strictly convex penalty functions, an instance of n jobs with equal Smith ratios, i.e. $w_i/p_i$ equal to a constant for all job $i=1,\ldots ,n$, admits an optimal schedule where the jobs are ordered in non-increasing weight.

Theorem 2

Consider a strictly convex penalty function f(t) and two jobs $i,j \in \mathcal {J}$. If $w_i/p_i=w_j/p_j$ and $p_i > p_j$, then $i\prec _{\ell [0,\infty )}j$

Proof

Let A, B be two arbitrary job sequences. Suppose that $i, j \in \mathcal {J}$ are adjacent in an optimal schedule and let t be the largest completion time of the jobs in A. The claim states that the order i, j generates a cost strictly smaller than the order j, i, i.e.

$$\begin{aligned}&F(AjiB)>F(AijB)\\&\quad \equiv w_jf(t+p_j)+w_if(t+p_i+p_j)>w_if(t+p_i)+w_jf(t+p_i+p_j)\\&\quad \equiv (w_i-w_j)f(t+p_i+p_j)+w_jf(t+p_j)>w_if(t+p_i)\\&\quad \equiv \left( 1- \frac{w_j}{w_i}\right) f(t+p_i+p_j)+ \frac{w_j}{w_i}f(t+p_j)>f(t+p_i)\\&\quad \equiv \left( 1- \frac{p_j}{p_i}\right) f(t+p_i+p_j)+ \frac{p_j}{p_i}f(t+p_j)>f(t+p_i)\\&\quad \equiv \nu _{ij}(t)>f(t+p_i), \end{aligned}$$

which holds for $p_i>p_j$ and f strictly convex for all $t\in [0,\infty )$. $\square$

From Theorem 2, we obtain the following statement.

Corollary 4

Consider a strictly convex penalty function f(t) and jobs with equal Smith ratio, i.e $w_i/p_i$ equal to a constant for all job $i=1,\dots , n$. This problem admits an optimal schedule where the jobs are ordered in non-increasing weight.

Note that Corollary 4 applies to the problem of minimizing the sum of weighted mean squared deviation of the completion times with respect to a common due date, where the penalty function is strictly convex.

4 Future research

Based on our results, we provide some insights into three future research directions. First, we observe that a reduction of the number of steps $O(n2^n)$ required by an exact exponential algorithm for the non-preemptive single-machine scheduling problem [see Theorem 3.1 in Fomin and Kratsch (2010)] could be possible by using Corollary 1. In particular, we leave open the question about the use of this result in the recursive form of algorithm cost described in Fomin and Kratsch (2010) for sets of three jobs, which can be reduced to $2{n\atopwithdelims ()3}$ from $3{n\atopwithdelims ()3}$.

Second, we note that the dominance properties introduced in this work can be translated to valid inequalities, which can be used in a mathematical formulation to speed up implicit enumeration methods such as branch-and-cut algorithm by iteratively strengthening its linear relaxation [see Bansal et al. (2017), Pereira and Vásquez (2017), Díaz-Núñez et al. (2018) for models and implementation examples].

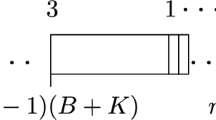
Third, we present an idea to show the computational complexity of the problem of minimizing the sum of weighted mean squared deviation of the completion times with respect to a common due date, whose status is open for jobs with arbitrary weights, in the sense that neither polynomial time algorithms nor NP-hardness proofs are known (Vásquez, 2014). This follows previous NP-hardness proofs for the scheduling problem with some convex and concave penalty functions, which had involved almost equal Smith ratio instances [see Jinjiang (1992); Vásquez (2014) for example]. Specifically, we are focused on the definition of a particular instance based on dominance properties, which allows us to reduce the search space and restrict the cases to be analyzed. Formally, we define an instance $\mathcal {I}^C$ as follows: Consider the strictly convex penalty function $f(t):=(t-d)^2$ with due date $d \in \mathbb {N}^+$ and a set $\mathcal {J}$ with $2n+1$ jobs where $\mathcal {B} \subseteq \mathcal {J}$ with $\mathcal {B}=\{1,\ldots ,2n\}$ with equal Smith ratios and $p_{i}<p_{i+1}$ for $i=1,\ldots , 2n-1$ and a job $k=2n+1$ with $w_k>p_k$, $p_k \ge \max _{i \in \mathcal {B}} p_i$, and $\sqrt{w_k \min _{i\in \mathcal {B}}p_i} \ge p_k$. By considering the global properties from Corollary 1 in Pereira and Vásquez (2017) and Theorem 1 in Bansal et al. (2017), and Theorem 1, in the optimal solution of these instances $\mathcal {I}^C$, the completion time of job k belongs to the interval $(d-p_k-\min _{i\in \mathcal {B}}p_i, d+\min _{i\in \mathcal {B}}p_i)$, all jobs preceding k are scheduled in a non-decreasing processing time, and all jobs following k are scheduled in a non-increasing processing time.

Based on Theorem 2, we focus on the necessary condition so that the problem does not become easy given by the sequence of three jobs that respect the local precedence among them, which is defined as follows: the job k and two jobs $i'+1$ and $i' (p_{i'}<p_{i'+1})$, which are immediately executed before and after job k, respectively. Given the above sequence, we consider Theorem 1 and have that at most one of these job sequences defined by (a) $i',k,i'+1$, (b) $k,i'+1,i^\prime$, or (c) $i^\prime +1,i^\prime ,k$, respects the local precedence among them. We consider the case (a) $i', k, i'+1$ in order to have a partition among the jobs with equal Smith ratio, excluding the sequence (b) by choosing sequence (c), and vice-versa based on Corollary 1. This result allows us to investigate systematically the configuration of an optimal solution of instances $\mathcal {I}^C$ focused on these cases (see Fig. 2). Numerical experiments show that the resolution might depend on where the jobs lie in the schedule and also on the value of due date d.

Fig. 2

Graphical representation of instance $\mathcal {I}^C$