For the airplane refueling problem local precedence implies global precedence

Abstract

We are given $n$ airplanes, which can refuel one another during the flight. Each airplane has a specific tank volume and gas consumption rate. The goal of the airplane refueling problem is to find a drop out permutation for the planes that maximizes the distance traveled by the last plane to drop out. This paper studies some structural properties of the problem and proposes pruning rules for an exact resolution.

1 Introduction

The Airplane refueling problem is motivated by George Gamow and Marvin Stern in the aeronautica chapter of the book “Puzzle-Math” [6]. They describe the problem as follows:

“Well, here’s another problem which may interest you fellows”, said another pilot.

“Suppose you have to deliver a bomb in some distant point of the globe, the distance being much greater than the range of the plane you are going to use. Thus, you have to use the technique of refueling in the air. Starting with several identical planes which refuel one another, and gradually drop out of the flight until the single plane carrying the bomb reaches the target, how would you plan the refueling program, and how many planes will you need to carry out the operation? We will assume for simplicity that airplane fuel consumption can be measured in miles per gallon and is independent of load.”

“Oh, just tell us,” said one of the pilots. “We are all too tired to work out these problems”.

On a Dagstuhl scheduling workshop in 2010, Woeginger [20] presented a generalization of this problem and proposed the following mathematical formulation: we are given $n$ airplanes. Each airplane $j$ has a full reservoir of capacity $w_j$ liters and consumption rate of $p_j$ liters per kilometer. At time zero, the airplanes fly at the same speed in the same straight direction, and can freely redistribute the fuel between their reservoirs. As soon as one airplane runs out of fuel, it is dropping out of the flight, and the goal is to reach a maximal distance with the last plane in the air.

A solution is completely described by a drop out ordering $\sigma$ as follows. Initially all planes leave the origin with total fuel $\sum w_j$ and with total consumption rate $\sum p_j$. We assume without loss of generality that all airplanes first fully use the tank of one of the airplanes, then fully use a second tank, and so on. As a consequence, the first time airplane $\sigma (1)$ can drop out is the time $t$ such that $w_{\sigma (1)} = t/\sum p_j$, since by the limited capacity of the other planes it is impossible to empty his reservoir earlier. Also it does not make sense to drop out $\sigma (1)$ later, because it will consume fuel which will be missed later on. Therefore the objective value of the drop out order $\sigma$ is

$$\begin{aligned} \sum _{j=1}^n\left( w_{\sigma (j)}\big /\sum _{k=j}^n p_{\sigma (k)}\right) . \end{aligned}$$

Phrased as a scheduling setting, the problem is equivalent to finding a permutation $\pi$ (the reverse of $\sigma$), which maximizes

$$\begin{aligned} \sum _{j=1}^n \left( w_{\pi (j)} \big / \sum _{k=1}^j p_{\pi (k)}\right) = \sum _{j=1}^n w_j/C_j, \end{aligned}$$

where $C_j$ is the completion time of job $j$, $p_j$ its processing time and $w_j$ its weight.

The problem is known to be easy for agreeable instances, i.e. whenever $w_i> w_j$ implies $p_i\le p_j$, while the computational complexity for general instances is open. Recently, Wiebke Höhn on a Dagstuhl scheduling workshop in 2013 [8], used this problem to motivate the study of a larger class of scheduling problems with the goal of minimizing $\sum w_j f(C_j)$ for some given concave and increasing monotone penalty function. For example the function $f(t)= -1/t, t\in \mathbb R^+$ models precisely the Airplane refueling problem.

For most problems of this form the complexity status is open (see [19]), except two special cases. The first case is the penalty function $f(t)=t$ where scheduling jobs in order of decreasing Smith ratio $w_j/p_j$ leads to the optimal schedule, as has been found out 60 years ago [16]. The another special case is the penalty function $f:t \mapsto 1-e^{-rt}$ for a constant $r$, which was considered by Rothkopf [13] in the context of minimizing total flow time, with continuously discounted linear waiting costs. Here a schedule is optimal if and only if it sequences jobs in order of non-increasing order of $\frac{r w_j e^{-r p_j}}{1-e^{-r p_j}}$.

In absence of a polynomial algorithm for an optimal resolution of the Airplane refueling problem, two approaches could be considered: approximation algorithm and branch and bound methods. In literature, approximation algorithms have been proposed for the more general problem $1||\sum f(C_j)$. Epstein et al. [5] provided a $4+\epsilon$ approximation algorithm for the setting where $f$ is an arbitrary increasing differentiable penalty function chosen by the adversary after the schedule has been produced. A polynomial time approximation scheme has been provided by Megow and Verschae [11] for general monotone penalty functions $f$, whereas Höhn and Jacobs [10] derived a method to compute the tight approximation factor of the Smith-ratio-schedule for any particular monotone increasing convex or concave cost function.

For branch-and-bound algorithms pruning rules were proposed which reduce the number of nodes in the search graph, having a direct effect on the running time. For example, if we knew, that without loss of generality in an optimal schedule, job $i$ is never scheduled after job $j$ then we could eliminate roughly half of the potential orderings, and reduce the number of explored nodes.

2 Pruning rules

Formally, we distinguish two kind of properties.

• We say that jobs $i,j$ satisfy local precedence at time $t$—denoted $i\prec _{\ell (t)} j$—if whenever in a schedule $S$ job $j$ starts at time $t$ and is followed immediately by job $i$ then $S$ is not optimal.

• We say that jobs $i,j$ satisfy global precedence in the time interval $[a,b]$—denoted by $i\prec _{g[a,b]} j$—if whenever in a schedule $S$ we have $a\le C_j-p_j \le C_i-p_i-p_j\le b$, then $S$ is sub-optimal, no matter if $i,j$ are adjacent or not.

We use the notation $i\prec _g j$ as a shorthand for $i\prec _{g[0,\infty )} j$. In addition $i\prec _{\ell [a,b]}j$ means $i\prec _{\ell (t)} j$ for all $t\in [a,b]$, and $i\prec _{\ell } j$ stands for $i\prec _{\ell [0,\infty )} j$.

3 Related work

An extensive literature have been devoted to finding stronger dominance property, which are weaker conditions on the job characteristics that would still imply $i\prec _g j$. Mainly, the branch-and-bound approaches with pruning rules implying order properties have been focused on the quadratic penalty function $f(t):=t^2$ (see [1–3, 9, 12, 15, 17, 18]).

Recently, Dürr and Vásquez [4] provided new rules and generalized existing ones for a general penalty function $f(t):=t^\beta ,\beta >0$. An extensive experimental study analyzed the effect of these rules to the performance of the branch-and-prune search.

For the Airplane refueling problem, we distinguish the following known rules:

• Sen–Dileepan–Ruparel [15] for any increasing penalty function $f(t)$, if $w_i>w_j$ and $p_i\le p_j$, then $i\prec _g j$.

• Dürr-Vásquez [4] for any increasing concave penalty function $f(t)$, if $w_i<w_j$ and $w_i/w_j\ge p_i/p_j$, then $i\prec _g j$.

In addition to the above rules found in the literature, Dürr and Vásquez [4] stated the conjecture local precedence implies global precedence for the scheduling problems with a penalty function $f(t):=t^\beta ,\beta >0$. Formally, the conjecture was stated as follows.

Conjecture 1

(Dürr and Vásquez [4]) Consider a penalty function $f(t):=t^\beta$ and fix an arbitrary constant $\beta >0$. Then for all jobs $i,j$, $i\prec _\ell j$ implies $i\prec _g j$.

The conjecture was based on the statement that for any increasing penalty function $f(t)$ and $i\prec _{\ell [a,b]} j$, if $p_i \le p_j$ then $i\prec _{g[a,b]}j$ (Theorem 1 in [4]) and the numerous instances of tests where the conjecture was verified. In addition, the same authors gave a proof for the case $\beta =2$ and showed that the stronger implication $i\prec _{\ell [a,b]} j \Rightarrow i\prec _{g[a,b]}j$ does not hold with a counterexample.

In this paper, we show the above stronger implication for the Airplane refueling problem and provide an experimental evaluation of their impact on an exact brute force resolution.

4 Preliminaries

We consider the problem of minimizing $\sum w_j f(C_j)$ for the penalty function $f(t)= -1/t, t\in \mathbb R^+$, which models the Airplane refueling problem. Following the approach proposed in [4], we introduce two functions, $F(S)$ the cost of schedule $S$ and the following function, parameterized by jobs $i,j$ and depending on $t\in \mathbb R^+$,

$$\begin{aligned} \phi _{ij}(t)=\frac{f(t+p_i+p_j)-f(t+p_j)}{f(t+p_i+p_j)-f(t+p_i)}=&\frac{\frac{1}{t+p_j}-\frac{1}{t+p_i+p_j}}{\frac{1}{t+p_i}-\frac{1}{t+p_i+p_j}}\\ =&\frac{p_i}{p_j} \cdot \frac{(t+p_i)(t+p_i+p_j)}{(t+p_j)(t+p_i+p_j)}\\ =&\frac{p_i}{p_j} \cdot \frac{t+p_i}{t+p_j}. \end{aligned}$$

Note that $\phi _{ij}(t)$ is well defined since the durations $p_i,p_j$ are non-zero. By definition we have the following equivalence.

$$\begin{aligned} i \prec _{\ell (t)} j\,\Leftrightarrow \,\phi _{ij}(t) < \frac{w_i}{w_j}. \end{aligned}$$

We start by analyzing properties of $\phi _{ij}(t)$.

Lemma 1

For any jobs $i,j$, we have

$$\begin{aligned} \lim _{t \rightarrow \infty } \phi _{ij}(t) = p_i/p_j. \end{aligned}$$

Proof

$$\begin{aligned} \lim _{t \rightarrow \infty }\phi _{ij}(t)=\lim _{t \rightarrow \infty }\frac{p_i}{p_j}\frac{t+p_i}{t+p_j}=\frac{p_i}{p_j}\lim _{t \rightarrow \infty }\frac{1+p_i/t}{1+p_j/t}=\frac{p_i}{p_j}. \end{aligned}$$

$\square$

Lemma 2

If $p_i\ne p_j$ then $\phi _{ij}(t)$ is strictly monotone and bounded, in particular:

• If $p_i>p_j$, then $\phi _{ij}(t)$ is strictly decreasing, convex and $\phi _{ij}(t) \in \left( \frac{p_i}{p_j},\left( \frac{p_i}{p_j}\right) ^2\right]$.

• If $p_i<p_j$, then $\phi _{ij}(t)$ is strictly increasing, concave and $\phi _{ij}(t) \in \left[ \left( \frac{p_i}{p_j}\right) ^2,\frac{p_i}{p_j}\right)$.

Proof

To prove the monotonicity of $\phi _{ij}(t)$, we use its first and second derivative

$$\begin{aligned} \phi _{ij}'(t)= \frac{p_i}{p_j}\frac{p_j-p_i}{(t+p_j)^2}, \phi _{ij}''(t)= -2\frac{p_i}{p_j}\frac{p_j-p_i}{(t+p_j)^3}. \end{aligned}$$

Clearly, the function $\phi _{ij} (t)$ is strictly decreasing and convex when $p_i>p_j$ and strictly increasing and concave when $p_j>p_i$.

To bound the function $\phi _{ij}(t)$, we analyze its codomain. Since $\phi _{ij} (t)$ is strictly monotone, it is suffices to evaluate its extreme points. At $t=0$, we have $\phi _{ij}(0)=\left( \frac{p_i}{p_j}\right) ^2$, whereas the limit of $\phi _{ij}(t)$ when $t$ tends to infinity is $\frac{p_i}{p_j}$ by Lemma 1. $\square$

Lemma 3

Fix two jobs $i$ and $j$. If there exists $t^*\in \mathbb R^+$ such that

$$\begin{aligned} \frac{w_i}{w_j}=\phi _{ij}(t^*), \end{aligned}$$

then $t^*$ is unique and equal to

$$\begin{aligned} \frac{w_j p_i^2-w_ip_j^2}{w_ip_j-w_jp_i} \end{aligned}$$

Proof

We assume that there exists $t^*\in \mathbb R^+$ such that $w_i/w_j=\phi _{ij}(t^*).$ The strict monotonicity of $\phi _{ij}(t)$ by Lemma 2 implies uniqueness of $t^*$. We have

$$\begin{aligned} \frac{w_i}{w_j}=\phi _{ij}(t^*)=\frac{p_i}{p_j}\cdot \frac{t^*+p_i}{t^*+p_j}, \end{aligned}$$

and arranging the above expression, we obtain

$$\begin{aligned} t^*=\frac{w_j p_i^2-w_ip_j^2}{w_ip_j-w_jp_i} \end{aligned}$$

$\square$

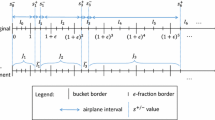
See Fig. 1 for an illustration of the claimed properties.

Fig. 1

Function $\phi _{ij}(t)$ in case $p_i>p_j$ (left) and case $p_i<p_j$ (right)

5 Main result

In 2014, Dürr and Vásquez [4] have stated the conjecture local precedence implies global precedence for the scheduling problem with a penalty function $f(t):=t^\beta ,\beta >0$. They proved it for the case $\beta =2$ and showed that the stronger implication $i\prec _{\ell [a,b]} j \Rightarrow i\prec _{g[a,b]} j$ does not hold with a counterexample.

The main result of our paper is to prove the above stronger implication for the Airplane refueling problem, which is stated formally as follows.

Theorem 1

For all jobs $i,j$ and time points $a,b$ the property $i\prec _{\ell [a,b]} j$ implies $i\prec _{g[a,b]} j$.

Proof

Rule 1 in [4] covered the case $p_i\le p_j$ and then, the remainder of the proof is to show the statement for the case $p_i>p_j$.

We consider time points $a,b$ and an arbitrary instance $I$ containing jobs $i,j$. Assume that there is an optimal schedule $S:=AjBiD$ for some job sequences $A,B,D$. Let $a$ be the total length of $A$ and $b$ be the total length of $AB$. Then we have $a = C_j-p_j \le C_i-p_i -p_j = b$ where $C_i,C_j$ are the respective completion times in $S$. We show that exchanging the jobs $i$ and $j$ decreases the cost of the schedule, contradicting optimality.

For this purpose, we will show

$$\begin{aligned} 0<F(ABjiD)-F(ABijD)<F(AjBiD)-F(AiBjD), \end{aligned}$$

where the former inequality follows from local precedence assumption $i\prec _{\ell (a)}j$, hence to conclude the proof it suffices to show

$$\begin{aligned} F(ABjiD)-F(AjBiD)<F(ABijD)-F(AiBjD). \end{aligned}$$

For every job $k\in B$ we denote by $t_k$ the completion time of $k$ in the schedule $ABijD$ and consider the following inequality by optimality assumption of $AjBiD$

$$\begin{aligned} 0<F(ABjiD)-F(AjBiD)&=\frac{w_j}{a+p_j}+\sum _{k \in B} \frac{w_k}{t_k+p_j}-\frac{w_j}{b+p_j}-\sum _{k\in B} \frac{w_k}{t_k} \nonumber \\&=\frac{w_j (b-a)}{(a+p_j)(b+p_j)}-\sum _{k\in B}\frac{w_k p_j}{(t_k+p_j)t_k} \end{aligned}$$

(1)

We consider the Lemma 2 which implies

$$\begin{aligned} \left( \frac{p_i}{p_j}\right) ^2 \ge \max _{t \in [a,b]}\phi _{ij}(t) \end{aligned}$$

and the locality assumption

$$\begin{aligned} \frac{w_i}{w_j} >\max _{t \in [a,b]}\phi _{ij}(t). \end{aligned}$$

Thus, we have

$$\begin{aligned} (1)<&\frac{w_i}{w_j} \left( \frac{p_i}{p_j}\right) ^2 \phi _{ji}(a)\phi _{ji}(b) \left( \frac{w_j (b-a)}{(a+p_j)(b+p_j)}-\sum _{k\in B}\frac{w_k p_j}{(t_k+p_j)t_k}\right) \nonumber \\ =&\frac{w_i (b-a)}{(a+p_i)(b+p_i)}-\frac{w_i}{w_j}\left( \frac{p_i}{p_j}\right) ^2 \phi _{ji}(a)\phi _{ji}(b) \left( \sum _{k\in B}\frac{w_k p_j}{(t_k+p_j)t_k}\right) \nonumber \\ =&\frac{w_i (b-a)}{(a+p_i)(b+p_i)}-\frac{w_i}{w_j}\phi _{ji}(a)\phi _{ji}(b) \left( \sum _{k\in B}\frac{w_k p_i}{(t_k+p_i)t_k}\phi _{ij}(t_k)\right) \end{aligned}$$

(2)

Now, we consider the from strict monotonicity of $\phi _{ij}(t)$ implied by Lemma 2 when $p_i>p_j$, therefore

$$\begin{aligned} \min _{t \in [a,b]}\phi _{ij}(t)=\phi _{ij}(b)=\frac{1}{\phi _{ji}(b)}, \end{aligned}$$

and

$$\begin{aligned} (2)&< \frac{w_i (b-a)}{(a+p_i)(b+p_i)}-\frac{w_i}{w_j}\phi _{ji}(a)\phi _{ji}(b) \min _{t \in [a,b]}\phi _{ij}(t) \left( \sum _{k\in B}\frac{w_k p_i}{(t_k+p_i)t_k}\right) \nonumber \\&= \frac{w_i (b-a)}{(a+p_i)(b+p_i)}-\frac{w_i}{w_j}\phi _{ji}(a)\phi _{ji}(b) \phi _{ij}(b) \left( \sum _{k\in B}\frac{w_k p_i}{(t_k+p_i)t_k}\right) \nonumber \\&= \frac{w_i (b-a)}{(a+p_i)(b+p_i)}-\frac{w_i}{w_j}\phi _{ji}(a) \left( \sum _{k\in B}\frac{w_k p_i}{(t_k+p_i)t_k}\right) \end{aligned}$$

(3)

Finally, we use the locality assumption $w_i/w_j>\phi _{ij}(a)$, which implies

$$\begin{aligned} \frac{w_i}{w_j}\phi _{ji}(a)>1 \end{aligned}$$

and obtain

$$\begin{aligned} (3)&< \frac{w_i (b-a)}{(a+p_i)(b+p_i)}-\sum _{k\in B}\frac{w_k p_i}{(t_k+p_i)t_k}\\&= \frac{w_i}{a+p_i}-\frac{w_i}{b+p_i}+\sum _{k\in B}\frac{w_k}{t_k+p_i}-\sum _{k\in B}\frac{w_k}{t_k}\\&= \frac{w_i}{a+p_i}+\sum _{k\in B}\frac{w_k}{t_k+p_i}-\sum _{k\in B}\frac{w_k}{t_k}-\frac{w_i}{b+p_i} \\&= F(ABijD)-F(AiBjD). \end{aligned}$$

Therefore, we have

$$\begin{aligned} F(ABjiD)-F(AjBiD)<F(ABijD)-F(AiBjD), \end{aligned}$$

concluding the proof. $\square$

Finally, we refine the above statement using the $\phi _{ij}$ properties and obtain the following precedence rules.

Corollary 1

(Our rules) For any two jobs $i,j$ with $w_i>w_j$:

Figure 2 illustrates the contribution of our rules.

Fig. 2

Job $j$ compared to a fixed job $i$. Labels of particular functions: a $w_j=w_i (p_i/p_j)^2$, b $w_j=p_j w_i/p_i$

6 Experimental study

In the absence of a polynomial time algorithm we solve the problem using the algorithm A*, which uses the following shortest path modelization [7]. This approach was initiated by [14] and developed further in [4, 9] for a related scheduling problem.

Formally, we model of scheduling problem as a directed acyclic graph consisting of all subsets $S\subseteq \{1,\ldots ,n\}$. In this graph for every vertex $S$ there is an arc to $S\backslash \{j\}$ for any $j\in S$. It is labeled with $j$, and has cost $w_j t^\beta$ for $t=\sum _{i\in S} p_i$. Every directed path from the root $\{1,\ldots ,n\}$ to $\{\}$ corresponds to a schedule with an objective value being the total arc cost and so the goal is to compute the shortest path distance between these vertices.

We use the algorithm A* for the above purpose, which explores the graph using a priority queue containing arcs pointing to vertices that still need to be visited. An arc $(S',S)$ has a weight corresponding to the distance from the root to $S$ through this arc plus a basic lower bound of the optimum cost. In our case, we choose to be simply $\sum _{j\in S} w_j p_j^\beta$.

In essence the algorithm A* applied to our problem use the local and global precedence relations as follows. Let $S$ be a vertex and $j\in S$ a job such that there is a shortest path from the source to $S$ where $S\backslash \{j\}$ is the predecessor of $S$ on this path. Then we prune the arc from $S$ to $S\cup \{i\}$ in the graph if $i\prec _{\ell (t)} j$ for $t$ being total processing time in $S\backslash \{j\}$. This modification preserves the validity of the graph modelization, since there by definition of the relation $\prec _{\ell (t)}$ there is no shortest path using this arc.

In addition we remove an arc from $S$ to $S\cup \{j\}$, if there is a vertex $k\not \in S$ with $k\ne j$ and $k\prec _{g[t_0,t_1]} j$, where $t_0$ is the total processing time of $A$ while $t_1$ is the total processing time over all jobs different from $j,k$. This modification is again valid, as any shortest path from the source to the target using that arc will correspond to a schedule where $j$ is scheduled before $k$, violating the global precedence relation $k\prec _{g[t_0,t_1]} j$.

6.1 Data sets

We implemented the algorithm described above to measure the impact of the prunning rules, and tested it against randomly generated instances. We adopt the model of random instances described by Dürr and Vásquez [4]. The processing time was generated uniformly between $1$ and $100$, whereas the Smith-ratio of the jobs was chosen according to distribution $2^{N(0,\sigma ^2 )}$, where $N(0,\sigma ^2)$ is the normal distribution of mean $0$ and standard deviation $\sigma$. This model is based on that $i\prec _g j$ of our rule can be approximated when $p_j/p_i$ tends to infinity by the relation $w_i/p_i \ge 2 w_j/p_j$. Thus, the $\sigma$ value permitted to tune the hardness of the instances, as for small $\sigma$, jobs tend to have similar Smith-ratios. In our experiments, we generated a data set, which contains 25 instances of 60 jobs each per $\sigma$ value from $\{0.1, 0.2, \ldots , 1\}$.

6.2 Results

In the above described graph modelization vertices correspond to prefixes of schedules, i.e a backward approach. An alternative forward approach would have been to construct schedules from the end, where vertices would correspond to suffixes of schedules. We implemented both approaches as well, and run the experiments on the first data set. We have that the forward alternative approach generated a smaller number of nodes in the search tree as is shown in Fig. 3. We believe that the reason of the forward approach dominance is that the early jobs of a schedule contribute with a higher value to the objective than the later jobs, and therefore it is more important to determine the prefix of an optimal schedule than the suffix.

Fig. 3

Proportion of instances for which the forward variant generated less nodes than the backward variant. The values are plotted as function of $\sigma$, both for the resolution with our new rules and without

In order to run the experiments in a reasonable time, we stopped the algorithm after a timeout of a million generated nodes. Every instance was solved twice, with and without the precedence rules provided by this paper. Without our rules, we considered the Sen–Dileepan–Ruparel and Dürr–Vásquez. Our experiments showed that with our rules, instances of up to 60 jobs can be solved within the selected timeout, while without our rules some instances with 60 jobs are not solved, see Fig. 4.

Fig. 4

Fraction of instances solved within the timeout limit of a million nodes as function of the number of jobs per instance, when the algorithm is run with or without the rules of this paper

We measure the influence on the number of nodes generated during a resolution when our rules are used. From Fig. 3, we fixed the forward direction for both cases without and with our rules, and excluded instances where the timeout was reached without the use of our rules. Figure 5 shows the ratio between the average number of generated nodes when the algorithm is run with and without our rules.

Fig. 5

Average improvement factor as function of $\sigma$

From Fig. 5, we observe that the the improvement factor trend is increasing in $\sigma$. Note that this improvement ratio is a pessimistic measurement, since we average only over instances which could be solved within the time limit, so in the statistics we filtered out the really hard instances.

Furthermore we measured the behavior of our algorithm in terms of number of nodes for a $\sigma$ fixed, exposing an expected running time which directly depends on the $\sigma$ value. Results are depicted in Fig. 6.

Fig. 6

Average number of nodes generated for solving random instances, as a function of $\sigma$