1 Introduction

Statistical process control (SPC) charts can be used to assure the quality of a product or process in the manufacturing industry or service industry. Statistical process control charts are primarily used to monitor a production process or service process and detect process shifts as soon as possible. Based on our understanding, the reliability and quality of a product are highly interrelated. Reliability means quality over time. A high-quality product will regularly be of high reliability. Practically, the higher the level of quality, the greater the product will be reliable. Control charts are very useful tools to improve productivity and product quality. Shewhart (1931) first introduced the Shewhart control chart to detect relatively large shifts in the process mean (\(\ge 1.5\sigma\)). Page first introduced the cumulative sum (CUSUM) control chart in (1954). The EWMA control chart was introduced by Roberts (1959). The EWMA technique gives the weighted averages of past observations with more weight to recent observations and less weight to past observations. Roberts used simulation to evaluate its properties and revealed that the EWMA control chart is more sensitive to detect small shifts in the process mean. The EWMA control chart has found wide application in the manufacturing industries. The CUSUM and EWMA control charts accumulate information over time to detect small shifts in the process mean. These two control charts are well-known memory-type control charts as they use past information to set up the control charts. The Shewhart control chart, CUSUM control chart, and EWMA control chart are three of the most widely used process control charts. It has been observed that the CUSUM and EWMA control charts surpass the Shewhart control charts to detect small shifts in the process mean (Crowder, 1987; Hunter, 1986; Lucas & Saccucci, 1990; Ng & Case, 1989; Woodall, 1997). The adaptive EWMA (AEWMA) control chart which combines an EWMA and a Shewhart chart is introduced by Capizzi and Masarotto (2003). The AEWMA is very powerful to detect both large and small process shifts. For more details about the EWMA control charts, the reader is referred to the works of Liu and Xue (2015) and Mitra et al. (2019).

The double EWMA (DEWMA) control chart was first introduced by Shamma and Shamma (1992). The triple EWMA (TEWMA) control chart was introduced by Alevizakos et al. (2021). Haq (2012) introduced a new hybrid exponentially weighted moving average (HEWMA) control chart for monitoring the process mean shifts. The result shows that the TEWMA control chart is better than the EWMA control chart and the DEWMA control chart for detecting small shifts in the process mean. The DEWMA control chart is better than the EWMA control chart for detecting small shifts in the process mean. The quadruple exponentially weighted moving average (QEWMA) control chart was introduced by Alevizakos et al. (). The result shows that the (QEWMA) is better than the EWMA control chart, DEWMA control chart, and the TEWMA control chart for detecting small shifts in the process mean.

Sheu and Lin (2003) used the concept of Sheu and Griffith (1996) and Sheu (1988) to extend the EWMA control chart to the GWMA control chart for monitoring the small process mean shifts of independent observations. Their results indicated that the GWMA control chart is more sensitive than the EWMA control chart for detecting process mean shifts of independent observations. Yang and Sheu (2007) showed that the GWMA median control chart surpasses the corresponding EWMA median control chart. Sheu and Chiu (2007) indicated that the GWMA c control chart surpasses the corresponding Shewhart and EWMA c control charts for detecting small shifts in the process mean. Sukparungsee (2018) proposed the GWMA p control chart and showed that it surpasses the corresponding EWMA p control chart for detecting small shifts in the process mean.

The originated GWMA control chart has been further extended to the double GWMA (DGWMA) control chart by Sheu and Hsieh (2008). The DGWMA control chart outperforms GWMA control charts and double exponentially weighted moving average (DEWMA) control charts for detecting small shifts in the process mean. For more details about the double GWMA control charts, the reader is referred to the works of Alevizakos et al. (2018), Karakani et al. (2018), Alevizakos et al. (2022a, 2022b) and Chatterjee et al. (2023).

Sheu and Tai (2006) first introduced the GWMA \({S}^{2}\) control chart to monitor process variability and indicated that the GWMA control chart is more sensitive than the EWMA control chart to detect the variance of process. Yang and Sheu (2006) introduced the multivariate generally weighted moving average (MGWMA) control chart which is the extended version of the multivariate exponentially weighted moving average (MEWMA) control chart. Yang and Sheu (2006) showed that integrating a multivariate engineering process control (MEPC) with multivariate generally weighted moving average (MGWMA) control chart is more sensitive than the MEPC with MEWMA control chart to detect the small shifts of the mean vector. Sheu et al. (2013) proposed the maximum GWMA (Max GWMA) control chart to simultaneously detect both increases and decreases in the mean and/or variance of a process. Mabude et al. (2020a, 2020b, 2020c) provided an overview and perspectives of the GWMA control charts. For more details about the GWMA control charts, the reader is referred to the works of Ali and Haq. (2017), Alevizakos and Koukouvinos (2019), Chen et al. (2019), Mabude et al. (2020a, 2020b, 2020c), Haq and Abidin (2020), Mabude et al. (2020a, 2020b, 2020c), Chatterjee et al. (2021), Li et al. (2021) and Mabude et al. (2022).

A fundamental assumption in the traditional application of statistical process control (SPC) is that the observations are independent (uncorrelated). In practical application, the independence assumption is often violated in the continuous manufacturing process for the chemical and pharmaceutical industries. The autocorrelation has a great influence on the control charts. Ignoring autocorrelation, the effect of constructing a control chart for the autocorrelated observations is that it produces control limits that are much tightened than desired. Hence, this decreases the ability of detecting the process mean shifts and generates a high false alarm rate.

We can use two different approaches to solve the problem for detecting the process mean shifts of autocorrelated observations. Firstly, the model-free approach, it uses the classical standard control charts, and adjusts the control limits to take account of the autocorrelation, and estimate the true process variance (see e.g., Vasilopoulos & Stamboulis, 1978; Schmid, 1995, 1997; Schmid & Schore, 1997; VanBrackle & Reynolds, 1997). Secondly, the model-based approach, applies an appropriate time series model to fit the autocorrelated observations so that forecasts of each observation can be made using the previous observations. Hence, we can get the residuals and then use the traditional control charts for the residuals (see e.g., Alwan & Roberts, 1988; Montgomery & Mastrangelo, 1991; Harris & Ross, 1991; Mastrangelo & Montgomery, 1995; Lu & Reynolds, 1999a, 1999b; Koehler et al., 2001; MacCarthy & Wasusri, 2001).

The work that has been published on residual control charts indicates that the EWMA control chart of residuals will usually offer better performance than the Shewhart control chart of residuals. Lu and Reynolds (1999a, 1999b) considered the performance of the EWMA control chart of the residuals and an EWMA control chart of the observations for monitoring processes that produce autocorrelated data. Sheu and Lu (2008, 2009a, 2009b) and Lu (2016) introduced GWMA control charts for monitoring autocorrelation data and showed that the GWMA control chart is more sensitive than the EWMA control chart for detecting small shifts in the process mean of autocorrelation data. Since 2003, the year of publication of the GWMA control chart paper, there have been a total of 183 publications on the GWMA-related monitoring control charts and their enhancements.

In this paper, the definition, and properties of the GWMA control chart are being further analyzed and investigated for detecting small process mean shifts of autocorrelated observations. The GWMA control chart, for detecting small process mean shifts of independent observations is extended to the GWMA control chart for detecting small process mean shifts of autocorrelated observations. This paper is structured as follows: Sect. 2 presents the generally weighted moving average technique. The GWMA control chart for detecting small process mean shifts of autocorrelated observations is shown in Sect. 3. An example is shown in Sect. 4. Conclusions are drawn in Sect. 5.

2 The generally weighted moving average technique

Sheu and Lin (2003) used the concept of Sheu and Griffith (1996) and Sheu (1988) to extend the EWMA control chart to the GWMA control chart. Their results indicated that the GWMA control chart is more sensitive than the EWMA control chart for detecting small process mean shifts of independent observations. Now we give the precise definition of the GWMA technique and investigate its properties of GWMA technique.

Suppose events S and F are mutually exclusive and complementary events. Let \(T\) count the number of periods until the first occurrence of event S since the last occurrence of event S. Let \({\overline{P} }_{t}=P(T>t)\) as the survival function of \(T\). That is, \({\overline{P} }_{t}\) is the probability of only event F occurring in the first \(t\) periods. We assume that \(1 = \overline{P}_{0} \ge \overline{P}_{1} \ge \overline{P}_{2} \ge \overline{P}_{3} \ldots\)

The symbol {\({\overline{P} }_{t}\)} is an abbreviation for the probabilities of a sequence. The sequence {\({\overline{P} }_{t}\)} is supposed to be known. Let

$$ \theta_{t} = P\left( {T = t} \right) = P\left( {T > t - 1} \right) - P\left( {T > t} \right) = \overline{P}_{t - 1} - \overline{P}_{t} = \overline{P}_{t - 1} \left( {1 - \frac{{\overline{P}_{t} }}{{\overline{P}_{t - 1} }}} \right), $$
(1)

where \(t = 1,2,3, \ldots\)

Equation (1) shows that event F occurs with probability \({q}_{t}=\frac{{\overline{P} }_{t}}{{\overline{P} }_{t-1}}\) at the t-th period whereas event S occurs with probability \({p}_{t}=1-{q}_{t}=1-\frac{{\overline{P} }_{t}}{{\overline{P} }_{t-1}}\). Evidently, the probability of event S occurrence depends on time \(t\). If \({\overline{P} }_{t}={q}^{t}\) which is a geometric distribution, then \({q}_{t}=\frac{{\overline{P} }_{t}}{{\overline{P} }_{t-1}}=\frac{{q}^{t}}{{q}^{t-1}}=q\) and \({p}_{t}=1-{q}_{t}=1-q\) which does not depend on time \(t\).

Thus, the sum of the probabilities is given below:

$$ \begin{aligned} \mathop \sum \limits_{j = 1}^{\infty } P\left( {T = j} \right) & = P\left( {T = 1} \right) + P\left( {T = 2} \right) + \cdots + P\left( {T = t} \right) + P\left( {T > t} \right) \\ & = \left( {\overline{P}_{0} - \overline{P}_{1} } \right) + \left( {\overline{P}_{1} - \overline{P}_{2} } \right) + \cdots + \left( {\overline{P}_{t - 1} - \overline{P}_{t} } \right) + \overline{P}_{t} = \overline{P}_{0} = 1, \\ \end{aligned} $$
(2)

whereas \(\left\{ {P\left( {T = j} \right)} \right\}_{j = 1,2, \ldots }\) can be considered as the weight of GWMA technique. The weighted averages of past observations with more weight to recent observations and less weight to the past observation. In other words, the weight of the current period is \(P(T=1)\). The weights of GWMA technique depend on the time. Thus, there is no recursive formula for the GWMA technique. The GWMA technique has no Markovian property. The GWMA control chart is more practical to monitor the process mean shifts of the production process or service process. The GWMA technique can be parameterized as below. We consider the random vector \(X\) of size \(t\) is given by:

$$ X = \left[ {X_{1} ,X_{2} , \ldots ,X_{t} } \right]_{1 \times t}^{\prime } = \left[ {\begin{array}{*{20}c} {X_{1} } \\ {X_{2} } \\ \vdots \\ {X_{t} } \\ \end{array} } \right]_{t \times 1} , $$
(3)

The mean of the random vector \(X\) is vector μ. The variance–covariance matrix of the random vector \(X\) is \(\sum \). We also assume that \(X_{1} ,X_{2} , \ldots ,X_{t}\) have the same mean \(u\) and same variance \({\sigma }_{X}^{2}\). The GWMA technique can be defined by the linear transformation

$$ Y = AX + y_{0} C, $$
(4)

where \(Y\) is \(t\times 1\) random vector and

$$ A = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\overline{P}_{0} - \overline{P}_{1} } & 0 & 0 \\ {\overline{P}_{1} - \overline{P}_{2} } & {\overline{P}_{0} - \overline{P}_{1} } & 0 \\ {\overline{P}_{2} - \overline{P}_{3} } & {\overline{P}_{1} - \overline{P}_{2} } & { \overline{P}_{0} - \overline{P}_{1} } \\ \end{array} } & \cdots & {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ \vdots & \ddots & \vdots \\ {\begin{array}{*{20}c} { \overline{P}_{t - 1} - \overline{P}_{t} } & {\overline{P}_{t - 2} - \overline{P}_{t - 1} } & {\overline{P}_{t - 3} - \overline{P}_{t - 2} } \\ \end{array} } & \cdots & {\overline{P}_{0} - \overline{P}_{1} } \\ \end{array} } \right]_{t \times t} , $$
(5)

is \(t\times t\) matrix and C is \(t\times 1\) vector with the form

$$ C = \left[ {\overline{P}_{1} ,\overline{P}_{2} , \ldots ,\overline{P}_{t} } \right]_{1 \times t}^{\prime } = \left[ {\begin{array}{*{20}c} {\overline{P}_{1} } \\ {\overline{P}_{2} } \\ {\overline{P}_{3} } \\ \vdots \\ {\overline{P}_{t} } \\ \end{array} } \right]_{t \times 1} , $$
(6)

where \({y}_{0}\) is an initial scalar value that can be represented as the starting value for the GWMA technique.

From Eq. (4), we can get

$$Y=\left[\begin{array}{c}{Y}_{1}\\ {Y}_{2}\\ {Y}_{3}\\ \vdots \\ {Y}_{t}\end{array}\right]={\left[\begin{array}{c}\left({\overline{P} }_{0}-{\overline{P} }_{1}\right){X}_{1}+{\overline{P} }_{1}{y}_{0} \\ \left({\overline{P} }_{1}-{\overline{P} }_{2}\right){X}_{1}+\left({\overline{P} }_{0}-{\overline{P} }_{1}\right){X}_{2}+{\overline{P} }_{2}{y}_{0} \\ \left({\overline{P} }_{2}-{\overline{P} }_{3}\right){X}_{1}+\left({\overline{P} }_{1}-{\overline{P} }_{2}\right){X}_{2}+\left({\overline{P} }_{0}-{\overline{P} }_{1}\right){X}_{3}+{\overline{P} }_{3}{y}_{0} \\ \vdots \\ \left({\overline{P} }_{t-1}-{\overline{P} }_{t}\right){X}_{1}+\left({\overline{P} }_{t-2}-{\overline{P} }_{t-1}\right){X}_{2}+\cdots +\left({\overline{P} }_{0}-{\overline{P} }_{1}\right){X}_{t}+\overline{{P }_{t}}{y}_{0}\end{array}\right]}.$$
(7)

Hence, the GWMA statistic at the t-th period is given below

$$ Y_{t} = \mathop \sum \limits_{j = 1}^{t} P\left( {T = j} \right)X_{t - j + 1} + P\left( {T > t} \right)y_{0} = \mathop \sum \limits_{j = 1}^{t} \left( {\overline{P}_{j - 1} - \overline{P}_{j} } \right)X_{t - j + 1} + \overline{P}_{t} y_{0} . $$
(8)

Remark 1

  1. a.

    For easy computation, consider the case \({\overline{P} }_{t}={q}^{{t}^{\alpha }}\), for \(t = 0,1,2, \ldots ,0 \le q < 1\) and \(\alpha > 0\) which is a discrete Weibull distribution (Nakagawa & Osaki, 1975). In this case, if we put \({\overline{P} }_{t}={q}^{{t}^{\alpha }}\) in Eq. (8), we can get:

    $$ Y_{t} = \mathop \sum \limits_{j = 1}^{t} \left( {q^{{\left( {j - 1} \right)^{\alpha } }} - q^{{j^{\alpha } }} } \right)X_{t - j + 1} + q^{{t^{\alpha } }} y_{0} . $$
    (9)
  2. b.

    If we consider the case \({\overline{P} }_{t}={q}^{{t}^{\alpha }}\), for \(t = 0,1,2, \ldots ,0 \le q < 1\) and \(\alpha =1\), then \({\overline{P} }_{t}={q}^{t}\) which is a geometric distribution. If we put \({\overline{P} }_{t}={q}^{t}\) in Eq. (8), we get:

    $$ \begin{aligned} Y_{t} & = \mathop \sum \limits_{j = 1}^{t} \left( {q^{{\left( {j - 1} \right)}} - q^{j} } \right)X_{t - j + 1} + q^{t} y_{0} \\ & = \left( {1 - q} \right)\mathop \sum \limits_{j = 1}^{t} q^{{\left( {j - 1} \right)}} X_{t - j + 1} + q^{t} y_{0} . \\ \end{aligned} $$
    (10)

    If we put \(q=1-\lambda \) and \(1-q=\lambda \) in Eq. (10), we can get:

    $$ Y_{t} = \lambda \mathop \sum \limits_{j = 1}^{t} \left( {1 - \lambda } \right)^{j - 1} X_{t - j + 1} + \left( {1 - \lambda } \right)^{t} y_{0} , $$
    (11)

    which is the EWMA technique. Hence the EWMA technique is a special case of our GWMA technique

  3. c.

    Consider the k-term weighted moving average (WMA) with the weight \({w}_{1}\ge {w}_{2}\ge \cdots \ge {w}_{k}\) and \(\sum_{i=1}^{k}{w}_{i}=1\), then \({\overline{P} }_{0}=1\), \({\overline{P} }_{1}=1-{w}_{1}\), \({\overline{P} }_{2}=1-{w}_{1}-{w}_{2}\), \(\overline{P}_{3} = 1 - w_{1} - w_{2} - w_{3} , \ldots ,\) \( {\overline{P} }_{k-1}=1-{w}_{1}-{w}_{2}-\cdots -{w}_{k-1}, {\overline{P} }_{k}=1-{w}_{1}-{w}_{2}-\cdots -{w}_{k}=0\) and \({\overline{P} }_{j}=0\) for\(j\ge k\). In this case, if we put \({\overline{P} }_{0}=1\), \({\overline{P} }_{1}=1-{w}_{1}\),\({\overline{P} }_{2}=1-{w}_{1}-{w}_{2}\), \({\overline{P} }_{3}=1-{w}_{1}-{w}_{2}-{w}_{3},\) \(\cdots , {\overline{P} }_{k-1}=1-{w}_{1}-{w}_{2}-\cdots -{w}_{k-1}, {\overline{P} }_{k}=1-{w}_{1}-{w}_{2}-\cdots -{w}_{k}=0\) and \({\overline{P} }_{j}=0\) for \(j\ge k\) in Eq. (10), we can get:

    $$ Y_{t} = \mathop \sum \limits_{j = 1}^{k} w_{j} X_{t - j + 1} ;\quad {\text{for}}\quad t = k, k + 1, \ldots , $$
    (12)

    which is the weighted moving average (WMA) technique. Hence WMA technique is a special case of our GWMA technique. Consider the special case where \({w}_{j}=1/k\) with all \(j\), then this yields the k-term simple moving average below

    $$ Y_{t} = \frac{1}{k}\mathop \sum \limits_{j = 1}^{k} X_{t - j + 1} ;\quad {\text{for}}\quad t = k,k + 1, \ldots , $$
    (13)

    which is the arithmetic average of the k-terms

  4. d.

    If \({\overline{P} }_{0}=1, {\overline{P} }_{j}=0\) for \(j\ge 1\), then \(Y=X\). This is clear from Eq. (4), when \({\overline{P} }_{0}=1, {\overline{P} }_{j}=0\) for \(j\ge 1\) we have \(A=I\) (where \(I\) is the identity matrix) and \(C=0\) which is a zero vector and thus has all components equal to zero, so that,

    $$ Y = AX + y_{0} C = IX + y_{0} 0 = X, $$
    (14)

    which is a random walk without a drift.

  5. e.

    Since the weight of GWMA technique depends on time t, thus, there is no recursive formula for the GWMA technique. The GWMA technique has no Markovian property. The GWMA control chart is more practical for detecting small process mean shifts of autocorrelated observations.

Properties

By applying the expectation operation to Eq. (4), we can get

$$ \begin{aligned} E\left( {Y_{t \times 1} } \right) & = E\left( {A_{t \times t} X_{t \times 1} + y_{0} C_{t \times 1} } \right) = A_{t \times t} E\left( {X_{t \times 1} } \right) + y_{0} C_{t \times 1} \\ & = A_{t \times t} \mu_{t \times 1} + y_{0} C_{t \times 1} , \\ \end{aligned} $$
(15)

and by letting \({\mu }_{t\times 1}=u{1}_{t\times 1}\) and \({y}_{0}=u\) then

$$ E\left( Y \right) = A\mu 1_{t \times 1} + \mu C_{t \times 1} = u\left( {A1_{t \times 1} + C_{t \times 1} } \right) = u1_{t \times 1} , $$
(16)

where \({1}_{t\times 1}\) is the vector of ones.

The variance covariance matrix of random vector \(Y\) is given as follows:

$$Var\left(Y\right)=Var\left(AX+{y}_{0}C\right)=A\Sigma {A}^{^{\prime}}={\sigma }_{X}^{2}AR{A}^{^{\prime}},$$
(17)

where R represents the autocorrelation matrix of random vector \(X\). The variance of the GWMA statistic at the time i is the i-th diagonal element of (17). The autocovariance of the GWMA statistic at \({\mathrm{lag}}_{\left(i-j\right)}={\mathrm{lag}}_{\left(j-i\right)}\) is the (i, j)-th off-diagonal element of (17). We can show that the variance of GWMA statistic \({Y}_{t}\) at any time \(t>0\) is given as follows:

$$ Var\left( {Y_{t} } \right) = \sigma_{X}^{2} \left[ {\mathop \sum \limits_{i = 1}^{t} \left( {\overline{P}_{i - 1} - \overline{P}_{i} } \right)^{2} + 2\mathop \sum \limits_{i = 1}^{t - 1} \mathop \sum \limits_{j = i + 1}^{t} \left( {\overline{P}_{i - 1} - \overline{P}_{i} } \right)\left( {\overline{P}_{j - 1} - \overline{P}_{j} } \right)\rho_{j - i} } \right]. $$
(18)

where \({\sigma }_{X}^{2}\) is the variance of original process \(\{{X}_{t}\}\), and \({\rho }_{n}={\rho }_{-n}\) represents the lag \(n\) autocorrelation of original process \(\{{X}_{t}\}\).

Remark 2

  1. a.

    For easy computation, we can consider the case \(\overline{P}_{t} = q^{{t^{\alpha } }}\), \(t = 0,1,2, \ldots ,0 \le q < 1\), \(\alpha > 0\) which is a discrete Weibull distribution. If we put \({\overline{P} }_{t}={q}^{{t}^{\alpha }}\) in Eq. (18), then we can get:

    $$ Var\left( {Y_{t} } \right) = \sigma_{X}^{2} \left[ {\mathop \sum \limits_{i = 1}^{t} \left( {q^{{\left( {i - 1} \right)^{\alpha } }} - q^{{i^{\alpha } }} } \right)^{2} + 2\mathop \sum \limits_{i = 1}^{t - 1} \mathop \sum \limits_{j = i + 1}^{t} \left( {q^{{\left( {i - 1} \right)^{\alpha } }} - q^{{i^{\alpha } }} } \right)\left( {q^{{\left( {j - 1} \right)^{\alpha } }} - q^{{j^{\alpha } }} } \right)\rho_{j - i} } \right]. $$
    (19)
  2. b.

    If we consider the case \({\overline{P} }_{t}={q}^{{t}^{\alpha }}\), \(t=\mathrm{0,1},2,\dots ,0\le q<1\), \(\alpha =1\), then \({\overline{P} }_{t}={q}^{t}\) which is a geometric distribution. If we put \({\overline{P} }_{t}={q}^{t}\) in Eq. (18), we can get:

    $$ Var\left( {Y_{t} } \right) = \sigma_{X}^{2} \left[ {\mathop \sum \limits_{i = 1}^{t} \left( {\left( {1 - q} \right)q^{i - 1} } \right)^{2} + 2\mathop \sum \limits_{i = 1}^{t - 1} \mathop \sum \limits_{j = i + 1}^{t} q^{i - 1} \left( {1 - q} \right)q^{j - 1} \left( {1 - q} \right)\rho_{j - i} } \right], $$
    (20)

    If we put \(q=1-\lambda \) and \(1-q=\lambda \) in Eq. (20), we can get:

    $$ Var\left( {Y_{t} } \right) = \sigma_{X}^{2} \lambda^{2} \left[ {\mathop \sum \limits_{i = 1}^{t} \left( {1 - \lambda } \right)^{{2\left( {i - 1} \right)}} + 2\mathop \sum \limits_{i = 1}^{t - 1} \mathop \sum \limits_{j = i + 1}^{t} \left( {1 - \lambda } \right)^{{\left( {i - 1} \right) + \left( {j - 1} \right)}} \rho_{j - i} } \right], $$
    (21)

    which agrees with Eq. (9) in Perry (2010).

    Assume that \(Var\left( {Y_{t} } \right) \to \sigma_{Y}^{2} ,\) as \(t \to \infty\), where \(\sigma_{Y}^{2}\) denotes the steady-state variance of the EWMA process \(\left\{ {Y_{t} ,t > 0} \right\}\). As \(\left| {\left( {1 - \lambda } \right)^{{\left( {i - 1} \right) + \left( {j - 1} \right)}} \rho_{j - i} } \right| < 1\) for all \(j\) and \(i\), \({\sigma }_{Y}^{2}\) can be written as

    $$ \sigma_{Y}^{2} = \sigma_{X}^{2} \left( {\frac{\lambda }{{\left( {2 - \lambda } \right)}} + 2\lambda^{2} \mathop \sum \limits_{i = 1}^{\infty } \mathop \sum \limits_{j = i + 1}^{\infty } \left( {1 - \lambda } \right)^{{\left( {i - 1} \right) + \left( {j - 1} \right)}} \rho_{j - i} } \right), $$
    (22)

    which agrees with Eq. (10) in Perry (2010).

  3. c.

    If \(X_{1} ,X_{2} ,X_{3} \ldots\) are independent (i.e., uncorrelated process), then

    1. 1.

      Equation (18) reduces to

      $$ Var\left( {Y_{t} } \right) = \sigma_{X}^{2} \mathop \sum \limits_{i = 1}^{t} \left( {\overline{P}_{i - 1} - \overline{P}_{i} } \right)^{2} , $$
      (23)
    2. 2.

      Equation (19) reduces to

      $$ Var\left( {Y_{t} } \right) = \sigma_{X}^{2} \mathop \sum \limits_{i = 1}^{t} \left( {q^{{\left( {i - 1} \right)^{\alpha } }} - q^{{i^{\alpha } }} } \right)^{2} $$
      (24)
    3. 3.

      Equation (20) reduces to

      $$ Var\left( {Y_{t} } \right) = \sigma_{X}^{2} \left( {1 - q} \right)^{2} \mathop \sum \limits_{i = 1}^{t} q^{{2\left( {i - 1} \right)}} , $$
      (25)
    4. 4.

      Equation (21) reduces to

      $$ Var\left( {Y_{t} } \right) = \sigma_{X}^{2} \lambda^{2} \mathop \sum \limits_{i = 1}^{t} \left( {1 - \lambda } \right)^{{2\left( {i - 1} \right)}} , $$
      (26)
    5. 5.

      Equation (22) reduces to

      $$ \sigma_{Y}^{2} = \sigma_{X}^{2} \left( {\frac{\lambda }{2 - \lambda }} \right), $$
      (27)

      which agrees with Eq. (11) in Perry (2010).

The initial value for \({y}_{0}\).

The impact of \({y}_{0}\) on \({Y}_{t}\) for large \(t\) is insignificant. Therefore, if \(t\) is large, we can select any value for \({y}_{0}\) and its influence on \({Y}_{t}\) should be negligible. In practice, we can use the arithmetic average of historical data for the initial value \({y}_{0}=\overline{X }=\frac{\sum_{i=1}^{t}{X}_{i}}{t}\). We also can select \({y}_{0}={X}_{1}\).

In the next section, we will discuss the applications of the GWMA technique in quality engineering.

3 The GWMA control chart for detecting small process mean shifts of autocorrelated observations

Roberts first proposed the EWMA control chart to monitor the process mean in 1959. The EWMA control chart is also called the geometric moving average (GMA) control chart. Sheu and Lin (2003) proposed the GWMA control chart, which is the extended version of the EWMA control chart. A numerical simulation comparison shows that the GWMA control chart is more sensitive than the EWMA control chart for detecting small process mean shifts of independent observations. Suppose that \(L\) is the width of control limits. The \(L\) is usually selected based upon an acceptable false alarm rate and is the distance of the control limits from the center line, expressed in standard deviation units. If \({u}_{0}\) represents the target value of the process mean used as the center line of the control chart, then the LCL (lower control limit), the UCL (upper control limit), and the CL (center line) of a GWMA control chart can be written as follows:

$$ \begin{aligned} UCL & = u_{0} + L\sqrt {Var\left( {Y_{t} } \right)} \\ CL & = u_{0} \\ LCL & = u_{0} - L\sqrt {Var\left( {Y_{t} } \right),} \\ \end{aligned} $$
(28)

where \(Var({Y}_{t})\) can choose one of these Eqs. (18), (19), (20), (21), (22), for detecting small process mean shifts of autocorrelated observations and \(Var({Y}_{t})\) can choose one of these Eqs. (23), (24), (25), (26), and (27) for detecting small process mean shifts of independent observations. The GWMA control chart would be built by plotting \({Y}_{t}\) versus the sample time t. If \({Y}_{t}\) exceeds one of these control limits, then the process is considered out-of-control and some corrective action needed to be taken.

Observations from continuous manufacturing process in the chemical and pharmaceutical industries are frequently autocorrelated. The autocorrelation has a great influence on the control charts. An effect of autocorrelation is to decrease the ability of detecting the process mean shifts and generates a high false alarm rate. Here we use a model-free approach to solve the problem of detecting the small process mean shifts of autocorrelated observations. We use the classical standard control charts and adjust the control limits to take account of the autocorrelation and estimate the true process variance.

For an autocorrelated process, an ARIMA (p, d, q) model may be appropriate for the observations from the autocorrelated process. We will restrict our work to control chart for autocorrelated observations that can be modeled with an autoregressive AR(1) model. The AR(1) model can be represented as follows:

$$ X_{t} - u_{0} = \phi \left( {X_{t - 1} - u_{0} } \right) + \varepsilon_{t} ,\quad {\text{or}} $$
(29)
$$ X_{t} = \left( {1 - \phi } \right)u_{0} + \phi X_{t - 1} + \varepsilon_{t} , $$
(30)

where \({X}_{t}\) is the observed time series at time \(t\), \(\phi \) is the autocorrelation coefficient satisfying \(\left|\phi \right|<1\), \({\varepsilon }_{t}\) is assumed to be independent and identically normally distributed with mean 0 and variance \({\sigma }_{\varepsilon }^{2}\) (i.e., \({\varepsilon }_{t}\sim N\left(0,{\sigma }_{\varepsilon }^{2}\right)\)). It is assumed that \({X}_{t}\) will be normal distribution with a mean of \({u}_{0}\) and a variance

$$ \sigma_{X}^{2} = Var\left( {X_{t} } \right) = \frac{{\sigma_{\varepsilon }^{2} }}{{\left( {1 - \phi^{2} } \right)}}\quad {\text{for}}\,{\text{all}}\quad t \ge 1. $$
(31)

The covariance between \({X}_{t-i}\) and \({X}_{t}\) is \({{\phi }^{i}\sigma }_{X}^{2}\) for \(t\ge i\), and from this, it follows that the correlation coefficient between \({X}_{t-i}\) and \({X}_{t}\) is \({\phi }^{i}\).

A process that is operating in the presence of assignable causes is said to be out of control. When an assignable cause occurs, the effect of this assignable cause is to shift the process mean from \({u}_{0}\) to \({u}_{0}+\delta .\) Here, we assume \({u}_{0}=0\). The GWMA control chart and EWMA control chart were developed for monitoring small shifts in the process mean.

The following dataset simulation illustrates the unexpected variation in the process of autocorrelated observation on the EWMA control chart and GWMA control chart respectively.

From the Eqs. (8) and (30), the GWMA statistics at the time t is defined as

$$ Y_{t} = \mathop \sum \limits_{j = 1}^{t} \left( {\overline{P}_{j - 1} - \overline{P}_{j} } \right)X_{t - j + 1} + \overline{P}_{t} y_{0} , $$
(32)

where \({X}_{t}\) is the observed time series at time \(t\). The initial value \({y}_{0}\) is the mean of \({X}_{t}\). Hence, we have \({Y}_{0}={u}_{0}\) and

$$ Y_{t} = \mathop \sum \limits_{j = 1}^{t} \left( {\overline{P}_{j - 1} - \overline{P}_{j} } \right)X_{t - j + 1} + \overline{P}_{t} u_{0} . $$
(33)

The expected value of GWMA statistic \({Y}_{t}\) computed as

$$ E\left( {Y_{t} } \right) = E\left[ {\mathop \sum \limits_{j = 1}^{t} \left( {\overline{P}_{j - 1} - \overline{P}_{j} } \right)X_{t - j + 1} + \overline{P}_{t} u_{0} } \right] = u_{0} . $$
(34)

From the Eq. (18), the variance of GWMA statistic \({Y}_{t}\) is

$$ Var\left( {Y_{t} } \right) = \sigma_{X}^{2} \left[ {\mathop \sum \limits_{i = 1}^{t} \left( {\overline{P}_{i - 1} - \overline{P}_{i} } \right)^{2} + 2\mathop \sum \limits_{i = 1}^{t - 1} \mathop \sum \limits_{j = i + 1}^{t} \left( {\overline{P}_{i - 1} - \overline{P}_{i} } \right)\left( {\overline{P}_{j - 1} - \overline{P}_{j} } \right)\rho_{j - i} } \right], $$
(35)

where \({\sigma }_{X}^{2}=\frac{{\sigma }_{\varepsilon }^{2}}{\left(1-{\phi }^{2}\right)}\) is the variance of the original process \(\left\{{X}_{t}\right\}\) and \({\rho }_{n}={\rho }_{-n}={\phi }^{n}\) represents the lag n autocorrelation of the original process \(\left\{{X}_{t}\right\}\). For easy computation, we can consider the case \({\overline{P} }_{t}={q}^{{t}^{\alpha }}, t=\mathrm{0,1},2,.. , 0\le q<1, \alpha >0\) which is a discrete Weibull distribution. If we put \({\overline{P} }_{t}={q}^{{t}^{\alpha }}\) in Eq. (33), then the GWMA statistics at time t is

$$ Y_{t} = \mathop \sum \limits_{j = 1}^{t} \left( {q^{{\left( {j - 1} \right)^{\alpha } }} - q^{{j^{\alpha } }} } \right)X_{t - j + 1} + q^{{t^{\alpha } }} u_{0} . $$
(36)

If we put \({\overline{P} }_{t}={q}^{{t}^{\alpha }},{\sigma }_{X}^{2}=\frac{{\sigma }_{\varepsilon }^{2}}{\left(1-{\phi }^{2}\right)}\) and \({\rho }_{j-i}={\phi }^{j-i}\) in Eq. (35), then we can get:

$$ Var\left( {Y_{t} } \right) = \frac{{\sigma_{\varepsilon }^{2} }}{{\left( {1 - \phi^{2} } \right)}}\left[ {\mathop \sum \limits_{i = 1}^{t} \left( {q^{{\left( {i - 1} \right)^{\alpha } }} - q^{{i^{\alpha } }} } \right)^{2} + 2\mathop \sum \limits_{i = 1}^{t - 1} \mathop \sum \limits_{j = i + 1}^{t} \left( {q^{{\left( {i - 1} \right)^{\alpha } }} - q^{{i^{\alpha } }} } \right)\left( {q^{{\left( {j - 1} \right)^{\alpha } }} - q^{{j^{\alpha } }} } \right)\phi^{j - i} } \right]. $$
(37)

The time-varying control limits of the GWMA control chart for monitoring the small process mean shifts of autocorrelated observations can be written as follows:

$$ \begin{aligned} UCL & = u_{0} + L\sqrt {Var\left( {Y_{t} } \right)} \\ CL & = u_{0} \\ LCL & = u_{0} - L\sqrt {Var\left( {Y_{t} } \right)} \\ \end{aligned} $$
(38)

where \(Var({Y}_{t})\) is given by Eq. (37), \(L\) denotes the width of the control limits, and is determined by the professional to achieve the desired in-control ARL for GWMA control charts. If we consider the case \({\overline{P} }_{t}={q}^{{t}^{\alpha }},\) for \(t=\mathrm{0,1},2..,0\le q<1, \mathrm{and }\alpha =1,\) then \({\overline{P} }_{t}={q}^{t}\) which is a geometric distribution. If we put \({\overline{P} }_{t}={q}^{t}\) in Eq. (33), we get the EWMA statistic \({Z}_{t}\) at the time \(t:\)

$$ Z_{t} = \mathop \sum \limits_{j = 1}^{t} \left( {q^{{\left( {j - 1} \right)}} - q^{j} } \right)X_{t - j + 1} + q^{t} u_{0} , = \left( {1 - q} \right)\mathop \sum \limits_{j = 1}^{t} q^{{\left( {j - 1} \right)}} X_{t - j + 1} + q^{t} u_{0} . $$
(39)

If we put \(q=1-\lambda \) and \(1-q=\lambda \) in Eq. (39), we can get

$$ Z_{t} = \lambda \mathop \sum \limits_{j = 1}^{t} \left( {1 - \lambda } \right)^{j - 1} X_{t - j + 1} + \left( {1 - \lambda } \right)^{t} u_{0} . $$
(40)

Hence, the EWMA statistic \({Z}_{t}\) is the special case of our GWMA statistic \({Y}_{t}.\)

If we put \({\overline{P} }_{t}={q}^{t},{\sigma }_{X}^{2}=\frac{{\sigma }_{\varepsilon }^{2}}{\left(1-{\phi }^{2}\right)}\) and \({\rho }_{j-i}={\phi }^{j-i}\) in Eq. (35), then we can get:

$$ Var\left( {Z_{t} } \right) = \frac{{\sigma_{\varepsilon }^{2} }}{{\left( {1 - \phi^{2} } \right)}}\left[ {\mathop \sum \limits_{i = 1}^{t} \left( {\left( {1 - q} \right)q^{i - 1} } \right)^{2} + 2\mathop \sum \limits_{i = 1}^{t - 1} \mathop \sum \limits_{j = i + 1}^{t} q^{i - 1} \left( {1 - q} \right)q^{j - 1} \left( {1 - q} \right)\phi^{j - i} } \right]. $$
(41)

If we put \(q=1-\lambda \) and \(1-q=\lambda \) in Eq. (41), we can get

$$ Var\left( {Z_{t} } \right) = \frac{{\sigma_{\varepsilon }^{2} }}{{\left( {1 - \phi^{2} } \right)}}\lambda^{2} \left[ {\mathop \sum \limits_{i = 1}^{t} \left( {1 - \lambda } \right)^{{2\left( {i - 1} \right)}} + 2\mathop \sum \limits_{i = 1}^{t - 1} \mathop \sum \limits_{j = 1}^{t} \left( {1 - \lambda } \right)^{{\left( {i - 1} \right) + \left( {j - 1} \right)}} \phi^{j - i} } \right]. $$
(42)

The time-varying control limits of the EWMA control chart for monitoring the small process mean shifts of autocorrelated observations can be written as follows:

$$ \begin{aligned} UCL & = u_{0} + L\sqrt {Var\left( {Z_{t} } \right)} \\ CL & = u_{0} \\ LCL & = u_{0} - L\sqrt {Var\left( {Z_{t} } \right)} \\ \end{aligned} $$
(43)

where \(Var({Z}_{t})\) is given by Eq. (41) or (42).

The average run length (ARL) is defined as the average number of the sample (subgroups) taken before an out-of-control signal is given on the control chart. The ARL is a performance measure of the ability of a control chart to detect process mean shifts. When the process is in control, we want the control chart to produce fewer false alarms, i.e., to have a large in-control ARL. When a process is out of control, we want the control chart to signal quickly, i.e., to have a small out-of-control ARL. The parameters for each control chart were defined such that the in-control ARL is set to be nearly 370. The out-of-control is then compared for a given process mean shift. According to the performance measure of the control chart, a smaller out-of-control ARL corresponds to greater detection ability. The computation of the ARL of an EWMA control chart has been studied by many authors. Crowder (1989) used the integral equation method to evaluate run-length distributions of the EWMA control chart. Lucas and Saccucci (1990) proposed the Markov chain method to compute the accurate ARL of the EWMA control chart with fixed control limits. Since the control limits of the GWMA control chart vary over time, it is difficult to use the Markov chain method or integral equation method to compute the exact ARL for given control limits. Hence, we use the simulation method to compute the ARL of the GWMA control chart. Sheu and Lu (2009a, 2009b) recommended the following simulation steps:

  1. (a)

    Give parameters \(\phi \), the magnitude of \({\sigma }_{\varepsilon }^{2}\) and the charting parameter \((q,\alpha ,L)\)

  2. (b)

    Generate a set of simulation data under an AR(1) process and compute the GWMA statistics \({Y}_{j}\) by Eq. (40) at the target value \({u}_{0}+\delta .\)

  3. (c)

    Record the run length when \({Y}_{j}\) exceeds the control limits and the trial halts. Run 20,000 iterations, we can obtain the ARL along with the specific parameters.

  4. (d)

    We use the bisection method to modify the control limit constant (L) to reach the desired in-control ARL.

  5. (e)

    When the process means shifts, we apply the in-control parameters to monitor the process mean shifts and compute out-of-control ARL.

In practice, we can use the GWMA control chart to detect the small process mean shifts of autocorrelated observations. We run the following simulations to compare the performance of various GWMA control charts in detecting the small process mean shifts of autocorrelated observations. Herein, the values of \(\phi \) which quantify the correlation coefficient between \({X}_{j-1}\) and \({X}_{j}\) under AR(1) process are set to 0.1, 0.2, 0.3, 0.4, 0.8. We use the bisection approach to obtain the control limit constant \((L)\) corresponding to the desired in-control ARL. We adjust the control limit constant \((L)\) based on 20,000 iterations to maintain the in-control ARL at approximately 370.4. The out-of-control ARLs of various GWMA control charts are used for comparison. Table 1 presents the ARL values for the GWMA control chart for detecting small process mean shifts of autocorrelated observations with time-varying control limits when the process mean shifts from \({u}_{0}\) to \({u}_{0}+\delta (\delta =0.25, 0.5, 0.75, 1.00, 1.25, \mathrm{2,00}, 3.00),\) the design parameter \(q(q=0.8, 0.85, 0.9),\) the correlation coefficient \((\phi =0.1, 0.2, 0.3, 0.4, 0.8)\) and the adjustable parameter \(\alpha (\alpha =0.5, 0.6, 0.7, 0.8, 0.9, 1.0)\). When \(\alpha =1,\) the GWMA control chart reduces to the EWMA control chart. We conduct a sensitivity analysis by comparing the out-of-control ARLs for one (\(q,\alpha ,L)\) combination to those associated with another \((q,\alpha ,L)\) combination. The optimal parameters are designed in the sense that for a fixed in-control ARL, they yield the least possible out-of-control ARL for a specific process mean shift \(\delta \) and a given autocorrelation coefficient \(\phi \). The numerical results in Table 1 show that the GWMA control chart outperforms the corresponding EWMA control chart for detecting small process mean shifts of autocorrelated observations with time-varying control limits. The smallest ARLs value obtained to detect shifts \(\delta \) in the process mean is highlighted with boldface in Table 1. For example, when \(\phi =0.3, q=0.85,\) the process mean shift \(\delta =0.5\), the ARL of the GWMA control chart with \(\alpha =0.6\), and \(L=2.811\) is 46.03, which compares with the ARL of the EWMA control chart with \(\alpha =1, L=2.733\) is 55.63.

Table 1 ARLs of GWMA control charts with time-varying control limits
Full size table

4 An example

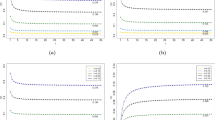
We use a set of simulated data to illustrate the GWMA control charts for detecting small process mean shifts of autocorrelated observations. In Tables 2, 3, and 4, we use \({X}_{j}\) to represent autocorrelated observations, \({Z}_{j}\) to represent EWMA statistics, and \({Y}_{j}\) to represent GWMA statistics. In Table 2 we consider the GWMA control chart for detecting small process mean shifts of autocorrelated observations which follow the AR(1) process with \(\phi =0.2, {\sigma }_{\varepsilon }^{2}=1\). We assume that the process mean shift \(\delta =0.5\) and 50 samples are generated. Within Table 2, the threshold for in-control ARL is set to ARL \(\cong 370.\) The parameters \(q=0.85, \alpha =0.7, L=2.813\) for the GWMA statistics and the parameters \(q=0.85, \alpha =1, L=2.703\) for the EWMA statistics. In Table 2 the EWMA control charts detect an out-of-control signal at observation 37 whereas the GWMA control chart detects an out-of-control signal at observation 33. In Table 3 we consider the GWMA control chart for detecting small process mean shifts of autocorrelated observations which follow the AR(1) process with \(\phi =0.4, {\sigma }_{\varepsilon }^{2}=1\). In Table 3 we assume that the process means shift \(\delta =0.5\) and 65 samples are generated. Within Table 3, the threshold for in-control ARL is set to ARL \(\cong 370.\) The parameters \(q=0.9, \alpha =0.6\) and \(L=2.688\) for the GWMA statistics and the parameters and \(q=0.9, \alpha =1\) and \(L=2.609\) for the EWMA statistics. In Table 3 the EWMA control chart detects an out-of-control signal at observation 62 whereas the GWMA control chart detects an out-of-control signal at observation 10. In Table 4 we consider the GWMA control chart for detecting small process mean shifts of autocorrelated observations which follow the AR(1) process with \(\phi =0.8, {\sigma }_{\varepsilon }^{2}=1\). In Table 4 we assume that the process mean shift \(\delta =1\) and 50 samples are generated. Within Table 4, the threshold for in control ARL is set to ARL \(\cong 370\). The parameters \(q=0.9 \alpha =0.6\) and \(L=2.420\) for the GWMA statistics and the parameters \(q=0.9\) \(\alpha =1\) and \(L=2.453\) for the EWMA statistics. In Table 4, the EWMA control chart detects an out-of-control signal at observation 42 whereas the GWMA control chart detects an out-of-control signal at observation 27. Figure 1 plots the GWMA and EWMA control charts for detecting small process mean shifts of autocorrelated observations from AR(1) when \(\phi \)=0.2 and process mean shift \(\delta \)=0.5. The parameters \(q=0.9, \alpha =0.6\) and \(L=2.688\) for the GWMA statistics. The parameters \(q=0.9, \alpha =1\) and \(L=2.609\) for the EWMA statistics. Figure 2 plots the GWMA and EWMA control charts for detecting small process mean shifts of autocorrelated observations from AR(1) when \(\phi \)=0.4 and process mean shift \(\delta \)=0.5. The parameters \(q=0.9, \alpha =0.6\) and \(L=2.688\) for the GWMA statistics. The parameters \(q=0.9, \alpha =1\) and \(L=2.609\) for the EWMA statistics. Figure 3 plots the GWMA and EWMA control charts for detecting small process mean shifts of autocorrelated observations from AR(1) when \(\phi \)=0.8 and process mean shift \(\delta \)=1. The parameters \(q=0.9 \alpha =0.6\) and \(L=2.420\) for the GWMA statistics. The parameters \(q=0.9 \alpha =1\) and \(L=2.453\) for the EWMA statistics. The solid line in Figs. 1, 2, and 3 is GWMA statistics and the dashed line is the EWMA statistics. From Figs. 1, 2, and 3 we can see that the GWMA control chart for detecting small process mean shifts of autocorrelated observations needs less time to obtain an out-of-control signal than the EWMA control chart. That is, the GWMA control chart outperforms the EWMA control chart for detecting small process mean shifts of autocorrelated observations.

Table 2 Example of GWMA and EWMA control charts for detecting small process mean shifts of autocorrelated observations from AR(1) when \(\phi \) = 0.2 and process mean shift \(\delta \)=0.5
Full size table
Table 3 Example of GWMA and EWMA control charts for detecting small process mean shifts of autocorrelated observations from AR(1) when \(\phi \)=0.4 and process mean shift \(\delta \)=0.5
Full size table
Table 4 Example of GWMA and EWMA control charts for detecting small process mean shifts of autocorrelated observations from AR(1) when \(\phi \)=0.8 and process mean shift \(\delta \)=1
Full size table
Fig. 1
figure 1

GWMA and EWMA control chart for detecting small process mean shifts of autocorrelated observations from AR(1) when \(\phi = 0.2\) and process mean shift \(\delta = 0.{5}\). The parameters \(q = 0.9, \alpha = 0.6\) and \(L = 2.688\) for the GWMA statistics. The parameters and \(q = 0.9, \alpha = 1\) and \(L = 2.609\) for the EWMA statistics

Full size image
Fig. 2
figure 2

GWMA and EWMA control chart for detecting small process mean shifts of autocorrelated observations from AR(1) when \(\phi = 0.{4}\) and process mean shift \(\delta = 0.{5}\). The parameters \(q = 0.9, \alpha = 0.6\) and \(L = 2.688\) for the GWMA statistics. The parameters and \(q = 0.9, \alpha = 1\) and \(L = 2.609\) for the EWMA statistics

Full size image
Fig. 3
figure 3

GWMA and EWMA control chart for detecting small process mean shifts of autocorrelated observations from AR(1) when \(\phi = 0.{8}\) and process mean shift \(\delta = {1}\). The parameters \(q = 0.9, \alpha = 0.6\) and \(L = 2.420\) for the GWMA statistics. The parameters \(q = 0.9, \alpha = 1\) and \(L = 2.453\) for the EWMA statistics

Full size image

5 Conclusion

The statistical process control chart is primarily applied to monitor the production process or service process and detect the process change as soon as possible. The EWMA (exponentially weighted moving average) control chart has been widely used to detect small shifts in the process mean. Sheu and Lin (2003) proposed the GWMA (generally weighted moving average) control chartfor detecting small process mean shifts of independent observations. The GWMA control chart is the extended version of the EWMA control chart. The GWMA control chart has been widely investigated. In this paper, the definition, and properties of the GWMA control chart are being further analyzed and investigated for detecting small process mean shifts of autocorrelated observations. The weight of GWMA technique depends on time t, thus, there is no recursive formula for the GWMA technique and the GWMA technique has no Markovian property. The GWMA control chart is more practical for detecting small process mean shifts of autocorrelated observations. The EWMA technique and the weighted moving average (WMA) technique can be shown to be special cases of the GWMA technique. We also provided some properties of the GWMA technique, including its variance and expected value. Finally, we discuss the applications of the GWMA technique in quality engineering. A numerical simulation comparison shows that the GWMA control chart outperforms the EWMA control chart for detecting small process mean shifts of autocorrelated observations.