Hybrid Exponentially Weighted Moving Average Control Chart with Measurement Error

Abstract

A control chart is a significant statistical technique that is used to monitor the production process. When measurement error is present in the data, it affects the performance of the control chart. In this study, we described the impact of measurement error on the HEWMA control chart by using (1) covariates, (2) multiple measurements and (3) linear increasing variance method. We compare the performance of the HEWMA control chart and the EWMA control chart on the basis of average run lengths when the data are contaminated with the measurement error. The results revealed that the HEWMA control chart deals with the measurement error more efficiently than the EWMA control chart. Two real-life examples are also given to show the application of the HEWMA control chart in the presence of measurement error.

1 Introduction

Control charts are an important tool to observe the production process. They are useful to detect the assignable causes of variation in the process parameters. Shewhart control charts are popular, but they do not work to detect the small shifts in the process parameters. The memory-type control charts such as exponentially weighted moving average (EWMA) and hybrid exponentially weighted moving average (HEWMA) control charts are useful to observe the small and moderate shifts in the process parameters. One may refer to Qiu (2013) for in-depth detail on EWMA working procedures. The HEWMA control chart is suggested by Haq (2013) which is further improved by Noor-ul-Amin et al. (2019a). Haridy et al. (2019) considered some EWMA-type schemes for monitoring attributes. Graham et al. (2012, 2017) discussed distribution-free EWMA-type charts based on precedence statistic. Recently, Mukherjee et al. (2019) compared some distribution-free CUSUM and EWMA-type charts for monitoring location parameters. When dealing with control charts, accurate measurements are important. The ability of control charts to detect the shifts in the process parameters can be reduced due to measurement error. In practice, the measurement error is often expressed by gauge capability and repeatability studies as discussed by Montgomery and Runger (2010) and Senvar and Firat (2010). Mittag and Stemann (1998) studied the effect of stochastic measurement error (gauge imprecision) on the performance of Shewhart-type $\bar{X} - S$ control charts. It was noticed that the measurement error can badly affect the ability of the chart to quickly detect process disturbances and chart performance can be reduced.

The usual measurement error model presented in the literature is

$$Y = X +\upvarepsilon$$

where X is the quality characteristic to be observed, and $\varepsilon$ is the random error, such that with 0 mean and $\sigma_{m}^{2}$ variance. The random error enters into the process due to the imprecise measurement, and Y is the observed result of the measurement operation. In the described model, Y is assumed to be normally distributed with mean µ and variance $\sigma_{Y}^{2}$. The variance $\sigma_{Y}^{2}$ is divided into two components: $\sigma^{2}$ and $\sigma_{m}^{2}$, due to the variability in quality characteristics and error in the measurement system. This model was discussed by Mittag (1995), Mittag and Stemann (1998) and Linna and Woodall (2001). Some authors have studied the effect of measurement error on control charting techniques. Linna and Woodall (2001) developed a linear covariate model to study the effect of measurement error on Shewhart control charts. It was concluded that the presence of measurement error can result in inefficiency of control charts in detecting the shift in process parameters.

Linna et al. (2001) examined the effect of measurement error using different measurement error parameters (A, B) on the performance of Shewhart control charts and also on multivariable control charts. They also concluded that measurement error can be controlled by measuring each quality characteristic multiple times.

The effect of measurement error on the performance of EWMA control chart is studied by Maravelakis et al. (2004). They examined the effect of measurement error by using the covariate model and multiple measurements. Moreover, linearly increasing variance model was also discussed. It was concluded that the presence of measurement error significantly affected the performance of EWMA control chart. Moameni et al. (2012) introduced a process in which $\tilde{X}$-$\tilde{R}$ fuzzy control chart is used for monitoring. They used a linear covariate model to study the efficiency of fuzzy control chart in detecting an out-of-control process considering measurement error. Tran et al. (2017) studied the effect of measurement error on Shewhart-$\bar{X}$ chart by applying a linear covariate error model. They concluded that the performance of the control chart decreased as the amount of measurement error increased. They also suggested that the measuring of each observation several times can also enhance the performance of the chart. Cheng and Wang (2018) implied that measurement error often occurs in statistical process control. They studied the effect of a linear covariate error model on the EWMA median and cumulative sum (CUSUM) median charts. It was concluded that measurement error has a noticeable effect on the performance of the EWMA median and CUSUM median charts and recommended CUSUM median for small shifts and EWMA median chart should be used for large shifts when considering the measurement error. Recently, Noor-ul-Amin et al. (2019b) and Riaz et al. (2019) studied the effect of measurement error on EWMA control chart and mixed EWMA–CUSUM control chart by considering the auxiliary information.

Haq (2013) stated that HEWMA control chart is more efficient as compared to conventional memory-type control charts, while detecting the shifts in process parameters. The effect of measurement error on HEWMA control chart has not been explored. We examine the performance of the HEWMA control chart in the presence of measurement error under a linear covariate error model and by taking multiple measurements of a single unit of the quality characteristic. Furthermore, a linearly increasing variance model is also used to investigate the effect of measurement error on HEWMA control chart.

The rest of this paper is given as follows: In Sect. 2, HEWMA control is described in detail. In Sect. 3, the HEWMA control chart with the linear covariate error model is described; Sect. 4 provides the impact of measurement error on HEWMA control chart while taking multiple measurements. Section 5 gives the results on HEWMA control chart when linearly increasing variance model is used. Proceeding to Sect. 6, an application of the control chart is given considering numerical data. A comparative study is presented in Sect. 7.

2 HEWMA control chart

Suppose X₁, X₂….X_n be the independently and identically distributed random variables. From this, we can define a sequence HE₁, HE₂…HE_n by using the formula given by

$$E_{t} = \lambda_{2} X_{i} + (1 - \lambda_{2} )E_{t - 1} \quad 0 < \lambda_{2} \le 1$$

(1)

$$HE_{t} = (1 - \lambda_{1} )HE_{t - 1} + \lambda_{1} E_{t} \quad 0 < \lambda_{1} \le 1$$

(2)

where λ₁ and λ₂ are smoothing constants in (1) and (2), respectively. The HE_t is an EWMA statistic that requires another EWMA statistic E_t. The initial values are taken such that HE₀ = E₀ = µ₀, HE_t statistic is proposed by Haq (2013) and the control chart consisting on this statistic is named the HEWMA control chart.

Let X be the random variable and quality characteristic of the process having a normal distribution with mean µ₀ and standard deviation $\sigma_{0}$. The shift of the process mean has a magnitude $\delta = \frac{{|\mu_{1} - \mu_{0} |}}{\sigma }$, where µ₀ is the in-control mean, µ₁ is the mean after the shift has occurred in the process and $\sigma$ is the standard deviation of the process.

Haq (2017) described the mean and variance of HE_t as

$$\begin{aligned} & E\left( {{\text{HE}}_{t} } \right) = \, \mu_{0} \\ & {\text{VAR}}({\text{HE}}_{t} ) = \frac{{\lambda_{1}^{2} \lambda_{2}^{2} }}{{(\lambda_{1} - \lambda_{2} )^{2} }}\left\{ {\begin{array}{*{20}l} {\frac{{(1 - \lambda_{1} )^{2} (1 - (1 - \lambda_{1} )^{2i} }}{{1 - (1 - \lambda_{1} )^{2} }} + \frac{{(1 - \lambda_{2} )^{2} (1 - (1 - \lambda_{2} )^{2i} )}}{{1 - (1 - \lambda_{2} )^{2} }}} \hfill \\ { - \frac{{2(1 - \lambda_{1} )(1 - \lambda_{2} )(1 - (1 - \lambda_{1} )^{i} (1 - \lambda_{2} )^{i} )}}{{1 - (1 - \lambda_{1} )(1 - \lambda_{2} )}}} \hfill \\ \end{array} } \right\}\sigma^{2} \\ \end{aligned}$$

(3)

The upper control limit (UCL), center line (CL) and the lower control limit (LCL) of the statistic HE_t based on the above parameters are given by

$$\begin{aligned} & {\text{UCL}} = \mu_{0} + L\sqrt {{\text{VAR}}({\text{HE}}_{t} )} \\ & {\text{CL}} = \mu_{0} \\ & {\text{LCL}} = \mu_{0} - L\sqrt {{\text{VAR}}({\text{HE}}_{t} )} \\ \end{aligned}$$

(4)

Various methods have been proposed to measure the performance of a control chart. The most reliable and widely used performance measurement tool is the average run length (ARL) which is the average number of points needed to detect an out-of-control point. For more details on ARL, readers can consult Crosier (1986) and Lucas and Saccucci (1990). A good production procedure has a large value of ARL when the process is in control (ARL₀) and a small value of ARL when the process is not in control (ARL₁). In Eq. 4, the value of L is calculated in such a way that the ARL₀ of HEWMA control chart reaches a pre-defined level

2.1 HEWMA control chart Using Covariates

Consider that we have a process where the true quality characteristic is taken as X which is normally distributed with mean $\mu_{0}$ and variance $\sigma^{2}$, but there is another observable value Y which is related to this true value through a relation $Y = A + BX + \varepsilon$, where A and B are known constants and $\varepsilon$ is a random error distributed independently with mean 0 and variance $\sigma_{m}^{2}$. Now, we have to study the effect of random variable Y which consists of the variable X having mean A + Bµ₀ and variance $B^{2} \sigma^{2} + \sigma_{m}^{2}$ under the HEWMA controlling statistic.

In this case, we compute the HEWMA statistic as follows:

$$E_{t} = \lambda_{2} Y_{i} + (1 - \lambda_{2} )E_{t - 1} \quad 0 < \lambda_{2} \le 1,$$

(5)

$${\text{where}}\quad E_{0} = A + B\mu_{0}$$

$${\text{HE}}_{t} = (1 - \lambda_{1} ){\text{HE}}_{t - 1} + \lambda_{1} E_{t} \quad 0 < \lambda_{1} \le 1,$$

(6)

$${\text{where}}\quad E\left( {{\text{HE}}_{t} } \right) = {\text{HE}}_{0} = A + B\mu_{0}$$

$${\text{VAR}}({\text{HE}}_{t} ) = \frac{{\lambda_{1}^{2} \lambda_{2}^{2} }}{{(\lambda_{1} - \lambda_{2} )^{2} }}\left\{ {\begin{array}{*{20}l} {\frac{{(1 - \lambda_{1} )^{2} (1 - (1 - \lambda_{1} )^{2i} }}{{1 - (1 - \lambda_{1} )^{2} }} + \frac{{(1 - \lambda_{2} )^{2} (1 - (1 - \lambda_{2} )^{2i} )}}{{1 - (1 - \lambda_{2} )^{2} }}} \hfill \\ { - \frac{{2(1 - \lambda_{1} )(1 - \lambda_{2} )(1 - (1 - \lambda_{1} )^{i} (1 - \lambda_{2} )^{i} )}}{{1 - (1 - \lambda_{1} )(1 - \lambda_{2} )}}} \hfill \\ \end{array} } \right\}\frac{{B^{2} \sigma^{2} + \sigma_{m}^{2} }}{n}$$

(7)

The control limits of the HEWMA statistic are given by

$$\begin{aligned} & {\text{UCL}} = A + B\mu_{0} + L\sqrt {{\text{VAR}}({\text{HE}}_{t} )} \\ & {\text{CL}} = A + B\mu_{0} \\ & {\text{LCL}} = A + B\mu_{0} - L\sqrt {{\text{VAR}}({\text{HE}}_{t} )} \\ \end{aligned}$$

(8)

where λ₁ and λ₂ both are the smoothing parameters and L specifies the width of the control limits. Following Steiner (1999), Monte Carlo simulations are used for the calculation of average run lengths (ARLs) in Tables 1, 2, 3, 4, 5, 6 and 7 by fixing the in-control ARL as ARL₀ = 370. The ARL and standard deviation of run length (SDRL) values are calculated for λ₁ = 0.1, λ₂ = 0.25, fixing L = 2.768, and λ₁ = 0.5, λ₂ = 0.25, fixing L = 2.43.

Table 1 ARL and SDRL for covariate model under different values of σ²_m/σ²

Table 2 ARL and SDRL for covariate model under different values of B

Table 3 ARL and SDRL for multiple measurements k = 5, B = 1 under different values of σ²_m/σ²

Table 4 ARL and SDRL for multiple measurements k = 5, σ²_m/σ² = 1 for different values of B

Table 5 ARL and SDRL for multiple measurements under different values of k

Table 6 ARL and SDRL for linearly increasing variance for different values of D

Table 7 ARL and SDRL for linearly increasing variance for different values of C

In Table 1, the ARLs are calculated using different ratios of $\sigma_{m}^{2} /\sigma^{2}$, keeping A = 0 and B = 1. It can be observed that while we increase the ratio $\sigma_{m}^{2} /\sigma^{2}$, the amount of ARL increases. Table 2 displays the effect of measurement error on the results of the covariate model when the value of B is changing, keeping A = 0 and $\sigma_{m}^{2} /\sigma^{2} = 1$. We can see from the results that the smaller value of B has more effect on the ARL. As we increase the value of B, the effect on the ARL reduces. This shows that a strong correlation between the variables is a cause, to improve the results.

3 Multiple Measurements

Sometimes, it is more desirable to take certain measurements on a single sampling unit from a statistical point of view. Taking multiple measurements per item is a technique used by Linna and Woodall (2001), Maravelakis et al. (2004) and Abbasi (2010), evidently taking more than one measurement per item to compensate for the effect of measurement error. The average of the multiple measurements can represent more accurately to the variable of interest as compared to a single measurement, and this has been proved in previously mentioned researchers. The variance of the average of numerous measurements has a measurement error component that has a smaller variability than taking a single measurement. Measuring an item multiple times will also increase its cost and time. Moreover, it should be kept in mind that if there is no measurement error present in the process, taking several measurements will be of any use. It will only increase the time and cost of measuring the extra observation, so before taking multiple measurements, these factors should be considered very carefully. If there is no time and cost issue, it would be very ideal to take several measurements.

HEWMA statistic is calculated under the assumption that each of n observations of Y is measured k number of times, and find out the overall mean of these quantities as $\bar{\bar{Y}}_{i}$. The HEWMA statistic is given by

$${\text{QE}}_{t} = \lambda_{2} \bar{\bar{Y}}_{i} + (1 - \lambda_{2} )Q_{t - 1,} \quad 0 < \lambda_{2} \le 1$$

(9)

$${\text{where}}\quad {\text{QE}}_{0} = A + B\mu_{0}$$

$${\text{QHE}}_{t} = \lambda_{1} {\text{QE}}_{t} + (1 - \lambda_{1} ){\text{QHE}}_{t - 1,} \quad 0 < \lambda_{1} \le 1$$

(10)

$${\text{where}}\quad {\text{QHE}}_{0} = A + B\mu_{0}$$

where λ₁ and λ₂ are a smoothing parameter which takes values between 0 and 1. We encounter the same measurement case as in Sect. 3 if by any chance k = 1.

Following Linna and Woodall (2001), the variance of the overall mean in case of multiple measurements is given by

$$\frac{{B^{2} \sigma^{2} }}{n} + \frac{{\sigma_{m}^{2} }}{nk}$$

Therefore, the variance of HEWMA statistic is given as

$${\text{VAR}}({\text{QHE}}_{t} ) = \frac{{\lambda_{1}^{2} \lambda_{2}^{2} }}{{(\lambda_{1} - \lambda_{2} )^{2} }}\left\{ \begin{aligned} \frac{{(1 - \lambda_{1} )^{2} (1 - (1 - \lambda_{1} )^{2i} }}{{1 - (1 - \lambda_{1} )^{2} }} + \frac{{(1 - \lambda_{2} )^{2} (1 - (1 - \lambda_{2} )^{2i} )}}{{1 - (1 - \lambda_{2} )^{2} }} \hfill \\ - \frac{{2(1 - \lambda_{1} )(1 - \lambda_{2} )(1 - (1 - \lambda_{1} )^{i} (1 - \lambda_{2} )^{i} )}}{{1 - (1 - \lambda_{1} )(1 - \lambda_{2} )}} \hfill \\ \end{aligned} \right\}\frac{{B^{2} \sigma^{2} }}{n} + \frac{{\sigma_{m}^{2} }}{nk}$$

(11)

The control limits of the HEWMA statistic in case of multiple measurements are given by:

$$\begin{aligned} & {\text{UCL}}_{Q} = A + B\mu_{0} + L\sqrt {{\text{VAR}}({\text{QHE}}_{t} )} \\ & {\text{CL}}_{Q} = A + B\mu_{0} \\ & {\text{LCL}}_{Q} = A + B\mu_{0} + L\sqrt {{\text{VAR}}({\text{QHE}}_{t} )} \\ \end{aligned}$$

(12)

Table 3 provides the results of ARL and SDRL for the covariate model with multiple measurements for different values of $\sigma_{m}^{2} /\sigma^{2}$ keeping A = 0, B = 1 and k = 5. As we can see, due to k = 5 measurements the ARL is not affected at various values of $\sigma_{m}^{2} /\sigma^{2}$, that is, less than 0.3; even when the values are larger than 0.3, it has a small impact on the ARL values. For values larger than 0.3, the effect is greater when k = 1. Table 4 corresponds to the multiple measurements for different values of B, keeping k = 5 and $\sigma_{m}^{2} /\sigma^{2}$ = 1. From the results, it can be witnessed that the effect on the ARL reduces as the value of B becomes larger. When the value of B reaches 5, the effect on the ARL almost diminishes. Table 5 displays the values for multiple measurements for different values of k keeping A = 0, B = 1 and $\sigma_{m}^{2} /\sigma^{2}$ = 1. The ARL decreases by increasing the number of measurements per unit. This leads us to a desirable situation when time and cost per item are not a problem.

4 Linearly Increasing Variance

We considered a covariate model in Sect. 3 which assumes a constant variance. Let’s assume the same model as $Y = A + BX +\upvarepsilon$, and here, the variance changes linearly with the change in the variable Y, and $\upvarepsilon$ is distributed normally with mean 0 and variance C + Dµ. Consequently, Y is distributed normally with mean A + Bµ₀ and variance $B^{2} \sigma^{2} + C + D\mu_{0}$. All the model parameters are assumed to be known.

The HEWMA statistic is

$${\text{VE}}_{t} = \lambda_{2} \bar{Y}_{t} + (1 - \lambda_{2} ){\text{VE}}_{t - 1,} \quad 0 < \lambda_{2} \le 1$$

(13)

$${\text{where}}\quad {\text{VE}}_{0} = A + B\mu_{0}$$

$${\text{VHE}}_{t} = \lambda_{1} {\text{VE}}_{t} + (1 - \lambda_{1} ){\text{VHE}}_{t - 1} ,\quad 0 < \lambda_{1} \le 1$$

(14)

$${\text{where}}\quad {\text{VHE}}_{0} = A + B\mu_{0}$$

$$E\left( {{\text{VHE}}_{t} } \right) = A + B\mu_{0}$$

$${\text{VAR}}({\text{VHE}}_{t} ) = \frac{{\lambda_{1}^{2} \lambda_{2}^{2} }}{{(\lambda_{1} - \lambda_{2} )^{2} }}\left\{ {\begin{array}{*{20}l} {\frac{{(1 - \lambda_{1} )^{2} (1 - (1 - \lambda_{1} )^{2i} }}{{1 - (1 - \lambda_{1} )^{2} }} + \frac{{(1 - \lambda_{2} )^{2} (1 - (1 - \lambda_{2} )^{2i} )}}{{1 - (1 - \lambda_{2} )^{2} }}} \hfill \\ { - \frac{{2(1 - \lambda_{1} )(1 - \lambda_{2} )(1 - (1 - \lambda_{1} )^{i} (1 - \lambda_{2} )^{i} )}}{{1 - (1 - \lambda_{1} )(1 - \lambda_{2} )}}} \hfill \\ \end{array} } \right\}\frac{{B^{2} \sigma^{2} + C + D\mu }}{n}$$

(15)

Now, the control limits of the HEWMA statistic are given by

$$\begin{aligned} & {\text{UCL}}_{v} = A + B\mu_{0} + L\sqrt {{\text{VAR}}({\text{VHE}}_{t} )} \\ & {\text{CL}}_{v} = A + B\mu_{0} \\ & {\text{LCL}}_{v} = A + B\mu_{0} + L\sqrt {{\text{VAR}}({\text{VHE}}_{t} )} \\ \end{aligned}$$

(16)

where L is a constant used to decide the width of the control limits. The results using the linearly increasing variance are given in Tables 6 and 7.

From Table 6, it can be seen that as soon as a measurement error is introduced through D, the ARL changes with a serious effect. Moreover, the effect is more serious for the larger values of D. In simple words, we can say that as the value of D increases, the effect on the variance of error component in the model increases.

In Table 7, results with linearly increasing variance for A = 0, B = 1, D = 1, $\sigma_{m}^{2} /\sigma^{2} = 1$ and different values of C are presented. We can see from the results shown in Table 7 that the changing value of C has an effect on the ARL values. The effect increases with the increase in the value of C, but the effect is not serious as compared to D due to the position of C in the variance of the error component.

5 Application on Real-Life Data

5.1 Example 1

In this section, we present a real dataset to show the implementation of HEWMA control chart with measurement error in a real-life situation. In the semiconductor manufacturing process, development is followed through a hard bake process to increase resistance. The quality characteristic of the process to monitor is flow width of the hard bake.

A data of forty-five samples of wafers, each of size five, have been taken from this process when the process was thought to be in control. The time interval between samples or subgroups is 1 h. The complete details of the dataset are given in Montgomery (2009). The flow width measurements are taken in microns.

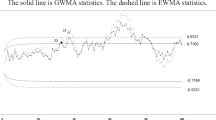
After combining all the 45 groups, each of size five, we get 225 observations. According to Haq et al. (2015), the combined dataset follows the normality assumption. The data of 225 observations were considered as the population. The parameters of the process are calculated using all the 225 observations. For our example, we selected 15 samples, each of size five, from the complete dataset. For this purpose, we again draw ten samples, each of size five, and introduce a shift of 0.5σ in the mean of these ten sample values considering something wrong in the process. Figure 1 displays the HEWMA chart under $\sigma_{m} /\sigma = 0.28$, A = 0, B = 1. The in-control ARL of the HEWMA chart is fixed at 370 with $\lambda_{1} = 0.1$, λ₂ = 0.25 and L = 2.43. It is evident from Fig. 1 that HEWMA chart generates an out-of-control signal at 17th sample. Therefore, HEWMA chart detects the fault soon after the shift in the process was introduced at 16th sample value.

Fig. 1

HEWMA control chart using covariate method

5.2 Example 2

We considered a 125 g yogurt cup filling process where the weight of each cup is taken as the quality characteristic to monitor for the out-of-control points. For details about data, Hu et al. (2015) can be consulted. The first ten subgroups are selected considering the process as in control, and when the process gets out of control, again ten subgroups are selected. The parameters of the data are found to be µ = 124.9, σ = 0.76, with n = 5 and k = 2. The data showed an estimated measurement error standard deviation as σ_m = 0.24, so that we have σ_m/σ = 0.316.

It is depicted from Fig. 2 that HEWMA chart triggered an out-of-control signal at the first sample. Therefore, the HEWMA chart can detect the fault in the process at 14^th sample.

Fig. 2

HEWMA control chart using multiple measurement method

6 Comparison in the Presence of Measurement Error

In this section, HEWMA chart is compared with EWMA chart. The comparison is made to decide the best suitable option of a control chart to use in case of measurement error problem in a practical situation. The EWMA statistic provided by Maravelakis et al. (2004) is given by

$$E_{t} = \lambda X_{t} + (1 - \lambda )E_{t - 1} \quad 0 < \lambda \le 1,$$

(17)

$${\text{where}}\quad E_{0} = A + B\mu_{0}$$

The control limits are given by

$$\begin{aligned} & {\text{UCL}} = A + B\mu_{0} + L\sqrt {\frac{\lambda }{2 - \lambda }\{ 1 - (1 - \lambda )^{2i} \} \frac{{B^{2} \sigma^{2} + \sigma_{m}^{2} }}{n}} \\ & {\text{LCL}} = A + B\mu_{0} - L\sqrt {\frac{\lambda }{2 - \lambda }\{ 1 - (1 - \lambda )^{2i} \} \frac{{B^{2} \sigma^{2} + \sigma_{m}^{2} }}{n}} \\ \end{aligned}$$

(18)

The results described in Sects. 2 to 4 go hand in hand with the results of EWMA chart. Some of the results for EWMA with comparison to HEWMA control chart are given in Tables 8, 9 and 10. In Table 8, the results are provided for changing values of σ²_m/σ², keeping A = 0, B = 1. ARL₀ is fixed at 370 for both EWMA and HEWMA control charts for the purpose of a fair comparison, when σ²_m/σ² = 0.1, 0.2, 0.3, 1 and the shift occurs in the data; the ARL values of HEWMA chart are smaller than the EWMA chart. It is observed from Table 9 when σ²_m/σ² = 0.1 and data show a shift of 0.5 magnitude, the EWMA chart produced an ARL₁ = 45.00, while for HEWMA chart, the ARL₁ = 41.92. We can witness a similar pattern for the other values of σ²_m/σ²

Table 8 Measurements and their corresponding statistics

Table 9 Comparison between EWMA and HEWMA charts using covariate model

Table 10 Comparison between EWMA and HEWMA charts using multiple measurements method

Table 10 provides the performance comparison between EWMA and HEWMA charts for the case of multiple measurements by keeping k = 5, B = 1 and varying σ²_m/σ². We can see that for taking multiple measurements, the error ratio has a minor effect on the ARL values. When the error ratio becomes large as 1, ARL₁ = 49.26 for EWMA and for HEWMA it drops to ARL₁ = 41.33 at shift 0.5. Tables 9 and 10 show that the HEWMA control chart is quick in shift detection as compared to EWMA control chart in the presence of measurement error.

7 Conclusion

In this paper, we studied the effect of measurement error on the HEWMA control chart using three methods suggested by Linna and Woodall (2001). By using the covariates, the results showed that the HEWMA chart is greatly affected by the measurement error. We also examined the situation of measurement error by taking multiple measurements. The use of multiple measurements reduces the effect of measurement error on the chart’s performance. In other words, taking multiple measurements for a particular condition provides a more accurate representation of the response as compared to one measurement. We studied the HEWMA chart for the mean with linearly increasing variance model and concluded that the performance of the chart is also affected. In the end, we compared the performance of the EWMA and HEWMA charts for the mean in conditions of the measurement error and concluded that HEWMA chart should be preferred over EWMA chart for data containing measurement error. The performance of HEWMA control chart with measurement error in case of estimated parameters under the covariate error model needs to be acknowledged.