A heuristic approach for the double row layout problem

Abstract

In the double row layout problem, we wish to position n machines on two parallel rows in order to minimize the cost of material flow among machines. The problem is NP-hard and has applications in industry. Here, an algorithm is presented, which works in two phases: (1) applying an improvement heuristic to optimize a random double row layout of a certain type and, then, (2) adjusting the absolute position of each machine in the layout via Linear Programming. Four variants of this two-phase algorithm are proposed and their efficiency is demonstrated by computational tests on several instances from the literature with sizes up to 50 machines.

1 Introduction

Facility layout problems (FLPs) are generally NP-hard and have many practical applications in industry (Drira et al. 2007). A class of FLPs called row layout problems consists of arranging facilities (machines in the present context) along rows. When machines are located on two parallel rows, we refer to this configuration as a double row layout (e.g. Zuo et al. 2014, 2016; Wang et al. 2015; Ahonen et al. 2014; Amaral 2012, 2013b). Given n machines of known lengths and the flow cost between any two machines, the double row layout problem (DRLP) is the problem of positioning machines on a double row layout so as to minimize the total cost of material flow among machines.

Many applications of the DRLP are related to the layout of machines in flexible manufacturing systems (FMS), where a material-handling device transports materials among machines (Heragu and Kusiak 1988; Tubaileh and Siam 2017). Chung and Tanchoco (2010) described an application of the DRLP within a fabrication line that produces liquid crystal display (LCD). The problem also has relevant applications in semiconductor manufacturing (Zuo et al. 2014; Wang et al. 2015).

Research on the DRLP may benefit from work done for the single row facility layout problem (SRFLP), since the DRLP and SRFLP share some structure. In the SRFLP all of the facilities have to be arranged on a single row. Some studies on the SRFLP have presented exact methods such as a branch-and-bound algorithm (Simmons 1969); dynamic programming (Picard and Queyranne 1981); mixed integer programming (MIP) (Amaral 2006, 2008b; Heragu and Kusiak 1991; Love and Wong 1976); a cutting plane algorithm (Amaral 2009); a branch-and-cut algorithm (Amaral and Letchford 2013); and semidefinite programming (SDP) (Anjos and Vannelli 2008; Anjos and Yen 2009; Anjos et al. 2005; Hungerländer and Rendl 2012).

Metaheuristics have also been utilized for the SRFLP. Heragu and Alfa (1992) developed a simulated annealing approach; de Alvarenga et al. (2000) presented simulated annealing and tabu search algorithms; Solimanpur et al. (2005) proposed an algorithm based on ant colony optimization; Amaral (2008a) used enhanced local search; Samarghandi et al. (2010) worked with particle swarm optimization; tabu search algorithms have been implemented in (Samarghandi and Eshghi 2010; Kothari and Ghosh 2013b); genetic algorithms in Ozcelik (2012); Datta et al. (2011), Kothari and Ghosh (2013a); scatter search algorithms in Kumar et al. (2008), Kothari and Ghosh (2014); Palubeckis (2015) used variable neighborhood search; Guan and Lin (2016) developed a hybrid algorithm based on variable neighborhood search and ant colony optimization; Palubeckis (2017) developed a multi-start simulated annealing algorithm; and Cravo and Amaral (2019) proposed a GRASP approach.

Problems such as the corridor allocation problem (CAP)(Amaral 2012; Ahonen et al. 2014) and the parallel row ordering problem (PROP) (Amaral 2013b; Yang et al. 2018) also arrange facilities along two rows, as it is the case for the DRLP. However, in the CAP and the PROP the left walls of the left-most facilities of each row must be aligned; and there must not be any space between two adjacent facilities. The PROP has a further restriction in that each facility is pre-assigned to a certain row. The CAP and the PROP are mostly applied to the arrangement of rooms in office-buildings, schools, hospitals, etc.

Concerning the DRLP, Chung and Tanchoco (2010) presented a MIP model (See also, Zhang and Murray 2012). Amaral (2013a, 2018) proposed more efficient models. Secchin and Amaral (2018) proposed improvements for the model in Amaral (2013a). In these studies, the largest DRLP instance that has been solved to optimality has size $n=15$. This is due to the hardness of the problem. Therefore, there is a quest for efficient heuristic methods that can handle larger DRLP instances in an acceptable amount of time.

In this context, this paper presents four variants of a two-phase algorithm for obtaining good approximate solutions for the DRLP. In a first phase, a random double row layout is optimized by an improvement heuristic. Then, in the following phase, the layout obtained in the first phase may be further improved by solving a linear program that adjusts absolute positions of machines. In the first phase, two perturbation schemes are employed for escaping local minima: one, called Shuffle, has a large perturbation strength and favors diversification of the search; the other, specialized for the DRLP, called Inversion, is less disruptive and is meant to retain previous knowledge of the search. The four variants of the two-phase algorithm were tested on DRLP instances with sizes up to $n=50\ \hbox {machines}$.

In the next section, the DRLP is presented in detail. In Sect. 3, four improvement heuristic procedures are proposed for the first phase of the solution method. In Sect. 4, the two-phase algorithms are presented. Section 5 discusses the computational experiments, followed by conclusions.

2 The double row layout problem

Let us consider the following notation: n is the given number of machines; $N=\{1,2,\ldots ,n\}$ is the set of machines; $R=\{\hbox {Row}\ 1, \hbox {Row}\ 2\}$ is the set of rows; $c_{ij}$ is the amount of flow between machines i and j; $\ell _{i}$ is the length of machine i.

Assumptions:

• The corridor is situated with its length along the x-axis on the interval $[0,\,L]$;

• The width of the corridor is negligible;

• The distance between two machines is taken as the x-distance between their centers.

Then, the Double Row Layout Problem (DRLP) is the problem of assigning the n machines to locations on either side of the corridor so that the total cost of transporting materials among machines is minimized. This is:

$$\begin{aligned} \min \limits _{\varphi \in \varPhi _{n}}\quad \sum \limits _{1\le i<j\le n} c_{ij}d_{ij}^{^{\varphi }} \end{aligned}$$

(1)

where $\varPhi _{n}$ is the set of all double row layouts on the set N; and $d_{ij}^{^{\varphi }}$ is the distance between the centers of machines i and j with reference to a layout $\varphi \in \varPhi _{n}$. Thereafter, we assume that $n\ge 4$, otherwise the problem is trivial.

3 Improvement heuristics for the DRLP

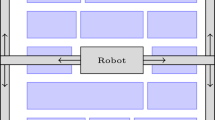
Suppose that the required clearance between any two machines is a constant, whose value is included in the lengths of the machines. On that account, the resulting problem can be treated as a problem without clearances (e.g. Amaral 2018). Then, a feasible double row layout might look like the one shown in Fig. 1. The quantity r denotes the leftmost point of the arrangement at Row 1 (similarly, for the quantity s in relation to Row 2). The layouts of the type shown in Fig. 1 can be represented by $(\pi ,\,t,\,r,\,s)$, where $\pi$ is a vector containing the machine sequence at Row 1, followed by the machine sequence at Row 2; and t is an integer, which indicates that the first t machines of $\pi$ are at Row 1 (and, consequently, the next $(n-t)$ machines are at Row 2).

Fig. 1

A feasible double row layout and its representation by means of parameters $(\pi ,\,t,\,r,\,s)$

3.1 Auxiliary routines

Let the cost of a layout $(\pi ,\,t,\,r,\,s)$ be given by $f(\pi ,\,t,\,r,\,s)$.

3.1.1 2OPT_LS

The 2-opt local search presented here, called 2OPT_LS, performs 2-opt moves in the vector $\pi$ for fixed values of $(t,\,r,\,s)$ in order to improve the cost of an initial double row layout $(\pi ,\,t,\,r,\,s)$ received as an input (See Algorithm 1). Note that a first improving 2-opt move is sought at each iteration (Lines 4–13), which might take $O(n^{2})$ in the worst case, but which in practical terms is much faster.

3.1.2 A routine that shuffles the arrangement $\pi$

A routine that shuffles the machine sequence vector $\pi$ is shown in Algorithm 2. The Shuffle routine uses the function ${ Random}(1,\,n)$, which randomly returns one value in $\{1, 2,..., n\}$. Note that by applying Shuffle, machines can change their location more than once.

3.1.3 A routine that inverts portions of $\pi$

A useful auxiliary routine called Inversion is proposed here. It randomly chooses a position i of $\pi$ and a number q of elements of $\pi$. From these choices, the inversion routine sets:

$$\begin{aligned} j={\left\{ \begin{array}{ll} i+q-1, &{} \text {if}\quad i+q-1\le n;\\ (i+q-1)-n, &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

Then, the routine executes the following sequence of statements $\lfloor \frac{q}{2}\rfloor$ times: swap the machines at positions $(i,\;j)$; increase i by one ( if i becomes greater than n, set i to 1); decrease j by one ( if j becomes less than 1, set j to n).

For problem instances with size $n\ge 20$, the routine sets q to a random number in $(1+\lfloor \frac{n}{8} \rfloor ,\lfloor \frac{n}{4}\rfloor )$. This is intended not to move more than $\lfloor \frac{n}{4}\rfloor$ elements of $\pi$, in order not to perturb too much the arrangement $\pi$. For problem instances with size $n<20$, the routine sets q to a random number in $(3,\,4)$ (this assumes $n\ge 4$ ). The Inversion routine is presented in Algorithm 3.

As an example, a vector $\pi$ given by (1, 2, 3, 4, 5, 6, 7, 8) would become (1, 2, 6, 5, 4, 3, 7, 8) if $i=3$, $q=4$, $j=6$. Another example is a vector $\pi$ given by (1, 2, 3, 4, 5, 6, 7, 8, 9, 10) and $i=9$, $q=4$. Then, $j=i+q-1=12>n=10$. Thus, the following adjustment is made: $j\leftarrow j-n =12-10=2$ and $\pi$ would become (10, 9, 3, 4, 5, 6, 7, 8, 2, 1).

3.2 Heuristic1

A heuristic called Heuristic1 is presented in Algorithm 4, which repeatedly calls 2OPT_LS with input arguments $(\pi ,\,t,\,r,\,s)$, while adjusting values of $(t,\,r,\,s)$ so as to try to find the best layout among all layouts of the type shown in Fig. 1. Heuristic1 uses the operator Shuffle, which disarranges the current machine sequence in $\pi$, thus creating a new random sequence in $\pi$; and the function Random(-1,+1), which randomly returns one value in {$-1$, 0, $+1$}.

For each value of t ($T_{1}\le t\le T_{2}$), a number ITER of iterations is carried out, each of which starts by shuffling the machine sequence in $\pi$ and setting $(r,\,s)$ to (0, 0). Next, for Max_k iterations, 2OPT_LS is called with input argument $(\pi ,\,t,\,r,\,s)$ and, then, the values $(r,\,s)$ are modified. Thus, Max_k adjustments of $(r,\,s)$ are tried for each random $\pi$.

Note that in lines 14-15 of Algorithm 4, the values of r and s could become negative. This is acceptable, because a layout having negative values for r and/or s is equivalent to a layout having nonnegative values for r and s (obtained as a result of a translation in the positive x-axis direction).

Whenever a call to 2OPT_LS produces an improved layout, the corresponding layout data is stored to be returned at the end of Heuristic1.

3.3 Heuristic2

A heuristic called Heuristic2 is presented in Algorithm 5. It differs from Heuristic1 because, within the loop 7-18 of Heuristic2, the less disruptive Inversion operator is called in place of the Shuffle operator. The Shuffle operator is now called just before loop 7-18. Thus, within loop 7-18 each new configuration $\pi$ will be obtained from a small perturbation on a previous configuration $\pi$. The idea is to preserve some past knowledge of the search.

3.4 Heuristic3

Algorithm 6 presents a heuristic called Heuristic3, which is attained by removing the outer loop of Heuristic2 and introducing some structure to adjust t after adjusting $(r,\,s)$.

3.5 Heuristic4

A heuristic called Heuristic4 is presented in Algorithm 7, which differs from Heuristic3 because Heuristic4 does not adjust the pair $(r,\,s)$. It adjusts r, always keeping s fixed at some value (here, we fixed $s=0$).

4 Two-phase algorithms

A layout such as that produced by each of the four heuristics presented in Sects. 3.2–3.5 may be further improved by using the values $(\pi ,\,t)$ to fix the integer variables of a mixed-integer programming (MIP) formulation of the DRLP and, then, solving the resulting linear program (e.g. Chung and Tanchoco 2010; Murray et al. 2013).

The MIP model given in Amaral (2018) has continuous variables $x_{i}$ (abscissa of machine i) and $d_{ij}$ (distance between machines i and j) and 0-1 integer variables ( $u_{ij}$, $t_{ij}$). Using the values $(\pi ,\,t)$, the 0-1 integer variables can be fixed in the following way. For each i, j ($1\le i<j\le n$) in the layout:

• if machines i and j are in the same row, set $u_{ij}$=1 and then set $t_{ij}$ (if i is to the left of j, set $t_{ij}=1$ ; else if i is to the right of j, set $t_{ij}=0$ );

• Otherwise, if machines i and j are not in the same row, set $u_{ij}$ to zero and, then it is indifferent to set $t_{ij}$ to either 1 or 0; we set $t_{ij}$ to zero for that matter.

For example, fixing the integer variables according to the values $(\pi ,\,t)$ corresponding to the layout in Fig. 1, we have: machines 2 and 6 are in different rows, then the integer variables $u_{26}$ and $t_{26}$ are set to zero; machines 1 and 3 are in the same row, then $u_{13}$ is set to 1 and $t_{13}$ is set to 1 because machine 1 is to the left of machine 3; etc. A linear program on the continuous variables $x_{i}$ and $d_{ij}$ is then solved, which might give us an improved layout.

The two-phase algorithm called $Heuristic1+LP$ operates by finding a layout via Heuristic1 and trying to improve it via linear programming. The two-phase algorithms $Heuristic2+LP$, $Heuristic3+LP$ and $Heuristic4+LP$ are analogously defined.

5 Computational results

The experiments with the two-phase algorithms presented in Sect. 4 were carried out on an Intel$\text{\textregistered}$ Core$^{\mathrm{TM}}$ i7-3770 CPU 3.40 GHZ with 8 GB of RAM with the Windows 8 operating system. The linear programs were solved by the CPLEX 12.7.1.0 solver.

5.1 Experiments with two-phase algorithms on instances having implicit clearances and symmetric flow matrices

In this subsection, we consider instances, which have implicit clearances (Amaral 2018) and symmetric flow matrices. The instances of sizes $n\ \in \ \{9, 10, 11\}$ are from Simmons (1969); of sizes n $\in$ {11, 12, 13} from Amaral (2018); of size $n=14$ from Secchin and Amaral (2018); of size $n=15$ from Amaral (2006); and of size $n=17$ from Amaral (2008b).

Large instances of sizes $n=30$ given in Anjos and Vannelli (2008) are also tested. Additionally, seven larger random instances with size $n=40$, introduced here, are tested. Data for all of the instances tested in this paper is available from the author.

For each problem instance, the two-phase algorithms were run ten times in order to determine the minimum, average, and standard deviation solution value among the 10 runs. The average, and standard deviation time was also calculated.

5.1.1 Parameter setting

The parameters used for the heuristics in Sects. 3.2–3.5 were set as follows. Assuming that in a good layout (of the type shown in Fig. 1) the length of the machine sequence at either row tends to be distributed around half the sum of all machine lengths, the parameter t was varied in the range $[T_{1},\,T_{2}]=[\lfloor \frac{n}{2}\rfloor ,\,\lfloor \frac{n}{2}\rfloor +4]$. This may be a plausible assumption as the instances have machine lengths uniformly distributed on a certain interval.

It was decided that the parameters ITER and $MAX\_k$ would be set to the same value. Then, preliminary tests with the largest instances $(n=40)$ were carried out in which the value of ITER was increased from 50 in steps of 25 and the times taken by $Heuristic1+LP$ were recorded. Then, ITER = $MAX\_k$ = 200 was chosen, because it was verified that with that setting, the computing time required by $Heuristic1+LP$ on the largest instances was about one hour. This value of 200 was also adopted for the other two-phase algorithms.

5.1.2 Experiments with two-phase algorithms on instances of sizes $9\le n\le 17$

First, the two-phase algorithms were tested on instances of sizes $9\le n\le 17$. In these tests, it was observed that the best solution value out of 10 runs found by each two-phase algorithm equals the known optimal value for all considered instances. The optimal value for the instance with $n=17$ is not known and for this instance the four two-phase algorithms give the same best value (4655).

Table 1 shows that for the instances with $9\le n\le 15$ each two-phase algorithm reaches the known optimal solution in all runs, with just a few exceptions. Therefore, for each two-phase algorithm the best and average solution values are equal or very close.

Table 1 Average (Avg.) and standard deviation (SD) solution value out of 10 runs obtained by each two-phase algorithm

Table 2 shows a comparison of average and standard deviation times in seconds required by each algorithm on the instances with $9\le n\le 17$. It can be seen that, for every instance, ${ Heuristic}4+LP$ was the fastest algorithm, followed by ${ Heuristic}3+LP$, ${ Heuristic}2+LP$ and ${ Heuristic}1+LP$. For the largest instance in this table ($n=17$), the fastest algorithm, ${ Heuristic}4+LP$, requires an average time of 63.15 s, while the slowest one, ${ Heuristic}1+LP$, requires 89.28 s.

Table 2 Average (Avg.) and standard deviation (SD) time out of 10 runs required by each two-phase algorithm

5.1.3 Experiments with two-phase algorithms on instances of sizes $n\in \{30,\,40\}$

Table 3 compares the best solution values out of 10 runs given by each two-phase algorithm on the instances with $n\in \{30,\,40\}$. The minimum value in each row of Table 3 is identified in boldface and will be used later on as a reference value for its corresponding instance. It is noted that ${ Heuristic}1+LP$ provides the minimum value among the algorithms for 7 instances; ${ Heuristic}2+LP$ for 8 instances; ${ Heuristic}3+LP$ for 3 instances and ${ Heuristic}4+LP$ for 4 instances. Moreover, only ${ Heuristic}3+LP$ provides the minimum value among those values shown in the row of Instance 40-6; and only ${ Heuristic}4+LP$ provides the minimum value in the row of Instance 40-3.

Table 3 Minimum solution value out of 10 runs obtained by each two-phase algorithm

Denote by $v*$ the reference value for an instance (this is taken as a value in boldface in Table 3). In order to see how consistent the convergence of an algorithm to a good solution is, the following quantities are determined. The percent deviation of the average value from the reference value:

$$\begin{aligned} Avg\,dev = 100\times \frac{Avg-v*}{v*} \end{aligned}$$

(2)

And the relative standard deviation (of ten solution values):

$$\begin{aligned} rSD = 100\times \frac{SD}{Avg} \end{aligned}$$

(3)

Table 4 presents the quantities $Avg\,dev$ and rSD. It can be seen that for each algorithm, the average values are very close to the reference values (the maximum $Avg\,dev$ observed was 0.147%). For each algorithm, the value of $Avg\,dev$ averaged over all instances are 0.038%, 0.032%, 0.033%, and 0.029%, respectively, as shown in the last row of Table 4. The relative standard deviations are also very small. These results indicate that all of the algorithms consistently converge to a high-quality solution, with a slightly advantage for ${ Heuristic}4+LP$.

Table 4 Percent deviation of the average value from the reference value (${ Avg}\,{ dev}$) and relative standard deviation (${ rSD}$) solution value for each two-phase algorithm

Table 5 shows a comparison of the times (in seconds) required by the two-phase algorithms for the instances with $n\in \{30,\,40\}$. It is seen that ${ Heuristic}4+LP$ performs faster than the other algorithms for the three first instances of the table; and ${ Heuristic}2+LP$ is the fastest for all other instances. The last row of this table (averages over all instances) indicates that for the instances with $n\in \{30,\,40\}$, ${ Heuristic}2+LP$ would be the fastest algorithm (2310.9 s), followed by ${ Heuristic}1+LP$ (2663.8 s), ${ Heuristic}4+LP$ (2,897.4 s) and ${ Heuristic}3+LP$ (2,925.5 s).

Table 5 Average (Avg.) and standard deviation (SD) time out of 10 runs required by each two-phase algorithm

5.2 Experiments with two-phase algorithms on instances having explicit clearances and asymmetric flow

In this subsection, we consider five of the largest instances presented by Murray et al. (2013), which have size $n= 50$. These instances have explicit clearances (Amaral 2018) and asymmetric flow. The use of these instances allows a comparison with the best method in Murray et al. (2013), which is called LS-minFFasym.

As in the previous section, the parameter t was allowed to vary in the range $[T_{1},\,T_{2}]=[\lfloor \frac{n}{2}\rfloor ,\,\lfloor \frac{n}{2}\rfloor +4]$ and the parameters ${ ITER}$ and $MAX\_k$ were set to the same value. However, since a comparison is intended with the LS-minFFasym method (Murray et al. 2013), which was run in a short runtime, in order to permit a fair comparison, we should allow to our algorithms a similar amount of time. Therefore, we had to recalculate the value of ${ ITER}$.

Murray et al. (2013) used a HP 8100 Elite desktop PC with a quad-core Intel i7-860 processor. For one of the instances with $n=50$ (i.e., 50-1-ID322), the LS-minFFasym method of Murray et al. (2013) runs in 356 seconds on their machine, which corresponds to 293 seconds on ours. Taking this into account, ${ Heuristic}1+LP$ was run on that instance, each time with the value of ${ ITER}$ increased in steps of 5 from 10. Then, it was observed that, for ${ ITER} = { MAX}\_k = 30$, the computing time required by ${ Heuristic}1+LP$ was about 286 seconds (which is close to 293). Thus, the setting ${ ITER} = { MAX}\_k = 30$ was chosen for ${ Heuristic}1+LP$. The setting ${ ITER} = { MAX}\_k = 30$ was also used for the other two-phase algorithms.

In Table 6, the best solution values out of 10 runs given by each two-phase algorithm on the instances with $n=50$ is compared with the solution value of the LS-minFFasym method. The minimum value in each row of Table 6 is identified in boldface. It can be seen that ${ Heuristic}3+LP$ provides the minimum value among the algorithms for all of the instances.

Table 6 Minimum solution value out of 10 runs obtained by each two-phase algorithm and solution values obtained by the LS-minFFasym method in Murray et al. (2013) on the instances with $n=50$

Table 7 Percent deviation of the average value from the reference value (${ Avg}\,{ dev}$) and relative standard deviation (${ rSD}$) solution value for each two-phase algorithm; and percent deviation of the solution value of LS-minFFasym from the reference value (${ dev}$)

Table 8 Time required by the LS-minFFasym method and the average (Avg.) and standard deviation (SD) time out of 10 runs required by each two-phase algorithm

A value in boldface in Table 6 will be now used as a reference solution value $v*$ for the corresponding instance, allowing the determination of ${ Avg}\,{ dev}$ and ${ rSD}$ for the two-phase algorithms (via Equations (2)–(3)). Also, letting v be the solution value of LS-minFFasym, we compute the percent deviation ${ dev}$ of v from $v*$ as $dev=100\times \frac{v-v*}{v*}$. These quantities are presented in Table 7, which shows that the two-phase algorithms produce significantly better solutions than the LS-minFFasym method for all of the instances. For each two-phase algorithm, the average values and the reference values are in close proximity (the maximum ${ Avg}\,{ dev}$ observed was 0.5 % for ${ Heuristic}1+LP$). The last row of Table 7 shows that the value of $r\,SD$ averaged over all instances is 0.13%, 0.10%, 0.10% and 0.07%, respectively, for each two-phase algorithm. These outcomes indicate that the two-phase algorithms reliably converge to a very good solution, with some, albeit only marginal, advantage for ${ Heuristic}4+LP$.

Table 8 presents the runtimes of the two-phase algorithms and of the LS-minFFasym method on the instances with $n=50$. It can be noted that the runtimes of ${ Heuristic}2+LP$, ${ Heuristic}3+LP$ and ${ Heuristic}4+LP$ are shorter than those of the LS-minFFasym method. The runtimes of ${ Heuristic}1+LP$ are (by construction) similar to LS-minFFasym runtimes. Among the two-phase algorithms, ${ Heuristic}3+LP$ and ${ Heuristic}4+LP$ are the fastest.

5.3 Assessing the usefulness of LP

It is interesting to assess the usefulness of LP within the two-phase algorithms. In this regard, we compare ${ Heuristic}1+LP$ with ${ Heuristic}1$, and so on, looking at their average and standard deviation times; and best, average and standard deviation solution values out of ten runs. We will refer to Tables 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, and 20 in the Appendix.

Tables 9, 10, 11 and 12 show that, for the majority of the instances with size $9\le n\le 15$, the heuristic procedures without LP reach the known optimal solutions in every run and, thus, for these instances, the heuristic procedures present an average solution value out of ten runs equal to the optimal solution value. In the few cases, when the heuristic procedures do not reach the optimal solutions, calling LP may reduce average solution values. Tables 13, 14, 15, and 16 show that, for the instances with size $n\in \{30,\,40\}$, there are more cases in which LP reduces average solution values.

From Tables 9, 10, 11, 12, 13, 14, 15 and 16, it is noted that for the instances with $n\le 40$, the improvement on average solution values was not substantial. The maximum improvement observed was 0.020% (see Row 4 of Table 15). However, using LP requires only very small extra computational time.

Finally, it is interesting to assess the usefulness of LP within the two-phase algorithms on the largest instances with size $n=50$. Tables 17, 18, 19 and 20 show that, for the the largest instances, using LP improves average solution values, while requiring only negligible extra computational time. Again, the improvement on average solution values is not substantial (the maximum improvement observed was 0.028%—see Row 3 of Table 17). This might be due to the way in which LP is used here, i.e., it is used to refine the solution of the heuristic, perhaps correcting a possibly bad decision made by the heuristic, if any. When the solution of the heuristic is already good there is not much room for LP to work. If an LP solver is available, it is recommended to use Heuristic+ LP, because the time required by LP is negligible anyway.

6 Conclusions

Four variants of a two-phase algorithm have been presented in this paper. For instances of sizes $9\le n\le 15$, each two-phase algorithm produces an average solution value (out of ten runs) that is equal in most cases to the known optimal solution value. Experiments with larger instances of sizes $n\in \{30,\,40\}$ showed that the two-phase algorithms consistently converged to high-quality solutions within reasonable time. Moreover, for even larger instances of size $n=50$, the two-phase algorithms have been able to improve on their best-known solutions.

In the literature, the largest DRLP that has been solved exactly has size $n=15$. Therefore, the two-phase algorithms presented here should be a very useful heuristic approach to deal with larger problems.

Appendix A

See Tables 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19 and 20

Table 9 Average and standard deviation times and minimum, average and standard deviation solution values out of 10 runs for ${ Heuristic}1$ and ${ Heuristic}1+LP$ on DRLP instances with sizes $9\le n\le 17$

Table 10 Average and standard deviation times and minimum, average and standard deviation solution values out of 10 runs for ${ Heuristic}2$ and ${ Heuristic}2+LP$ on DRLP instances with sizes $9\le n\le 17$

Table 11 Average and standard deviation times and minimum, average and standard deviation solution values out of 10 runs for ${ Heuristic}3$ and ${ Heuristic}3+LP$ on DRLP instances with sizes $9\le n\le 17$

Table 12 Average and standard deviation times and minimum, average and standard deviation solution values out of 10 runs for ${ Heuristic}4$ and ${ Heuristic}4+LP$ on DRLP instances with sizes $9\le n\le 17$

Table 13 Average and standard deviation times and minimum, average and standard deviation solution values out of 10 runs for ${ Heuristic}1$ and ${ Heuristic}1+LP$ on DRLP instances with sizes $n\in \{30,\,40\}$

Table 14 Average and standard deviation times and minimum, average and standard deviation solution values out of 10 runs for ${ Heuristic}2$ and ${ Heuristic}2+LP$ on DRLP instances with sizes $n\in \{30,\,40\}$

Table 15 Average and standard deviation times and minimum, average and standard deviation solution values out of 10 runs for ${ Heuristic}3$ and ${ Heuristic}3+LP$ on DRLP instances with sizes $n\in \{30,\,40\}$

Table 16 Average and standard deviation times and minimum, average and standard deviation solution values out of 10 runs for ${ Heuristic}4$ and ${ Heuristic}4+LP$ on DRLP instances with sizes $n\in \{30,\,40\}$

Table 17 Average and standard deviation times and minimum, average and standard deviation solution values out of 10 runs for ${ Heuristic}1$ and ${ Heuristic}1+LP$ on DRLP instances with sizes $n=50$

Table 18 Average and standard deviation times and minimum, average and standard deviation solution values out of 10 runs for ${ Heuristic}2$ and ${ Heuristic}2+LP$ on DRLP instances with sizes $n=50$

Table 19 Average and standard deviation times and minimum, average and standard deviation solution values out of 10 runs for ${ Heuristic}3$ and ${ Heuristic}3+LP$ on DRLP instances with sizes $n=50$

Table 20 Average and standard deviation times and minimum, average and standard deviation solution values out of 10 runs for ${ Heuristic}4$ and ${ Heuristic}4+LP$ on DRLP instances with sizes $n=50$